Journal of Quantum Information Science, 2013, 3, 107-119
http://dx.doi.org/10.4236/jqis.2013.33015 Published Online September 2013 (http://www.scirp.org/journal/jqis)
Solution of the Time Dependent Schrödinger Equation
and the Advection Equation via Quantum Walk with
Variable Parameters
Shinji Hamada, Masayuki Kawahata, Hideo Sekino
Toyohashi University of Technology, Toyohashi, Japan
Received June 10, 2013; revised July 10, 2013; accepted August 1, 2013
Copyright © 2013 Shinji Hamada et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
We propose a solution method of Time Dependent Schrödinger Equation (TDSE) and the advection equation by quan-
tum walk/quantum cellular automaton with spatially or temporally variable parameters. Using numerical method, we
establish the quantitative relation between the quantum walk with the space dependent parameters and the “Time De-
pendent Schrödinger Equation with a space dependent imaginary diffusion coefficient” or “the advection equation with
space dependent velocity fields”. Using the 4-point-averaging manipulation in the solution of advection equation by
quantum walk, we find that only one component can be extracted out of two components of left-moving and right-mov-
ing solutions. In general it is not so easy to solve an advection equation without numerical diffusion, but this method
provides perfectly diffusion free solution by virtue of its unitarity. Moreover our findings provide a clue to find more
general space dependent formalisms such as solution method of TDSE with space dependent resolution by quantum
walk.
Keywords: Quantum Walk; Quantum Cellular Automaton; Time Dependent Schrödinger Equation; Advection
Equation
1. Introduction
Quantum walk is a mechanical system evolved by a dis-
crete local unitary transformation and is regarded as a
quantum version of the classical random walk [1,2]. In
recent years, relations between the quantum walk and
continuous quantum wave equations were shown [3-9]
and more recently a certain view point was added to the
relation between the quantum walk and the Time De-
pendent Schrödinger Equation (TDSE) [10].
There are some formalisms on the broadly-defined
quantum walk. Here we use the formalism usually called
as quantum cellular automaton (QCA). Namely, we
simply consider it as a mechanical system evolved by a
unitary transformation by a banded matrix.
A quantum walk can be most easily conceived by
comparing it with classical random walk. One-dimen-
sional classical random walk is defined by a transition
probability matrix applying a probability distribu-
tion
ˆij
P
i

.
 
ˆ
iij
j
ttP t   

j
(1.1)
The conservation of probability requires
ˆ1
ij
i
P

 (1.2)
And the requirement that
between neighboring grid points means that should
be
e
l
the transition occurs only
ˆij
P
a banded matrix.
In quantum walk, where probability amplitud evolves
instead, this transition probability matrix is repaced by
the unitary banded matrix. Namely,




*
,
ˆˆ ˆ
iijjkikjij
jk
ttUt UU


 
 (1.3)
Incidentally the difference between a random
and a quantum process is that in the latter case the pro-
ba
process
bility is given by squaring the amplitude. In order to
conserve total probability, the transformation must be
unitary,
2
ˆ1
ij
U
 (1.4)
i
and therefore formally the correspondence relation
C
opyright © 2013 SciRes. JQIS

S. HAMADA ET AL. 108
2
ˆˆ
ij ij
PU holds.
While it is apparently easy to make some transition
f pro-
bability ((1.2)), it requires some devices to
con
probability matrix that satisfies the conservation o
Equation
struct a unitary banded matrix.
However we note that the unitary banded matrix re-
presented on discrete space is quite similar to the two-
scale transformation matrix in an orthogonal wavelet
with compact support [11].
One of the easiest way to construct the unitary banded
matrix is to use the product of trivial unitary banded
matrices as shown in Figure 1. Here we refer to a block
diagonal matrix whose block diagonal components are 2
× 2 unitary matrices as a trivial unitary banded matrix.
By using the product of trivial unitary matrices in the
RHS, we can construct a non-trivial unitary banded
matrix in the LHS of Figure 1. In fact, reversely it is true
that any translationally invariant unitary banded matrix
can be factorized in the form of the RHS (see Appendix
B).
In general we can introduce space dependent para-
meters  

,,
x
xbx  in the quantum walk (see
Appendix A).
  



cos sin
si cos
ix
ib x
xi xe
Ux e
ix x







(1.5)


nix e




Here we use U in place of E and F in Figure 1.
In these parameters, b(x) means potential te
TDSE (see Appendix A).
rm in


x

is a local gauge transformation pa
amely redefinition of the phase of wave functio
rameter
(nn), but
we don’t discuss space dependent


x

here while it is
an interesting subject.
2. Time Dependent Schrödinger Equation
with Space Dependent Imaginary
Diffusion Coefficient
Here we discuss space dependent parameters






,
x
bx  in the TDSE-type quantum walk.

cos xi  
  
sin cosix x 


tion


sin ib x x
Ux e



(2.1)
By the rela1tanm

 (see Appendix A),


x

can be interpreted as a parameter for the space dependent
A B
A B
A B
A
B A
B
E
E
E
EF
F
F
F
E
E
E
0
0
0
0
0
0
0
0
0
0
0
0
Figure 1. Product of trivial unitary banded matrices (E, F
are 2 × 2 unitary matrices).
imaginary diffusion coefficient 

12m.
erges in the cThe Hamiltonian that emontinuum limit
evolution equation


,, xt
iHxt
  (2.2
and/or their linear com-
rmitian an
t
may have the following form
)
binations because H must be Hed
2
1
2
H
D
m
 for constant A(x).
 
 

222(
1
2)x
  

22
2
1
2
1
x
x
AxAx x
HA xDAxDAx
A
AxAx DAxD
x






where

 
 (2.3)
 
1
A
xmx
,

,
x
xx
Ax Ax
pects to space x
are first and
second derivatives with res and .D

x


We show some examples as follows.
 
 
 
 

0
2
1,
2
1,
1
2
H DAxAxD
HAxDDAx
12
1
1
22
H
AxDAxD A
 x
AxDAx



(2.4
By making
)
1
2
H
as a basis for which theoretical solu-
tion can be obtained easily,
H

can be rewritten as
 
1
2
2
2
11 1
HH
22 2
x
xx
A
xAxAx 



 
 
 



 

(2.5)
onages We must note that additil potential term emer
when

is changed.
H

For the case of H as the linear combination of , we
have more general form
 


2
1
2
x
xx
H
HAxAxAx  

 (2.6)
Since analytical derivationof ,

 is not straight-
forwarbecause of the d broken traslational invariance,
w
n
e determine,


using a numerical method.
Namely, the solution for
 


2
x
xx
H
AxAx Ax  

 is calculated usin
type quantum walk with space dependent
g TDSE-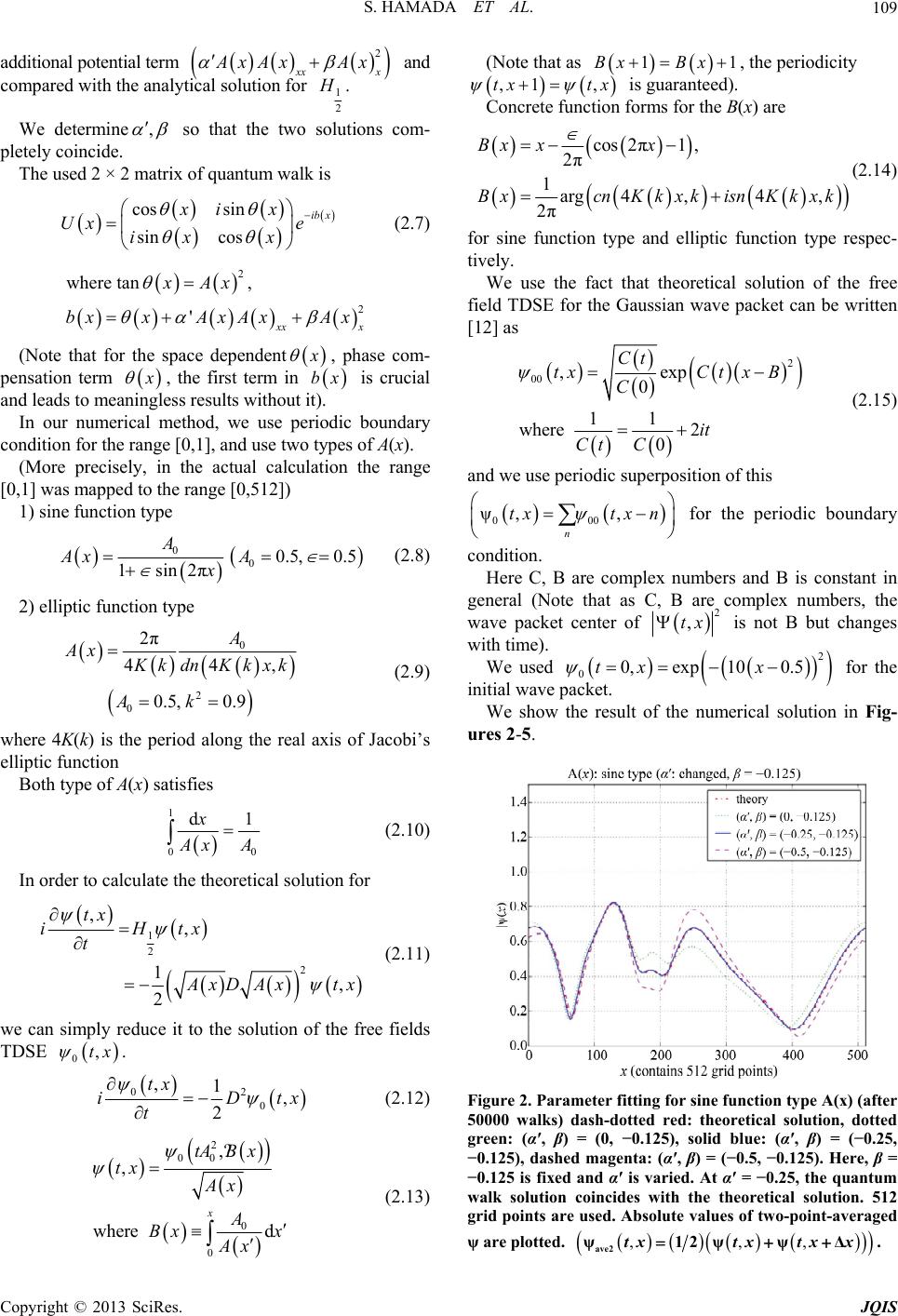


x
 with

S. HAMADA ET AL. 109
additional potential term  

2

x
xx
A
x Ax 
 and
compared with the analytical solution for
Ax
1
2
H
.
We determine,

 so that the two solutions com-
pletely coincide.
The used 2 × 2 matrix of quantum

walk is
 
 
cos s
sin cos
xi
Ux e
ix x





(2.7)


in ib x x 

 

wheretan,
  
2
'
2
x
xx
xAx
x
 
bx AxAx Ax    
(Note that for the space dependent

x

, phase com-
pensation term

x

, the first term in


bx is crucial
and leads to mss results without it).
In our numerical method, we use periodic boundary
condition for the range [0,1], and use two types of A(x).
(More precisely, in the actual calculation the range
[0,1] was mapped to the range [0,512])
1) sine function type
eaningle
  
0
0
0.5,5
1sin2π
A
Ax A
x


 (2.8)
0.  
2) elliptic function type
  


0.5,0A 

2
0.9k

(2.9)
where 4K(k) is the period along the real axis of
elliptic function
s
0
2π
44,
A
Ax Kk dnKkx k

Jacobi’s
Both type of A(x) satisfie

1
0 0
d1x
A
xA

 (2.10)
In order to calculate the theoretical solution for
 
 


1
2
,
2
2
1
, , tx
iH tx
t
A
xD Axtx  
(2.11)
we can simply reduce it to the solution of the free fields
TD
 

SE


0,tx

.
 
02
0
,1,
2
tx
iD
t
 
tx
(2.12)
 



 
2
00
0
0
wh
,?
edre
xA
(2.13)


11Bx Bx


,
tAB x
tx
Ax
Bx x
Ax






(Note that as , the periodicity




,tx is guaranteed).
nction forms for the B(
,1tx  
Concrete fux) are
  
    

cos 2π1,
2π
1arg 4,4,
2π
Bx xx
Bxcn Kkxkisn Kkxk

 

(2.14)
for sine function type and elliptic function type respec-
tiv
We use the fact olution of the free
fien be written
[12] as
ely.
that theoretical s
ld TDSE for the Gaussian wave packet ca
 
  

 
2
00 ,exp
0
11
Ct
txCt x B
C
 
(2.15)
an

condition.
Here C, B are complex numbers and B is constant in
general (Note that as C, B are complex n
wave packet center of
where 2
0it CtC

d we use periodic superposition of this
 
0
ψ,,txtx n 




 for the periodic boundary
00
n
umbers, the

2
,tx is not B but changes
with time).

for the
We show the result of th
ures 2-5.
We used
 

 00,exp 100.tx x
  
initial wave packet.


2
5
e numerical solution in Fig-
Figure 2. Parameter fitting for sine function type A(x) (after
50000 walks) dash-dotted red: theoretical solution, dotted
green: (α′, β) = (0, −0.125), solid blue: (α′, β) = (−0.25,
−0.125), dashed magenta: (α′, β) = (−0.5, −0.125). Here, β =
−0.125 is fixed and α′ is varied. At α′ = −0.25, the quantum
walk solution coincides with the theoretical solution. 512
grid points are used. Absolute values of two-point-averaged
ψ are plotted.  



,,,
ave2
ψ12 ψψΔtxtxtx x.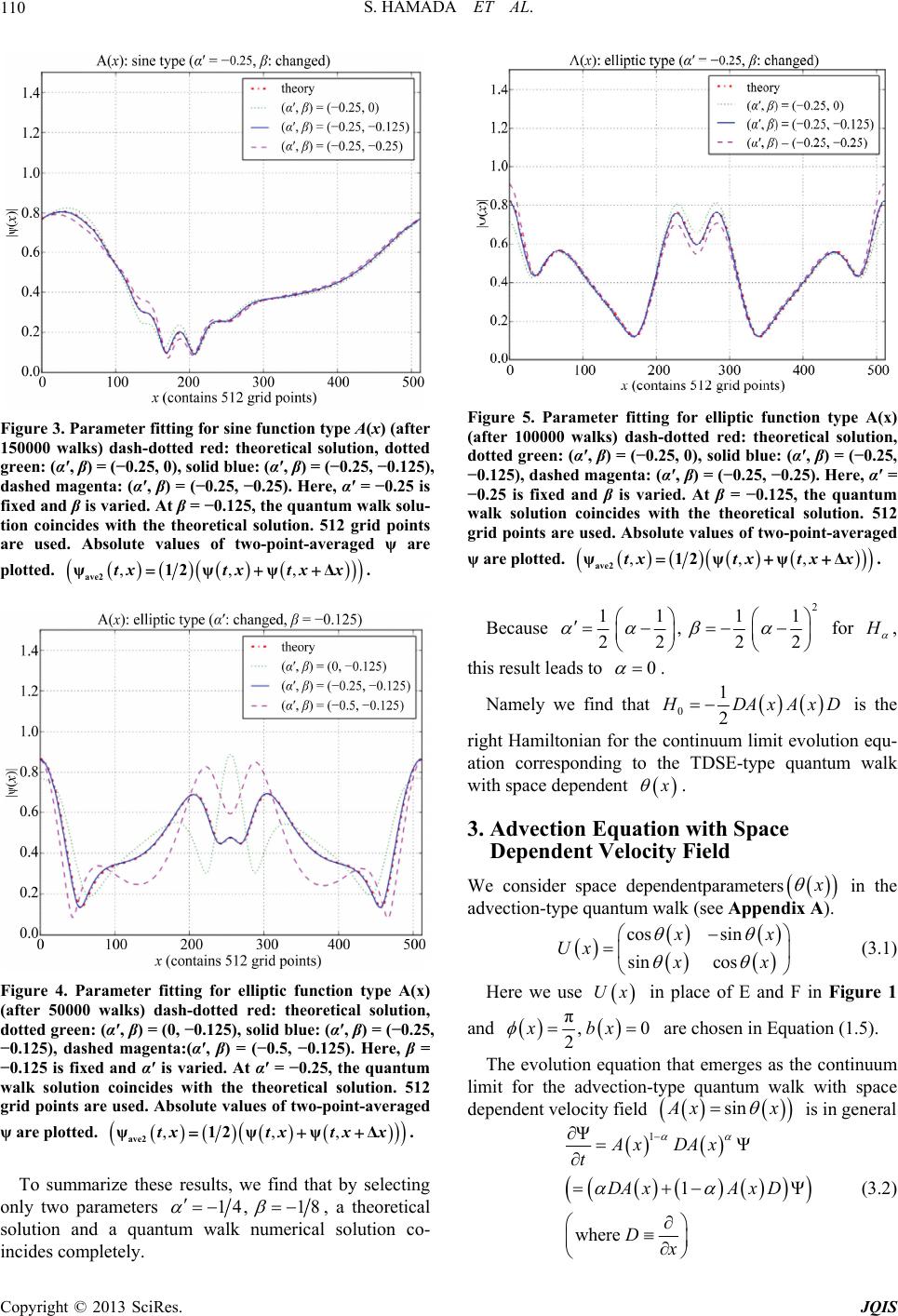

S. HAMADA ET AL. 110
Figure 3. Parameter fitting for sine function type A(x) (after
150000 walks) dash-dotted red: theoretical solution, dotted
green: (α′, β) = (−0.25, 0), solid blue: (α′, β) = (−0.25, −0.125),
dashed magenta: (α′, β) = (−0.25, −0.25). Here, α′ = −0.25 is
fixed and β is varied. At β = −0.125, the quantum walk solu-
tion coincides withints the theoretical solution. 512 grid po
are used. Absolute values of two-point-averaged ψ are
plotted.
  

,,,
ave2
ψ12 ψψΔtxtxtx x.

Figure 4. Parameter fitting for elliptic function type A(x)
(after 50000 walks) dash-dotted red: theoretical solution,
dotted green: (α′, β) = (0, −0.125), solid blue: (α′, β) = (−0.25,
−0.125), d
−0.125 is
ashed magenta:(α′, β) = (−0.5, −0.125). Here, β =
fixed and α′ is varied. At α′ = −0.25, the quantum
alk solution coincides with the theoretical solution. 512
points are used. Absolute values of two-point-averaged
ψ are plotted.
w
grid
 
 
,,,
ave2
ψ12 ψψΔtxtxtx x.
 
To summarize these results, we find that by selecting
only two parameters 14, 18


,
tum walk num
Figure 5. Parameter fitting for elliptic function type A(x
(after 100000 walks) dash-dotted red: theoretical solution,
dotted green: (α′, β) = (−0.25, 0), solid blue: (α′, β) = (−0.25,
−0.125), dashed magenta: (α′, β) = (−0.25, −0.25). Here, α′ =
−0.25 is fixed and β is varied. At β = −0.125, the quantum
walk solution coincides with the theoretical solution. 512
grid points are used. Absolute values of two-point-averaged
ψ are plotted. 
)
 



,,,
ave2
ψ12 ψψΔtxtxtx x.
Because
2
11 11
,
2 2
 
 
 



for
22

H

,
this result leads to 0


.
Namely we find that
 
0
1
2
H
DA xA xD is the
right Hamiltonian for the continuum limit evolution equ-
ation corresponding to the TDSE-type quantum walk
with space dependent


x

.
3. Advection Equation with Space
Dependent Velocity Field
We consider space dependentparameters 



x

x A).
in the
advection-type quantum walk (see Appendi



 
cossin
sin cos

x
x
Ux
x
x






(3.1)
Here we use


Ux in place of E and F in Figure 1
and
 
π,0
2
xbx


 are chosen in Equation (1.5).
The evolution equation that emerges as the continuum
limit for the advection-type quantum walk with space
dependent velocity field  


sin
A
xx   is in general
 
   

1
ΨΨ
1Ψ
Ax DAx
t
DA xA x D







(3.2)
a theoretical
solution and a quanerical solution co-
incides completely. where Dx






S. HAMADA ET AL. 111
Especiall 1
0, 1
2and
 y correspond to
y-type and conserving-type advection
ely (Note that there is a relation
non-con-
serving-type, unitar
equations respectiv

  between unitard con- y-type solution an

serving-type solution

).
However since quantum walk is a unitary transforma-
tion, only the unitary-type advection equation is allowed.
In the following, wvee instigate using a numerical
ion indeed
e periodic boundary
follow
(More precisely, in the actual calculation the range
[0,1] was mapped to the range [0,512])
method if the unitary-type advection equat
emerges as a solution for continuum limit.
In our numerical method, we us
condition for the range [0,1], and use the ing type
of A(x).
  
0
0.50.5Ax A  ， (3.3)
0
1s in2π
A
 
an
x
d this satisfies

1
0
d1x
Ax
 (3.4)
0
A

In order to calculate the theoretical solution for


 
1
,, tx
A
xDAx tx
t




 (3.5)
we can simply reduce it to the solution of the constant
velocity field (


1Ax

x
(w
) adve
here F
ction equation
 
,txFt(x) is an arbitrary periodic
0

function of which period = 1).
 
0
0
,, tx
D
tx
t
 
 (3.6)
 


 
00
,?
,tAB x tx

 
0
where d
x
Ax
A
Bx x



(3.7)
0Ax

(Note that as



11Bx Bx 
, the periodicity

tx  

,1 ,tx   is guaranteed).
We used
  


2
00,exp 10tx x
  0.5 for the
initial wave packet.
In fact, in the case of advection type quantu
both left moving and right moving components emerge.
that using the 4-point-averaging mani-
ract only the one component (see
Appendix C).
4-point-averaging is an aver
four neighboring grid points in space-time.
m walk,
However we find
pulation, we can ext
aging manipulation over


  
 

Δ ,Δ,Δtt x ttxx 
  
Now, if we a
4, ave tx

1,,Δ
4tx txx
 
ssume
(3.8)




,,Δtxtx x   then 1



Δ,Δcossin 1 ttxx   




Δ ,sin cos1
cos
cos sin
ttx










sin


(3.9)


and therefore

2
4
1cos
,c
2
os
ave tx

2



 . It means
that by 4-point-averaging the wave function
factor of
scales with a
2
cos 2

.
In order to sotions by using quan
int-averaging, we
lve advection equa-
tum walk with 4-po must consider this
faot straightforward to deduce the ri
scripto account the factor in a purely th
e examined three different prescrip-
tio
ctor. It is nght pre-
tion to take ineo-
retical way. We her
ns to account the factor using numerical method.
Here we refer to the wave function of quantum walk as


,tx 
, and refer to the solution of the advection
equation to be solved as


,tx 
.
Three methods we use follows (At initial time are as


0t

,


0,tx  
 is loaded to


0,tx   with/
without scaling factor, and at any time
(0)t


4, ave tx is

copied to


,tx with/w 
ithout
ng). scaling factor for plotti



,:tx  


2
ave4
0,
0, :,
cos 2
ψ,
tx
tx
tx





(Method 1)


 
ave4
0,
0, :,
cos 2
ψ,
,:
cos 2
tx
tx
tx
tx








(Method 2)




 
ave4
2
cos2

We show the numerical solutions in Figures 6-8 using
the above prescriptions.
To summarize, from the numerical examination we
find that method 2 is the right prescription.
0,:0,,tx tx  

ψ,
,: tx tx  
 (Method 3)

S. HAMADA ET AL. 112
Figure 6. Comparison of three methods for different scal-
ings (after 100 walks) dash-dotted red: theoretical solution,
dotted green: method1 solid blue: met
genta: method 3, solid cyan: velocity A(x). When the wave
packet locates the region where A(x) is small, the solution of
all methods coincide with the theoretical solution with good
accuracy.
hod 2, dashed ma-
Figure 7. Comparison of three methods for different scal-
ings (after 200 walks) dash-dotted red: theoretical solution,
dotted green: method 1 solid blue: method 2, dashed ma-
genta: method 3, solid cyan: velocity A(x). As the wave
packet comes close to the region where A(x) ≈ 1, the differ-
ences among these methods become non-negligible and only
the solution of method 2 coincides with the theoretical solu-
tion.
he mathematics of quantum walk with variable para-
meters is not well established and difficult to derive
space-time equation for its continuum limit by purely
In general it is not so easy to solve an advection equ-
ation without numerical diffusion, but this method pro-
vides perfectly diffusion free solution by virtue of its uni-
tarity.
4. Conclusion
T
Figure 8. Comparison of three methods for different scal-
ings (after 350 walks) dash-dotted red: theoretical solution,
dotted green: method 1 solid blue: method 2, dashed ma-
genta: method 3, solid cyan: velocity A(x). When the wave
packet locates around the region where A(x) ≈ 1, the dif-
ferences among these methods become large and only the
solution of method 2 coincides with the theoretical solution.
mathematical method. And it is indispensable to compare
th
is work, we propose clear-cut numerical methods
to identify the right relation between the quantum walk
ndent parameters and the continuous
velocity fields”.
Using the 4-point-averaging manipulation in the solu-
tion of advection equation by quantum walk, we find that
only one component can be extracted out of two compo-
nents of left-moving and right-moving solutions.
In the present work, we employ QCA formalism where
extended space generated by combining original physical
space and coin space (internal degree of freedom) is
used.
On the extended discrete space, mathematics of quan-
tum walks becomes more clear.
The extension to the multidimensional space is straight-
forward and currently we are applying the methodology
to more realistic inhomogeneous quantum system in or-
his research was supported in part by TUT Programs on
eories with numerical methods especially in the case of
space dependent parameters or broken translational in-
variance.
In th
with the space depe
space-time evolution equations. Using the method we
establish the right relation between quantum walk and
“TDSE with a space dependent imaginary diffusion coef-
ficient” or “the advection equation with space dependent
der to examine its practicality. Moreover our findings
provide a clue to find more general space dependent
formalisms such as solution method of TDSE with space
dependent resolution by quantum walk/QCA.
5. Acknowledgements
T

S. HAMADA ET AL. 113
Advanced Simulation Engineering, Toyohashi University
of Technology.
REFERENCES
[1] Y. Aharonov, L. Davidovich and N. Zagury, “Quantum
Random Walks,” Physical Review A, Vol. 48, No. 2, 1993,
pp. 1687-1690. doi:10.1103/PhysRevA.48.1687
[2] N. Konno, “Mathematics of Quantum Walk,” Sangyo-
Tosho, 2008.
[3] P. L. Knight, E. Roldán and J. E. Sipe, “Quantum Walk
on the Line as Interference Phenomenon,” Physical Re-
view A, Vol. 68, No. 2, 2003, Article ID: 020301(R).
doi:10.1103/PhysRevA.68.020301
[4] David A. Meyer, “Quantum Mechanics of Lattice gas
Automation: One Particle Plane Waves and Potential,”
Physical Review E, Vol. 55, No. 5, 1997, pp. 5261-5269.
doi:10.1103/PhysRevE.55.5261
[5] B. M. Boghosian and W. Taylor, “Quantum Lattice-Gas
Model for the Many-Particle Schrödinger Equation in d
Dimensions,” Physical Review E, Vol. 57, No. 1, 1998,
pp. 54-66. doi:10.1103/PhysRevE.57.54
[6] F. W. Strauch, “Relativistic Quantum Walks,” Physical
Review A, Vol. 73, No. 6, 2006, Article ID: 069908.
doi:10.1103/PhysRevA.73.069908
[7] A. J. Bracken, D. Ellinas and I. Smyrnakis, “Free-Dirac-
particle Evolution as a Quantum Random Walk,” Physi-
cal Review A, Vol. 75, No. 2, 2007, Article ID: 022322.
doi:10.1103/PhysRevA.75.022322
[8] C. M. Chandrashekar, S. Banerjee andR. Srikanth, “Rela-
tionship between Quantum Walks and Relativistic Qu
tum Mechanics,” Physical Review A
an-
, Vol. 81, No. 6, 2010,
Article ID: 062340.
doi:10.1103/PhysRevA.81.062340
[9] A. Ahibrecht, H. Vogts, A. H. Werner, and R. F. Werner,
“Asymptotic Evolution of Quantum Walks with Random
Coin,” Journal of Mathematical Physics, Vol. 52, No. 4,
2011, Article ID: 042201. doi:10.1063/1.3575568
[10] H. Sekino, M. Kawahata and S. Hamada, “A Solution of
Time Dependent Schrödinger Equation by Quantum
3
Walk,” Journal of Physics Conference Series (JPCS), Vol.
352, No. , 2012, Article ID: 012013.
doi:10.1088/1742-6596/352/1/01201
[11] I. Daubechies, “Ten Lectures on Wavelets,” SIAM, Phil-
adelphia, 1992. doi:10.1137/1.9781611970104
[12] R. P. Feynman and A. R. Hibbs, “Quantum Mechanics
and Path Integrals,” McGraw Hill, 1 965.
[13] R. Courant, K. Friedrichs and H. Lewy, “On the Partial
Difference Equations of Mathematical Physics,” IBM
Journal of Research and Development, Vol. 11, No. 2,
1967, pp. 215-234.
[14] P. Høyer, “Efficient Quantum Transforms,” Unpublished,
1997.
http://arxiv.org/abs/quant-ph/9702028v1

S. HAMADA ET AL. 114
Appendix
Appendix A (Continuum Limit of Quantum
Walk with Constant Parameters)
Here we briefly review the way how an evolution equa-
tion can be derived as a continuum (zero wave number)
limit of a quantum walk with constant parameters. This
derivation technique is also used when 4-point-averaging
is introduced (Appendix C).
In the method described here, the time evolution gen-
erator is expanded with respect to wavenumber k around
k = 0. This treatment is essentially the same described in
other literatures [4,6].
In the latter, the effective mass

1
2
2
0
dtan
dk
k
mk









 was given from the dispersion
relation cosω(k) = cosθcosk (though their model is diffe-
rent from ours and their θ corresponds to our π
2


).
Note that the derivation in this appendix is athnot me-
m
uous function
atically rigorous, we rather provide an outline of the
derivation needed to explain or interpret the background
and results of our numerical experiments.
We regard the wavefunction as a contin


x

in spa
, when the shape of the wavefunction varies slowly
ce as compared with the grid spacing of the quan-
tum walk. We show the continuous space-time evolution
equation thus introduced.
First we consider the continuum limit of the classical
ra
tin
ndom walk, classical counterpart of the quantum walk.
It is well known that by central limit theorem, the con-
uum limit of the classical random walk is a diffusion
equation (If the left-right balance of the walk is broken, it
leads to an advection-diffusion equation with an advec-
tive term)
2
2
AB
tx
x
 


 (A.1)
First, we review how this equation can be derived.
We assume that the transition probability matrix ˆ
P
is
translationally invariant. Namely ˆ
P
commutes withne-
grid shift (to the negative directiooperation matrix ˆ S.
Below is a simplest example of classical random wlk
o
a
n)
w
yclic lattice of size N or periodic
bo
ith probabilities of both left and right walks being the
equivalent value 1/2.
Here we assume c
undary condition.
012

0 012
120 1200
012012 0
ˆ
00120 0
12
12 00012 0
P














(A.2)


0100 0
0010 0
0001 0
0000 0
1
1000 0 0
ˆ
S















(A.3)
0
ˆ
,
ˆ PS


 (A.4)
In treating translationally invariant
is usual technique to diagonalize
discrete system, it
both ˆ S and ˆ
P
si-
multaneously using Z-transformation.


1
0
ˆ1
2
i
i
i
PsPss s



w


Ps is the diagonal element of the diagonalized here
ˆ
P
corresponding to the eigenvalue s of ˆ S.
Next we extend the problem from discrete time to con-
tinuous time and assume this leads to the fllowing con-
tinuous time evolution equation
o


s
H
ss
t
 
 (A.5)
(In this appendix we use ,
H
H for genrators e
,i
tt



 respectively).
As transition probability matrix for a unit time is


Hs
P
se,


Hs can be calculated by




logHsPs
e colong
range limuse the relation bet
shift ope differential operator
(A.6)
In order to investigate thntinuum limit (or
it) behavior, we ween the
erator (ˆ S) and th
(D
x



)ˆ
D
Se

 and we have only to expand H(s) in a
ik
s
e around k = 0. Taylor series with respect to k of
In this example,






 
22
44
loglog cos
log
Hs Psk
kk
ok ok


 
 (A.7)
1

Therefore in the real space representation by replacing
22

ik
x



we obtain a diffusion en quatio
2
2
1
2t
x





In the case of quantum walk, we can use basically the
sa
has
translational invariance.
(A.8)
me technique. the difference is that the quantum walk
not an 1-grid translational invariance but a 2-grid

S. HAMADA ET AL. 115
2
,0,
ˆˆ
ˆˆ
,0US US



(A.9)
We 2 × 2-block-diagonalize both and simul-
taneously by Z-transformation.
This time, unlike the case of classical random walk,
w
(A.10)
a t
ndices) of
Z-transformation of U is obtained by the matrix
multiplication of Z-transformation of each factor.
ˆ
Uˆ S
e use Z-transformation of 2 × 2 matrix unit.

22
0:1,2 :21
22
ˆ
ˆ
i
ii
i
Us U s



0:1,2 :212
01
0
i
ii
i
Ss Ss s







Here 0:1,2 :21
ˆii
U denotes 2 × 2 subm trix (0 o 1 row
indices and 2i to 2i + 1 column iˆ
U.
If we use the factorization form 1
ˆˆ ˆˆˆ
USESF

 of
Figure 1.
 
1
2222
201
0
UsSsEsSs Fs
sEF







2
20
10 s




(A.11)
E, F beingNow we assume the 2 × 2 matrix form of
A
B

EF CD 


(A.12)

2
1
2
2
11
0
0
AB
s
Us CD
s
Cs Ds
As Bs








 





Then we regard the square root ofas 1-walk
evolution matrix.

(A.13)

2
Us


11
2 CsDs
Us Us
A
sBs





(A.14)
The logarithm of U(s) is obtained by dec
into the scalar part and the traceless part as follows.
omposing U(s)
 
22
22
exp
arctan








(A.15)
arccos
UsI ii  

 


 

 


(,, C

 ,:22 matrix with trace


0 and
2I )
 
22
logi
log logHsUsI i

 
 .16)
As has eigenvalues +1 and −1, we can obtain

(A
Δ
,


fro




1
trace 2UsCs Bs



(A.17)







22
det UsAD BC
ii








(A.18)
Now we cder mA, B, C
b 
H


are Pauli’s matri-
ces.
Then using
onsiore concrete form for (, D).


expcos sin
cos sin
sin cos
xy
i
ib
i
AB ii
CD
ie
e
ie













ere, 
(A.19)
01 0
,
10 0
xy
i
i


 

 
 
ik
s
e

we have



1tracesin cos
2
ib
Us ike 

 (A.20)


22 detiib
Us e 

 (A.21)
and therefore






22
222
π,
2
arccos sincos0π
sin1sincos
cos
m
sin sin
Hsbi i
k
k
k










 

(A.22)


sin sincos
1
sincossin sin
ik
ik
ke
ek
 
 



 



(A.23)
In order to investigate the continuum
ehavior, we expand
limit (or long
range limit) b


s
 in a Taylor
series with respect to k of ik
s
e around k = 0 and we
have


 



22
2
23
3
22
2
arccos sincos
sin sin
arccos sincos
1s
1sin coscos
21sin co
in cos
s
ik
kok
e
k
k







 







(A.24)
Here we use the Taylor expansion of arccos,






2
3
3
222
arccos ax
1
arccos 2
11
0 arccosπ.
xax
aox
aa
 



S. HAMADA ET AL. 116
Two cases (0

 or π
2
 ) are particularly impor-
tant, and from now on we restrict our arguments to these
cases.




24
arccos sincos
π1tan
22
for 0
ik
ek
ko






k
(A.25)



3
arccos sinsin
πsin
2
π
for 2
ik
ek  
kok


 




(A.26)

01sincos
0,
1cossin
k0
2
π
for0, respectively




 

(A.27)





  


Now we consider eigenfunctions of


k or (which
is the same)


ik
H
e



 ik
ek 

 


k
The equation of motion for wavenumber represen-
tation is
(A.28)


,tk 

 


2
ππ 1tan
22
for
2
0
H
t
ib k








 
 
  



 (A.29)
  
ππ sin
22
πand 0
2

So the equf m

for
Hi
tx
b



 

 
 







(A.30)
ation ootion for real space representation
is

,tx 

 


2
2
ππ 1tan
22
r
2
o0
t
bx 









 









(A.31)
iH



  
ππ sin
22
πand 0
2
for
Hi
t
b



 

 
 







 x



(A.32)
Thus we obtain the TDSE with potential term


for 0 

and advection equation.
πandf0
2
or b






.
Here we drop higher-order terms.
cribe the physical meaning of

Now we des


briefly.
For TDSE-type (0


),

01
010 k  

and its
eigenvector are 1
1




.
It is plausible that the eigenvector corresponds to
the wave function slowly varying in space,
1
1



namely




,,Δtxtx x   .
On the contrary, for advection-type
(π
2


),

0cos sin ksincos




  

and 1


is not
r, so the wave functio


1

the eigenvecton slowly varying in
space must have both

Ψ

and components corre-
sponding to left-md rig wave packets.
on relation for the
TD
that if we shift the horizontal axis by

Ψ
ght-movinoving an
In Figure A1 we plot the dispersi
SE type quantum walk (Equation (A.25)).
Note π
2

, we
caph as the dispersion rela
advection type quantum walk (Equation (A. 26)).
se,
n regard this gration for
In the TDSE caascomes close to π
2

, the dis-
persion relation around 0k

changesfrom quadratic to
linear and this corresponds to the one-dimensional Dirac
equation with a small mass 1π
tan 2
m


 .
This can be seen as follows (shown by the article [6]).

 

1
0
log exp
0
ππ
x
z
s
Hi
s
i

 









factor
log expexp
π
xx
ik  



log exp?
2
zx
ii ki    

 




(A.33)
22
zx
ik 
   




π
ifbothandare small
2k




 



Therefore in a real space representation without the
constant phase rotation π  in Equation (A.33),
2

S. HAMADA ET AL. 117
Figure A1. dispersion relation for TDSE (or advection) type
quantum walk.
we have
2
zx
ii
tx


 
 

 
 



(A.34)
Finally we comment about unit system. By comparing
the continuum limit evolution equation for the TDSE-
type quantum walk with

and b



2
2
1tan
2
it
H
b
x

















(A.35)
and the usual TDSE
2
2
ψ1
HψiV
2tmx



 

 (A.36) 

y that the correspondence relation we can sa
1tanand Vb
m

   hold. It is true if we u
units system of where means the time
in
se the
1txt
terval of each step and Δ
x
means the grid interval. If
we use more general units system, we must say that

2
1tanand tVt b
mx



using dimensionless
quantities.
Throughout this article we call 1
2m as imaginary





diffusion coefficient.
One more important comment to say is that in a finite
difference (leap-frog) method

2
Δ,
2Δ
,Δ,Δ2
1
2Δ
ttx
it
tx xtx x
mx
 

 

there is a sharp stability
nondimensionalized imag
Δ,ttx  
,tx (A.37)
condition (CFL condition) for
inary diffusion coefficient

2
11
2
t
mx


 [1uantum walk there is no such
limitation.
3], but in q
Appendix B (Factorization of Unitary
Hon
la.
trix can be found in articles such as
Banded
Matrix)
ere we briefly review the factorizatiof 2-grid trans-
tionally invariant unitary banded matrix
Factorization of ma
[14].
We will show

 
224221
ˆˆˆˆˆˆˆˆˆ ˆˆ ˆˆ
SABSCSSDSSES F

  (B.1)
that corresponds to Figure A2, or equivalently.
24
ˆˆ ˆˆˆˆ ˆˆˆˆ
A
BS CSDSESF (B.2)
(Note that 2
ˆ
S commutes with any matrix dealt here).
By the unitarity




24 24
ˆˆ ˆˆ ˆˆˆ
ˆˆˆ
ˆ
A
BSCSABSCSI



(B.3)
or equivalently (after Z-transformation)



24 24
ABs ABsCs Cs

 

2
I
  

24 4
AA BB CCAB BC
BA CBACCAs
s
ss


 


(B.4)

get we can
C
BC
AB C
AB C
AB
B
A
A
C
D
D
D
D
D
=x
E
E
E
E
x
F
F
F
F
F
EE
EE
Figure A2. Factorization of unitary banded matrix.

S. HAMADA ET AL. 118
0
0
AA BB CCI
ABBCBA CB
CA AC

 




erscript (+) denotes Hermitian conjugate).
efine Hermitian matrices
and P, Q can be diagonalized simul-
taneously unitary matrix diagonalized P,
Q have the forms of
(B.5)
(Here sup
Now we d
,AQCC

 .
As 0PQ QP
PA
by someD,
1
2
00 0,0
00
DPDDQD






 
 
(B.6)
Namely


1
2
0
00
00
0
DADA
DC DC












(B.7)
Therefore,
D
A
 and should have the form of DC 

222 2
12
, ab cd
00
,
00
ab
DADC cd

  

 

 
 (B.8)
the above equations can Figure A3.
(bwer half of
k-w
This can be expressed by


be illustrated as
A oth lo and upper half of C are zero).
Namely by applying from the left D to U, the band
width can be reduced from 3-blocidth to 2-block-
width.




24
ˆˆˆˆˆˆ ˆˆ ˆ
DABS CSSXYS
 2
(B.9)
or


24
ˆˆˆˆ ˆˆ
ˆˆ
ˆˆ2
A
BSCSDS XYS (B.10)
Next similar procedure can be applied to


2
ˆ ˆˆ
X
YS
and we can say that
2
ˆˆ ˆˆˆˆ
X
YS (B.11) ESF
so finally Equation (B.2)
24
ˆˆˆˆ ˆˆ ˆˆˆˆ
A
BS CSDSESF
is obtained.
r four
ne
Appendix C (4-Point-Averaging)
4-point-averaging is an averaging manipulation ove
ighboring grid points in space-time.




1,,
4tx t
 
ave4
ψ,tx

 

Δ
Δ ,Δ,Δ
x x
ttx ttxx 

 
(C.1)
we let the 2 × 2 unitary matrix of a constant para-
meter quantum walk
Now
A
B
UCD




and
t, es at grid
let o, p, q, r, s,
u, v, w, x, y, z be the wave function valu
points as shown in Figure A4.
Namely
,,
,
rABouABq
s
CDpvCD r
wABsyABv
x
CD tzCDw











  



(C.2)
ed values.

 

and let a, c, d, e be their 4-point-averag





4arvuq 
4
4
4
cstwx
doprs
evw zy



(C.3)
a, c, d, e, can be represented by q, r, s, t as follows.
A
A
B
B
C
C
A
A
B
B
C
C
Figure A3. Band-width reduction of unitary banded matrix.
abc
d
yz
e
op
qr s
t
uv wx
x
t
Figure A4. Illustration of 4-point averaging.

S. HAMADA ET AL. 119

 
11 00
0011
1111
01 1A0
where
AC BD aq
AC BD cr
CACDACABDBBD
es
DC B
dt
AD BC


 

 

 
 

 

 
 

 

 
 


(C.4)
By a simple calculation , we can find that this matrix is
singular and can have a relation

11
Cs Ds
Us
A
sBs




(C.10)
we can find that
eCaBcd

 (C.5)
If we regard the change




,, ,,adcaec
rall one-step evolution e
(We refer to this ma
as a one-
step time evolution, ovequation
can be written as follows trix as ˆ
F








).
*
(C.6)
ep evolution matrix can
be written as
s
1
1
**
*1
aa
eC Bd
cc
CB


 
 
 
 

 
 
 
 
   
1
det det,
tracetrace
TsUs
TsUsCs Bs





(C.11)
and therefore both


Ts and


Us have the same
**C 
  
Using shift matrix ˆ
S, two-st
eigenvalues.
Therefore if we use
b 
(C.12)
w
 
expcossin
cos sin
sin cos
xy
i
ib
i
AB ii
CD
ie
e
ie













e can derive TDSE or advection equation for 0


1
ˆ ˆ
TSFSF

 (C.7)
And Z-transformation (by 2 × 2 matrix unit) of thi is
obtained as
ˆ ˆˆ
 
1
22222
2
22
2
11
100110
0
0
10
0
TsSsFs Ss Fs
s
CBss CBs
CsDs s
s
2


(C.8)
















Now we consider its square root as 1-step evolution
matrix.


11
Bs s



2
0
Ts Tss 


(C.9)
Cs

Comparing with the Z-transformation of the original
quantum walk
and π
2


respectively in the same way shown in
Appendix A.
The only difference between T(s) and U(s) is the
eigenfunctions of


Δik e.
s)) In this case (T(

sin101
1
0,
1sin10
cos
0, respectively
i
ki




 




Therefore this time, the advection-type quantum walk
has an eigenvector and we can assume that the
wave function spatially-varying slowly must have only
one component out of two

forπ 



(C.13)
2

1
1






Ψ components.