Intelligent Information Management, 2013, 5, 162-170
http://dx.doi.org/10.4236/iim.2013.55017 Published Online September 2013 (http://www.scirp.org/journal/iim)
Bayesian and Frequentist Prediction Using Progressive
Type-II Censored with Binomial Removals
Ahmed A. Soliman1, Ahmed H. Abd Ellah2, Nasser A. Abou-Elheggag2,
Rashad M. El-Sagheer3*
1Faculty of Science, Islamic University, Madinah, Saudi Arabia
2Mathematics Department, Faculty of Science, Sohag University, Sohag, Egypt
3Mathematics Department, Faculty of Science, Al-Azhar University, Cairo, Egypt
Received June 30, 2013; revised July 27, 2013; accepted August 9, 2013
Copyright © 2013 Ahmed A. Soliman et al. This is an open access article distributed under the Creative Commons Attribution Li-
cense, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
In this article, we study the problem of predicting future records and order statistics (two-sample prediction) based on
progressive type-II censored with random removals, where the number of units removed at each failure time has a dis-
crete binomial distribution. We use the Bayes procedure to derive both point and interval bounds prediction. Bayesian
point prediction under symmetric and symmetric loss functions is discussed. The maximum likelihood (ML) prediction
intervals using “plug-in” procedure for future records and order statistics are derived. An example is discussed to illus-
trate the application of the results under this censoring scheme.
Keywords: Bayesian Prediction; Burr-X Model; Progressive Censoring; Random Removals
1. Introduction
In many practical problems of statistics, one wishes to
use the results of previous data (past samples) to predict
a future observation (a future sample) from the same
population. One way to do this is to construct an interval
which will contain the future observation with a specified
probability. This interval is called a prediction interval.
Prediction has been applied in medicine, engineering,
business, and other areas as well. Hahn and Meeker [1]
have recently discussed the usefulness of constructing
prediction intervals. Bayesian prediction bounds for a
future observation based on certain distributions have
been discussed by several authors. Bayesian prediction
bounds for future observations from the exponential dis-
tribution are considered by Dunsmore [2], Lingappaiah
[3], Evans and Nigm [4], and Al-Hussaini and Jaheen [5].
Bayesian prediction bounds for future lifetime under the
Weibull model have been derived by Evans and Nigm
[6,7], and Bayesian prediction bounds for observable
having the Burr type-XII distribution were obtained by
Nigm [8], Al-Hussaini and Jaheen [9,10], and Ali Mousa
and Jaheen [11,12]. Prediction was reviewed by Patel
[13], Nagraja [14], Kaminsky and Nelson [15], and Al-
Hussaini [16], and for details on the history of statistical
prediction, analysis, and applications, see, for example,
Aitchison and Dunsmore [17], Geisser [18]. Bayesian
prediction bounds for the Burr type-X model based on
records have been derived from Ali Mousa [19], and
Bayesian prediction bounds from the scaled Burr type X
model were obtained by Jaheen and AL-Matrafi [20].
Bayesian prediction with Outliers and random sample
size for the Burr-X model was obtained by Soliman [21],
Bayesian prediction bounds for order statistics in the one
and two-sample cases from the Burr type X model were
obtained by Sartawi and Abu-Salih [22]. Recently, Ah-
madi and Balakrishnan [23] discussed how one can pre-
dict future usual records (order statistics) from an inde-
pendent Y-sequence based on order statistics (usual re-
cords) from an independent X-sequence and developed
nonparametric prediction intervals. Ahmadi and Mir Mo-
stafaee [24], Ahmadi et al. [25] obtained prediction in-
tervals for order statistics as well as for the mean lifetime
from a future sample based on observed usual records
from an exponential distribution using the classical and
Bayesian approaches, respectively.
The rest of the paper is as follows. In Section 2, we
present some preliminaries as the model, priors and the
posterior distribution. In Section 3, Bayesian predictive
distribution for the future lower records (two-sample pre-
diction) is based on progressive type-II censored with
*Corresponding author.
C
opyright © 2013 SciRes. IIM

A. A. SOLIMAN ET AL. 163
random removals. In Section 4, the ML prediction both
point and interval prediction using “plug-in” procedure
are derived. In Section 5, Bayesian predictive distribution
for the future order statistics based on progressive type-II
censored with random removals. In Section 6, the ML
prediction both point and interval prediction using “plug-
in” procedure for the future order statistics are derived. A
practical example using generating data set Progressively
type-II censored random sample from Burr-X distribu-
tion, and a simulation study has been carried out in or-
der to compare the performance of different methods of
prediction are presented in Section 8. Finally we con-
clude the paper in Section 8.
2. The Model, Prior and Posterior
Distribution
Let random variable X have an Burr-X distribution with
Parameter
 . the probability density function and the
cumulative distribution function of X are respectively

  
 
1
22
2
2exp1exp, ,0
( )1exp,,0.
fx xxxx
Fxx x






 


,
(1)
Suppose that denote a
progressively type-II censored sample, where 12
  
112 2
,,, ,,,
mm
xRxRx R
x
x


m
x

Rr
with pre-determined number of removals, say
112 2 the conditional likelihood
function can be written as,
,,Rr, ,
mm
R r

 
1
;1
i
mr
ii
i
LxRrCfx Fx 

  

,


(2)
where





112 1
12,,m C nnrnr rnrr 
 
11
0ii rnmr r

 
2,3,,1im

i
U
p
x
1m
1,
and for
,
substituting (1), (2) into (3) we get
 
1
100 1
exp1 ln,
m
m
r rm
mi
kk i
Gk  
 




 
 (3)
where

 
112
1
1, 1ex
m
kk mii
m
r r
GU
kk
 

 
 

. (4)
If the parameter
 is unknown, from the In-likelihood
function given by (3), the MLEs, MLE
ˆˆ

  can be ob-
tained by the following equations,


1
1001
lnln1 ln.
m
m
r rm
i
kki
mGk 

 

 i U (5)
The first derivative of

ln

with respect to  is


1
1001
ln 1ln ,
m
m
r rm
i
kki
mGk U



 



setting


ln 0 





we get the maximum likelihood
estimator of
 as the following

1
1
MLE
001
ˆ,
1ln
m
m
r rm
ii
kki
m
Gk U







(7)
consider a gamma conjugate prior for  in the form




1
π,exp,0,,0




.
(8)

From (3) and (8) the conditional posterior (pdf) of  is
given by




1
1
1
1
1
00
00
exp
πx
m
m
m
m
r rmk
kk
r rm
k
kk
Gq
mGq

















(9)
where

1
1ln
m
ki
i
qk 

 
i
U
.
3. Bayesian Prediction for Record Value
Suppose n independent items are put on a test and the
lifetime distribution of each item is given by (2). Let
123
,,,,
m
X
XX X be the ordered m-failures observed
under the type-II progressively censoring plan with bi-
nomial removals


1,, m
RR, and that 1
12 be
a second independent sample (of size m1) of future lower
record observed from the same distribution (future sam-
ple). Our aim is to make Bayesian prediction about the
,,,
m
YY Y
,
th
s
then the marginal pdf of is given by see
Ahmadi and Mir Mostafaee [24] is
S
V
 
 
1
log
1!
s
S
V
FY
fY fY
S

 

 (10)
where





  
2
1
22
1exp ,
2exp1 exp,
s
ss s
FY Y
fY YYY




 

(11)







2
2
2
1exp, log,
2exp .
1exp
sss
ss
s
s
UYq
YY
YY
 







s
U
(12)
Applying (11), (12) in (10) we obtain





1
exp .
s
S
Ss
Vss s
q
fYq Y
S





(13)
i
(6)

A. A. SOLIMAN ET AL. 164
Combining the posterior density (9) with (13) and in-
tegrating out  we obtain the Bayes predictive density

 

 



1
1
1
1
0
1
00
00
d
.
,
xx
s
m
m
m
m
sVs
r rmS
S
ss ks
kk
r rm
k
kk
fYf Y
qY Gqq
BSm Gq



















(14)
The Bayesian prediction bounds for the future
1
,
S
Y
1, 2,,
s
m are obtained by evaluating 1 Pr x
S
Yt



for some given value of t1, It follows from (14) that




1
1
1
1
1
1
1
00
00
Prxxd
,
,
m
m
m
m
SSs
t
r r
ts
kk
r rm
k
kk
YtfV Y
GI Y
BSm Gq















(15)
where






11
1
d.
S
s
tss s
mS
tis
q
I
Y
qq






YY
(16)
The predictive bounds of a two-sided interval with
cover


100% 

for the future lower record S, may
thus obtained by solving the following two equation for
the lower
Y
s
L and upper
s
U bounds:



1
1
1
1
00
00
1,
2
,
m
m
m
m
r r
LS
kk
r rm
k
kk
GI Y
BSm Gq













(17)
and



1
1
1
1
00
00
1,
2
,
m
m
m
m
r r
US
kk
r rm
k
kk
GI Y
BSm Gq













(18)
where

L
S
I
Y and

US
I
Y are given by Equation (16).
Now by using (14) the Bayesian point prediction of the
future lower record values YS under SE (BS) and LINEX
loss functions (BL) are given, respectively, as





1
1
1
1
0
1
00
00
d
,
,
x
m
m
m
m
sSs sBS
r r
s
kk
r rm
k
kk
YYfVY
GI Y
BSm Gq















(19)
and

 



1
1
1
1
0
2
00
00
1Log expd
1Log
,
x
m
m
m
m
sS s
sBL
r r
s
kk
r rm
k
kk
YcYfV
c
GI Y
cBSm Gq







 


Y






















(20)
where





1
1
0
d,
S
ss
s
ss
mS
is
Yq
I
YY
qq






Y
(21)
and






1
2
0
exp d.
S
ss
s
ss
mS
is
qcY
I
YY
qq







Y (22)
One can use a numerical integration technique to get
the above integration, given by (21), (22).
Special case: In special case it is important to predict
the first unobserved lower record value .
1
When s = 1, in (17) and (18), the lower and upper
Bayesian prediction bounds with cover
Y

of 1 Y are
obtained from the numerical solution of the following
equations



1
1
1
1
1
00
00
1,
2
1,
m
m
m
m
r r
L
kk
r rm
k
kk
GI Y
Bm Gq













(23)
and



1
1
1
1
1
00
00
1,
2
1,
m
m
m
m
r r
U
kk
r rm
k
kk
GI Y
Bm Gq













(24)
where


1L
I
Y and


1U
I
Y given by Equation (16), and
solving the resulting equations numerically.
4. ML Prediction for Record Value
The commonly used frequentist approaches such as the
maximum likelihood estimate and the “plug-in” proce-
dure, which is to substitute a point estimate of the un-
known parameters into the predictive distribution are
reviewed and discussed. In this section the ML prediction
both point and interval using “plug-in” procedure for
future lower record based on progressive type-II cen-
sored sample defined by (2). By replacing  in the mar-
ginal pdf of S (13) by Vˆ

which we can find it from
the numerical solution of the Equation (7), then

A. A. SOLIMAN ET AL. 165





1
1
ˆˆ
exp .
s
S
Ss
Vss s
qOne can use a numerical integration technique to get
the above integration, given by (32).

f
YY
S


 
q (25)
The ML prediction bounds for the future S are ob-
tained by evaluating
Y
2
Pr x
S
Yt  

5. Bayesian Prediction for Order Statistics


for some given
value of t2, It follows from (25) that



1
2
2
1
PrxdIngamma; ,1
s
SVss
t
Yt fYYtS
S

 
  



2
(26)
Order statistics arise in many practical situations as well
as the reliability of systems. It is well-known that a sys-
tem is called a k-out-of-m system if it consists of m
components functioning satisfactorily provided that at
least


km components function. If the lifetimes of
the components are independently distributed, then the
lifetime of the system coincides with that of the


1thmk order statistic from the underlying distri-
bution. Therefore, order statistics play a key role in stu-
dying the lifetimes of such systems. See Arnold et al. [26]
and David and Nagaraja [27] for more details concerning
the applications of order statistics.
where Ingamma is the incomplete gamma
function defined by

12
;,tt 



1
12
12
2
0
Ingamma; ,
ˆ
expd .,andlog1exp.
t
tt
ztzztt






 



(27)
The predictive bounds of a two-sided interval with
cover

for the future lower record S, may thus ob-
tained by solving the following two equation for the
lower
Y
s
L and upper
s
U bounds:


1
Ingamma; ,1,
2
s
LS
S
1



 (28)
and


11
Ingamma; ,1.
2
s
US
S



 (29)
Suppose n independent items are put on a test and the
lifetime distribution of each item is given by (2). Let
123
,,,,
m
X
XX X be the ordered m-failures observed
under the type-II progressively censoring plan with bi-
nomial removals


1,, m
RR
, .
m
Y
, and that 2
12 be
a second independent random sample (of size m2) of fu-
ture order statistics observed from the same distribution.
Our aim is to obtain Bayesian prediction about some
functions of
,,,
m
YY Y
2
12
Let
,,YY th
s
Special case
When S = 1, in (28) and (29), the lower and upper ML
prediction bounds with cover

of 1 are obtained
from the numerical solution of the following equations:
Y

1
1
Ingamma ;1,1,
2
L


 (30)
and

1
1
Ingamma ;1,1.
2
U


 (31)
The ML point prediction of the lower record value
is given, from (25), as
S
Y






1
0
1
0
d
ˆˆ
expd .
s
sV ss sML
SS
s
sss s
YYfYY
qqYY
S









Y
(32)
s
Y be the ordered lifetime in the future sam-
ple of m2 lifetimes. The density function of
s
Y for given
 is of the form


   
21
1,
s
ms s
ss
hY
D sFYFYfY

s







(33)
where

2.
m
Ds s
s



For the Burr-X model, substi-
tuting (11) and (12) in (22), we obtain


 



21
22
0
12exp
s
ms lls
sss
l
hY
ms
DsYY U
l











 


(34)
Therefore, from (9) and (34), the Bayes predictive
density function of
s
Y will be (see Equation (35)).
where and

22
0
1
ms ms
l
l
l
lDs




 


 


s
Y,
s
U
 







1
1
1
1
0
1
00
00
xxd
log
,
m
m
m
m
ss
r rm
ks
kk
sr
rm
k
kk
fY hY
Gqs lU
lYm
Gq


 


 






 





(35)

A. A. SOLIMAN ET AL. 166
are given by Equation (12).
The Bayesian prediction bounds for the future
are obtained by evaluating
for some given value of 1

2
, 1,2,,
s
Ys m
1
Pr x
S
Y 



 , It follows
from (35) that




 



1
1
1
1
1
2
00
Prxx d
log 1exp
m
m
Sss
r rm
m
kk
r
kk
YfYY
lGqqsl
sl





















The predictive bounds of a two-sided interval with
cover
100
m
kk


1
.
m
rm
k
Gq
 




(36)


100%  for the future order statistics ,
may thus obtained by solving the following two equation
for the lower
S
Y
s
LL and upper
s
UU bo unds:



 



1
1
1
1
2
00
00
k
kk
sl Gq
...log 1exp1,
2
m
m
m
m
r
rm
m
kk s
kk
r rm
lGqqsl LL













 



(37)






 



1
1
1
1
2
00
00
log 1exp1.
2
m
m
m
m
r rm

m
kk s
kk
r rm
k
kk
lGqqslUU
sl Gq





















(38)
Now by using (35) the Bayesian point prediction of the
future order statistics
s
Y
n, res
under SE (BS) and LINEX loss
functions (BL) are givepectively, as


 


1
1
0
00
xd
m
m
sss sBS
r r
1
1
1
00
m
m
s
kk
r rm
k
GI Y
lm
Gq
kk
YYfYY










(39)







and



 


1
1
1
1
0
2
00
00
1Logexpx d
m
m
m
m
s
ss
Y
sB L
r r
s
kk
r rm
k
kk
YcYfY
c
GI Y
lm
Gq


















(40)
where
  


1
1
0
logd ,
m
s
skss s
IYYqslUY Y



 (41)
and


 



2
0
explogd .
s
m

1
s
ks
IY
cYqs lUYY


 


(42)
ss
We can use a numerical integration technique to get
the above integration, given by (41), (42).
6. ML Prediction for Order Statistics
In this section the ML prediction both point and in
using “plug-in” procedure for the future order
based on progressive type-II censored sample defined by
(2). From (34) by replacing  in the density function of
terval
statistics
for given  by ˆ

h
s
Ywhich we can find it from the nu-
lution of t e Equation (7), then the density
n of
merical so
functio foen r givˆ

s
Y






2
1
ˆ1
22
0
ˆ
ˆ
12exp
s
ms lls
sss
l
hY
ms .sYYU
l






D




 


(43)
The ML prediction bounds for the future

s
Y are ob-
tained by evaluating 2 Pr x
S
Y 




 fore given
value of
som
2,

It follows from (43) that

A. A. SOLIMAN ET AL. 167






2
2
ˆ
2
1
Pr x
ˆd11exp
S
ls
ss
Y
l
hYY ls













2
. 


(44)
The predictive bounds of a two-sided interval with
cover

for the future order statistics
s
Y
q
, may thus
obtaineby solving the following two euation for the d
lower
s
LL and upper
s
UU bounds:


 

ˆ
21
11exp ,
2
ls
s
lLL
ls






 


(45)
and





ˆ
21
11exp .
2
ls
s
lUU
ls






 


(45)
From (43 ML point) the prediction of the order statis-
tics YS is given by



 

ˆ1
2
0
ˆ
2exp.
ls
1
ML
0
ˆd
d
ss s
s
s
ssss
lY YY U



 

One case a numerical integration tec
YYhYY
Y





(46)
n uhnique to get
the above integration, given by (46)
7. Illustrative Example and Simulation
Study
E
.
Algorithm 1.
1) Specify the value of n.
2) Specify the value of m.
Specify the value of parameters
 and p
Generate a random sample with size m from Burr-X
and sort it.
5) Generate a random number r1 from

,

for each .
7) Set rm according to the following relation,
1
the exact value of
and P are respectively 1.6374, 0.4 and n = 10 and m = 7,
xample 1: In this example, a progressive type-II cen-
sored sample with random removals from the Burr-X
distribution have been generated using the following al-
gorithm
3)
4)

,.bio nm p
6) Generate a random number ri from
1
,
i
i
bio nmrp





1l 
,2,3,, 1ii m
1
11
if0
0.
ii
ll
ll
m
nm rnm r
r
ow








In these sample, we assumed that 
the sample obtained is given as follows


,
ii
X
R
(1.2655,1)
:
(0.0.5449,1), (0.6728,0), (0.9914,0), ,
95% Bayesian prediction intervals of the
4406,1), (
(1.3680,0), (1.4271,0).
We used the above sample to compute:
1) Bayesian point prediction, under SE and LINEX
loss function;
2) The th
s
unecords (order statistics);
d prediction ML;
elihood prediction intervals
of
observed lower r
3) The maximum likelihoo
4) The 95% maximum lik
the th
s
unobserved lower records (order statistics);
Simulation Study In this example, we
diparing the pe
fo d in this paper.
Firstly we generate (wer record values (order
statistics) from the Burr-X distribution  = 1.63. By
usingenend 95%
Bervations
lower record (order statistics) from the the Burr-X
ution and by repeated the generations 100 time
we can find the Percentage (C.P) and we use prior
5) The results obtained are given in Tables 1-4.
Example 2:
scuss results of a simulation study comr-
rmance of the prediction results obtaine
m1 = 5) lo
74
g the rating data we predict the 90% a
ayesian prediction intervals for the future obs
th
S
distrib 0


,

 equal (2,3). Tables 5-8 show the 90% and 95%
Bayesian (B) and maximum likelihood (ML) prediction
intervals for the future th
S lower record (order statis-
tics). The sample obtained is given as follows, (0.4640,1),
(0.5124,1), (0.7323,0), (0.8293,1), (0.8665,0), (0.8713,1),
(1.1322,0), (1.4969,0).
8.
In on
ensored sam-
stribution
fo
pr
ate
i n
y.
using “plug-in” procedure (MLPI)
ediction intervals using Bayes
results show that, for all cases (low-
Conclusions
this paper, we consider the two-sample predicti
wherein the observed progressive Type-II c
ples with random removals from the Burr-X di
rm the informative samples and discussed how point
prediction and prediction intervals can be constructed for
fud MLture lower records (order statistics). Bayesian an
edictions both the point prediction and the prediction
intervals are presented and discussed in this paper.
The commonly used frequentist approaches such as the
maximum likelihood estimate and the “plug-in” proce-
dure, which is to substitute a point estimate of the un-
known parameters into the predictive distribution are
reviewed and discussed. Numerical example using simu-
ld data were used to illustrate the procedures devel-
oped here. Finally, simulation studies are presented to
compare the performance of different methods of predic-
t o. A study of 1000 randomly generated future samples
from the same distribution shows that the actual predic-
tion levels are satisfactorFrom the results we note the
following:
1) The results in Tables 1-4 show that the lengths of
the prediction intervals
are shorter than that of pr
procedure.
2) The simulation
er records and order statistics), the proposed prediction
levels are satisfactory compared with the actual predic-
tion levels 90% and 95%.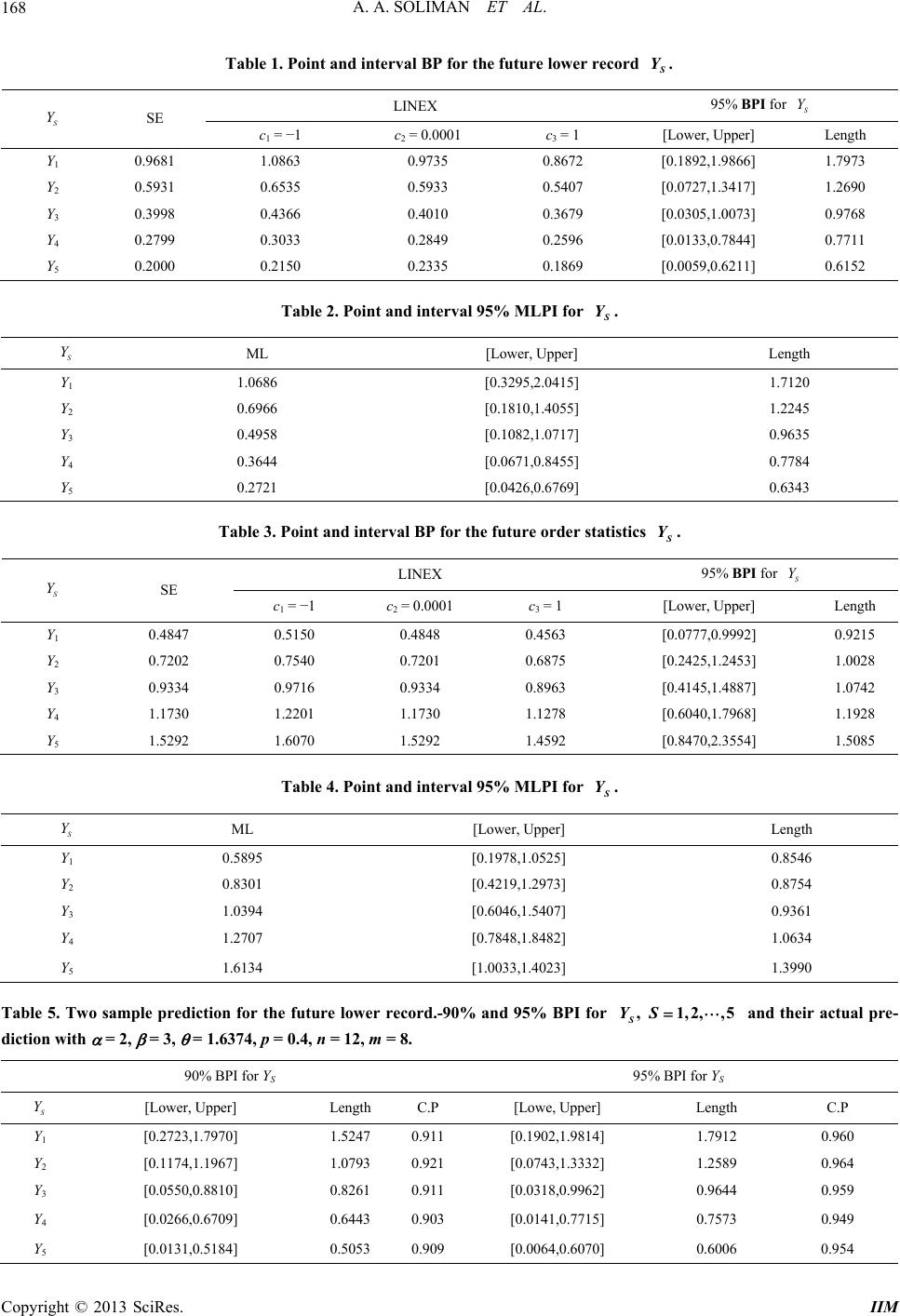

A. A. SOLIMAN ET AL. 168
for
Table 1. Point and interval BP
LINEX
the future lower record S Y.
95% BPI for S
Y
S
Y SE c1 = −1 c2 = 0.00c01 3 = 1 [Lower, Upper] Length
Y1 0.9681 1.0863 0.9735 0.8672 [0.1892,1.9866] 1.7973
Y2 0.5931 0.6535 0.5933
Y3 0.3998 0.4366 0.4010
Y4 0.2799 0.3033 0.2849
Y5 0.2000 0.2150 0.233
[0.0305,1.0073] 0.9768
5
0.5407 [0.0727,1.3417] 1.2690
0.3679
0.2596 [0.0133,0.7844] 0.7711
0.1869 [0.0059,0.6211] 0.6152
Table 2. Point and interva
Length
l 95% MLPI for S Y.
S
Y ML [Lower, Upper]
Y1 1.0686 [0.3295,2.0415] 201.71
Y2 0.6966 [0.1810,1.1.2245
3 0.4958 [0.1082,1.0.9635
4 0.3644 [0.0671,0.0.7784
5 0.2721 [0.0426,0.0.6343
4055]
Y0717]
Y8455]
Y6769]
Tablet and intervae futuretatistics
LINEX 95% BPI for
S Y 3. Poinl BP for th order s.
S
Y
S
Y SE c[Lower, Upper] Length
1 = −1 c2 = 0.0001 c3 = 1
Y1 0.4847 0.5150 0.4848 [0.0777,0.9992] 0.9215 0.4563
Y0.7202 7540 0.7201 [0.2425,1.2453] 1.0028
Y0.9334 9716 0.9334 [0.4145,1.4887] 1.0742
Y1.1730 2201 1.1730 [0.6040,1.7968] 1.1928
Y1.5292 6070 1.5292 [0.8470,2.3554] 1.5085
2 0.0.6875
3 0.0.8963
4 1.1.1278
5 1.1.4592
Table 4. Point and interval 95
Length
S
Y. % MLPI for
S
Y ML [Lower, Upper]
Y1 0.5895 [0.1978,1.0525] 0.8546
Y2 0.8301 [0.4219,1.0.8754
3 1.0394 [0.6046,1.0.9361
4 1.2707 [0.7848,1.0634
5 1.6134 [1.0033,1.3990
2973]
Y5407]
Y1.8482]
Y1.4023]
Table 5. Two sample pion for thre lower reco and 95% for d their actue-
tion with  = 2,  = 3, 374, p = 0.4 = 12, m = 8.
90% BPI for YS 95% BPI for YS
,1,2,,
S
YS 5 anal prredicte futurd.-90% BPI
 = 1.6, n dic
S
Y [Lower, UppeLength C.P per] Length C.P r] [Lowe, Up
Y1 [0.2723,1.791.5247 0.911 1.7912 0.960 70] [0.1902,1.9814]
Y2 [0.1174,1.191.0793 0.921 1.2589 0.964
Y3 [0.0550,0.880.8261 0.911 0.9644 0.959
Y4 [0.0266,0.670.6443 0.903 0.7573 0.949
Y5 [0.0131,0.5184] 0.5053 0.909[0.0064,0.6070] 0.6006 0.954
67] [0.0743,1.3332]
10] [0.0318,0.9962]
09] [0.0141,0.7715]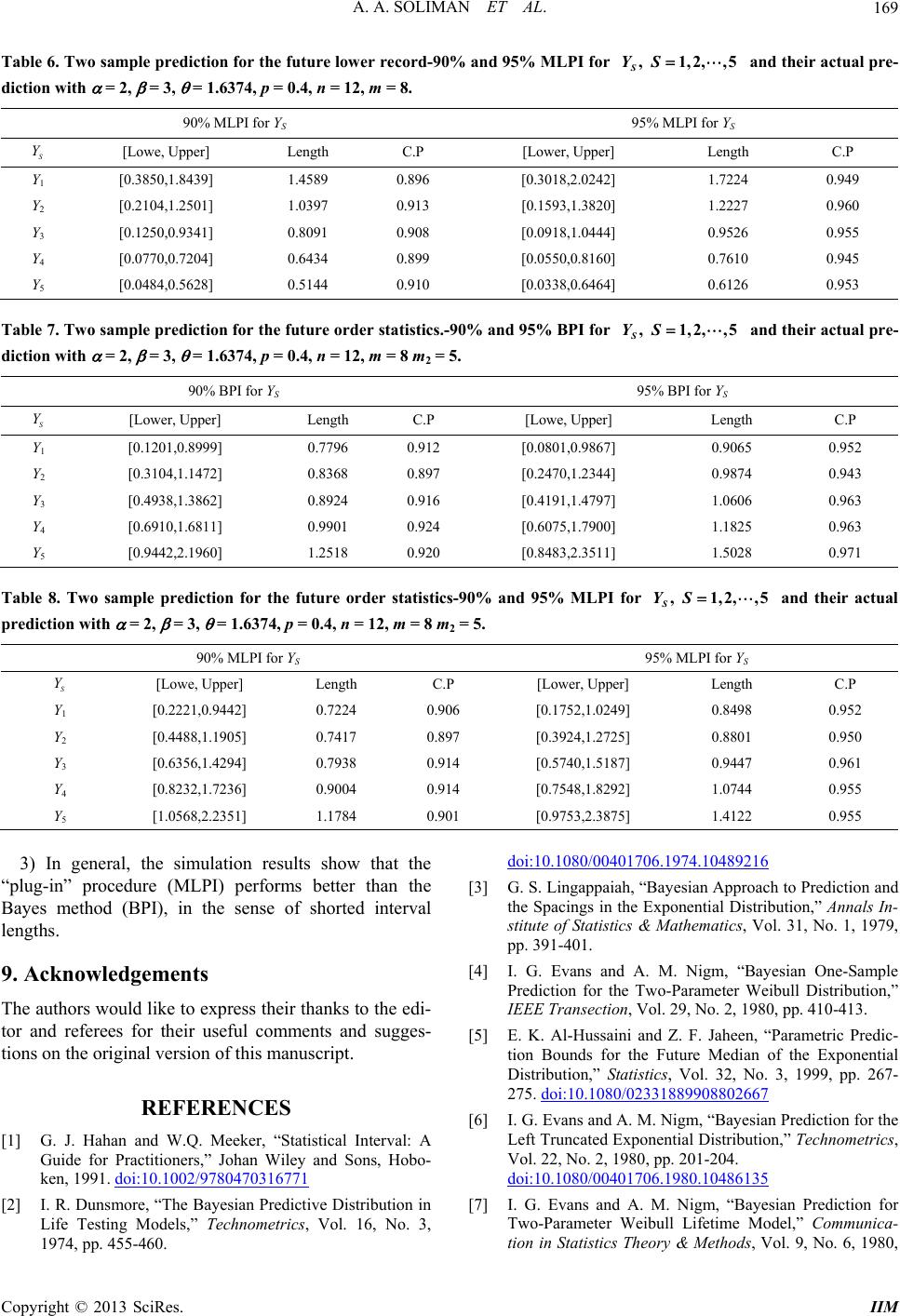

A. A. SOLIMAN ET AL. 169
Table 6. To sample predictioe future lower record-90%I for 5wn for th and 95% MLP ,1,2,,
S
YS

 anactual pre-
iction with  = 2,  = 3,  = 1.6374, p = 0.4, n = 12, m = 8.
95% MLPI for YS
d their
d
90% MLPI for YS
S
Y [L] Length C.owe, UpperP [Lower, Upper] Length C.P
Y1 [0.3850,1.1.4589 0.896 [0.3018,2.0242] 24 0.949 8439] 1.72
Y221.0397 0.913 ]
[0.10.8091 0.]
[0.00.6434 0.]
[0.00.5144 0.]
[0.104,1.2501] [0.1593,1.38201.22270.960
Y3 250,0.9341] 908 [0.0918,1.04440.95260.955
Y4 770,0.7204] 899 [0.0550,0.81600.76100.945
Y5 484,0.5628] 910 [0.0338,0.64640.61260.953
Tab Two sample pe future tatis-90% andle 7.rediction for thorder stics. 95% BPI for ,1,2,,
S
YS 5

 and their are-
dictwith  = 2, 4, p = 0.4, n = 8 5.
95% BPI for YS
ctual p
ion  = 3,  = 1.637 = 12, mm =
2
90% BPI for YS
S
Y [Lower, Upper] Length C.P [Lowe, Upper] LC.P ength
Y11201,0.0.7796 0.912 [0.0801,0.9867] 0.952 [0.8999] 0.9065
Y2] 8 7
4
1
8
[0.3104,1.14720.8360.89[0.2470,1.2344] 0.9874 0.943
Y3 [0.4938,1.3862]0.8920.916[0.4191,1.4797] 1.0606 0.963
Y4 [0.6910,1.6811]0.9900.924[0.6075,1.7900] 1.1825 0.963
Y5 [0.9442,2.1960]1.2510.920[0.8483,2.3511] 1.5028 0.971
Table 8. Two san for thrder statistics-90% anor 5and their actual
rediction with  = 2,  = 3,  = 1.6374, p = 0.4, n = 12, m = 8 m = 5.
95% MLPI for YS
mple predictioe future od 95% MLPI f ,
S
YS 1,2,,
p2
90% MLPI for YS
S
Y [Lowe, Upper] Length C.P [Lower, Upper] Length C.P
Y1 [0.220.7224 0.906 [0.1752,1.0249] 98 0.952
2 5] 97 ]
Y3 4] 4 ]
Y4 6] 4 ]
Y5 1] 1 ]
21,0.9442] 0.84
Y[0.4488,1.1900.74170.8[0.3924,1.2725 0.8801 0.950
[0.6356,1.4290.79380.91[0.5740,1.5187 0.9447 0.961
[0.8232,1.7230.90040.91[0.7548,1.8292 1.0744 0.955
[1.0568,2.2351.17840.90[0.9753,2.3875 1.4122 0.955
3) In generalon results show that
plug-in” procedure (MLPI) performs better than the
9. Acknowledgemen
The auwould like to eheir thanks to the edi-
tor and referees foments and sugges
tions oe originas manus
RES
] G. J. Hahan an, “Statiserval: A
, the simulatithe
“
Bayes method (BPI), in the sense of shorted interval
lengths.
ts
thors xpress t
r their useful com-
n thl version of thicript.
EFERENC
[1 d W.Q. Meekertical Int
Guide for Practitioners,” Johan Wiley and Sons, Hobo-
ken, 1991. doi:10.1002/9780470316771
[2] I. R. Dunsmore, “The Bayesian Predictive Distribution in
Life Testing Models,” Technometrics, Vol. 16, No. 3,
1974, pp. 455-460.
d1706.1974.16oi:10.1080/0040048921
[3] G. S. Lingappaiah, “Bayesian Approach to Prediction and
xponential Distri
stitute of Statistics & Mathematics, Vol. 31, No. 1, 1979,
pp. 391-401.
[4] I. G. Evans and Aayesian One-Sample
PredTwo-Parameibull Dision,”
IEEE Transectio, No. 2, pp. 410-
[5] E. K.Z. F. J “Parametricedic-
tione Future Median of the Ential
Dis stics, Vol.. 3, 1999267-
275 33188990 7
the Spacings in the Ebution,” Annals In-
. M. Nigm, “B
iction for the eter Wtribut
n, Vol. 29, 1980413.
Al-Hussaini and
Bounds for th
aheen, Pr
xpone
tribution,” Stati 32, No, pp.
. doi:10.1080/02880266
[6] I. G Nigm, an Predicr the
Left Truncated Exponential Distribution,” Tech rics,
Vol. 22, No. 2, 1980, pp. 201-204.
86135
. Evans and A. M.“Bayesition fo
nomet
doi:10.1080/00401706.1980.104
igm, “Bayesian Prediction for [7] I. G. Evans and A. M. N
Two-Parameter Weibull Lifetime Model,” Communica-
tion in Statistics Theory & Methods, Vol. 9, No. 6, 1980,

A. A. SOLIMAN ET AL. 170
pp. 649-658. doi:10.1080/03610928008827909
[8] A. M. Nigm, “Prediction Bounds for the Burr Model,”
Communicatio Methods, Vol.
No. 1, 1988, p
n in Statistics Theory &
p. 287-297.
17,
doi:10.1080/03610928808829622
[9] E. K. Al-Hussaini and Z. F. Jaheen, “Bayesian Prediction
Bounds for Burr Type XI Model,” Communication in
d Z. F. Jaheen, “Bayesian Prediction
in the Presence of
Sta-
tistics Theory & Methods, Vol. 24, No. 7, 1995, pp. 1829-
1842.
[10] E. K. Al-Hussaini an
Bounds for Burr Type XII Distribution
Outliers,” S tati stic al Planning and Infe rence, Vol. 55, No.
1, 1996, pp. 23-37. doi:10.1016/0378-3758(95)00184-0
[11] M. A. M. Ali Mousa and Z. F. Jaheen, “Bayesian Predic-
tion Bounds for Burr Type XII Model Based on Doubly
ic-
eview,” Commu-
tial Distribution
of Mathematics and
Censored Data,” Statistics, Vol. 48, No. 2, 1997, pp. 337-
344.
[12] M. A. M. Ali Mousa and Z. F. Jaheen, “Bayesian Pred
tion for the Two Parameter Burr Type XII Model Based
on Doubly Censored Data,” Applied Statistics of Science,
Vol. 7, No. 2-3, 1998, pp. 103-111.
[13] J. K. Patel, “Prediction Intervals—A R
nication in Statistics Theory & Methods, Vol. 18, No. 7,
1989, pp. 2393-2465.
[14] H. N. Nagaraja, “Prediction Problems,” In: N. Balakrish-
nan and A. P. Basu, Eds., The Exponen:
Theory and Applications, Gordon and Breach, New York,
1995, pp. 139-163.
[15] K. S. Kaminsky and P. I. Nelson, “Prediction on Order
Statistics,” In: N. Balakrishnan and C. R. Rao, Eds.,
Handbook of Statistics, Elsevier Science, Amsterdam,
1998, pp. 431-450.
[16] E. K. Al-Hussaini, “Prediction: Advances and New Re-
search,” International Conference
21st Century, Cairo, 15-22 January 2000, pp. 25-33.
[17] J. Aitchison and I. R. Dunsmore, “Statistical Prediction
Analysis,” Cambridge University Press, Cambridge, 1975.
doi:10.1017/CBO9780511569647
[18] S. Geisser, “Predictive Inference: An Introduction,”
15-425.
Chapman and Hall, 1993.
[19] M. A. M. Ali Mousa, “Inference and Prediction for the
Burr Type X Model Based on Records,” Statistics, Vol.
35, No. 4, 2001, pp. 4
doi:10.1080/02331880108802745
[20] Z. F. Jaheen and B. N. AL-Matrafi, “Bayesian Prediction
Bounds from the Scaled Burr Type X Model,” Computers
and Mathematics, Vol. 44, No. 5, 2002, pp. 587-594.
[21] A. A. Soliman, “Bayesian Prediction with Outliers and
Random Sampel Size for the Burr Type X Model,”
Mathematics & Physics Socity, Vol. 73, No. 1, 1998, pp.
1-12.
[22] H. A. Sartawi and M. S. Abu-Salih, “Bayesian Prediction
Applied Statistics,
tics
Bounds for Burr Type X Model,” Communication in Sta-
tistics Theory & Methods, Vol. 20, No. 7, 1991, pp. 2307-
2330.
[23] J. Ahmadi and N. Balakrishnan, “Prediction of Order
Statistics and Record Values from Two Independent Se-
quences,” Journal of Theoretical and
Vol. 44, No. 4, 2010, pp. 417-430.
[24] J. Ahmadi and S. M. T. K. Mir Mostafaee, “Prediction
Intervals for Future Records and Order Statistics Coming
from Two Parameter Exponential Distribution,” Statis
Probability Letters, Vol. 79, No. 7, 2009, pp. 977-983.
doi:10.1016/j.spl.2008.12.002
[25] J. Ahmadi, S. M. T. K. Mir Mostafaee and N. Balakrish-
nanb, “Bayesian Prediction of Order Statistics Based on
ourse in Order Statistics,” Wiley, New York, 1992.
k-Record Values from Exponential Distribution,” Statis-
tics, Vol. 45, No. 4, 2011, pp. 375-387.
[26] B .C. Arnold, N. Balakrishnan and H. N. Nagaraja, “A
First C
[27] H. A. David and H. N. Nagaraja, “Order Statistics,” Wi-
ley, New York, 2003.