Journal of Applied Mathematics and Physics, 2013, 1, 28-36
http://dx.doi.org/10.4236/jamp.2013.13006 Published Online August 2013 (http://www.scirp.org/journal/jamp)
Comparison of Solution Methods for some Classical Flow
Problems in Rarified Gas Dynamics
Ignatius N. Njoseh1, Alex Musa2
1Department of Mathematics and Computer Science, Delta State University, Abraka, Nigeria
2Department of Mathematics and Statistics, University of Port-Harcourt, Port-Harcourt, Nigeria
Received July 216, 2013; revised August 19, 2013; accepted September 10, 2013
Copyright © 2013 Ignatius N. Njoseh, Alex Musa. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
A comparison of two methods of solution to classical flow problem in rarefied gas dynamics was presented. The two
methods were chosen to examine the effect of the following transport phenomena (pressure gradient and temperature
difference) viz Poiseuille and Thermal creep respectively on the flow of rarefied gas. The governing equations were
approximated using BGK model. It was shown that while the Discrete Ordinate Method could consider more values of
the accommodation coefficients, the Finite Difference Method can only take accommodation coefficient of one. It was
also shown that the flow rate has its minimum in both solution methods at Kn = 0.1 in the transition regime and that as
the channels get wider, the Thermal creep volume flow rates get smaller.
Keywords: Discrete Ordinate; Finite Difference; Pressure Gradient; Temperature Difference; Knudsen Number
1. Introduction
In the recent literature there is a growing interest to solve
problems in rarefied gas dynamics. The reader is referred
to [1-6], and other references therein for an overview of
the recent work in this area. Earlier researches [7-12]
solved rarefied gas dynamics problems using different
methods. It has been shown that these methods yield
good results. The main objective of this work is to do a
comparison of two of the most widely used methods in the
numerical study of rarefied gas flow problem: the Dis-
crete Ordinate method (DOM) and the Finite Difference
Method (FDM). Though the literature concerning our area
of study is very intensive, we shall review a few of them.
Barichello, et al. [13] studied a version of the dis-
crete-ordinates method to solve in a unified manner some
classical flow problems based on the Bhatnagar, Gross
and Krook model in the theory of rarefied gas dynamics.
In particular, the thermal-creep problem and the viscous-
slip (Kramer’s) problem are solved for the case of a
semi-infinite medium, and the Poiseuille-flow problem,
the Couette-flow problem and the thermal-creep problem
are all solved for a wide range of the Knudsen number.
Also Scherer and Barichello [14] studied an analytical
version of the discrete-ordinates method, the ADO
method, to solve two problems in the rarefied gas dy-
namics field, which describe evaporation/condensation
between two parallel interfaces and the case of a semi-
infinite medium. The modeling of the problems is based
on a general expression which may represent four dif-
ferent kinetic models.
In [15], the problem of heat transfer and temperature
distribution in a binary mixture of rarefied gases between
two parallel plates with different temperatures on the
basis of kinetic theory was investigated. Under the as-
sumptions that the gas molecules are hard spheres and
undergo diffuse reflection on the plates, the Boltzmann
equation was analyzed numerically by means of an ac-
curate finite difference method, in which the complicated
nonlinear collision integrals are computed efficiently by
the deterministic numerical kernel method. As a result,
the overall quantities are obtained accurately for a wide
range of the Knudsen number. At the same time, the be-
havior of the velocity distribution function is clarified
with high accuracy.
Muljadi and Yang [16] obtained a direct method for
solving rarefied flow of gases of arbitrary particle statis-
tics. The method is based on semi-classical Boltzmann
equation with BGK relaxation time approximation. The
discrete ordinate method is first applied to render the
Boltzmann equation into hyperbolic conservation laws
with source terms, and then classes of explicit and im-
plicit time integration sch emes are applied to evalu ate the
C
opyright © 2013 SciRes. JAMP

I. N. NJOSEH, A. MUSA 29
discretized distribution function. The method is tested on
both transient and steady flow problems of gases of arbi-
trary statistics at varying relaxation times.
Also worthy of no te are th e work s of [17- 22] and oth er
references therein.
2. The Linearized Boltzmann Equation
The non-linearity form of the Boltzmann equation is es-
sential in application if the gas is far from thermal equi-
librium. However, if the state of the gas is near thermal
equilibrium, a linearized form of the Boltzmann equation
will provide a reasonably accurate description of the
transport phenomena. This form assumed that the per-
turbation of the velocity distribu tion from its equilibrium
form is small.
Following the work in [23] a linearized form of the
Boltzma nn e qu at i on was given as
 

22
0
0
2 0
3
2
22 2
33
2
22
d, ,
d
dexp ,
23 23
12 32 32
x
xx xz
x
zz
cckR cK ccK
chxc
cRh xc
x
cchxc
ccccc



 
 
  
 

 
  




 

 
  
z
 



(1)
where h is a disturbance caused to the local Maxwellian,
Rx is the relative density in the x-direction, Kx is the
temperature gradient in the x-direction,
1
2
2
m
cv
K
T



and
1
2
02
m
K
T




.
3. Discrete Ordinate Method
Consider the flow of rarefied gas in z-direction between
two parallel plates separated by a distance d. the orig in is
chosen in the middle of the channel so that the coordinate
y varies from 2
d to 2 d.
Following the linearized Boltzmann Equation (1), we
seek the solution to the equation:



12
2
,,exp ,
zd
x
Zxu Zxu u
x
 


 
 (2)
For ,
22
dd
x 


and


,  , subject to the
boundary conditions:
1) For Couette flow



 
,1 ,Za Za



  (3)



 
,1 ,Za Za



  (4)
2) Poiseuille flow






2
,1 ,2Za Zaa


    (5)






2
,1 ,2ZaZa a


     (6)
3) Thermal flow
 
2
1
,1, 22 Za Za
 

 


1


(7)

2
1
,1,
22
Za Za


 


1


(8)
Rewriting (2) we have

 

,,
,,d
zZx Zx
x
Zx Zx


 









where

12
2exp



 




(10)
for ,
22
dd
x 


and

, 

 .
Define = weight and kk
W

= nodes for
1, 2,k,N

, then the integral term on the right hand
side of (9) can be approximated to obtain

 
1
,,
,,
N
kk kk
k
zZx Zx
x
WZxZx

 









(11)
for ,
22
dd
x 


and


, 

 .
To satisfy the requirements of the right hand side of
(11) the left hand side was evaluated at the points
i



 to obtain a system of differential equatio ns

 
1
,,
,,
iii
N
kk kk
k
zZx Zx
x
WZxZx

 









(12)
and

 
1
,,
,,
iii
N
kk kk
k
zZx Zx
x
WZxZx

 










(13)
for 1, 2,,,iN

 where is the quadrature points. N
Seeking exponential solutions to Equations (12) and
(13), set

I. N. NJOSEH, A. MUSA
30

,,exp
ii
x
Zx v 

 



(14)
Substituting Equation (14) into Equations (12) and
(13), we have

 
1
,,
,,
i

 ii
N
kk i k
k
vv
v
Wvv

  

  
 


(15)
and

 
1
,,
,,
i
ii
N
kk ik
k
vv
v
Wvv

 


 



(16)
For convenience, let

,,
i
v 
 
 
12
, ,
,diagonals, ,,
i
ijj iN
v
WWM



 
  
Then (15) and (16) can be written as

 

1MIWW 
v
(17)

1MIWW
v


(18)
where
I
is an N × N identity matrix
Now let
(19)
and
(20)
Adding (17) and (18) and substi

,,,,,vv 



T
12, N
v 



U

Y 
tuting (19) gives

112
M
YWU
v (21)
Subtracting (18) from (17) and substitutin g (20) gives
1
M
YY
v

(22)
Eliminating Y from (21) an d (22) we ha v e

11
1
22
M
UDMWMMU
v (23)
where T with diagonal



22 2
12
diagonals,,, N D  
 

iplying (23) by a diagonal matriMultx
elements given by

1
2
iii
TW 
 

2
1
2DVX X
v
 (25)
where
VMTWTM



and
X
TMU
With the elements isade sym-
m12
,, ,tt T
n write the eigenv
,
N
t mV
aetric and hence we calue in the form


T
2DZZX X

 (26)
where
2
11
V
v



and
 

T
112 2
12 1
,,,
NN
N
W
WW
Z

 











Considering that the required eigenvalues has been ob-
ta
I
ined in (26), a normalization condition is therefore im-
posed, that is,

N
W 
 
1
,,
kk k k
k
vv  



 

 (27)
Hence the discrete ordinate solution is written as

 
1
,ee
jj
jj
ij j
jji ji
Zx A B
vv


ax ax
Nvv
vv






 

 


(28)

 
1
,e
jj
ax ax
Nvv
jj
ij j
jjiji
vv
Zx AB
vv




e




 

 



(29)
where


j
A
and


j
Bou are arbitrary constants to be
determinrom the bndary conditions. ed f
j
v is separa-
tion constants and is equal to the reciprocaf the posi-
tive square root of the eigenvalues as defined by (26), the
separation constants
l o


j
v will not be allowed to be
equal to one of the qrature points

uad
j

and a is
the arbitrary scaling constant which we aring as 2a
for the full chann el width.
The problem based on (2) is “conservative” since
e tak

d
I
 



For this reason we expect that one of the eigenvalues
defined by Equation (26) will tend to zero as N tends to
infinity. Taking this fact into account, ,
N
v which is the
largest of the computed separation conts stan


j
v will
have to be neglected, hence (28) and (29) are written as




 
1
1
,ii ZxA Bx   
ee
jj
ax ax
Nvv
jj
jj
jji ji
vv
AB
vv 

 



(24)
we have








 (30)

I. N. NJOSEH, A. MUSA 31
 
 
1
1
,
ee
jj
ii
ax ax
Nvv
jj
jj
jjiji
ZxA Bx
vv
AB
vv



 

 



 


The constants
(31)

,,
j
A
BA and

j
B
itions. Equat
will be deter-
mined fromions (30) and
(31) represent the discrete ordinate solutions.
To solve the problem of Couette, Poiseuille and Ther-
mal creep, we consider the boundary conditions as de-
finnd write
the boundary cond
ed in (3) to (8) a

1
,1 ,ZaZaF

   (32)
and








2
,1 ,ZaZa F

   (33)
for From (32) and (33), we can
bouitions as stated in (3) to (8) as

0, .  
ndary cond express the

1
F

  (34)
and

2
F

  (35)
for Couette flow,
 
2
12Fa





 (36)
and

2
F
 
22a





   (37)
for Poiseuille flow and

2
111
22
F





(38)
and

2
211
2
F


 


2

(39)
for Thermal creep.
bstituting (30) and (31) into the boundary conditions
(32) and (33), and evaluate at the quadrature points gives
the system of linear algebraic equation
Su
s
 
,,
1
1
2
ij jij j
j
i
AB a F
2
ej
a
v
i
A NB
1 N
M





 


and

 


  

(40)
 
2
1
,,
1
2
e
2
a
N
vj
ij jij j
j
ii
MA NB
AB aF

 








 

 (41)
for , and the matrix elements 1, 2,,iN

,22
2
ji
ij j
ji
v
Mv v













 (42)
and

,22
2
ji
v
v
ij j
ji
Nv













 (43)
Adding (40) and (41) we have

 
2
1
,,
1
12
2e
j
a
Nv
jj ijij
j
AABMN
FF


 





 
 







ave
 (44)
Subtracting (41) from (40) we h

 
2
1
,,
1
12
e2
j
a
Nv
j jijij
j
AB MNBa
FF

2
i

 






 
  







(45)
for 1, 2,,.iN


Solving (44) and (45) simultaneously to find the val-
ues of the constants A, B,

j
A
and

j
B
rious pr
. Hence we
can establish the solutions t vaoblems as
follows
For Poiseuille flow, we have
Velocity profile
o the
1)



22 0
11
2
p
qaY



     (46)
where

 
1N 
0
YAB 
1
ee
jj
aa
vv
jj
J
A B
 






 




 (47)
and iseuille Volume Flow Rate 2) Po

2
1
21
2
121
2
12
1
e
j
a
Nv
pjjj
j
QAvAB
a








23
a
a
 
 







 (48)
For Couette flow, we compute the stress given by



1
2
1
2
xz
PB

 
and for Thermal Creep, we compute the Velocity profile
(49)


01T
qY

  (50)
and the flow rate

I. N. NJOSEH, A. MUSA
32


2
1
2
121
2
a
N
Tjj
QAvA
a







4. Finite Difference Method
zed two dimensional approach in [7]
with the Bhatnagar-Gross-Krook Model (BGK) in [24,
25], the Boltzmann equation to be solved is reduce
1 j

e
j
v
j
B
 

 (51)
Using the lineari
d to


2
0
3
2222
0
3
22
d
exp
2
zz
xyz
hq h
yz
qF
h
Fh
m
hkT


 






 

0
20
3d
2hv F
 
d
z
F

 






















 


 








(52)
where




relativechangein velocity distribution function
,,the molecular volecity
,,the ga s ve lo city
relative change in the particle density
lative change in temperature
the collision f
xyz
xyz
qq q q
re

 


 



requency
 
The perturbation terms  and  depend only on z (flow
direction) and are related to the pressure and temperature
gradient. They are
21
,
zz
Tkv k
dd

 

 
 
where is proportional to pressure gradient and
is
boundary conditions are:
1
k 2 k
proportional to temperature gradient, and both are
small compared to unity. The velocity of the reflecting
molecules from the wall is specified by the Maxwellian
distribution; then the

2
122
13
Sgn, ,
22
y
zz
dzkk kh
dd
 (53)
where
1, if0
Sgn 1, if0
y
y







  

 

A solution in the form

y 

 
01
,, ,
z
y
zy
d






 (54
was sought where
)

2
0125
2
kkh  

 


(55)
Substituting Equation (54) into Equation (52) we have

1
d,
d
yy
y

 
2
12 52
2
kk
hh q
z



zdd









(56)

Multiplying both sides of Equation (56) by

22
exp
zzx
hh










and integrating over fu ll ranges, we have
2
12 2
d1
2
d2
yz
kkk F
y
F
hq h
yh ddd
 

 


(57)
where the function F is defined by



22
1
,exp ,

dd
z
zx
h
Fyhy yxz


 




 

(58)
oundary condi-
tions
Integrating Equation (57) under the b
11Sgn, ,0
2y
dz 





(59)
we have




1112 2
sgn
22
ex
ydd d
 

,
2
22
1
p d
y
y
d
yzy
y
Fy
kk k
hhq h
yt













he gas velocity qz is expressed by
(60)
When t


1
22
sgnexp d
z
yy
h
qyFh









 (61)
Equation (61) now re duces to


1
2
11 12
1
222
11
1
2 22
1
1
d
22
d
z
d
d
d
hq y
1
2 22 2
11
z
d
kk
22
2
J
hythqt 



  




t
dh dh
kJhytt





 



 



(62)
dh



I. N. NJOSEH, A. MUSA 33
n
J
where is defined by
2
0exp d
n
n
x
J
yy
y




 y
Let
1
21
2
2,dh




 
 
11
22
, ,yh yT dht

  
 
1
11
22 12
1
21 2
zp
hq dhkk 






T

 
 
 


(63)
then Equation (62) will be written as two integral e
quations, i.e.,

 
11
2 22
1
2
d1
d
pp d
J
hytt  




 



 (64)
and
 
11
2 22
1
2
11
2 22
1
1d
2
d
d
2
d
d
TT d
J
hytt  





 





where
Jhytt 



  



(65)
the inverse Knudsen number


From
induc Equation (63), we have the velocity of the gas ed by the pressure gradient as,

1
2
1
21
2
z
P
hq



P
(66)
and that induced by temperature gradient as
1
2
1
21
22
z
TT
hq








 (67)
The volume flow rate is then given by


2
2
11
2
d
d
d
Pz P d
Gqyy
p
z








22
22
2d
2
4hd


 



 


d

(68)


2
2
Tz T
d

11
222
20
22
d
d
d
4d 4
d
T
Gpqyy
T
hnkdz 














(69)
Expressing Equations (68) and (69) in non-dimen-
sional for m gives;

1
12
2
1
2
2d
24
x
PP
x
Q







 
 (70)
and

1
12
2
1
2
2d
44
x
TT
Q



x




 
 (71)
ectively.
Next, is to solve numerically the unknown functions
The subscripts P and T imply Poiseuille flow and
Thermal creep resp
and T

r to s
P

in Equations (64) and (65)
ordeolve Equations (64) and (
ference method was utilized after discretization as
respectively.
65), a finite dif- In

11
21
11
0
1d1
2
k
k
n
PhPkn n
k
J


 








 (72)



11
2
12
2
211
22
nn
1
11
0
1
2
11 d
k
k
n
ThTkn n
k
J
J


d 
 









 









 




(73)

where
P
k

is the stepwise function of
P

and Tk

e stepwise function of T th

he consnt value of th e functions Tta
P
k

and Tk

on
each interval is interpreted as the value at the midpoint.
The transcendental function

x
T has a singularity
when
According to the obvious way of differences,
tions (72) and (73) reduce to the matrix
0.x Equa-
1
01 for 0,1,2,,1
n
hk pk
k
A
nn 




 (74)
1
0 for 0,1,2 ,,1
Tk
n
hk h
k
Bgn n 




 (75)
where


22
1
2
222
2
121 d
2
kn
n
kn
n
hk hk
hn
AJ
n


 

 




(76)

hk hk
A
B

(77)
1
2
2
21
121
d
22
h
hn
gJ
n







 


 (78)


Integrating Equations (76) and (78) using
ties of the proper-
n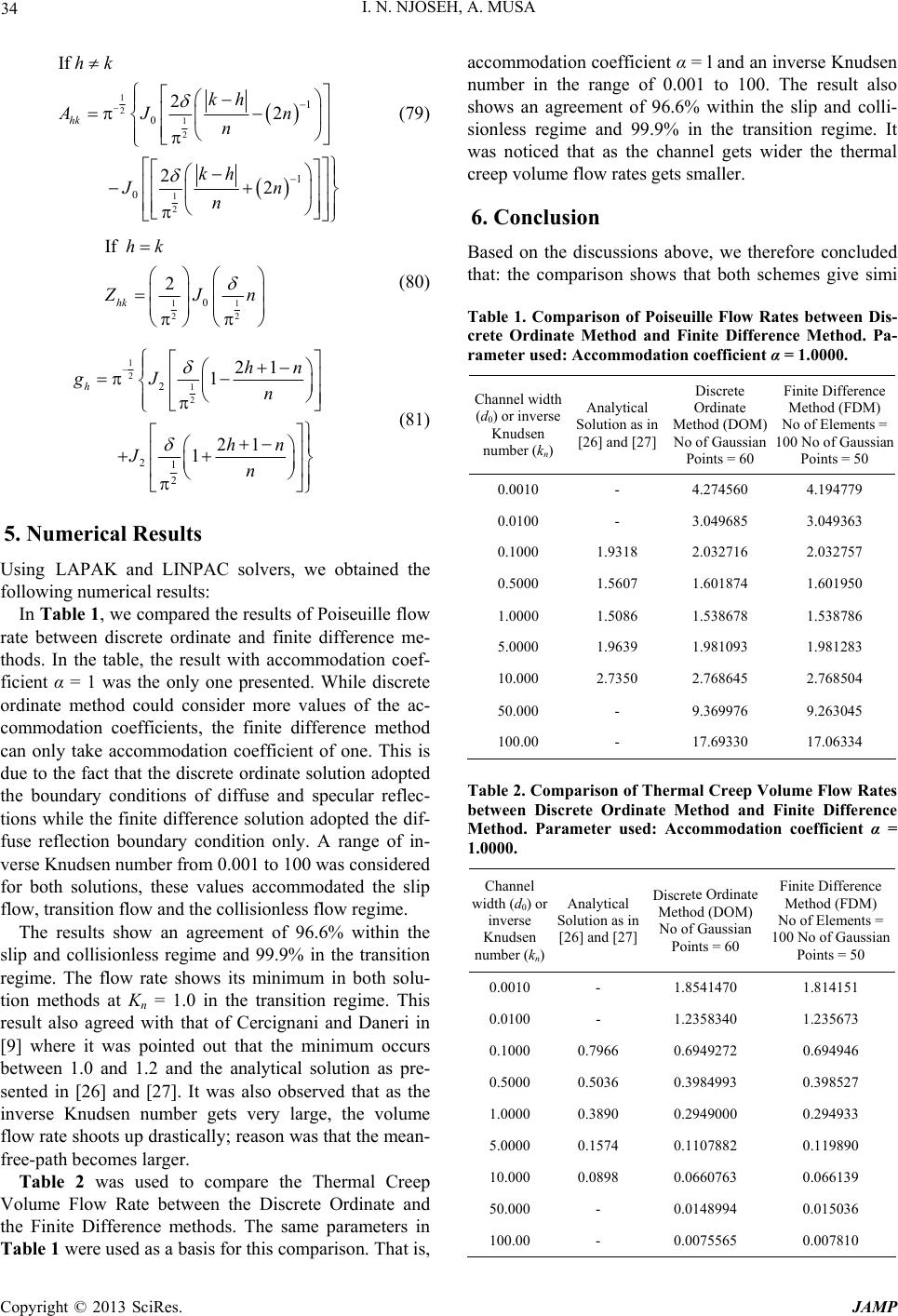
J
we have;

I. N. NJOSEH, A. MUSA
34


1
21
2
1
2
1
0
1
0
If
22
22
hk
hk
kh
AJ n
n
kh
Jn
n








 









 



 




 











(79)



11
22
0hk
If
2
hk
Jn


 
 

  

 
(80)
Z
1
21
2
2
21
2
21
1
21
1
h
hn
gJ n
hn
Jn





  








 


 




 


5. Numerical Results
Using LAPAK and LINPAC solvers, we obtained the
following numerical results:
In Ta ble 1, we compared the results of Poiseuille flow
rate between discrete ordinate and finite difference me
thods. In the table, the result with accommodation coef-
ficient α = 1 was the only one presented. While discrete
ordinate method could consider more values of the ac-
commodation coefficients, the finite diffe
can only take accommodation coefficient of one. This is
due to the fact that the discrete ordinate solution adopted
the boundary conditions of diffuse and specular reflec-
tions while the finite difference solution adopted the dif-
ndition only. A range of in-
T
(81)
-
rence method
fuse reflection boundary co
verse Knudsen number from 0.001 to 100 was considered
for both solutions, these values accommodated the slip
flow, transition flow and the collisionless flow regime.
The results show an agreement of 96.6% within the
slip and collisionless regime and 99.9% in the transition
regime. The flow rate shows its minimum in both solu-
tion methods at Kn = 1.0 in the transition regime. This
result also agreed with that of Cercignani and Daneri in
[9] where it was pointed out that the minimum occurs
between 1.0 and 1.2 and the analytical solution as pre-
sented in [26] and [27]. It was also observed that as the
inverse Knudsen number gets very large, the volume
flow rate shoots up drastically; reason was that the mean-
free-path becomes larger.
Table 2 was used to compare the Thermal Creep
Volume Flow Rate between the Discrete Ordinate and
the Finite Difference methods. The same parameters in
able 1 were used as a basis for this comparison. That is,
accommodation coefficient α = l and an inverse Knudsen
number in the range of 0.001 to 100. The result also
shows an agreement of 96.6% within the slip and colli-
sionless regime and 99.9% in the transition regime. It
was noticed that as the channel gets wider the thermal
creep volume flow rates gets smaller.
6. Conclusion
Based on the discussions above, we therefore concluded
that: the comparison shows that both schemes give simi
Table 1. Comparison of Poiseuille Flow Rates between Dis-
crete Ordinate Method and Finite Difference Method. Pa-
rameter used: Accommodation coefficient α = 1.0000.
Channel width
(d0) or inverse
Knudsen
number (kn)
Analytical
Solution as in
[26] and [27]
Discrete
Ordinate
Method (DOM)
No of Gaussian
Points = 60
Finite Difference
Method (FDM)
No of Elements =
100 No of Gaussian
Points = 50
0.0010 - 4.274560 4.194779
0.0100 - 3.049685 3.049363
1.0000 1.5086 1.538678 1.538786
4
0.1000 1.9318 2.032716 2.032757
0.5000 1.5607 1.601874 1.601950
5.0000 1.9639 1.981093 1.981283
10.000 2.7350 2.768645 2.76850
50.000
100.00
-
-
9.369976
17.69330
9.263045
17.06334
Table 2. Comparison of Thermal Creep Volume Flow Rates
betwiscrete Oinate Md Finince
Merametersed: Acc coα =
1.0000.
Channel
wid
inver
K
num
Ana
Solution as in
[26] a
Discre
Method (
No of
Points = 60
Finite Difference
Me)
No o
100 No of Gaussian
P
een Drdethod ante Differe
thod. Pa uommodationefficient
th (d0) or
se
nudsen
ber (kn)
lytical
nd [27]
te Ordinate
DOM)
Gaussian
thod (FDM
f Elements =
oints = 50
01.8.0010 - 541470 1.814151
0- 1.2
00.7966 0.6
0.5000 0.5036 0.3984993 0.398527
0898 0.0660763 0.066139
50.000 - 0.0148994 0.015036
100.00 - 0.0075565 0.007810
.0100 358340 1.235673
.1000 949272 0.694946
1.0000 0.3890 0.2949000 0.294933
5.0000 0.1574 0.1107882 0.119890
10.000 0.

I. N. NJOSEH, A. MUSA 35
la when computinge
m m
toc n
fch m
comparable to the discrete ordinate solutions even up to
99% accuracy. However, differ
could not take accommodatient of order greater
than onebecause consi
bo cond
FERS
[1] Haualyticaor Three-Dimensional
icanss of chanic,
ary 2012p. 1-5.
aamech.org/PACAM
[2] Schere. F. Prol L. B. B“An
. Aoki, “Numerical Analysis of Rarefied
Gas Flow induced around a Flat Plate with a Single
Heated Side ins,” Proceedings of
27th Internatiofied Gas Dynamics
r results
Knudsen nu
give ex
lows at a r
with the rang
nite difference es of the invers ethod was ab ber; the fi
ellent results
elatively mu
le
on Poiseuille a
shorter cod Thermal creep putation and was
the finiteence method
ion coeffic
undary of the ition. deration of only the diffuse
RE ENCE
E. B.ser, “Anl Solution f
Discrete Ordinates Problems,”
Amer
Proceedings
Applied Me
of 12th Pan-
Trinidad, Congre 2-6
Janu
http://www. , p12/Documents/73.pdf
C. S.r, Jo Fihlo andarichello,
Analytical Approach to the Unified Solution of Kinetic
Equations in Rarefied Gas Dynamics. I. Flow Problems”.
Zeitschrift für Angewandte Mathematik und Physik ZAMP,
Vol. 60, No. 1, 2009, pp. 70-115.
[3] C. S. Scherer, J. F. Prolo Filho and L. B. Ba richello, “An
Analytical Approach to the Unified Solution of Kinetic
Equations in the Rarefied Gas Dynamics. II. Heat Trans-
fer Problems” Zeitschrift für Angewandte Mathematik
und Physik ZAMP, Vol. 60, No. 4, 2009, pp. 651-687.
[4] S. Taguchi and K
Rarefied Gas Dynamic
nal Symposium on Rare,
Pacific Grove, 10-15 July 2010, pp. 790-795.
[5] V. A. Titarev, “Efficient Deterministic Modeling of
Three-Dimensional Rarefied Gas Flow,” Communications
in Computational Physics, Vol. 12, No. 1, 2012, pp. 162-
192.
[6] J. Y. Yang, B. P. Muljadi, Z. H. Li and H. X. Zhang, “A
Direct Solver for Initial Value Problems of Rarefied Gas
Flows of Arbitrary Statistics,” Communications in Com-
putational Physics, Vol. 14, No. 1, 2013, pp. 242-264.
C. Cercignani, “Mathematical M[7] ethods in Kinetic The-
ory,” Plenum Press, New York, 1969.
[8] C. Cercignani “Rarefied Gas Dynamics: From Basic
Concepts to Actual Calculations,” Cambridge University
Press, Cambridge, 2000.
[9] C. Cercignani and A. Daneri, “Flow of Rarefied Gas be-
tween two Parallel Plates,” Journal of Applied Physics,
Vol. 34 No. 12, 1962. pp. 3509-3513
doi:10.1063/1.1729249
[10] C. E. Siewert and L. B. Barichello, “A Discrete-Ordinate
Solution for Poiseuille Flow in Plan Channel,” Zeitschrift
für Angewandte Mathematik und Physik ZAMP, Vol. 50,
No. 6, 1999, pp. 972-981. doi:10.1007/s000000050189
[11] S. K. Stefanov, V. M. Roussinov and C. Cerciginani,
p.
between Non-Par-
, 2001, pp.
“Three-Dimensional Rayleigh-Benard Convection of a
Rarefied Gas: DSMC and Navier-Stokes Calculations,”
AIP Conference Proceedings of 24th International Sym-
posium on Rarefied Gas Dynamics, Vol. 762, 2004, p
529-534.
[12] Y. Sone, “Rarefied Gas Flow Induced
allel Plane Walls with Different Temperature,” In: M.
Becker and M. Fiebig, Eds., Rarefied Gas Dynamics,
DFVLR Press, Porz-Wahn, 1974.
[13] L. B. Barichello, M. Camargo, P. Rodrigues and C. E.
Siewert, “Unified Solutions to Classical Flow Problems
Based on the BGK Model,” Zeitschrift für Angewandte
Mathematik und Physik ZAMP, Vol. 52, No. 3
517-534.
[14] C. S. Scherer and L. B. Barichello, “An Analytical Ap-
proach to the Unified Solution of Kinetic Equations in
Rarefied Gas Dynamics. III. Evaporation and Condensa-
tion Problems,” Zeitschrift für Angewandte Mathematik
und Physik ZAMP, Vol. 61, No. 1, 2012, pp. 95-117.
[15] S. Kosuge, K. Aoki and S. Takata, “Heat Transfer in a
Gas Mixture between Two Parallel Plates: Finite-Differ-
ence Analysis of the Boltzmann Equation,” 22nd Interna-
tional Symposium on Rarefied Gas Dynamics, Sydney,
9-14 July 2000, pp. 289-296.
[16] B. P. Muljadi and J. Y. Yang, “Deterministic Solver for
Rarefied Flow Problems of Gases of Arbitrary Statistics
Based on the Semiclassical Boltzmann-BGK Equation,”
7th International Conference on Computational Fluid
Dynamics, Big Island, 9-13 July 2012, p. 1404.
[17] R. D. M. Garcia and C. E. Siewert, “Particular Solutions
of the Linearized Boltzmann Equation for A Binary Mix-
ture of Rigid Spheres,” Zeitschrift für Angewandte Mathe-
matik und Physik ZAMP, Vol. 59, No. 2, 2008, pp. 281-
292.
[18] C. Henri, “Couette Flow for a Gas with a Discrete Veloc-
ity Distribution” Journal of Fluid Mechanics, Vol. 76, No.
2, 1976, pp. 273-287. doi:10.1017/S0022112076000633
[19] S. L. Lorenzani, A. Gibelli, A. Frezzotti, A. Frangi and C.
Cercignani, “Kinetic Approach to Gas Flows in Micro-
channels,” Nanoscale and Microscale Thermophysical
Engineering, Vol. 11, No. 1-2, 2007, pp. 211-226.
doi:10.1080/15567260701333489
[20] S. K. Loyalka, “Motion of a Sphere in a Gas: Numerical
Solution of the Linearized Boltzmann Equation,” Physics
of Fluids A: Fluid Dynamics, Vol. 4, No. 5, 1992, p. 1049.
doi:10.1063/1.858256
[21] S. Kubota and Y. Yoshizawa, “Couette Flow Problems by
cs, Vol. 152, No. 1, 1999, pp. 251-263.
Thirteen Moment Equations,” Proceedings of Rarefied
Gas Dynamics, DFVLR Press, Porz-Wahn, 1974.
[22] C. E. Siewert, “A Discrete-Ordinate Solution for Heat
Transfer in a Plan Channel,” Journal of Computational
Physi
doi:10.1006/jcph.1999.6244
[23] M. M. R. Williams, “A Review of the Rarefied Gas Dy-
namics Theory Associated with Some Classical Problems
elfor
mall Amplitude Proc-
in Flow and Heat Transfer,” Zeitschrift für Angewandte
Mathematik und Physik ZAMP, Vol. 52, No. 3, 2001, pp.
500-516.
[24] P. L. Bhatnagar, E. P. Gross and M. Krook, “A Mod
Collision Processes in Gases. 1. S
esses in Charge and Neutral One-Component Systems,”

I. N. NJOSEH, A. MUSA
36
arefied Gas Past a Sphere on
Physical Review, Vol. 94, No. 3, 1954, pp. 511-525.
[25] S. Takata, Y. Sone and K. Aoki, “ Numerical Analysis of
a Uniform Flow of a Rthe
Basis of the Boltzmann Equation for Hard-Sphere Mole-
cules,” Physics of Fluids A: Fluid Dynamics, Vol. 5, No.
3, 1993, p. 716. doi:10.1063/1.858655
[26] S. K. Lokalka and K. A. Hickey, “Kinetic Theory of
Thermal Transpiration and Mechanocaloric Effect: Planar
Flow of a Rigid Sphere Gas with Arbitrary Accommoda-
tion at the Surface,” Journal of Vacuum Science & Tech-
nology A, Vol. 9, No. 1, 1991, p. 158.
doi:10.1116/1.577119
[27] D. Valougeorgis, “An Analytic Solution of S-Model Ki-
netic Equations,” Zeitschrift für Angewandte Mathematik
und Physik ZAMP, Vol. 54, No. 1, 2003, pp. 112-124.
doi:10.1007/PL00012627