 American Journal of Operations Research, 2013, 3, 431-438 http://dx.doi.org/10.4236/ajor.2013.35041 Published Online September 2013 (http://www.scirp.org/journal/ajor) On Cost Based Algorithm Selection for Problem Solving Edilson F. Arruda1, Fabrício Ourique2, Anthony Almudevar3, Ricardo C. Silva4 1Federal University of Rio de Janeiro, Alberto Luiz Coimbra Institute-Graduate School and Research in Engineering, Industrial Engineering Program, Rio de Janeiro, RJ, Brazil 2Federal University of Santa Catarina, Campus Araranguá, Araranguá, SC, Brazil 3Department of Biostatistics, University of Rochester Medical Center, Rochester, NY, USA 4Institute of Science and Tehcnology, Federal University of Sao Paulo, So Jos dos Campos, SP, Brazil Email: efarruda@po.coppe.ufrj.br, Almudevar@urmc.rochester.edu, ricardo.coelho@unifesp.br, fabricio.ourique@ufsc.br Received July 9, 2013; revised August 9, 2013; accepted August 16, 2013 Copyright © 2013 Edilson F. Arruda et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT This work proposes a novel framework that enables one to compare distinct iterative procedures with known rates of convergence, in terms of the computational effort to be employed to reach some prescribed vicinity of the optimal solu- tion to a given problem of interest. An algorithm is introduced that decides between two competing algorithms, which algorithm makes the best use of the computational resources for some prescribed error. Several examples are presented that illustrate the trade-offs involved in such a choice and demonstrate that choosing an algorithm over another with a higher rate of convergence can be perfectly justifiable in terms of the overall computational effort. Keywords: Decision Analysis; Computational Effort; Numerical Analysis Optimization 1. Introduction It is not automatic that the runner with the longest stride will win a marathon, although it can be ascertained that she will complete the distance with the fewest number of strides. The same analysis can be applied to numerical algorithms: it is certain that the algorithm with the faster convergence rate will take fewer steps to converge, but it does not necessarily follow that its convergence is the fastest. This happens because convergence rate is often defined in terms of the iteration counter. Hence, an analysis based solely on such a rate is equivalent to pick- ing as the marathon winner the runner with the longest stride. This paper is concerned with proposing new measures for algorithm efficiency based on the computational ef- fort. Such a measure can be more appropriate than the usual convergence rate with respect to the iteration coun- ter. It permits us to assess how efficiently an algorithm employs the computational resources at hand, while searching for a solution to a given problem. That, in turn, allows one to compare algorithms not in terms of how many steps they employ to reach a solution, but based on how much computational effort (time) they apply to reach the solution. Alternatively, one can compare algo- rithms based on their usage of limited available computa- tional effort, i.e. given a fixed amount of computational effort, one would wish to identify which algorithms get closer to the solution while applying at most the pre- scribed effort. In terms of our initial analogy, that would be equivalent to letting an athlete run for a fixed amount of time, declaring the winner as the athlete who covers more ground in that prescribed time. We stress that this paper strives to classify algorithms for a given specific application. Hence, the rationale is to compare competing algorithms that can be used to solve a given problem up to some prescribed error tolerance, from a given starting point, with a view to identifying the alternative that makes the best use of the computational resources available. One could equivalently state that the proposed approach is instance-based, i.e. it focuses on identifying the best algorithm for a specific instance of a given problem. That can be viewed as a complement to the theory of computational complexity [1-3], which at- tempts to establish bounds—typically worst case scena- rio bounds—for the convergence time for general classes of algorithms, typically based on the dimension of the solution domain. Such an approach can be described as algorithm based, since it strives to classify algorithms based on their performance bounds, and individual prob- lem instances may have very little to do with these bounds, see for example [4,8], and [1,27]. It is worth pointing out that, under the proposed approach, the com- putational effort of an algorithm is no longer determined C opyright © 2013 SciRes. AJOR  E. F. ARRUDA ET AL. 432 by its convergence rate. Rather, it is determined by the total number of elementary operations (Floating point operations—FLOP, for example) iteration times per the total number of iterations [5-7]. The idea of identifying iterative procedures that en- hance the efficiency of the search for the solution of a given problem is hardly new. Multigrid methods [8,9], in which a system is first discretized on a grid, following which the grid resolution is systematically refined, are commonly used in the numerical solution of partial dif- ferential equations [8,9]. The objective is to save compu- tational resources in the process of reaching a vicinity of the optimal solution. Heuristic procedures, such as ge- netic algorithms [10], also rely on an efficient use of the computational resources, aiming at getting within a vi- cinity of the optimal solution in reduced time. However, when advocating for a given method over another one, one has often to rely on extensive empirical data or do- main specific mathematics, e.g. [11]. The novel feature in this paper is that it proposes a general framework to compare distinct iterative procedures with known rates of convergence based on the overall computational effort prior to convergence. The main contributions of this paper are twofold. Firstly, considering that the convergence time of an algo- rithm is not based on its iteration count, but rather on the overall computational effort it employs, we propose a framework for algorithm comparison based on how much of the (limited) computational resources each algorithm applies to reach a desired precision. Secondly, given two algorithms starting from the same initial point, we pro- pose a routine that identifies which algorithm requires less computational effort to converge, for any given error tolerance. The proposed routine requires a previous knowledge of the properties of both algorithms: order of convergence and rate of convergence; as well as the ratio of the computational efforts per iteration of the algo- rithms under consideration. This approach addresses directly a trade-off commonly encountered in the design of iterative algorithms. A higher rate or order of convergence is usually achieved at the cost of an increased computation time per iteration. If we specify a desired tolerance , we can expect the number of iterations required to achieve this tolerance to be smaller for a faster converging algorithm for all small enough . If we instead adopt total computation time as a metric, the question becomes whether or not faster convergence with respect to iteration will always over- come the disadvantage of an increased computation time per iteration, promising greater efficiency for all small enough . We show that this is not the case, that is, an algorithm may have both higher rate and higher order of convergence than an alternative and still require greater computation time to achieve tolerance for all 0 , provided the computation effort per iteration exceeds that of the alternative by a large enough factor. This paper is organized as follows. Section 2 addresses the properties of iterative algorithms. Section 3 derives bounds on the number of iterations to reach a desired precision. Section 4 makes use of these bounds to derive a framework for algorithm comparison based on the overall computational effort, and shows that, under some circumstances, algorithms with lower order of conver- gence can always converge faster than higher converging ones, provided the computation time per iteration of the latter algorithm exceeds that of the alternative by a large enough factor. Numerical experiments that illustrate the proposed approach are presented in Section 5. Finally, Section 6 concludes the paper. 2. Numerical Formulation This paper deals with numerical algorithms which take the form a convergent iterative sequence 1,1,2, kk VTV k (1) given a starting element , where 00 is an operator on a normed linear space VvV :TVV , V, and V is the solution domain. The objective is to converge to a fixed point , which provides the solution to a given problem of inter- est. ,VTVV V When assessing how many evaluations of mapping in Equation (1) are necessary until we found ourselves within a prescribed vicinity of the fixed point T V , two important attributes stand out, namely the order of con- vergence and the convergence rate, which are defined below: Definition 1 (Order of Convergence) The algorithm converges with order if d 1 lim , kd kk VV VV (2) for some scalar , e.g. [12]. Definition 2 (Convergence Rate) An algorithm is said to have convergence rate , if satisfies Equation (2). If 1d and 1 , the algorithm is said to be line- arly convergent. Observe that both the order of conver- gence and the convergence rate d are defined with respect to the iteration counter. Remark 1 Note that both order of convergence and convergence rate are indicative of how fast an algorithm converges to the solution in terms of the number of itera- tions. While they may be used to obtain an estimate of how many iterations are needed for the algorithm to converge, they are not sufficient to determine the con- vergence time, for the latter depends also on how much Copyright © 2013 SciRes. AJOR  E. F. ARRUDA ET AL. 433 time each iteration takes up to be completed. Typically, one lets Algorithm (1) run for a finite num- ber of iterations, until a prescribed vicinity of the solu- tion is reached. Let V, 0 be a prescribed error tolerance. We can define the total number of itera- tions needed for convergence as 0 min :. k k kVV (3) Let represent the computational effort of iteration of Algorithm (1). Then, the overall compu- tational effort of Algorithm (1) to attain a desired preci- sion , 0 k gk k is defined as 1 . k n n G g (4) In the present analysis, we assume that the overall computational time to attain precision is proportional to the overall computational effort G . Hence, the following analysis can be solely based on the overall computational effort. We also stress that computational time and computational cost are used interchangeably in this paper. Let , 0,1, kk VVk (5) be a sequence of iteration errors with respect to the solu- tion. Without loss of generality, we employ a normalized error sequence 0 , 0,1, k kk (6) Note that, regardless of the value of 0, 0 V1 . That greatly simplifies our subsequent analysis. Moreover, k can be seen as the ratio of improvement at iteration with respect to the initial solution. For the sake of simplicity, we assume that k 1, 0. kd k VVMk VV That can be accomplished by having an arbitrarily high index relabeled as zero. Hence, we have k 1, 0, d kk Mk which implies 1 10 , d kk Md MM (7) Observe that a sufficient condition for the convergence of Algorithm (1) is . 1M Remark 2 We note that , defined in Equatio n (7), is a renormalization of the convergence rate that takes into account the initial error 0 M , defined in (5). Such a renormalization is intended to simplify the subsequent analysis. Moreover, it enables us to assess the perfor- mance of the algorithm at iteration by evaluating the attained relative improvement with respect to the initial solution k k , as defined in (7). On the Definition of Computational Effort and Its Relation with the Computation Time It must be acknowledged that the actual computation time of an algorithm does depend on the platform run- ning the algorithm. Indeed, complexity theory acknow- ledges this issue and typically addresses it in two distinct ways: Assuming that the analysis is carried on for a single platform, see for example [4]. By defining computational complexity (effort) in terms of elementary operations performed by the al- gorithm, e.g. [13]. In this text we assume that the computational effort is defined in terms of elementary operations. We also as- sume that the elementary operations are defined in such a way that does not depend on the platform. Additionally, the overall computational time (cost) is assumed to be proportional to the overall computational effort, with the platform determining only what the constant of propor- tionality is. The definition of elementary operation is left to the user. Since our analysis is focused on the problem, the function G could be tailor-made for the problem. Or it could, alternatively, be a general function, such as a counter of floating point operations. 3. An Upper Bound on the Iteration Counter Prior to Convergence In this paper, we represent an iterative algorithm of the form in (1) by the pair , d. Hence, , Md describes a convergence rate with respect to the iteration count, with an iterative algorithm of order . d We start this section with an upper bound on the error achieved by an iterative Algorithm , Md, of the form in (1), formalized in Theorem 1 below. Theorem 1 Let , kk1 , be the sequence in (6). Then 1 , 1 ki id k M (8) where is the quantity defined in (7). M Proof. It follows from (7) that Equation (8) holds for 1k . Assume it also holds for . Then, Equation (2) implies kn 1 d nn M 1d 1 1 ni id n MM 1 1 1 ni id n M Copyright © 2013 SciRes. AJOR  E. F. ARRUDA ET AL. 434 11 1 1 ni id n M Hence, Equation (8) also holds for and that completes the proof. 1n Let be a prescribed error and assume . Suppose also that after of iterations we have 2d n 1 1. ni id n M The expression above yields: 1 1 log log ni i d MM M 1log 1 n d d M 11 log n dd M 1 loglog log dd nd M If , Equation (8) implies: 1d n M . log n M Consequently, an appropriate bound k on the number of iterations of Algorithm to reach a tole- rance is ,1 log 1, log log d d kd M M2, (9) which we refer to as the iteration cost. 4. Algorithm Comparison Based on the Overall Computational Effort For the analysis in this section, we assume that the com- putational effort of Algorithm (1) does not change with the iteration counter, i.e. , 1 k ggk . In the analysis that follows, we use k , defined in (9), as an estimate for the quantity defined in (3), which indicates the num- ber of iterations required for a given Algorithm , Md to reach a prescribed normalized error . The objective is to assess the efficiency of the algorithm based on the overall computational effort prior to reach- ing the prescribed error . Such an effort is defined as ,1 log 1, log log d d EA Ggkgd 2, M M (10) where is the per iteration effort (PIE): the computa- tional effort of a single iteration of Algorithm , and is the order of convergence of d , and function is defined in (4). :G Now, suppose we have an alternative algorithm , Md , with PIE . Then, in order to choose the best algorithm for a given problem, one can seek an in- terval for values of that yield .EA EA (11) If both algorithms have convergence orders higher than 1 ,1dd , Equation (11) implies 11 log logloglog dd gg MM 11 log logloglog dd gg MM 1log log. 1log log d d M M Hence, 1log log 1log log d d M M (12) is a threshold that indicates a situation when both algo- rithms are equivalent in terms of computational cost for a prescribed error . Whenever g , algorithm is more economical in terms of computational effort. Otherwise, is the more efficient algorithm to reach the prescribed error. When both ,1AM and are linearly convergent, the threshold ,1AM becomes: log log . log log M M M M (13) Observe that, in such case, the threshold is indepen- dent of the tolerance, but it does depend on the initial solution through , defined in (7). If only M ,1AM is linear, the threshold becomes log . 1log log d M M (14) With the results above, one can define a general proce- dure for selecting between any two competing algorithms , Md and , Md , the one with the fastest convergence with respect to the overall computational effort. Such a procedure is centered on the per iteration effort ratio , (15) with and denoting, respectively the PIE of Al- gorithms and . The procedure is summarized in Algorithm 1 below. Algorithm 1 (Algorithm Selection Procedure) 1) Initialize , Md and , Md , and . 2) Choose an appropriate error 0 . 3) Evaluate , by using Equation (15). Copyright © 2013 SciRes. AJOR  E. F. ARRUDA ET AL. 435 4) Determine by choosing the appropriate ex- pression from Equation (12)-(14). 5) Define . ,I 6) If , select Algorithm and terminate. 7) Select Algorithm and terminate. In the following sections, we present some experi- ments which illustrate the tradeoffs for choosing from two iterative algorithms for solving a given problem. The experiments illustrate the thresholds for per iteration ra- tios and demonstrate the existence of situations for which the choice of a lower convergence algorithm is more effi- cient in terms of computational effort. 4.1. A Perspective on the Proposed Approach We argue that the proposed approach to selecting algo- rithms for problem solving is instance-based in the sense that, given a problem and an initial solution, and fixed a desired tolerance, it guides the choice of which algorithm to apply. It enables us to select a priori which of the two alternatives converges employing less computational effort. So far as we know, no equivalent formulation has been introduced in the literature, which would be directly comparable. A related approach that could be contrasted with the present formulation is complexity theory. However, com- plexity theory is typically centered on the algorithms, often providing worst-case bounds on the convergence time of algorithms for classes of problems. Such bounds can have very little to do with the particular instance of interest [4,8]. Moreover, the responses obtained would be of different nature: complexity theory would identify, for a given problem, which of two algorithms has a better performance in a worst-case scenario. Hence, the re- sponse would be static and a single algorithm would be identified. The proposed approach, on the other hand, could identify different algorithms as the best alternative for different problem instances. In fact, an example is presented in the next section where two different prob- lem instances yield two different responses. Such an an- swer would not be possible within a complexity theory framework. 4.2. Asymptotic Comparison of Algorithms Suppose and are two linearly convergent algo- rithms. Note that the ratio in Equation (13) does not depend on . Thus, even if has the theoretic- cally faster convergence rate, if it also has a PIE sufficiently larger than that applicable to , it will be the inferior choice for all tolerance values . In this section we consider this type of comparison for arbitrary order of convergence . d A common intuiton is that an algorithm with the better rate or order of convergence will eventually outperform an alternative, in the sense that the computation time will be smaller for all small enough . Accordingly, we say that overtakes if for any two PIEs , there exists 0 such that gkgk for all 0 , where k , k are the respective itera- tion costs. If neither algorithm overtakes the other, we say they are computationally equivalent. Interestingly, this relation can be resolved by consider- ing the order of convergence alone. To see this, we first note that the question reduces analytically to an evaluation of the the limit d 0 lim , where kk , since if then over- takes , while if 0 then and are computationally equivalent. We next state the main re- sult. Theorem 2 Let , Md and , Md 1d be two algorithms. Then if , or if and 1dd 1d then and are computationally equivalent. Conversely, if 1d and then 1d overtakes . Proof. As remarked above, we proceed by evaluating 0 lim . The case of follows di- rectly from Equation (13). Then suppose 1 dd ,dd 1 . The derivative of k may be evaluated as d 1 dd nln lk . Using L’Hôpital’s rule we obtain 0 ln lnln lim , ln lnln dd dd which is a positive finite constant, thus the theorem holds for the case ,dd1 . Finally, suppose 1d and 1d . Then we similarly argue that 0 ln ln lim , ln d M so that overtakes . 5. Numerical Examples In order to grasp the meaning of the proposed analysis, a series of numerical experiments are presented in this sec- tion, which make comparisons between an incumbent algorithm , Md with PIE and a challenging algorithm , Md , with PIE . The experiments depict a curve of threshold values, as defined in Equations (12)-(14), for a prescribed range o conver- gence rates , for fixed values of and dM ,d . Such a curve is here called the effort ratio frontier. We recall that the )( represents the per iteration effort ratio for which both and are equivalent in terms of the overall computational effort. For our experiments, we apply an initial point with 01 in (6), which im- plies M M in (7), for each considered algorithm. Figure 1 comprises the effort ratio frontier for linearly Copyright © 2013 SciRes. AJOR 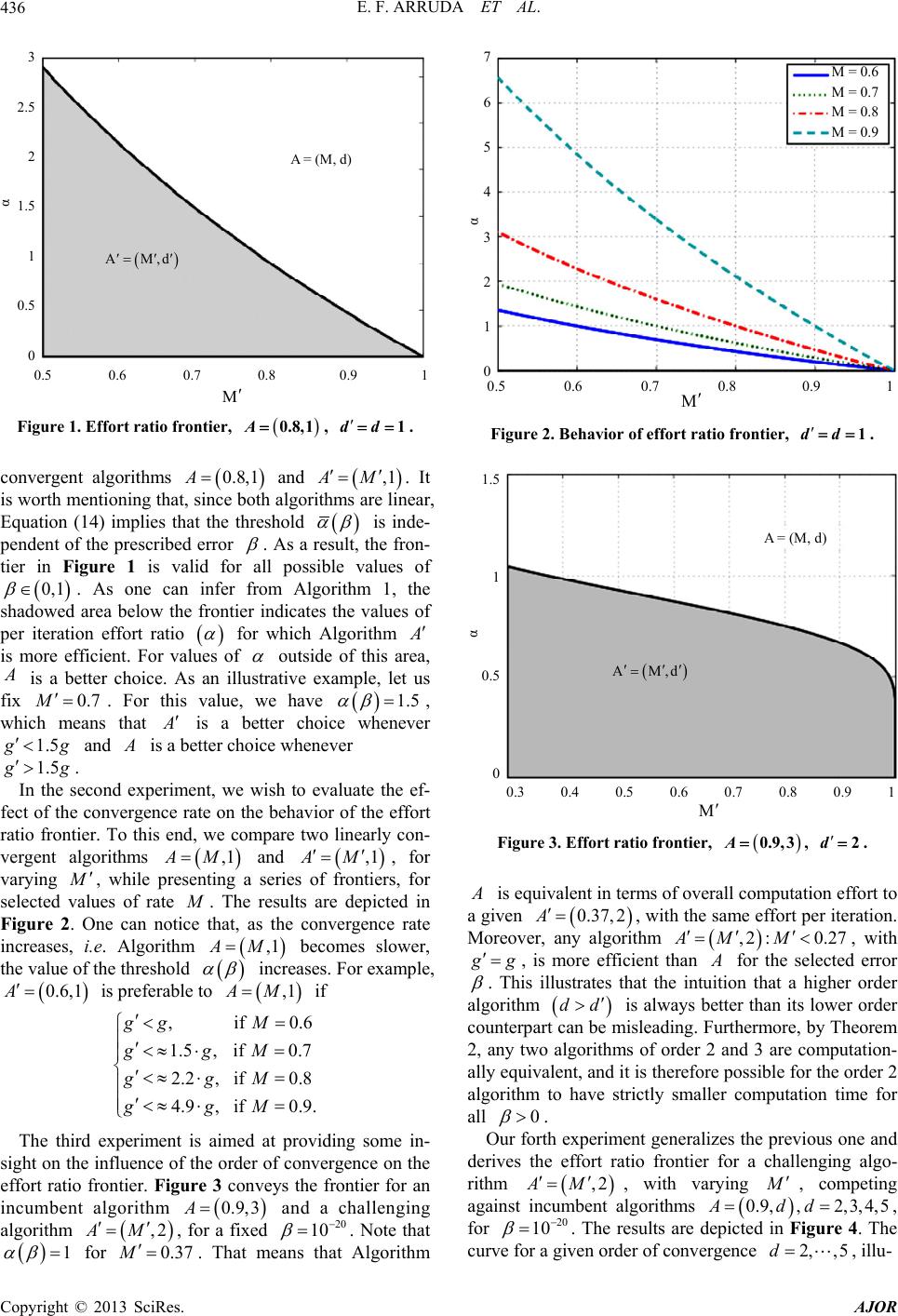 E. F. ARRUDA ET AL. 436 0.5 0.6 0.7 0.8 0.9 1 α 3 2.5 2 1.5 1 0.5 0 A = (M, d) AM,d M Figure 1. Effort ratio frontier, A0.8,1, dd 1. convergent algorithms and . It is worth mentioning that, since both algorithms are linear, Equation (14) implies that the threshold 0.8,1A ,1AM is inde- pendent of the prescribed error . As a result, the fron- tier in Figure 1 is valid for all possible values of . As one can infer from Algorithm 1, the shadowed area below the frontier indicates the values of per iteration effort ratio 0,1 for which Algorithm is more efficient. For values of outside of this area, is a better choice. As an illustrative example, let us fix . For this value, we have , which means that 0.7M 1.5 is a better choice whenever 1.5 g and is a better choice whenever 1.5 g . In the second experiment, we wish to evaluate the ef- fect of the convergence rate on the behavior of the effort ratio frontier. To this end, we compare two linearly con- vergent algorithms and , for varying ,1AM ,1AM , while presenting a series of frontiers, for selected values of rate . The results are depicted in Figure 2. One can notice that, as the convergence rate increases, i.e. Algorithm becomes slower, the value of the threshold ,1 AM increases. For example, is preferable to if 0.6A .6 ,1 ,1AM ,if0 1.5,if0.7 2.2,if0.8 4.9,if0.9. gg M ggM ggM ggM The third experiment is aimed at providing some in- sight on the influence of the order of convergence on the effort ratio frontier. Figure 3 conveys the frontier for an incumbent algorithm and a challenging algorithm , for a fixed . Note that for . That means that Algorithm 0.9,3A 37 ,2AM 0.M 20 10 1 0.5 0.6 0.7 0.8 0.9 1 M α 7 6 5 4 3 2 1 0 M = 0.6 M = 0.7 M = 0.8 M = 0.9 Figure 2. Behavior of effort ratio frontier, dd 1. A = (M, d) α 1.5 1 0.5 0 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 M AM,d Figure 3. Effort ratio frontier, A0.9,3, d 2. is equivalent in terms of overall computation effort to a given 0.37, 2A, with the same effort per iteration. Moreover, any algorithm , with ,2 :0.27AM M g , is more efficient than for the selected error . This illustrates that the intuition that a higher order algorithm dd 0 is always better than its lower order counterpart can be misleading. Furthermore, by Theorem 2, any two algorithms of order 2 and 3 are computation- ally equivalent, and it is therefore possible for the order 2 algorithm to have strictly smaller computation time for all . Our forth experiment generalizes the previous one and derives the effort ratio frontier for a challenging algo- rithm ,2AM , with varying 9, ,Ad , competing against incumbent algorithms , for 0. 2,3,4,5d 20 10 . The results are depicted in Figure 4. The curve for a given order of convergence , illu- 2, ,5d Copyright © 2013 SciRes. AJOR 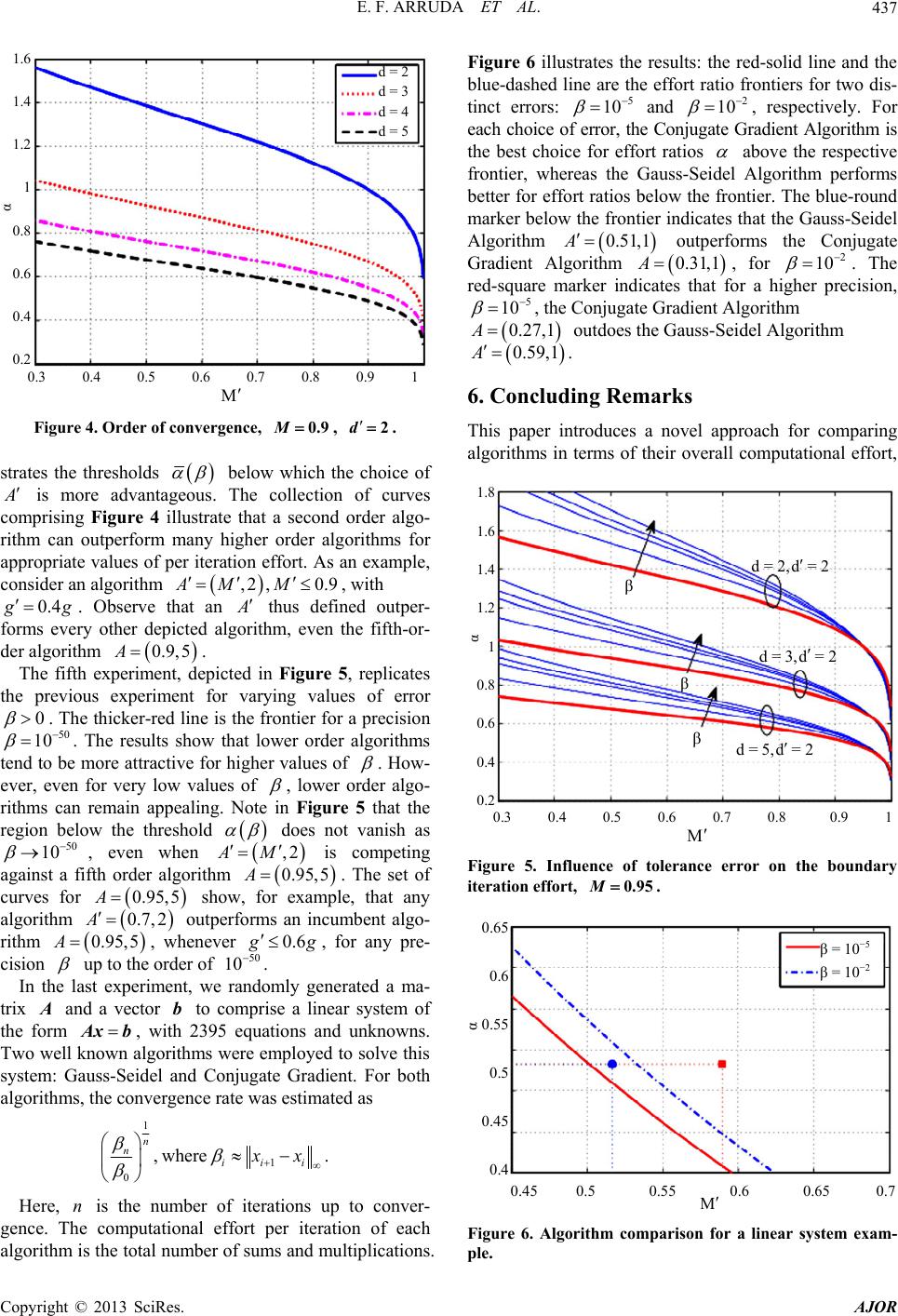 E. F. ARRUDA ET AL. 437 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 M 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 α d = 2 d = 3 d = 4 d = 5 Figure 4. Order of convergence, , M0.9 d 2. strates the thresholds below which the choice of is more advantageous. The collection of curves comprising Figure 4 illustrate that a second order algo- rithm can outperform many higher order algorithms for appropriate values of per iteration effort. As an example, consider an algorithm , with ,2, 0.9AM M 0.4 g . Observe that an thus defined outper- forms every other depicted algorithm, even the fifth-or- der algorithm . 0.9,5A The fifth experiment, depicted in Figure 5, replicates the previous experiment for varying values of error 0 10 . The thicker-red line is the frontier for a precision . The results show that lower order algorithms tend to be more attractive for higher values of 50 . How- ever, even for very low values of , lower order algo- rithms can remain appealing. Note in Figure 5 that the region below the threshold does not vanish as , even when 50 10 AM ,2 0. A is competing against a fifth order algorithm . The set of curves for show, for example, that any algorithm outperforms an incumbent algo- rithm , whenever 95 0.6 ,5 0.95,5A 0.7, 2A 0.95,5A g , for any pre- cision up to the order of . 50 10 In the last experiment, we randomly generated a ma- trix and a vector to comprise a linear system of the form , with 2395 equations and unknowns. Two well known algorithms were employed to solve this system: Gauss-Seidel and Conjugate Gradient. For both algorithms, the convergence rate was estimated as b Ax b 1 1 0 , where . n niii xx Here, is the number of iterations up to conver- gence. The computational effort per iteration of each algorithm is the total number of sums and multiplications. Figure 6 illustrates the results: the red-solid line and the blue-dashed line are the effort ratio frontiers for two dis- tinct errors: n 5 10 and , respectively. For each choice of error, the Conjugate Gradient Algorithm is the best choice for effort ratios 2 10 above the respective frontier, whereas the Gauss-Seidel Algorithm performs better for effort ratios below the frontier. The blue-round marker below the frontier indicates that the Gauss-Seidel Algorithm 10.51,A outperforms the Conjugate Gradient Algorithm 0.31,1A, for 2 10 . The red-square marker indicates that for a higher precision, 5 10 , the Conjugate Gradient Algorithm 0.27,A1 outdoes the Gauss-Seidel Algorithm 0.59A,1 . 6. Concluding Remarks This paper introduces a novel approach for comparing algorithms in terms of their overall computational effort, 0.3 1.8 1.6 1.4 1.2 1 0.8 0.6 0.4 0.2 0. 0. 14 0.5 0.6 0.7 M 8 0.9 α β M β βd= d=2 d= 5, ,d =2 3,d =2 d =2 Figure 5. Influence of tolerance error on the boundary iteration effort, 0.95. α 0.65 0.6 0.55 0.5 0.45 0.4 β = 10 β = 10 0.65 −5 −2 0.45 0.7 0.5 0.5 5 0.6 M Figure 6. Algorithm comparison for a linear system exam- ple. Copyright © 2013 SciRes. AJOR  E. F. ARRUDA ET AL. Copyright © 2013 SciRes. AJOR 438 rather than in terms of the convergence-order, conver- gence-rate pair. A threshold is derived for the ratio be- tween the per-iteration effort of two competing algo- rithms that indicate which of the competing algorithm makes the more efficient use of the computational re- sources available. In addition, an algorithm is proposed for choosing between two competing algorithms under the proposed setting, which makes use of this threshold. The derived results are applied in a few examples that provide an insight on the compromises involved in the proposed approach. The experiments illustrate that a low- er order algorithm can be more advantageous in terms of the overall computational effort to reach a prescribed error than a higher order counterpart. In particular, even as we let the prescribed error approach the order of , using a lower order algorithm can be more advan- tageous under suitable conditions. This demonstrates that an analysis of algorithms based only on their order and rate of convergence can be very misleading. By applying an analysis based on the computational effort, on the other hand, one can identify the algorithm that makes the best use of the (limited) computational resources made available. 50 10 7. Acknowledgments This work was partially supported by the Brazilian Na- tional Research Council-CNPq, under Grant No. 302716/ 2011-4. REFERENCES [1] T. H. Cormen, C. Stein, R. L. Rivest and C. E. Leiserson, “Introduction to Algorithms,” 3rd Edition, MIT Press, Cambridge, 2009. [2] J. Hartmanis and R. E. Stearns, “On the Computational Complexity of Algorithms,” Transactions of the Ameri- can Mathematical Society, Vol. 117, No. 5, 1965, pp. 285-306. doi:10.1090/S0002-9947-1965-0170805-7 [3] J. Belanger, A. Pavan and J. Wang, “Reductions Do Not Preserve Fast Convergence Rates in Average Time,” Al- gorithmica, Vol. 23, No. 4, 1999, pp. 363-378. [4] M. R. Garey and D. S. Johnson, “Computers and Intrac- tability: A Guide to the Theory of NP-Completeness,” Freeman and Company, New York, 1979. [5] D. B. Lloyd Trefethen, “Numerical Linear Algebra,” SIAM, Philadelphia, 1997. doi:10.1137/1.9780898719574 [6] J. W. Demmel, “Applied Numerical Linear Algebra,” SIAM, Philadelphia, 1997. doi:10.1137/1.9781611971446 [7] N. J. Higham, “Accuracy and Stability of Numerical Al- gorithms,” SIAM, Philadelphia, 2002. doi:10.1137/1.9780898718027 [8] W. Hackbusch, “Multi-Grid Methods and Applications,” 2nd Edition, Springer Series in Computational Mathe- matics, Springer-Verlag, Berlin, 2003. [9] Y. Shapira, “Matrix-Based Multigrid: Theory and Appli- cations,” 2nd Edition, Springer Publishing Company, New York, 2008. doi:10.1007/978-0-387-49765-5 [10] M. Mitchell, “Introduction to Genetic Algoritms,” MIT Press, Cambridge, 2008. [11] C. Chow and J. N. Tsitsiklis, “An Optimal One-Way Multigrid Algorithm for Discrete-Time Stochastic Con- trol,” IEEE Transactions on Automatic Control, Vol. 36, No. 8, 1991, pp. 898-914. doi:10.1109/9.133184 [12] J. Nocedal and S. Wright, “Numerical Optimization,” Springer, New York, 1999. doi:10.1007/b98874 [13] M. Hofri, “Analysis of Algorithms: Computational Me- thods and Mathematical Tools,” Oxford University Press, New York, 1995.
|