Applied Mathematics
Vol.3 No.10A(2012), Article ID:24144,6 pages DOI:10.4236/am.2012.330213
Harmony Search and Cellular Automata in Spatial Optimization
Faculty of Engineering, Aristotle University of Thessaloniki, Thessaloniki, Greece
Email: nontas@topo.auth.gr
Received July 11, 2012; revised August 11, 2012; accepted August 18, 2012
Keywords: Harmony Search; Cellular Automata; Spatial Optimization; Resource Allocation
ABSTRACT
The combined optimization problem of resource production and allocation is considered. The spatial character of the problem is emphasized and cellular modeling is introduced. First a new enhanced harmony search algorithm is applied combined with cellular concepts. Then another new approach is presented involving a cellular automaton combined with harmony search. This second approach renders solutions with greater compactness, a desirable characteristic in spatial optimization. The two algorithms are compared and discussed.
1. Introduction
In spatial optimization the combined problem of resource production and allocation is particularly challenging. It presents the difficulty of non-linearity in the objective function, if the production process is to be represented realistically and, also, the undesirable effects of high complexity.
Characteristic problems of this category, involving water extraction and allocation, have been treated by the author and collaborators by means of cellular automata combined with meta-heuristics, such as genetic algorithms [1-3], simulated annealing [4] and stochastic and simulated evolution [5].
The introduction of cellular automata enables the representation of the spatial character of the problem, while the meta-heuristics serve the purpose of guiding the cellular automaton toward optimal arrangements or configurations.
Harmony Search (HS) is a relatively new metaheuristic [6] that has been studied intensively during the recent years and has been applied to a great variety of optimization problems [7-10]. This paper presents a new variant of harmony search designed for the solution of the spatial optimization problem just outlined.
The next (second) section reviews the HS algorithm introducing notation that paves the way toward subsequent developments. The third section gives a description of the problem, demonstrating at the same time the applicability of HS. The fourth section presents a new enhanced version of HS for spatial optimization. This version performs the so called “pitch adjustment” within cellular neighborhoods and it introduces local perturbations on all members of the harmony memory, contrary to the conventional HS version.
The fifth section presents a new alternative cellular— operative approach, combining the concept of cellular automaton with HS. The operative concept has been presented by the author in connection to a genetic algorithm [1,2] and it is again utilized here in connection to HS. Results and discussion are given in the sixth section, where the two approaches are compared and it is noted that the operative method yields more compact configurations.
2. Review of the Harmony Search Algorithm
The Harmony Search (HS) algorithm is presented in this section in a notation suitably adapted to the needs of the problem under study.
Let f be a function to be minimized and
 (1)
(1)
be a possible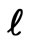 —component argument of f. This may also be considered as a possible solution to the optimization of f.
—component argument of f. This may also be considered as a possible solution to the optimization of f.
A set of I such “solutions”
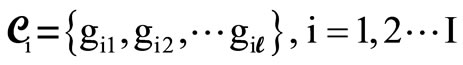 (2)
(2)
will be called the “harmony memory”:
 (3)
(3)
and its members “harmonies”, according to the terminology of the HS (harmony search) algorithm [6], while fi denotes the value of :
:
 (4)
(4)
The harmony memory is obtained initially by randomly taking each gij, j = 1, 2, ···,  in Equation (1) from its respective domain Gj (
in Equation (1) from its respective domain Gj ( ). Subsequently the following steps are executed:
). Subsequently the following steps are executed:
1) A new harmony is generated as follows:
Let hmcr be a preset parameter of the algorithm called the “harmony considering rate”. A typical value of hmcr is 0.9.
For j = 1, 2, ···, 
Let rj be a random number with 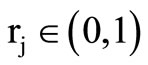
If rj < hmcr, then
Let sj be an integer with 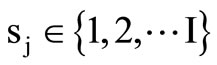
and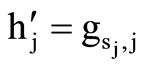 , i.e.
, i.e.  is taken from
is taken from
the existing elements of the HM.
Else  is taken at random from its
is taken at random from its
respective domain Gj.
End If
Next For
2) The new harmony
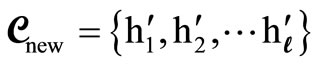 (5)
(5)
thus formed is further modified by the so called “pitch adjustment rate”, which is another preset parameter of HS denoted as par.
For j = 1, 2, ···, 
Let rp be a random number with 
If rp < par, then
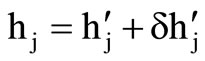
Else, 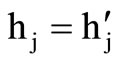 ,
,
End If
Next For
where 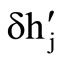 is a perturbation of
is a perturbation of 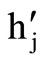 within a preassigned allowable “bandwidth” and always inside the respective domain Gj. The bandwidth is another parameter of HS. Thus the new harmony of Equation 5 becomes
within a preassigned allowable “bandwidth” and always inside the respective domain Gj. The bandwidth is another parameter of HS. Thus the new harmony of Equation 5 becomes
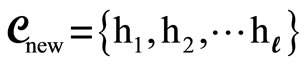 (6)
(6)
and its corresponding value, just as in Equation (4), is denoted as
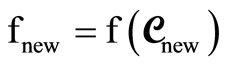 (7)
(7)
3) In order to decide whether the new harmony will enter the harmony memory, let max be the index of the harmony with the largest fi (Equation 4).
If fnew < fmax, then Cnew is introduced into the harmony memory and Cmax is deleted. The HM is now renewed and control is transferred to step 1).
The whole process is repeated for a maximum number of iterations.
The HS algorithm has been tested for a large number of optimization problems [7]. A number of improvements have been suggested, mainly in the domain of continuous optimization. These improvements and/or variants concerned the adaptive, dynamic adjustment of parameters involved, such as the pitch adjustment rate and the bandwidth [8,9], as well as the application of concepts from particle swarm optimization [10].
The present optimization problem does not involve any continuous decision variables. It is a combinatorial optimization problem with a predominantly spatial character and the application of HS will require the formulation of a variant that will take special account of the spatial character. The problem is defined in the next section.
3. Problem Description
A two-dimensional array of cells may be employed in order to represent a rectangular area divided into land blocks. Each one of the cell-blocks receives a commodity from one of a certain number of production points.
Let 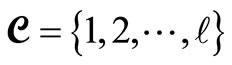 be the set of cells numbered consecutively and let
be the set of cells numbered consecutively and let
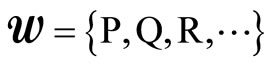 be the set of production points.
be the set of production points.
Let w: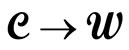 be a function assigning to each one of the cells the production point to which it is connected, i.e.
be a function assigning to each one of the cells the production point to which it is connected, i.e.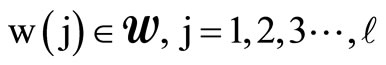 .
.
The function w may be called a configuration or a mosaic, if each one of the cells takes the color of the production point to which it is connected, as shown in Figure 1. If this whole cell arrangement is considered as a cellular automaton [1], then w(j) may be considered to be the state of cell j.
A neighborhood structure and a local transition rule will be needed in order to complete the definition of the cellular automaton. This issue will be addressed to later, in Section 5, in connection to a purely cellular approach. The present section will demonstrate the adaptation of the HS to the present problem, taking into account its spatial character.
A cost s will be assigned to every configuration w. The cost s will be divided into a production cost sP and a cost of transportation sT:
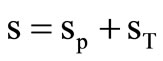 (8)
(8)
The cost s is a functional mapping the set of all configurations to the set of positive reals:

Figure 1. Problem representation.

The functional s is determined as follows:
Let q(j) be a function from the set of cells to the set of positive reals, expressing the quantity of the commodity supplied to cell j:

If v is a production point,  , then
, then
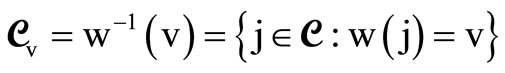
is the inverse image of v under the mapping w. It represents the set of cells connected to production point v.
It follows that the total quantity required at production point v will be equal to
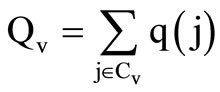 (9)
(9)
The total production sp cost of Equation (8) is a function of the quantities of Equation (9), Q1, Q2, ···, QJ, where J is the number of production points. Thus,
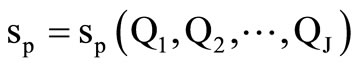 (10)
(10)
The present treatment considers a nonlinear function in Equation (10). One typical example of nonlinear production function is the case of groundwater as the requisite commodity, as presented in [1,2]. In the latter case, the cost of production is the extraction or pumping cost of groundwater and the function of Equation (10) is formed through an appropriate model of groundwater movement. This paper deals with the same nonlinear problem by means of a different method, namely HS.
The transport cost sT of Equation (8) is expressed as:
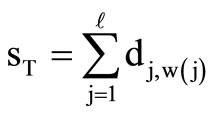 (11)
(11)
where (xj, yj) are the coordinates of the center of cell j, 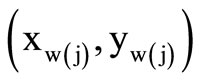 the coordinates of the production point, to which cell i is connected and
the coordinates of the production point, to which cell i is connected and
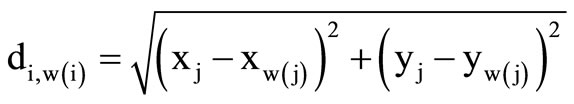
the distance of cell i from the production point.
It is obvious from Equations (9)-(11), that both types of cost, sP and sT, are functionals of w.
The objective of the problem is to find the configuration that minimizes the cost s. The same problem has been solved by Sidiropoulos and Fotakis [1,2] by means of genetic algorithms, and recently by the same authors [5] using simulated and stochastic evolution. A similar spatial nonlinear problem was presented by Sidiropoulos [4] using simulated annealing.
This paper presents another evolutionary procedure for the problem, competitive to the ones mentioned above, based on HS. Two alternative formulations are developed. The first one, described in the next section, is a more straightforward application of HS, while the second one is more indirect and more closely related to the cellular automaton concept.
4. Solution through an Enhanced HS
A small population of configurations or mosaics is initialized. Each one of these may be identified as a harmony, while their set forms the harmony memory, according to the definitions given in Section 2. Thus the set
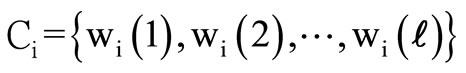 (12)
(12)
where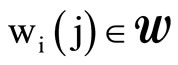 , j = 1, 2, ···,
, j = 1, 2, ···, 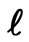 forms the harmony memory with wi(j) I = 1, 2, ···, I denoting I different possible configurations.
forms the harmony memory with wi(j) I = 1, 2, ···, I denoting I different possible configurations.
The generation of new harmonies from the harmony memory may now proceed in the standard fashion as described in the Section 2. However, a specific definition is now needed for the pitch adjustment process. A natural proposal for this purpose is to consider each one of the cells in succession and apply pitch adjustment with a probability equal to par, as outlined above.
In view of the cellular representation of the problem, it is also plausible to confine the pitch adjustment of each cell to its own neighborhood. Indeed, for each cell j a neighborhood N(j) is defined in the sense of von Neumann, as in [2] (Figure 2).
The pitch adjustment process will be defined as follows:
Let rp be a random number with .
.
If rp < par, then pick one of the neighbors of the cell in question at random and exchange attributes between the cell and the chosen neighbor, Specifically.
Let  be the randomly chosen neighbor of the cell j. Then
be the randomly chosen neighbor of the cell j. Then
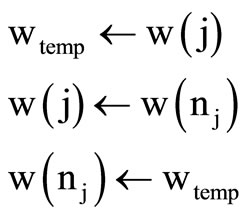
End If

Figure 2. Von Neumann neighborhood.
The above process is applied to all cells j (j = 1, 2, ···, ) in succession and in a synchronous fashion.
) in succession and in a synchronous fashion.
Although the spatial element was introduced into the algorithm through the pitch adjustment process, the overall approach did not yield satisfactory results presenting premature convergence to suboptimal solutions. For that reason the following novel modification to HS is introduced:
Let 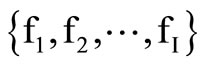 be the set of objective function values corresponding to the members of the harmony memory, sorted in ascending order.
be the set of objective function values corresponding to the members of the harmony memory, sorted in ascending order.
If , where ε is a pre-assigned problemdependent small number, the harmony memory is considered to have stagnated and it is subjected to perturbation. The perturbation is the same as described above for the pitch adjustment and it is applied to all members of the harmony memory, except the first one. The latter remains unaltered as an elite member.
, where ε is a pre-assigned problemdependent small number, the harmony memory is considered to have stagnated and it is subjected to perturbation. The perturbation is the same as described above for the pitch adjustment and it is applied to all members of the harmony memory, except the first one. The latter remains unaltered as an elite member.
The purpose of this device is to escape local minima by giving a mild restart to the harmony memory. A similar idea is applied in the so called micro-genetic algorithms [11], in which the small population undergoes frequent restarts with the exception of the best member.
This additional new characteristic helped in obtaining definitely improved results. The procedure described in this section may be termed an HS enhanced method. A cellular HS method will be presented in the next section.
5. A Cellular-Operative Approach
As in the previous section, let N(j) be the neighborhood of the cell j and let  be one of the neighbors of cell j. Then the set
be one of the neighbors of cell j. Then the set
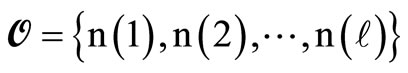 (13)
(13)
can be considered as an operator acting on a configuration
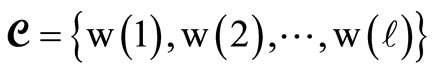 (14)
(14)
like the ones of Equation (12), as follows:
Let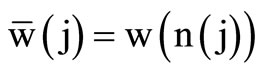 . Then the derived configuration
. Then the derived configuration
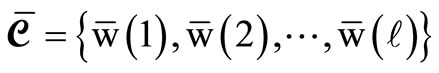
may be thought of as the product of an operation of the set  of Equation (13) on the configuration
of Equation (13) on the configuration  of Equation (14) and thus be denoted as
of Equation (14) and thus be denoted as
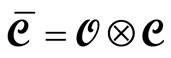 (15)
(15)
This operative concept expressed by Equation (15) has been introduced in conjunction to a genetic algorithm for spatial optimization problems in [2], where more details can be found. Here, it will be embedded into an HS process. In this new approach the harmony memory will consist of a small population of operators of the type of Equation (13), instead of configurations of the type of Equation (12), as in the previous section.
These operators will be applied to a base configuration (mosaic) generating an equal number of new mosaics. The latter are evaluated and the best one is singled out in order to form the next base mosaic. At the same time, the where  is randomly initialized, along with a random “best” configuration Cbest of the type of Equation (14). Then
is randomly initialized, along with a random “best” configuration Cbest of the type of Equation (14). Then
1) Obtain a new operator 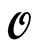 I+1 through generation of a new harmony and subsequent pitch adjustment, according to the HS scheme.
I+1 through generation of a new harmony and subsequent pitch adjustment, according to the HS scheme.
2) Operate with the I + 1 operators on the best mosaic and obtain I + 1 new, derived mosaics: harmony memory of operators is renewed by the generation of a new operator according to the standard HS scheme. These operators act again on the current best mosaic and the process is repeated for a number of iterations. More specificallyA population of I operators of the type of Equation (13)
 (16)
(16)
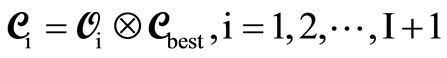
3) Evaluate the I + 1 mosaics: 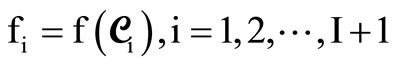
4) Sort the I + 1 fi’s in ascending order and let “new” be the index such that
 and worst be the index such that
and worst be the index such that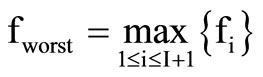 .
.
5) Drop  worst from the harmony memory. Thus I operators remain.
worst from the harmony memory. Thus I operators remain.
6) Single out 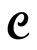 new and let
new and let 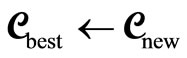
7) With 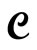 best from step 6 and with the I operators of step (5) go to step (1).
best from step 6 and with the I operators of step (5) go to step (1).
Repeat the above steps for a maximum number of iterations.
Figure 3 shows a schematic representation of the cellular-operative HS.
6. Results—Discussion
A fictive rectangular area is considered with 15 × 15 rectangular blocks with three wells placed in the following positions:

The hydraulic data of the problem are given in [5].
The problem of minimizing the combined water extraction-transport cost was treated by means of the HS enhanced algorithm of Section 4 and by the cellular-operative HS of Section 5 presented in this paper.
Figure 4 shows the initial randomly generated mosaic, Figure 5 the resulting mosaic given by HS enhance
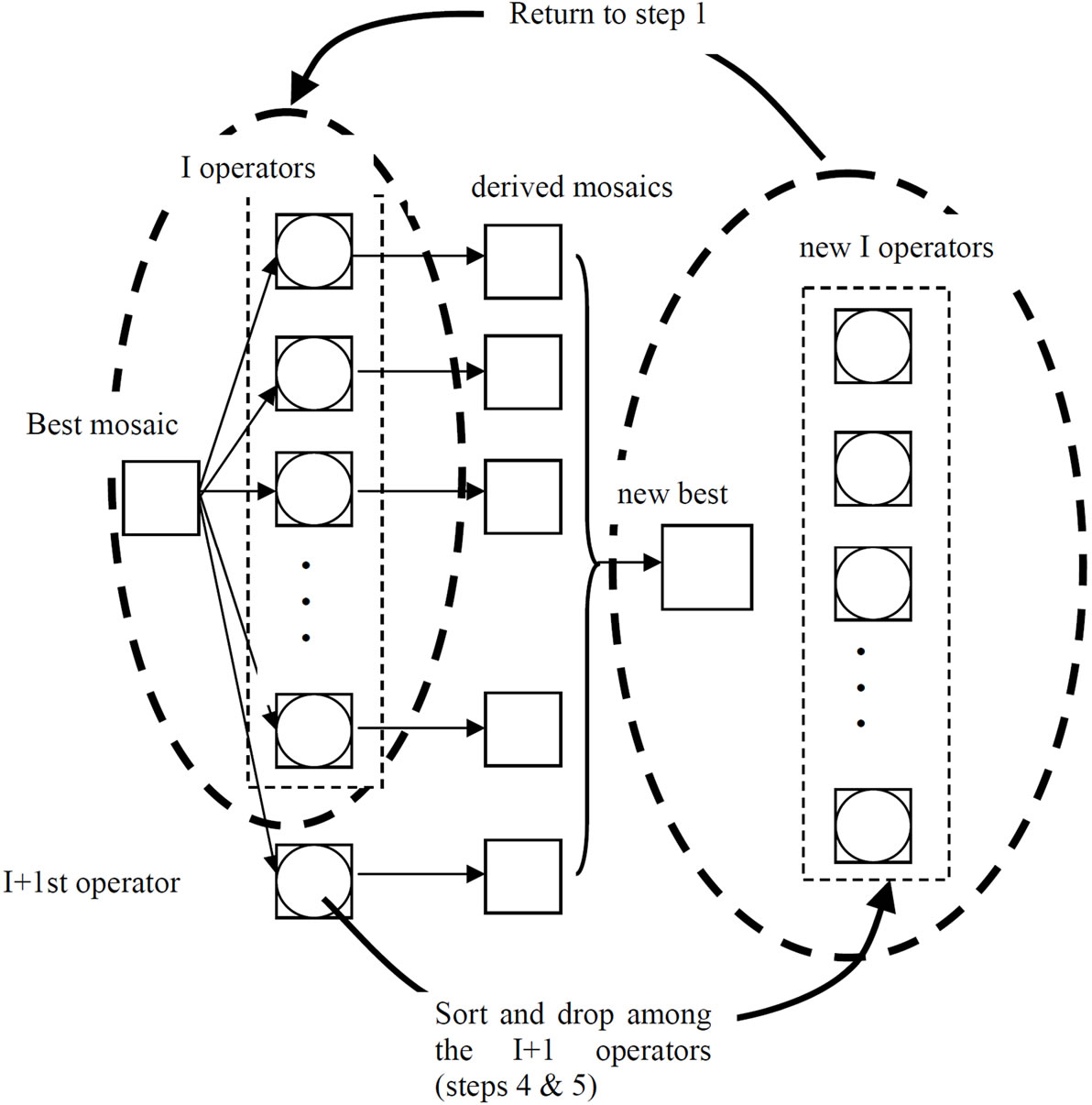
Figure 3. Cellular-operative algorithm.

Figure 4. Initial configuration.

Figure 5. HS enhanced method.
method and Figure 6 the corresponding result of the cellular approach.

Figure 6. Cellular-operative approach.
The cellular-operative approach of Section 5 yields within a relatively small number of iterations satisfactory results that are also compact. Compactness of configurations is important in spatial optimization, as documented in [12]. The HS enhanced method, after a large number of iterations, gave results with slightly better objective function values, but inferior in terms of compactness.
It is important to stress that the operative approach is fully consistent with the notion of the cellular automaton, in the sense that the cellular automaton is identified with the “best” mosaic and the HS scheme of the operators selects each time the most suitable operator that will carry the current best mosaic to the next. It also needs to be noted that the operators may be considered as the carriers of the local rules that transform mosaics.
Finally, since the harmony search method does not seem to have been applied to problems of spatial optimization, more research is needed in terms of extensive comparisons to other methods and for many more realworld problems of this category.
REFERENCES
- E. Sidiropoulos and D. Fotakis, “Cell-Based Genetic Algorithm and Simulated Annealing for Spatial Groundwater Allocation,” WSEAS Transactions on Environment and Development, Vol. 4, No. 5, 2009, pp. 1-10.
- E. Sidiropoulos and D. Fotakis, “Spatial Optimization and Resource Allocation in a Cellular Automata Framework,” In: A. Salcido, Ed., Cellular Automata: Simplicity behind Complexity, INTECH Scientific Publishing, Rijeka, 2011.
- E. Sidiropoulos and D. Fotakis, “A New Multi-Objective Self-Organizing Optimization Algorithm (MOSOA) for Spatial Optimization Problems,” Applied Mathematics and Computation, Vol. 218, No. 9, 2012, pp. 5168-5180. doi:10.1016/j.amc.2011.11.003
- E. Sidiropoulos, “Spatial Resource Allocation via Simulated Annealing on a Cellular Automaton Background,” 2011 World Congress on Engineering and Technology, Shanghai, 28 October-2 November 2011, Vol. 2, p. 137.
- E. Sidiropoulos and D. Fotakis, “Spatial Groundwater Allocation via Stochastic and Simulated Evolution on a Cellular Background,” 11th International Conference on Protection and Restoration of the Environment, Thessaloniki, 3-6 July 2012, pp. 34-43.
- Z. W. Geem, J. H. Kim and G. V. Loganathan, “A New Heuristic Optimization Algorithm: Harmony Search,” Simulation, Vol. 76, No. 2, 2001, pp. 60-68. doi:10.1177/003754970107600201
- K. S. Lee and Z. W. Geem, “A New Meta-Heuristic Algorithm for Continuous Engineering Optimization: Harmony Search Theory and Practice,” Computer Methods in Applied Mechanics and Engineering, Vol. 194, No. 36-38, 2005, pp. 3902-3933. doi:10.1016/j.cma.2004.09.007
- M. Mahdavi, M. Fesanghary and E. Damangir, “An Improved Harmony Search Algorithm for Solving Optimization Problems,” Applied Mathematics and Computation, Vol. 188, No. 2, 2007, pp. 1567-1579. doi:10.1016/j.amc.2006.11.033
- Q.-K. Pan, P. N. Suganthan, M. F. Tasgetiren and J. J. Liang, “A Self-Adaptive Global Best Harmony Search Algorithm for Continuous Optimization Problems,” Applied Mathematics and Computation, Vol. 216, No. 3, 2010, pp. 830-848. doi:10.1016/j.amc.2010.01.088
- M. G. H. Omran and M. Mahdavi, “Global-Best Harmony Search,” Mathematics and Computation, Vol. 198, No. 2, 2008, pp. 643-656.
- K. Krishnakumar, “Micro-Genetic Algorithms for Stationary and Non-Stationary Function Optimization,” SPIE Intelligent Control and Adaptive Systems, Philadelphia, Vol. 1196, 1989, pp. 289-296.
- P. Vanegas, D. Cattrysse and J. Van Orshoven, “Compactness in Spatial Decision Support: A Literature Review,” Lecture Notes in Computer Science, Springer 2010, pp. 414-429.

