Computational Molecular Bioscience, 2013, 3, 66-79
http://dx.doi.org/10.4236/cmb.2013.33009 Published Online September 2013 (http://www.scirp.org/journal/cmb)
Evaluation of Quantum Chemical Meth ods and Basis Sets
Applied in the Molecular Modeling of Artemisinin
Cleydson B. R. dos Santos1,2,3*, Cleison C. Lobato1, Josinete B. Vieira1,
Davi S. B. Brasil1,4, Alaan U. Brito1, Williams J. C. Macêdo1,3,
José Carlos T. Carvalho1,2, José C. Pinheiro3
1Laboratory of Modelling and Computational Chemistry, Federal University of Amapá, Macapá, Brazil
2Postgraduate Program in Biotechnology and Biodiversity-Network BIONORTE, Campus Universitário Marcos Zero,
Macapá, Brazil
3Laboratory of Theoretical and Computational Chemistry, Institute of Exact and Natural Sciences,
Federal University of Pará, Belém, Brazil
4Institute of Technology, Federal University of Pará, Belém, Brazil
Received July 28, 2013; revised August 29, 2013; accepted September 7, 2013
Copyright © 2013 Cleydson B. R. dos Santos et al. This is an open access article distributed under the Creative Commons Attribu-
tion License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly
cited.
ABSTRACT
In this paper, we evaluate semiempirical methods (AM1, PM3, and ZINDO), HF and DFT (B3LYP) in different basis
sets to determine which method best describes the sign and magnitude of the geometrical parameters of artemisinin in
the region of the endoperoxide ring compared to crystallographic data. We also classify these methods using statistical
analysis. The results of PCA were based on three main components, explaining 98.0539% of the total variance, for the
geometrical parameters C3O13, O1O2C3, O13C12C12a, and O2C3O13C12. The DFT method (B3LYP) corresponded
well with the experimental data in the hierarchical cluster analysis (HCA). The experimental and theoretical angles were
analyzed by simple linear regression, and statistical parameters (correlation coefficients, significance, and predictability)
were evaluated to determine the accuracy of the calculations. The statistical analysis exhibited a good correlation and
high predictive power for the DFT (B3LYP) method in the 6-31G** basis set.
Keywords: Artemisinin; Molecular Modeling; Quantum Chemical Methods; Statistical Analysis; B3LYP/6-31G**
1. Introduction
Artemisinin (or Qinghaosu, QHS, Figure 1) represents
the most relevant advance in the treatment of malarial
disease for the last 20 years [1]. Artemisinin is a ses-
quiterpene lactone with an endoperoxide group, which
has been used in traditional Chinese medicine for many
centuries as a natural product for fever and malarial
treatment. This drug was isolated by Chinese chemists in
the early 1970s from the ancient Artemisia annua L.
Nowadays, artemisinin and derivatives are widely used
around the world because of their potent antimalarial
activity, fast action, and low toxicity. As a result, arte-
misinin and its derivatives have become recognized as a
new generation of antimalarial drugs [2].
Many studies on the rational design of new antimalar-
ial drugs have been performed using molecular modeling.
However, complex molecular systems containing exter-
nal and internal transition atoms, proteins, polymers, or
compounds with a higher molecular weight overestimate
the ability of these methods and basis sets to obtain mo-
lecular properties, which can lead to inaccurate results
when compared with experimental data. Therefore, an
evaluation of these methods and basis sets will be
strongly dependent on the system under consideration
[3].
Costa et al. studied the interaction between heme and
artemisinin using the PM3 method, which exhibited a
potential energy barrier for the relative rotation of the
artemisinin-heme complex being studied both in vacuo
and partially solvated. The authors observed that the in-
clusion of water molecules did not significantly affect the
stability of the heme-artemisinin complex [4].
Leite et al. conducted studies of 18 natural compounds
from Brazilian flora, which possess a peroxide group and
*Corresponding author.
C
opyright © 2013 SciRes. CMB

C. B. R. D. SANTOS ET AL. 67
Figure 1. Artemisinin (structure) and region essential for
the expression of biological activity (pharmacophore).
are assumed to act in heme protein, leading to a reduction
in peroxide binding and the production of radicals that
can kill the etiological agents of malaria (Plasmodium
falciparum strains). These findings motivated the re-
searchers to study the interactions among 18 natural per-
oxides. They initially performed a conformational search
using the MM3 method for each molecule, and the most
stable conformers were optimized by the PM3 (tm) me-
thod. The interactions between the peroxide-heme groups
were then evaluated, and the results indicated that four of
the compounds may exhibit desirable antimalarial activ-
ity [5].
Recent studies on 51 peroxides were conducted to
identify correlations between in silico parameters and
experimental data for identifying new antimalarial agents
from natural sources. The interaction of the heme group
was studied by molecular docking refinement followed
by conformational analysis using semiempirical paramet-
ric method 6 (PM6). The results indicated that two of
these compounds are promising antimalarials [6].
Artemisinin derivatives with antimalarial activity
against Plasmodium fa lciparum, which is resistant to me-
floquine, were studied using quantum chemical methods
(HF/6-31G*) and the partial least-squares (PLS) method.
Three main components explained 89.55% of the total
variance, with Q2 = 0.83 and R2 = 0.92. From a set of 10
proposed artemisinin derivatives (artemisinin derivatives
with unknown antimalarial activity against Plasmodium
falciparum), a novel compound was produced with supe-
rior antimalarial activity compared to the compounds
previously described in the literature [7].
Recently, Cristino et al. [8] used the B3LYP/6-31G*
method to model artemisinin and 19,10-substituted de-
oxoartemisinin derivatives, with different degrees of ac-
tivity against the Plasmodium falciparum D-6 strains of
Sierra Leone. Chemometric methods (PCA, HCA, KNN,
SIMCA, and SDA) were employed to reduce the dimen-
sionality and to determine which subset of descriptors is
responsible for the classification between more and less
active agents.
Figueiredo et al. [9] conducted studies using the
B3LYP/6-31G* method for antimalarial compounds
against Plasmodium falciparum K1. These studies led to
multivariate models for artemisinin derivatives and series
of dispiro-1,2,4-trioxolanes. The application of these
models has enabled the prediction of activity for com-
pounds designed without known biological activity.
Moreover, a new series of antimalarial compounds is
currently in the study phase.
Araújo et al. [10] used density functional theory (6-
31G*) to verify the performance of a basis set in repro-
ducing experimental data, particularly geometrical pa-
rameters, and to calculate the interaction energies, elec-
tronic states, and geometrical arrangements for com-
plexes composed of a heme group and artemisinin. The
results demonstrated that the interaction between arte-
misinin and the heme group occurs at long distances
through a complex in which the iron atom of the heme
group retains its electronic characteristics, with the quin-
tet state being the most stable. These results suggest that
the interaction between artemisinin and heme is thermo-
dynamically favorable.
In this paper, we propose to identify the best method
and basis set for molecular modeling of the pharmaco-
phoric group of artemisinin and its derivatives. There is
currently a diversity of methods and basis sets that can be
applied to reproduce experimental data and to elucidate
the biological significance of this compound. An identi-
fication of the best theoretical method for data acquisi-
tion is critical in achieving credible in silico results with
respect to biological action. Artemisinin was modeled
using five methods and seven basis sets (6-31G, 6-31G*,
6-31G**, 3-21G, 3-21G*, 3-21G**, and 6-311G) based
on the properties of the endoperoxide group present in
artemisinin, which is responsible for the biological activ-
ity, and the results were evaluated via principal compo-
nent analysis (PCA), hierarchical cluster analysis (HCA),
and statistical analysis using simple linear regression.
2. Experimental
2.1. Molecular Modeling of Artemisinin
The artemisinin compound was constructed as follows:
initially, the structure of artemisinin was established with
the Gauss View 3.0 program [11] and optimized using
different methods and basis sets: semiempirical (AM1,
PM3, and ZINDO), Hartree-Fock (HF/6-31G, HF/6-31G*,
HF/6-31G**, HF/3-21G, HF/3-21G*, HF/3-21G**, and
HF/6-311G), and DFT (B3LYP/6-31G, B3LYP/6-31G*,
B3LYP/6-31G**, and B3LYP/3-21G) implemented with
the Gaussian 03 program [12]. These calculations were
performed to determine which methods and basis sets
provide the best compromise between computational
time and accuracy compared to the experimental data
[13]. The experimental structure of artemisinin was re-

C. B. R. D. SANTOS ET AL.
68
moved from the Database Cambridge Structural CSD
with REFCODES: QNGHSU10, crystallographic R fac-
tor 3.6 [14]. The numbering of atoms adopted in this
study is shown in Figure 1 (artemisinin).
When measurements are made on a number of objects,
the results are typically organized in a data matrix. The
measures in this study (geometrical parameters) were
organized in rows, and the objects (quantum chemical
methods and basis sets) were organized in columns. Sta-
tistical analysis was conducted with the Piroutte 3.10 and
Statistica 6.2 programs [15,16].
The statistical analysis of the geometrical parameters
was based on the studies of Silva et al., in which density
functional theory (DFT) calculations (B3PW91/DGD-
ZVP) were employed to determine 13C and 1H nuclear
magnetic resonance (NMR) chemical shifts for the two
dihydrochalcones: 3,4,5-tetramethoxydihydrochalcone and
2,3,4,4-trimethoxydihydrochalcone. The theoretical and
experimental NMR data were analyzed by simple linear
regression, and the most relevant parameters were se-
lected. In addition, other statistical parameters (correla-
tion coefficients, significance, and predictability) were
employed to verify the accuracy of the calculations. The
statistical analysis indicated a good correlation between
the NMR experiment results and the theoretical data,
with high predictive power [17].
2.2. Principal Component Analysis (PCA)
PCA was performed with autoscaled processing for a
maximum of three factors (3PCS), using the “leave-one-
out validation method and cross-validation” procedure.
The data matrix was constructed from the combinations
of methods and basis sets, resulting in a 15 × 18 matrix.
Each column was related to five methods and seven basis
sets, and one column was related to the experimental
geometrical parameters [13]. Each row represents 18
geometrical parameters of the 1,2,13-trioxane ring (bond
lengths, bond angles, and torsion angles). The final PCA
results led to the selection of a small number of geomet-
rical parameters that were most strongly related to the
dependent variable, which was the standard deviation of
the methods and basis sets in this case.
2.3. Hierarchical Cluster Analysis (HCA)
Similar to the PCA results, the HCA results are qualita-
tive and are arranged in the form of a dendrogram to dis-
play the methods studied and the variables (geometrical
parameters of artemisinin) in a two-dimensional space.
The results illustrate the combinations or divisions made
in each successive stage of analysis. The samples (meth-
ods and basis sets) are represented by the bottom branch
of the dendrogram. The similarity between agglomerates
is given by the length of each branch such that methods
and basis sets with low levels of similarity have long
branches and methods and basis sets with high similarity
have short branches [18]. In HCA, the distance between
these variables is calculated and transformed into a simi-
larity matrix S. A hierarchical cluster analysis aims to
display data in a manner that accentuates the natural
groupings and patterns. Statistical analysis was required
in this study to group similar methods and basis sets in
their respective categories. HCA is a statistical method
that was developed for this purpose.
2.4. Statistical Analysis
Statistical analysis via simple linear regression can cor-
relate data from more relevant parameters to estimate and
predict values using a model built with a full dataset and
actual values of yi (r), the explained variance (, i.e.,
adjusted R2), Fisher ratio values (F), and the standard
error of estimation (SEE). The equations were also tested
for their predictive power using a cross-validation pro-
cedure. Cross-validation is a practical and reliable me-
thod for verifying the predictive power. In the so-called
“leave-one-out” approach, a number of models are de-
veloped with one sample omitted in each step. After de-
veloping each model, the omitted data are predicted and
the differences between the actual and predicted y values
are calculated. The sum of squares of these differences is
computed, and finally, the performance of the model (its
predictive ability) can be given by the prediction residual
error sum of squares (PRESS) and standard deviation of
the cross-validation (SPRESS), as shown in Equations (1)
and (2) [19]:
2
A
R

2
1
PRESS
n
i
i

y
y


 (1)
PRESS
PRESS
1
Snk  (2)
where yi is the experimental value, y is the predicted val-
ue, n is the number of samples used to build the model,
and k is the number of geometrical parameters. The pre-
dictive ability of the model can also be quantified in
terms of the cross-validated correlation coefficient (Q2),
which is defined as [19]

2
mean
2
1
PRESS
1.0; where,
n
i
i
Qy
yy

 

y
(3)
In addition, other statistical parameters are available to
verify the accuracy of the calculation, but none of these
parameters are fully satisfactory if taken alone. For each
system, we present parameters a and b from linear re-
gression

calcd = a + b

expt1; the mean absolute error
(MAE) defined as exp 1ncalcdt , and the
corrected mean absolute error, CMAE [20], defined as
MAE n   

C. B. R. D. SANTOS ET AL.
69
exp 1
CMAE ncorrtn   , where

corrcalcd ab
 
to correct for systematic errors.
tween B3LYP/6-31G and B3LYP/6-31G*, ±0.260 be-
tween B3LYP/6-31G and B3LYP/6-31G**, and ±0.124
between B3LYP/6-31G* and B3LYP/6-31G**.
3. Results and Discussion 3.2. PCA and HCA
3.1. Determination of the Theoretical
Geometrical Parameters of Artemisinin The advantage of the PCA and HCA methods in this
study is that all structural parameters are considered si-
multaneously and all of their correlations are considered.
We determined the geometrical parameters for the 1,2,
13-trioxane ring of artemisinin (bond length, bond angle,
and torsion angle of atoms in this ring), as shown in Ta-
ble 1. Table 1 illustrates that for the DFT method, all
four basis sets (B3LYP/6-31G, B3LYP/6-31G*, B3LYP/
6-31G**, and B3LYP/3-21G) can accurately describe all
of the structural parameters with respect to their magni-
tude and sign when compared with the experimental val-
ues. Meanwhile, the semiempirical (AM1, PM3, and
ZINDO) and Hartree-Fock (HF/6-31G, HF/6-31G*, HF/
6-31G**, HF/3-21G, HF/3-21G*, HF/3-21G**, and
HF/6-311G) methods exhibited standard deviations of
4.776, 8.388, and 4.372 and 1.663, 2.484, 1.762, 1.722,
1.714, 1.797, and 1.658, respectively. By comparing
these methods with the DFT method, we find that all of
the basis sets (B3LYP/6-31G, B3LYP/6-31G*, and
B3LYP/6-31G**) have low standard deviations in rela-
tion to the semiempirical and Hartree-Fock methods at
0.843 (B3LYP/6-31G), 1.227 (B3LYP/6-31G*), and
1.103 (B3LYP/6-31G**). The variation was ±0.384 be-
Figure 2 presents the PC1-PC2 scores for the five
methods and seven basis sets and one score related to the
experimental geometrical parameters of the 1,2,13-tri-
oxane ring. The methods are divided into two groups
according to PC2, where the semiempirical and Har-
tree-Fock methods are located at the bottom and the ex-
perimental data and the DFT/B3LYP method and basis
sets (B3LYP/6-31G, B3LYP/6-31G*, B3LYP/6-31G**,
and B3LYP/3-21G) are located at the top.
Figure 3 presents the PC1-PC2 loading for the four
most important geometrical parameters related to the
trioxane ring, namely, C3O13, O1O2C3, O13C12C12a,
and O2C3O13C12. These geometrical parameters are
responsible for the separation of the methods and basis
sets into three groups, namely, semiempirical, Hartree-
Fock, and DFT methods, as shown in Figure 2. The four
geometrical parameters related to the trioxane ring are
identified by atoms C3O13, which provides the interpla-
nar distance between these two atoms (bond length),
Figure 2. Plot of PC1-PC2 scores for the five methods and seven basis sets and the experimental geometrical parameters of
the 1,2,13-trioxane ring.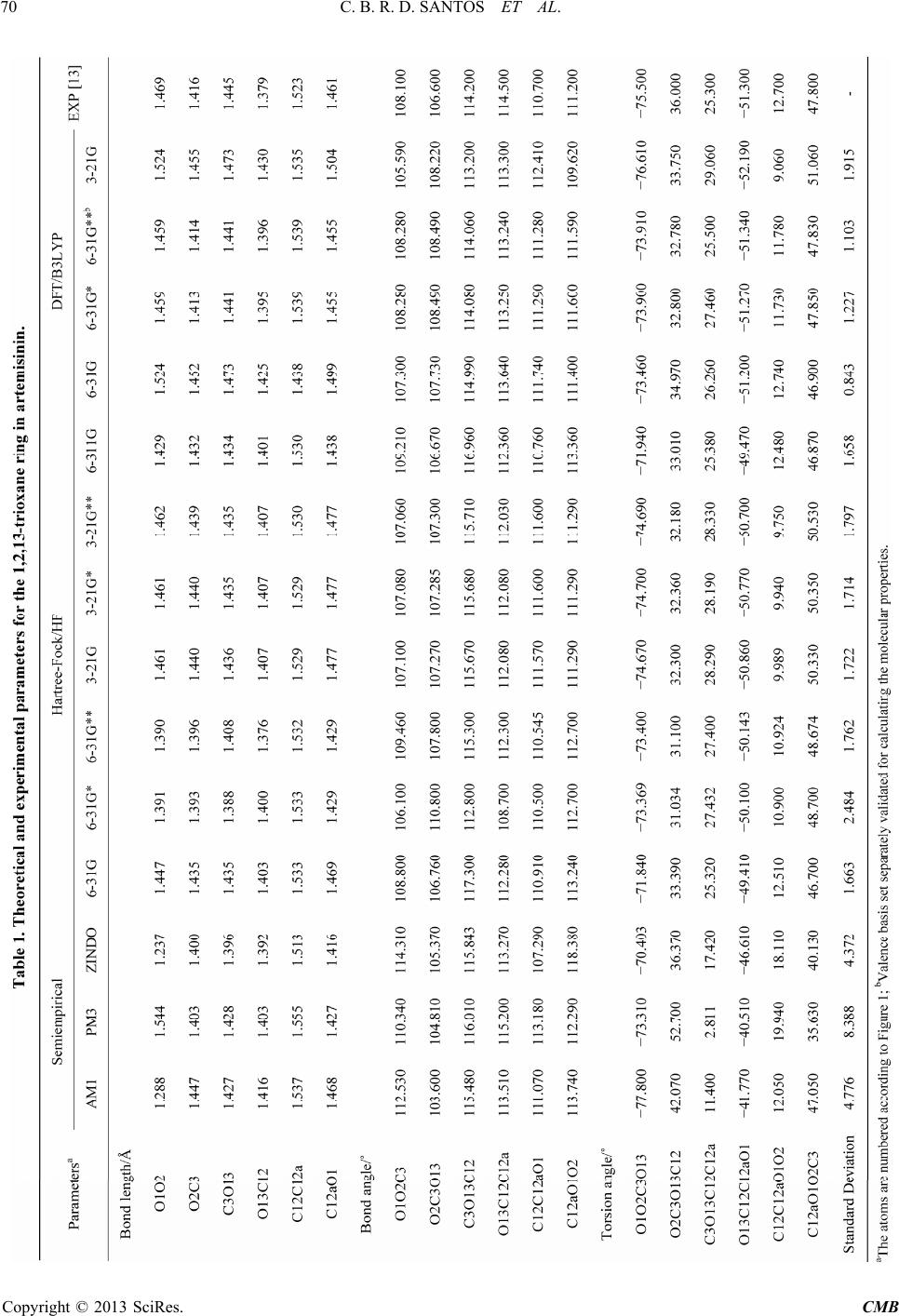

C. B. R. D. SANTOS ET AL.
70

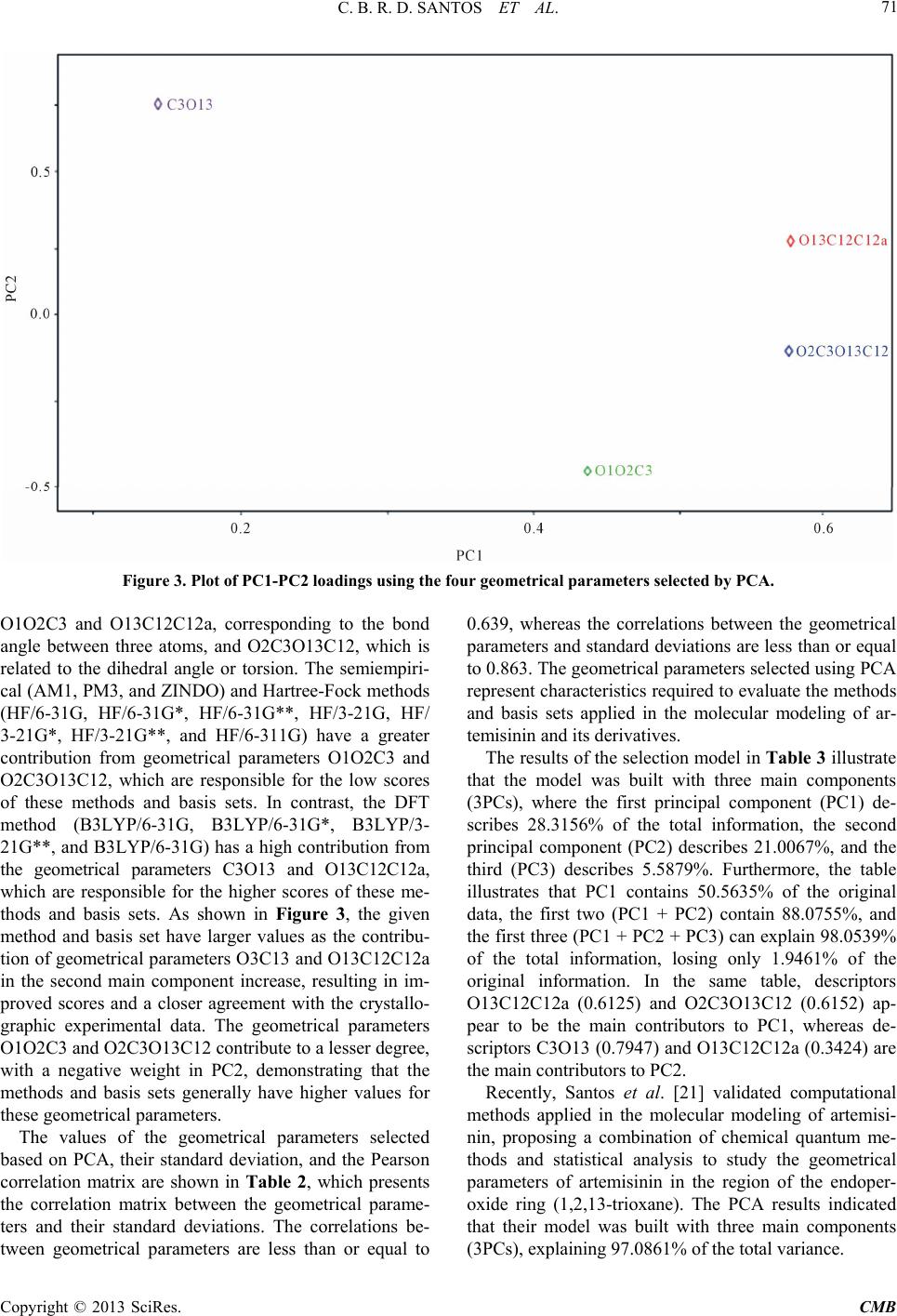C. B. R. D. SANTOS ET AL.
71
Figure 3. Plot of PC1-PC2 loadings using the four geometrical parameters selected by PCA.
O1O2C3 and O13C12C12a, corresponding to the bond
angle between three atoms, and O2C3O13C12, which is
related to the dihedral angle or torsion. The semiempiri-
cal (AM1, PM3, and ZINDO) and Hartree-Fock methods
(HF/6-31G, HF/6-31G*, HF/6-31G**, HF/3-21G, HF/
3-21G*, HF/3-21G**, and HF/6-311G) have a greater
contribution from geometrical parameters O1O2C3 and
O2C3O13C12, which are responsible for the low scores
of these methods and basis sets. In contrast, the DFT
method (B3LYP/6-31G, B3LYP/6-31G*, B3LYP/3-
21G**, and B3LYP/6-31G) has a high contribution from
the geometrical parameters C3O13 and O13C12C12a,
which are responsible for the higher scores of these me-
thods and basis sets. As shown in Figure 3, the given
method and basis set have larger values as the contribu-
tion of geometrical parameters O3C13 and O13C12C12a
in the second main component increase, resulting in im-
proved scores and a closer agreement with the crystallo-
graphic experimental data. The geometrical parameters
O1O2C3 and O2C3O13C12 contribute to a lesser degree,
with a negative weight in PC2, demonstrating that the
methods and basis sets generally have higher values for
these geometrical parameters.
The values of the geometrical parameters selected
based on PCA, their standard deviation, and the Pearson
correlation matrix are shown in Table 2, which presents
the correlation matrix between the geometrical parame-
ters and their standard deviations. The correlations be-
tween geometrical parameters are less than or equal to
0.639, whereas the correlations between the geometrical
parameters and standard deviations are less than or equal
to 0.863. The geometrical parameters selected using PCA
represent characteristics required to evaluate the methods
and basis sets applied in the molecular modeling of ar-
temisinin and its derivatives.
The results of the selection model in Table 3 illustrate
that the model was built with three main components
(3PCs), where the first principal component (PC1) de-
scribes 28.3156% of the total information, the second
principal component (PC2) describes 21.0067%, and the
third (PC3) describes 5.5879%. Furthermore, the table
illustrates that PC1 contains 50.5635% of the original
data, the first two (PC1 + PC2) contain 88.0755%, and
the first three (PC1 + PC2 + PC3) can explain 98.0539%
of the total information, losing only 1.9461% of the
original information. In the same table, descriptors
O13C12C12a (0.6125) and O2C3O13C12 (0.6152) ap-
pear to be the main contributors to PC1, whereas de-
scriptors C3O13 (0.7947) and O13C12C12a (0.3424) are
the main contributors to PC2.
Recently, Santos et al. [21] validated computational
methods applied in the molecular modeling of artemisi-
nin, proposing a combination of chemical quantum me-
thods and statistical analysis to study the geometrical
parameters of artemisinin in the region of the endoper-
oxide ring (1,2,13-trioxane). The PCA results indicated
that their model was built with three main components
(3Cs), explaining 97.0861% of the total variance. P

C. B. R. D. SANTOS ET AL.
72
Table 2. Geometrical parameters selected by PCA, standard deviations, and the Pearson correlation matrix.
Bond length/Å Bond angle/˚ Bond angle/˚ Torsion angle/˚
METHODS
C3O13 O1O2C3 O13C12C12a O2C3O13C12
Standard deviation
AM1 1.427 112.530 113.510 42.070 4.776
PM3 1.428 110.340 115.200 52.700 8.388
ZINDO 1.396 114.310 113.270 36.370 4.372
HF/6-31G 1.435 108.800 112.280 33.390 1.663
HF/6-31G* 1.388 106.100 108.700 31.034 2.484
HF/6-31G** 1.408 109.460 112.300 31.100 1.762
HF/3-21G 1.436 107.100 112.080 32.300 1.722
HF/3-21G* 1.435 107.080 112.080 32.360 1.714
HF/3-21G** 1.435 107.060 112.030 32.180 1.797
HF/6-311G 1.434 109.210 112.360 33.010 1.658
B3LYP/6-31G 1.473 107.300 113.640 34.970 0.843
B3LYP/6-31G* 1.441 108.280 113.250 32.800 1.227
B3LYP/6-31G** 1.441 108.280 113.240 32.780 1.103
B3LYP/3-21G 1.473 105.590 113.300 33.750 1.915
Experimental 1.445 108.100 114.500 36.000 0.000
C3O13 ˗0.453 0.522 ˗0.002 ˗0.360
O1O2C3 0.360 0.483 0.564
O13C12C12a 0.639 0.281
O2C3O13C12 0.863
Table 3. PCA of selection model for the methods and basis
sets.
Principal component
PC1 PC2 PC3
Variance/% 28.3156 21.0067 5.5879
Cumulative Variance/% 50.5635 88.0755 98.0539
Contribution
Geometrical Parameters
PC1 PC2
C3O13 0.0806 0.7947
O1O2C3 0.4898 ˗0.4989
O13C12C12a 0.6125 0.3424
O2C3O13C12 0.6152 ˗0.0478
The main components can be written as linear combi-
nations of the four geometrical parameters selected by
PCA. The mathematical expressions for PC1 and PC2 are
shown:




PC10.0806 C3O130.4898O1O2C3
0.6125 O13C12C12a
0.6152 O2C3O13C12




(4)




PC20.7947 C3O130.4989 O1O2C3
0.3424 O13C12C12a
0.0478 O2C3O13C12




(5)
The geometrical parameters C3O13, O1O2C3,
O13C12C12a, and O2C3O13C12 are of great importance
in this study because according to the proposal made by
Jefford et al., the iron in heme attacks artemisinin at po-
sition O1 and generates a free radical at position O2. Af-
ter the ligation at C3-C4 is broken, a home carbon radical
is generated at C4 [22]. This free radical at C4 has been
suggested as an important substance in antimalarial ac-
tivity [23]. The study of molecular docking between ar-
temisinin and its receptor, heme, conducted by Tonmun-
phean et al. also indicated that heme iron preferentially
interacts with O1 rather than O2 [24]. This phenomenon

C. B. R. D. SANTOS ET AL. 73
leads to the importance of geometry parameters C3O13
and O1O2C3, which were selected to be associated with
the suggested mechanism in this model.
Table 4 presents the geometrical parameters selected
by PCA, the methods, the basis sets, and the variations in
the geometrical parameters with respect to the experi-
mental data (Δ and Δ%). The semiempirical and Har-
tree-Fock methods do not exhibit a good agreement be-
tween the theoretical and experimental values for the
bond angles and torsion angles, particularly for the an-
gles formed by atoms O13C12C12a and O2C3O13C12,
respectively.
The semiempirical methods (AM1, PM3, and ZINDO)
present deviations of Δ = 0.990˚ (Δ% = 0.864), Δ =
−0.700˚ (Δ% = −0.611), and Δ = 1.230˚ (Δ% = 1.074),
respectively, in relation to the angle O13C12C12a. For
angle O2C3O13C12, deviations of Δ = −6.070˚ (Δ% =
−16.861), Δ = −16.700˚ (Δ = −46.388%), and Δ = −0.370˚
(Δ% = −1.027) were observed. For the Hartree-Fock
methods (HF/6-31G, HF/6-31G*, HF/6-31G**, HF/
3-21G, HF/3-21G*, HF/3-21G**, and HF/6-311G), the
angle formed by atoms O13C12C12a have deviations of
Δ = 2.220˚ (Δ% = 1.938), Δ= 5.800˚ (Δ% = 5.065) and Δ
= 2.200˚ (Δ% = 1.921), Δ = 2.420˚ (Δ% = 2.113), Δ =
2.420˚ (Δ% = 2.113), Δ = 2.470˚ (Δ% = 2.157), and Δ =
2.140˚ (Δ% = 1.868), respectively. For the angle
O2C3O13C12, deviations of Δ = 2.610˚ (Δ% = 7.250), Δ
= 4.966˚ (Δ% = 13.794), Δ = 4.900 (Δ% = 13.611), Δ =
3.700˚ (Δ% = 10.277), Δ = 3.640˚ (Δ% = 10.111), Δ =
3.820˚ (Δ% = 10.611), and Δ = 2.990˚ (Δ% = 8.305)
were obtained. For the DFT/B3LYP method, the four
levels (6-31G, 6-31G*, 6-31G**, and 3-21G) exhibited
excellent results for the bond angle O1O2C3, with devia-
tions of Δ = −0.800˚ (Δ% = −0.740) for DFT/B3LYP
6-31G, Δ = −0.180 (Δ% = −0.166) for DFT/B3LYP
6-31G*, Δ = 0.180˚ (Δ% = −0.166) for DFT/B3LYP
6-31G**, and Δ = 2.510˚ (Δ% = 2.321) for DFT/B3LYP
3-21G, as shown in Table 4.
As also shown in Table 4, by accounting for the fea-
tures of the basis sets B3LYP/6-31G* and B3LYP/
6-31G**, excellent results were obtained in relation to
the bond length C3O13 and bond angle O1O2C3, which
exhibited good agreement with the experimental values
reported in the literature. Thus, for the 6-31G* and
6-31G** bases, these parameters are close to the crystal-
lographic experimental data in the region of the endoper-
oxide ring of artemisinin.
HCA was used to explore and more appropriately
group the methods and basis sets according to their simi-
larities. A dendrogram was obtained with autoscaled
processing based on the Euclidean distance and incre-
mental method, as shown in Figure 4. This figure illus-
trates the grouping of the three classes: semiempirical
(AM1, PM3, and ZINDO), Hartree-Fock (HF/6-31G,
HF/6-31G*, HF/6-31G**, HF/3-21G, HF/3-21G*, HF/
3-21G**, and HF/6-311G), and DFT (B3LYP/6-31G,
B3LYP/6-31G*, B3LYP/6-31G**, and B3LYP/3-21G).
The semiempirical method has long branches, indicating
a low similarity with the experimental data. However, the
Hartree-Fock method exhibits similarity between the
basis sets, indicated by short branches, for the HF/
3-21G**, HF/3-21G*, and HF/3-21G bases. Cardoso et
al. [25] studied artemisinin and some of its derivatives
with activity against D-6 strains of Plasmodium falcipa-
rum using the HF/3-21G method. To verify the reliability
of the geometry obtained, Cardoso et al. compared the
structural parameters of the artemisinin trioxane ring
with theoretical and experimental values from the litera-
ture. Ferreira et al. [26] also studied artemisinin and 18
derivatives with antimalarial activity against W-2 strains
of Plasmodium falciparum through quantum chemistry
and multivariate analysis. The geometry optimization of
structures was realized using the Hartree-Fock method
and the 3-21G** basis set.
The DFT/B3LYP method exhibits high similarity be-
tween the basis sets, particularly for the B3LYP/6-31G*
and B3LYP/6-31G** basis sets, as indicated by the short
branches between them, shown in Figure 4.
The results of the theoretical methods and experimen-
tal data exhibited a distribution similar to that obtained
with PCA. Thus, HCA confirmed the results achieved by
PCA.
3.3. Statistical Analysis of Parameters
In this step, regression models with high values of r (%),
(%), Q2, and F (a statistic assessing the overall sig-
nificance) and low values of MAE, CMAE, SEE, PRESS,
and SPRESS were selected.
2
A
R
The most relevant statistical parameters are given in
Table 5. When comparing the semiempirical methods,
the best values were found for ZINDO (r = 99.7039%,
= 99.3496%, Q2 = 99.3909, F = 1681.28, SEE =
5.3983, MAE = 4.335, CMAE = 4.0998, PRESS =
305,773, and SPRESS = 1.7486). Among the basis sets for
the Hartree-Fock method, the best values were observed
for HF/6-31G (r = 99.9609%, = 99.9142%, Q2 =
99.9118%, F = 12811.33, SEE = 1.9641, MAE = 1.491,
CMAE = 1.4715, PRESS = 44.286, SPRESS = 0.6654),
HF/6-311G (r = 99.9606%, = 99.9134%, Q2 =
99.9124%, F = 12705.14, SEE = 1.9733, MAE = 1.492,
CMAE = 1.4626, PRESS = 43.985, SPRESS = 0.6632), and
HF/3-21G* (r = 99.9532%, = 99.8970%, Q2 =
99.9063%, F = 10679.82, SEE = 2.1638, MAE = 1.647,
CMAE = 1.6311, PRESS = 47.017, SPRESS = 0.6856).
2
A
R
2
A
R
2
A
R
2
A
R
The DFT method using B3LYP, with the valence-
separate basis sets B3LYP/6-31G, B3LYP/6-31G*, and
B3LYP/6-31G**, achieved the best results among all of
the methods and basis sets studied herein (semiempirical

C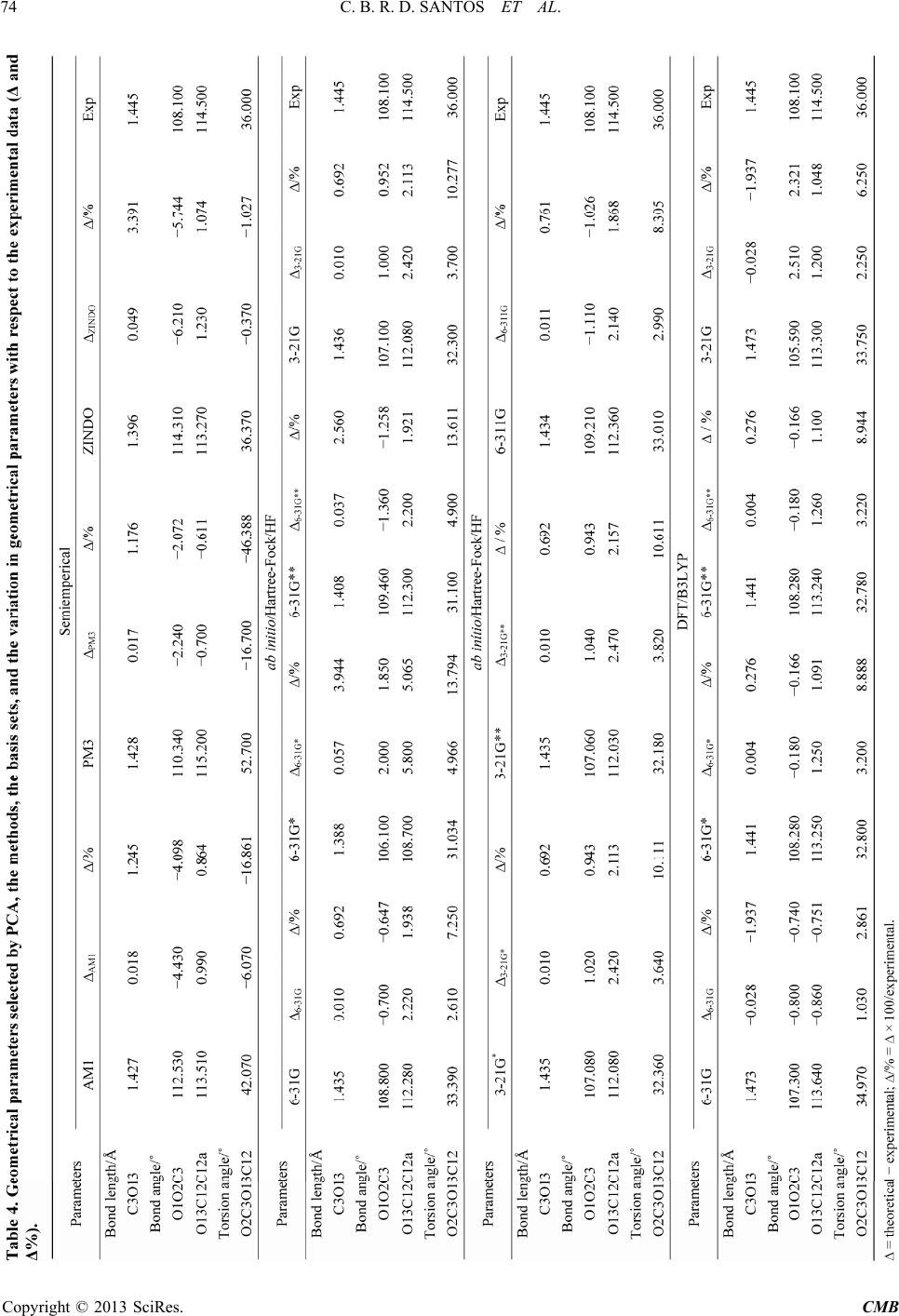. B. R. D. SANTOS ET AL.
74

C. B. R. D. SANTOS ET AL. 75
Figure 4. Dendogram for five methods, seven basis sets, and one factor related to the experimental geometrical parameters of
the 1,2,13-trioxane ring.
and Hartree-Fock), as shown in Table 5. However, these
minimum bases (6-31G and 3-21G) have several defi-
ciencies; thus, a polarization function was included to
improve upon these bases (i.e., p orbitals represented by
*). These orbitals follow restricted functions that are cen-
tered at the nuclei. However, it was found that the atomic
orbitals become distorted or polarized when a molecule
is formed. For this reason, one must consider the possi-
bility of a non-uniform displacement of electric charges
outside of the atomic nucleus, i.e., polarization. Thus, it
is possible to obtain a better description of the charges
and deformations of atomic orbitals within a molecule. A
mode of polarization can be considered by introducing
functions for which the values of l (quantum number of
the orbital angular momentum) are larger than those of
the fundamental state of a given atom. For these types,
the basis set names denote the polarization functions.
Thus, 6-31G* refers to basis set 6-31G with a polariza-
tion function for heavy atoms (i.e., atoms other than hy-
drogen), and 6-31G** refers to the inclusion of a po-
larization function for hydrogen and helium atoms [27].
When basis sets with polarization functions are used in
calculations involving anions, good results are not ob-
tained due to the electronic cloud of anionic systems,
which tend to expand. Thus, appropriate diffuse func-
tions must be added because they allow for a greater or-
bital occupancy in the region of space. Diffuse functions
are important in the calculations of transition metals be-
cause metal atoms have “d” orbitals, which tend to dif-
fuse. It then becomes necessary to include diffuse func-
tions in the basis function associated with the configura-
tion of a neutral metal atom to obtain a better description
of the metal complex. The 6-31G** basis is particularly
useful in the case of hydrogen bonds [27-30].
Pereira et al. (2008) studied four structures of artemis-
inin by reductive decomposition A, B1, B2, and B3 with
13 species (QHS, 1/2, 3, 4, 5, 5a, 6, 7, 18, 18a, 19, 20,
and 21), and the structures of the studied species were
analyzed in terms of geometrical parameters, Löwdin
bond orders, atomic partial charges, spin densities, elec-
tronic energies, free energies, and entropy. These studies
were carried out at the B3LYP/6-31G** level [31].
Barbosa et al. (2011) performed molecular modeling
and chemometric studies involving artemisinin and 28
derivatives exhibiting anticancer activity against human
hepatocellular carcinoma HepG2. The calculations of the
studied compounds were performed at the B3LYP/
6-31G** level [32].
Carvalho et al. (2011) used the B3LYP/6-31G** me-
thod to study artemisinin and 31 analogues with an- ti-
leishmanicidal activity against Leishmania donovani.
The authors proposed a set of 13 artemisinins, seven of
which are less active and six of which that have not been
tested; of these six, one is expected to be more active
against L. donovani [33].
The statistical analysis revealed good correlations (r >

C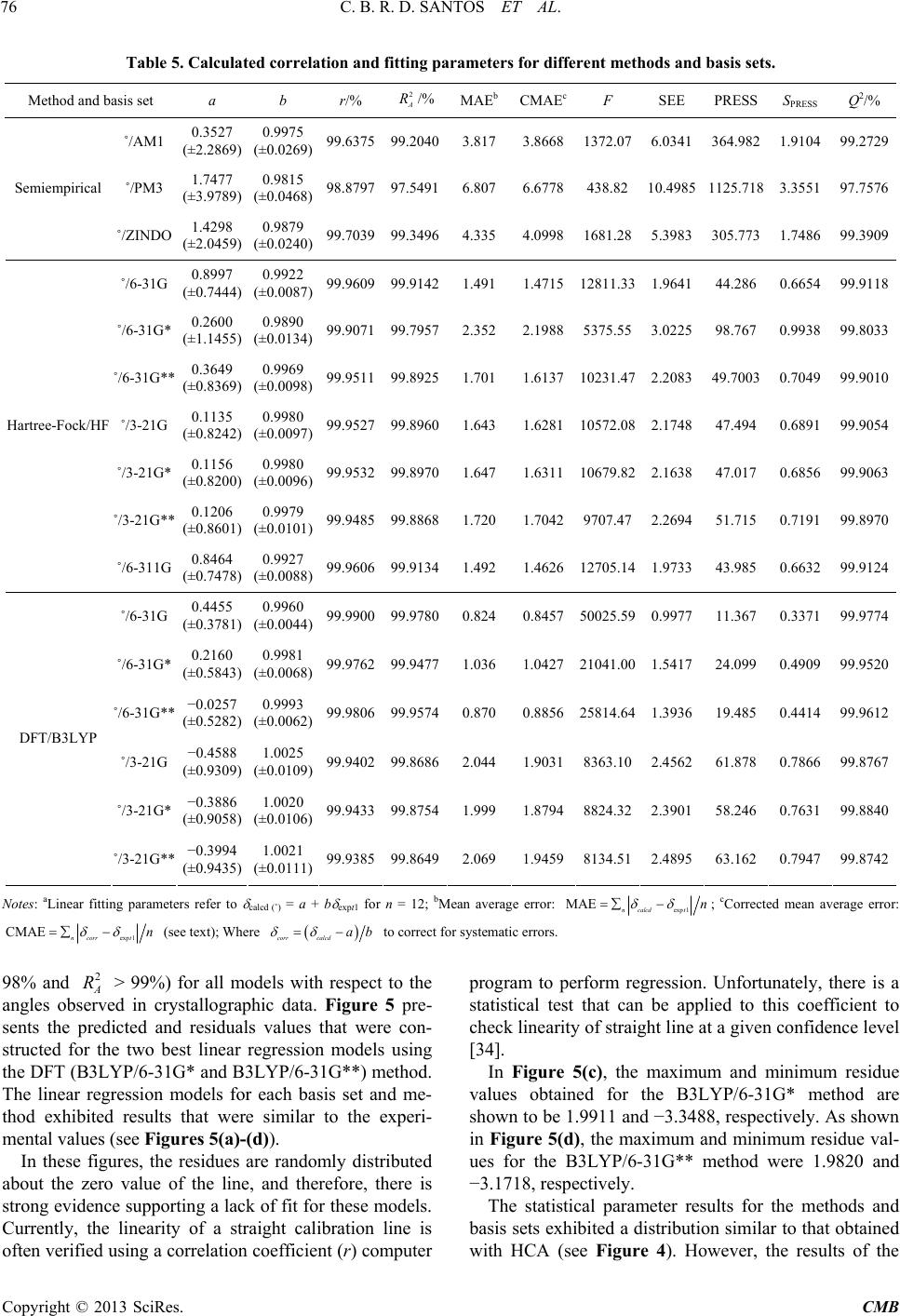. B. R. D. SANTOS ET AL.
76
Table 5. Calculated correlation and fitting parameters for different methods and basis sets.
Method and basis set a b r/% 2
A
R
/% MAEbCMAEcF SEE PRESS SPRESS Q2/%
˚/AM1 0.3527
(±2.2869)
0.9975
(±0.0269) 99.637599.20403.817 3.8668 1372.07 6.0341 364.982 1.9104 99.2729
˚/PM3 1.7477
(±3.9789)
0.9815
(±0.0468) 98.879797.54916.807 6.6778438.8210.4985 1125.718 3.355197.7576Semiempirical
˚/ZINDO 1.4298
(±2.0459)
0.9879
(±0.0240) 99.703999.34964.335 4.0998 1681.28 5.3983 305.773 1.7486 99.3909
˚/6-31G 0.8997
(±0.7444)
0.9922
(±0.0087) 99.960999.9142 1.491 1.471512811.331.9641 44.286 0.665499.9118
˚/6-31G* 0.2600
(±1.1455)
0.9890
(±0.0134) 99.907199.7957 2.352 2.19885375.553.0225 98.767 0.993899.8033
˚/6-31G** 0.3649
(±0.8369)
0.9969
(±0.0098) 99.951199.89251.701 1.613710231.472.2083 49.7003 0.7049 99.9010
˚/3-21G 0.1135
(±0.8242)
0.9980
(±0.0097) 99.952799.8960 1.643 1.628110572.082.1748 47.494 0.689199.9054
˚/3-21G* 0.1156
(±0.8200)
0.9980
(±0.0096) 99.953299.8970 1.647 1.631110679.822.1638 47.017 0.685699.9063
˚/3-21G** 0.1206
(±0.8601)
0.9979
(±0.0101) 99.948599.8868 1.720 1.70429707.472.2694 51.715 0.719199.8970
Hartree-Fock/HF
˚/6-311G 0.8464
(±0.7478)
0.9927
(±0.0088) 99.960699.9134 1.492 1.462612705.141.9733 43.985 0.663299.9124
˚/6-31G 0.4455
(±0.3781)
0.9960
(±0.0044) 99.990099.9780 0.824 0.845750025.590.9977 11.367 0.337199.9774
˚/6-31G* 0.2160
(±0.5843)
0.9981
(±0.0068) 99.976299.9477 1.036 1.042721041.001.5417 24.099 0.490999.9520
˚/6-31G** −0.0257
(±0.5282)
0.9993
(±0.0062) 99.980699.9574 0.870 0.885625814.641.3936 19.485 0.441499.9612
˚/3-21G −0.4588
(±0.9309)
1.0025
(±0.0109) 99.940299.8686 2.044 1.90318363.102.4562 61.878 0.786699.8767
˚/3-21G* −0.3886
(±0.9058)
1.0020
(±0.0106) 99.943399.8754 1.999 1.87948824.322.3901 58.246 0.763199.8840
DFT/B3LYP
˚/3-21G** −0.3994
(±0.9435)
1.0021
(±0.0111) 99.938599.8649 2.069 1.94598134.512.4895 63.162 0.794799.8742
Notes: aLinear fitting parameters refer to 
calcd (˚) = a + b

expt1 for n = 12; bMean average error: exp 1
MAEncalcdt n   ; cCorrected mean average error:
exp 1
CMAE ncorrt n    (see text); Where 
corrcalcd ab
  to correct for systematic errors.
98% and > 99%) for all models with respect to the
angles observed in crystallographic data. Figure 5 pre-
sents the predicted and residuals values that were con-
structed for the two best linear regression models using
the DFT (B3LYP/6-31G* and B3LYP/6-31G**) method.
The linear regression models for each basis set and me-
thod exhibited results that were similar to the experi-
mental values (see Figures 5(a) - (d)).
2
A
R
In these figures, the residues are randomly distributed
about the zero value of the line, and therefore, there is
strong evidence supporting a lack of fit for these models.
Currently, the linearity of a straight calibration line is
often verified using a correlation coefficient (r) computer
program to perform regression. Unfortunately, there is a
statistical test that can be applied to this coefficient to
check linearity of straight line at a given confidence level
[34].
In Figure 5(c), the maximum and minimum residue
values obtained for the B3LYP/6-31G* method are
shown to be 1.9911 and −3.3488, respectively. As shown
in Figure 5(d), the maximum and minimum residue val-
ues for the B3LYP/6-31G** method were 1.9820 and
−3.1718, respectively.
The statistical parameter results for the methods and
basis sets exhibited a distribution similar to that obtained
with HCA (see Figure 4). However, the results of the

C. B. R. D. SANTOS ET AL. 77
(a) (b)
(c) (d)
Figure 5. Correlation between the calculated and experimental angle data; predicted values for the DFT/B3LYP method and
the 6-31G* and 6-31G** basis sets (a) and (b) and residual values (c) and (d).
DFT method for the B3LYP/6-31G** basis set exhibited
the lowest values for MAE, CMAE, SEE, PRESS, and
SPRESS; in comparison with B3LYP/6-31G*, the two sets
have a variation of MAE = ±0.166, CMAE = ±0.1571,
SEE = ±0.1481, PRESS = ±4.614, and SPRESS = ±0.0495.
The molecular properties obtained depend on the me-
thod and basis set used, which represent a number of
functions used in the expansion monoelectronics (orbital)
and parameter characteristics that must be optimized.
Therefore, it is of fundamental importance that these
functions be carefully evaluated to obtain accurate results.
Many studies have been performed to develop methods
and basis sets that can provide more accurate results. In
recent years, other sets have been employed in electronic
structure calculations in addition to the methods and ba-
sis sets described previously [30]. Generally, the inclu-
sion of polarization functions in the molecular basis al-
lows for a greater probability of better results for many
chemical properties of interest, such as the dissociation
energy and dipole moment. In practice, the inclusion of
polarization functions with d and f symmetry for small s
and p basis sets has been shown to be unsatisfactory; thus,
polarization functions should only be added to saturated
basis sets.
These results confirm the relevance of theoretical data
used to calculate the angles of crystallographic data for
this compound (artemisinin) for the method and basis set
DFT/B3LYP 6-31G**. HCA confirmed the results ob-
tained by statistical analysis. Therefore, we conclude that
the DFT method combined with the B3LYP/6-31G**

C. B. R. D. SANTOS ET AL.
78
basis set can be used for the calculation of molecular
properties and for the molecular modeling of artemisinin
and its derivatives with biological activity based on the
mechanism of action in the region of the endoperoxide
ring (1,2,13-trioxane).
4. Conclusions
The statistical analysis techniques of PCA and HCA
were vital in enabling the classification of methods and
basis sets into three separate groups. The geometrical
parameters that were found to be the most important in
the classification of methods and basis sets were related
to the trioxane ring: C3O13, O1O2C3, O13C12C12a,
and O2C3O13C12. The HCA results were similar to
those obtained with PCA.
The DFT/B3LYP method with valence-separate basis
set 6-31G** exhibited the best results and high predictive
ability compared to the methods and basis sets studied
herein (semiempirical, Hartree-Fock, and DFT). This
method is suitable for molecular modeling studies of
artemisinin and for determining the conformation of its
derivatives along with their biological activity and me-
chanism of action in the region of the endoperoxide ring.
The DFT/B3LYP 6-31G** method can be used for future
calculations of molecular properties, which represent a
means of obtaining chemical information contained in
the molecular structure of a compound for chemical,
pharmacological, and toxicological studies on quantita-
tive structure-activity and structure-property relation-
ships.
5. Acknowledgements
We gratefully acknowledge the support provided by the
Brazilian Agency National Council of Scientific and
Technological Development and the Institute of Exact
and Natural Sciences of Federal University of Para for
use of the GaussView and Gaussian software. The au-
thors would like to thank the Postgraduate Program in
Biotechnology and Biodiversity-Network BIONORTE,
the Laboratory of Modeling and Computational Chemis-
try, Federal University of Amapá for computational sup-
port, and especially Professor Dr. José Walkimar de
Mesquita Carneiro of Federal University Fluminense for
his contributions.
REFERENCES
[1] S. R. Meshnick, C. W. Jefford, G. H. Posner, M. A. Ave-
ry and W. Peters, “Second-Generation Antimalarial Endo-
peroxides,” Parasitology Today, Vol. 12, No. 2, 1996, pp.
79-82. http://dx.doi.org/10.1016/0169-4758(96)80660-0
[2] D. L. Klayman, “Qinghaosu (Artemisinin): An Antima-
larial Drug from China,” Science, Vol. 228, No. 4703,
1985, pp. 1049-1055.
http://dx.doi.org/10.1126/science.3887571
[3] A. A. C. Braga and N. H. Morgon, “Cálculos Teóricos de
Afinidades por Próton De N-Alquilaminas Usando o
Método Oniom,” Quimica Nova, Vol. 29, No. 2, 2009, pp.
187-193.
http://dx.doi.org/10.1590/S0100-40422006000200002
[4] M. S. Costa, R. Kiralj and M. M. C. Ferreira, “Estudo
Teórico da Interação Existente Entre a Artemisinina e o
Heme,” Quimica Nova, Vol. 30, No. 1, 2007, pp. 25-31.
http://dx.doi.org/10.1590/S0100-40422007000100006
[5] F. H. A. Leite, A. G. Taranto, M. C. Santos Junior, A.
Branco, M. T. Araujo and J. W. M. Carneiro, “Search for
New Antimalarial Compounds Obtained From Natural
Sources by Molecular Modeling,” International Journal
of Quantum Chemistry, Vol. 110, No. 11, 2010, pp.
2057-2066.
[6] F. H. A. Leite, J. W. M.Carneiro, M. T. Araujo, M. Co-
mar Jr. and A. G. Taranto, “Docking Between Natural
Peroxides and Heme Group by Parametric Method 6,”
International Journal of Quantum Chemistry, Vol. 1012,
No. 20, 2012, pp. 3390-3397.
http://dx.doi.org/10.1002/qua.24247
[7] J. C. Pinheiro, R. Kiralj, M. M. C. Ferreira and O. A. S.
Romero, “Artemisinin Derivatives with Antimalarial Ac-
tivity against Plasmodium falciparum Designed with the
aid of Quantum Chemical and Partial Least Squares
Methods,” QSAR & Combinatorial Science, Vol. 22. No.
8, 2003, pp. 830-842.
http://dx.doi.org/10.1002/qsar.200330829
[8] M. G. G. Cristino, C. C. F. Meneses, M. M. Soeiro, J. E.
V. Ferreira, A. F. Figueiredo, J. P. Barbosa, R. C. O. Al-
meida, J. C. Pinheiro and A. L. R. Pinheiro, “Computa-
tional Modeling of Antimalarial 10-Substituted Deoxoar-
temisinins,” Journal of Theoretical and Computational
Chemistry, Vol. 11, No. 2, 2012, pp. 241-263.
http://dx.doi.org/10.1142/S0219633612500162
[9] A. F. Figueiredo, J. E. V. Ferreira, J. P. Barbosa, W. J. C.
Macêdo, M. G. G. Cristino, M. S. Lobato, J. C. Pinheiro
and R. T. A. Serra, “A Computational Study on Antima-
larial Dispiro-1,2,4-Trioxolanes,” Journal of Computa-
tional and Theoretical Nanoscience, Vol. 8, No. 9, 2011,
pp. 1847-1856. http://dx.doi.org/10.1166/jctn.2011.1892
[10] J. Q. Araújo, J. W. M. Carneiro, M. T.Araújo, F. H. A.
Leite and A. G. Taranto, “Interaction between Artemisi-
nin and Heme. A Density Functional Theory Study of
Structures and Interaction Energies,” Bioorganic & Me-
dicinal Chemistry, Vol. 16, No. 9, 2008, pp. 5021-5029.
http://dx.doi.org/10.1016/j.bmc.2008.03.033
[11] GaussView 3.07, Gaussian, Inc.; Pittsburgh, PA, 1997.
[12] M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria,
M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T.
Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S.
Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G.
Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M.
Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M.
Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M.
Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C.
Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O.
Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Och-

C. B. R. D. SANTOS ET AL.
79
terski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salva-
dor, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A.
D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D.
Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q.
Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Ste-
fanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R.
L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y.
Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B.
Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A.
Pople, “Gaussian 03”, Revision C.02; Gaussian, Inc.,
Wallingford, 2004.
[13] J. N. Lisgarten, B. S. Potter, C. Bantuzeko and R. A. Pal-
mer, “Structure, Absolute Configuration, and Conforma-
tion of the Antimalarial Compound, Artemisinin,” Jour-
nal of Chemical Crystallography, Vol. 28, No. 7, 1998,
pp. 539-543. http://dx.doi.org/10.1023/A:1023244122450
[14] F. H. Allen, “The Cambridge Structural Database: A
Quarter of a Million Crystal Structures and Rising,” Acta
Crystallographica Section B, Vol. 58, No. 01, 2002, pp.
380-388. http://dx.doi.org/10.1107/S0108768102003890
[15] Pirouette Software, Version 3.01, Infometrix Inc., 2001.
[16] STATISTICA (Data Analysis Software System); Version
6.1, StatSoft, Inc., 2004. http://www.statsoft.com
[17] S. O. Silva, M. J. C. Corrêa, H. R. Bitencourt, W. R. Mon-
teiro, J. Lameira, L. S. Santos, G. M. S. P. Guilhon and D.
S. B. Brasil, “Density Functional Theory Calculations of
the Nuclear Magnetic Resonance Parameters for Two
Dihydrochalcones,” Journal of Computational and Theo-
retical Nanoscience, Vol. 9, No. 7, 2012, pp. 953-956.
http://dx.doi.org/10.1166/jctn.2012.2123
[18] M. M. C. Ferreira, “Multivariate QSAR,” Journal of Bra-
zilian Chemical Society, Vol. 13, No. 6, 2002, pp. 742-
753.
http://dx.doi.org/10.1590/S0103-50532002000600004
[19] A. C. Gaudio and E. Zandonade, “Proposição, Validação
e Análise dos Modelos que Correlacionam Estrutura
Química e Atividade Biológica,” Quimica Nova, Vol. 24,
No. 5, 2001, pp. 658-671.
http://dx.doi.org/10.1590/S0100-40422001000500013
[20] P. Cimino, P. L. D. Gomez, R. R. Duca and G. Bifulco,
“Comparison of Different Theory Models and Basis Sets
in the Calculation of 13C NMR Chemical Shifts of Natural
Products,” Magnetic Resonance in Chemistry, Vol. 42,
No. S1, 2004, pp. S26-S33.
http://dx.doi.org/10.1002/mrc.1410
[21] C. B. R. Santos, J. B. Vieira, A. S. Formigosa, E. V. M.
Costa, M. T. Pinheiro, J. O. Silva, W. J. C. Macêdo and J.
C. T. Carvalho, “Validation of Computational Methods
Applied in Molecular Modeling of Artemisinin with Anti-
malarial Activity,” Journal of Computational and Theo-
retical Nanoscience, Vol. 11, No. 3, 2014, pp. 1-9.
[22] C. W. Jefford, “Why Artemisinin and Certain Synthetic
Peroxides are Potent Antimalarials. Implications for the
Mode of Action,” Current Medicinal Chemistry, Vol. 8,
No. 15, 2001, pp.1803-1826.
http://dx.doi.org/10.2174/0929867013371608
[23] G. H. Posner, A. J. McRiner, I. H. Paik, S. Sur, K. Bor-
stnik, S. Xie, T. A. Shapiro, A. Alagbala and B. Foster,
“Anticancer and Antimalarial Efficacy and Safety of Ar-
temisinin-Derived Trioxane Dimers in Rodents,” Journal
of Medicinal Chemistry, Vol. 47, No. 5, 2004, pp. 1299-
1301. http://dx.doi.org/10.1021/jm0303711
[24] S. Tonmunphean, V. Parasuk and S. Kokpol, “Automated
Calculation of Docking of Artemisinin to Heme,” Journal
of Molecular Modeling, Vol. 7, No. 4, 2001, pp. 26-33.
[25] F. J. B. Cardoso, A. F. Figueiredo, M. S. Lobato, R. M.
Miranda, R. C. O. Almeida and J. C. Pinheiro, “A Study
on Antimalarial Artemisinin Derivatives Using MEP
Maps and Multivariate QSAR,” Journal of Molecular
Modeling, Vol. 14, No. 1, 2008, pp. 39-48.
http://dx.doi.org/10.1007/s00894-007-0249-9
[26] J. E. V. Ferreira, A. F. Figueiredo, J. P. Barbosa, M. G. G.
Cristino, W. J. C. Macêdo, O. P. P. Silva, B. V. Malheiros,
R. T. A. Serra and J. C. Pinheiro, “A Study of New An-
timalarial Artemisinins Through Molecular Modeling and
Multivariate Analysis,” Journal of the Serbian Chemical
Society, Vol. 75, No. 11, 2010, pp. 1533-1548.
http://dx.doi.org/10.2298/JSC100126124F
[27] A. Leach, “Molecular Modelling—Principles and Appli-
cations,” 2nd Edition, Pearson Education Limited, Upper
Saddle River, 2001.
[28] W. J. Hehre, “A Guide to Molecular Mechanics and Qu-
antum Chemical Calculations,” Wavefunction, Inc., Ir-
vine, 2003.
[29] R. S. Mulliken and B. Liu, “Self-Consistent-Field Wave
Functions of P2 and PO, and the Role of d Functions in
Chemical Bonding and of s-p Hybridization in N2 and
P2,” Journal of the American Chemical Society, Vol. 93,
No. 25, 1971, pp. 6738-6744.
http://dx.doi.org/10.1021/ja00754a004
[30] I. N. Levine, “Quantum Chemistry,” 4th Edition, Pren-
tice-Hall, New York, 1991.
[31] M. S. C. Pereira, R. Kiralj and M. M. C. Ferreira, “Theo-
retical Study of Radical and Neutral Intermediates of Ar-
temisinin Decomposition,” Journal Chemical Information
and Modeling, Vol. 48, No. 1, 2008, pp. 85-98.
http://dx.doi.org/10.1021/ci700011f
[32] J. P. Barbosa, J. E. V. Ferreira, A. F. Figueiredo, R. C. O.
Almeida, O. P. P. Silva, J. R. C. Carvalho, M. G. G. Cris-
tino, J. C. Pinheiro, J. L. F. Vieira and R. T. A. Serra,
“Molecular Modeling and Chemometric Study of Anti-
cancer Derivatives of Artemisinin,” Journal of the Ser-
bian Chemical Society, Vol. 76, No. 9, 2011, pp. 1263-
1282. http://dx.doi.org/10.2298/JSC111227111B
[33] J. R. C. Carvalho, J. E. V. Ferreira, J. P. Barbosa, M. S.
Lobato, C. C. F. Meneses, M. M. Soeiro, M. S. Farias, R.
C. O. Almeida, K. C. Ventura, J. C. Pinheiro and A. L. R.
Pinheiro, “Computational Modeling of Artemisinins with
Antileishmanial Activity,” Journal of Computational and
Theoretical Nanoscience, Vol. 8, No. 11, 2011, pp. 2193-
2203. http://dx.doi.org/10.1166/jctn.2011.1943
[34] L. M. Z. G. Passari, P. K. Soares, R. E. Bruns and I. S.
Scarminio, “Estatística Aplicada à Química: Dez Dúvidas
Comuns,” Quimica Nova, Vol. 34, No 5. 2011, pp. 888-
892.
http://dx.doi.org/10.1590/S0100-40422011000500028