Open Journal of Composite Materials, 2013, 3, 89-96
http://dx.doi.org/10.4236/ojcm.2013.34009 Published Online October 2013 (http://www.scirp.org/journal/ojcm)
89
Effective Elastic Properties of Honeycomb Core with
Fiber-Reinforced Composite Cells
F. Ernesto Penado
Department of Mechanical Engineering, Northern Arizona University, Flagstaff, USA.
Received August 18th, 2013; revised September 10th, 2013; accepted September 18th, 2013
Copyright © 2013 F. Ernesto Penado. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
Sandwich construction incorporating a honeycomb cellular core offers the attainment of structures that are very stiff and
strong in bending while the weight is kept at a minimum. Generally, an aluminum or Nomex honeycomb core is used in
applications requiring sandwich construction with fiber-reinforced composite facesheets. However, the use of a fiber-
reinforced composite core offers the potential for even lower weight, increased stiffness and strength, low thermal dis-
tortion compatible with that of the facesheets, the absence of galvanic corrosion and the ability to readily modify the
core properties to suit specialized needs. Furthermore, the material of the core itself will exhibit anisotropic material
properties in this case. In order to design, analyze and optimize these structures, knowledge of the effective mechanical
properties of the core is essential. In this paper, the effective three-dimensional mechanical properties of a composite
hexagonal cell core are determined using a numerical method based on a finite element analysis of a representative unit
cell. In particular, the geometry of the simplest repeating unit of the core as well as the appropriate loading and bound-
ary conditions that must be applied is presented.
Keywords: Lightweight Structures; Composite Mirrors; Sandwich Construction; Hexagonal Cell Core; Effective Core
Properties
1. Introduction
Sandwich structures can be used advantageously where
low weight and high stiffness and strength are required,
such as the traditional case in aerospace applications.
Composite materials, such as carbon fiber reinforced
plastics (CFRP), are well suited for sandwich construc-
tion methods due to their low weight, high stiffness, high
strength, dimensional stability, and ease of manufacture.
For example, complex structural designs can be fabri-
cated in CFRP directly and do not need massive material
removal to achieve the desired shape, which would be
the case with traditional materials such as aluminum. A
sandwich structure consisting of two face-sheets (skins)
bonded to a framework of ribs between them is much
lighter than a solid sheet of the same material but retains
most of the stiffness in bending. The stiffness against
bending out of plane is a strong function of the facesheet
planar stiffness and the distance between the two face-
sheets (e.g., the moment of inertia), providing the core
carries the entire shear load. Sandwich construction is
very common in a wide variety of applications, including
aircraft components, space structures, and other weight
sensitive applications. More recently, other non-tradi-
tional applications have emerged, such as in land and sea
transportation [1] and in the construction of optical tele-
scope composite mirrors [2,3]. The latter requires very
tight tolerances of dimensional stability and low weight,
so a core made of CFRP material that is very stiff and at
the same time has thermal expansion compatible with
that of the facesheets can be used advantageously. In or-
der to facilitate the analysis and design of these structures,
the core can be represented as a homogeneous layer with
equivalent mechanical properties.
The effective properties of the core can be found ana-
lytically, numerically or experimentally [4]. Existing an-
alytical methods to find the equivalent homogeneous
properties of the core are based on isotropic material
properties (e.g. aluminum) and use a variety of simpli-
fying assumptions. Notably, Kelsey et al. [5] used the
unit displacement and unit load methods in conjunction
with simplifying assumptions to derive simple expres-
sions for the upper and lower limits of the shear moduli
of honeycomb sandwich cores. Hoffman [6] used an en-

Effective Elastic Properties of Honeycomb Core with Fiber-Reinforced Composite Cells
90
ergy method to derive an expression for the in-plane
Poisson ratio. Zhang and Ashby [7] adapted the analysis
of Gibson and Ashby [8] for honeycombs with a pair of
doubled walls in each hexagonal cell to derive effective
out-of-plane properties. Later, Masters and Evans [9]
combined the three mechanisms of flexing, hinging and
stretching to derive in-plane effective properties of the
core for the tensile and shear moduli, and Poisson’s ratio.
Grediac [10] used finite element analyses and the upper
and lower bounds to determine a least squares approxi-
mation for the transverse shear moduli. However, due to
the complexities involved, analytical solutions for a core
with walls made of CFRP materials, which are anisot-
ropic in nature, are not currently available.
In a previous paper, Penado et al. [2] presented a nu-
merical method to find the mechanical properties of a
triangular isogrid core with composite (anisotropic) walls.
In the present paper, a practical method is presented to
determine the effective elastic properties of a hexagonal
cell core from a finite element analysis of the simplest
repeating unit of the core, including the proper boundary
conditions that must be used in the model. In applications
that require structural stability, such as composite mirrors,
hexagonal cells offer the advantage of higher out-of-
plane shear stiffness over triangular cells of the same
density.
2. Unit Cell Method
A hexagonal cell core exhibits a regular, periodic pattern.
Although a full core can be difficult or impractical to
model due to its complexity, a significant amount of
simplification can be achieved by considering only the
representative structural unit, or unit cell, as shown in
Figure 1. However, this unit cell is not the simplest re-
peating unit that must be used in the finite element model,
as shown later. By proper selection of boundary condi-
tions and loading, the properties obtained by using the
unit cell equal those of the full core. It should be noted
that, due to the expansion process used in the manufac-
ture of hexagonal-cell cores, the thickness of the hori-
(a) (b)
Unit cell
x
y
t = wall thickness
2t
w = cell size
a
t
Figure 1. (a) Plan view of full hexagonal cell core; (b) Unit
cell.
zontal cell wall is usually twice the thickness of the in-
clined cell walls, and this is the case considered herein
(see Figure 1).
The effective stiffnesses of the core are determined by
finding the force necessary to produce an unit displace-
ment in a given direction, determining the resulting stress
and strain, and then calculating the corresponding engi-
neering constants. This process can be used to find the
nine effective engineering constants, Ex, Ey, Ez, Gxy, Gxz,
Gyz,

xy,

xz, and

yz. In equation form,
iii
iiii
F
A
EuL


 (1)
j
ij j
ij iii
uL
uL


  (2)
ijj i
ij ijji
F
A
GuL


 (3)
where i, j = x, y or z directions; Ei=extension modulus in
i-direction; 
ij = Poisson’s ratio; Gij = shear modulus in
i-j plane; 
i = normal stress in i-direction;

i = normal
strain in i-direction;

ij = shear stress in i-j plane;

ij =
shear strain in i-j plane; Ai, Aj = projected area of core on
a plane perpendicular to i-, j-direction; Li, Lj = length of
core in i-, j-direction; Fi, Fj = force needed to produce a
unit displacement ui, uj; ui, uj = unit displacement in i-,
j-direction = 1; and uij = resulting displacement in j-di-
rection when a unit displacement is applied in i-direction.
For example,
(1)
x
xx xx
x
x
xx x
F
AFL
EuL A


 (4)
(1)
y
xyyxy x
xy
x
xx y
uL uL
uL L

   (5)
(1)
x
yyxyx
xy
x
yyxx
F
AFL
GuL A


 (6)
The application of the appropriate boundary conditions
and unit displacements to the unit cell is discussed in the
next section. It should be noted that, as part of the verifi-
cation process involving symmetry conditions, the fol-
lowing six additional effective engineering constants
were also calculated: Gyx, Gzx, Gzy,

yx,

zx, and

zy.
3. Finite Element Model and Boundary
Conditions
3.1. Finite Element Model of Unit Cell
Closed form solutions for the effective properties of a
core with hexagonal cells can be found in the literature
only for the special case of isotropic walls, such as those
made of aluminum [7,9,11]. Cell walls made of compos-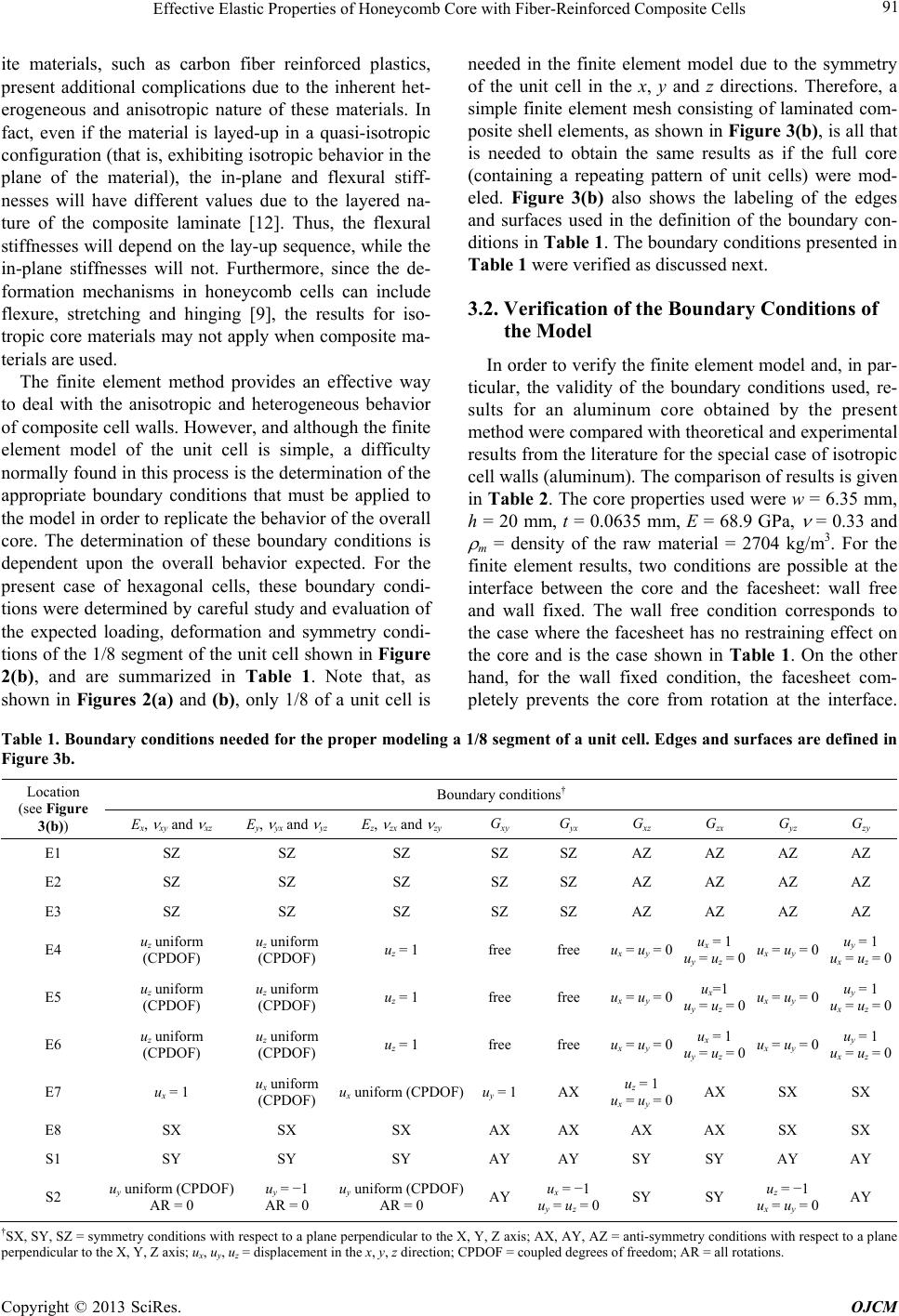

Effective Elastic Properties of Honeycomb Core with Fiber-Reinforced Composite Cells
91
ite materials, such as carbon fiber reinforced plastics,
present additional complications due to the inherent het-
erogeneous and anisotropic nature of these materials. In
fact, even if the material is layed-up in a quasi-isotropic
configuration (that is, exhibiting isotropic behavior in the
plane of the material), the in-plane and flexural stiff-
nesses will have different values due to the layered na-
ture of the composite laminate [12]. Thus, the flexural
stiffnesses will depend on the lay-up sequence, while the
in-plane stiffnesses will not. Furthermore, since the de-
formation mechanisms in honeycomb cells can include
flexure, stretching and hinging [9], the results for iso-
tropic core materials may not apply when composite ma-
terials are used.
The finite element method provides an effective way
to deal with the anisotropic and heterogeneous behavior
of composite cell walls. However, and although the finite
element model of the unit cell is simple, a difficulty
normally found in this process is the determination of the
appropriate boundary conditions that must be applied to
the model in order to replicate the behavior of the overall
core. The determination of these boundary conditions is
dependent upon the overall behavior expected. For the
present case of hexagonal cells, these boundary condi-
tions were determined by careful study and evaluation of
the expected loading, deformation and symmetry condi-
tions of the 1/8 segment of the unit cell shown in Figure
2(b), and are summarized in Table 1. Note that, as
shown in Figures 2(a) and (b), only 1/8 of a unit cell is
needed in the finite element model due to the symmetry
of the unit cell in the x, y and z directions. Therefore, a
simple finite element mesh consisting of laminated com-
posite shell elements, as shown in Figure 3(b), is all that
is needed to obtain the same results as if the full core
(containing a repeating pattern of unit cells) were mod-
eled. Figure 3(b) also shows the labeling of the edges
and surfaces used in the definition of the boundary con-
ditions in Ta ble 1. The boundary conditions presented in
Table 1 were verified as discussed next.
3.2. Verification of the Boundary Conditions of
the Model
In order to verify the finite element model and, in par-
ticular, the validity of the boundary conditions used, re-
sults for an aluminum core obtained by the present
method were compared with theoretical and experimental
results from the literature for the special case of isotropic
cell walls (aluminum). The comparison of results is given
in Table 2. The core properties used were w = 6.35 mm,
h = 20 mm, t = 0.0635 mm, E = 68.9 GPa,  = 0.33 and

m = density of the raw material = 2704 kg/m3. For the
finite element results, two conditions are possible at the
interface between the core and the facesheet: wall free
and wall fixed. The wall free condition corresponds to
the case where the facesheet has no restraining effect on
the core and is the case shown in Table 1. On the other
hand, for the wall fixed condition, the facesheet com-
pletely prevents the core from rotation at the interface.
Table 1. Boundary conditions needed for the proper modeling a 1/8 segment of a unit cell. Edges and surfaces are defined in
Figure 3b.
Boundary conditions†
Location
(see Figure
3(b)) Ex,

xy and

xz Ey,

yx and

yz Ez,

zx and

zy Gxy G
yx G xz G zx G yz G zy
E1 SZ SZ SZ SZ SZ AZ AZ AZ AZ
E2 SZ SZ SZ SZ SZ AZ AZ AZ AZ
E3 SZ SZ SZ SZ SZ AZ AZ AZ AZ
E4 uz uniform
(CPDOF)
uz uniform
(CPDOF) uz = 1 free free ux = uy = 0ux = 1 uy = uz = 0 ux = uy = 0uy = 1 ux = uz = 0
E5 uz uniform
(CPDOF)
uz uniform
(CPDOF) uz = 1 free free ux = uy = 0ux=1 uy = uz = 0 ux = uy = 0uy = 1 ux = uz = 0
E6 uz uniform
(CPDOF)
uz uniform
(CPDOF) uz = 1 free free ux = uy = 0ux = 1 uy = uz = 0 ux = uy = 0uy = 1 ux = uz = 0
E7 ux = 1 ux uniform
(CPDOF) ux uniform (CPDOF)uy = 1 AX uz = 1 ux = uy = 0AX SX SX
E8 SX SX SX AX AX AX AX SX SX
S1 SY SY SY AY AY SY SY AY AY
S2 uy uniform (CPDOF)
AR = 0
uy = −1
AR = 0
uy uniform (CPDOF)
AR = 0 AY ux = −1 uy = uz = 0SY SY
uz = −1
ux = uy = 0AY
†SX, SY, SZ = symmetry conditions with respect to a plane perpendicular to the X, Y, Z axis; AX, AY, AZ = anti-symmetry conditions with respect to a plane
perpendicular to the X, Y, Z axis; ux, uy, uz = displacement in the x, y, z direction; CPDOF = coupled degrees of freedom; AR = all rotations.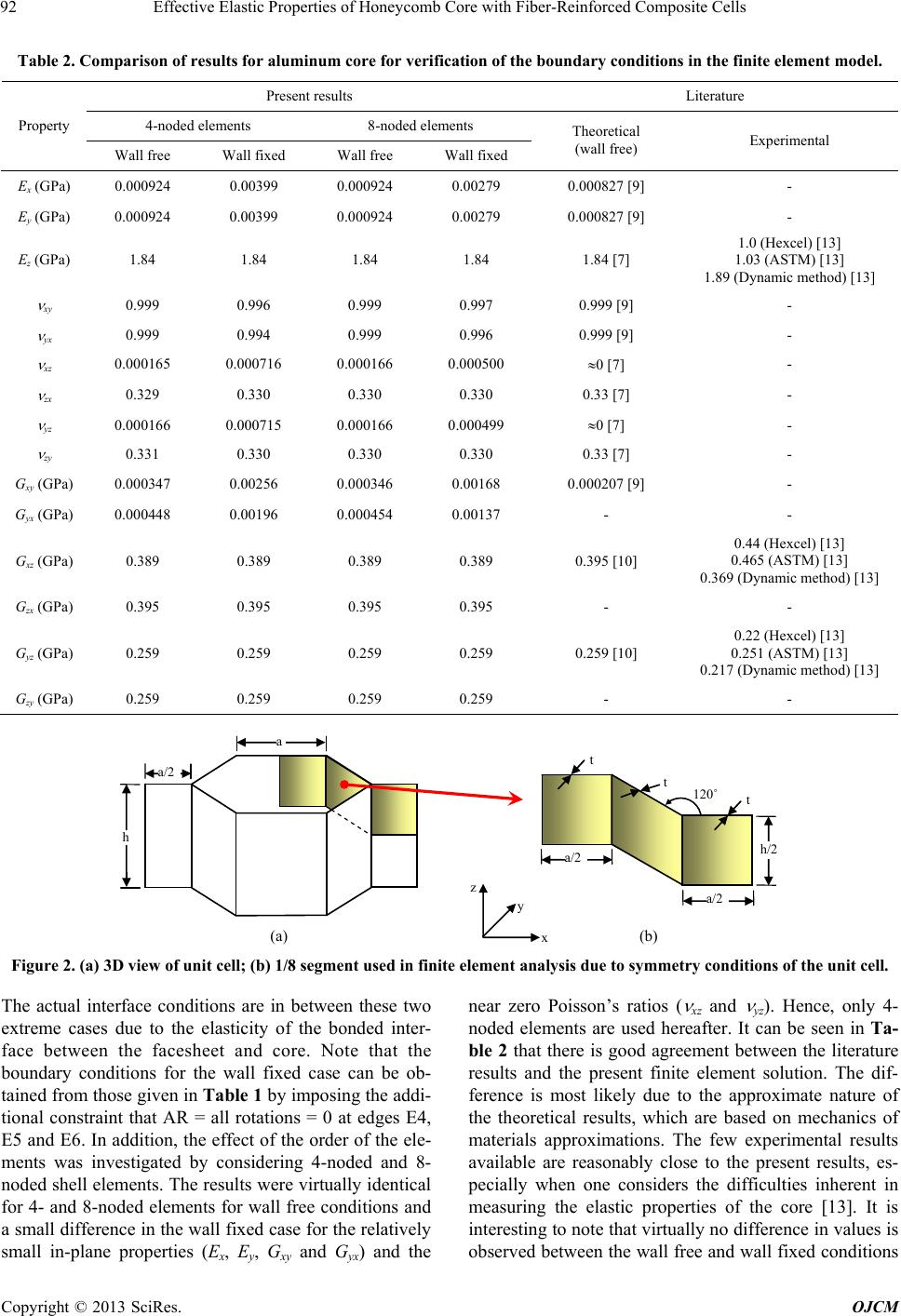

Effective Elastic Properties of Honeycomb Core with Fiber-Reinforced Composite Cells
92
Table 2. Comparison of results for aluminum core for verification of the boundary conditions in the finite element model.
Present results Literature
4-noded elements 8-noded elements
Property
Wall free Wall fixed Wall free Wall fixed
Theoretical
(wall free) Experimental
Ex (GPa) 0.000924 0.00399 0.000924 0.00279 0.000827 [9] -
Ey (GPa) 0.000924 0.00399 0.000924 0.00279 0.000827 [9] -
Ez (GPa) 1.84 1.84 1.84 1.84 1.84 [7]
1.0 (Hexcel) [13]
1.03 (ASTM) [13]
1.89 (Dynamic method) [13]

xy 0.999 0.996 0.999 0.997 0.999 [9] -

yx 0.999 0.994 0.999 0.996 0.999 [9] -

xz 0.000165 0.000716 0.000166 0.000500 0 [7] -

zx 0.329 0.330 0.330 0.330 0.33 [7] -

yz 0.000166 0.000715 0.000166 0.000499 0 [7] -

zy 0.331 0.330 0.330 0.330 0.33 [7] -
Gxy (GPa) 0.000347 0.00256 0.000346 0.00168 0.000207 [9] -
Gyx (GPa) 0.000448 0.00196 0.000454 0.00137 - -
Gxz (GPa) 0.389 0.389 0.389 0.389 0.395 [10]
0.44 (Hexcel) [13]
0.465 (ASTM) [13]
0.369 (Dynamic method) [13]
Gzx (GPa) 0.395 0.395 0.395 0.395 - -
Gyz (GPa) 0.259 0.259 0.259 0.259 0.259 [10]
0.22 (Hexcel) [13]
0.251 (ASTM) [13]
0.217 (Dynamic method) [13]
Gzy (GPa) 0.259 0.259 0.259 0.259 - -
(a) (b)
x
z
y
120˚
a/2
a/2 h/2
t
a
h
a/2
t
t
Figure 2. (a) 3D view of unit cell; (b) 1/8 segment used in finite element analysis due to symmetry conditions of the unit cell.
The actual interface conditions are in between these two
extreme cases due to the elasticity of the bonded inter-
face between the facesheet and core. Note that the
boundary conditions for the wall fixed case can be ob-
tained from those given in Table 1 by imposing the addi-
tional constraint that AR = all rotations = 0 at edges E4,
E5 and E6. In addition, the effect of the order of the ele-
ments was investigated by considering 4-noded and 8-
noded shell elements. The results were virtually identical
for 4- and 8-noded elements for wall free conditions and
a small difference in the wall fixed case for the relatively
small in-plane properties (Ex, Ey, Gxy and Gyx) and the
near zero Poisson’s ratios ( 
xz and

yz). Hence, only 4-
noded elements are used hereafter. It can be seen in Ta-
ble 2 that there is good agreement between the literature
results and the present finite element solution. The dif-
ference is most likely due to the approximate nature of
the theoretical results, which are based on mechanics of
materials approximations. The few experimental results
available are reasonably close to the present results, es-
pecially when one considers the difficulties inherent in
measuring the elastic properties of the core [13]. It is
interesting to note that virtually no difference in values is
observed between the wall free and wall fixed conditions

Effective Elastic Properties of Honeycomb Core with Fiber-Reinforced Composite Cells
93
x
z
y
120˚
a/2
a/2 h/2
t
S2
S1
E7
E1
E3
E8
E4
E2
E5
E6
master node
for CPDOF
(a)
(b)
t
t
Figure 3. (a) 1/8 segment used in finite element analysis; (b)
Typical finite element mesh used showing the labeling of
edges (E) and surfaces (S).
for the properties not small or near zero (Ez,

xy,

yx,

zx,

zy, Gxz, Gzx, Gyz and Gzy). However, this is not necessar-
ily the case with other cell dimensions, wall thicknesses,
and when composite cells are considered, as seen in Ta-
bles 4 and 6, especially for the Poisson’s ratios. However,
the difference is small and either the wall free or wall
fixed boundary conditions can be used to approximate
the effective elastic properties of the core.
An additional check is provided by noting that the
symmetry of the stiffness constants requires that the fol-
lowing relations be satisfied [12]:
,,
x
yxyxzzxyzzy
GGGGGG (7)
,,
yzz
y
xxyzxxzzyyz
xxy
EEE
EEE

   (8)
In order to perform this check, the properties Gyz, Gzx,
Gzy, 
yx,

zx and

zy were additionally calculated. The ap-
propriate boundary conditions for these cases are also
given in Table 1 . It can be seen that the results in Table
2 either equally or very nearly satisfy Equations (7), (8),
providing an additional check on the results. The only
case where there is a small discrepancy is in the in-plane
shear modulus, Gxy. This discrepancy may be explained
by the relatively small value of Gxy with respect to the
out-of-plane shear moduli, Gxz and Gyz, which are rough-
ly 2 - 3 orders of magnitude smaller. It should be noted
that Chamis [14] noticed a similar small discrepancy
between Gxy and Gyx using a completely different ap-
proach based on a three dimensional detailed finite ele-
ment model of the honeycomb that included multiple
cells. His results were based on “wall free” conditions for
the cells. Chamis also observed a much smaller discrep-
ancy between Gxz and Gzx and exact equality between Gyz
and Gzy, all consistent with the present results.
4. Results for Anisotropic Cells and
Discussion
The 1/8 segment of a unit cell shown in Figure 3(a) was
modeled using version 2.95 of the finite element code
COSMOS/M [15]. This finite element code includes, in
its library, a layered composite element with a capacity
of up to fifty layers, and is suitable for the analysis of
structures made of composite materials. The finite ele-
ment mesh used herein is shown in Figure 3(b) and con-
sisted of 1,701 nodes and 1,600 four-noded composite
shell elements. The boundary conditions used are those
shown in Table 1. A cell size of 25.4 mm and three la-
yups ([45/−45]s, [0/±60]s, and [0 ± 53.5/90]s) were con-
sidered. All of the layups used result in a relatively low
coefficient of thermal expansion in the walls of the core
and were chosen because they provide different condi-
tions of practical importance. The [45/-45]s laminate has
the smallest thickness and highest in-plane shear, but its
other elastic properties are relatively low. The [0/±60]s
laminate is a quasi-isotropic laminate with intermediate
thickness. The [0/±53.5/90]s laminate has near zero coef-
ficient of thermal expansion in the x-direction (see foot-
note under Table 3), but has the highest thickness. In
each case, a larger thickness means higher density. For
the various cell sizes, the cell height used was the same
as the cell size, h = a. The same number of elements and
nodes were used in each case, although the element size
was scaled up or down depending on the cell size. The
ply (lamina) material used consisted of a high modulus
pitch fiber with a cyanate ester matrix, and has the prop-
erties given in Table 5 [16]. As a result of its high stiff-
ness and dimensional stability due to its hygrophobic
nature, this material system is well suited for use in
composite mirror applications. Furthermore, the thermoe-
lastic laminate properties for each laminate, calculated
from laminated plate theory [12], are given in Table 3
along with the corresponding properties of aluminum for
comparison. The equivalent stiffnesses for the core re-
sulting from the analysis are given in Tables 4 and 6,
respectively, for the cases of free and fixed boundary
conditions at edges E4, E5 and E6 (Figure 3b). The re-
sults for the composite (anisotropic) core are compared
with those of aluminum core of the same density. For a
hexagonal core, the dimensionless relative density, de-
fined as the ratio of the core density
 to the density of
the raw material

m, can be expressed in terms of the wall
thickness and cell size as:



wallwallwall
cellcellcell
22 8
33
32 222
m
mm
mVA
cmVA
aaat t
a
aaaa
 

 




(9)
where the cell used corresponds to the 1/8 segment in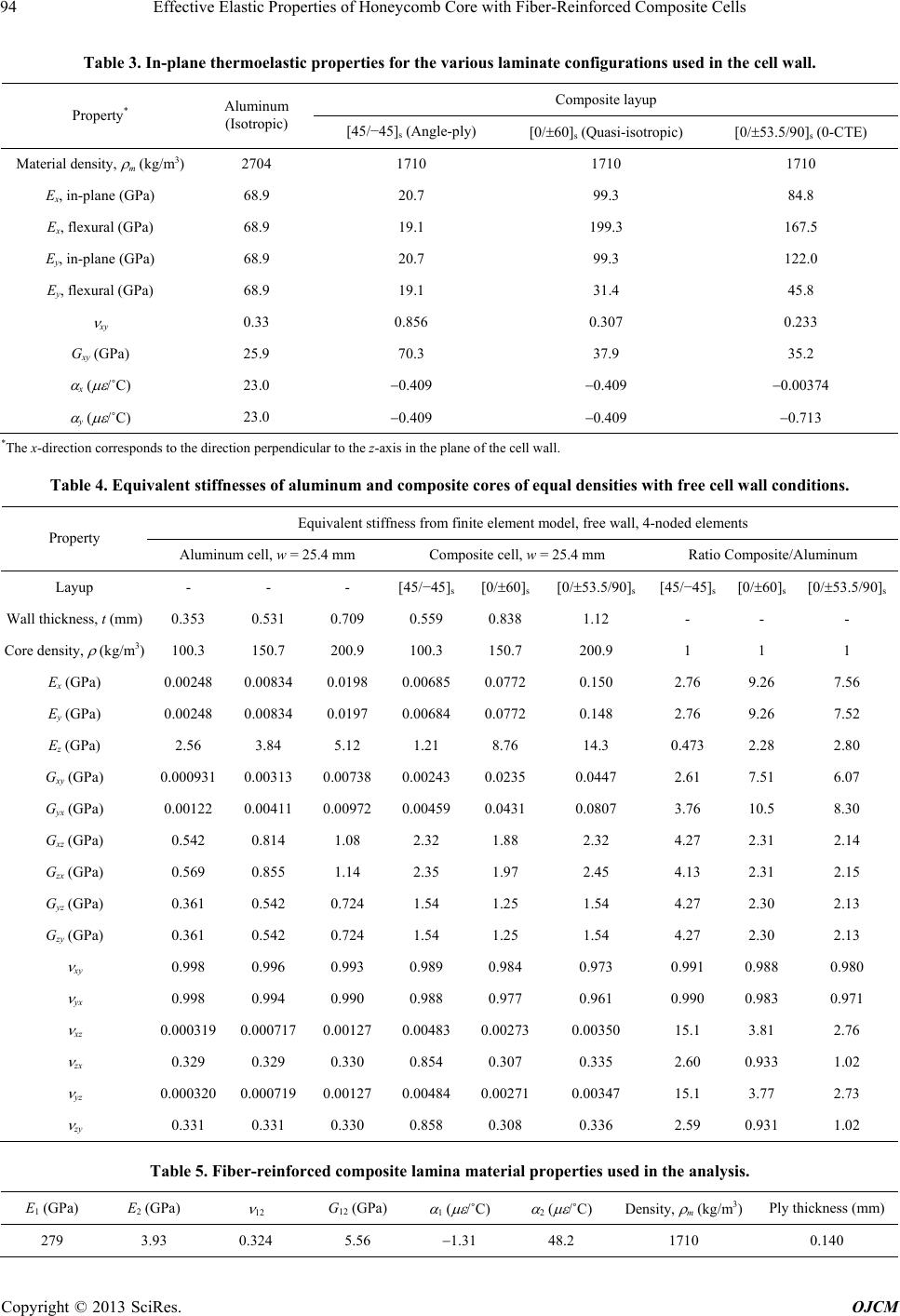

Effective Elastic Properties of Honeycomb Core with Fiber-Reinforced Composite Cells
94
Table 3. In-plane thermoelastic properties for the various laminate configurations used in the cell wall.
Composite layup
Property* Aluminum
(Isotropic) [45/−45]s (Angle-ply) [0/60]s (Quasi-isotropic) [0/53.5/90]s (0-CTE)
Material density, 
m (kg/m3) 2704 1710 1710 1710
Ex, in-plane (GPa) 68.9 20.7 99.3 84.8
Ex, flexural (GPa) 68.9 19.1 199.3 167.5
Ey, in-plane (GPa) 68.9 20.7 99.3 122.0
Ey, flexural (GPa) 68.9 19.1 31.4 45.8

xy 0.33 0.856 0.307 0.233
Gxy (GPa) 25.9 70.3 37.9 35.2

x (
 /˚C) 23.0 0.409 0.409 0.00374

y (
 /˚C) 23.0 0.409 0.409 0.713
*The x-direction corresponds to the direction perpendicular to the z-axis in the plane of the cell wall.
Table 4. Equivalent stiffnesses of aluminum and composite cores of equal densities with free cell wall conditions.
Equivalent stiffness from finite element model, free wall, 4-noded elements
Property
Aluminum cell, w = 25.4 mm Composite cell, w = 25.4 mm Ratio Composite/Aluminum
Layup - - - [45/−45]s[0/60]s [0/53.5/90]s[45/−45]s [0/60]s [0/53.5/90]s
Wall thickness, t (mm) 0.353 0.531 0.709 0.559 0.838 1.12 - - -
Core density,  (kg/m3) 100.3 150.7 200.9 100.3 150.7 200.9 1 1 1
Ex (GPa) 0.00248 0.00834 0.0198 0.00685 0.0772 0.150 2.76 9.26 7.56
Ey (GPa) 0.00248 0.00834 0.0197 0.00684 0.0772 0.148 2.76 9.26 7.52
Ez (GPa) 2.56 3.84 5.12 1.21 8.76 14.3 0.473 2.28 2.80
Gxy (GPa) 0.000931 0.00313 0.00738 0.00243 0.0235 0.0447 2.61 7.51 6.07
Gyx (GPa) 0.00122 0.00411 0.00972 0.00459 0.0431 0.0807 3.76 10.5 8.30
Gxz (GPa) 0.542 0.814 1.08 2.32 1.88 2.32 4.27 2.31 2.14
Gzx (GPa) 0.569 0.855 1.14 2.35 1.97 2.45 4.13 2.31 2.15
Gyz (GPa) 0.361 0.542 0.724 1.54 1.25 1.54 4.27 2.30 2.13
Gzy (GPa) 0.361 0.542 0.724 1.54 1.25 1.54 4.27 2.30 2.13

xy 0.998 0.996 0.993 0.989 0.984 0.973 0.991 0.988 0.980

yx 0.998 0.994 0.990 0.988 0.977 0.961 0.990 0.983 0.971

xz 0.000319 0.000717 0.00127 0.00483 0.00273 0.00350 15.1 3.81 2.76

zx 0.329 0.329 0.330 0.854 0.307 0.335 2.60 0.933 1.02

yz 0.000320 0.000719 0.00127 0.00484 0.00271 0.00347 15.1 3.77 2.73

zy 0.331 0.331 0.330 0.858 0.308 0.336 2.59 0.931 1.02
Table 5. Fiber-reinforced composite lamina material properties used in the analysis.
E1 (GPa) E2 (GPa)

12 G12 (GPa)

1 (
 /˚C) 
2 (
 /˚C) Density, 
m (kg/m3) Ply thickness (mm)
279 3.93 0.324 5.56 1.31 48.2 1710 0.140

Effective Elastic Properties of Honeycomb Core with Fiber-Reinforced Composite Cells
95
Table 6. Equivalent stiffnesses of aluminum and composite cores of equal densities with fixed cell wall conditions.
Equivalent stiffness from finite element model, fixed wall, 4-noded elements
Property
Aluminum cell, w = 25.4 mm Composite cell, w = 25.4 mm Ratio Composite/Aluminum
Layup - - - [45/−45]s [0/±60]s[0/±53.5/90]s[45/−45]s [0/±60]s [0/±53.5/90]s
Wall thickness, t (mm) 0.353 0.531 0.709 0.559 0.838 1.12 - - -
Core density,
 (kg/m3) 100.3 150.7 200.9 100.3 150.7 200.9 1 1 1
Ex (GPa) 0.0596 0.186 0.403 0.0275 0.101 0.199 0.462 0.544 0.493
Ey (GPa) 0.0585 0.179 0.379 0.0274 0.100 0.195 0.468 0.558 0.515
Ez (GPa) 2.56 3.84 5.12 1.21 8.76 14.3 0.473 2.28 2.80
Gxy (GPa) 0.0412 0.125 0.265 0.0137 0.0389 0.0724 0.333 0.312 0.273
Gyx (GPa) 0.0290 0.0896 0.194 0.0182 0.0599 0.111 0.629 0.668 0.573
Gxz (GPa) 0.542 0.814 1.08 2.32 1.88 2.32 4.27 2.31 2.14
Gzx (GPa) 0.570 0.855 1.14 2.35 1.98 2.46 4.12 2.31 2.15
Gyz (GPa) 0.361 0.542 0.724 1.54 1.25 1.54 4.27 2.30 2.13
Gzy (GPa) 0.363 0.547 0.731 1.56 1.28 1.61 4.30 2.35 2.20

xy 0.958 0.913 0.859 0.956 0.979 0.964 0.998 1.07 1.12

yx 0.941 0.879 0.808 0.951 0.970 0.949 1.01 1.10 1.17

xz 0.00767 0.0160 0.0259 0.0194 0.003560.00465 2.53 0.223 0.180

zx 0.330 0.330 0.330 0.856 0.307 0.335 2.59 0.930 1.02

yz 0.00753 0.0154 0.0244 0.0193 0.003530.00457 2.56 0.229 0.187

zy 0.330 0.330 0.330 0.856 0.307 0.335 2.59 0.930 1.02
Figure 2b, V = volume and A = cross-sectional area.
The above equation indicates that in order to achieve
the same density for aluminum and composite cores, the
thickness of the aluminum core wall must be made small-
er by the ratio of raw material densities as follows:



composite
Alcomposite composite
Al
0.633
m
m
tt t


 (10)
Tables 4 and 6 also show the ratio of the composite
and aluminum cell properties. A ratio higher than one
indicates that the corresponding property of the compos-
ite cell is larger than that of the aluminum. It can be seen
that in most cases the composite has higher properties,
especially for the transverse shear moduli (Gxz and Gyz),
which are always higher for the composite core. These
transverse moduli are essential in the design of sandwich
panels since the core must be stiff enough in shear to
ensure that the facesheets do not slide over each other
when bending is present. In addition, no significant dif-
ference is seen between the “free wall” and “fixed wall”
results for the properties not small or near zero (Ez,

xy,

yx,

zx,

zy, Gxz, Gzx, Gyz and Gzy) in Tables 4 and 6.
5. Summary and Conclusions
A simplified finite element procedure to determine the
equivalent engineering elastic moduli of a hexagonal cell
core has been presented, including the appropriate bound-
ary conditions that must be applied to a 1/8 segment of a
unit cell in order to replicate the behavior of the overall
core. Using this method, values for the effective proper-
ties of hexagonal cell cores made of composite materials
of various layups were presented. It was shown that the
present method provides an accurate and practical way to
incorporate the anisotropic and heterogeneous behavior
of composite materials in the analysis of core properties.
Furthermore, accurate values for the effective core prop-
erties are particularly important in the design of sand-
wich composite structures such as optical composite mir-
rors. Results for composite core showed that the trans-
verse shear moduli are always higher than those of alu-
minum for the same core density. Additionally, if sand-
wich panels incorporate both composite facesheets and
core, instead of aluminum core, then lower weights, in-
creased stiffness, lower thermal distortion compatible
with that of the facesheets, the absence of galvanic cor-

Effective Elastic Properties of Honeycomb Core with Fiber-Reinforced Composite Cells
96
rosion and the ability to readily modify the core proper-
ties to suit specialized needs can be achieved.
REFERENCES
[1] R. Atkinson, “Innovative Uses for Sandwich Construc-
tions,” Reinforced Plastics, Vol. 41, No. 2, 1997, pp. 30-
33.
[2] F. E. Penado, J. H. Clark III, J. P. Walton, R. C. Romeo
and R. N. Martin, “Calculation of the Elastic Properties of
a Triangular Cell Core for Lightweight Composite Mir-
rors,” Proceedings of SPIE: New Developments in Opto-
mechanics, San Diego, 26-30 August 2007, pp. B1-B8.
[3] R. C. Romeo and R. N. Martin, “Progress in 1 m-Class
Lightweight CFRP Composite Mirrors for the ULTRA
Telescope,” Proceedings of SPIE: Optomechanical Tech-
nologies for Astronomy, Orlando, 24 May 2006, p.
62730S.
[4] J. Hohe and W. Becker, “Effective Stress-Strain Relations
for Two-Dimensional Cellular Sandwich Cores: Homog-
enization, Material Models, and Properties,” Applied Me-
chanics Reviews, Vol. 55, No. 1, 2002, pp. 61-87.
http://dx.doi.org/10.1115/1.1425394
[5] S. Kelsey, R. A. Gellatly and B. W. Clark, “The Shear
Modulus of Foil Honeycomb Cores: A Theoretical and
Experimental Investigation on Cores Used in Sandwich
Construction,” Aircraft Engineering and Aerospace Tech-
nology, Vol. 30, No. 10, 1958, pp. 294-302.
http://dx.doi.org/10.1108/eb033026
[6] G. Hoffman, “Poisson’s Ratio for Honeycomb Sandwich
Cores,” Journal of the Aerospace Sciences, Vol. 25, No. 8,
1958, pp. 534-535. http://dx.doi.org/10.2514/8.7765
[7] J. Zhang and M. F. Ashby, “The Out-of-Plane Properties
of Honeycombs,” International Journal of Mechanical
Sciences, Vol. 34, No. 6, 1992, pp. 475-489.
http://dx.doi.org/10.1016/0020-7403(92)90013-7
[8] L. J. Gibson and M. F. Ashby, “Cellular Solids: Structure
and properties,” Pergamon Press, Oxford, 1988.
[9] I. G. Masters and K. E. Evans, “Models for the Elastic
Deformation of Honeycombs,” Composite Structures, Vol.
35, No. 4, 1996, pp. 403-422.
http://dx.doi.org/10.1016/S0263-8223(96)00054-2
[10] M. Grediac, “A Finite Element Study of the Transverse
Shear in Honeycomb Cores,” International Journal of
Solids and Structures, Vol. 30, No. 13, 1993, pp. 1777-
1788. http://dx.doi.org/10.1016/0020-7683(93)90233-W
[11] B. Kim and R. M. Christensen, “Basic Two-Dimensional
Core Types for Sandwich Structures,” International Jour-
nal of Mechanical Sciences, Vol. 42, No. 4, 2000, pp.
657-676.
http://dx.doi.org/10.1016/S0020-7403(99)00028-4
[12] R. F. Gibson, “Principles of Composite Material Me-
chanics,” McGraw-Hill, New York, 1994.
[13] C. W. Schwingshackl, G. S. Aglietti and P. R. Cunning-
ham, “Determination of Honeycomb Material Properties:
Existing Theories and an Alternative Dynamic Approach,”
Journal of Aerospace Engineering, Vol. 19, No. 3, 2006,
pp. 177-183.
http://dx.doi.org/10.1061/(ASCE)0893-1321(2006)19:3(1
77)
[14] C. C. Chamis, R. A. Aiello and P. L. N. Murthy, “Fiber
Composite Sandwich Thermostructural Behavior: Com-
putational Simulation,” Journal of Composites Technol-
ogy & Research, Vol. 10, No. 3, 1988, pp. 93-99.
http://dx.doi.org/10.1520/CTR10135J
[15] “COSMOS/M User Guide,” Version 2.95, Structural Re-
search and Analysis Corporation, Los Angeles, 2007.
[16] J. R. Andrews, F. E. Penado, S. T. Broome, C. C. Wilcox,
S. R. Restaino, T. Martinez, S. W. Teare and F. Santiago,
“Characterization of the Lightweight Telescope Devel-
oped for the NPOI,” Proceedings of SPIE: Ground-Based
and Airborne Telescopes , Orlando, 24 May 2006, p. 62673Q.