Advances in Remote Sensing, 2013, 2, 247-257
http://dx.doi.org/10.4236/ars.2013.23027 Published Online September 2013 (http://www.scirp.org/journal/ars)
Towards an Intelligent Predictive Model for Analyzing
Spatio-Temporal Satellite Image Based
on Hidden Markov Ch ain
Houcine Essid1,2, Imed Riadh Farah1,3, Vincent Barra2
1Research Laboratory in Computer Integrated Documentation and Arabized-Documentiel Geniuses and Software, National
School of Computer Science Campus, Universitaire de Manouba, Tunis, Tunisie
2Limos, Laboratory of Computer Modeling and System Optimization UMR CNRS 6158-Campus Scientifique des
Cézeaux-Office, Aubiere, France
3TELECOM-Bretagne, Département ITI Technopôle Brest Iroise, Brest, France
Received May 5, 2013; revised June 5, 2013; accepted July 8, 2013
Copyright © 2013 Houcine Essid et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
Nowadays remote sensing is an important technique for observing Earth surface applied to different areas such as, land
use, urban planning, remote monitoring, real time deformation of the soil that can be associated with earthquakes or
landslides, the variations in thickness of the glaciers, the measurement of volume changes in the case of volcanic erup-
tions, deforestation, etc. To follow the evolution of these phenomena and to predict their future states, many approaches
have been proposed. However, these approaches do not respond completely to the specialists who process yet more
commonly the data extracted from the images in their studies to predict the future. In this paper, we propose an innova-
tive methodology based on hidden Markov models (HMM). Our approach exploits temporal series of satellite images in
order to predict spatio-temporal phenomena. It uses HMM for representing and making prediction concerning any ob-
jects in a satellite image. The first step builds a set of feature vectors gathering the available information. The next step
uses a Baum-Welch learning algorithm on these vectors for detecting state changes. Finally, the system interprets these
changes to make predictions. The performance of our approach is evaluated by tests of space-time interpretation of
events conducted over two study sites, using different time series of SPOT images and application to the change in
vegetation with LANDSAT images.
Keywords: Satellite Image; Remote Sensing; Hidden Markov Model; Change Detection; Image Processing
1. Introduction
During the last decade there have been many improve-
ments and significant technical breakthroughs in the field
of remote sensing to improve the quality of available
observations [1]. The use of sensors with multi-temporal,
multi-resolution and multi-spectral images has yielded
new data essential to understanding the mechanics of
earthquakes, volcanoes dynamics and functioning of
major active tectonic structures. As a result, several re-
searches are conducted to extract useful information and
represent knowledge in order to interpret and analyze
dynamic scenes. Indeed, precise measurements taken
from a satellite image require a rigorous assessment of
uncertainty and robust methods to achieve operational
results. All these reasons have encouraged researchers to
focus their studies to detect, explain, interpret and predict
temporal variations in scenes of satellite images.
The aim of this paper is to present a methodological
framework for analyzing and predicting many joint space-
time events that occur in the time series of satellite im-
ages. This analysis is dedicated to automatically label
spatiotemporal structures and discover new events. To
achieve this goal, we exploit two areas: the extraction of
information from satellite images and stochastic analy-
ses.
Using satellite images that cover part of the Earth in
different times for the same place we thus first use image
processing and segmentation tools to get various de-
scriptors of satellite images. These descriptors then serve
as an input of a stochastic modeling process. The hidden
Markov model (HMM) allows the dynamic of objects to
be represented from a sequence of images to manage the
C
opyright © 2013 SciRes. ARS

H. ESSID ET AL. 248
change in sensor resolution. We thus model all the hid-
den states and descriptors in the form of a HMM whose
parameters are estimated by a learning based on time
series satellite images. Once estimated, these parameters
allow interpretation of variations and prediction to be
performed.
This article consists of three sections. The current sec-
tion introduces the context of our study by providing a
quick review of technical information extraction and ana-
lysis systems by spatiotemporal stochastic tools. The se-
cond section deals with our contributions for the ex-
ploitation of time series of satellite images, in coopera-
tion with the techniques for extracting information for
the spatiotemporal analysis based on a HMM. In the third
section we present the results of two applications of our
approach: SPOT imagery with various applications and
LANDSAT imagery applied to vegetation variation.
Now, we present a synthetic state of the art of remote
sensing images interpretation. The goal is to highlight
different strategies in the literature to achieve spatiotem-
poral modeling. These systems offer predictive analytics
solutions helping photo interpreters to predict future
events, and take advantage of different types of image
descriptors to characterize the dynamics of objects. We
focus our study on stochastic models. Several authors [2]
[3,4] have proposed a comprehensive review of existing
approaches to change detection in remote sensing. If me-
thods detecting changes using only two images are very
common, methods dedicated to the temporal trajectory
analysis are very few and generally correspond to adap-
tations of bi-dates methods to multiple dates. In general,
two images methods are rather used for the analysis of
abrupt changes at a local level and exploit data at high
spatial resolution. Conversely, multi temporal methods
focused on the analysis of slow changes or large-scale
phenomena. In the spatiotemporal domain analysis, Lazri
[5] developed an analytical model of rainfall data by a
Markovian approach. The data used consist of a series of
images collected by weather radar. The results show that
rainfall is well described by Markov chains of high order
both on land and sea and whatever the climate prevailing
in the region. In agriculture data mining, Mari [6] devel-
oped a Markov model to understand and explain the pro-
cess that produces the succession of crops. He used the
Peano curve [7] to perform spatial segmentation of ho-
mogeneous geographic regions in terms of spatial densi-
ties of crops and he used a second order HMM to study
the consequences of crops. In image recognition, Slimane
[8] designed a hybrid algorithm for learning images by
HMM. Aurdal et al. [9] as for them proposed a super-
vised classification method adapted to high dimensional
data from spatially correlated with LANDSAT satellite
images. The authors introduced a statistical model based
on the hidden Markov random field which took into ac-
count spatial dependencies between data. In statistical
image processing, Pieczynski [10-12] introduced new
systems dedicated to image segmentation by Markov
models such as pairwise Markov chains and triplet Mar-
kov chains. These particular models can better take into
account the boundaries between classes, which can be of
great interest for the segmentation of satellite images.
But, the complexity of these models is higher than the
conventional model. An application in detecting changes
between radar images was developed by Carincotte [13]
based on a fuzzy Markovian segmentation of images.
The same kind of idea has been studied by Derrode [14]
who designed two HMM-based algorithms, a fuzzy one
and a sliding window-based one. In the same study area,
Wijanarto [15] developed a technique for Markov change
detection that can be used to predict future changes based
on the rate of changes in the past and generating prob-
abilities of changes between classes. These probabilities
were calculated using a transition matrix of pixels be-
tween the classes for two periods of time. In the field of
automatic information extraction, Lacoste [16] presented
a method for unsupervised extraction of line networks,
such as roads or water systems, from satellite images.
This system modeled the line network in the image by a
Markov process. The density of this process was built to
exploit the best properties of the network topology and
radiometric data properties. An algorithm for Monte Car-
lo Markov chain reversible jump was proposed for opti-
mization.
Most of these systems have addressed the component
of change detection which aims to generate an image re-
presenting the areas of changes/no changes between two
images I1 and I2 (or sequences of images) acquired at
two different times (or time intervals), commonly called
image map changes. Few of them have solved the prob-
lem of explanation and prediction of space-time events
from time series of satellite images. The prediction mod-
els are generally stochastic models using the calculation
of probabilities. They can describe and predict the char-
acteristics of a given system under different configura-
tions. Once these characteristics are known, the best so-
lution among the alternatives evaluated is selected. This
choice is simplified by a technique for detecting changes.
However, we note the existence of a variety of tech-
niques such as spectral mixture analyses [17]. And since
the digital change detection is affected by spatial, spec-
tral, thematic and temporal features, the selection of a
suitable method or algorithm, for a given research project,
is very important. Many systems use HMM in speech
recognition, audiovisual detection, isolated character re-
cognition and degraded printed character recognition, but
not in satellite image analysis. In our approach, we chose
to use the HMM because the processing of satellite im-
ages representing natural scenes brought a large volume

H. ESSID ET AL. 249
of information. HMM is a statistical tool allowing
complex stochastic phenomena to be modeled. They are
used in a lot of areas including speech recognition and
synthesis, biology, scheduling, information retrieval, re-
cognition image, temporal series prediction.
2. Proposed Approach
The main contribution of our work lies in the use of
HMM for both change detection in satellite images and
prediction. The proposed approach is composed of three
phases. The first one is a segmentation and preprocessing
step of a series of satellite images. In the second step we
measure and normalize descriptors for using them in
HMM learning. Finally, in the third step we use the
HMM structure to predict events.
Phase 1:
The method begins with a processing chain that starts
from the acquisition of a series of satellite images

12
,,,
n

I
II where Ik denotes the kth image of size
M × N. Each image is composed of a set of pixels each of
them being represented by a vector of n radiometric com-
ponents xj. From these vectors, the matrix SN×M,n featur-
ing the all dataset can be formed. Since the large amount
of data carried out by these vectors may not optimaly
represent the available information, we applied a reduc-
tion dimension technique and more precisely a principal
component analysis (PCA) [18]. PCA is a method widely
used in the field of remote sensing. Besides, the images
of the same scene registered according to the various
spectral ranges of the sensor are highly correlated. The
purpose of PCA is to condense the original data into new
groups so that the variace explained by these groups is
maximized. This allows to tranform the matrix SN×M,n
into SN×M,d, where (d represents the number of
descriptors i.e., principal components). This more infor-
mative matrix is then partitioned by SCFCM (spatially
constrained fuzzy c-means algorithm [19]), a fuzzy clus-
tering algorithm based on the optimization of a quadratic
criterion of classification where each class is represented
by its center. This allows the coexistence of hard pixels
(obtained with the classical HMM segmentation) and
fuzzy pixels (obtained with the fuzzy measure) in the
same image [13].
dn
SCFCM allows a fuzzy partition UN×M,C = (uik), uik in
[0,1] of the image to be computed. More precisely, let C
the number of classes, V = {Vi} be the set of unknown
class centroids, M × N the number of individuals and m a
fuzzy exponent (m > 1). The objective of the method is to
find U and V minimizing the cost function:
2
11 11
2j
MNC MNC
mm
SCFCMij jiik
ji jikN
J
ux vu


 


with
1
11,,
C
ik
i
uk


n
U and V are iteratively found using

1
21
j
m
m
ji ik
kN
j
j
i
mx vu
u






And
1
1
MN m
ij j
j
iMN
j
uX
V






And





11
2
11
1j
m C
mm
jjiik
kN
i
mxv u 






where Nj is the set of neighbours of pixel j (except j). The
parameter β controls the trade-off between minimizing
the standard FCM objective function and obtaining
smooth membership functions [20]. SCFCM allows each
pixel j to be represented by a set of C membership’s uij
describing the way the pixel j belongs to region i, 1 ≤ i ≤
C. We focus on classes such that harvesting of a field, the
evolution of the forest in autumn, the maturation of a
field of rapeseed and the changing river. Following this
segmentation, each image is quantified; isolated objects
are measured by the descriptors chosen. This information
is collected to form the raw data set of our Markov model.
Phase 2:
During this phase, measurements of descriptors are
stored as vectors describing each region of the study area
at a time t. These vectors will serve to build the database
of our model. We perform a smoothing and a normaliza-
tion of the data to obtain the characteristic vectors.
The feature vectors obtained are continuous and they
can be quantified using a dictionary coding. The alterna-
tive is to include densities of continuous observations in
the model using a continuous HMM. But the large num-
ber of parameters to be determined is a serious drawback
of the model. Feature vectors are thus discretized using a
Kohonen network [21]. This allows obtaining a dozen
possible observations. Some of these observations serve
as input for the HMM training phase. The choice is pro-
portional to the surface of each class (see Figure 1).
The obtained data are then used in a hidden Markov
chain to model the variation of the tracked object. A first
order stationary hidden Markov model corresponds to
two stochastic processes: one is a homogeneous Markov
chain and the second depends on the first process.
Let be


1,, p
H
hh the set of P hidden states of
the system. Let


1,, T
SS S be a T-uple of random

H. ESSID ET AL. 250
R1
R2
R4
R3
R5
R6
R1
R2
R4
R3
R5
R6
R1
R2
R4
R3
R5
R6
Image T1 Image T2 Image Tn
…………………………………………..…
R1
R2
R3
R4
R5
R6
R1
R2
R3
R4
R5
R6
R1
R2
R3
R4
R5
R6
………… R1 at t1
R1 at t2
R1 att n
………… R2 at t1
R2 at t2
R2 at t n
…………………………
………… R6 at t1
R6 at t2
R6 at t n
Filtering
Ve c tors
extraction
Vectors / imagesRegions/ imagesVectors / regions
Image afterthe FCMImage afterthe FCMImage afterthe FC
M
100
150
50
100
150
50
50
100
150
50 100150 50100 150 50 100 150
……………………………..…………………..
………… …………
Coding
Classification SOM
Class A, Class B, Class C…
…………
R1 at t1 C
R1 at t2 A
R1 at tn B
R2 at t1 D
R2 at t2 B
R2 at tn B
R6 at t1 E
R6 at t2 A
R6 at tn C
Coded vectors
(HMM Observations)
Construction of observations
Figure 1. Extraction and selection of training data.
variables defined on S. Let be the set of

1,, q
Oo o



1i
PS s
Q symbols that can be emitted by the system. Let  the probabilities of transiting between two states:


1,, T
Vv v be a T-uple of random variables defined


1tjt i
PSs Ss


on V. A hidden Markov model is then defined by the
following probabilities:
 the probabilities of emitting a particular symbol for a
particular state:
 the probabilities of starting the sequence with a par-
ticular state:

H. ESSID ET AL. 251

tjti
PVv Ss
If the HMM is a first order stationary hidden Markov
model then many simplifications can be done. Let:

1
iip


 with


it
PSs  
i

,1, ij ij p
Aa  with

,1ijtj ti
aPSsS s

 ,
 
1,1
iip jq
Bbj
 
 with


itjti
bjPV vSs
A first order stationary hidden Markov model  is then
completely defined by the triple (A,B,∏). In the fol-
lowing, we will consider the notation  = (A,B,∏) and
we note HMM a first order stationary.
We note a hidden state se-

1,, T
T
Qqq S
quence and an observed sequence

1,, T
T
Ooo V
of symbols. The probability that a state sequence Q and
an observed sequence of symbols O occurs given a
HMM  is

,VOSQ


 . Probability dependencies
allow to write:



,,,PVOSQPVOSQPS Q


   
With


1
,, T
tttt
t
PVOSQPVo Sq 

 


and
 
1
111 1
1
,
T
tttt
t
PSQPSqPSqSq





 

From a HMM  , a state sequence Q and an observed
sequence of symbols O, we can compute the adequacy
between the model  and the two sequences Q and O.
For so, we need to compute the probability

,PVOS Q

 . When the state sequence is un-
known, it is possible to compute the likelihood of the
observed sequence O given a model  by evaluating the
probability:



,
QS
PV OPVOSQ



 

When manipulating hidden Markov models, we com-
monly need to solve three kind of problems (for a given
HMM  ) :
 computing the likelihood,

O
 determining the state sequence * Q that is the most
likely followed to emit the observed sequence O: the
state sequence * Q defined by the following equation
is efficiently computed by the Viterbi algorithm with
a complexity of


2
OpT;

*arg max,
T
Qs
QPVOSQ



 Adjusting one or many HMMs from one or many
observed sequences when the number of hidden state
in HMMs is known: training can be viewed as a con-
strained optimization problem for which we try to
maximize some criterion. There exist many criteria
used for HMMs training [8]. When considering the
maximization of the likelihood, we search a HMM
*

satisfying the equation

*arg maxPV O





Up to now, there is no general solution to this problem
but algorithms, such as the Baum-Welch algorithm [22]
which is an iterative re-estimation which counted the
number of times each state, each transition and each sym-
bol was attached to the statements used in all sequences.
We can also use the gradient descent [23] to improve an
initial solution. Training algorithm for HMMs are iterative
methods such that when iterating the algorithm, only a
local optimum of the criterion can be found. This article
attempts to show that it is reasonable to adopt a new pol-
icy of learning so that the time series of satellite images
provide a good prediction of space-time events.
Note that change detection may be of different types of
origin and of varying lengths, which allows distinguish-
ing different families of applications:
 Monitoring of land use, which corresponds to the
characterization of the development of vegetative tis-
sue, or the detection of seasonal changes in vegeta-
tion;
 The management of natural resources, which corre-
sponds to the characterization of urban development,
monitoring of deforestation...
 Mapping of damages, which corresponds to the loca-
tion of the damages caused by natural disasters e.g. a
volcanic eruption, a tsunami, an earthquake, a flood.
Thus the hidden states of our model change depending
on the application domain. Let consider the database
system already constructed from phase 1 and containing
a set V of data vectors describing each region in the study
area at a time t:
PV

 , of an ob-
served sequence O given a model : this problem is
efficiently solved by the Forward algorithm or by the
Backward algorithm with a complexity of


2
OpT
[22];


11211 12
at ,at ,,at;;at,at,,at
mnnm
VRtRtRtRtRt Rt 
n
Following an unsupervised classification by Kohonen network, we obtain a set C of classes including the vec-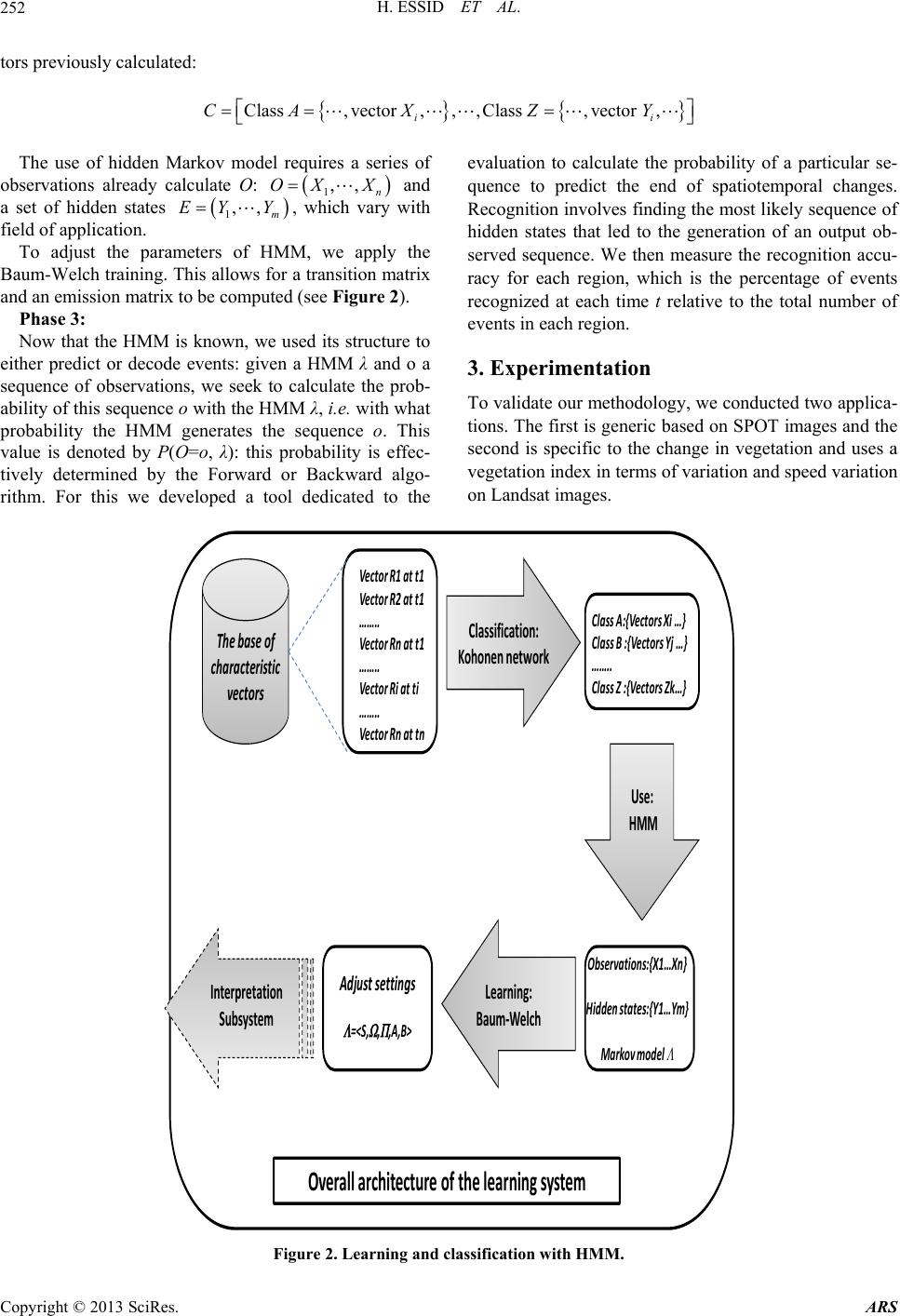

H. ESSID ET AL. 252
tors previously calculated:




Class ,vector ,,,Class ,vector ,
ii
CA XZY

  


 
The use of hidden Markov model requires a series of
observations already calculate O:


1,, n
OX X

m
Y
and
a set of hidden states , which vary with
field of application.

1,,EY
To adjust the parameters of HMM, we apply the
Baum-Welch training. This allows for a transition matrix
and an emission matrix to be computed (see Figure 2).
Phase 3:
Now that the HMM is known, we used its structure to
either predict or decode events: given a HMM λ and o a
sequence of observations, we seek to calculate the prob-
ability of this sequence o with the HMM λ, i.e. with what
probability the HMM generates the sequence o. This
value is denoted by P(O=o, λ): this probability is effec-
tively determined by the Forward or Backward algo-
rithm. For this we developed a tool dedicated to the
evaluation to calculate the probability of a particular se-
quence to predict the end of spatiotemporal changes.
Recognition involves finding the most likely sequence of
hidden states that led to the generation of an output ob-
served sequence. We then measure the recognition accu-
racy for each region, which is the percentage of events
recognized at each time t relative to the total number of
events in each region.
3. Experimentation
To validate our methodology, we conducted two applica-
tions. The first is generic based on SPOT images and the
second is specific to the change in vegetation and uses a
vegetation index in terms of variation and speed variation
on Landsat images.
Overall architecture of the learning system
The base of
characteristic
vecto r s
VectorR1 att1
VectorR2 att1
……..
VectorRn att1
……..
VectorRi atti
……..
VectorRn attn
Classification:
Kohonen network
Class A:{Vectors Xi …}
Class B :{VectorsYj…}
……..
Class Z :{Vectors Zk…}
Use:
HMM
Observations:{X1…Xn}
Hidden states:{Y1…Ym}
Markov model 
Learning:
Baum-Welch
Adjustsettings
 =<S,  ,  ,A,B>
Interpretati on
Subsystem
Figure 2. Learning and classification with HMM.

H. ESSID ET AL. 253
3.1. First Experiment
The methodology described in the previous section is
implemented using Matlab programming language,
MS-Excel spreadsheet, free software for processing and
image analysis: Multispec (normalization of multispec-
tral satellite images), Image Analyzer (principal compo-
nent analysis), UTHSCSA ImageTool (used to extract
feature vectors of each region and to record in the learn-
ing database) and TANAGRA (used to classify and
quantify all feature vectors using Kohonen maps). We
tested our methodology on a sample of four sequences of
time series of satellite images of Gueguen ADAM pro-
ject in 2007 [24]. The image acquisition was daily for a
period of 10 months, from October 2000 to July 2001 by
Spot 1, 2 and 4 and concerns the area located in the Iflov
departement at the East of Bucharest in Romania. Each
series consists of 10 images of size 200 × 200. These
sequences exhibit some phenomena that can be observed
in the series. The first one is the harvesting of a field that
is the human activity most observable sky. The second
shows the evolution of the forest in autumn. The third is
the maturation of a field of rapeseed which appears in
white. Finally, the fourth shows a changing river.
We began by analyzing each image time series to ex-
tract feature vectors of each region such as area, cen-
troid, compactness, and save them in the learning data-
base (see Table 1).
All these vectors were classified using Kohonen maps
using data mining software TANAGRA. Thereafter each
vector was identified by a code representing the class.
Finally, our system tried to learn a HMM for each time
series of satellite images from sequences of observations,
when we set in the learning database the number of hid-
den states, (i.e. a state for each type of spatiotemporal
event), the transition matrix, the emission matrix and
initial probabilities of departure. Once learning is com-
pleted, we interpreted spatiotemporal events on regions
of interest based on HMM. Figure 3 shows an example
HMM
Viterbi algorithm
ExpansionStabilization Regression
A0.0000 0.5776 0.2737
B0.0000 0.0000 0.7263
C0.7504 0.1367 0.0000
D0.2496 0.2858 0.0000
ExpansionStabilization Regression
010
ExpansionStabilization Regression
Expansion0.4168 0.0000 0.5832
Stabilization0.6720 0.3280 0.0000
Regression0.00000.4445 0.5555
at t1: D
att2: C
att3: C
att4: A
att5: A
att7: C
att6: D
att8: B
att9: A
att10: A
DCCAADCBAA
at T1: Stabilization, at T2: Expansion, atT3: Stabilization, at T4: Regression, at T5: Regression,
atT6: Re
g
ression
,
at T7: Ex
p
ansion, atT8: Ex
p
ansion, atT9: Re
g
ression and at T10: Re
g
ression.
Figure 3. General scheme for the interpretation of spatiotemporal events.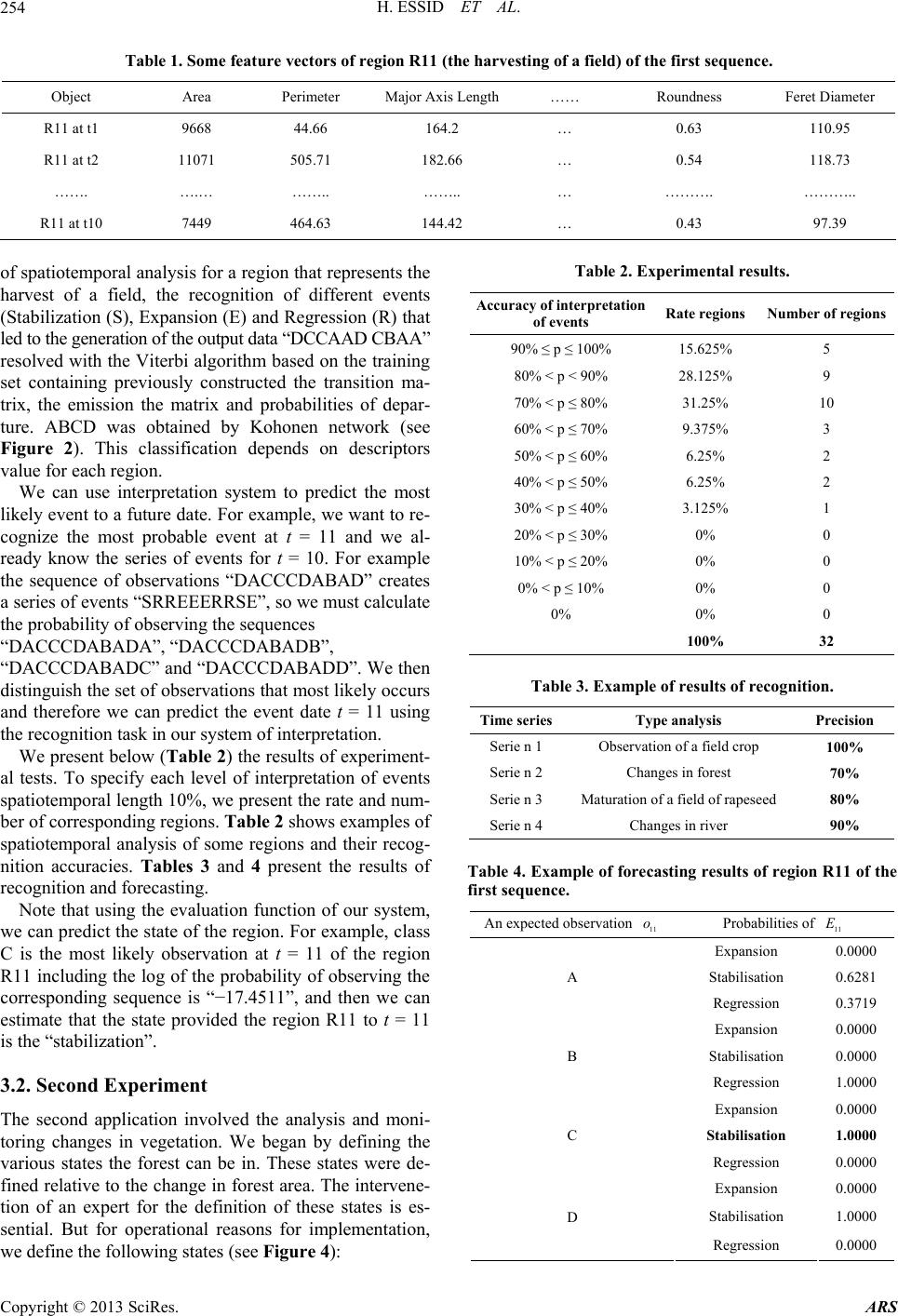

H. ESSID ET AL. 254
Table 1. Some feature vectors of region R11 (the harvesting of a field) of the first sequence.
Object Area Perimeter Major Axis Length …… Roundness Feret Diameter
R11 at t1 9668 44.66 164.2 … 0.63 110.95
R11 at t2 11071 505.71 182.66 … 0.54 118.73
……. ….… …….. …….. … ………. ………..
R11 at t10 7449 464.63 144.42 … 0.43 97.39
of spatiotemporal analysis for a region that represents the
harvest of a field, the recognition of different events
(Stabilization (S), Expansion (E) and Regression (R) that
led to the generation of the output data “DCCAAD CBAA”
resolved with the Viterbi algorithm based on the training
set containing previously constructed the transition ma-
trix, the emission the matrix and probabilities of depar-
ture. ABCD was obtained by Kohonen network (see
Figure 2). This classification depends on descriptors
value for each region.
We can use interpretation system to predict the most
likely event to a future date. For example, we want to re-
cognize the most probable event at t = 11 and we al-
ready know the series of events for t = 10. For example
the sequence of observations “DACCCDABAD” creates
a series of events “SRREEERRSE”, so we must calculate
the probability of observing the sequences
“DACCCDABADA”, “DACCCDABADB”,
“DACCCDABADC” and “DACCCDABADD”. We then
distinguish the set of observations that most likely occurs
and therefore we can predict the event date t = 11 using
the recognition task in our system of interpretation.
We present below (Table 2) the results of experiment-
al tests. To specify each level of interpretation of events
spatiotemporal length 10%, we present the rate and num-
ber of corresponding regions. Table 2 shows examples of
spatiotemporal analysis of some regions and their recog-
nition accuracies. Tables 3 and 4 present the results of
recognition and forecasting.
Note that using the evaluation function of our system,
we can predict the state of the region. For example, class
C is the most likely observation at t = 11 of the region
R11 including the log of the probability of observing the
corresponding sequence is “−17.4511”, and then we can
estimate that the state provided the region R11 to t = 11
is the “stabilization”.
3.2. Second Experiment
The second application involved the analysis and moni-
toring changes in vegetation. We began by defining the
various states the forest can be in. These states were de-
fined relative to the change in forest area. The intervene-
tion of an expert for the definition of these states is es-
sential. But for operational reasons for implementation,
we define the following states (see Figure 4):
Table 2. Experimental results.
Accuracy of interpretation
of events Rate regions Number of regions
90% ≤ p ≤ 100% 15.625% 5
80% < p < 90% 28.125% 9
70% < p ≤ 80% 31.25% 10
60% < p ≤ 70% 9.375% 3
50% < p ≤ 60% 6.25% 2
40% < p ≤ 50% 6.25% 2
30% < p ≤ 40% 3.125% 1
20% < p ≤ 30% 0% 0
10% < p ≤ 20% 0% 0
0% < p ≤ 10% 0% 0
0% 0% 0
100% 32
Table 3. Example of results of recognition.
Time seriesType analysis Precision
Serie n 1 Observation of a field crop 100%
Serie n 2 Changes in forest 70%
Serie n 3 Maturation of a field of rapeseed 80%
Serie n 4 Changes in river 90%
Table 4. Example of forecasting results of region R11 of the
first sequence.
An expected observation 11
oProbabilities of
11
E
Expansion 0.0000
Stabilisation 0.6281
A
Regression 0.3719
Expansion 0.0000
Stabilisation 0.0000
B
Regression 1.0000
Expansion 0.0000
Stabilisation 1.0000
C
Regression 0.0000
Expansion 0.0000
Stabilisation 1.0000
D
Regression 0.0000

H. ESSID ET AL. 255
CA
DN
HN
Vv
TVv
Vvs
π
1
π
2
π
3
HA
DA
CN
Usual
Critical
Gradient
Vv
TVv
Vvs
Vv
TVv
Vvs
Figure 4. Model for monitoring changes in vegetation.
 Usual (H) is the state of the forest when its surface is
in the range of 100% and 75% of the initial surface.
 Gradient (D) is the state of the forest when its surface
becomes in the range of 75% and 60% of the initial
surface
 Critical (C) is the state of the forest when the surface
becomes less than 60% of the initial surface.
Note: the initial surface was defined by the forest area
corresponding to the first image in the chronological or-
der of the series. This surface is updated if we met in the
series of images a larger area.
Each of these three states can have two different in-
stances of speed variation of the surface. This speed was
defined by the variation of the surface to the moment
chosen from the surface to the moment before. We de-
fined the following two instances:
 Normal (N) when the variation is less than 10% of the
surface vegetation at the previous moment.
 Illness (M): When this variation is greater than 10%
of the surface vegetation at the previous moment.
In Figure 4 Vv, TVv and Vvs descriptors were respec-
tively surface variation, vegetation rate change and heal-
thy vegetation variation. The oriented arcs connecting the
different states represent transitions from one state to
another, this transitions can occur from one of two in-
stances belonging to this state. The outgoing arrows rep-
resent each state emissions or comments made by this
state and summarized by the descriptors change.
Note: The different thresholds for switching from one
state to another (75% and 60%) and to move from one
jurisdiction to another (10%) are chosen in an empirical
way, so it was domain expert landlines.
We used a series of Landsat images from different re-
gions, whose shape and surface randomly and continu-
ously changed. For this, we created 15 time series each
with ten images each two months between avril 2008 and
march 2010. These series formed the sequence learning
model and represent the area of North Africa (Tunisia,
Algeria and Egypt). At this stage, we should extract the
region of interest in each image of the 15 time series to
detect the change from one image to another, then to
calculate the descriptors of variation. For this, we choose
vegetation indices to be used to discriminate forest from
the rest of the scene. The first index was the NDVI
(Normalized Difference Vegetation Index) [25]. The in-
dex is strongly correlated with the chlorophyll activity of
the vegetation, and is used to quickly and simply identify
plant surfaces. The NDVI is typically 0.3 to 0.8 for bare
soil and dense vegetation. It was therefore essential to set
a threshold for the NDVI (0.4 used in literature [26]); the
pixels with a value above this threshold were classified
as vegetation. The remaining pixels were considered as
the rest of the scene. The second index was the RVI (Ra-
tio Vegetation Index) [25]. This index highlighted areas
where vegetation was under stress, or not healthy, and
sharpens between vegetation and soil. The overall RVI
varies from 1 for bare floors to over 20 for dense vegeta-
tion. It is also essential to set a threshold for the RVI
(equal to the average of RVI for all the pixels of the re-
gion), the pixels with a value above this threshold will be
classified as healthy vegetation, and the rest will be con-
sidered unhealthy vegetation. We varied the threshold
but it did not give conclusive results because of certain
values (which are close to 0.4), we no longer distinguish
between bare soil and vegetation. The descriptors calcu-
lated from sequences of images were considered as the
observations of a HMM. From these observations, was
possible to determine the hidden states associated with
them. This was done using rules like: IF “descriptor1
belongs to interval-X” AND “descriptor 2 belongs to
interval-Y” THEN “state-Z”. The different intervals and
states were defined based on thresholds already set. Ob-
servations and corresponding hidden states were used as
training data model. This training used Baum-Welch
algorithm. This practice considered the continuous emis-
sion and thus provided “a probability distribution of gen-
eration according to a normal” in addition to the transi-
tion matrix between states A and the vector of initial
probabilities Pi. In this HMM, the number of states is six
because we have three hidden states (usual, gradient and
critical) each one is composed by two instances (normal
and illness).
The Probability of First Visit states: Pi = (0.4 0 0.1 0.2
0 0.3)
The matrix of transition probabilities between states:
0.710.080.080.09 0 0.02
0.620.370 0 0 0
0.36 0.090.2700.18 0.09
0.36 0.1800.36 0.090
0 0.25 00.25 00.5
0.1800.27 0.09 0.09 0.36
A











H. ESSID ET AL. 256
To test the robustness and reliability of the model after
learning, we used the model to generate the correct path
to a given observation randomly selected. This was done
using the Viterbi algorithm. Then, we determined the
actual path corresponding to the same observation using
the rules defined above. Finally, we compared both re-
sults to calculate the error of the model.
Let the observation test defined by its descriptors:
Observation test = [100 48.17 93.51 59.9 90.18 77.71
68.78 100 69.18 100 41.85 75.37 71.12 61.63 86.04
53.78 89.88 89.12; 0 51.83 0 35.95 0 13.83 11.48 0 30.82
0 58.15 0 5.631 13.35 0 37.5 0 0.8397]
The corresponding path generated by the model
Viterbi path: [1 6 1 6 1 4 4 1 6 1 6 3 3 6 1 6 1 1]
The actual path calculated by the Rules
Real path: [1 6 1 6 1 2 4 1 4 1 6 1 3 4 1 6 1 1]
The error was computed for eleven different observa-
tions; and we obtained a mean error of 8.38%. We noted
that the error happened in different locations. These re-
sults show the efficiency of our system and indicate that
NDVI can provide a useful index of vegetation variability.
The final step was to operate the predictive power of
Markov models in general, and especially that of our mo-
del. Indeed, knowing the current state of the object track-
ing “a forest”, and indicating to the system after how long
we want to predict the condition of the forest, the system
will give us the probabilities of being in each of the six
states previously defined.
Example of current state of a forest gradient-normal
(DN), corresponding state vector is [0 0 1 0 0 0]. After a
period, probability vector of states becomes [0.364 0.09 0
0.273 0.182 0.09]. Note that a period is defined by time
incurred between two successive acquisitions of satellite
images constructing time series used for model training.
For example, 0.364 means that we will translate to the
state one with a probability of 36.4%.
4. Conclusions
The work of interpretation is complicated when analyz-
ing changes from a series of satellite images spaced in
time. It would be interesting to have one (or several)
model(s) making the link between observations and real-
ity for a specific purpose, and that even when observa-
tions are incomplete and/or inaccurate. In addition, to
interpret the formal results and simply to explain to non-
specialists, these results should be presented in sum-
mary form. In this paper, we presented an approach that
involves applying a number of pre-processing satellite
images. We then built a hidden Markov model whose pa-
rameters were estimated by learning. Finally, we moved to
the phase of interpretation, evaluation and forecasting.
Our approach is validated by two experiences.
The results of the first experiment were quite accept-
able. Indeed, 75% of events have been recognized with at
least an accuracy of 70% and 15.625% of events have
been interpreted with an accuracy of 100%. For the sec-
ond experiment, the evaluation of the robustness and
reliability of the model provided satisfactory results with
a reasonable error rate. Therefore, the methodology pre-
sented in this study is promising.
It provides a good prediction of spatiotemporal changes
in conjunction with the monitoring of the latter. Besides,
it is transferable to multiple applications such as moni-
toring and management of natural resources, dynamic
monitoring of land use, risk assessment, mapping of da-
mage, assessment of urban expansion, updating of to-
pographic maps, etc. The model can be improved by in-
corporating knowledge of an expert in the field of appli-
cation.
Several researches and developments emerge from this
work. The integration of technical change detection sub-
system in the learning and assess the effect of this im-
provement on system performance. It will also be inter-
esting to extend our approach to spatio-temporal opera-
tion of other models such as pairwise or triplets Markov
chains.
REFERENCES
[1] J. Rodriguez, F. Vos and R. Below, “Annual Disaster
Statistical Review 2008: The Numbers and Trends,” Cen-
tre for Research on the Epidemiology of Disasters, 2009,
pp. 1-33.
[2] A. Singh, “Digital Change Detection Techniques Using
Remotely-Sensed Data,” International Journal of Remote
Sensing, Vol. 10, No. 6, 1989, pp. 989-1003.
doi:10.1080/01431168908903939
[3] D. Lu, P. Mausel, E. Brondizio and E. Moran, “Change
Detection Techniques,” International Journal of Remote
Sensing, Vol. 25, No. 12, 2004, pp. 2365-2407.
doi:10.1080/0143116031000139863
[4] P. Coppin, I. K. Jonckheere, B. Nackaerts and B. Muys,
“Digital Change Detection Methods in Ecosystem Moni-
toring: A Review,” International Journal of Remote
Sensing, Vol. 25, No. 9, 2004, pp. 1565-1596.
doi:10.1080/0143116031000101675
[5] M. Lazri, S. Ameur and B. Haddad, “Analyse de Données
de Précipitations par Approche Markovienne,” Larhyss
Journal, Vol. 6, 2007, pp. 7-20.
[6] J. F. Mari and F. Le Ber, “Temporal and Spatial Data
Mining with Second-Order Hidden Markov Models,” Soft
Computing, Vol. 10, No. 5, 2006, pp. 406-414.
doi:10.1007/s00500-005-0501-0
[7] H. Sagan, “Space-Filling Curves,” Springer-Verlag, Ber-
lin, 1994.
[8] S. Aupetit, M. Slimane and N. Monmarche, “Utilisation
des Chaînes de Markov Cachées à Substitution de Sym-
boles Pour l’Apprentissage et la Reconnaissance Ro-
buste d’Images,” 2nd Proceeding of MAJECSTIC, 13-15
October 2004, Calais, pp. 245-269.

H. ESSID ET AL. 257
[9] L. Aurdal, R.B. Huseby, D. Vikhamar, L. Eikvil and A.
Solberg, “Use of Hidden Markov Models and Phenology
for Multitemporal Satellite Image Classification: Applica-
tions to Mountain Vegetation Classification,” 3rd Inter-
national Workshop on the Analysis of Multi-Temporal
Remote Sensing Images, Biloxi, 16-18 May 2005, pp.
220-224.
[10] W. Pieczynski, “Triplet Markov Chains and Image Seg-
mentation,” Draft of Chapter 4 in Inverse Problems in Vi-
sion and 3D Tomography, Wiley, Hoboken, 2010.
[11] W. Pieczynski, “Pairwise Markov Chains,” IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
Vol. 25, No. 5, 2003, pp. 634-639.
doi:10.1109/TPAMI.2003.1195998
[12] W. Pieczynski, C. Hulard and T. Veit, “Triplet Markov
Chains in Hidden Signal Restoration,” Proceedings of
SPIE 4885, Image and Signal Processing for Remote
Sensing VIII, Crete, 22-27 September 2002, pp. 58-68.
[13] C. Carincotte, S. Derrode and S. Bourennane, “Unsuper-
vised Change Detection non SAR Images Using Fuzzy
Hidden Markov Chains,” IEEE Transactions on Geo-
sciences and Remote Sensing, Vol. 44, No. 2, 2005, pp.
432-441.
[14] S. Derrode and W. Pieczynski, “Signal and Image Seg-
mentation Using Pairwise Markov Chains,” IEEE Trans-
actions on Signal Processing, Vol. 52, No. 9, 2004, pp.
2477-2489. doi:10.1109/TSP.2004.832015
[15] A. B. Wijanarto, “Application of Markov Change Detec-
tion Technique for Detecting Landsat ETM Derived Land
Cover Change over Banten Bay,” Jurnal Ilmiah Geo-
matika, Vol. 12, No. 1, 2006, pp. 11-21.
[16] C. Lacoste, X. Descombes, J. Zerubia and N. Baghdadi,
“Extraction Automatique des Réseaux Linéiques à Partir
d’Images Satellitaires et Aériennes par Processus Markov
Objet,” Bulletin de la SFPT, Vol. 170, 2003, pp. 13-22.
[17] C. Song, “Spectral Mixture Analysis for Subpixel Vege-
tation Fractions in the Urban Inveronment: How to In-
corporate Endmember Variability?” Remote Sensing of
Inveronment, Vol. 95, No. 2, 2005, pp. 248-263.
doi:10.1016/j.rse.2005.01.002
[18] V. Michel, “Analyse des Données,” 4th Edition, Eco-
nomica, Paris, 1997.
[19] B.-Y. Kang, D.-W. Kim and Q. Li, “Spatial Homogene-
ity-Based Fuzzy c-Means Algorithm for Image Segmen-
tation,” Proceedings of Second International Conference
on Fuzzy Systems and Knowledge Discovery, Changsha,
27-29 August 2005, Part I.
[20] D. L. Phum, “Spatial Models for Fuzzy Clustering,”
Computer Vision and Image Understanding, Vol. 84, No.
2, 2001, pp. 285-297. doi:10.1006/cviu.2001.0951
[21] T. Kohonen, “Self-Organizing Maps,” Springer-Verlag,
Berlin, 1995.
[22] L. R. Rabiner, “A Tutorial on Hidden Markov Models
and Selected Applications in Speech Recognition,” Pro-
ceeding of the IEEE, Vol. 77, No. 2, 1989, pp. 257-286.
doi:10.1109/5.18626
[23] S. Kapadia, “Discriminative Training of Hidden Markov
Models,” Ph.D. Dissertation, Downing College-Univer-
sity of Cambridge, Cambridge, 1998.
[24] L. Gueguen, “Extraction d’Information et Compression
Conjointes des Séries Temporelles d’Images Satelli-
taires,” Ph.D. Dissertation, l’École Nationale Supérieure
des Télécommunications de Paris, Paris, 2007.
[25] J. G. Lyon, D. Yuan, R. S. Lunetta and C. D. Elvidge, “A
Change Detection Experiment Using Vegetation Indices,”
Photogrammetric Engineering and Remote Sensing, Vol.
64, 1998, pp. 143-150.
[26] B. M. Ranga, G. H. Forrest, J. S. Piers and L. M. Alex-
ander, “The Interpretation of Spectral Vegetation In-
dexes,” IEEE Transactions on Geosiences and Remote
Sensing, Vol. 33, No. 2, 1995, pp. 481-486.