 Materials Sciences and Applications, 2013, 4, 528-537 http://dx.doi.org/10.4236/msa.2013.49065 Published Online September 2013 (http://www.scirp.org/journal/msa) Chromium-Doped ZnO Nanoparticles Synthesized by Co-Precipitation: Chromium Effects Santi Septiani Sartiman, Nadia Febiana Djaja, Rosari Saleh Departement Fisika, FMIPA-Universitas Indonesia, Depok, Indonesia. Email: rosari.saleh@ui.ac.id, rosari.saleh@gmail.com Received November 3rd, 2012; revised June 8th, 2013; accepted June 30th, 2013 Copyright © 2013 Santi Septiani Sartiman, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT The influence of chromium doping on the physical properties of ZnO nanoparticles synthesized using a low temperature co-precipitation technique is presented. In particular, we have studied the correlation between the structural and the magnetic properties as a function of chromium concentrations. In order to investigate the magnetic properties, vibrating sample magnetometry and electron spin resonance were employed. X-ray diffraction, energy-dispersive X-ray spec- troscopy, Fourier transform infrared spectroscopy and UV-Vis spectroscopy were used. X-ray diffraction patterns of all the samples showed peaks consistent with a hexagonal wurzite structure. The structure and composition analyses re- vealed that chromium is incorporated into the lattice structure, forming a solid solution instead of precipitates. All of the samples in this study exhibit ferromagnetic behavior. The implications of the effects of chromium are also dis- cussed. Keywords: Nanocrystalline ZnO Particles; Chromium; Room-Temperature-Ferromagnetic; ESR; Co-Precipitation 1. Introduction The possibility to achieve both semiconducting and mag- netic properties within a single material system by dop- ing semiconducting materials with small concentrations of transition metals has spawned a new field of elec- tronics known as spintronics [1-4]. The discovery of fer- romagnetism at temperatures above 100 K in III-V-based ferromagnetic semiconductors such as Mn-doped GaAs has made it possible to fabricate spin injecting structures as well as structures for electrical or optical control of ferromagnetism [5-8]. However, most of the III-V-based ferromagnetic semiconductors have a highest Currie tem- perature (TC) of 110 K, still far from room temperature, which is required for practical device applications [9-11]. Since Dietl et al. [12] predicted that p-type ZnO would be a promising candidate for high-TC ferromagnetic semiconductors, there has been considerable research and progress on transition metal-doped ZnO for the realization of a room temperature TC. Thereafter, there has been considerable research and progress on transition metal doped ZnO for the realization of a TC at or above room temperature. Experimentally, room temperature ferromagnetism has been observed in Cr-, Mn-, Fe-, Co-, Ni-, and Cu-doped ZnO [13-18]. However, the results are inconsistent and controversial, both in experiments and in theory. This inconsistency suggests that room tem- perature ferromagnetism in transition metal-doped ZnO is highly sensitive to the synthesis procedures and con- ditions. Another suspicion is that ferromagnetism might be caused by a secondary phase, such as the doping ele- ments or their oxides, rather than by the substitution of transition metal ions into Zn sites [19-21]. There are several theoretical explanations of the origin of room temperature ferromagnetism in transition metal- doped ZnO. Dietl et al. [12] first predicted that a high TC for transition metal doped ZnO would require a large density of mobile holes to induce the ferromagnetic exchange interaction. However, a high concentration of hole is difficult to achieve due to the compensation of the wide band gap ZnO. Additionally, such a theory cannot explain the RT ferromagnetism in n-type TM-doped ZnO. Therefore, Sato and Katayama-Yoshida [22] suggested a theory based on a combination of the Korringa-Kohn- Rostoker (KKR) method and the coherent potential ap- proximation (CPA) to explain the origin of ferromag- netism in n-type TM-doped ZnO. Recently, Coey et al. [23] have argued that a carrier mediated exchange inter- action cannot produce long-range magnetic order when Copyright © 2013 SciRes. MSA  Chromium-Doped ZnO Nanoparticles Synthesized by Co-Precipitation: Chromium Effects 529 the doping level of magnetic ions is only a few percent. They proposed a spin-split impurity band theory derived from the bound magnetic polarons (BMPs). In this model, the ferromagnetic exchange interaction is mediated by shallow donor electrons, which are treated in two-sub- lattice mean field approximation. The only remaining option to obtain a higher TC is to increase the donor elec- trons in the impurity band that will delocalize onto the TM ions. Despite a number of reports available, confusion still persists on the existence and origin of room temperature ferromagnetism in transition metal doped ZnO. Hence, an attempt was made to reinvestigate Cr-doped ZnO. For synthesis, a co-precipitation method was chosen because it is cost effective, it requires low temperatures for pro- cessing, and it has a higher degree of solubility. The powder samples were characterized with regard to their composition, structure and phase (EDX, XRD, and UV- Vis), and magnetic properties (VSM and ESR). 2. Experimental The following starting materials were used without fur- ther purification: zinc (II) sulfate (ZnSO4.7H2O, 99%, Merck)and chromium (III) chloride (CrCl3.6H2O, 99% Merck). To obtain the desired degree of doping of Cr, ZnSO4·7H2O was mixed in distilled water with CrCl3·6H2O. This solutions were designated as solution A. Solution A was placed in an ultrasonic cleaner oper- ating at 57 kHz for 2 h. Solution B was obtained by add- ing 44 mmol of NaOH to 440 mL of de-ionized water. After sonication, solution A was mixed with a magnetic stirrer at room temperature, and solution B was added to solution A until a pH of 12 was reached. The resulting solution was magnetically stirred for 0.5 h, and then it was allowed to stand at room temperature for 18 h. Sub- sequently, the solution was centrifuged and washed sev- eral times with ethanol and distilled water to remove re- sidual and unwanted impurities. The final product was dried in a vacuum oven at 200˚C for 1 h to yieldCr-doped ZnO powder. Elemental analyses of the samples were performed by energy dispersive X-ray (EDX) spectroscopy using a scanning electron microscope. Magnetic measurements were performed at room temperature using an Oxford Type 1.2 T vibrating sample magnetometer (VSM). The powder samples were tightly packed in a clear plastic drinking straw. Magnetization data were recorded as a function of an applied magnetic field, 0 ± 1T. The data reported in this study were corrected because background signalswere introduced from the sample holder. To evaluate the phase purity of the samples, X-ray diffraction (XRD) measurements were performed using a Philips PW 1710 and monochromatic Cu-Ka (l = 1.54060 Å) radiation operated at 40 kV and 20 mA in the range of 10˚ to 80˚.The instrumental broadening, including the instrumental symmetry, was calibrated using a Si pow- der standard. The X-ray diffraction patterns were ana- lyzed by means of the MAUD program using Rietveld whole profile fitting to determine the crystal structure and lattice parameters. To study the electronic interactions near the optical band gap resulting from the addition of dopant atoms, diffuse reflectance UV-Vis measurements were performed using a Shimadzu UV-Vis spectrophotometer with an integrating sphere and a spectral reflectance standard over a wavelength range of 250 - 800 nm. The diffuse re- flectance, R, of the sample is related to the Kubelka- Munk function, F(R), according to the following equa- tion: 2 12 RR R (1) The energy band gap of the samples was calculated from the diffuse reflectance spectra by plotting the F(R)2 as a function of energy and extrapolating to F(R)2 = 0. To obtain information regarding the oxidation state and site occupancy of the Cr ions in the ZnO matrix, electron spin resonance (ESR) was performed using an X-band JEOL JES-RE1X at room temperature and an X-band spectrometer equipped with a 9.1 GHz field mo- dulation unit. The resonance was optimized for the mo- dulation amplitude, receiver gain, time-constant and scan time. The amount of powder used in all measurements was the same. DPPH was used as the standard. The shape and area of the ESR spectra were analyzed using stan- dard numerical methods. 3. Results and Discussion 3.1. Chemical Analysis EDX measurement were used to determine the chemical composition of the Cr-doped ZnO samples. Figure 1 shows EDX spectra of the Cr-doped ZnO samples. The content of different elements in the sample can be ob- served in the spectra, confirming the incorporation of Cr atoms into the nanocrystalline ZnO particles. Calculat- ing the area of the corresponding spectral K lines en- abled quantitative characterization of the Cr/Zn ratios. The amounts of Cr in the nanocrystalline ZnO parti- cles were determined to vary between 3 and 16 at.%. The results were obtained by averaging four values from dif- ferent regions of a sample. The inset of Figure 1 illus- trates how the Cr incorporated into the nanocrystalline ZnO particles varied as a function of the initial cations ratio used in the synthesis.The EDX results indicate that the amounts of Cr incorporated in the samples were slightly lower than the amounts of Cr introduced in the synthesis. Copyright © 2013 SciRes. MSA 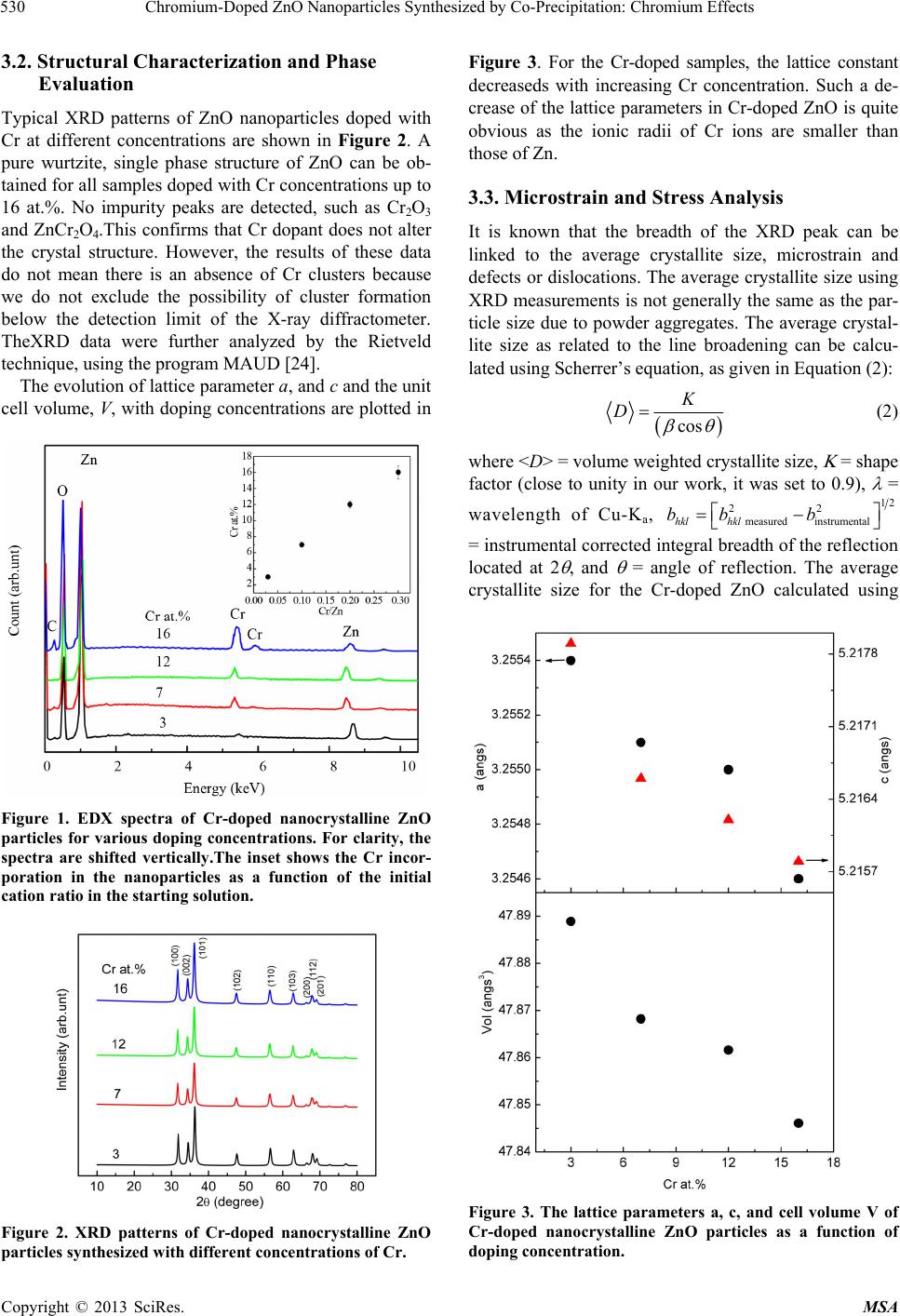 Chromium-Doped ZnO Nanoparticles Synthesized by Co-Precipitation: Chromium Effects 530 3.2. Structural Characterization and Phase Evaluation Typical XRD patterns of ZnO nanoparticles doped with Cr at different concentrations are shown in Figure 2. A pure wurtzite, single phase structure of ZnO can be ob- tained for all samples doped with Cr concentrations up to 16 at.%. No impurity peaks are detected, such as Cr2O3 and ZnCr2O4.This confirms that Cr dopant does not alter the crystal structure. However, the results of these data do not mean there is an absence of Cr clusters because we do not exclude the possibility of cluster formation below the detection limit of the X-ray diffractometer. TheXRD data were further analyzed by the Rietveld technique, using the program MAUD [24]. The evolution of lattice parameter a, and c and the unit cell volume, V, with doping concentrations are plotted in Figure 1. EDX spectra of Cr-doped nanocrystalline ZnO particles for various doping concentrations. For clarity, the spectra are shifted vertically.The inset shows the Cr incor- poration in the nanoparticles as a function of the initial cation ratio in the starting solution. Figure 2. XRD patterns of Cr-doped nanocrystalline ZnO particles synthesized with different concentrations of Cr . Figure 3. For the Cr-doped samples, the lattice constant decreaseds with increasing Cr concentration. Such a de- crease of the lattice parameters in Cr-doped ZnO is quite obvious as the ionic radii of Cr ions are smaller than those of Zn. 3.3. Microstrain and Stress Analysis It is known that the breadth of the XRD peak can be linked to the average crystallite size, microstrain and defects or dislocations. The average crystallite size using XRD measurements is not generally the same as the par- ticle size due to powder aggregates. The average crystal- lite size as related to the line broadening can be calcu- lated using Scherrer’s equation, as given in Equation (2): cos K D (2) where <D> = volume weighted crystallite size, = shape factor (close to unity in our work, it was set to 0.9), = wavelength of Cu-Ka, 12 22 measuredinstrumental hkl hkl bb b = instrumental corrected integral breadth of the reflection located at 2 , and = angle of reflection. The average crystallite size for the Cr-doped ZnO calculated using Figure 3. The lattice parameters a, c, and cell volume V of Cr-doped nanocrystalline ZnO particles as a function of doping concentration. Copyright © 2013 SciRes. MSA  Chromium-Doped ZnO Nanoparticles Synthesized by Co-Precipitation: Chromium Effects Copyright © 2013 SciRes. MSA 531 Scherrer’s equation is presented in Table 1. By plotting the value of 4sin along the x-axis and hklcos along the y-axis, the lattice strain and the aver- age crystallite size can be calculated through a linear fit. The UDM for Cr-doped ZnO are shown in Figure 4. It is clear that there is a decrease in the lattice strain with increasing doping concentrations. However, the UDM becomes less valid because the material properties vary with crystallographic directions. The other modified forms of the WH plot, that consider the anisotropic na- ture of the crystals are the uniform stress deformation model (USDM) and the uniform deformation energy density model (UDEDM). USDM and UDEDM give an idea of the stress-strain relation and the strain as a func- tion of energy density, respectively. In USDM the ani- sotropic strain direction hkl can be related with the de- formation stress using Young’s modulus: The strain arising from crystal imperfections and dis- tortions, such as vacancies and lattice deformations, can also induce a broadening in the XRD profile. Therefore, the line broadening is a combination of crystallite size and strain. Although the separation of these two phe- nomena is not straightforward, the contribution of each type of broadening can be determined by constructing a modified form of William and Hall (W-H) plot [25], namely UDM. In this form the strain was assumed to be uniform in all crystallographic direction, thus the mate- rial is considered to be isotropic. Strain-induced broad- ening is calculated by the equation: 4tan hkl (3) where = the lattice strain. The UDM approach considers the case of both the domain effect and lattice deformation operating simulta- neously, and their combined effects give the final line broadening, which is the sum of Equation (2) and Equa- tion (3): hklhkl hkl E (6) where Ehkl is Young’s modulus in the direction perpen- dicular to the (hkl) plane and hkl is the anisotropic lattice strain. In this model the WH equation becomes: 4sin cos hkl hkl K DE (7) 4tan cos hkl K D (4) The deformation stress can be estimated from the slope of the linear fit of the graph which is plotted be- tween hklcos and 4sin /Ehkl, and the crystallite size <D> from the intercept. For samples with a hexagonal crystal phase, Young’s modulus Ehkl is related to: Rearranging the equation, the following equation can be obtained: cos4 sin hkl K D (5) 22 2 2 22 42 22 113313 44 2 3 22 2 33 hkl hk al hc Ehk hk al al ShSS Sh cc where a and c are lattice parameters and S11, S33, S13 and S44 are the elastic compliance of ZnO with values of 7.858 × 10−12, −2.206 × 10−12, 6.940 × 10−12 and 23.57 × 10−12 m2N−1, respectively [26]. The USDMs for Cr-doped ZnO are also plotted in Figure 4. Using the linear fits of Figure 4, the strain in anisotropic hexagonal crystals is calculated from the peak position, which is different from the USDM and UDM, their values are tabulated in Table 1. Table 1. The average crystallite size, Young’s modulus strain, stress, and anisotropic energy density of Cr-doped na nocrystalline ZnO particles calculated using William-Hall approximation. Debye Scherrer UDM USDM UDEDM Sample at.% <D> nm <D> nm e (10−4)<D> nm (MPa)e (10−4) <D> nmu (kJm−3) (MPa)e (10−4) 3 22 18 0.0007 17 71 0.0009 17 16 45 0.0005 7 20 15 0.0001 16 64 0.0008 16 13 41 0.0004 12 18 15 0.0001 15 11 0.0002 15 1 13 0.0001 Cr doped ZnO 16 17 14 0.0003 13 9 0.0001 14 4 23 0.0002 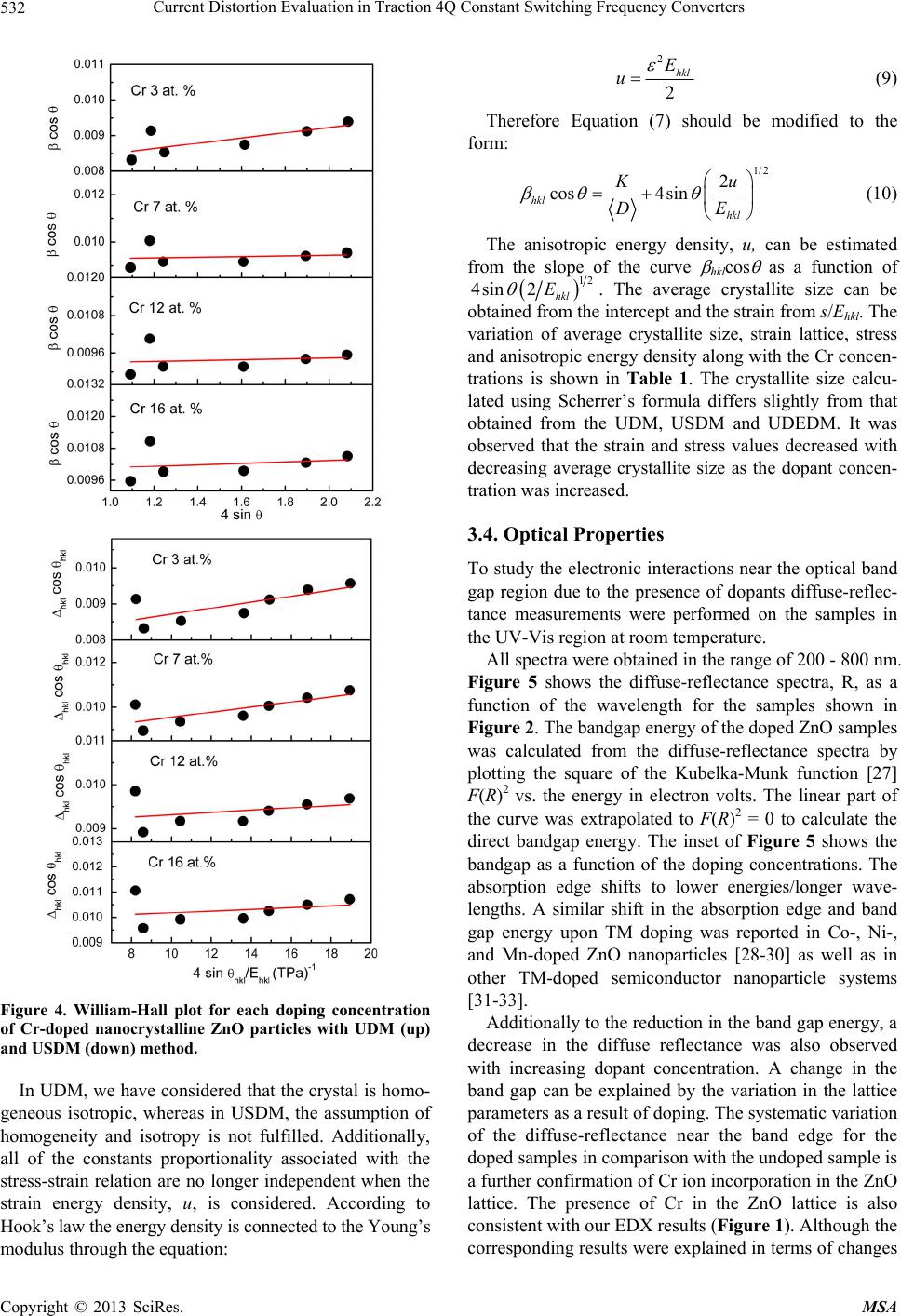 Current Distortion Evaluation in Traction 4Q Constant Switching Frequency Converters 532 Figure 4. William-Hall plot for each doping concentration of Cr-doped nanocrystalline ZnO particles with UDM (up) and USDM (down) method. In UDM, we have considered that the crystal is homo- geneous isotropic, whereas in USDM, the assumption of homogeneity and isotropy is not fulfilled. Additionally, all of the constants proportionality associated with the stress-strain relation are no longer independent when the strain energy density, u, is considered. According to Hook’s law the energy density is connected to the Young’s modulus through the equation: 2 2 hkl E u (9) Therefore Equation (7) should be modified to the form: 1/2 2 cos 4sin hkl hkl K DE u (10) The anisotropic energy density, u, can be estimated from the slope of the curve hklcos as a function of 12 4sin2 hkl E . The average crystallite size can be obtained from the intercept and the strain from s/Ehkl. The variation of average crystallite size, strain lattice, stress and anisotropic energy density along with the Cr concen- trations is shown in Table 1. The crystallite size calcu- lated using Scherrer’s formula differs slightly from that obtained from the UDM, USDM and UDEDM. It was observed that the strain and stress values decreased with decreasing average crystallite size as the dopant concen- tration was increased. 3.4. Optical Properties To study the electronic interactions near the optical band gap region due to the presence of dopants diffuse-reflec- tance measurements were performed on the samples in the UV-Vis region at room temperature. All spectra were obtained in the range of 200 - 800 nm. Figure 5 shows the diffuse-reflectance spectra, R, as a function of the wavelength for the samples shown in Figure 2. The bandgap energy of the doped ZnO samples was calculated from the diffuse-reflectance spectra by plotting the square of the Kubelka-Munk function [27] F(R)2 vs. the energy in electron volts. The linear part of the curve was extrapolated to F(R)2 = 0 to calculate the direct bandgap energy. The inset of Figure 5 shows the bandgap as a function of the doping concentrations. The absorption edge shifts to lower energies/longer wave- lengths. A similar shift in the absorption edge and band gap energy upon TM doping was reported in Co-, Ni-, and Mn-doped ZnO nanoparticles [28-30] as well as in other TM-doped semiconductor nanoparticle systems [31-33]. Additionally to the reduction in the band gap energy, a decrease in the diffuse reflectance was also observed with increasing dopant concentration. A change in the band gap can be explained by the variation in the lattice parameters as a result of doping. The systematic variation of the diffuse-reflectance near the band edge for the doped samples in comparison with the undoped sample is a further confirmation of Cr ion incorporation in the ZnO lattice. The presence of Cr in the ZnO lattice is also consistent with our EDX results (Figure 1). Although the orresponding results were explained in terms of changes c Copyright © 2013 SciRes. MSA 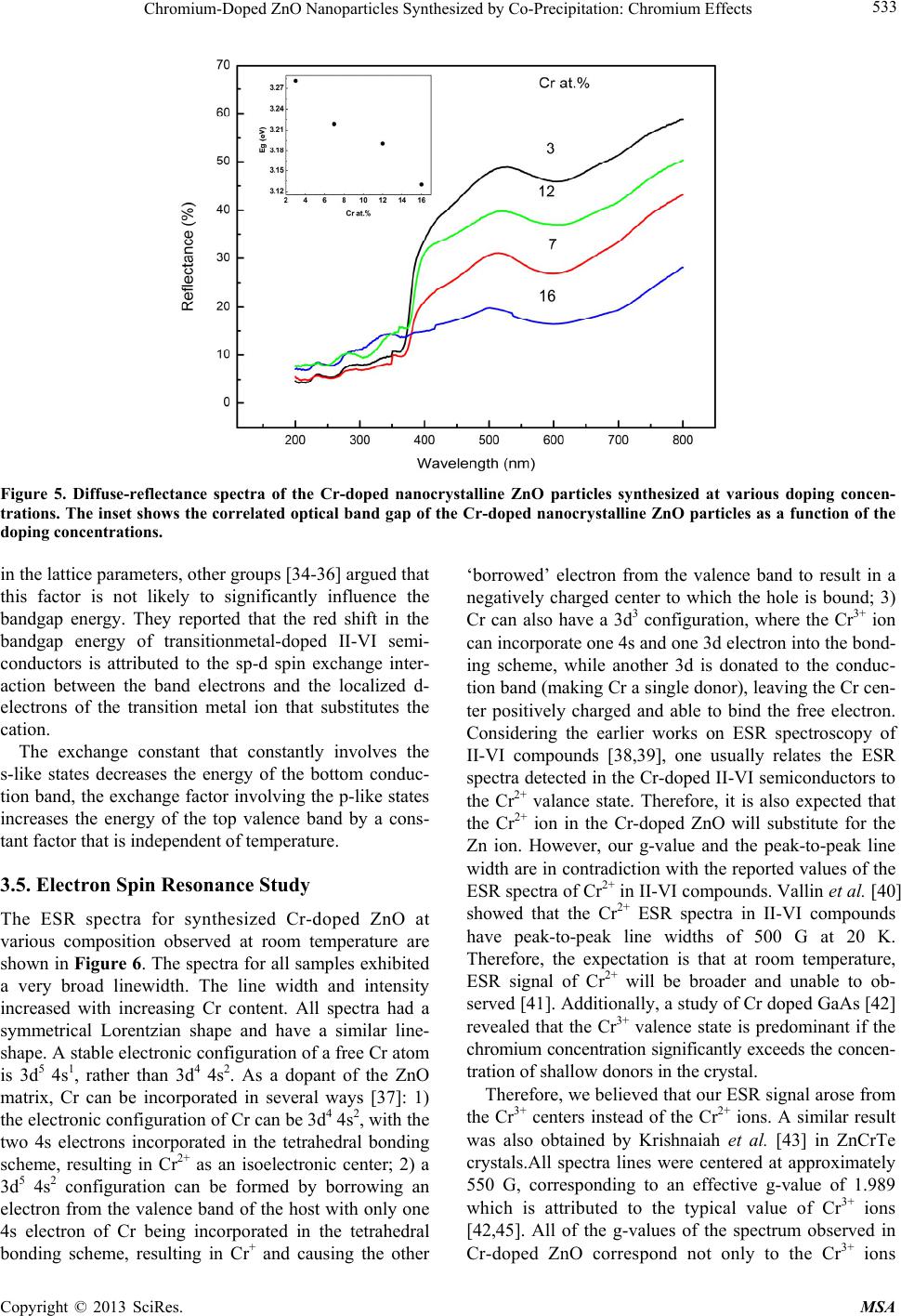 Chromium-Doped ZnO Nanoparticles Synthesized by Co-Precipitation: Chromium Effects Copyright © 2013 SciRes. MSA 533 Figure 5. Diffuse-reflectance spectra of the Cr-doped nanocrystalline ZnO particles synthesized at various doping concen- trations. The inset shows the correlated optical band gap of the Cr-doped nanocrystalline ZnO particles as a function of the doping concentrations. in the lattice parameters, other groups [34-36] argued that this factor is not likely to significantly influence the bandgap energy. They reported that the red shift in the bandgap energy of transitionmetal-doped II-VI semi- conductors is attributed to the sp-d spin exchange inter- action between the band electrons and the localized d- electrons of the transition metal ion that substitutes the cation. ‘borrowed’ electron from the valence band to result in a negatively charged center to which the hole is bound; 3) Cr can also have a 3d3 configuration, where the Cr3+ ion can incorporate one 4s and one 3d electron into the bond- ing scheme, while another 3d is donated to the conduc- tion band (making Cr a single donor), leaving the Cr cen- ter positively charged and able to bind the free electron. Considering the earlier works on ESR spectroscopy of II-VI compounds [38,39], one usually relates the ESR spectra detected in the Cr-doped II-VI semiconductors to the Cr2+ valance state. Therefore, it is also expected that the Cr2+ ion in the Cr-doped ZnO will substitute for the Zn ion. However, our g-value and the peak-to-peak line width are in contradiction with the reported values of the ESR spectra of Cr2+ in II-VI compounds. Vallin et al. [40] showed that the Cr2+ ESR spectra in II-VI compounds have peak-to-peak line widths of 500 G at 20 K. Therefore, the expectation is that at room temperature, ESR signal of Cr2+ will be broader and unable to ob- served [41]. Additionally, a study of Cr doped GaAs [42] revealed that the Cr3+ valence state is predominant if the chromium concentration significantly exceeds the concen- tration of shallow donors in the crystal. The exchange constant that constantly involves the s-like states decreases the energy of the bottom conduc- tion band, the exchange factor involving the p-like states increases the energy of the top valence band by a cons- tant factor that is independent of temperature. 3.5. Electron Spin Resonance Study The ESR spectra for synthesized Cr-doped ZnO at various composition observed at room temperature are shown in Figure 6. The spectra for all samples exhibited a very broad linewidth. The line width and intensity increased with increasing Cr content. All spectra had a symmetrical Lorentzian shape and have a similar line- shape. A stable electronic configuration of a free Cr atom is 3d5 4s1, rather than 3d4 4s2. As a dopant of the ZnO matrix, Cr can be incorporated in several ways [37]: 1) the electronic configuration of Cr can be 3d4 4s2, with the two 4s electrons incorporated in the tetrahedral bonding scheme, resulting in Cr2+ as an isoelectronic center; 2) a 3d5 4s2 configuration can be formed by borrowing an electron from the valence band of the host with only one 4s electron of Cr being incorporated in the tetrahedral bonding scheme, resulting in Cr+ and causing the other Therefore, we believed that our ESR signal arose from the Cr3+ centers instead of the Cr2+ ions. A similar result was also obtained by Krishnaiah et al. [43] in ZnCrTe crystals.All spectra lines were centered at approximately 550 G, corresponding to an effective g-value of 1.989 which is attributed to the typical value of Cr3+ ions [42,45]. All of the g-values of the spectrum observed in Cr-doped ZnO correspond not only to the Cr3+ ions  Chromium-Doped ZnO Nanoparticles Synthesized by Co-Precipitation: Chromium Effects 534 observed in Cr-doped II-VI compounds, but also to an unpaired electron trapped at an oxygen vacancy site. It is possible that the broad line of the Cr3+ ions overlap with the resonance line of an unpaired electron trapped on an oxygen vacancy site. However, the deconvolution would be problematic because an accurate estimate of the inten- sity under the broad resonance line is difficult. 3.6. Magnetic Characterization The magnetic properties of the Cr-doped ZnO samples were investigated using VSM in the magnetic field range of 0 to ±1 T. The magnetization (M) versus the magnetic field (H) measured at room temperature is illustrated in Figure 7. The magnetization is plotted as a function of magnetic field for different doping concentrations. All of the Cr-doped samples in this study exhibit ferromagnetic behavior. An interesting feature is observed when we analyze the magnetization data of Cr-doped samples studied in this work. The 7, 12 and 16 at.% Cr-doped samples showed the a remnant magnetizations of 0.35, 0.35, and 0.34 (×10−2) emu/g and coercive field of 482, 322 and Figure 6. Experimental ESR spectra of the Cr-doped nano- crystalline ZnO particles prepared at various Cr concen- trations. Figure 7. Room temperature M-H curves for Cr-doped nanocrystalline ZnO particles sy nthe sized with various dop- ing concentrations. 164 Oe, respectively. The magnetization increased for samples doped with higher Cr concentrations. The 7 at.%, 12 at.% and 16 at.% Cr-doped samples possessed net moments of 0.060, 0.077 and 0.144 µB/Cr, respectively. The Cr-doped samples also had net moments far below the theoretical values. However, only a small fraction of Cr atoms contribute to ferromagnetism. The low mag- netic moment values might be a result of the competition between the ferromagnetic and antiferromagnetic coupling that occurs at short distances between a pair of Cr ions. Similar to ZnO doped with other transition metals, the secondary phase in our samples is thought to be the source of the spurious magnetic signal. In principle, as the Cr concentration increases, a number of antiferromagnetic phases may occur, such as ZnCr2O4 (TN 11K), Cr metal clusters, Cr2O3 and Cr3O4 [46-48]. However, none of the phases can be detected via XRD. Even, if these phases are present in small quantities, none of them to ferro- magnetism, except the CrO2 phase (TC ~386 K) [49]. Therefore, room temperature ferromagnetism in our Cr- doped sample cannot be explained by the secondary phases. Xu et al. [50] observed ferromagnetism in Cr- doped ZnOnanorods. They observed a uniform incorpo- ration of Cr into Zn with no secondary phases and sug- gested that the combined effects of structural defects and exchange interactions of the Cr ions substituting for Zn in the ZnO matrix were responsible for the magnetization in their Cr-doped ZnO samples. The existence of compressive stress/and/or strain due to the oxygen vacancies may also be a factor that to in- fluences the shift of the XRD peaks position. Defects are known to play a primary role in ferromagnetic ordering in transition metal-doped semiconductors such as ZnO [23,46,51]. An increasing number of studies have dem- onstrated that the formation of oxygen vacancies and zinc interstitial could lead to room temperature ferro- magnetism or enhanced ferromagnetism [52-54]. Ac- cording to the donor impurity band exchange model, the ferromagnetic-exchange between transition-metal ions and semiconductors is mediated by shallow donor elec- trons that form bound magnetic polarons which overlap to create a spin-split impurity band. With regard to the origin of the ferromagnetism ob- served in our samples and considering the above meas- urements, we conclude that ferromagnetism in our Cr- doped samples is an intrinsic property of Cr-doped ZnO. Our data support the hypothesis that the magnetic be- havior observed is related to the presence of intrinsic defects. This can be understood via the BMP model dis- cussed above. 4. Summary In summary, a series of Cr-doped ZnO nanoparticle sam- ples with different doping concentrations were success- Copyright © 2013 SciRes. MSA  Chromium-Doped ZnO Nanoparticles Synthesized by Co-Precipitation: Chromium Effects 535 fully synthesized and characterized by EDX, XRD, UV-Vis, ESR and VSM. The XRD patterns suggested the formation of a wurtzite structure in theCr-doped ZnO. The XRD results also indicated that Cr-ions were incur- porated into the ZnO matrix. The XRD line broadening due to the combination of the coherent scattering of X- rays from a particular lattice plane and the random dis- placement of atoms from their original positions, which generates strain was analyzed by Scherrer’s formula and by a modified form of W-H analysis. The three modified W-H analyses were helpful in approximating the strain, stress and energy density values. The results show that the strain, stress and energy density values decreased with increasing doping concentrations. The magnetic measurements show that the Cr-doped ZnO samples are ferromagnetic in nature with a well- defined hysteresis at room temperature and the coercive field (HC) and the remnant magnetization increase with increasing doping concentrations. The analysis shows that the room temperature ferromagnetic in Cr-doped ZnO might be explained by BMP model. REFERENCES [1] G. A. Prinz, “Magnetoelectronics,” Science, Vol. 282, No. 5394, 1998, pp. 1660-1663. doi:10.1126/science.282.5394.1660 [2] A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnár, M. L. Roukes, A. Y. Chtchel- kanova and D. M. Treger, “Spintronics: A Spin-Based Electronics Vision for the Future,” Science, Vol. 294, No. 5546, 2001, pp. 1488-1495. doi:10.1126/science.1065389 [3] S. J. Pearton, C. R. Abernathy, M. E. Overberg, G. T. Thaler, D. P. Norton, N. Theodoropoulou, A. F. Hebard, Y. D. Park, F. Ren, J. Kim and L. A. Boatner, “Wide Band Gap Ferromagnetic Semiconductors and Oxides,” Journal of Applied Physics, Vol. 93, No. 1, 2003, 13 p. doi:10.1063/1.1517164 [4] K. Ueda, H. Tabata and T. Kawai, “Magnetic and Electric Properties of Transition-Metal-Doped ZnO Films,” Ap- plied Physics Letters, Vol. 79, No. 7, 2001, pp. 988-990. doi:10.1063/1.1384478 [5] H. Ohno, “Making Nonmagnetic Semiconductors Ferro- magnetic,” Science, Vol. 281, No. 5379, 1998, pp. 951- 956. doi:10.1126/science.281.5379.951 [6] H. Ohno, H. Munekata, T. Penney, S. Von Molnár and L. L. Chang, “Magnetotransport Properties of p-Type (In, Mn)As Diluted Magnetic III-V Semiconductors,” Physi- cal Review Letters, Vol. 68, No. 17, 1992, pp. 2664-2667. doi:10.1103/PhysRevLett.68.2664 [7] H. Ohno, A. Shen, F. Matsukura, A. Oiwa, A. Endo, S. Katsumoto and Y. Iye, “(Ga,Mn)As: A New Diluted Magnetic Semiconductor Based on GaAs,” Applied Phys- ics Letters, Vol. 69, No. 3, 1996, pp. 363-365. doi:10.1063/1.118061 [8] F. Matsukura, H. Ohno, A. Shen and Y. Sugawara, “Tran- sport Properties and Origin of Ferromagnetism in (Ga,Mn) As,” Physical Review B, Vol. 57, No. 4, 1998, pp. R2037- R2040. doi:10.1103/PhysRevB.57.R2037 [9] Y. Matsumoto, M. Murakami, T. Shono, T. Hasegawa, T. Fukumura, M. Kawasaki, P. Ahmet, T. Chikyow, S. Ko- shihara and H. Koinuma, “Room-Temperature Ferromag- netic in Transparent Transition Metal-Doped Titanium Dioxide,” Science, Vol. 291, No. 5505, 2001, pp. 854-856. doi:10.1126/science.1056186 [10] T. Wakano, N. Fujimura, Y. Morinaga, N. Abe, A. Ashida and T. Ito, “Magnetic and Magneto-Transport Properties of ZnO:Ni Films,” Physica E: Low-Dimensional Systems and Nanostructures, Vol. 10, No. 1-3, 2001, pp. 260-264. doi:10.1016/S1386-9477(01)00095-9 [11] P. Sharma, A. Gupta, K. V. Rao, F. J. Owens, R. Sharma, R. Ahuja, J. M. Osorio, B. Johansson and G. A. Gehring, “Ferromagnetism above Room Temperature in Bulk and Transparent Thin Films of Mn-Doped ZnO,” Nature Matter, Vol. 2 , No. 10, 2003, pp. 673-677. doi:10.1038/nmat984 [12] T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand, “Zener Model Description of Ferromagnetism in Zinc- Blende Magnetic Semiconductors,” Science, Vol. 287, No. 5455, 2000, pp. 1019-1022. doi:10.1126/science.287.5455.1019 [13] R. Saleh, S. P. Prakoso and A. Fishli, “The Influence of Fe Doping on the Structural, Magnetic and Optical Prop- erties of Nanocrystalline Zno Particles,” Journal of Mag- netism and Magnetic Materials, Vol. 324, No. 5, 2012, pp. 665-670. doi:10.1016/j.jmmm.2011.07.059 [14] G. Glaspell, P. Dutta and A. A Manivanna, “A Room- Temperature and Microwave Synthesis of M-Doped ZnO (M = Co, Cr, Fe, Mn & Ni),” Journal of Cluster Science, Vol. 16, No. 4, 2005, pp. 523-536. doi:10.1007/s10876-005-0024-y [15] O. D. Jayakumar, H. G. Salunke, R.M. Kadam, M. Mo- hapatra, G. Yaswant and S. K. Kulshreshtha, “Magnetism in Mn-doped ZnO Nanoparticles Prepared by A Co-Pre- cipitation Method,” Nanotechnology, Vol. 17, No. 5, 2006, p. 1278. doi:10.1088/0957-4484/17/5/020 [16] R. Elilaressi and G. Chandrasekaran, “Structural, Optical, and Magnetic Properties of Nanoparticles of ZnO:Ni— DMS Prepared by Sol-Gel Method,” Materials Chemistry Physics, Vol. 123, No. 2-3, 2010, pp. 450-455. doi:10.1016/j.matchemphys.2010.04.039 [17] D. B. Buchholz, R. P. H. Chang, J.-Y. Song and J. B. Ketterson, “Room-Temperature Ferromagnetism in Cu- Doped ZnO Thin Films,” Applied Physics Letters, Vol. 87, No. 8, 2005, Article ID: 082504. doi:10.1063/1.2032588 [18] L.-H. Ye, A. J. Freeman and B. Delley, “Half-Metallic Ferromagnetism in Cu-Doped ZnO: Density Functional Calculations,” Physical Review B, Vol. 73, No. 3, 2006, Article ID: 033203. doi:10.110x3/PhysRevB.73.033203 [19] K. P. Bhatti, S. Chaudhary, D. K. Pandya and S. C. Ka- shyap, “Intrinsic and Extrinsic Origin of Room Tempera- ture Ferromagnetism in ZnO:Co (5 at. %),” Journal of Applied Physics, Vol. 101, No. 10, 2007, Article ID: 103919. doi:10.1063/1.2740343 [20] J. Zhang, R. Skomski and D. J. Sellmyer, “Sample Preparation and Annealing Effects on the Ferromagnetism Copyright © 2013 SciRes. MSA  Chromium-Doped ZnO Nanoparticles Synthesized by Co-Precipitation: Chromium Effects 536 in Mn-Doped ZnO,” Journal of Applied Physics, Vol. 97, No. 10, 2005, Article ID: 10D303. [21] D. P. Norton, M. E. Overberg, S. J. Pearton, K. Pruessner, J. D. Budai, L. A. Boatner, M. F. Chisholm, J. S. Lee, Z. G. Khim, Y. D. Park and R. G. Wilson, “Ferromagnetism in Cobalt-Implanted ZnO,” Applied Physics Letters, Vol. 83, No. 26, 2003, p. 5488. doi:10.1063/1.1637719 [22] K. Sato and H. Katayama-Yoshida, “Ferromagnetism in a Transition Metal Atom Doped ZnO,” Physica E: Low- Dimensional Systems and Nanostructures, Vol. 10, No.1, 2001, pp. 251-255. doi:10.1016/S1386-9477(01)00093-5 [23] J. M. Coey, M. Venkatesan and C. B. Fitzgerald, “Donor Impurity Band Exchange in Dilute Ferromagnetic Ox- ides,” Nature Matter, Vol. 4, No. 2, 2005, pp. 173-179. doi:10.1038/nmat1310 [24] L. Lutterotti, “MAUD (Material Analysis Using Diffrac- tion) version 2.33,” 2010. http://www.ing.unitn.it/~luttero/maud [25] G. K. Williamson and W. H. Hall, “X-Ray Line Broad- ening from Filled Aluminium and Wolfram,” Acta Met- allurgica, Vol. 1, No. 1, 1953, pp. 22-31. doi:10.1016/0001-6160(53)90006-6 [26] J. F. Nye, “Physical Properties of Crystals: Their Repre- sentation by Tensors and Matrices,” Oxford University Press, Oxford, New York, 1985. [27] B. Hapke, “Theory of Reflectance and Emittance Spec- troscopy,” University Press, Cambridge, 1993. [28] P. Koidl, “Optical Absorption of Co2+ in ZnO,” Physical Review B, Vol. 15, No. 5, 1977, pp. 2493-2499. doi:10.1103/PhysRevB.15.2493 [29] J. Anghel, A. Thurber, D. A. Tenne, C. B. Hanna and A. Punnoose, “Correlation Between Saturation Magnetiza- tion, Bandgap, and Lattice Volume of Transition Metal (M = Cr, Mn, Fe, Co, or Ni) doped Zn1-XMXO Nanopar- ticles,” Journal of Applied Physics, Vol. 107, No. 9, 2010, Article ID: 09E314. doi:10.1063/1.3360189 [30] Z. H. Wang, D. Y. Geng and Z. D. Zhang, “Room-Tem- perature Ferromagnetism and Optical Properties of Zn1- XMnXO Nanoparticles,” Solid State Communication, Vol. 149, No. 17-18, 2009, pp. 682-684. doi:10.1016/j.ssc.2009.02.016 [31] M. Bouloudenine, N. Viart, S. Colis and A. Dinia, “Bulk Zn1-XCoXO MAGNETIC Semiconductors Prepared by Hydrothermal Technique,” Chemical Physics Letters, Vol. 397, No. 1-3, 2004, pp. 73-76. doi:10.1016/j.cplett.2004.08.064 [32] K. J. Kim and Y. R. Park, “Spectroscopic Ellipsometry Study of Optical Transitions in Zn1-XCoXO Alloys,” Applied Physics Letters, Vol. 81, No. 8, 2002, p. 1420. doi:10.1063/1.1501765 [33] A. J. Hays, A. Punnoose, R. Baldner, M. H. Engelhard, J. Peloquin, K. M. Reddy, “Relationship between the Structural and Magnetic Properties of Co-Doped SnO2 Nano-particles,” Physical Review B, Vol. 72, No. 7, 2005, Article ID: 075203. doi:10.1103/PhysRevB.72.075203 [34] Z. W. Zhao, B. K. Tay, J. S. Chen, J. F. Hu, B. C. Lim and G. P. Li, “Large Magnetic Moment Observed in Co-Doped ZnO Nanoclusters-Assembled Thin Films at Room Temperature,” Applied Physics Letters, Vol. 90, No. 15, 2007, Article ID: 152502. doi:10.1063/1.2721140 [35] A. Parra-Palomino, O. Perales-Perez, R. Singhal, M. To- mar, J. Hwang, P. M. Voyles, “Structural, Optical, and Magnetic Characterization of Monodisperse Fe-Doped ZnO Nanocrystals,” Journal of Applied Physics, Vol. 103, No. 7, 2008, Article ID: 07D121. doi:10.1063/1.2834705 [36] Z. H. Wang, D. Y. Geng, and Z. D. Zhang, “Room-Tem- perature Ferromagnetism and Optical Properties of Zn1-X MnXO Nanoparticles,” Solid State Communications, Vol. 149, No. 17-18, 2009, pp. 682-684. doi:10.1016/j.ssc.2009.02.016 [37] X. Lu, S. Tsoi, I. Miotkowski, S. Rodriguez, H. Alawadhi and A. K. Ramdas, “Raman Electron Paramagnetic Reso- nance in Zn1−xCrxTe and Cd1−xCrxTe,” Physical Review B, Vol. 75, No. 15, 2007, Article ID: 155206. doi:10.1103/PhysRevB.75.155206 [38] J. T. Vallin and G. D. Watkins, “The Spin Hamiltonian for Cr2+ in CdS,” Physics Letters A, Vol. 37, No. 4, 1971, pp. 297-298. doi:10.1016/0375-9601(71)90678-5 [39] T. L. Estle and W. C. Holton, “Electron-Paramagnetic- Resonance Investigation of the Superhyperfine Structure of Iron-Group Impurities in II-VI Compounds,” Physical Review, Vol. 150, No. 1, 1966, pp. 159-167. doi:10.1103/PhysRev.150.159 [40] J. T. Vallin and G. D. Watkins, “EPR of Cr2+ in II-VI Lattices,” Physical Review B, Vol. 9, No. 5, 1974, pp. 2051-2072. doi:10.1103/PhysRevB.9.2051 [41] M. E. J. Boonman, W. Mac, A. Twardowski, A. Wittlin, P. J. M. van Bentum, J. C. Maan and M. Demianiuk, “High-Magnetic-Field EPR of Cr-Based Diluted Mag- netic Semiconductors,” Physical Review B, Vol. 61, No. 8, 2000, pp. 5358-5368. doi:10.1103/PhysRevB.61.5358 [42] J. J. Kerbs and G. H. Strauss, “EPR of Cr(3d3) in GaAs—Evidence for Strong Jahn-Teller Effects,” Physi- cal Review B, Vol. 15, No. 1, 1977, pp. 17-22. doi:10.1103/PhysRevB.15.17 [43] G. Krishnaiah, N. MadhusudhanaRao, D. R. Reddy, B. K. Reddy and P. S. Reddy, “Growth and Structural Proper- ties of Zn1−xCrxTe Crystals,” Journal of Crystal Growth, Vol. 310, No. 1, 2008, pp. 26-30. doi:10.1016/j.jcrysgro.2007.10.013 [44] A. Franco Jr. and R. C. Santana, “Electron Paramagnetic Resonance (EPR) of Antiferromagnetic Nanoparticles of La1−xSrxCrO3 (0.000 ≤ x ≤ 0.020) Synthesized by Combustion Reaction,” Materials Chemistry and Physics, Vol. 120, No. 1, 2010, pp. 225-228. doi:10.1016/j.matchemphys.2009.10.052 [45] G. Krishnaiah, N. MadhusudhanaRao, B. K. Reddy, D. R. Reddy, T. M. Babu, S. Sambasivam and P. S. Reddy, “EPR and Magnetic Properties of Vapour Phase Grown Zn1−xCrxTe Crystals,” Physics Letters A, Vol. 372, No. 42, 2008, pp. 6429-6433. doi:10.1016/j.physleta.2008.08.039 [46] H. Liu, X. Zhang, L. Li, Y. X. Wang, K. H. Gao, Z. Q. Li, R. K. Zheng, S. P. Ringer, B. Zhang and X. X. Zhang, “Role of Point Defects in Room-Temperature Ferromag- netism of Cr-Doped ZnO,” Applied Physics Letters, Vol. 91, No. 7, 2007, Article ID: 072511. Copyright © 2013 SciRes. MSA  Chromium-Doped ZnO Nanoparticles Synthesized by Co-Precipitation: Chromium Effects Copyright © 2013 SciRes. MSA 537 doi:10.1063/1.2772176 [47] X. H. Chen, H. T. Zhang, C. H. Wang, X. G. Luo and P. H. Li, “Effect of Particle Size on Magnetic Properties of Zinc Chromite Synthesized by Sol-Gel Method,” Applied Physics Letters, Vol. 81, No. 23, 2002, p. 4419. doi:10.1063/1.1526921 [48] B. K. Roberts, A. B. Pakhomov and K. M. Krishnan, “Effect of Hydrogen Codoping on Magnetic Ordering and Conductivity in Cr:ZnO Thin Films,” Journal of Applied Physics, Vol. 103, No. 7, 2008, Article ID: 07D133. [49] R. Bhargava, P. K Sharma, A. K Chawla, S. Kumar, R. Chandra, A. C Pandey and N. Kumar, “Variation in Structural, Optical and Magnetic Properties of Zn1-XCrXO (x= 0.0, 0.10, 0.15, and 0.20) Nanoparticles: Role of Do- pant Concentration on Non-Saturation of Magnetiza- tion,” Materials Chemistry and Physics, Vol. 125, No. 3, 2011, pp. 664-671. doi:10.1016/j.matchemphys.2010.09.075 [50] C. Xu, K. Yang, Y. Liu, L. Huang, H. Lee, J. Cho and H. Wang, “Buckling and Ferromagnetism of Aligned Cr- Doped ZnO Nanorods,” The Journal of Physical Chemis- try C, Vol. 112, No. 49, 2008, pp. 19236-19241. doi:10.1021/jp806164b [51] C. Song, K. W. Geng, F. Zeng, X. B. Wang, Y. X. Shen, F. Pan, Y. N. Xie, T. Liu, H. T. Zhou and Z. Fan, “Giant Magnetic Moment in an Anomalous Ferromagnetic Insu- lator: Co-Doped ZnO,” Physical Review B, Vol. 73, No. 2, 2006, Article ID: 024405. doi:10.1103/PhysRevB.73.024405 [52] J. L. MacManus-Driscoll, N. Khare, Y. Liu and M. E. Vickers, “Structural Evidence for Zn Intersititials in Fer- romagnetic Zn1–xCoxO Films,” Advanced Materials, Vol. 19, No. 19, 2007, pp. 2925-2929. [53] H. S. Hsu, J. C. A. Huang, S. F. Chen and C. P. Liu, “Role of Grain Boundary and Grain Defects on Ferro- magnetism in Co:ZnO Films,” Applied Physical Letters, Vol. 90, No. 10, 2007, Article ID: 102506. doi:10.1063/1.2711763 [54] J. M. D. Coey, “Dilute Magnetic Oxide,” Current Opin- ion in Solid State and Materials Science, Vol. 10, No. 2, 2006, pp. 83-92. doi:10.1016/j.cossms.2006.12.002.
|