J. Biomedical Science and Engineering, 2009, 2, 80-85
Published Online April 2009 in SciRes. http://www.scirp.org/journal/jbise JBiSE
A novel approach in ECG beat recognition using
adaptive neural fuzzy filter
Glayol Nazari Golpayegani1, Amir Homayoun Jafari1
1Biomedical Engineering Department, Islamic Azad University, Science and Research Branch, Tehran, Iran.
Received Jan. 5th, 2009; revised Jan. 16th, 2009; accepted Feb. 10th, 2009
ABSTRACT
Accurate and computationally efficient means
of electrocardiography (ECG) arrhythmia detec-
tion has been the subject of considerable re-
search efforts in recent years. Intelligent com-
puting tools such as artificial neural network
(ANN) and fuzzy logic approaches are demon-
strated to be competent when applied individu-
ally to a variety of problems. Recently, there has
been a growing interest in combining both of
these approaches, and as a result, adaptive
neural fuzzy filters (ANFF) [1] have been evolved.
This study presents a comparative study of the
classification accuracy of ECG signals using
(MLP) with back propagation training algorithm,
and a new adaptive neural fuzzy filter architec-
ture (ANFF) for early diagnosis of ECG ar-
rhythmia. ANFF is inherently a feed forward
multilayered connectionist network which can
learn by itself according to numerical training
data or expert knowledge represented by fuzzy
if-then rules [1]. In this paper we used an adap-
tive neural fuzzy filter as an ECG beat classifier.
We combined 3 famous wavelet transforms and
used them mid 4 the order AR model coefficient
as features. Our results suggest that a new
proposed classifier (ANFF) with these features
can generalize better than ordinary MLP archi-
tecture and also learn better and faster. The
results of proposed method show high accu-
racy in ECG beat classification (97.6%) with
100% specificity and high sensitivity.
Keywords: Adaptive Neural Fuzzy Filter, ECG
Arrhythmia Classification, Pattern Recognition,
Multilayer Perceptron.
1. INTRODUCTION
Electrocardiography deals with the electrical activity of
the heart. Bio-signals being non-stationary signals, the
reflection may occur at random in the time-scale. There-
fore, for effective diagnostic, ECG pattern and heart rate
variability may have to be observed over several hours.
Thus the volume of the data being enormous, the study
is tedious and time consuming. Therefore, com-
puter-based analysis and classification of cardiac dis-
eases can be very helpful in diagnostic [1]. Several algo-
rithms have been developed in the literature for detection
and classification of ECG beats. One of ECG beat rec-
ognition is neural network classification method [2-9].
Multilayer perceptron (MLP), has been shown to be able
to recognize and classify ECG signals more accurately.
However conventional Neural Networks with Back
Propagation algorithm (BPNN) suffers from slow con-
vergence to local and global minima and from random
settings of initial of weights, which may make the neural
networks have very poor mappings from inputs to output.
More over in conventional neural networks, users have
to determine the structure of network such as the num-
bers of hidden layer before training and it is too hard to
select proper structure. Another ECG classification
method is Fuzzy Hybrid Neural Network [10]. In this
structure a FCM algorithm is used to clustering the fea-
tures and the center of clusters will be used as the input
of MLP neural network. This structure made the results
conventional MLP better but because of using MLP as
final classifier, the shortcomings of MLP are still exist.
To overcome the shortcomings encountered in neural
networks, while still keeping their advantages, an adap-
tive neural fuzzy filter, (ANFF) has been developed in
[1]. The ANFF is a feed forward multilayer network that
integrates the basic elements and functions of a tradi-
tional fuzzy system into a connectionist structure. An
important feature of this adaptive filter is that it can dy-
namically partition the input space and output space us-
ing irregular fuzzy hyper box [11]. For the adaptation of
membership functions in the ANFF, the back propaga-
tion algorithm is used to find the optimal parameters
under the mean square error (MSE) criterion. Hence, in
the ANFF, the Fuzzy ART is used for structure learning
and the back propagation algorithm for parameter learn-
ing. The ANFF can thus on-line partition the in-
put-output spaces, tune membership functions, and find
proper fuzzy logic rules dynamically on the fly. Users
need not give the initial fuzzy partitions, membership
functions, or fuzzy logic rules except for the case that
SciRes Copyright © 2009

81 G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 80-85
SciRes Copyright © 2009 JBiSE
expert knowledge is available and is used as the initial
fuzzy rules. Hence, there are no hidden nodes in the be-
ginning of learning; they are created and begin to grow
as the training signal arrives. Since the structure of the
ANFF is constructed from fuzzy if-then rules, once the
input-output relationship is constructed, it will not be
destroyed and, thus, no knowledge forgetting may hap-
pen while in conventional neural network we might had
this event. These properties can make the ANFF more
suitable for on-line classification than neural networks.
Therefore in this paper we decided to use this filter as a
classifier instead of a filter. More over, in this paper we
used the fuzzy combination of 3 wavelets which were:
Daubechies, Symlet, Biorthogonal mid 4th order AR
model coefficients as features. These features beside
ANFF had more efficient results than MLP. This algo-
rithm was faster and more reliable than MLP and it has
high mean accuracy 97.6% and also high sensitivity and
specificity.
This paper organized as follows. Section 1 describes
the basic structure and functions of ANFF in brief. The
on-line structure/parameter learning algorithm of the
ANFF, which combines fuzzy ART and back propaga-
tion learning algorithm under the MSE criterion is pre-
sented in Section 3. In Section 4 we describe the feature
extraction method. In Section 6 we will show the results
of this method and compare this method with conven-
tional neural network (MLP). Finally conclusions are
summarized in the last section.
2. THE STRUCTURE OF ADAPTIVE
NEURAL FUZZY FILTER
2.1. Adaptive Neural Fuzzy Filters
In this section, we will describe the structure and func-
tions of ANFF briefly. The ANFF (see Figure 1) has five
layers with node and link numbering defined by the
brackets on the left-hand side of the figure.
Layer-1 nodes are input nodes representing input
variables. Layer-5 nodes are output nodes representing
output variables. Layer-2 and layer-4 nodes are term
nodes that act as membership functions representing the
terms of respective input and output variables. Each
layer-3 node is a rule node representing one fuzzy logic
rule. Thus, together all the layer-3 nodes will be as a
fuzzy rule base. The links between layers 3 and 4 func-
tion as a connectionist inference engine. Layer-3 links
define the preconditions of rule nodes, and layer-4 links
define the consequents of the rule nodes. Therefore, each
rule node has at most one link to some term node of a
linguistic node, and may have no such links. This is true
both for precondition links (link in layer 3) and conse-
quent links (links in layer 4). The links in layers 2 and 5
are fully connected between linguistic nodes and their
corresponding term nodes. The arrows indicate the nor-
mal signal flow directions when the network is in opera-
tion (after it has been built and trained). When we are in
structure learning step, ANFF operates in Up-Down
mode and when we want to obtain estimated output,
ANFF operates in Down-Up mode.
The ANFF uses the technique of complement coding
from fuzzy ART [12] to normalize the input-output
training vectors. Complement coding is a normalization
process that rescales an n-dimensional vector, x=(x1,
x2… xn), to its 2n-dimensional complement coding such
that
(
)
()
nn
c
nn
cc
xxxxxx
xxxxxxx
−−−≡
≡
′
1,,,,1,,1,
,,,,,,
2211
2211
L
L (1)
where 12
( ,,...) n
x
xxxx x
x
′≡== and
c
i
x is the
complement of i
x
, i.e., c
ii
x
x=−1. As mentioned in
[11], complement coding helps avoid the problem of
category proliferation when using fuzzy ART cluster-
ing. It also preserves training vector amplitude infor-
mation. In applying the complement coding technique
to the ANFF, all training vectors (either input state
vectors or desired output vectors) are transformed to
their complement coded form in the preprocessing
process, and the transformed vectors are then used for
training.
A typical network consists of nodes with some finite
number of fan-in connectionist from other nodes repre-
sented by weight values, and fan-out connectionists to
other nodes. Associated with the fan-in of a node is an
integration function f which combines information, acti-
vation, or evidence from other nodes, and provides the
net input, i.e.,
()()() ()()()
121 2
(,, ...;,,...)
kkkk kk
pp
netinputf zzzwww−= (2)
where
(
)
(
)
,...
k
i
Z
ip is the ith input to a node in layer k,
and w(i) is the weight of the associated link. The super-
script in the above equation indicates the layer number.
This notation will be also used in the following equa-
tions. Each node also outputs an activation value as a
function of its net-input.
()outputaf= (3)
The description of the functions of nodes in each of five
layers of the ANFF can be obtained from Reference [1].
2.2. The Structure-Learning Step
The structure learning step consists of three learning
processes: input fuzzy clustering process, output fuzzy
clustering process, and mapping process. The first two
processes are performed simultaneously on both sides of
network, and are described below.
2.2.1. Input Fuzzy Clustering Process
For input fuzzy clustering, ANFF uses the fuzzy ART
fast learning algorithm [11,12] to find the input mem-
bership function parameters )2()2( ,ijij UV . For this purpose,
first, the values of choice functions, Tj, for each com-
plement coded vector are computed by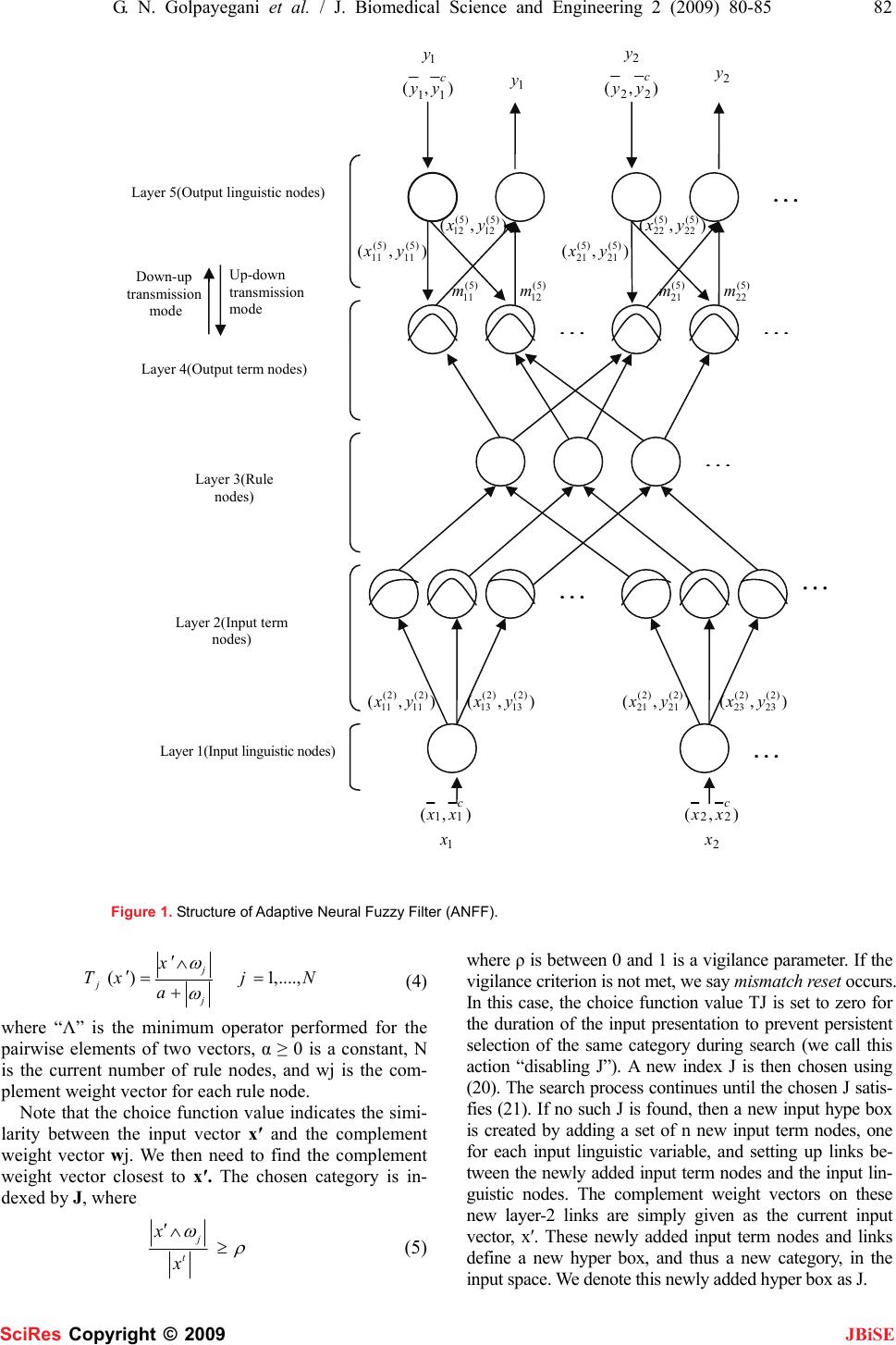

G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 80-85 82
SciRes Copyright © 2009 JBiSE
Figure 1. Structure of Adaptive Neural Fuzzy Filter (ANFF).
( )1,....,
j
j
j
x
Txj N
a
ω
ω
′∧
′==
+ (4)
where “Λ” is the minimum operator performed for the
pairwise elements of two vectors, α ≥ 0 is a constant, N
is the current number of rule nodes, and wj is the com-
plement weight vector for each rule node.
Note that the choice function value indicates the simi-
larity between the input vector x′ and the complement
weight vector wj. We then need to find the complement
weight vector closest to x′. The chosen category is in-
dexed by J, where
j
t
x
x
ω
ρ
′∧≥ (5)
where ρ is between 0 and 1 is a vigilance parameter. If the
vigilance criterion is not met, we say mismatch reset occurs.
In this case, the choice function value TJ is set to zero for
the duration of the input presentation to prevent persistent
selection of the same category during search (we call this
action “disabling J”). A new index J is then chosen using
(20). The search process continues until the chosen J satis-
fies (21). If no such J is found, then a new input hype box
is created by adding a set of n new input term nodes, one
for each input linguistic variable, and setting up links be-
tween the newly added input term nodes and the input lin-
guistic nodes. The complement weight vectors on these
new layer-2 links are simply given as the current input
vector, x′. These newly added input term nodes and links
define a new hyper box, and thus a new category, in the
input space. We denote this newly added hyper box as J.
Layer 5(Output linguistic nodes)
Down-up
transmission
mode
Up-down
transmission
mode
Layer 4(Output term nodes)
Layer 3(Rule
nodes)
Layer 2(Input term
nodes)
Layer 1(Input linguistic nodes)
),(22
2
c
yy
y
2
y
1
y
),( 11
1
c
yy
y
),( )5(
11
)5(
11 yx
),( )5(
12
)5(
12 yx
)5(
11
m
)5(
12
m
),( )5(
21
)5(
21 yx
),( )5(
22
)5(
22 yx
)5(
21
m
)5(
22
m
…
…
…
…
…
…
),( )2(
11
)2(
11 yx
),( )2(
13
)2(
13 yx
),( )2(
21
)2(
21 yx
),( )2(
23
)2(
23 yx
…
1
11),(
x
xx c
2
22),(
x
xx c

83 G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 80-85
SciRes Copyright © 2009 JBiSE
2.2.2. Output Fuzzy Clustering Process
The output fuzzy clustering process is exactly the same
as the input fuzzy clustering process except that it is
performed between layers 4 & 5 which are working in
the up-down transmission mode.
2.2.3. Mapping Process
After the two hyper boxes in the input and output spaces
are chosen in the input and output fuzzy clustering proc-
esses, the next step is to perform the mapping process
which decides the connections between layer-3 and
layer-z4 nodes. This mapping process is described by the
following algorithm, wherein connecting rule node J
output hyper box K we means connecting the rule node J
to the output term nodes that constitutes the hyper box K
in the output space.
Step 1: IF rule node J is a newly added node THEN
connect rule node J to output hyper box K.
Step 2: ELSE IF rule node J not connected to output
hyper box K originally THEN disable J and perform In-
put Fuzzy Clustering Process to find the next qualified J.
Step 3: ELSE no structure change is necessary. In the
mapping process, hyper boxes J and K are resized ac-
cording to the fast learning rule [40] by updating weights,
WJ and WK, as
)()()()( ,old
k
new
k
old
J
new
JWxWWxW ∧
′
=∧
′
= (6)
2.3. The Parameter-Learning Step
After the network structure has been adjusted according
to the current training pattern in the structure-learning
step, it is then necessary to fine tune the network pa-
rameters using the same training pattern. Basically, the
back propagation algorithm is used to find node output
errors, which are then analyzed to guide parameter ad-
justment. As mentioned above, the goal of training the
ANFF is to minimize the error function
() ()
ESKSK
∧
⎛⎞
=−
⎜⎟
⎝⎠
2
1
2 (7)
where s(k) is the desired signal, and s ˆ(k) is the filtered
signal. Based upon this MSE criterion and in analogy to the
back propagation algorithm, we can derive the following
w
f
f
E
W
F
F
E
W
E
w
E
KWKWKWKW
∂
∂
⋅
∂
∂
⋅
∂
∂
−=
∂
∂
⋅
∂
∂
−=
∂
∂
−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−+=Δ+=+
α
α
η )()()()1(
(8)
where W is the adjustable parameter in the filter.
The adapting equations of the parameters of each layer
can be obtained from [1] in more details.
3. DATA ACQUISITION AND FEATURE
EXTRACTION METHOD
We had 4 kinds of ECG beats. There were: Atrial Fibril-
lation beats (AF), Ventricular Tachycardia beats (VT),
Super Ventricular Tachycardia Arrhythmia beats (SVA)
and Normal beats. We selected 18 signals from each kind
of beat from MIT-BIH Arrhythmia database. So we had
72 signals totally. The arrhythmia database of MIT-BIH,
have been preprocessed in such away that they are clean
from any corrupting noise. Therefore we did not need to
do any additional preprocessing on our ECG signals. The
sampling frequency of MIT-BIH Arrhythmia database is
250Hz. We used a 1000 point moving window with 200
point overlap between each two windows for each ECG
signal. So each ECG signal converted to 24 segments
which each segment had 1000 point. Therefore we had
1728 segment totally. We used 80% of these segments
for training ANFF and 20% of that to test the perform-
ance of ANFF.
We used a fuzzy combination of 3 wavelet transform
which were: Daubechies (db4), Symlets (sym8) and
Biorthoginal (bior4.4). A 4 level decomposition was done
with each wavelet transform. And then we selected the
maximum value between these 3 wavelets in each level.
Therefore, 4 wavelet coefficients were obtained for each
segment with this fuzzy combination if wavelet trans-
forms. We also used the 4th order AR model coefficients
as another feature extraction method so 4 features were
obtained for each segment by this method. Therefore
finally we had an 8 dimensional feature vector for each
segment. Then we used these features as input for ANFF.
We also defined the target for each segment and used
them as output variable for ANFF.
4. RESULTS
We considered following values for the constants in
ANFF: learning parameter (η)=0.1, fuzziness parameter
(γ)=0.6, choice function parameter (α)=0.7.
In the first step of process we used only the Daube-
chies wavelet coefficients as ECG features. In the second
step of process we used Daubechies wavelet mid 4th
order AR model coefficient as ECG features. In third step
of process we used only the fuzzy combination of three
wavelets as ECG features. And finally we used fuzzy
combination of wavelets mid 4th order AR model coeffi-
cient as ECG features. Table 1 shows the results of using
these features with ANFF separately. Then also did these
steps with an MLP with 40 hidden nodes. Table 2 shows
the results of using these features with MLP. In both
methods (ANFF and MLP) we calculated specificity and
sensitivity and accuracy for each kind of features. We
selected 1382 segments for training and 346 segments
for test randomly.
As we can see from Table 1 and Table 2, among 4
kinds of features extracted, the fuzzy combination of 3
pre nominate wavelet transforms mid 4th order AR
model coefficients provided best results for both ANFF
and MLP structures. Also we can see that in compare
with MLP, ANFF had much better results. ANFF had
high accuracy about 97.6% and also it had higher speci-
ficity and sensitivity than MLP. Furthermore unlike the
MLP, ANFF did not need to have pre determined struc-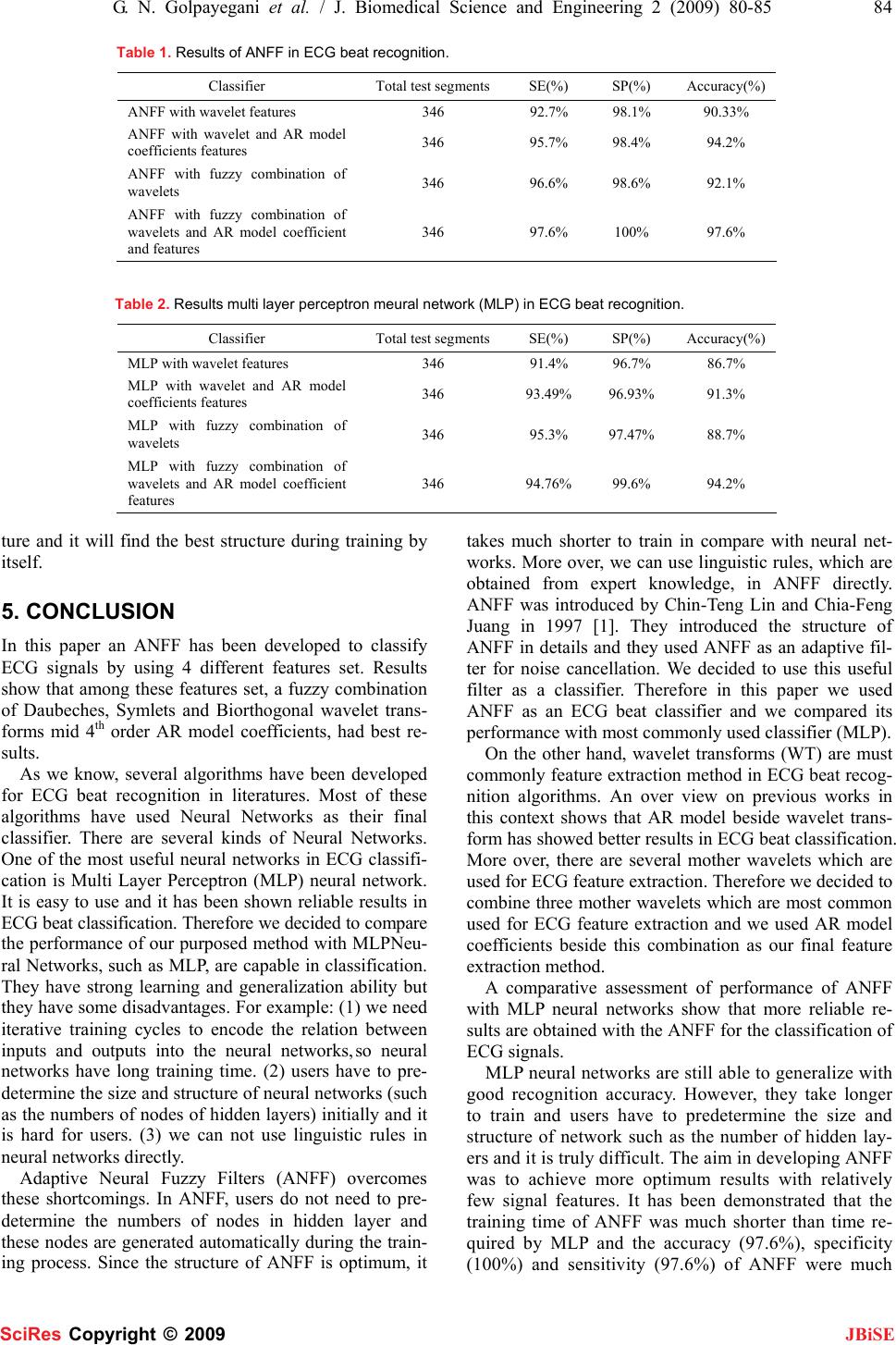

G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 80-85 84
SciRes Copyright © 2009 JBiSE
Table 1. Results of ANFF in ECG beat recognition.
Classifier Total test segments SE(%) SP(%) Accuracy(%)
ANFF with wavelet features 346 92.7% 98.1% 90.33%
ANFF with wavelet and AR model
coefficients features 346 95.7% 98.4% 94.2%
ANFF with fuzzy combination of
wavelets 346 96.6% 98.6% 92.1%
ANFF with fuzzy combination of
wavelets and AR model coefficient
and features
346 97.6% 100% 97.6%
Table 2. Results multi layer perceptron meural network (MLP) in ECG beat recognition.
Classifier Total test segments SE(%) SP(%) Accuracy(%)
MLP with wavelet features 346 91.4% 96.7% 86.7%
MLP with wavelet and AR model
coefficients features 346 93.49% 96.93% 91.3%
MLP with fuzzy combination of
wavelets 346 95.3% 97.47% 88.7%
MLP with fuzzy combination of
wavelets and AR model coefficient
features
346 94.76% 99.6% 94.2%
ture and it will find the best structure during training by
itself.
5. CONCLUSION
In this paper an ANFF has been developed to classify
ECG signals by using 4 different features set. Results
show that among these features set, a fuzzy combination
of Daubeches, Symlets and Biorthogonal wavelet trans-
forms mid 4th order AR model coefficients, had best re-
sults.
As we know, several algorithms have been developed
for ECG beat recognition in literatures. Most of these
algorithms have used Neural Networks as their final
classifier. There are several kinds of Neural Networks.
One of the most useful neural networks in ECG classifi-
cation is Multi Layer Perceptron (MLP) neural network.
It is easy to use and it has been shown reliable results in
ECG beat classification. Therefore we decided to compare
the performance of our purposed method with MLPNeu-
ral Networks, such as MLP, are capable in classification.
They have strong learning and generalization ability but
they have some disadvantages. For example: (1) we need
iterative training cycles to encode the relation between
inputs and outputs into the neural networks, so neural
networks have long training time. (2) users have to pre-
determine the size and structure of neural networks (such
as the numbers of nodes of hidden layers) initially and it
is hard for users. (3) we can not use linguistic rules in
neural networks directly.
Adaptive Neural Fuzzy Filters (ANFF) overcomes
these shortcomings. In ANFF, users do not need to pre-
determine the numbers of nodes in hidden layer and
these nodes are generated automatically during the train-
ing process. Since the structure of ANFF is optimum, it
takes much shorter to train in compare with neural net-
works. More over, we can use linguistic rules, which are
obtained from expert knowledge, in ANFF directly.
ANFF was introduced by Chin-Teng Lin and Chia-Feng
Juang in 1997 [1]. They introduced the structure of
ANFF in details and they used ANFF as an adaptive fil-
ter for noise cancellation. We decided to use this useful
filter as a classifier. Therefore in this paper we used
ANFF as an ECG beat classifier and we compared its
performance with most commonly used classifier (MLP).
On the other hand, wavelet transforms (WT) are must
commonly feature extraction method in ECG beat recog-
nition algorithms. An over view on previous works in
this context shows that AR model beside wavelet trans-
form has showed better results in ECG beat classification.
More over, there are several mother wavelets which are
used for ECG feature extraction. Therefore we decided to
combine three mother wavelets which are most common
used for ECG feature extraction and we used AR model
coefficients beside this combination as our final feature
extraction method.
A comparative assessment of performance of ANFF
with MLP neural networks show that more reliable re-
sults are obtained with the ANFF for the classification of
ECG signals.
MLP neural networks are still able to generalize with
good recognition accuracy. However, they take longer
to train and users have to predetermine the size and
structure of network such as the number of hidden lay-
ers and it is truly difficult. The aim in developing ANFF
was to achieve more optimum results with relatively
few signal features. It has been demonstrated that the
training time of ANFF was much shorter than time re-
quired by MLP and the accuracy (97.6%), specificity
(100%) and sensitivity (97.6%) of ANFF were much

85 G. N. Golpayegani et al. / J. Biomedical Science and Engineering 2 (2009) 80-85
SciRes Copyright © 2009 JBiSE
better than those of MLP. Furthermore the ANFF can be
trained by numerical data and linguistic information
expressed by fuzzy if-then rules. Another key feature of
ANFF is that, without any given initial structure, the
ANFF can construct itself automatically from numerical
training data.
The proposed method, which incorporates the tech-
niques of Adaptive Neural Fuzzy Filter and back propa-
gation learning and combines their advantages, can be
said to be more capable of recognizing other biological
signals than conventional Neural Networks with Back
Propagation algorithm (BPNN) such as Multi Layer Per-
ceptron (MLP).
REFERENCES
[1] C.T. Lin, C.F. Juang, (2001) “An adaptive neural fuzzy filter and
its applications,” IEEE Transactions On Systems, MAN, And
Cybernetics, VOL. 27, NO. 4, 1103-1110.
[2] S. Osowaki, T.H. Linh, (2001) “ECG beat recognition using
fuzzy hybrid neural network,” IEEE Trans. Biomed. Eng. 48 (11)
1265-1271.
[3] Y. Ozbay, B. Karlik, (2001) “A reconition of ECG arrhythmias
using artificial neyral network,” Proceedings of the 23rd Annual
Conference, IEEE/EMBS, Istanbul, Turkey, pp. 76-80.
[4] Y. Ozbay, “Fast recognition of ECG arrhythmias,” (1999) Ph.D.
Yhesis, Institute of Natural and Applied Science, Selcuk Univer-
sity,.
[5] S.Y. Foo, G. Harvey, A. Meyer-Baese, (2002) “Neural network-
based ECG pattern recognition”, Eng. Appl. Artif. Intell. 15,
353-360.
[6] V. Pilla, H.S. Lopes, (1999) “Evolutionary training of a
neuro-fuzzy network for detection of a P wave of the ECG,”
Proceeding of the third international conference on computational
intelligence and multimedia applications, New Dehli, India,
102-106.
[7] M. Engin, S. Demirag, (2003) “Fuzzy-hybrid neural network
based ECG beat recognition using three different types of feature
sets,” Cardiovasc. Eng. Int. J. 3 (2) 71-80.
[8] S. Hykin, (1994) Neural Networks: A comperhensive Foundation,
Macmillan, New York.
[9] B. Karlik, m.o. Tokhi, M. Alci, (2003) “A fuzzy clustering neural
network architecture for multifunction upper-limb prosthesis,”
IEEE Trans. Biomed. Eng. 50 (11), 1255-1261.
[10] R. Acharya, P.S. Bhat, S.S. Iyengar, A. Roo, S. Dua, (2001)
“Classification of heart rate data using artificial neural network
and fuzzy equivalence relation,” J. Pattern Recognition Soc, 4,
238-244.
[11] G. A. Carpenter, S. Grossberg, and D. B. Rosen, (2001) “Fuzzy
ART: Fast stable learning and categorization of analog patterns
by an adaptive adaptive resonance system,” Neural Networks, 4,
759-771.
[12] G. A. Carpenter, S. Grossberg, N. Markuzon, J. H. Reynolds, and
D. B. Rosen, (2002) “Fuzzy ARTMAP: A neural network
architecture for incremental supervised learning of analog
multidimensional maps,” IEEE Trans. Neural Networks, vol. 3,
pp. 698-712.