p
f
J
ournal o
f
B
i
doi:10.4236/jb
n
Copyright ©
2
Heati
n
Parti
c
Badia Fasla
Macromolecul
a
m
Received Nove
m
ABSTRA
C
This paper d
e
These sphere
s
non. The sing
l
p
roportional
t
reach a finite
is treated as
a
f
erent space
d
coverage of
m
ing the borde
r
highlight the
i
medical team.
Keywords: H
y
1. Introdu
c
Thermal ther
a
variety of t
u
heated papyr
u
tions [1]. No
w
one of the ma
j
The method i
soft matter k
n
tion absorbin
g
b
in and mela
n
therapy aims
as an alternat
i
the advantag
e
rapid recover
y
involving a c
quire mathe
m
of the system
Energy deliv
e
meters like l
a
Thermal effe
c
of tissues, th
e
as well as on
sue damage c
a
i
omaterials a
n
n
b.2011.21007
P
2
011 SciRes.
ng
of
B
c
les: E
f
, Assia Rac
h
a
r Research Lab
o
m
m
ber 4th, 2010;
C
T
e
als with hyp
e
s
are heated
w
l
e sphere pro
b
t
o the sphere
s
range when t
r
a
convolution
p
d
istribution f
u
m
edium heatin
g
r
s of the treat
e
i
mpacts of the
y
per Thermal
T
c
tion
a
py has been
u
u
mors. Many
u
s to treat br
e
w
adays, laser
j
or tools of
t
r
e
s based on th
e
n
owing that bi
o
g
agents such
n
in with diffe
r
at eliminating
i
ve to convent
i
e
s of being no
n
y
[3-6]. It is
ombination o
f
m
atical models
behavior at d
e
red by radiati
a
ser power, be
a
c
ts depend o
n
e
ir optical an
d
biological de
n
a
n be evaluate
n
d Nanobiotec
h
P
ublished Onlin
B
iolo
gi
f
fects
o
h
ida Senoud
i
o
ratory, Depart
m
com
revised Novem
b
e
r thermal the
r
w
ith a laser be
a
b
lem gives a s
u
s
urface and in
v
r
aveling into t
h
p
roduct of the
u
nctions of na
n
g
while a Ga
u
e
d region. Lo
r
obtained res
u
T
herapy, Gol
d
u
sed for a lon
g
years ago,
E
e
ast cancer a
n
thermal thera
p
e
ating a variet
y
e
interaction
o
o
logical tissu
e
as water, pro
r
ent absorptio
n
g
cancerous tis
ional surgical
n
invasive, si
m
however a c
o
f
distinct phe
n
to improve o
u
d
ifferent stage
s
on to tissue d
e
a
m diameter
a
n
the absorpti
o
d
thermo-
p
hy
s
n
aturation. T
h
d knowing th
e
h
nolo
gy
, 201
1
e January 2011
i
cal Ti
o
f Par
t
i
, Abdelhak
B
m
ent of Physics
b
er 23rd, 2010;
a
r
apy of tumo
r
a
m in the nea
r
u
rface temper
a
v
erse diffusivi
t
h
e
s
urroundin
g
sphere densit
y
n
o particles
a
u
ssian distribu
t
r
entzian distri
b
u
lts in develop
i
d
Nano Sphere
s
g
time to treat
E
gyptians us
e
n
d others infe
p
y is becomi
n
y
of diseases [
2
o
f radiation wi
t
e
s contain radi
teins, hemogl
o
n
spectra. Las
sues by heati
n
treatments wi
t
m
ple allowing
o
mplex proce
n
omena that
r
u
r understandi
n
s
of the proce
s
e
pends on pa
r
a
nd waveleng
t
o
n cross secti
o
s
ical paramete
h
e extend of t
i
e
time and spa
c
1
, 2, 49-54
(http://www.Sc
i
ssues
b
t
icle S
B
oussaid,
M
, Faculty of Sci
e
a
ccepted Dece
m
r
s in biologic
a
r
infrared ran
g
a
ture rise foll
o
t
y of the surr
o
g
medium wit
h
y
distribution
f
a
re con
s
idere
d
t
ion predicts
a
b
ution was als
i
ng strategies
f
s
, Laser, Heat
a
e
d
c-
n
g
2
].
t
h
a-
o
-
er
n
g
t
h
a
ss
e-
n
g
s
s.
a-
t
h.
o
n
rs
i
s-
c
e
temper
a
p
heno
m
leadin
g
fast up
o
The
dispers
damag
e
needs t
of hea
t
transfe
r
tions
o
from h
e
resona
n
the ne
a
genera
t
larger
t
ver, bi
o
good t
r
sibility
tumors
for sol
v
spheri
c
exami
n
sphere
i
RP.org/journal
/
by
Go
l
ize an
d
M
ustapha Be
n
e
nces Universit
y
m
ber 1st, 2010.
a
l tissues usin
g
g
e based on s
u
o
wing a unive
r
o
unding mediu
m
h
a certain tim
f
unction and
t
d
. A uniform
s
a
n important
d
o considered
f
f
or hyper ther
m
Transfe
r
a
ture depend
e
m
enon and e
n
g
to cell’s deat
h
o
n further hea
t
present pape
r
ion of gold
n
e
s to healthy
o design strat
e
t
ing sources
a
r
problem in s
p
o
f application
s
e
ated gold na
n
n
ce phenome
n
a
r infrared and
t
es photon c
a
t
han standard
p
o
logical tissu
e
r
ansparency in
to reach dee
p
deep inside t
h
v
ing the time
c
al coordinate
n
ed first to obt
a
surface and i
m
/
jbnb)
l
d Na
n
d
Dist
r
n
mouna, Re
d
y
Abou Bekr B
e
g
dispersions
u
rface plasmo
n
r
sal form with
m
. The tempe
r
e delay. The
m
t
he particle te
m
s
phere distrib
u
d
rop of tempe
r
f
or compariso
n
m
al therapy i
n
e
nce. For e
x
n
dothelial da
m
h
within seco
n
t
ing.
r
deals with
n
ano spheres.
tissues surro
u
e
gies that incl
u
a
nd a precise
p
ace and time
s
. [7-9] Ther
m
n
o spheres is
d
n
on where gol
release heat [
1
a
pture several
p
hoto therma
l
e
s are charac
t
the near infr
a
p
regions via
f
h
e body. A
m
and space he
s. The singl
e
a
in the rate of
m
mediate sur
r
n
o
r
ibuti
o
d
a Benmou
n
e
lkaid, Tlemcen
,
of gold nano
n
resonance p
a characteris
t
r
ature front is
f
m
any particles
p
m
perature pro
f
u
tion provide
s
r
ature when a
p
n
. An effort is
n
a joint effort
x
ample, vaso
d
m
ages appear
n
ds. Damages
s
laser therapy
In order to
m
u
nding the ta
r
u
de a good dis
t
resolution of
under practic
a
m
al ablation
r
d
ue to surface
d absorbs rad
1
0-13]. This r
e
orders of m
l
dyes [14,15]
.
t
erized by a r
a
red providing
f
iber optics fo
r
m
odel is prese
n
at transfer pr
o
e
particle pr
o
temperature r
i
r
oundings. Th
e
JBNB
49
o
n
n
a
,
Algeria
spheres.
henome-
t
ic time τ
f
ound to
p
roblem
f
ile. Dif-
s
a good
p
proach-
made to
with the
d
ilatation
at 45°C
s
peed up
using a
m
inimize
r
get, one
t
ribution
the heat
a
l condi-
r
esulting
plasmon
iation in
e
sonance
agnitude
.
Moreo-
elatively
the pos-
r
remote
n
ted here
o
blem in
o
blem is
i
se at the
e
case of

Heating of Biological Tissues by Gold Nano Particles: Effects of Particle Size and Distribution
50
a large number of nano spheres is then examined based
on selected particle distributions.
2. The Single Particle Problem
Conducting electrons of gold nano spheres exhibit a re-
sonance with the incident electromagnetic field and os-
cillate producing heat. Resonance at a specific frequency
of the applied field is called plasmon resonance. Optimi-
zation of process efficiency and enhancement of thermal
conversion require an adequate choice of the laser wave-
length consistent with the particle shape and size.[13,14]
In this section heating by a single gold sphere of radius a
is considered. The sphere is exposed to a laser beam of
wavelength  , intensity I0 (W/m2) and assumed to gener-
ate a power proportional to the absorption cross section

abs, Pabs=I0

abs (W). This cross section is different from
the geometric expression (i.e ., 4a2) and can be eva-
luated depending on dielectric properties of the medium.
When an electromagnetic radiation of wavelength  im-
pinges into the sphere, its intensity splits into absorption
and scattering. The absorption power which is more re-
levant for our purpose depends on the cross section 
abs.
According to the electro-dynamic theory of dielectric
media, absorption cross section is related to the polariza-
bility of the sphere  [16, 17] by 
abs = [(
  
½] Im
 ,
and the polarizability can be deduced from the Clau-
sius-Mossotti [18,19] relationship as  a3(  –

m)/(
 + 2 
m) where
 is the sphere dielectric permittivity
and 
m that of the biological medium in which it is em-
bedded (i.e., the physiological liquid for example). The
permittivity  is a complex quantity with real and imagi-
nary parts that can be evaluated in terms of gold parame-
ters and surrounding medium using Lorentz-Drude mod-
els. [20,21] It is not our attention to dwell more on this
question which is nevertheless important to complete our
understanding of the problem. A more detailed investiga-
tion along these lines is under progress and we hope to
report on some results in the near future essentially for
confronting the conversion efficiencies with those of
other metals such as iron, nickel, silver or hybrid spheres
containing polymers [22].
The problem now consists of solving the following
sets of equations
12
2
1








gg
abs
g
g
TT
P
r
trr rfor r < a (1)
12
2
10







TT
r
trr r for r  a (2)
Subscript g refers to gold while T is the temperature in
the surrounding medium; λ’s and  ’s are thermal diffu-
sivities (m2/s) and conductivities (W·m-1·K-1), respec-
tively. The focus is made on the resolution of Equation (2)
since T(r,t) is the relevant temperature. In addition, the
solution gives access to Ts at the sphere surface which is
sufficient to characterize the heating source. The solution
must satisfy the following initial and boundary conditions:
Initial condition 0
(, 0)Trt T (3)
Boundary conditions 0
(,) Trt T (4)
2
4






abs
ra
P
T
ra (5)
T0 is the initial temperature prior to laser exposure and
remains that of healthy tissue away from the infected
region. Equation 5 expresses the heat flux from the sphere.
To solve equation 2 subject to the indicated initial and
boundary conditions, we first make a change of variable
from T(r,t) to u(r,t) = r[T(r,t) – T0] then Laplace transform
the resulting equation. Resolution of the equation in u(r,t)
is straight forward. The final step is to go back to time
domain and noting that the inverse Laplace transform of
exp() ()akssas (k > 0) is tabulated in [23] as


2
2exp( )(2) erfck takaterfcatk t.
The result is




10
1
1max
11
1
,,
2
exp
2













 












 








TrtTrt T
ra
erfc
at a
Trra ra
terfc t
aat
(6)
where
1max 4



abs
P
Ta;
2


a;




p
c (7)
and cP represent the sphere density and specific heat,
respectively; erfc is the complementary error function
2
21



t
X
erfcXdt eerfX (8)
The subscript 1 is used to distinguish single particle
from many particle temperature fields to be discussed in
the next section; τ is the characteristic time of sphere
photo heating. The procedure used to solve this problem is
similar to that reported in [24] where the coupled equa-
tions for r < a and r > a were solved. Note that Equation (6)
is similar to the result of Kablinski et al. [10].
The characteristic time is proportional to the sphere
surface and inverse thermal diffusivity of the surrounding
medium meaning that it lasts longer to heat bigger spheres
embedded in poorly diffusing media. Moreover, T1max =
Pabs/4  a  is proportional to Pabs and inversely propor-
tional to sphere’s radius and tissue’s thermal conductivity.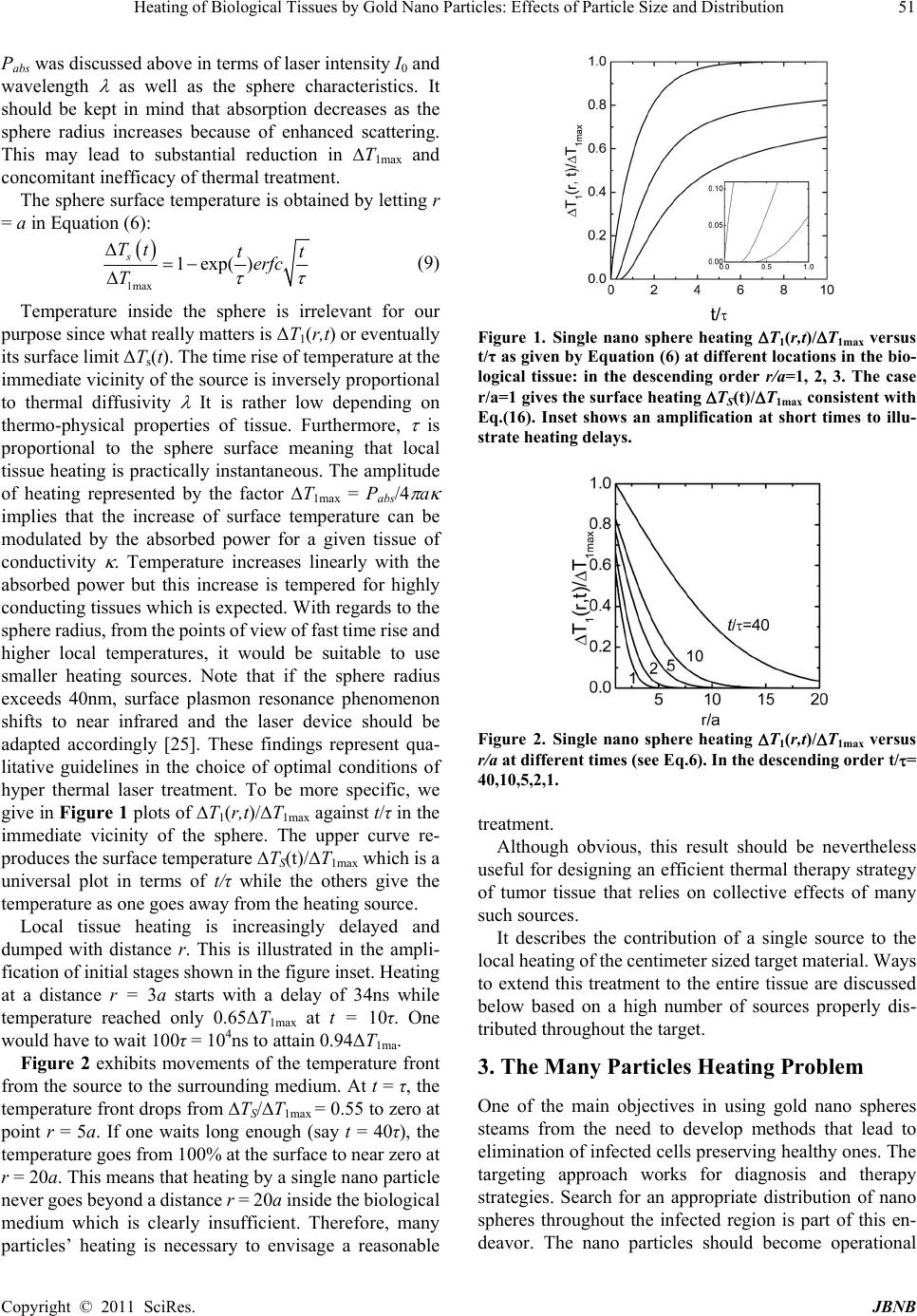

Heating of Biological Tissues by Gold Nano Particles: Effects of Particle Size and Distribution
51
Pabs was discussed above in terms of laser intensity I0 and
wavelength  as well as the sphere characteristics. It
should be kept in mind that absorption decreases as the
sphere radius increases because of enhanced scattering.
This may lead to substantial reduction in T1max and
concomitant inefficacy of thermal treatment.
The sphere surface temperature is obtained by letting r
= a in Equation (6):

1max
1exp()




s
Tt tt
erfc
T (9)
Temperature inside the sphere is irrelevant for our
purpose since what really matters is ΔT1(r,t) or eventually
its surface limit ΔTs(t). The time rise of temperature at the
immediate vicinity of the source is inversely proportional
to thermal diffusivity  It is rather low depending on
thermo-physical properties of tissue. Furthermore,  is
proportional to the sphere surface meaning that local
tissue heating is practically instantaneous. The amplitude
of heating represented by the factor T1max = Pabs/4  a 
implies that the increase of surface temperature can be
modulated by the absorbed power for a given tissue of
conductivity  . Temperature increases linearly with the
absorbed power but this increase is tempered for highly
conducting tissues which is expected. With regards to the
sphere radius, from the points of view of fast time rise and
higher local temperatures, it would be suitable to use
smaller heating sources. Note that if the sphere radius
exceeds 40nm, surface plasmon resonance phenomenon
shifts to near infrared and the laser device should be
adapted accordingly [25]. These findings represent qua-
litative guidelines in the choice of optimal conditions of
hyper thermal laser treatment. To be more specific, we
give in Figure 1 plots of T1(r,t)/T1max against t/τ in the
immediate vicinity of the sphere. The upper curve re-
produces the surface temperature TS(t)/T1max which is a
universal plot in terms of t/τ while the others give the
temperature as one goes away from the heating source.
Local tissue heating is increasingly delayed and
dumped with distance r. This is illustrated in the ampli-
fication of initial stages shown in the figure inset. Heating
at a distance r = 3a starts with a delay of 34ns while
temperature reached only 0.65ΔT1max at t = 10τ. One
would have to wait 100τ = 104ns to attain 0.94ΔT1ma.
Figure 2 exhibits movements of the temperature front
from the source to the surrounding medium. At t = τ, the
temperature front drops from TS/T1max = 0.55 to zero at
point r = 5a. If one waits long enough (say t = 40τ), the
temperature goes from 100% at the surface to near zero at
r = 20a. This means that heating by a single nano particle
never goes beyond a distance r = 20a inside the biological
medium which is clearly insufficient. Therefore, many
particles’ heating is necessary to envisage a reasonable
Figure 1. Single nano sphere heating T1(r,t)/T1max versus
t/τ as given by Equation (6) at different locations in the bio-
logical tissue: in the descending order r/a=1, 2, 3. The case
r/a=1 gives the surface heating TS(t)/T1max consistent with
Eq.(16). Inset shows an amplification at short times to illu-
strate heating delays.
Figure 2. Single nano sphere heating T1(r,t)/T1max versus
r/a at different times (see Eq.6). In the descending order t/=
40,10,5,2,1.
treatment.
Although obvious, this result should be nevertheless
useful for designing an efficient thermal therapy strategy
of tumor tissue that relies on collective effects of many
such sources.
It describes the contribution of a single source to the
local heating of the centimeter sized target material. Ways
to extend this treatment to the entire tissue are discussed
below based on a high number of sources properly dis-
tributed throughout the target.
3. The Many Particles Heating Problem
One of the main objectives in using gold nano spheres
steams from the need to develop methods that lead to
elimination of infected cells preserving healthy ones. The
targeting approach works for diagnosis and therapy
strategies. Search for an appropriate distribution of nano
spheres throughout the infected region is part of this en-
deavor. The nano particles should become operational

Heating of Biological Tissues by Gold Nano Particles: Effects of Particle Size and Distribution
52
under remote activation signals with the capacity to re-
spond to external commands in a predictable way. Intense
research efforts are currently focusing on the development
of novel technologies using nano metallic, organic or
hybrid sources synthesized in a way to be responsive to
remote electric, magnetic or electromagnetic fields. In our
case, these particles must fulfill in addition to the above
requirements other conditions that are related with their
biocompatibility with the least toxicity to the human body.
3.1. Uniform Particles Distribution
Figure 3 shows a schematic representation of a uniform
distribution of nano spheres throughout a centimeter sized
target supposed to be spherical. The first panel describes
the coordinates system while panel b shows projection of
the sphere onto the x-y plane. The z-axis gives the tem-
perature distribution and the amplification describes the
local heating due to a single particle.
As a typical example, if one considers the density of
nano spheres suggested in references [4,10], namely
1015particles/m3, then a spherical tumor of radius 1mm
would contain more than 4 millions spheres, which is high
number. Assuming that the laser intensity is 40W/cm2 and
approximating the sphere absorption cross section with
the geometric one, the power absorbed by a sphere of
radius 40nm would be about 10nW. A typical conductiv-
ity of a biological tissue such as prostate, kidney or liver is
in the order of 0.5 m-1K-1 [26]. This example yields a
single particle heating contribution 1ax 0.04
m
TK
which is of course too low for our purpose. The maximum
rise of temperature in the whole target reads:
R
max 1max1max
a

   
a
TNT T
R (10)
where volume fraction  and surface fractions  ’s are
defined as:
32
32
;


 
aa
RR
NV Na a
VRR
(11)
Figure 3. Schematic representation of temperature profiles
for a uniform nano spheres distribution: (a) The coordinates
system; (b) Temperature and nano spheres distributions; (c)
Amplification of the local heating due to a single nano
sphere.
The surface ratio appearing in Equation (10) means
that only gold particles respond to the laser beam. These
considerations are of course approximate but have the
merit of giving rough estimate of different quantities
involved in the therapy process. For example, one finds
that the maximum temperature rise in the tumor region is
in the order of ΔTma x =10K which is sufficient for thera-
peutic purposes.
Heating biological tissues at a distance r from the origin
is a combined effect of all spheres. For the Dirac delta
function distribution, the maximum rise of temperature in
the biological tissue ΔTmax is proportional to the volume
fraction of spheres  but for a modulated space dependent
distribution, one must take into account density varia-
tions in space and introduce an average temperature rise
due to the N particle system as:

3
1
(,)'' ( ',) 

NN
TrtdrD rTrrt (12)
where DN(r’)d3r’ is the probability of finding a particle at
a distance r’ in a small volume d3r’. Equation 12 describes
the response of the medium at point r due to a source
located at r’. Response of the biological tissue to the N
particle heating system has the form of a convolution
product involving the space variation of density distribu-
tion function



N
Dr and single particle heating temper-
ature. This problem is conveniently handled in Fourier
space by writing


1
,,
NN
Tqt DqTqt (13)
where q is the Fourier variable conjugate of r and Fourier
transform is defined as


3exp
NN
D
qdriqrDr (14)
The result of Equation (11) means that DN(r) is a uni-
form distribution of Dirac delta function, i.e.
  
1
()




 

N
R
Nj
ja
a
Drrr Nrr
R
Below, we will consider the case of a Gaussian distri-
bution of nano spheres.
3.2. Gaussian Distribution
Here we assume that the nano sphere density decreases
from the target center according to the Gaussian distribu-
tion represented in Figure 4.
Using a similar normalization as above, one finds:

32 2
22
33
exp
42 






N
ar
Dr N
RRR
(15)
Fourier transforming this expression and using the fol-
lowing integral [23]

2
2
exp 2



 

q
p
q
dx xpxqxe
pp (p > 0) (16)
r
a
T
1
(r)
X
Y
T(r)
a) b)c)
r
a
T
1
(r)
X
Y
T(r)
a) b)c)

Heating of Biological Tissues by Gold Nano Particles: Effects of Particle Size and Distribution
53
Figure 4. Nano sphere distribution function DN in terms of
r/R where R is the radius of heated tissue.
One finds

22
exp 6




N
Naq R
Dq R (17)
Hence, the temperature rise in the presence of N spheres
becomes
 
22
6
1
,,

 
qR
N
Na
Tqte Tqt
R (18)
The Gaussian factor exp(–q2R2/6) representing the
temperature drop with qR is shown in Figure 5. At qR=1
for example, this drop is quite substantial since.
1
exp 0.02778
6




Another density distribution of nano spheres that can be
considered for comparison would be

2
1
4 


r
R
N
Na e
Dr Rr
R
which is also represented in Figure 4. Fourier trans-
forming yields a Lorentzian distribution in terms of qR

22
1
1

N
Na
Dq RqR
We mention this form because it is often encountered in
soft matter physics and Brownian motion of colloidal
dispersions [27,28] although its relevance to therapeutic
applications could be subject to doubt. In this case, the
total rise of temperature would be
 
1
22
1
,,
1
 

N
Na
Tqt Tqt
RqR
where the factor (1+q2R2)-1 represents a space modulated
drop of temperature reminiscent of a Lorentzian distribu-
tion (see Figure 5). It shows that at tumor’s border, the
temperature drops by nearly a factor 2 which is expected
since the density of nano particles is lower in this region.
Throughout these discussions, Fourier transform of
Figure 5. Uniform (DN(q) = 1), Gaussian and Lorentzian
distribution functions in Fourier space DN(q) versus qR.
ΔT1(r,t) was not needed since this function could be ana-
lyzed directly in r-space.
4. Discussion and Conclusion
Hyper thermal therapy using laser heated nano sized gold
spheres is analyzed by solving the heat transfer problem.
It is found that the sphere temperature rises with a cha-
racteristic time that is proportional to its surface and in-
versely proportional to heat diffusivity of the surrounding
biological medium. Heat fronts move from the particle to
the medium with increasing delays as one goes away
from the surface. A simple numerical example shows that
heat generated by a single particle is too low to produce
any noticeable effect on the surrounding tissue but the
combined effects of a large number of particles is suffi-
cient for thermal ablation. Models are used for the particle
density distribution function D(r) and a mean temperature
rise defined as a convolution product of the distribution
and the single particle temperature front. The function
D(r-r’) is defined as the probability density of finding a
particle at point r’ knowing that there is one at point r. For
a uniform distribution of spheres, the probability distri-
bution would be a sum of Dirac delta functions and the
problem reduces to the single particle contribution T1(r,t)
within a constant factor. But if the density of spheres is
space modulated and decreases as one goes away from the
target center due to some specific long range inter particle
interactions, then the probability drops substantially. We
have examined the case of Gaussian and Lorentzian dis-
tributions. In the latter case, the probability distribution
decays according to a long 1/r tail damped exponentially as

e



r
R
Dr r
where  is normalization constant. A colloidal dispersion
of charged particles is an example of this distribution. In
the case of a Gaussian distribution, one has

2
2
32
2
2
2
3





r
R
Dr e
R

Heating of Biological Tissues by Gold Nano Particles: Effects of Particle Size and Distribution
54
an example of which would be spheres with a harmonic
potential interaction. For a uniform distribution, temper-
ature raised proportionally to T1(q) within a constant
factor defined by the volume fraction of spheres times
their fractional area. For Lorentzian and Gaussian distri-
butions, the temperature was also proportional to  T1
modulated by a space dependent factor reminiscent of the
drift in the concentration of spheres as the border of the
target region was approached. Lorentzian distribution
predicted a moderate drop of temperature rise compared to
the Gaussian case where a much stronger exponential
drop was obtained.
It is worthwhile to note that biological systems such as
proteins (10-100 nm), cells (10-100 mm) and bacteria
(1-10 mm) are characterized by a broad range of sizes.
Use of nano spheres of diameter between 10 and 40 nm in
hyper thermal therapy seems to be adequate and efficient
at the proteins level. It should be kept in mind that foreign
particles can react with the host medium selectively de-
pending on a variety of conditions related with the nature
of particles and biological tissue. Hydrophobic and hy-
drophilic particles react differently and can be covered
with molecular species present in blood. They can absorb
proteins and these effects should be taken into account to
define the right distribution and evaluate their stability
and efficiency in developing a therapy strategy [29] of
tumor tissues. Magnetic nano particles such as Fe3O4
exhibit a magnetization that oscillates up and down under
the influence of an external field and induce heating of the
surrounding medium. Other elements like cobalt and
nickel can also be used combined with polymers.
These results should be useful in prescribing efficient
treatments of tumors in close collaboration with the
medical team. It is hoped that these considerations will
trigger interest in collecting precise experimental data to
assess the validity of the results and the concomitant pre-
dictive models.
REFERENCES
[1] J. H. Breasted, “Edwin’s Smith Chirurgical Papyrus,”
University of Chicago, 1930.
[2] L. Goldman, et al., Adv. Biomed. Eng. Med. Phys., Vol. 1,
1968, pp. 317.
[3] M. Ferrari, Nat. Rev. Cancer, Vol. 5, pp. 161, 2005.
[4] I. R. Hirsh et al., Proc. Nat. Acad. Sci. USA, Vol. 100, pp.
13549, 2003.
[5] A.G. Cuenca et al., Am. Cancer Soc., Vol. 107, pp. 459
2006.
[6] O. V. Salata, J. Nanobiotech., Vol. 2, pp. 1, 2004.
[7] A. Hadj Sahraoui, et al., J. Appl. Phys., Vol. 82, pp. 12,
1997.
[8] A. Boudene, S. Khaldi, J. Appl. Polym. Sci. Vol. 89, pp.
481, 2003.
[9] X. Coqueret et al., Macromol. Theory Simul., Vol. 9, pp.
725, 2000.
[10] P. Keblinski al., J. Appl. Phys., Vol. 100, pp. 054305,
2006.
[11] C. M. Pitsillides et al. Biophys. J., Vol. 84, pp. 4023, 2003.
[12] L. E. Vlerken, M. M. Amiji, Expert Opin. Drug Deliv.,
Vol. 3, pp. 205, 2006.
[13] X. Huang et al., J. Adv. Res., Vol. 1, pp. 13, 2010.
[14] D. Lapotko, Nanomed., Vol. 4, pp. 253, 2009.
[15] S. Shenogin et al., J. Appl. Phys., Vol. 95, pp. 8136, 2004.
[16] G. Mie, Ann. Phys., Vol. 25, pp. 377, 1908.
[17] M. Kerker, “The Scattering of Light and Other Electromag
Netic Radiations,” Academic Press, New York, 1969.
[18] B.T. Draine et al., Astrophys. J., Vol. 405, pp. 685, 1993.
[19] B.T. Draine, “Light Scattering by Non-Spherical Particles:
Theory, Measurements and Applications,” Academic
Press, San Diego, 2000.
[20] U. Kreibig, M. Vollmer, “Optical Properties of Metal
Clusters,” Springer Verlag, Berlin, 1995.
[21] C.F. Bohren, D.R. Huffman, “Absorption and Scattering
of Light by Small Particles,” Wiley, New York, 1983.
[22] A. R. Sennoudi et al. unpublished.
[23] I.-S. Gradshteyn and I. W. Ryghik, “Tables of Integrals,
Series and Products,” Academic Press, New York, 1965.
[24] H. Goldenberg, C.J. Tranter, Brit. J. Appl. Phys. 296,
1952.
[25] G. Yin et al. , J. Kor. Phys. Soc., Vol. 49, pp. 2108, 2006.
[26] G. Brix et al , Magn. Res. Imag., Vol. 20, pp. 65, 2002.
[27] F. Hakem et al., Ber. Bunsenges. Phys. Chem., Vol. 100,
pp. 815, 1996.
[28] M. Benmouna et al., Phys. Chem. Liq., Vol. 16, pp. 235,
1987.
[29] J. M. Dobson, “Manual of Small Animal Oncology”, RAS
White Edit., Bsava, 1991.