Smart Grid and Renewable Energy, 2013, 4, 8-20
http://dx.doi.org/10.4236/sgre.2013.46A002 Published Online September 2013 (http://www.scirp.org/journal/sgre)
Vehicle to Grid Decentralized Dispatch Control Using
Consensus Algorithm with Constraints
Alexandre Lucas1, Sun Chang2
1MIT-Portugal Program, Instituto Superior Técnico, Lisbon, Portugal; 2Singapore MIT-Alliance, National University of Singapore,
Singapore, Singapore.
Received July 22nd, 2013; revised August 22nd, 2013; accepted August 29th, 2013
Copyright © 2013 Alexandre Lucas, Sun Chang. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
With the transition to electric vehicle technologies, large scale support infrastructure is being deployed. The vehicle-
to-grid (V2G) concept is an opportunity to take advantage from both infrastructure and electric vehicle drive. However,
coordinating large number of agents in a reasonable speed and lack of homogenous distribution of the service provided
by vehicle users to the grid have been left unattended. We apply consensus theory to the V2G concept presenting a de-
centralized control solution to assure that all vehicles within a region, regardless of their technology, positioning or state
of charge, can communicate with their neighbors and agree on how much energy each should individually exchange
with the grid. Applying constraints to the system, we considered a 25,000 vehicle fleet connected to a grid during peak
hours. Simulating power changes and vehicles entering and leaving the system, two groups of 5 vehicles were studied:
the first group remained in the system during all peak hours, while the second group only an hour. Results showed that
the two groups of vehicles despite connecting to the system at different times were able to reach consensus in t = 15 s,
and reported a maximum error of ε < 0.01% if left in the system during all peak hours.
Keywords: Vehicle-to-Grid; Smart-Grid; Consensus; Decentralized Control; Infrastructure
1. Introduction
Environmental concerns and oil dependency have en-
couraged electric drive technology transition and today,
it is no longer a plan but a reality. Several technologies
of varying maturity have been made available to different
markets, but main identified options are hybrids, battery
electric vehicles, and fuel cell vehicles. An extensive
charging infrastructure is being deployed to support these
new electric vehicles, and with it, the business world is
showing a newfound urgency to realize the promise of
these technologies.
The benefits of an electric transportation technology
transition can be seen in renewable energy systems for
electricity conversion. Due to their stochastic nature, it is
apparent that they can profit from the introduction of
electric vehicles (EV). This is due to their power storage
capacity particularly during night hours and capacity to
supply it back to the grid during high demand hours
when electricity is more expensive to produce; a concept
known as peak shaving. Kempton and Tomic [1,2] dem-
onstrate the potential electric vehicles may have in stabi-
lizing the grid and in the support of large-scale renewable
energy systems. White and Zhang [3] extend their work
to plug-in hybrids and defend that the greater incentive
for individuals to connect their vehicles to the grid is
when used in frequency regulation rather than exclu-
sively peak reduction. Several services such as regulation,
spinning reserves and power supply become relevant
with large market penetration of electric vehicles. A sys-
tem in which electric vehicles, communicate with the
power grid, to provide such services is called vehicle-
to-grid (V2G).
In addition to grid service opportunities, charging in-
frastructure can also profit from V2G, both in economic
and environmental terms. Lucas et al. [4] draw attention
to the impact energy supply infrastructures that may have
in both emissions and energy use life cycle analyses of
an electric vehicle, particularly the foreseen charging
infrastructure. Their study suggested that if more energy
were to flow through the charging infrastructure, the
higher the effective use and the lower carbon and energy
impact per kilometer each charger would have.
However, when considering V2G services and multi-
ple agents in a system, behavior control becomes a prob-

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints 9
lem. Decentralized control is a popular choice over cen-
tralized control for networked systems, as it tends to re-
duce communication or sensing requirements and it has
improved scalability, flexibility, reliability, and robust-
ness. The cooperative consensus problem is an option in
decentralized control and has attracted much interest in
the last few years. Consensus problem has been applied
to many different subjects such as physics, biology, and
mechanical engineering. The aim of cooperative control
is to achieve a consensus value for the cooperative vari-
ables for all agents in the network. Each agent of the
network updates its own variable, using values from its
neighbors, in such a way that drives the system towards a
consensus value [5].
In the consensus problem, a graph G(V,E) is used to
represent the communication network, where V is the set
of nodes and E is the set of edges. We call node j the
neighbor of node i if and only if ji denoted by
eE

j
Ni
i
and the number of neighbors is called the de-
gree of the node i, denoted by di. In this paper we make
use of the consensus algorithm in its discrete case. Sup-
pose that there are n nodes in the graph. Each node has a
state variable which they exchange within the network,
for the node it is denoted as
th k
i
x
at time step
The state variables follow the updating rule
0,1,2,k

1
1
n
kk kk
ii ijijji
j

x
xcax


 
x
. (1)
In this algorithm aij is the element in the adjacency
matrix of G(V,E), which is defined as if and
only if ji and j ≠ I, otherwise . We are
able to control cij under the condition that
1
ij
a
0
ij 
1
n
j
eEa
1
ij ij
ca


for all . 1, ,in
Consensus theory has been previously explored in the
literature [6-9] and they have proven the required condi-
tions for a deterministic network to achieve consensus.
There are also studies [5,10,11,] addressing consensus
under various disturbances such as topology changes and
communication delays. Also various applications such as
flocking theory and rendezvous problems have been
studied [5,12,13].
The current study demonstrates how consensus theory
can be applied to control the energy flux to or from
agents in V2G systems. The study considers the use of
public or private normal charging infrastructure, which
typically charge an electric vehicle in 6 to 8 hours [14].
Most of normal charging infrastructure is ready for smart
grid integration; however, integrating the V2G concept
would only require small adaptations to unprepared char-
gers. This study only addresses the power supply service,
simulated during peak hours, but it can however, be ap-
plied to other services as well. The only requirement is to
adjust the number of agents in the system or systems,
control variables, restrictions and consensus.
1.1. V2G Services
Peak power is the amount of electricity conversion at the
times of day when high levels of power are demanded. It
is typically generated by power plants that can be
switched on for short periods, typically only a few hun-
dred hours per year. At this stage, electricity conversion
cost per kWh is the highest when compared to other
times of day. Peak hours can vary from 3 to 5 hours, and
depending on the season, its length and amplitude may
change significantly. Studies [15-17] have shown that
V2G contribution to peak power supply needs, may be
economical viable.
An additional service that EV’s can provide is being a
substitute to the so called spinning reserves. Spinning
reserves refer to additional generating capacity that can
provide quick power, within a ten-minute response time
upon request from the grid operator. Generators provid-
ing spinning reserves run at low or partial speed and thus
are already synchronized to the grid. This service is paid
by the amount of time they are available and ready even
though no energy is actually delivered. According to
Shoup [18], vehicles are parked 95% of their time, so the
potential to work with the grid and provide such services
is significant.
In such circumstances, an even more pertinent applica-
tion would be the regulation service, which according to
Kempton and Tomic [2], is in fact the most profitable
service V2G can provide to the grid. This service is the
main option to adjust the grid’s frequency and voltage by
re-matching generation and load demand. This service
requires instantaneous control of the grid operator, trans-
mitting signals to generation centers. This communica-
tion and demand is fulfilled within a minute or less by
increasing or decreasing the output of the generator or
charge.
1.2. Impact of Charging/Discharging Rate
Main arguments against the V2G concept, are related to
both efficiency and the rapid deterioration of batteries
when increasing the number of charge/discharge cycles
and the depth of discharge. Peterson [19] reports values
showing that several thousand driving days/V2G incur
substantially less than 10% capacity loss regardless of
the amount of V2G support used. In his study, different
degrees of continuous discharge were imposed on the
cells to mimic afternoon V2G use to displace grid elec-
tricity. The tested cells showed promising capacity fade
performance: more than 95% of the original cell capacity
remained after thousands of driving days’ worth of use.
However, V2G modes that were more intermittent in na-
ture led to more rapid battery capacity fade and should be
avoided to minimize battery capacity loss over many
years of use. It becomes critical to mitigate the depth of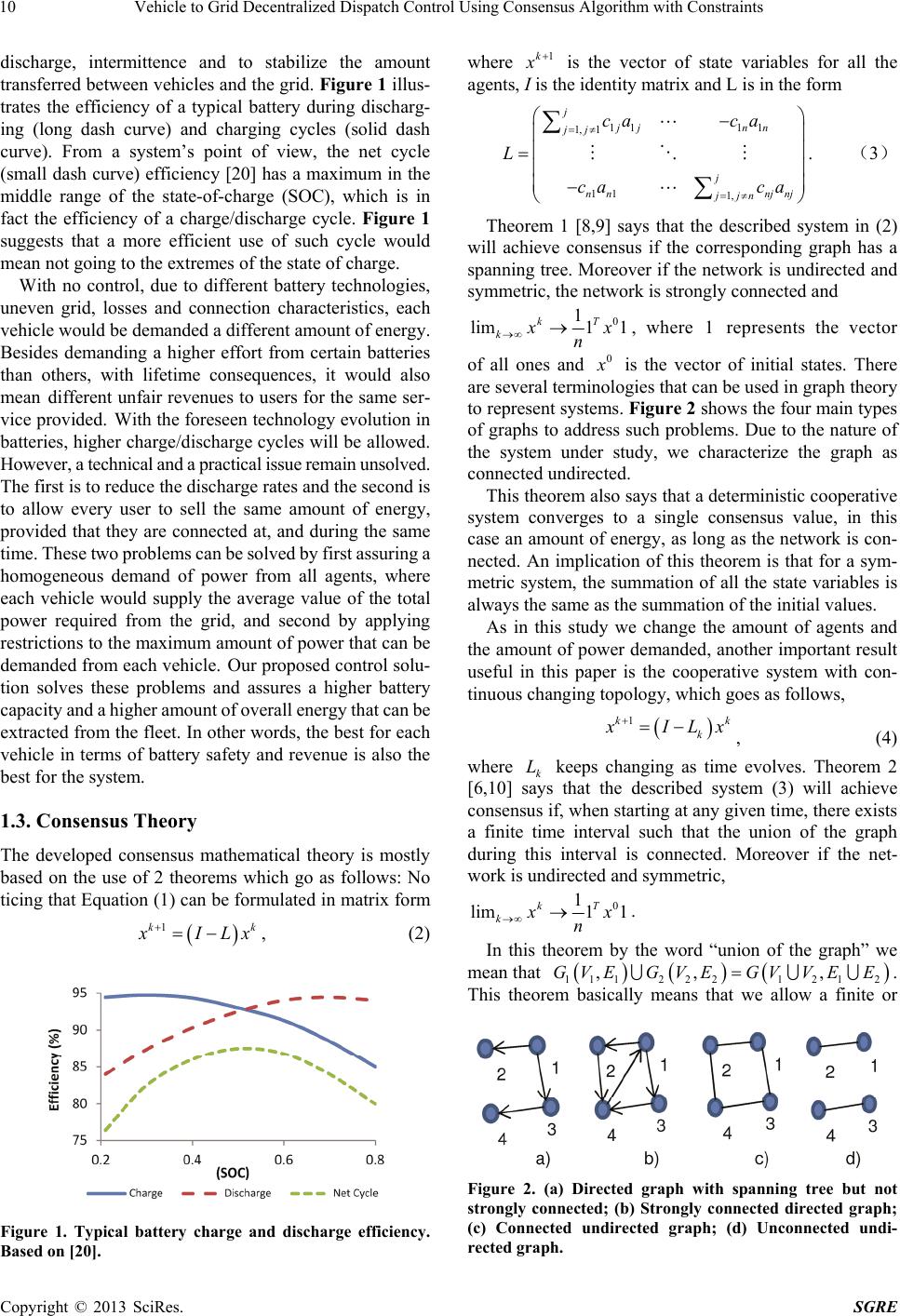

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints
10
discharge, intermittence and to stabilize the amount
transferred between vehicles and the grid. Figure 1 illus-
trates the efficiency of a typical battery during discharg-
ing (long dash curve) and charging cycles (solid dash
curve). From a system’s point of view, the net cycle
(small dash curve) efficiency [20] has a maximum in the
middle range of the state-of-charge (SOC), which is in
fact the efficiency of a charge/discharge cycle. Figure 1
suggests that a more efficient use of such cycle would
mean not going to the extremes of the state of charge.
With no control, due to different battery technologies,
uneven grid, losses and connection characteristics, each
vehicle would be demanded a different amount of energy.
Besides demanding a higher effort from certain batteries
than others, with lifetime consequences, it would also
mean different unfair revenues to users for the same ser-
vice provided. With the foreseen technology evolution in
batteries, higher charge/discharge cycles will be allowed.
However, a technical and a practical issue remain unsolved.
The first is to reduce the discharge rates and the second is
to allow every user to sell the same amount of energy,
provided that they are connected at, and during the same
time. These two problems can be solved by first assuring a
homogeneous demand of power from all agents, where
each vehicle would supply the average value of the total
power required from the grid, and second by applying
restrictions to the maximum amount of power that can be
demanded from each vehicle. Our proposed control solu-
tion solves these problems and assures a higher battery
capacity and a higher amount of overall energy that can be
extracted from the fleet. In other words, the best for each
vehicle in terms of battery safety and revenue is also the
best for the system.
1.3. Consensus Theory
The developed consensus mathematical theory is mostly
based on the use of 2 theorems which go as follows: No
ticing that Equation (1) can be formulated in matrix form

1kk
x
ILx
 , (2)
Figure 1. Typical battery charge and discharge efficiency.
Based on [20].
where 1k
x

is the vector of state variables for all the
agents, I is the identity matrix and L is in the form
11 11
1, 1
11 1,
j
jj nn
jj
j
nnnj nj
jjn
ca ca
L
ca ca















. （3）
Theorem 1 [8,9] says that the described system in (2)
will achieve consensus if the corresponding graph has a
spanning tree. Moreover if the network is undirected and
symmetric, the network is strongly connected and
01im 11l kT
k
x
x
n
 , where 1 represents the vector
of all ones and 0
x
is the vector of initial states. There
are several terminologies that can be used in graph theory
to represent systems. Figure 2 shows the four main types
of graphs to address such problems. Due to the nature of
the system under study, we characterize the graph as
connected undirected.
This theorem also says that a deterministic cooperative
system converges to a single consensus value, in this
case an amount of energy, as long as the network is con-
nected. An implication of this theorem is that for a sym-
metric system, the summation of all the state variables is
always the same as the summation of the initial values.
As in this study we change the amount of agents and
the amount of power demanded, another important result
useful in this paper is the cooperative system with con-
tinuous changing topology, which goes as follows,


1kk
k
x
ILx
 , (4)
where k keeps changing as time evolves. Theorem 2
[6,10] says that the described system (3) will achieve
consensus if, when starting at any given time, there exists
a finite time interval such that the union of the graph
during this interval is connected. Moreover if the net-
work is undirected and symmetric,
L
01im 11l kT
k
x
x
n
 .
In this theorem by the word “union of the graph” we
mean that




1112 2 21212
,, ,GVEGVEGV VEE


.
This theorem basically means that we allow a finite or
Figure 2. (a) Directed graph with spanning tree but not
strongly connected; (b) Strongly connected directed graph;
(c) Connected undirected graph; (d) Unconnected undi-
rected graph.

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints 11
countable disconnection during the process of consensus
seeking. If we consider as an example graphs (d) and (c)
from Figure 2 to be G1 and G2respectively, the corre-
sponding Laplacian matrices will be:

11
00
22
11 00
22
111
00 22
0011
22
LG

























,

211
0
333
12 1
0
33 3
212
0
33
112
0333
LG
















1
3












.
Note that G1 is not connected, and so consensus will
not be reached except in some very rare cases as depicted
in the Figure 3(a). However if we switch G1 and G2, in
order to follow the pattern G1G2G1G2…, then theorem
2 is satisfied. The system finally achieves consensus as
can be seen Figure 3(b).
Difficulties arise when trying to control the amount of
energy demanded by the grid and given by each of the
vehicles. As far as the final costumer is concerned, this
problem would cause different readings on the meters
and unfair payment to users even if ultimately, some
were to plug in at the same time and available to supply
the same amount of energy. This study develops a decen-
tralized control solution for the foreseen vehicle to grid
(V2G) technology, using consensus problem theory. The
Figure 3. Consensus variable only with G1 (a); Consensus
variable with switched topology (b).
objective is to estipulate the amount of power that each
EV discharges to the grid (when available as a V2G
agent), when requested a certain demand in peak hours,
also known as peak shaving. Consensus problem will be
proven to be a good control technique in such systems if:
1) Agents reach consensus with a dynamic and large
scale system; 2) if vehicles within the system provide the
same amount of energy to the grid; 3) if vehicles, despite
arriving at different moments to the system, can reach
consensus, 4) if the consensus is reached in a reasonable
convergence speed.
2. Methodology
Even though it has been demonstrated that some vehicles
are better suited than others for individual power markets
[17], this study makes no distinctions between EVs
FCHEV, PHEVs or other technologies, as it is not the
intention to distinguish them but to demonstrate the as-
sociated control that can be applied to different groups.
We consider that it should be the user’s responsibility to
make an efficient use of its technology according to each
service provided. Unlike argued by [20], that see a higher
efficiency of the system to be managed and controlled
upstream by utilities, deciding what to extract from vehi-
cles and always seeking higher SOC’s, we defend that if
the right incentives are given to the market, users will
behave in an optimized way, realizing that there are more
efficient ways, hence benefits to use their batteries, SOC
and times. That is after all what smart grid is all about.
Using MATLAB, a simulation was performed using
consensus algorithm theory. Considering a reference load
diagram (Figure 1 of the Appendix), it is assumed that
the marginal cost of generating electricity above 7350
kW, would be higher than purchasing it from the electric
vehicle fleet connected to the grid. A hydro plant was
used as leader agent to initiate the system and to com-
pensate the lack of capacity of the fleet. Peak hours last
for 3 hours from 17:45 h to 20:45 h. Figure 4 shows the
required power demanded to the fleet which is updated
every 15 minutes according to Table 1 of the Appendix.
Moreover, every minute the system incorporates new
vehicles or have vehicles leaving. Figure 5 shows the
Figure 4. Power de mande d by the grid.

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints
12
Table 1. Production by source during peak hours and energy requested to the fleet.
Hour Coal SSG
Hydro SSG Thermal SSG Wind Natural Gas Imports Run of river Reserv. Pump.Demand W/o pump. Demand > 7. 35 GW
17:45 1633.2 119.3 1048.5 905.7 936.8 950.8 1400.8437.4 0 7432.5 82.5
18:00 1570.8 117.6 1051.6 945 897.6 859.7 1418.4595.3 0 7456 106
18:15 1532.4 114.3 1056.3 952 865.6 835.3 1472.8654.9 0.8 7483.6 133.6
18:30 1532.8 114 1065 985.9 871.6 864.5 1479.8674.1 93 7587.7 237.7
18:45 1569.2 114.1 1060.6 991.9 888 863.4 1445.7691.8 93.5 7624.7 274.7
19:00 1633.2 112.2 1064.5 960.2 883.2 627.9 1531.3729 8 7541.5 191.5
19:15 1698.4 111.1 1072.7 977.3 795.6 620.6 1610.1660.8 0 7546.6 196.6
19:30 1701.2 109.6 1071.8 987.8 802.4 633.1 1580.2664 0 7550.1 200.1
19:45 1727.2 102.1 1070.8 962.9 851.6 635.6 1535.6661 0 7546.8 196.8
20:00 1654.4 103.6 1074.8 943.2 934 505.9 1516.7783.5 0 7516.1 166.1
20:15 1629.6 105.1 1080.1 923.8 948.4 461.2 1554.8761.6 0 7464.6 114.6
20:30 1674.4 105.2 1079 945.3 873.6 466.2 1541.8702.7 0 7388.2 38.2
Figure 5. Dynamics of vehicles entering and leaving the
system.
amount of vehicles in the system during peak hours. The
complete fleet dynamics can be observed in Table 2 of
the Appendix. Every time a vehicle connects to the grid,
the charging station’s smart meter will be turned on and
communicate its GPS location. This allows being recog-
nized by other meters as a neighbor.
The smart meter will communicate with its neighbors
and assume the state variable x, which is the consensus
value of the same power to be delivered by the complete
fleet.
The total output energy from the fleet plus the leader
agent is always equal to the total power demanded by the
grid i
x
P.
When a vehicle is disconnected either because it has
reached its user’s predetermined SOC, or leaves the
charging station, the system will stop assuming its Global
Positioning System (GPS) and will stop considering it as
a neighbor. As the number of vehicles change, the system
will communicate and reach once again a consensus.
The control process will ensure that all vehicles reach
a consensus value for the amount of power that each of
them can supply. However, due to battery and grid con-
nection power limitations, two scenarios can occur. The
first, is that the amount of power required by the grid is
such, that the number of cars in the system find the con-
sensus value to be perfectly within the connection and
batteries’ limits, hence all power is provided be the fleet.
The second scenario is that the consensus value is higher
than what the charging circuit connections can sustain
(assumed to be all 7.2 kW) or the amount of energy sur-
passes the batteries’ capacity (assumed 24 kWh). In this
case, the leader agent (hydro plant), which acts like an
agent at all times but has no restrictions, assumes the rest
of the power. The total amount of vehicles is hence n-1
(due to the existence of the leader agent). So that the
power demand to each vehicle does not exceed its limits
endangering the battery, a restriction of 80% of the bat-
tery capacity was assumed. This value is of course pro-
grammable in the control process.
In mathematical and programming terms, to address
this problem, we first define and undirected graph G(V,
E) associated with the network formed by the vehicles
and communication link between them. Each car is a
node in the graph and the communication links are sym-
metric, representing the edges in the graph. The state
variable k
i
x
, 1, ,in

, associated with
each car is a single variable indicating the power re-
quested to each car. Each car can only communicate with
their neighbors and exchange the information of their
state variables. Our problem can be formulated as a co-
operative system with constraint on each state variable
that must be satisfied at all time. In our model, there is a
quick response power plant that it is used as a leader, so
0,1,k

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints 13
Table 2. Fleet variation, vehicles entering and leaving the system.
Time Cars Arriving Cars Leaving Cars in the system
17:45 0 0 25,000 18:28 8 2 24,979
17:46 3 0 25,003 18:29 5 8 24,976
17:47 7 0 25,010 18:30 4 7 24,973
17:48 11 16 25,005 18:31 8 13 24,968
17:49 0 2 25,003 18:32 1 11 24,958
17:50 6 12 24,997 18:33 3 3 24,958
17:51 0 5 24,992 18:34 2 6 24,954
17:52 12 3 25,001 18:35 1 5 24,950
17:53 6 8 24,999 18:36 5 6 24,949
17:54 15 1 25,013 18:37 8 5 24,952
17:55 8 2 25,019 18:38 5 2 24,955
17:56 7 7 25,019 18:39 10 1 24,964
17:57 17 2 25,034 18:40 5 1 24,968
17:58 6 7 25,033 18:41 4 4 24,968
17:59 3 6 25,030 18:42 3 8 24,963
18:00 1 0 25,031 18:43 8 8 24,963
18:01 1 5 25,027 18:44 5 10 24,958
18:02 1 7 25,021 18:45 5
7 24,956
18:03 6 2 25,025 18:46 1 8 24,949
18:04 8 2 25,031 18:47 3 14 24,938
18:05 0 6 25,025 18:48 3 9 24,932
18:06 6 3 25,028 18:49 1 8 24,925
18:07 6 5 25,029 18:50 5 8 24,922
18:08 0 9 25,020 18:51 5 2 24,925
18:09 1 12 25,009 18:52 5 5 24,925
18:10 8 8 25,009 18:53 5 3 24,927
18:11 0 2 25,007 18:54 8 3 24,932
18:12 2 8 25,001 18:55 9 6 24,935
18:13 5 7 24,999 18:56 3 9 24,929
18:14 8 2 25,005 18:57 2 8 24,923
18:15 2 14 24,993 18:58 1 8 24,916
18:16 7 8 24,992 18:59 1 4 24,913
18:17 9 5 24,996 19:00 8 3 24,918
18:18 8 17 24,987 19:01 0 2 24,916
18:19 5 2 24,990 19:02 1 3 24,914
18:20 1 8 24,983 19:03 6 10 24,910

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints
14
Continued
18:21 7 7 24,983 19:04 0 3 24,907
18:22 8 8 24,983 19:05 1 3 24,905
18:23 2 9 24,976 19:06 10 2 24,913
18:24 7 14 24,969 19:07 1 1 24,913
18:25 2 8 24,963 19:08 1 8 24,906
18:26 7 3 24,967 19:09 1 2 24,905
18:27 8 2 24,973 19:10 11 4 24,912
19:11 2 10 24,904 19:57 0 1 25,015
19:12 1 8 24,897 19:58 0 8 25,007
19:13 6 9 24,894 19:59 4 8 25,003
19:14 13 4 24,903 20:00 11 1 25,013
19:15 16 12 24,907 20:01 6 1 25,018
19:16 8 5 24,910 20:02 12 8 25,022
19:17 3 1 24,912 20:03 6 1 25,027
19:18 9 2 24,919 20:04 1 1 25,027
19:19 9 1 24,927 20:05 8 5 25,030
19:20 6 1 24,932 20:06 3 1 25,032
19:21 0 1 24,931 20:07 9 1 25,040
19:22 1 4 24,928 20:08 2 2 25,040
19:23 0 3 24,925 20:09 2 17 25,025
19:24 16 2 24,939 20:10 16 0 25,041
19:25 3 2 24,940 20:11 6 7 25,040
19:26 8 2 24,946 20:12 12 2 25,050
19:27 3 6 24,943 20:13 8 8 25,050
19:28 2 6 24,939 20:14 11 1 25,060
19:29 7 8 24,938 20:15 8 1 25,067
19:30 6 1 24,943 20:16 7 3 25,071
19:31 5 1 24,947 20:17 3 10 25,064
19:32 5 9 24,943 20:18 8 2 25,070
19:33 9 9 24,943 20:19 2 1 25,071
19:34 1 9 24,935 20:20 1 7 25,065
19:35 12 1 24,946 20:21 2 1 25,066
19:36 1 7 24,940 20:22 1 1 25,066
19:37 14 1 24,953 20:23 1 2 25,065
19:38 9 1 24,961 20:24 7 3 25,069
19:39 7 11 24,957 20:25 0 2 25,067
19:40 1 1 24,957 20:26 0 2 25,065

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints
15
Continued
19:41 13 4 24,966 20:27 1 0 25,066
19:42 7 4 24,969 20:28 1 0 25,067
19:43 8 1 24,976 20:29 1 0 25,068
19:44 7 2 24,981 20:30 2 3 25,067
19:45 7 3 24,985 20:31 4 3 25,068
19:46 12 1 24,996 20:32 2 3 25,067
19:47 2 8 24,990 20:33 5 2 25,070
19:48 1 1 24,990 20:34 5 1 25,074
19:49 8 9 24,989 20:35 2 6 25,070
19:50 1 1 24,989 20:36 3 8 25,065
19:51 8 1 24,996 20:37 5 7 25,063
19:52 3 1 24,998 20:38 2 6 25,059
19:53 1 1 24,998 20:39 4 5 25,058
19:54 7 4 25,001 20:40 3 4 25,057
19:55 7 2 25,006 20:41 8 4 25,061
19:56 12 2 25,016 20:42 3 7 25,057
20:43 5 10 25,052
20:44 9 1 25,060
that it adjusts its own state value at any time in order to
satisfy the power demanded which is denoted as k for
the time step. Without loss of generality, we use
1
P
th
k
k
x
to denote its state variable. Except the leader node,
all the other nodes are representing cars and they all have
a limitation on the maximum power they can provide,
denoted by max
x
and assumed to be the same for all the
cars. With the notations introduced above, we can de-
scribe our model with the following constrained coopera-
tive system,
To initialize the system at , we set 0 0k0
1
x
P

and
00
i
x

for 2,, ,in


0k
it is easy to verify that (6) is
satisfied at

. Moreover by theorem 1 if there is no
change in power demanded and network topology, (6) is
satisfied following the updating rule (5).
Considering the dynamics introduced in the system,
such as power demand and variation of vehicles we have
the following behaviors:
When there is a change in power demand at time k and
1kk k
PP P


 , we set11
kk
k
x
x

1k
k
k
x
ILx
 (5)
P

 and continue up-
dating the state variable using (5). Then constraint (6) is
satisfied.
Subjected to constraints
1Tk
k
x
P (6)
Whenever there is a car entering the system at time k,
supposing it is the car,
we set 1

th
1n0
k
n
x

and
it will start to update its value according to equation (5).
We have again constraint (6) being satisfied.
max 2,,, 0,1,2,
k
i
xx ink 
k
 (7)
Whenever there is a car leaving the system at time k,
supposing it is the car, this car sends a message
that it is leaving the system and the value
th
m
kk
mm
x
d to all
its neighbors, where is the degree of node m at time
k. Then, before going to the next time step we set
k
m
d
In our case, the size of
x
and k will vary since
there will be cars plugged in or off during a particular
time period. This further complicates our model from the
standard consensus problem. However by theorem 1 we
can easily see that the constraint (6) can be satisfied if the
network is symmetric i.e. k is symmetric at any time
and the initial value of each state variable is set properly.
L
L

k
kk m
ii k
m
x
x
xiN
d
 m and delete the node m and all
Having assured that the system always reaches a con-
sensus, it is still required to initialize the system and re-
initialize the state variable.
the edges connected to it from the graph. One can verify
that constraint (6) is then satisfied.
Using switching control, we guarantee that vehicles do

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints
16
not exceed its limits. Now, we are able to guarantee that
the constraint (6) is satisfied by reinitializing the state
variable whenever there is a change in the network to-
pology or total power demanded. To satisfy constraint (7),
we need further control techniques. Recalling in Equa-
tion (1)

1
1
n
kk k
ii ijijji
j
k
x
xcaxx


 

ij
c s are the control variables that can be decided by
each agent under the condition that for all
11
ij ij
n
jca


i = 1,…,n. In our problem, we need a further regulation
that in order to keep the network symmetric.
ij ji
We propose a state dependent control on
cc


,
kk
ijji
cxx
which can be summarized as follows,

,0
kk
ijji
cxx if
max max
max max
min min
80%& 80%
kk
ij
x
xx xx
d
 
 
 
 
x
d



0
(8)
if otherwise. (9)

,
kk
ijji
cxx
In Equation (8), min refers to the minimum degree
in the network. In the case of 25000 agents we know that
the degree of each node is 80 - 100. Therefore we choose
min to be 80. We choose such a threshold number ba-
sically for two reasons. First of all, we want to make sure
that whenever there is a car leaving the system, the con-
sensus variable of its neighboring agents, which we reset
d
d
to
k
kk m
ii k
m
x
xxd  , will not exceed the limit. The 80%
coefficient is used to make the control more robust. One
can however change this value according to other char-
acteristics or system’s requirements. This function is
symmetric regarding to k
j
x
and k
i
x
, so
and whenever the value of the
state variable

,
kk kk
ijjijij i
cxxcxx
k
i

,
x
is greater than max
max
min
80%xx
d




of
the maximum power max
x
, i
k
x
will only decrease at the
next time step so it will not exceed max
x
. We can also
verify that starting from any time instant; there exists a
bounded time interval where the union of the graphs
within that time interval is connected. Therefore by
theorem 2, the system will reach consensus.
Having built the model, we applied it to two groups of
vehicles to confirm that they would reach consensus and
provide the same amount of energy under different start-
ing and ending points. The first group of 5 vehicles re-
mained connected to the grid during all 3 peak hours,
while the second group of vehicles joined the system one
hour after the beginning of the peak hour and left one
hour earlier. Since there is a time to reach consensus,
until it eventually happens there will be some vehicles
whose state variable will be higher than others. This dif-
ference will tend to decrease as communications between
neighbors happen and values are updated, until it eventu-
ally reaches a value of zero. The consequent final error
was measured from the two groups, to understand the
impact that the time vehicles remained in the system had.
Taking the maximum and minimum amount of energy
sold by the vehicles in each group, a relative error was
found. Regarding the dynamics of the system reaching
consensus, we analyzed the progression with and without
the switching control technique and verified the impact
that this can have in both making the system independent
of the consensus time and protecting the vehicle’s batter-
ies in exchange of little error between energy sold by
each agent.
3. Results and Discussion
The control algorithm demonstrated good adaptability to
a large scale system, considered here with 25,000 vehi-
cles and dynamics both of varying power demanded and
number of agents in the system. Figure 6 shows the pro-
gression of the consensus values in each agent. One can
observe a similar shape to the power demanded by the
grid in Figure 4. Since the power variable only upgrades
every 15 minutes, the fleet approximately assumes con-
stant state values between those intervals.
These intervals, in fact, are not constant at all, because
in each minute there is variability in the number of cars,
hence within those 15 minutes, there are 15 changes in
the state value. Figure 7, reflects this, showing the first
Figure 6. Power supplied by each vehicle during all peak
hours.
Figure 7. Power supplied by each vehicle in the first 15
minutes.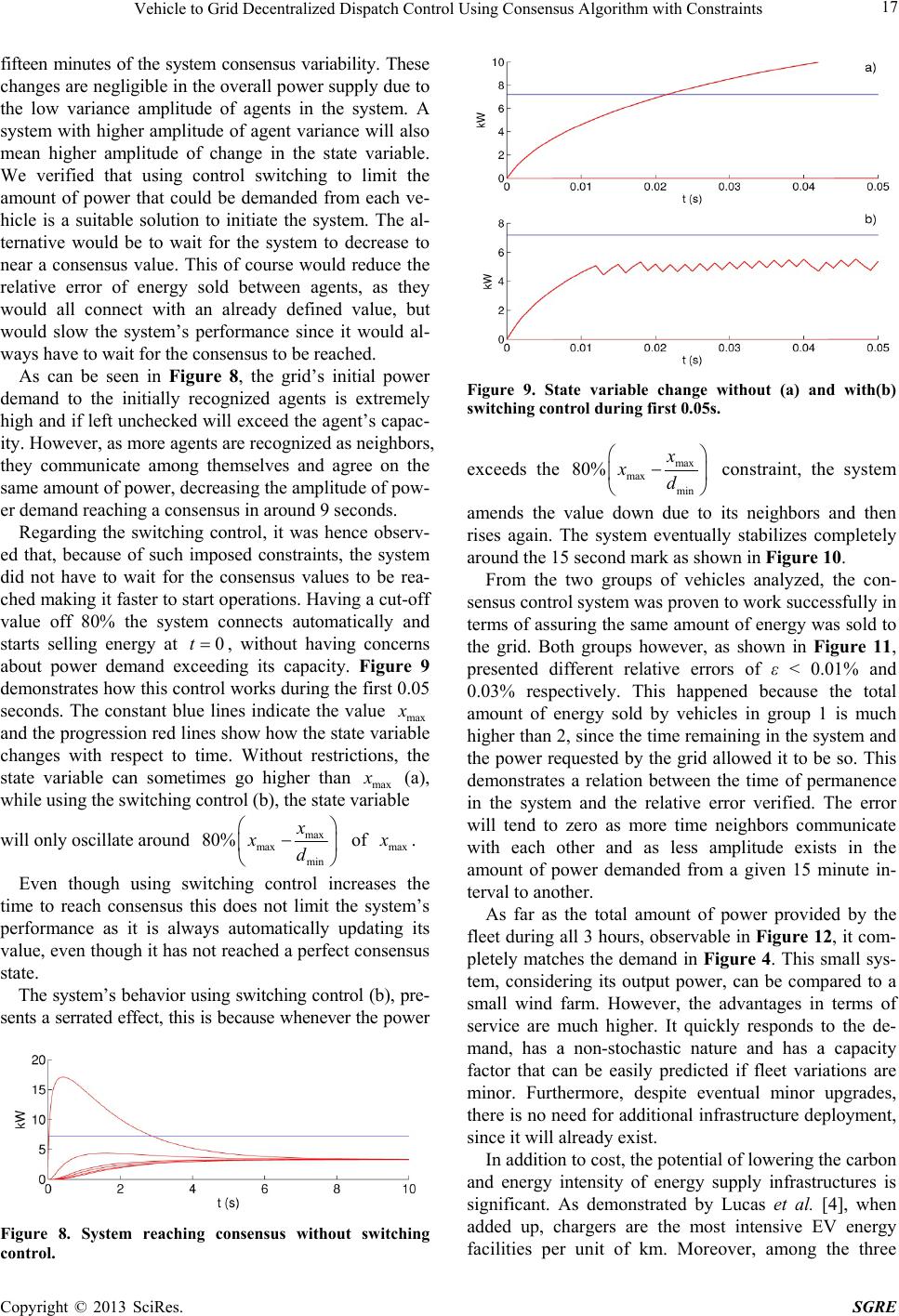

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints 17
fifteen minutes of the system consensus variability. These
changes are negligible in the overall power supply due to
the low variance amplitude of agents in the system. A
system with higher amplitude of agent variance will also
mean higher amplitude of change in the state variable.
We verified that using control switching to limit the
amount of power that could be demanded from each ve-
hicle is a suitable solution to initiate the system. The al-
ternative would be to wait for the system to decrease to
near a consensus value. This of course would reduce the
relative error of energy sold between agents, as they
would all connect with an already defined value, but
would slow the system’s performance since it would al-
ways have to wait for the consensus to be reached.
As can be seen in Figure 8, the grid’s initial power
demand to the initially recognized agents is extremely
high and if left unchecked will exceed the agent’s capac-
ity. However, as more agents are recognized as neighbors,
they communicate among themselves and agree on the
same amount of power, decreasing the amplitude of pow-
er demand reaching a consensus in around 9 seconds.
Regarding the switching control, it was hence observ-
ed that, because of such imposed constraints, the system
did not have to wait for the consensus values to be rea-
ched making it faster to start operations. Having a cut-off
value off 80% the system connects automatically and
starts selling energy at , without having concerns
about power demand exceeding its capacity. Figure 9
demonstrates how this control works during the first 0.05
seconds. The constant blue lines indicate the value max
0t
x
and the progression red lines show how the state variable
changes with respect to time. Without restrictions, the
state variable can sometimes go higher than max
x
(a),
while using the switching control (b), the state variable
will only oscillate around max
max
min
80% x xd



max

of
x
.
Even though using switching control increases the
time to reach consensus this does not limit the system’s
performance as it is always automatically updating its
value, even though it has not reached a perfect consensus
state.
The system’s behavior using switching control (b), pre-
sents a serrated effect, this is because whenever the power
Figure 8. System reaching consensus without switching
control.
Figure 9. State variable change without (a) and with(b)
switching control during first 0.05s.
exceeds the max
max
min
80% x xd





constraint, the system
amends the value down due to its neighbors and then
rises again. The system eventually stabilizes completely
around the 15 second mark as shown in Figure 10.
From the two groups of vehicles analyzed, the con-
sensus control system was proven to work successfully in
terms of assuring the same amount of energy was sold to
the grid. Both groups however, as shown in Figure 11,
presented different relative errors of ε < 0.01% and
0.03% respectively. This happened because the total
amount of energy sold by vehicles in group 1 is much
higher than 2, since the time remaining in the system and
the power requested by the grid allowed it to be so. This
demonstrates a relation between the time of permanence
in the system and the relative error verified. The error
will tend to zero as more time neighbors communicate
with each other and as less amplitude exists in the
amount of power demanded from a given 15 minute in-
terval to another.
As far as the total amount of power provided by the
fleet during all 3 hours, observable in Figure 12, it com-
pletely matches the demand in Figure 4. This small sys-
tem, considering its output power, can be compared to a
small wind farm. However, the advantages in terms of
service are much higher. It quickly responds to the de-
mand, has a non-stochastic nature and has a capacity
factor that can be easily predicted if fleet variations are
minor. Furthermore, despite eventual minor upgrades,
there is no need for additional infrastructure deployment,
since it will already exist.
In addition to cost, the potential of lowering the carbon
and energy intensity of energy supply infrastructures is
significant. As demonstrated by Lucas et al. [4], when
added up, chargers are the most intensive EV energy
facilities per unit of km. Moreover, among the three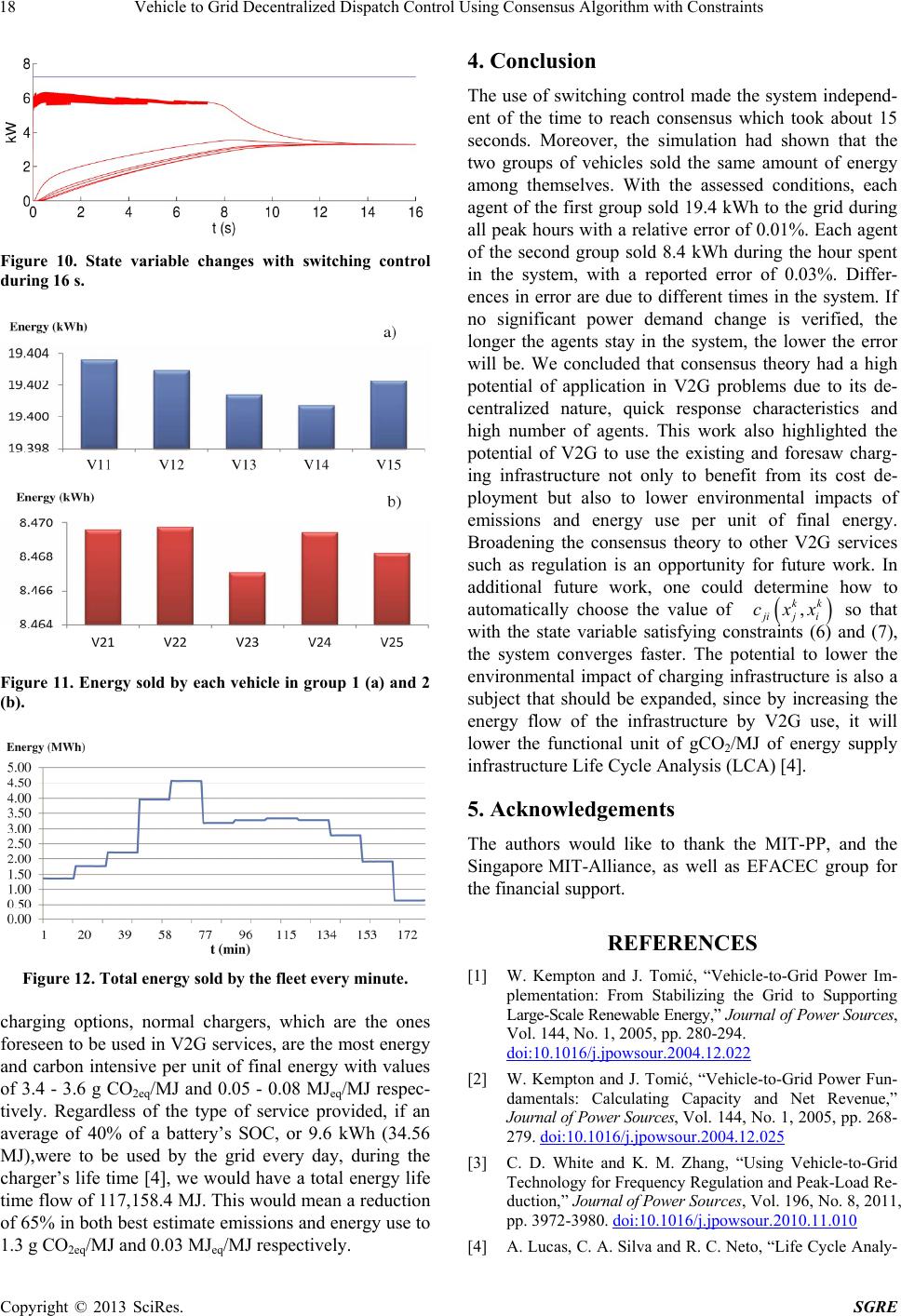

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints
18
Figure 10. State variable changes with switching control
during 16 s.
Figure 11. Energy sold by each vehicle in group 1 (a) and 2
(b).
Figure 12. Total energy sold by the fleet every minute.
charging options, normal chargers, which are the ones
foreseen to be used in V2G services, are the most energy
and carbon intensive per unit of final energy with values
of 3.4 - 3.6 g CO2eq/MJ and 0.05 - 0.08 MJeq/MJ respec-
tively. Regardless of the type of service provided, if an
average of 40% of a battery’s SOC, or 9.6 kWh (34.56
MJ),were to be used by the grid every day, during the
charger’s life time [4], we would have a total energy life
time flow of 117,158.4 MJ. This would mean a reduction
of 65% in both best estimate emissions and energy use to
1.3 g CO2eq/MJ and 0.03 MJeq/MJ respectively.
4. Conclusion
The use of switching control made the system independ-
ent of the time to reach consensus which took about 15
seconds. Moreover, the simulation had shown that the
two groups of vehicles sold the same amount of energy
among themselves. With the assessed conditions, each
agent of the first group sold 19.4 kWh to the grid during
all peak hours with a relative error of 0.01%. Each agent
of the second group sold 8.4 kWh during the hour spent
in the system, with a reported error of 0.03%. Differ-
ences in error are due to different times in the system. If
no significant power demand change is verified, the
longer the agents stay in the system, the lower the error
will be. We concluded that consensus theory had a high
potential of application in V2G problems due to its de-
centralized nature, quick response characteristics and
high number of agents. This work also highlighted the
potential of V2G to use the existing and foresaw charg-
ing infrastructure not only to benefit from its cost de-
ployment but also to lower environmental impacts of
emissions and energy use per unit of final energy.
Broadening the consensus theory to other V2G services
such as regulation is an opportunity for future work. In
additional future work, one could determine how to
automatically choose the value of

,
kk

j
iji
cxx so that
with the state variable satisfying constraints (6) and (7),
the system converges faster. The potential to lower the
environmental impact of charging infrastructure is also a
subject that should be expanded, since by increasing the
energy flow of the infrastructure by V2G use, it will
lower the functional unit of gCO2/MJ of energy supply
infrastructure Life Cycle Analysis (LCA) [4].
5. Acknowledgements
The authors would like to thank the MIT-PP, and the
Singapore MIT-Alliance, as well as EFACEC group for
the financial support.
REFERENCES
[1] W. Kempton and J. Tomić, “Vehicle-to-Grid Power Im-
plementation: From Stabilizing the Grid to Supporting
Large-Scale Renewable Energy,” Journal of Power Sources,
Vol. 144, No. 1, 2005, pp. 280-294.
doi:10.1016/j.jpowsour.2004.12.022
[2] W. Kempton and J. Tomić, “Vehicle-to-Grid Power Fun-
damentals: Calculating Capacity and Net Revenue,”
Journal of Power Sources, Vol. 144, No. 1, 2005, pp. 268-
279. doi:10.1016/j.jpowsour.2004.12.025
[3] C. D. White and K. M. Zhang, “Using Vehicle-to-Grid
Technology for Frequency Regulation and Peak-Load Re-
duction,” Journal of Power Sources, Vol. 196, No. 8, 2011,
pp. 3972-3980. doi:10.1016/j.jpowsour.2010.11.010
[4] A. Lucas, C. A. Silva and R. C. Neto, “Life Cycle Analy-

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints
19
sis of Energy Supply Infrastructure for Conventional and
Electric Vehicles,” Energy Policy, Vol. 41, 2012, pp. 537-
547. doi:10.1016/j.enpol.2011.11.015
[5] Z. Qu, “Cooperative Control of Dynamical Systems,” 2nd
Edition, Springer-Verlag, London, 2009, p. 325.
[6] A. Jadbabaie, J. Lin and A. S. Morse, “Coordination of
Groups of Mobile Autonomous Agents Using Nearest
Neighbor Rules,” IEEE Transactions on Automatic Con-
trol, Vol. 48, 2003, pp. 988-1001.
doi:10.1109/TAC.2003.812781
[7] J. A. Fax and R. M. Murray, “Information Flow and Co-
operative Control of Vehicle Formations,” IEEE Trans-
actions on Automatic Control, Vol. 49, 2004, pp. 1465-
1476. doi:10.1109/TAC.2004.834433
[8] R. Olfati-Saber and R. Murray, “Consensus Protocols for
Networks of Dynamic Agents,” Proceedings of the 2003
American Control Conference, Pasadena, 4-6 June 2003,
pp. 951-956.
[9] W. Ren, R. W. Beard and T. W. Mclain, “Coordination
Variables and Consensus Building in Multiple Vehicle
Systems,” In: V. Kumar, N. E. Leonard and A. S. Morse,
Eds., Cooperative Control, Vol. 309 Lectures Notes in
Control and Information Sciences, Springer-Verlag, Ber-
lin, 2005, pp. 171-188.
[10] A. Tahbaz-Salehi and A. Jadbabaie, “Consensus over
Ergodic Stationary Graph Processes,” IEEE Transactions
on Automatic Control, Vol. 55, 2010, pp. 225-230.
doi:10.1109/TAC.2009.2034054
[11] R. Olfati-Saber and R. Murray, “Consensus Problems in
Networks of Agents with Switching Topology and Time-
Delays,” IEEE Transactions on Automatic Control, Vol.
49, 2004, pp. 1520-1533. doi:10.1109/TAC.2004.834113
[12] J. Lin and A. S. Morse, “The Multi-Agent Rendezvous
Problem: The Asynchronous Case,” Proceedings of the
43rd IEEE Conference on Decision and Control, Atlantis,
14-17 December 2004.
[13] R. Olfati-Saber, “Flocking for Multi-Agent Dynamic Sys-
tems: Algorithms and Theory,” IEEE Transactions on
Automatic Control, Vol. 51, 2006, pp. 401-420.
doi:10.1109/TAC.2005.864190
[14] EFACEC Marketing and Communication Office, “EFA
CEC Electronic Systems, EFACEC EV Normal Chargers-
Technical Specification,” Porto, Portugal, 2010, 11 pages.
[15] W. Kempton and S. E. Letendre, “Electric Vehicles as a
New Power Source for Electric Utilities,” Transportation
Research Part D: Transport and Environment, Vol. 2, No.
3, 1997, pp. 157-175.
[16] W. Kempton and T. Kubo, “Electric-Drive Vehicles for
Peak Power in Japan,” Energy Policy, Vol. 28, No. 1,
2000, pp. 9-18. doi:10.1016/S0301-4215(99)00078-6
[17] W. Kempton, J. Tomic, S. Letendre A. Brooks and T.
Lipman, “Vehicle-to-Grid Power: Battery, Hybrid, and
Fuel Cell Vehicles as Resources for Distributed Electric
Power in California,” California Air Resources Board and
the California Environmental Protection Agency, and Los
Angeles Department of Water and Power, Electric Trans-
portation Program.
[18] D. C. Shoup, “The High Cost of Free Parking,” Planners
Press, Chicago, 2005, p. 733.
[19] S. B. Peterson, J. Apt and J. F. Whitacre, “Lithium-Ion
Battery Cell Degradation Resulting from Realistic Vehi-
cle and Vehicle-to-Grid Utilization,” Journal of Power
Sources, Vol. 195, No. 8, 2010, pp. 2385-2392.
doi:10.1016/j.jpowsour.2009.10.010
[20] M. Ehsani, Y. Gao, S. Gay and A. Emadi, “Modern Elec-
tric, Hybrid Electric, and Fuel Cell Vehicles Fundamen-
tals, Theory, and Design,” CRC Press, New York, 2004, p.
424.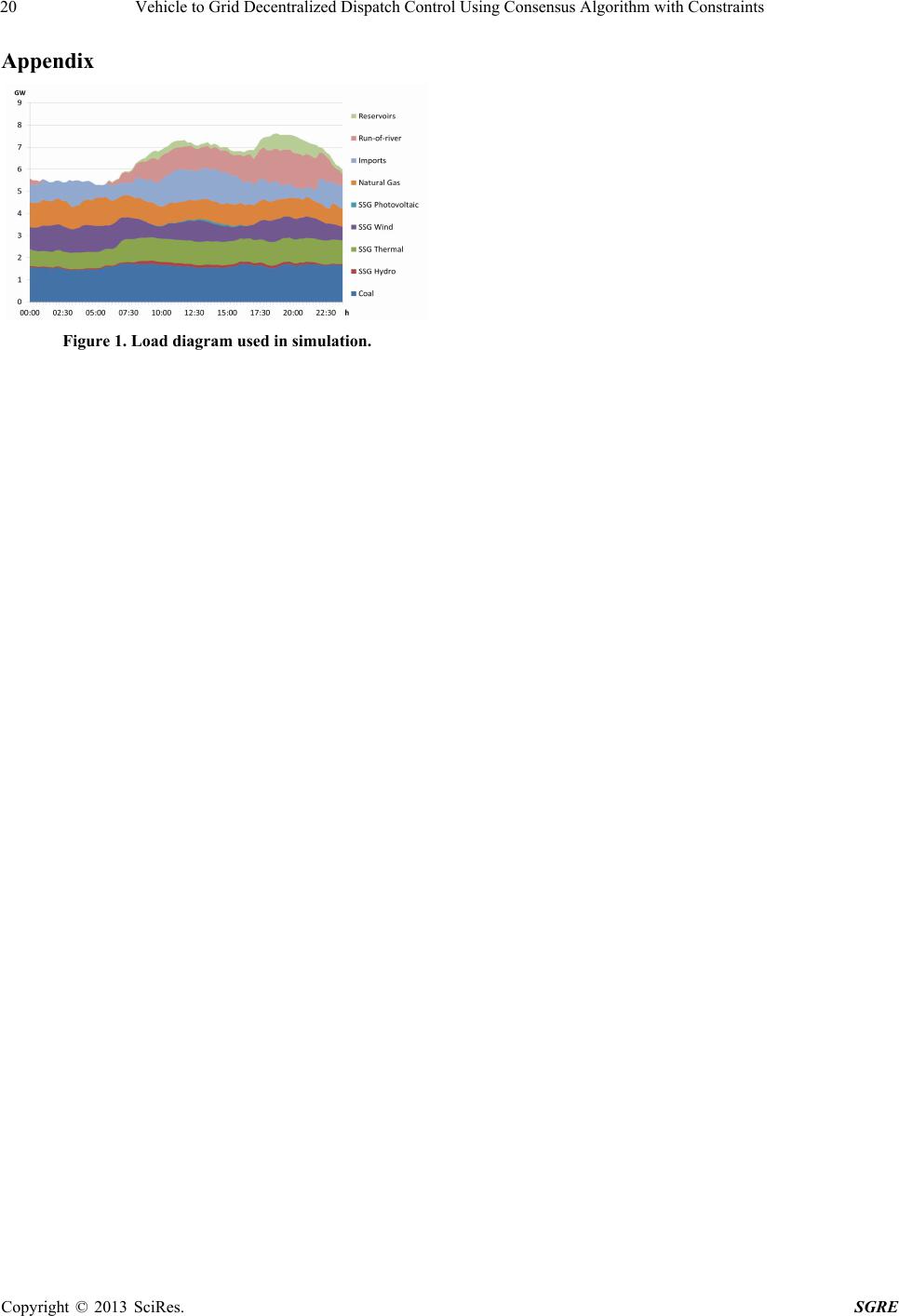

Vehicle to Grid Decentralized Dispatch Control Using Consensus Algorithm with Constraints
20
Appendix
Figure 1. Load diagram used in simulation.