Circuits and Systems, 2011, 2, 18-24
doi:10.4236/cs.2011.21004 Published Online January 2011 (http://www.SciRP.org/journal/cs)
Phase and Quadrature Puls ed Bias LC-CMOS VCO
Stefano Perticaroli1, Fabrizio Palma1, Adriano Carbone2
1Department of Information Engineering, Electronics and Telecommunications,
Sapienza Università di Roma, Rome, Italy
2Rhea System S. A., Louvain-La-Neuve, Belgium
Received October 8, 2010; revised October 27, 2010; accepted November 10, 2010
Abstract
Pulsed bias is an attempt to improve the performance of oscillators in integrated circuits as a result of archi-
tectural innovation. Given the relatively low value of resonator quality factor achievable on-chip, for a speci-
fied bias voltage level, pulsed bias may result in a lower power consumption and in an improvement of the
spectral purity of the oscillation. The main drawback of this approach is the need to introduce a certain time
delay in order to properly position pulses with respect to oscillation waveform. Delay accumulation requires
further energy dissipation and introduce additional jitter. In this paper we present a new architecture capable
to avoid unnecessary delay, based on the idea to apply the pulsed bias approach to a quadrature oscillator. A
first circuit-level implementation of this concept is presented with simulation results.
Keywords: Phase And Quadrature VCO, Pulsed Bias Oscillator, Floquet Eigenvectors Noise Decomposition
1. Introduction
All the recent theories of phase noise point out the intrin-
sic time-varying nature of its generation[1-4]. Ocillators
in fact are nonlinear systems with a periodically time-
variant steady state. For this reason, internal noise sources,
whose variances depend on the operating point, must be
described as cyclostationary processes. Furthemore, pe-
riodicity implies that also the conversion process of noise
sources into phase and orbital deviation is described by a
linear periodically time-variant (LPTV) system. Floquet
eigenvectors decomposition is widely acknowledged as a
correct approach for the analytical treatment of noise
sources in such LPTV systems [3].
Following the Floquet decomposition it can be stated
that determination of power density spectrum (PDS) of
oscillator depends on mean values of noise sources va-
riances multiplied by the square of noise sources projec-
tions onto the system’s Floquet eigenvectors. In particular,
projections onto the “first eigenvector”, i. e. the vector
tangent to the space state orbit, are indicated as the main
contributors to the PDS close to the fundamental [5].
In order to obtain a higher spectral purity, the men-
tioned mean values should be minimized. This result may
be achieved if noise sources are allowed to enter the sys-
tem only when their projections onto eigenvectors are
possibly around a minimum. Since noise in integrated
circuits is due mainly to active devices, we may search
for architectures that switch on bias currents, and thus add
noise, only in certain time intervals during the oscillation
period. These time intervals should be chosen to obtain a
minimum of the projection onto eigenvectors. We notice
that, in a single VCO this i mplies the need for a circuitry
which produces a delay between a threshold crossing and
the switching of devices: Additional noise is then intro-
duced as jitter in accumulation of delay time. Uncertainty
related to this jitter affects th e time instant when th e large
current needed to sustain oscillations is provided. For this
reason, jitter can be not negligible and may overwhelm
any improvem ent obt ai ned t h rou gh p ul sed b i asi ng.
In this paper we present a new architecture based on
the idea to apply the pulsed bias approach to a quadrature
oscillator including two resonators. In particular we pro-
pose to adopt a threshold at zero differential voltage of
one resonator and apply the consequent pulse, with no
delay, at the second one, taking advantage of the natural
phase relationship between the zero and the maximum in
quadrature signals.
Quadrature VCOs are fundamental components in ma-
ny RF transceiver systems. Especially when low-IF or
direct conversion architecture is required, the generation
of two periodic signal in quadrature of phase is a critical
issue. One of the main problems with quadrature oscilla-
tors, obtained clo s ing in a loop two identical resonators, is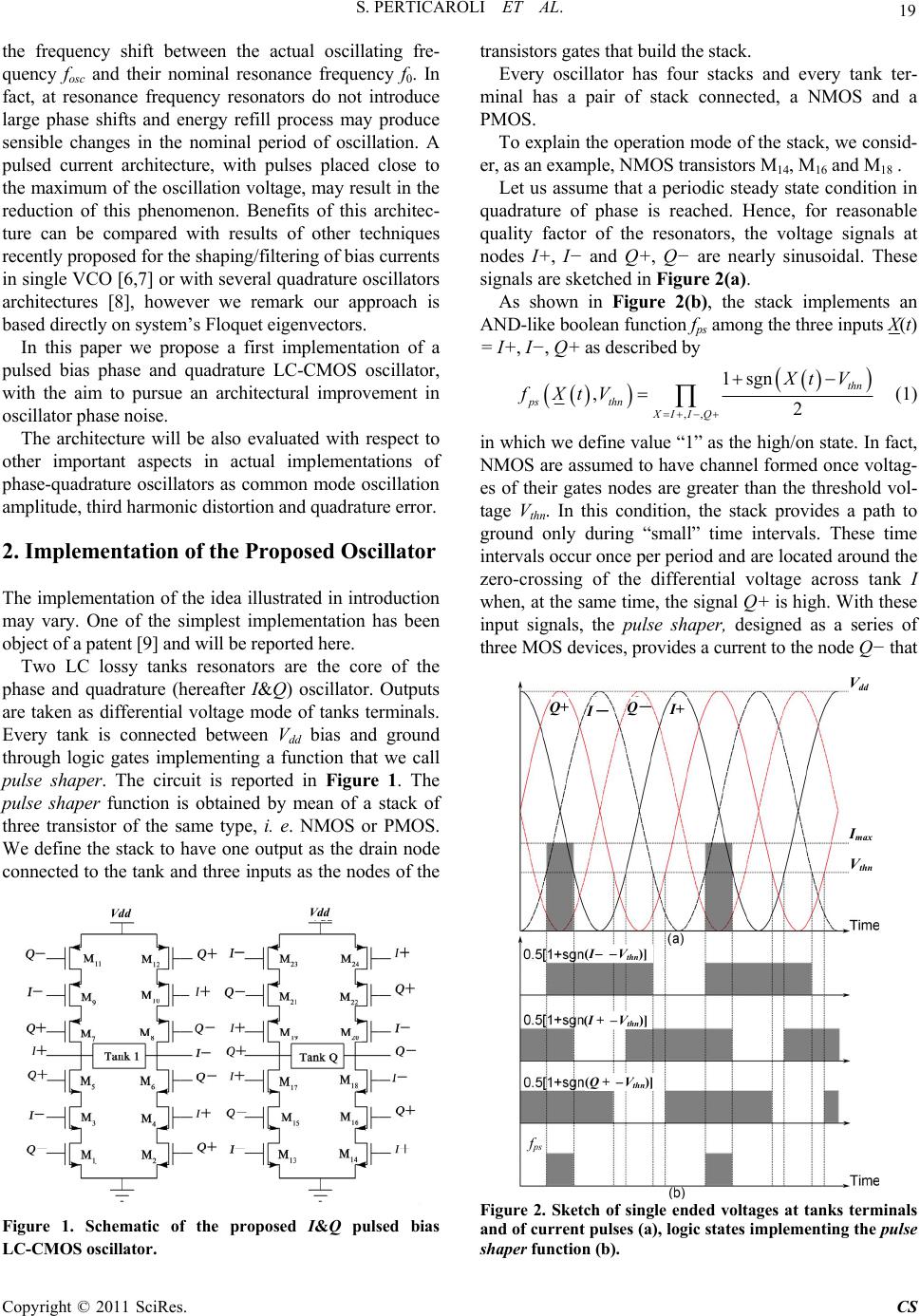

S. PERTICAROLI ET AL.
19
the frequency shift between the actual oscillating fre-
quency fosc and their nominal resonance frequency f0. In
fact, at resonance frequency resonators do not introduce
large phase shifts and energy refill process may produce
sensible changes in the nominal period of oscillation. A
pulsed current architecture, with pulses placed close to
the maximum of the oscillation voltage, may result in the
reduction of this phenomenon. Benefits of this architec-
ture can be compared with results of other techniques
recently proposed for the shaping/filtering of bias currents
in single VCO [6,7] or with several quadrature oscillato rs
architectures [8], however we remark our approach is
based directly on syst em’s Floquet eigenvec t ors.
In this paper we propose a first implementation of a
pulsed bias phase and quadrature LC-CMOS oscillator,
with the aim to pursue an architectural improvement in
oscillator phase noise.
The architecture will be also evaluated with respect to
other important aspects in actual implementations of
phase-quadrature oscillators as common mode oscillation
amplitude, t hi rd harmonic distorti on and q uadrature error.
2. Implementation of the Proposed Oscillator
The implementation of the idea illustrated in introduction
may vary. One of the simplest implementation has been
object of a patent [9] and will be reported here.
Two LC lossy tanks resonators are the core of the
phase and quadrature (hereafter I&Q) oscillator. Outputs
are taken as differential voltage mode of tanks terminals.
Every tank is connected between Vdd bias and ground
through logic gates implementing a function that we call
pulse shaper. The circuit is reported in Figure 1. The
pulse shaper function is obtained by mean of a stack of
three transistor of the same type, i. e. NMOS or PMOS.
We define the stack to have one output as the drain node
connected to the tank and three inputs as the nodes of the
Figure 1. Schematic of the proposed I&Q pulsed bias
LC-CMOS oscillator.
transistors gates that build the stack.
Every oscillator has four stacks and every tank ter-
minal has a pair of stack connected, a NMOS and a
PMOS.
To explain the operation mode of the stack, we consid-
er, as an example, NMOS transistors M14, M 16 and M 18 .
Let us assume that a periodic steady state cond ition in
quadrature of phase is reached. Hence, for reasonable
quality factor of the resonators, the voltage signals at
nodes I+, I− and Q+, Q− are nearly sinusoidal. These
signals are sketched in Figure 2(a).
As shown in Figure 2(b), the stack implements an
AND-like boolean function fps among the three inputs X(t)
= I+, I−, Q+ as described by
 


,,
1sgn
,2
thn
ps thn
XII Q
Xt V
fXtV
 

 (1)
in which we define value “1” as the high/on state. In fact,
NMOS are assumed to have channel formed once voltag-
es of their gates nodes are greater than the threshold vol-
tage Vthn. In this condition, the stack provides a path to
ground only during “small” time intervals. These time
intervals occur once per period and are located around the
zero-crossing of the differential voltage across tank I
when, at the same time, the signal Q+ is high. With these
input signals, the pulse shaper, designed as a series of
three MOS devices, provides a current to the node Q− that
V
thn
Figure 2. Sketch of single ended voltages at tanks terminals
and of current pulses (a), logic states implementing the pulse
shaper function (b).
Q+
I
－
Q－
I
+
Vdd Vdd
(I－ －Vthn)]
(I + －Vthn)]
(Q + －Vthn)]
fps
Vdd
I
max
Vthn

S. PERTICAROLI ET AL.
20
is a train of pulses at frequency fosc located exactly around
the minimum of the Q− voltage.
The amplitude of pulses depends on the width of MOS
devices and on tanks impedance at resonance. In the fol-
lowing discussion we approximate pulses using a rectan-
gular shape. The approximation is valid if pulse duration
is reasonably small compared to th e oscillation p eriod, so
that voltage Q− does not vary considerably around its
minimum.
Analogous description may be developed for a PMOS
stack. It has to be noticed that as long as Vthn < Vcm and
(Vdd – Vthp) > Vcm (where Vcm is the half-sum of tank ter-
minals voltages), a NMOS stack is “active” during the
same time intervals when the PMOS stack connected to
the other terminal of the same tank is also active, giving
rise to pulses of current IpI and IpQ respectively. In conclu-
sion, the stack formed by M14, M16 and M18 and the stack
formed by M19, M21 and M23 create a path from Vdd to
ground through the tank Q once time per period. This
path alternates with the one formed by M13, M15 and M17
and by M20, M22 and M24.
As overall result, the proposed circuit topology shown
in Figure 1 is able to generate trains of current pulses
injected in each tank synchronously with their peak of
differential voltages, thus accomplishing a positive feed-
back capable to sustain oscillations despite losses in the
tanks.
3. Phase Noise Evaluation Based on Floquet
Eigenvectors
In order to obtain an interpretation of the architecture
response to noise perturbatio n we present here a descrip-
tion of the orbital deviation based on the Floquet eigen-
vectors. Eigenvectors are obtained from the simplified
circuital model reported in Figure 3 which accounts for
the differential modes only.
The model presents four state variables, corresponding
to the capacitors voltages and the inductors currents of
two tanks. This assumption can be seen as a rather drastic
simplification for a model of a real oscillator, neverthe-
less, if the stacks do not introduce parasitics comparable
to those in tanks, the additional state variables can be
neglected. Moreover, the assumption is justified by the
fact that once a large differential oscillation is established,
any common mode oscillation is inhibited and remains
within negligible amplitudes.
In our treatment we derive the noise response by direct
considering contributions of noise projections onto Flo-
quet eigenvectors [5].
We recall that the “first eigenvector”, u1(t), is tangent
to the space state orbit and has unitary eigenvalue. In a
stable configuration other eigenvectors have corre-
sponding eigenvalues lower than 1.
The main contribution to the overall power density
spectrum at frequencies close to the fundamental is due
to noise projectio ns on first eigenvector. On the contrar y
contributions arising from other eigenvectors become
relevant only at high frequency offsets ω > γJ=2,3,4 (where
γJ=2,3,4 are the poles pulsations related to Floquet multi-
pliers of eigenvectors) due to their low-pass shape with
respect to the fundamental.
We assume noise perturbations to be independent re-
alizations of white process with zero time average. Since
we are dealing with a parallel RLC tanks, noise is intro-
duced as parallel current sources. Such noisy currents
cause a variation of the capacitors voltages, hence we
have two normalized noise perturbations through a con-
stant matrix Bw (4x2)
0010
1000
T
w
B






. (2)
The matrix maps perturbations at nodes [VI V
Q]T on
the vector of state variables defined as S(t) = [VC_I I
L_I
VC_Q IL_Q]T.
A dedicated MATLAB simulator has been developed
to compute Floquet eigenvalues and eigenvectors as well
as the projections of the components of matrix Bw onto
the eigenvectors. Simulator implements a shooting algo-
rithm on the differential equations of the nonlinear model
reported in Figure 3. Shooting is reached by the use of
Interface matrices correction [10] in the calculation of
the Monodromy matrix in every iterative step. Interface
matrices are essential to reach the convergence, since
they allow to properly take into account state variables
variations on non-derivable points. Computed eigenva-
lues are reported in Table 1 in the case we set resonators
parameters (QI = QQ = 18, LI = LQ = 912 pH, CI = CQ =
1.05 pF) to be comparable with simulation of implemen-
tation with real device models presented in section 4.
The working frequency predicted by shooting is fosc =
5.1275 GHz.
We want to remark that two very close eigenvalues are
found, i. e. 
2 and

3. This result suggests to perform the
circuital simulation with great care on such system in
order to avoid convergence difficulties.
In Figure 4(a) the shooting waveforms voltages are
reported whereas Figure 4(b) shows the projections of
matrix Bw components onto eigenvector u1(t). For the
sake of our treatment we choose to not express physical
Figure 3. Simplified differential mode model of the I&Q
pulsed bias oscillator.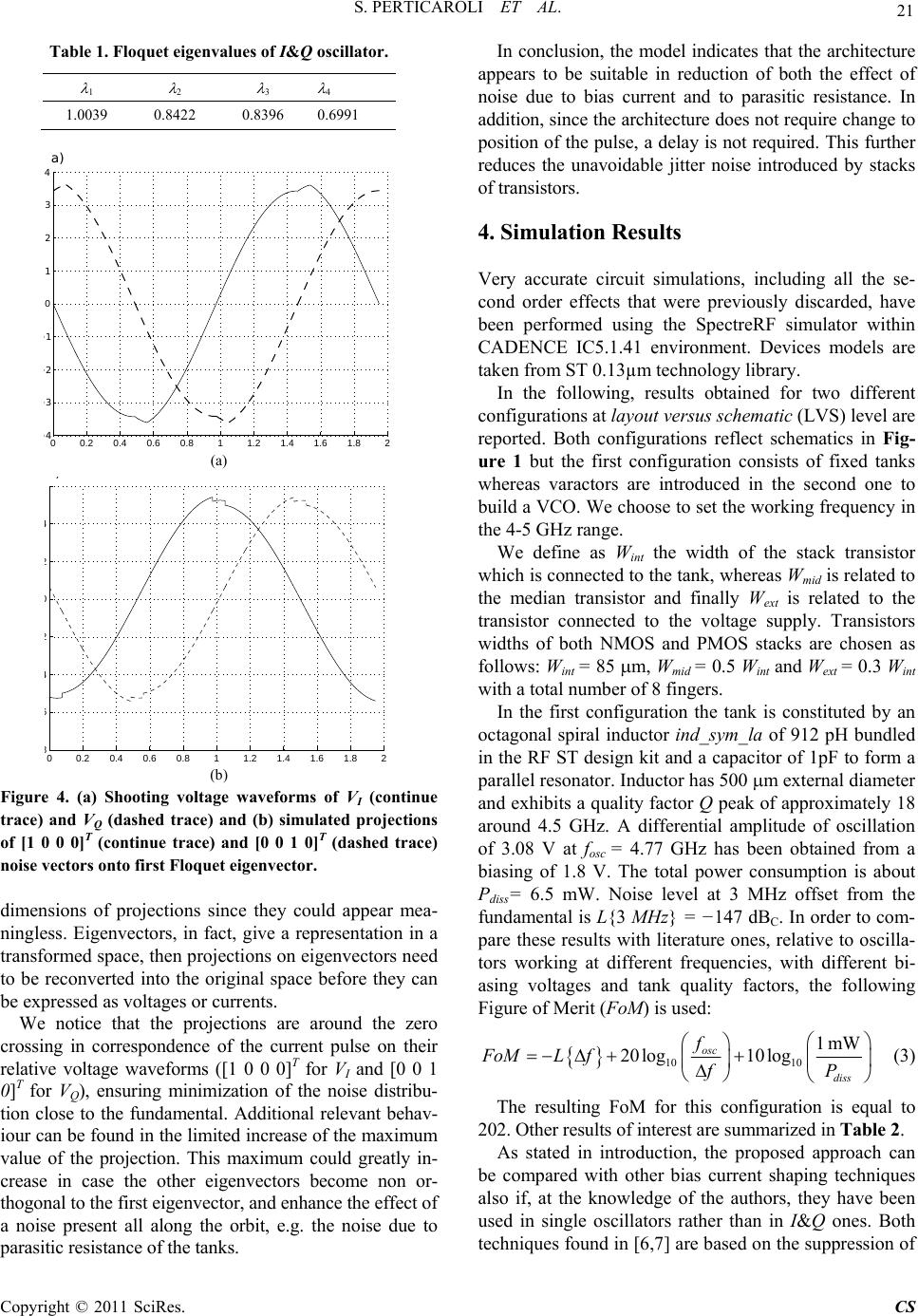

S. PERTICAROLI ET AL.
21
Table 1. Floquet eigenvalues of I&Q oscillator.

1

2

3

4
1.0039 0.8422 0.8396 0.6991
00.2 0.4 0.6 0.811.2 1.4 1.6 1.82
−
4
−
3
−
2
−
1
0
1
2
3
4
a)
(a)
0 0
.2
0
.4
0
.
6 0
.
8
11.2 1.4 1.
6
1.
8
2
8
6
4
2
0
2
4
)
(b)
Figure 4. (a) Shooting voltage waveforms of VI (continue
trace) and VQ (dashed trace) and (b) simulated projections
of [1 0 0 0]T (continue trace) and [0 0 1 0]T (dashed trace)
noise vectors onto first Floquet eigenvector.
dimensions of projections since they could appear mea-
ningless. Eigenvectors, in fact, give a representation in a
transformed space, then projections on eigenvectors need
to be reconverted into the original space before they can
be expressed as voltages or currents.
We notice that the projections are around the zero
crossing in correspondence of the current pulse on their
relative voltage waveforms ([1 0 0 0]T for VI and [0 0 1
0]T for VQ), ensuring minimization of the noise distribu-
tion close to the fundamental. Additional relevant behav-
iour can be fo und in the li mited increase of the maximum
value of the projection. This maximum could greatly in-
crease in case the other eigenvectors become non or-
thogonal to the first eigenvect or, an d en hance the effect of
a noise present all along the orbit, e.g. the noise due to
parasitic resistance of the tanks.
In conclusion, the model indicates that the architecture
appears to be suitable in reduction of both the effect of
noise due to bias current and to parasitic resistance. In
addition, since the architecture does not require change to
position of the pulse, a delay is not required. This further
reduces the unavoidable jitter noise introduced by stacks
of transistors.
4. Simulation Results
Very accurate circuit simulations, including all the se-
cond order effects that were previously discarded, have
been performed using the SpectreRF simulator within
CADENCE IC5.1.41 environment. Devices models are
taken from ST 0.13µm technology library.
In the following, results obtained for two different
configurations at layout versus schematic (LVS) level are
reported. Both configurations reflect schematics in Fig-
ure 1 but the first configuration consists of fixed tanks
whereas varactors are introduced in the second one to
build a VCO. We choose to set the working frequency in
the 4-5 GHz range.
We define as Wint the width of the stack transistor
which is connected to the tank, whereas Wmid is related to
the median transistor and finally Wext is related to the
transistor connected to the voltage supply. Transistors
widths of both NMOS and PMOS stacks are chosen as
follows: Wint = 85 m, Wmid = 0.5 Wint and Wext = 0.3 Wint
with a total number of 8 fingers.
In the first configuration the tank is constituted by an
octagonal spiral inductor ind_sym_la of 912 pH bundled
in the RF ST design kit and a capacitor of 1pF to form a
parallel resonator. Inductor has 500 m external diameter
and exhibits a qu ality factor Q peak of approximately 18
around 4.5 GHz. A differential amplitude of oscillation
of 3.08 V at fosc = 4.77 GHz has been obtained from a
biasing of 1.8 V. The total power consumption is about
Pdiss= 6.5 mW. Noise level at 3 MHz offset from the
fundamental is L{3 MHz} = −147 dBC. In order to com-
pare these results with literature ones, relative to oscilla-
tors working at different frequencies, with different bi-
asing voltages and tank quality factors, the following
Figure of Merit (FoM) is used:

1010 1mW
20log 10log
osc
diss
f
FoML ffP


 


 
(3)
The resulting FoM for this configuration is equal to
202. Other results of interest are summarized in Table 2.
As stated in introduction, the proposed approach can
be compared with other bias current shaping techniques
also if, at the knowledge of the authors, they have been
used in single oscillators rather than in I&Q ones. Both
techniques foun d in [6,7] are based on the suppression of

S. PERTICAROLI ET AL.
22
Table 2. Main characteristics of proposed oscillator.
Frequency 4.77 GHz
Differential mode amplitude 3.08 V
Phase Noise @ 3 MHz offset −147 dBC
Power consumption @ 1.8 V supply 6.53 mW
FoM as in (3) 202
Quadrature phase error 0.03°
Common mode amplitude @ 2fosc 37 mV
HD3 −40.4 dB
devices noise injected at 2fosc. Since architectures of [6,7]
require a tail current source, noise around second har-
monic is down-converted to the fundamental, thus in-
creasing phase noise. In [6] an LC filter is considered
whereas in [7] a phase displacement of pulsed current at
2fosc is used to reduce the down-conversion phenomenon.
In the proposed architecture instead there is no need of a
tail current source and pulsed biasing currents flow at
fundamental frequency. Results of comparison are re-
ported in Table 3.
For the second configuration a parallel branch is
added to the tanks. The branch is constituted of two
varactors in series and the control voltage VCTRL is the
common node in the series. The total area occupied by
varactors is 20 m2.
In Figure 5 transient waveforms are reported from
postlayout simulation in case fosc = 4.63 GHz for Vctrl =
1.5 V. Periodic steady state occurs in about 10ns without
any startup circuitry. A 600 mV difference in amplitude
between the two differential voltage modes I and Q is
observed, however quadrature of signals is maintained . A
close-up of pulsed currents bias is also reported. It has to
be noticed that these current waveforms result both from
displacement of parasitics as well as form conduction in
devices, since a single component cannot be isolated.
Moreover, when the peak of a pulse is expected, devices
of stack are pushed into triode region by the tank termin-
al voltage, giving rise to deformation of the pulse itself.
The obtained tuning range with the above mentioned
varactors dimensions is about 300 MHz around 4.55 GHz,
i. e. 7% relative tenability, and allows the comparison of
the proposed architecture with recent literature works as
shown in Table 4 Comparison is based on largely
adopted PTFN defined as

max min
10 10
20log10log B
diss
ff KT
PTFNL ffP

 





(4)
Table 3. Comparison with phase noise reduction tech-
niques.
Ref. L{
 f}@3 MHz
[dBc] Frequency
[GHz]
Power
consumption
[mW] FOM
[6] −153 1.2 9.25 195
[7] −135 1.77 2.25 186
This
work −147 4.77 6.53 202
Table 4. Comparison with literature I&Q VCO.
Ref.Technology
[m] Tuning range
[GHz]
Power
consumption
[mW] PTFN
[11]0.25 1.73−1.99 20
−2.44
[12]0.18 5.4−6.6 18
−1.84
[13]0.25 4.07−4.72 15
−3.17
This
work 0.13 4.3−4.64 14
−4.36
(a)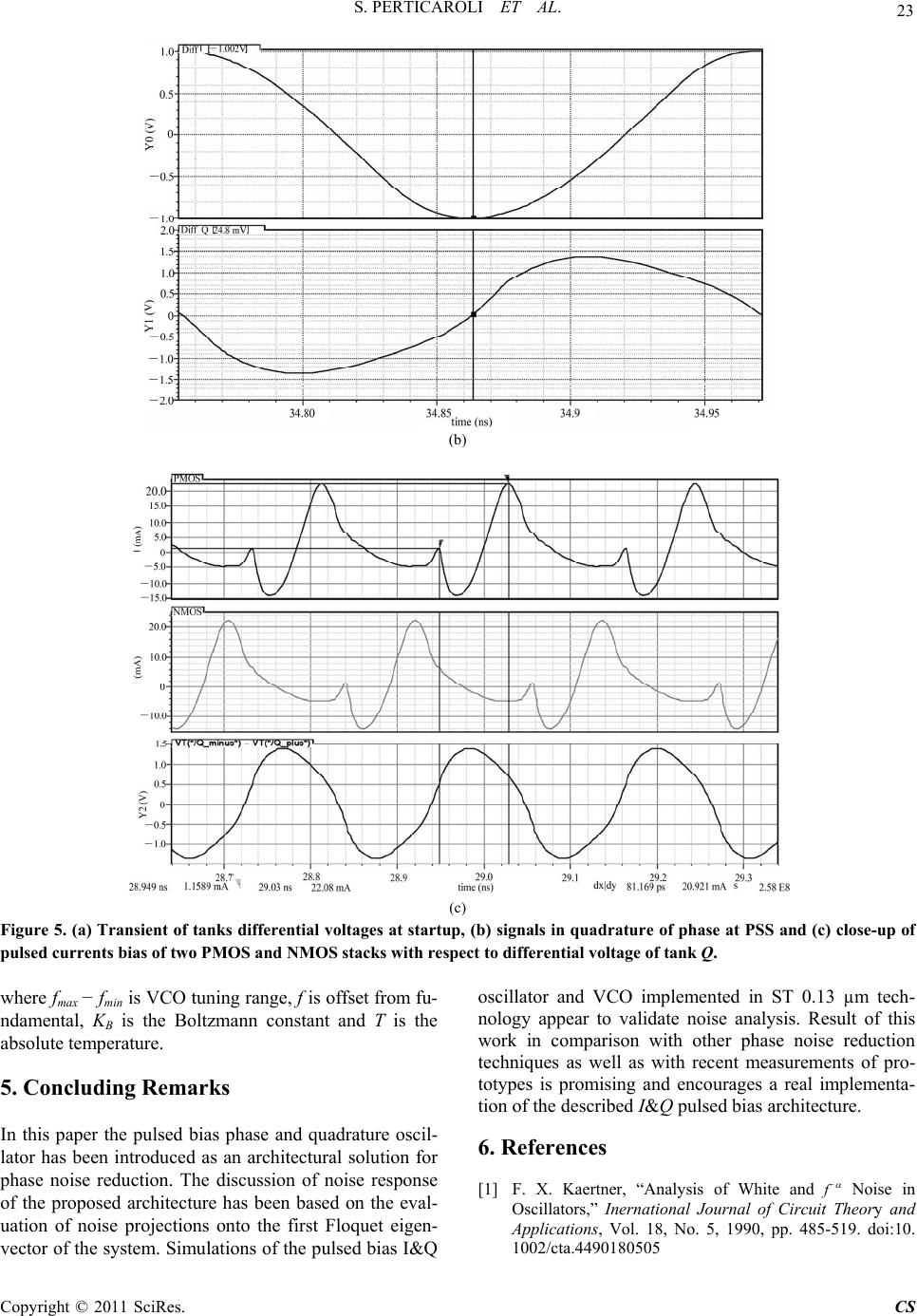

S. PERTICAROLI ET AL.
23
(b)
(c)
Figure 5. (a) Transient of tanks differential voltages at startup, (b) signals in quadrature of phase at PSS and (c) close-up of
pulsed currents bias of two PMOS and NMOS stacks with respect to differential voltage of tank Q.
where fmax − fmin is VCO tuning range, f is offset from fu-
ndamental, KB is the Boltzmann constant and T is the
absolute temperature.
5. Concluding Remarks
In this paper the pulsed bias phase and quadrature oscil-
lator has been introduced as an architectural solution for
phase noise reduction. The discussion of noise response
of the proposed architecture has been based on the eval-
uation of noise projections onto the first Floquet eigen-
vector of the system. Simulations of the pulsed bias I&Q
oscillator and VCO implemented in ST 0.13 µm tech-
nology appear to validate noise analysis. Result of this
work in comparison with other phase noise reduction
techniques as well as with recent measurements of pro-
totypes is promising and encourages a real implementa-
tion of the described I&Q pulsed bias architecture.
6. References
[1] F. X. Kaertner, “Analysis of White and f−

Noise in
Oscillators,” Inernational Journal of Circuit Theory and
Applications, Vol. 18, No. 5, 1990, pp. 485-519. doi:10.
1002/cta.4490180505

S. PERTICAROLI ET AL.
24
[2] A. Hajimiri and T. H. Lee, “A General Theory of Phase
Noise in Electrical Oscillators,” IEEE Journal Solid-State
Circuits, Vol. 33, No. 2, 1998, pp. 179-194. doi:10.1109
/4.658619
[3] A. Demir, “Floquet Theory and Non-linear Perturbation
Analysis Foroscillators with Differential-Algebraic Eq-
uations,” International Journal of Circuit and Theory
Applications, Vol. 28, No. 2, 2000, pp. 163-185. doi:
10.1002/(SICI)1097007X(200003/04)28:2<163::AID-CT
A101>3.0.CO;2-K
[4] A. Carbone, A. Brambilla and F. Palma, “Using Floquet
Eigenvectors in the Design of Electronic Oscillators,” Em-
erging Technologies: Circuits and Systems for 4 G Mo-
bile Wireless Communications, No. 6, 23-24 June 2005, pp.
100-103.
[5] A. Carbone and F. Palma, “Considering Orbital Devia-
tions on the Evaluation of Power Density Spectrum of
Oscill-Ators,” IEEE Transactions on Circuits and
Systems-II: Express Briefs, Vol. 53, No. 6, 2006, pp.
438-442. doi: 10.1109/TCSII.2006.873527
[6] E. Hegazi, H. Sjoland and A. Abidi, “A Filtering Tech-
nique to Lower LC Oscillator Phase Noise,” IEEE Journal
of Solid State Circuits, Vol. 36, No. 12, 2001, pp. 1921-
1930. doi:10.1109/4.972142
[7] B. Soltanian and P. Kinget, “Tail Current Shaping to
Improve Phase Noise in LC Voltage Controlled Os-
cillators,” IEEE Journal of Solid State Circuits, Vol. 41,
No. 8, 2006, pp. 1792-1802. doi:10.1109/JSSC.2006.8772
73
[8] L. B. Oliveira et al., “Analysis and Design of Quadrature
Oscillators,” Springer, Berlin, 2008. do i: 10 .1007/978-14020-
8516-1.
[9] United States Patent No. US 2008/0218280 A1.
[10] A. Carbone and F. Palma, “Discontinuity Correction in
Piece-Wise-Linear Models of Oscillators for Phase Noise
Characterization,” International Journal of Circuit Theory
and Applications, Vol. 35, No. 1, 2007, pp. 93-104. doi:10.
1002/cta.383
[11] M. Tiebout, “A Differentially Tuned Quadrature CMOS,”
Proceedings of the 26th European Solid-State Circuits
Conference, Montreux, 18-22 September 2006.
[12] J. H. Chang, et al., “A New 6 GHz Fully Integrated Low
Power Low Phase Noise LC Quadrature VCO,” Pro-
ceedings of 2003 Radio Frequency Integrated Circuits
Symposium Philadelphia, Philadelphia, 8-10 June 2003,
pp. 295-298.
[13] F. Yang et al., “A 4.8 GHz CMOS LC Balanced Oscillator
with Symmetry Noise Filtering Technique,” International
Conference on Solid-State Integrated Circuits Technology,
Vol. 2, No. 7, 2004, pp. 1315-1320. doi:10.1109/ICSICT.
2004.1436795