Paper Menu >>
Journal Menu >>
 Circuits and Systems, 2011, 2, 7-13 doi:10.4236/cs.2011.21002 Published Online January 2011 (http://www.SciRP.org/journal/cs) Copyright © 2011 SciRes. CS A Modified Eigenvector Method for Blind Deconvolution of MIMO Systems Using the Matrix Pseudo-Inversion Lemma* Mitsuru Kawamoto1, Kiyotaka Kohno2, Yujiro Inouye3, Koichi Kurumatani1 1Information Technology Research Institute, National Institute of Advanced Science and Technology, Tsukuba, Japan 2Department of Electronic Control Engineering, Yonago National College of Technology, Yonago-city, Japan 3Department of Electronic and Control Systems Engineering, Shimane University, Matsue, Japan E-mail: {m.kawamoto, k.kurumatani}@aist.go.jp, kohno@yonago-k.ac.jp, inouye@riko.shimane-u.ac.jp Received August 26, 2010; revised December 2, 2010; accepted December 8, 2010 Abstract Recently we have developed an eigenvector method (EVM) which can achieve the blind deconvolution (BD) for MIMO systems. One of attractive features of the proposed algorithm is that the BD can be achieved by calculating the eigenvectors of a matrix relevant to it. However, the performance accuracy of the EVM de- pends highly on computational results of the eigenvectors. In this paper, by modifying the EVM, we propose an algorithm which can achieve the BD without calculating the eigenvectors. Then the pseudo-inverse which is needed to carry out the BD is calculated by our proposed matrix pseudo-inversion lemma. Moreover, using a combination of the conventional EVM and the modified EVM, we will show its performances comparing with each EVM. Simulation results will be presented for showing the effectiveness of the proposed methods. Keywords: Blind Signal Processing, Blind Deconvolution, Eigenvector Methods, Super-Exponential Mthods, MIMO Systems, Matrix Pseudo-Inversion Lemma 1. Introduction In this paper, we deal with a blind deconvolution (BD) problem for a multiple-input and multiple-output (MIMO) infinite-impulse response (IIR) channels. A large number of methods for solving the BD problem have been pro- posed until now (see [1], and reference therein). In order to solve the BD problem, this paper focuses on the eigenvec- tor method (EVM). The first proposal of the EVM was done by Jelonnek et al. [2]. They have proposed the EVM for solving blind equa- lization (BE) problems of single-input single-output (SISO) channels and single-input multiple-output (SIMO) channels. The most attractive feature of the EVM is that its algorithm can be derived from a closed-form solution using reference signals. Then, a generalized eigenvector problem can be formulated and the eigenvector calculation is carried out in order to solve the BE problem. Owing to the property, dif- ferently from the algorithms derived from steepest descent methods, the EVM does not need many iterations to achieve the BE, but works so as to solve the BE problem with one iteration. Recently, we extended the EVM to the case of MI- MO-IIR channels [3,4]. Then we proved that the proposed EVM can work so as to recover all source signals from their mixtures with one iteration. However, in the EVM, its performance accuracy depends highly on computational results of the eigenvectors. In this paper, we modify the EVM and then an algo- rithm for solving the BD is proposed, in which the pro- posed algorithm can be carried out without calculating the eigenvectors. Namely, the proposed algorithm can achieve the BD with as less computational complexity as possible, compared with the conventional EVMs. More- over, a combination of the conventional EVM and the modified EVM is proposed. The combined EVM has su- ch properties that the BD can be achieved with as less computational complexity as possible and with good acc- uracy compared with each EVM. The present paper uses the following notation: Let Z de- note the set of all integers. Let C denote the set of all com- plex numbers. Let Cn denote the set of all n-column vectors with complex components. Let Cm×n denote the set of all mn matrices with complex components. The super- *A preliminary version of this paper was presented at the 2010 IEEE International Symposium on Circuits and Systems (ISCAS2010).  M. KAWAMOTO ET AL. Copyright © 2011 SciRes. CS 8 scripts T, *, and H denote, respectively, the transpose, the complex conjugate, and the complex conjugate transpose (Hermitian) of a matrix. The symbol † denotes a pseudo- inverse of a matrix. The symbols block-diag and diag denote respectively a block diagonal and a diagonal matrices with the block diagonal and the diagonal elements . The symbol cum{x1, x2, x3, x4} denotes the fourth- order cumulant of xi's. Let i = 1, n stand for 1, 2,,.In 2. Problem Formulation and Assumptions We consider a MIMO system with n inputs and m out- puts as described by () – ()() (),, k k ytHst knttZ (1) where s(t) is an n-column vector of input (or source) signals, y(t) is an m-column vector of system outputs, n(t) is an m-column vector of Gaussian noises, and {H(k)} is an m×n impulse response matrix sequence. The transfer function of the system is defined by H(z) = () – kk k H z , z ∈ C. To recover the source signals, we process the output signals by an n×m deconvolver (or equalizer) W(z) de- scribed by () – ()( ) k k vtWyt k () () –– kk kk Gstk Wntk , (2) where {G(k)} is the impulse response matrix sequence of G(z) := W(z)H(z), which is defined by G(z) = k kk z )( G, z ∈ C. The cascade connection of the unknown system and the deconvolver is illustrated in Figure 1. Here, we put the following assumptions on the system, the source signals, the deconvolver, and the noises. A1) The transfer function H(z) is stable and has full column rank on the unit circle |z| = 1, where the assump- tion A1) implies that the unknown system has less inputs than outputs, i.e., n ≤ m, and there exists a left stable inverse of the unknown system. Please do not revise any of the current designations. Figure 1. The composite system of the unknow n system H(z) and the deconvolver W(z), and the reference system f(z) with m inputs and single output x(t). It is the case of single reference. A2) The input sequence {s(t)} is a complex, ze- ro-mean and non-Gaussian random vector process with element processes {si(t)}, i = 1,n being mutually inde- pendent. Each element process {si(t)} is an i.i.d. process with a variance 0 2 i s and a nonzero fourth-order cumulant 0 i defined as ** cum, ,,0. iiiii stst s ts t (3) A3) The deconvolver W(z) s an FIR system, that is, W(z) = 2 1 )( L Lk kk zW, where the length L := L2 L1 + 1 is taken to be sufficiently large so that the truncation effect can be ignored. A4) The noise sequence {n(t)} is a zero-mean, Gaus- sian vector stationary process whose component processes {nj(t)}, j = 1,m have nonzero variances20 i n , j = 1,m. A5) The two vector sequences {n(t)} and {s(t)} are mutually statistically independent. Under A3), the impulse response {G(k)} of the cascade system is given by ,: 2 1 )()()( L Lτ kk HWG k ∈ Z (4) In a vector form, (4) can be written as ii g Hw , 1i,n (5) where i g is the column vector consisting of the i-th output impulse response of the cascade system defined by 12 : T TT T iiiin gg,g,,g , gij is expressed as : 1011 T ijijij ij g ,g,g,g,, j,n (6) where gij(k) is the (i, j)-th element of matrix G(k), and i w is the mL-column vector consisting of the tap coeffi- cients (corresponding to the i-th output) of the decon- volver defined by i w ~ := 12 [,,, ] TT TT ii in ww w∈ CmL, ij wis defined by 11 2 : 11 TL ij ijijij wwL,wL,,wLC,j ,m, (7) where wij(k) is the (i,j)-th element of matrix W(k), and H is the n×m block matrix whose (i,j)-th block ele- ment Hij is the matrix (of L columns and possibly infinite number of rows) with the (l,r)-th element [Hij]lr defined by[Hij]lr := hji(l r), l = 0, 1,2,, r = L1,L2, where hij(k) is the (i,j)-th element of the matrix H(k). In the MIMO deconvolution problem, we want to ad- just i w ~ 's (i= 1,n) so that 111 ,,,, ,, nnn ggHww δδP, (8) where P is an n×n permutation matrix, andi δ is the  M. KAWAMOTO ET AL. Copyright © 2011 SciRes. CS 9 n-block column vector defined by12 T TT T iii in δδ,δ,,δ ,i = 1,n, ˆ : ij i δδfor i = j, otherwise. ,0,0,0, T Here, i ˆis the column vector (of infinite elements) whose r-th element )( ˆ iis given by ˆiii drk , where t is the Kronecker delta function, di is a complex number standing for a scale change and a phase shift, and ki is an integer standing for a time shift. 3. The Conventional Eigenvector Algorithms Jelonnek et al. [2] have shown in the single-input case that from the following problem, that is, Maximize ** cum,, , i vxi i Dvtvtxtxt under , 22 iisv (9) a closed-form solution expressed as a generalized eigen- vector problem can be led by the Lagrangian method, where 2 i v and 2 i s denote the variances of the output vi(t) and a source signal)(ts i , respectively, i is one of integers 1, 2, n such that the set {12 ,,, n } is a permutation of the set 1, 2,, n, vi(t) is the i-th ele- ment of v(t) in (2), and the reference signal x(t) is given by T f zytusing an appropriate filter f(z) (see Fig- ure 1). The filter f(z) is called a reference system. Let a(z) := 12 ,,,T T n H zfza z azaz , then x(t) = . TT f zH zstazstThe element ai(z) of the filter a(z) is defined as () k ii k az akz and the reference system f(z) is an $m$-column vector whose elements are fj(z) = 2 1)( L Lk k jzkf , j = 1,m, where dif- ferently from the wij(k), the parameter fj(k) is any fixed value. In our case, i vx Dand 2 i v can be expressed in terms of the vectori w ~ as, respectively, i H ixvi DwBw ~ ~ ~ and i H i viwRw ~ ~ ~ 2 where B ~is the m×m block matrix whose (i,j)-th block element Bij is the matrix with the (l,r)-th element calculated by cum 11 j ytLr, * i1 1,ytLl *, x txt (l,r = 1,L) and *T REytyt is the covariance matrix of m-block column vector)( ~ tydefined by 12 :T TT TmL m ytyt,yt,..., ytC (10) where j1 12 : ,1,,, T L jjj ytytL ytLytLC j=1,m. It follows from (10) that()yt is expressed as )( ~ ty = Dc(z)y(t), where Dc(z) is an mL×m converter (consist- ing of m identical delay chains each of which has L delay elements when L1 = 1) defined by Dc(z) := block-diag ,, cc dz dz with m diagonal block elements all being the same L-column vector dc(z) de- fined by dc(z) = 12 ,, . T LL zz Therefore, by the simi- lar way to as in [2], the maximization of || xvi D under 22 ii sv leads to the following generalized eigenvec- tor problem; . ~ ~ ~ ~ iiiwRwB (11) Moreover, Jelonnek et al. have shown in [2] that the eigenvector corresponding to the maximum magnitude eigenvalue of B R ~ ~ †becomes the solution of the blind equalization problem, which is referred to as an eigen- vector algorithm (EVA). It has been also shown in [3] that the BD for MIMO-IIR systems can be achieved with the eigenvectors of B R ~ ~ †, using only one reference sig- nal. Note that since Jelonnek et al. have dealt with SI- SO-IIR systems or SIMO-IIR systems, the constructions of B, i w, and R in (11) are different from those pro- posed in [2]. Castella et al. [5] have shown that from (9), a BD can be iteratively achieved by using xi(t) =)( ~ ~ t iyw (i = 1,n) as reference signals (see Figure 2), where the number of reference signals corresponds to the number of source signals andi w ~ is a vector obtained byi BR ~ ~ †divided by i in the previous iteration, where i B represents B in (11) calculated by xi(t) = )( ~ ~ t iyw . Namely, they considered the following equation; . ~ ~ ~ ~ iiiiwwBR † (12) Then a deflation method was used to recover all source signals. However, the EVM proposed by Castella et al. requires the calculation of the eigenvectors of the matrix i BR ~ ~ †to achieve the BD. 4. The Proposed Algorithm Here, the Equation (12) can be interpreted as follows. Suppose that the value i w ~ in the left-hand side of (12) is a vector obtained by i BR ~ ~ † divided byi in the pre- vious iteration. Also, let i d ~denote . ~ ~ ii wB Then (12) can be expressed as  M. KAWAMOTO ET AL. Copyright © 2011 SciRes. CS 10 Figure 2. The composite system of the unknow n system H(z) and the deconvolver W(z), and the reference system with m inputs and n outputs, where Dc(z) is an mL×m converter. It is the case of multiple reference system. , ~ ~ 1 ~i i idRw † i = 1,n, (13) where on the details of iii dBw, see (30) in Appendix. Differently from the EVM in [5], (13) means that i w is modified iteratively by the value of the right-hand side of (13) without calculating the eigenvectors of i BR ~~ †where i w in both xi(t) and i d is the value of the left-hand side of (13) in the previous iteration. Moreover, the EVMs in [2,6] must select the appropriate parameter for the refer- ence system f(z), but our proposed algorithm does not need such a troublesome process. The scalari is fixed to be 1, but i w ~ obtained by (13) should be normalized at each iteration, that is i H i i i wRw w w~ ~ ~ ~ : ~, i = 1,n. (14) It can be seen that the iterative algorithm (13) is noth- ing but an iterative procedure of the super-exponential method (SEM) [7-9] (see Appendix), where the first pro- posal of the SEM was done by Shalvi and Weinstein [9]. Therefore, our proposed algorithm for achieving the BD is that the vectori w is modified by using the value i dR ~ ~ †in (13), and then the modified vector, that is, i w in the left-hand side of (13) is normalized by (14). Here, the calculation of† R ~ is implemented by using the following algorithm based on the matrix pseudo-inversion lemma proposed in [10]. The reason is that in the case that the pseudo-inverse is calculated using data block, the convergence speed is increased and the computational complexity is reduced, compared with the conventional pseudo-inverse algorithms, for example, the built-in func- tion “pinv” in MATLAB [11]. Therefore, in order to pro- vide a recursive formula based on block data for time-updating of pseudo-inverse, the block index “k” is defined, and then R ~ and † R ~are described as(k) ~ Rand P(k), respectively, where the k-th block of data is defined as t = kl + i, i = 1,l – 1, k ∈ Z (15) the parameters l and t denote the block length and the original discrete (or sample) time, respectively. The ma- trix Rk is obtained by (k),(k))1(k ~ )1((k) ~ * kk T YYRR (16) where Y(k) = k1k1 1k11yl,yl,,yll ∈ CmL×l (17) and k is a positive number close to, but greater than zero, which accounts for some exponential weighting factor or forgetting factor [12]. Moreover, the following parame- ters are defined; *, k YkY k (18) 111, Yk=Rk-Pk- Yk (19) 2()( 1)( 1).YkI RkPkYk (20) Then the pseudo-inverse P(k) can be explicitly ex- pressed, as follows: B PkP k † †1 12 12 kkkkkk H BD PY ,YPY ,Y †k B P (21) where B Pk †and 1 D Pk are respectively defined by 1 11 † k k1k1kkk1 k1 H A B PPYPYP P: †† 22 kk H YY, (22) and 11 2 1 11 121 ΔkkΔk k: kΔkk kΔk D P PIEE E (23) with 21 Δk:kk I EE, (24) where † 11 1 kkkk H B EBPB, (25) † 22 2 kkkk H B EBPB, We treat P(k) as , ~ † Rand i w is iteratively modified using (13) and (14), wherei in (13) is assumed to be fixed to 1 and : iii dBw in (13) is estimated by using Y(k). Thus, the proposed iterative algorithm for solving the BD problem is summarized, as follows: 1) Choose appropriate initial values of 0 i w, P(0), R0 , i d0, i=1,n and set k = 1. 2) Estimate 1Rk , dk1, i by their moving aver- ages, and 1Pk by (21). 1 1  M. KAWAMOTO ET AL. Copyright © 2011 SciRes. CS 11 3) Calculate the i wk, from i Pk-1wk, and then (k) ~ i wis normalized by kk1 k H ii wR w. 4) Put k = k + 1 and stock thei w obtained in (13). If k = k' (where k' denotes an appropriate iteration number), stop the iterations, otherwise go to 2). 5. Simulation Results To demonstrate the proposed algorithm, we considered a MIMO system H(z) with two inputs (n = 2) and three outputs (m = 3), and assumed that the system H(z) is FIR and the length of channel is three, that is H(k)'s in (1) were set to be H(z) = 2 0 )( k kkzH = 22 22 22 1.02.01.04.01.06.0 1.025.012.01.05.0 15.025.065.01.015.01 zzzz zzzz zzzz The source signals s1(t) and s2(t) were a sub-Gaussian signal which takes one of two values, –1 and 1 with equal probability 1/2. The parameters L1 and L2 in W(z) were set to be 0 and 9, respectively. As a measure of performances, we used the multichannel intersymbol interference (MISI) [8], which was the average of 50 Monte Carlo runs. In each Monte Carlo run, using 300 data samples, i w is modified by (13) and (14), and the total number of modification times is 10. About the block length l, the following two cases were considered: l = 1 and l = 2. For obtaining the pseudo-inverse of the correlation matrix, the initial values ofR i d, and P were estimated using 30 data samples. The value ofk was chosen asl k 1 k for each k. Figure 3 shows the results obtained by the convention- al EVM (ConEVM), the modified EVM (ModEVM), and their combined EVM (ComEVM) in the case of l = 1. As a ConEVM, we selected the EVM proposed by Castella et al.. Then, the pseudo-inverse ofR in (12) was calculated by the built-in function “pinv” in MATLAB and our pro- posed matrix pseudo-inversion lemma, denoted by “mpinvl”. In the ComEVM, the ConEVM was carried out at the first modification and from the second modification the ModEVM was carried out, where the pseu- do-inverse R in (12) was calculated by “mpinvl”. From the figure, the ConEVM with mpinvl provides a better performance compared with the other EVMs, except for the ComEVM. However, the average of the execution time of the ConEVM with mpinvl is longer than the one of the ModEVM with mpinvl (see Table 1). Figure 3. The performances of the proposed algorithm and the conventional methods (l = 1). On the other hand, the ComEVM with mpinvl is carried out with a little bit longer execution time than the Mod- EVM with mpinvl but the performance of the ComEVM with mpinvl is better than the other EVMs. From these results, we recommend to use the ComEVM with mpinvl to achieve the BD in the case of l = 1. Figure 4 shows the results obtained by the EVMs in the case of l = 2. From Figure 4, one can see that the ModEVMs with mpinvl provides better performances than the other EVMs. Therefore we recommend to use the ModEVM with mpinvl to achieve the BD in the case of l = 2. Table 1 shows the average of the execution times for the proposed method and the conventional EVM, using a personal computer (Windows machine) with 3.33 GHz processor and 3 GB main memories. From the Table 1, one can see that the execution time of the ModEVM with mpinvl is the fastest compared with other EVMs. The reasons are that the ModEVM is carried out without cal- culating the eigenvectors of i BR ~~ † in (12) and the mpinvl has a property written in [13]. 6. Conclusions In this paper, by modifying the EVM, we have proposed an algorithm which can achieve the BD without calcu- lating eigenvectors. Moreover, a combination of the modified EVM and the conventional EVM has been proposed. It can be seen that the combined EVM pro- vides a better performance than the other EVMs in the case of l = 1, and the ModEVA with mpinvl provides a better performance than the other EVMs in the case of l = 2, but the average of execution time of the combined EVM is a little bit longer than the modified EVM. Al- though there exists such a trade-off, we conclude that our proposed EVM is more useful for solving the BD prob- lem, because we consider that the performance accuracy is most important for achieving the BD. 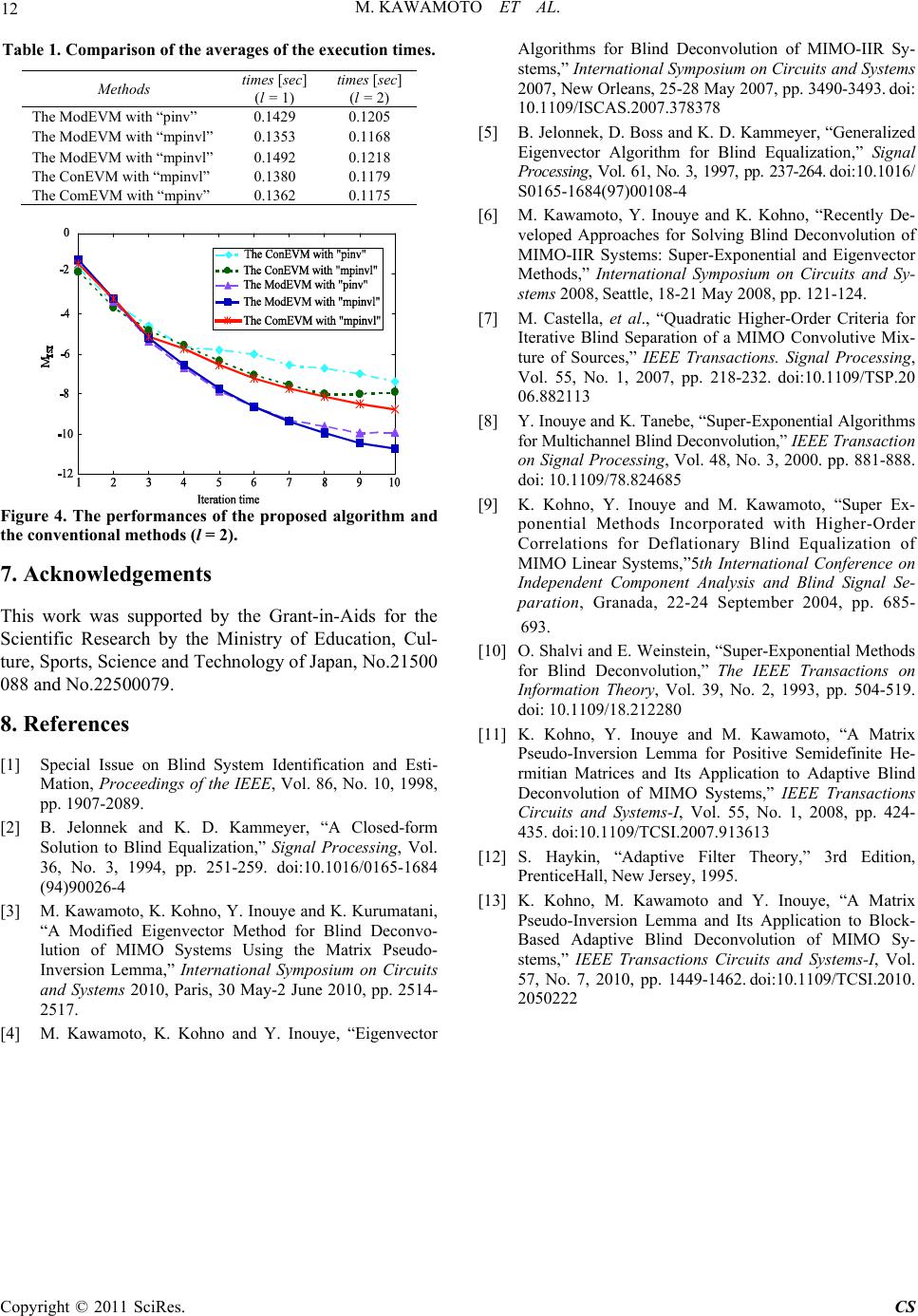 M. KAWAMOTO ET AL. Copyright © 2011 SciRes. CS 12 Table 1. Comparison of the averages of the execution times. Methods times [sec] (l = 1) times [sec] (l = 2) The ModEVM with “pinv” 0.1429 0.1205 The ModEVM with “mpinvl” 0.1353 0.1168 The ModEVM with “mpinvl” 0.1492 0.1218 The ConEVM with “mpinvl” 0.1380 0.1179 The ComEVM with “mpinv” 0.1362 0.1175 Figure 4. The performances of the proposed algorithm and the conventional methods (l = 2). 7. Acknowledgements This work was supported by the Grant-in-Aids for the Scientific Research by the Ministry of Education, Cul- ture, Sports, Science and Technology of Japan, No.21500 088 and No.22500079. 8. References [1] Special Issue on Blind System Identification and Esti- Mation, Proceedings of the IEEE, Vol. 86, No. 10, 1998, pp. 1907-2089. [2] B. Jelonnek and K. D. Kammeyer, “A Closed-form Solution to Blind Equalization,” Signal Processing, Vol. 36, No. 3, 1994, pp. 251-259. doi:10.1016/0165-1684 (94)90026-4 [3] M. Kawamoto, K. Kohno, Y. Inouye and K. Kurumatani, “A Modified Eigenvector Method for Blind Deconvo- lution of MIMO Systems Using the Matrix Pseudo- Inversion Lemma,” International Symposium on Circuits and Systems 2010, Paris, 30 May-2 June 2010, pp. 2514- 2517. [4] M. Kawamoto, K. Kohno and Y. Inouye, “Eigenvector Algorithms for Blind Deconvolution of MIMO-IIR Sy- stems,” International Symposium on Circuits and Systems 2007, New Orleans, 25-28 May 2007, pp. 3490-3493. doi: 10.1109/ISCAS.2007.378378 [5] B. Jelonnek, D. Boss and K. D. Kammeyer, “Generalized Eigenvector Algorithm for Blind Equalization,” Signal Processing, Vol. 61, No. 3, 1997, pp. 237-264. doi:10.1016/ S0165-1684(97)00108-4 [6] M. Kawamoto, Y. Inouye and K. Kohno, “Recently De- veloped Approaches for Solving Blind Deconvolution of MIMO-IIR Systems: Super-Exponential and Eigenvector Methods,” International Symposium on Circuits and Sy- stems 2008, Seattle, 18-21 May 2008, pp. 121-124. [7] M. Castella, et al., “Quadratic Higher-Order Criteria for Iterative Blind Separation of a MIMO Convolutive Mix- ture of Sources,” IEEE Transactions. Signal Processing, Vol. 55, No. 1, 2007, pp. 218-232. doi:10.1109/TSP.20 06.882113 [8] Y. Inouye and K. Tanebe, “Super-Exponential Algorithms for Multichannel Blind Deconvolution,” IEEE Transaction on Signal Processing, Vol. 48, No. 3, 2000. pp. 881-888. doi: 10.1109/78.824685 [9] K. Kohno, Y. Inouye and M. Kawamoto, “Super Ex- ponential Methods Incorporated with Higher-Order Correlations for Deflationary Blind Equalization of MIMO Linear Systems,”5th International Conference on Independent Component Analysis and Blind Signal Se- paration, Granada, 22-24 September 2004, pp. 685- 693. [10] O. Shalvi and E. Weinstein, “Super-Exponential Methods for Blind Deconvolution,” The IEEE Transactions on Information Theory, Vol. 39, No. 2, 1993, pp. 504-519. doi: 10.1109/18.212280 [11] K. Kohno, Y. Inouye and M. Kawamoto, “A Matrix Pseudo-Inversion Lemma for Positive Semidefinite He- rmitian Matrices and Its Application to Adaptive Blind Deconvolution of MIMO Systems,” IEEE Transactions Circuits and Systems-I, Vol. 55, No. 1, 2008, pp. 424- 435. doi:10.1109/TCSI.2007.913613 [12] S. Haykin, “Adaptive Filter Theory,” 3rd Edition, PrenticeHall, New Jersey, 1995. [13] K. Kohno, M. Kawamoto and Y. Inouye, “A Matrix Pseudo-Inversion Lemma and Its Application to Block- Based Adaptive Blind Deconvolution of MIMO Sy- stems,” IEEE Transactions Circuits and Systems-I, Vol. 57, No. 7, 2010, pp. 1449-1462. doi:10.1109/TCSI.2010. 2050222  M. KAWAMOTO ET AL. 13 Copyright © 2011 SciRes. CS Appendix The relationship between (13) and the SEM The matricesR ~ and i B ~ can be expressed as H Σ H R ~ ~ ~ ~ H , HΛHB ~ ~ ~ ~ i H i (28) whereΣ ~is a block-diagonal matrix which is denoted as 1 Σ:block -diagΣ,,Σ, n 22 Σ:diag ,,, , ii ss i =1,n, i Λ ~ is a block-diagonal matrix which is represented as i Λ ~ := block- 1 diag Λ,,Λ iin , 22 Λ:diag,(1),(0),, ijijj ijj gg (29) j = 1,n. Then, from (5) and (28), iii wBd ~ ~ ~ can be ex- pressed as . ~ ~ ~ ~ ~ ~ ii H iii gΛHwBd (30) It can be seen from (29) that the elements ofii gΛ ~ ~ are 2, ijij j gk gk k = –∞,∞. Here,we define the fol- lowing equation: 2 2. j j ijij ij s f kgkgk (31) This can be used for the SEM with respect to gij(k), using the 4th order cumulant. [7] Substituting (31) into (30), we obtain the following equation: , ~ ~ ~ ~ i H ifΣHd (32) where 12 101 TT TTT iiiinij ijij f f,f, ,f,f,f,f,. Moreover, substituting (28) and (32) into (13), then (13) can be expressed as †Σ HH ii wHΣ H Hf, (33) where i is assumed to be 1. (33) is the first step of the SEM with respect toi w ~ [8].In the SEM, the second step, that is, the normalization step is implemented using (14). Therefore, (13) and (14) are nothing but the iterative algorithm of the SEM. This completes the proof. |

