Paper Menu >>
Journal Menu >>
 Vol.5, No.9, 963-971 (2013) Natural Science http://dx.doi.org/10.4236/ns.2013.59117 Relationship of nine constants Michael Snyder Department of Physics and Astronomy, University of Louisville, Louisville, USA; m0snyd04@louisville.edu Received 25 June 2013; revised 25 July 2013; accepted 4 August 2013 Copyright © 2013 Michael Snyder. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Through the process of trial and error, four unitless equations made up of nine constants have been found with exact ans wers. The related constants are the Speed of Light [1], the Planck constant [2], Wien’s displacement constant [3], Avogadro’s number [4], the universal Gravity constant [5], the Ampere constant [6], the Fara- day constant [7], the G as constant [8] and Apery’s constant [9]. Keywords: Planck; Wien; Avogadro; Faraday; Apery; Ampere 1. INTRODUCTION At the end of the spring semester 2013, I had found an expression of a few physical constants that gave the cor- rect value of the universal Gravity constant [5]. I shared my findings with my classmates and they all pointed out the units were incorrect. This started the search for a unitless expression of physical constants similar in form to the Fine Structure constant but with more constants. In the context of this paper, the term unitless is defined as all the exponents of the units on the left hand side of the equation are equal to zero and the right hand side of the equation is represented by only a numeric expression. 2. MAIN BODY The first few equations were found by trial and error. One would literally examine a listing of physical con- stants and guess which set of constants multiplied to- gether and divided by another set of multiplied constants produces an answer with units raised to the zero power. I had the limited success of finding the Fine Structure constant over and over again. At this point I changed my strategy by writing a program that would try every com- bination of a set of constants within a certain integer range of exponents, with its dimensionality equal to a selected SI unit. This strategy worked in the sense that it produced a large set of equations, of the selected con- stants that had the required SI units of seconds or meters, etc. The programming process and the testing the programs happened over a few weeks and various sets of physical constants where tried. Overall the physical constants that produced the most equations were selected to be in the final set of nine presented in this paper. A few things happened concurrently that allowed me to find the equations presented in this paper. One was that I started using a unit of an ampere-mole as a range extender in my search programs. The derived unit could be removed from the final answers yet its presence in the program allowed more equations to be found. The second was that it occurred to me that the struc- ture of the programs that I had written; could search for unitless equations too. The third was that I added the Faraday constant to the primary set of search constants. I intended to use the Faraday constant as a more robust replacement for the derived ampere-mole constant, and was hoping for similar results. A few minutes later, the first of many unitless equa- tions appeared on the screen. Through the process of trial and error I had found a set of eight physical constants that produced unitless equations. Once a pattern was found in the first few equations, a new program in the Cuda GPU language was written to find unitless combinations expressed as the powers of the constants. A program listing is included for completeness as Appendix I. A set of 200 unitless equations are shown in Tab le 1 , and Eq.1 through Eq.4 are the results of the reduced row echelon form of Tab le 1 . The reduced row echelon op- eration on Table 1, results with two rows. Eq.1 represents the first row and Eq.2 represents the second row of the reduced row echelon form. Eq.3 represents the multiplication of the Eq.1 and Eq.2 and Eq.4 represents the quotient of Eq.1 and Eq. 2. One can Copyright © 2013 SciRes. OPEN ACCESS 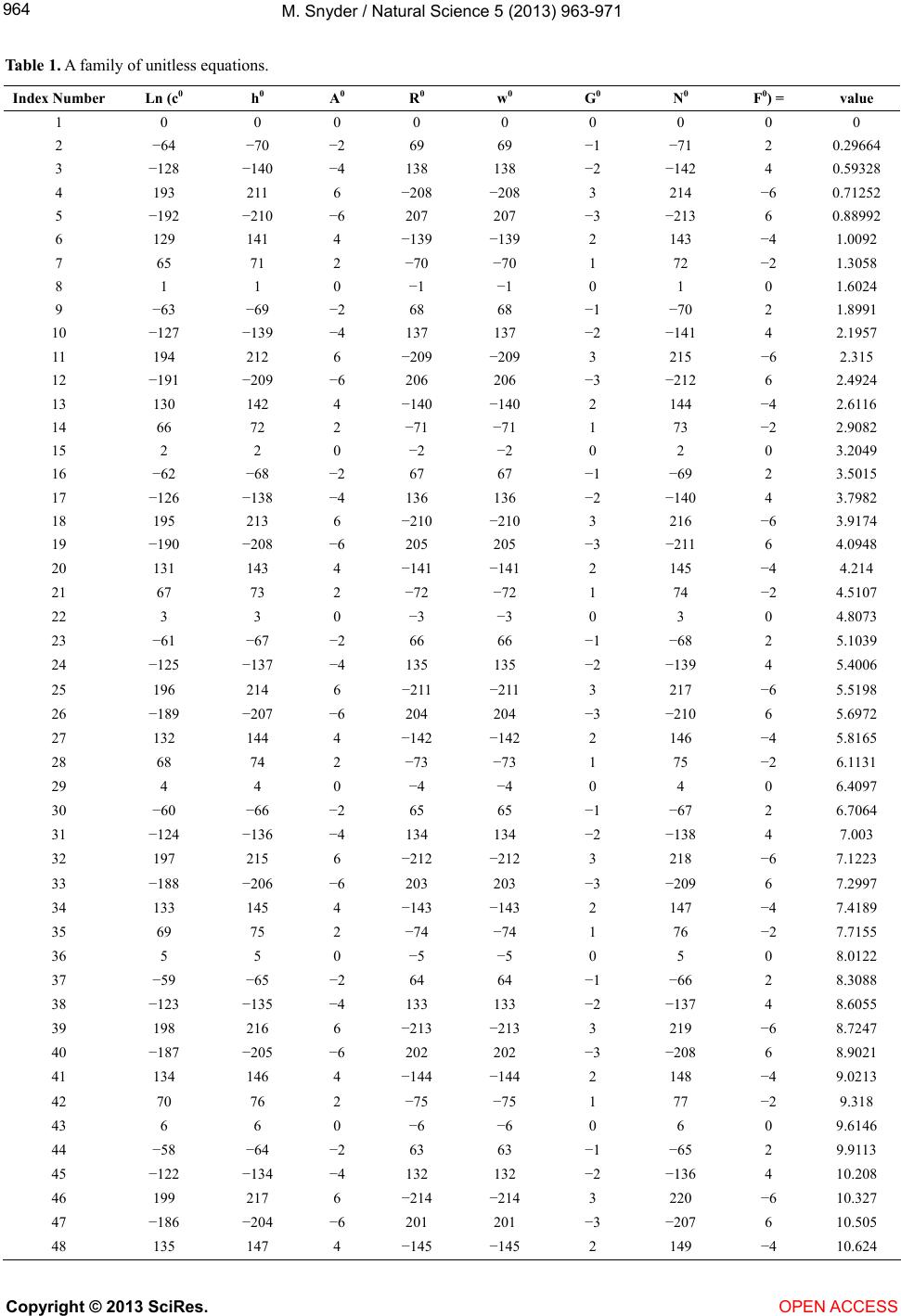 M. Snyder / Natural Science 5 (2013) 963-971 964 Table 1. A family of unitless equations. Index Number Ln (c0 h 0 A 0 R 0 w 0 G 0 N 0 F 0) = value 1 0 0 0 0 0 0 0 0 0 2 −64 −70 −2 69 69 −1 −71 2 0.29664 3 −128 −140 −4 138 138 −2 −142 4 0.59328 4 193 211 6 −208 −208 3 214 −6 0.71252 5 −192 −210 −6 207 207 −3 −213 6 0.88992 6 129 141 4 −139 −139 2 143 −4 1.0092 7 65 71 2 −70 −70 1 72 −2 1.3058 8 1 1 0 −1 −1 0 1 0 1.6024 9 −63 −69 −2 68 68 −1 −70 2 1.8991 10 −127 −139 −4 137 137 −2 −141 4 2.1957 11 194 212 6 −209 −209 3 215 −6 2.315 12 −191 −209 −6 206 206 −3 −212 6 2.4924 13 130 142 4 −140 −140 2 144 −4 2.6116 14 66 72 2 −71 −71 1 73 −2 2.9082 15 2 2 0 −2 −2 0 2 0 3.2049 16 −62 −68 −2 67 67 −1 −69 2 3.5015 17 −126 −138 −4 136 136 −2 −140 4 3.7982 18 195 213 6 −210 −210 3 216 −6 3.9174 19 −190 −208 −6 205 205 −3 −211 6 4.0948 20 131 143 4 −141 −141 2 145 −4 4.214 21 67 73 2 −72 −72 1 74 −2 4.5107 22 3 3 0 −3 −3 0 3 0 4.8073 23 −61 −67 −2 66 66 −1 −68 2 5.1039 24 −125 −137 −4 135 135 −2 −139 4 5.4006 25 196 214 6 −211 −211 3 217 −6 5.5198 26 −189 −207 −6 204 204 −3 −210 6 5.6972 27 132 144 4 −142 −142 2 146 −4 5.8165 28 68 74 2 −73 −73 1 75 −2 6.1131 29 4 4 0 −4 −4 0 4 0 6.4097 30 −60 −66 −2 65 65 −1 −67 2 6.7064 31 −124 −136 −4 134 134 −2 −138 4 7.003 32 197 215 6 −212 −212 3 218 −6 7.1223 33 −188 −206 −6 203 203 −3 −209 6 7.2997 34 133 145 4 −143 −143 2 147 −4 7.4189 35 69 75 2 −74 −74 1 76 −2 7.7155 36 5 5 0 −5 −5 0 5 0 8.0122 37 −59 −65 −2 64 64 −1 −66 2 8.3088 38 −123 −135 −4 133 133 −2 −137 4 8.6055 39 198 216 6 −213 −213 3 219 −6 8.7247 40 −187 −205 −6 202 202 −3 −208 6 8.9021 41 134 146 4 −144 −144 2 148 −4 9.0213 42 70 76 2 −75 −75 1 77 −2 9.318 43 6 6 0 −6 −6 0 6 0 9.6146 44 −58 −64 −2 63 63 −1 −65 2 9.9113 45 −122 −134 −4 132 132 −2 −136 4 10.208 46 199 217 6 −214 −214 3 220 −6 10.327 47 −186 −204 −6 201 201 −3 −207 6 10.505 48 135 147 4 −145 −145 2 149 −4 10.624 Copyright © 2013 SciRes. OPEN ACCESS 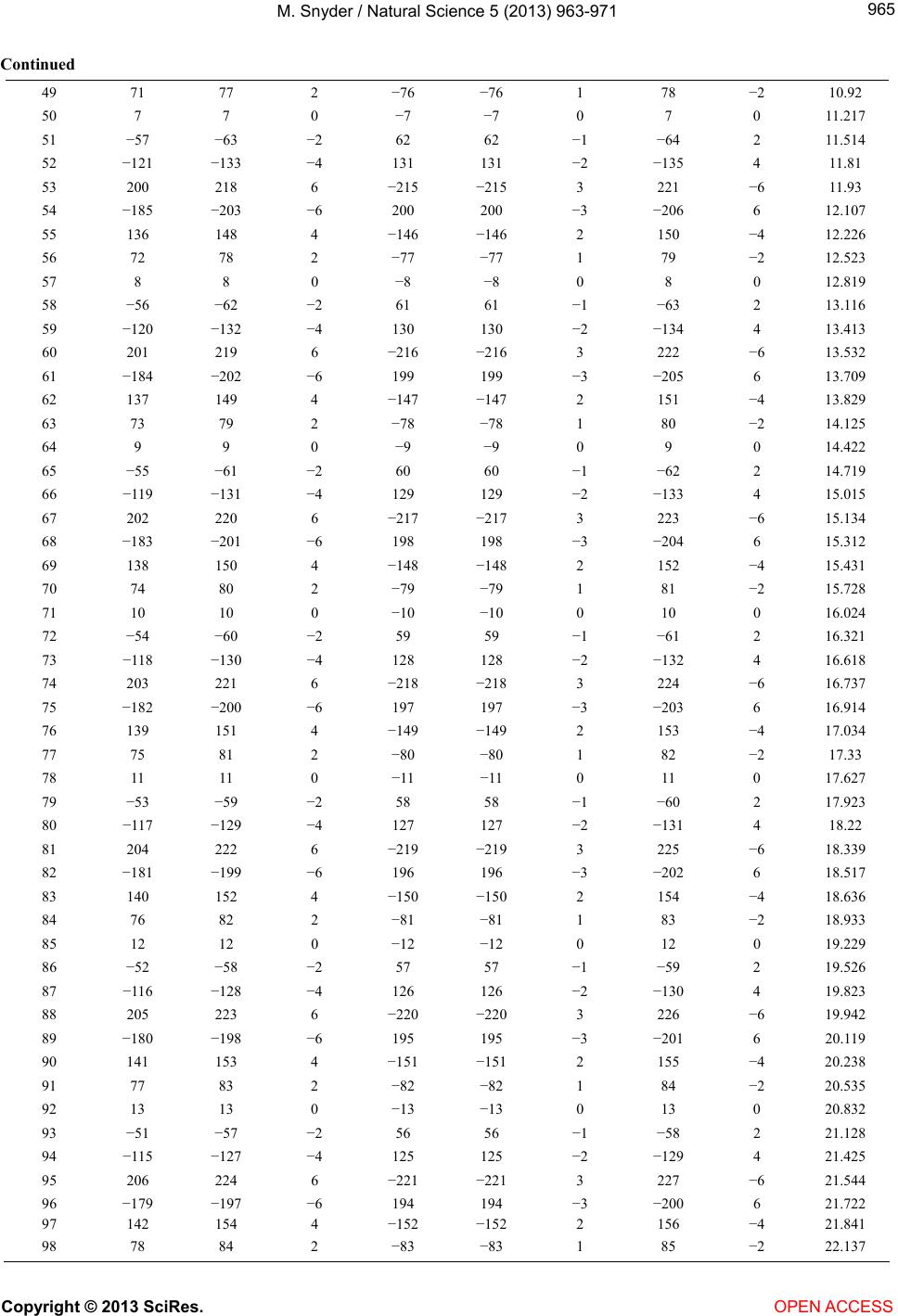 M. Snyder / Natural Science 5 (2013) 963-971 965 Continued 49 71 77 2 −76 −76 1 78 −2 10.92 50 7 7 0 −7 −7 0 7 0 11.217 51 −57 −63 −2 62 62 −1 −64 2 11.514 52 −121 −133 −4 131 131 −2 −135 4 11.81 53 200 218 6 −215 −215 3 221 −6 11.93 54 −185 −203 −6 200 200 −3 −206 6 12.107 55 136 148 4 −146 −146 2 150 −4 12.226 56 72 78 2 −77 −77 1 79 −2 12.523 57 8 8 0 −8 −8 0 8 0 12.819 58 −56 −62 −2 61 61 −1 −63 2 13.116 59 −120 −132 −4 130 130 −2 −134 4 13.413 60 201 219 6 −216 −216 3 222 −6 13.532 61 −184 −202 −6 199 199 −3 −205 6 13.709 62 137 149 4 −147 −147 2 151 −4 13.829 63 73 79 2 −78 −78 1 80 −2 14.125 64 9 9 0 −9 −9 0 9 0 14.422 65 −55 −61 −2 60 60 −1 −62 2 14.719 66 −119 −131 −4 129 129 −2 −133 4 15.015 67 202 220 6 −217 −217 3 223 −6 15.134 68 −183 −201 −6 198 198 −3 −204 6 15.312 69 138 150 4 −148 −148 2 152 −4 15.431 70 74 80 2 −79 −79 1 81 −2 15.728 71 10 10 0 −10 −10 0 10 0 16.024 72 −54 −60 −2 59 59 −1 −61 2 16.321 73 −118 −130 −4 128 128 −2 −132 4 16.618 74 203 221 6 −218 −218 3 224 −6 16.737 75 −182 −200 −6 197 197 −3 −203 6 16.914 76 139 151 4 −149 −149 2 153 −4 17.034 77 75 81 2 −80 −80 1 82 −2 17.33 78 11 11 0 −11 −11 0 11 0 17.627 79 −53 −59 −2 58 58 −1 −60 2 17.923 80 −117 −129 −4 127 127 −2 −131 4 18.22 81 204 222 6 −219 −219 3 225 −6 18.339 82 −181 −199 −6 196 196 −3 −202 6 18.517 83 140 152 4 −150 −150 2 154 −4 18.636 84 76 82 2 −81 −81 1 83 −2 18.933 85 12 12 0 −12 −12 0 12 0 19.229 86 −52 −58 −2 57 57 −1 −59 2 19.526 87 −116 −128 −4 126 126 −2 −130 4 19.823 88 205 223 6 −220 −220 3 226 −6 19.942 89 −180 −198 −6 195 195 −3 −201 6 20.119 90 141 153 4 −151 −151 2 155 −4 20.238 91 77 83 2 −82 −82 1 84 −2 20.535 92 13 13 0 −13 −13 0 13 0 20.832 93 −51 −57 −2 56 56 −1 −58 2 21.128 94 −115 −127 −4 125 125 −2 −129 4 21.425 95 206 224 6 −221 −221 3 227 −6 21.544 96 −179 −197 −6 194 194 −3 −200 6 21.722 97 142 154 4 −152 −152 2 156 −4 21.841 98 78 84 2 −83 −83 1 85 −2 22.137 Copyright © 2013 SciRes. OPEN ACCESS 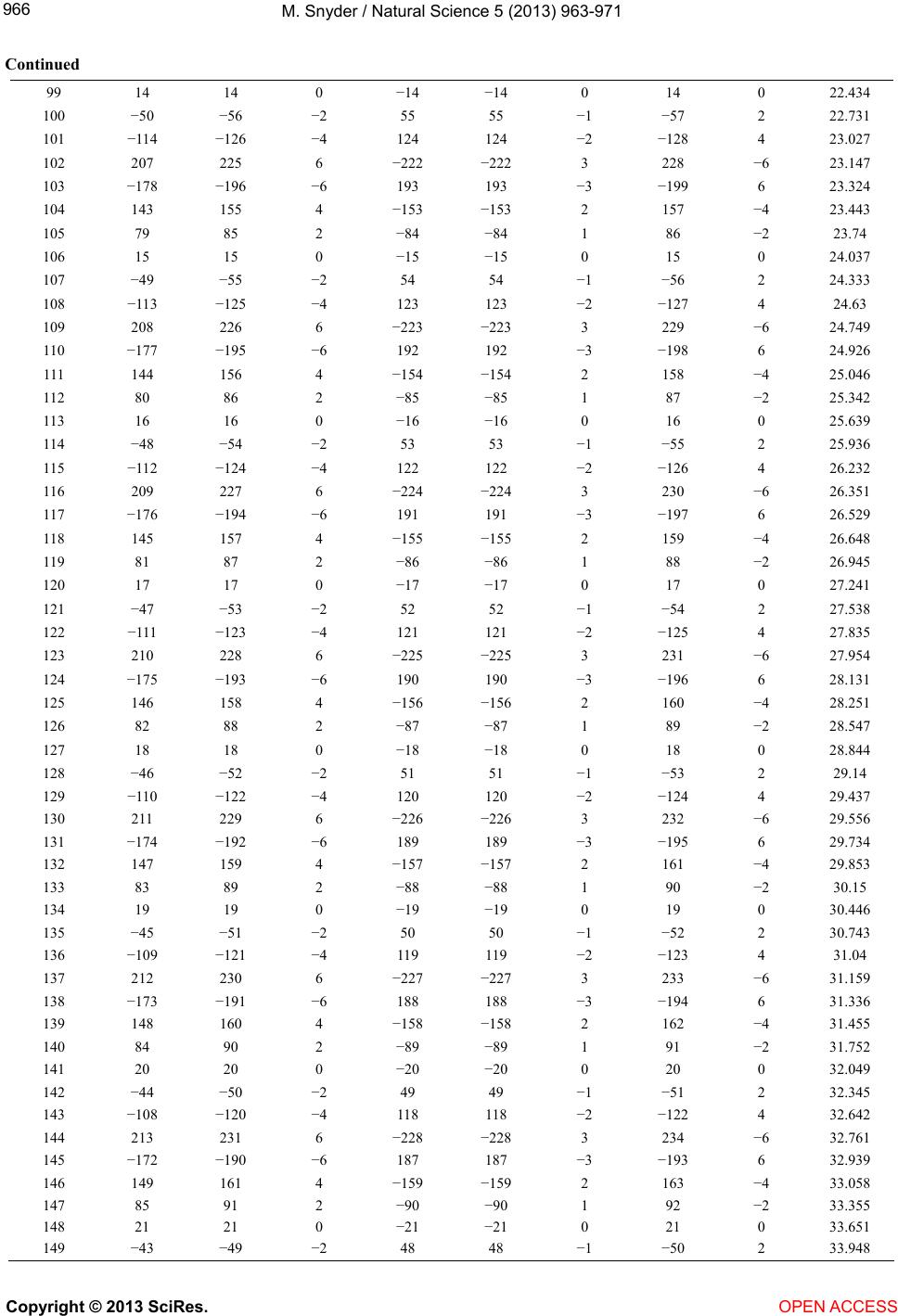 M. Snyder / Natural Science 5 (2013) 963-971 966 Continued 99 14 14 0 −14 −14 0 14 0 22.434 100 −50 −56 −2 55 55 −1 −57 2 22.731 101 −114 −126 −4 124 124 −2 −128 4 23.027 102 207 225 6 −222 −222 3 228 −6 23.147 103 −178 −196 −6 193 193 −3 −199 6 23.324 104 143 155 4 −153 −153 2 157 −4 23.443 105 79 85 2 −84 −84 1 86 −2 23.74 106 15 15 0 −15 −15 0 15 0 24.037 107 −49 −55 −2 54 54 −1 −56 2 24.333 108 −113 −125 −4 123 123 −2 −127 4 24.63 109 208 226 6 −223 −223 3 229 −6 24.749 110 −177 −195 −6 192 192 −3 −198 6 24.926 111 144 156 4 −154 −154 2 158 −4 25.046 112 80 86 2 −85 −85 1 87 −2 25.342 113 16 16 0 −16 −16 0 16 0 25.639 114 −48 −54 −2 53 53 −1 −55 2 25.936 115 −112 −124 −4 122 122 −2 −126 4 26.232 116 209 227 6 −224 −224 3 230 −6 26.351 117 −176 −194 −6 191 191 −3 −197 6 26.529 118 145 157 4 −155 −155 2 159 −4 26.648 119 81 87 2 −86 −86 1 88 −2 26.945 120 17 17 0 −17 −17 0 17 0 27.241 121 −47 −53 −2 52 52 −1 −54 2 27.538 122 −111 −123 −4 121 121 −2 −125 4 27.835 123 210 228 6 −225 −225 3 231 −6 27.954 124 −175 −193 −6 190 190 −3 −196 6 28.131 125 146 158 4 −156 −156 2 160 −4 28.251 126 82 88 2 −87 −87 1 89 −2 28.547 127 18 18 0 −18 −18 0 18 0 28.844 128 −46 −52 −2 51 51 −1 −53 2 29.14 129 −110 −122 −4 120 120 −2 −124 4 29.437 130 211 229 6 −226 −226 3 232 −6 29.556 131 −174 −192 −6 189 189 −3 −195 6 29.734 132 147 159 4 −157 −157 2 161 −4 29.853 133 83 89 2 −88 −88 1 90 −2 30.15 134 19 19 0 −19 −19 0 19 0 30.446 135 −45 −51 −2 50 50 −1 −52 2 30.743 136 −109 −121 −4 119 119 −2 −123 4 31.04 137 212 230 6 −227 −227 3 233 −6 31.159 138 −173 −191 −6 188 188 −3 −194 6 31.336 139 148 160 4 −158 −158 2 162 −4 31.455 140 84 90 2 −89 −89 1 91 −2 31.752 141 20 20 0 −20 −20 0 20 0 32.049 142 −44 −50 −2 49 49 −1 −51 2 32.345 143 −108 −120 −4 118 118 −2 −122 4 32.642 144 213 231 6 −228 −228 3 234 −6 32.761 145 −172 −190 −6 187 187 −3 −193 6 32.939 146 149 161 4 −159 −159 2 163 −4 33.058 147 85 91 2 −90 −90 1 92 −2 33.355 148 21 21 0 −21 −21 0 21 0 33.651 149 −43 −49 −2 48 48 −1 −50 2 33.948 Copyright © 2013 SciRes. OPEN ACCESS  M. Snyder / Natural Science 5 (2013) 963-971 967 Continued 150 −107 −119 −4 117 117 −2 −121 4 34.244 151 214 232 6 −229 −229 3 235 −6 34.364 152 −171 −189 −6 186 186 −3 −192 6 34.541 153 150 162 4 −160 −160 2 164 −4 34.66 154 86 92 2 −91 −91 1 93 −2 34.957 155 22 22 0 −22 −22 0 22 0 35.254 156 −42 −48 −2 47 47 −1 −49 2 35.55 157 −106 −118 −4 116 116 −2 −120 4 35.847 158 215 233 6 −230 −230 3 236 −6 35.966 159 −170 −188 −6 185 185 −3 −191 6 36.144 160 151 163 4 −161 −161 2 165 −4 36.263 161 87 93 2 −92 −92 1 94 −2 36.559 162 23 23 0 −23 −23 0 23 0 36.856 163 −41 −47 −2 46 46 −1 −48 2 37.153 164 −105 −117 −4 115 115 −2 −119 4 37.449 165 216 234 6 −231 −231 3 237 −6 37.569 166 −169 −187 −6 184 184 −3 −190 6 37.746 167 152 164 4 −162 −162 2 166 −4 37.865 168 88 94 2 −93 −93 1 95 −2 38.162 169 24 24 0 −24 −24 0 24 0 38.458 170 −40 −46 −2 45 45 −1 −47 2 38.755 171 −104 −116 −4 114 114 −2 −118 4 39.052 172 217 235 6 −232 −232 3 238 −6 39.171 173 −168 −186 −6 183 183 −3 −189 6 39.348 174 153 165 4 −163 −163 2 167 −4 39.468 175 89 95 2 −94 −94 1 96 −2 39.764 176 25 25 0 −25 −25 0 25 0 40.061 177 −39 −45 −2 44 44 −1 −46 2 40.358 178 −103 −115 −4 113 113 −2 −117 4 40.654 179 218 236 6 −233 −233 3 239 −6 40.773 180 −167 −185 −6 182 182 −3 −188 6 40.951 181 154 166 4 −164 −164 2 168 −4 41.07 182 90 96 2 −95 −95 1 97 −2 41.367 183 26 26 0 −26 −26 0 26 0 41.663 184 −38 −44 −2 43 43 −1 −45 2 41.96 185 −102 −114 −4 112 112 −2 −116 4 42.257 186 219 237 6 −234 −234 3 240 −6 42.376 187 −166 −184 −6 181 181 −3 −187 6 42.553 188 155 167 4 −165 −165 2 169 −4 42.672 189 91 97 2 −96 −96 1 98 −2 42.969 190 27 27 0 −27 −27 0 27 0 43.266 191 −37 −43 −2 42 42 −1 −44 2 43.562 192 −101 −113 −4 111 111 −2 −115 4 43.859 193 220 238 6 −235 −235 3 241 −6 43.978 194 −165 −183 −6 180 180 −3 −186 6 44.156 195 156 168 4 −166 −166 2 170 −4 44.275 196 92 98 2 −97 −97 1 99 −2 44.572 197 28 28 0 −28 −28 0 28 0 44.868 198 −36 −42 −2 41 41 −1 −43 2 45.165 199 −100 −112 −4 110 110 −2 −114 4 45.461 200 221 239 6 −236 −236 3 242 −6 45.581 Copyright © 2013 SciRes. OPEN ACCESS  M. Snyder / Natural Science 5 (2013) 963-971 Copyright © 2013 SciRes. 968 Figures 1 and 2 should prove that the family of unitless equations contained in Table 1 is not random but instead is a structure made up of periodic waveforms. use dimensional analysis to check that Eq.1 through Eq.4 are unitless equations. 75 19 62 12 2 6 22 49 π5 π3 cF AGNRw 2 (1) 3. DISCUSSION Once we know that the dimensionality of the left hand sides of the equations are correct, then our focus switches to the right hand side of the equations. One should note by definition all the physical constants on the left hand side are measurements and have limited accuracy. 2 113 255 7 6 2672 7 212 49 2 π5π FRw AGhN (2) 21 122 3222 72 3 234 22 492 5 π3 cF Rw AGhN (3) 55 9 62 22 2 8 7 π54 π 27 3 chN Rw Obviously the equations based physical measurements can not be more accurate than the measurements them- selves. My method was to give the Maple software pro- gram the benefit of the doubt when computing the right hand sides of the equations. 9 (4) For example while factoring and processing Eq.3 with Maple’s identify command, the Apery’s constant [9] ap- pears in the result. Apery’s constant can be expressed as a series, which means we could convert the right hand side of Eq.3 into a series just by redistributing some of the factors. For this reason I left Apery’s constant in the answer which propagated to other the equations. Figure 1 is a plot of Ta ble 1, and is intended to show that the system of equations in Table 1 is not random but very periodic. The green line represents the natural log of the right hand sides of the equations and the other lines represent the exponent powers of the physical constants. I view the form of the right hand sides of the equations as an idealized guess times an error term which was sup- plied by the reduced row echelon operation. Figure 2 is also a plot of Table 1, where the equations of the table have been resorted based on the values of the ninth column of the table, instead of the tenth column. Figure 1. Plot of Table 1 sorted by the right hand side values. OPEN ACCESS 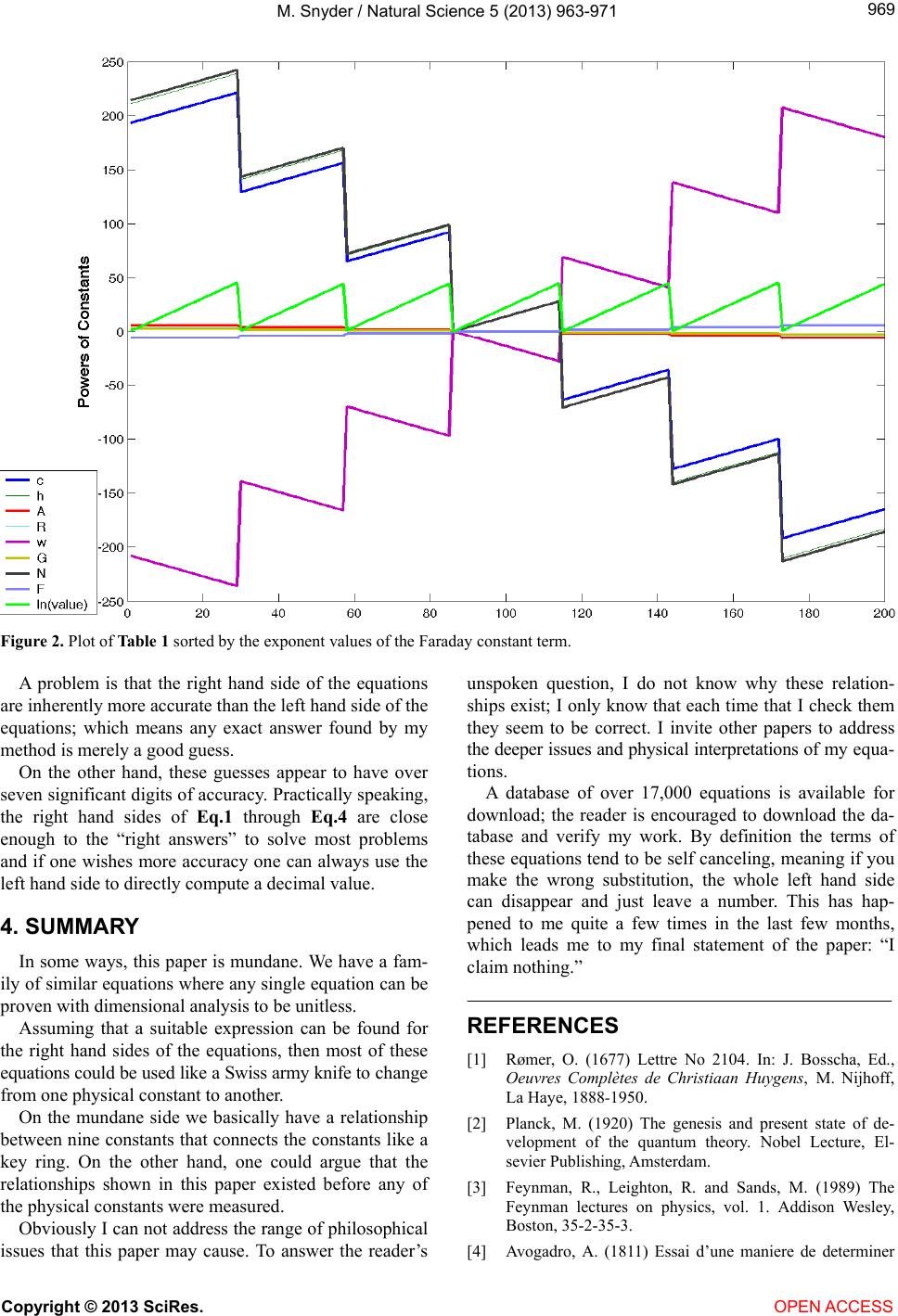 M. Snyder / Natural Science 5 (2013) 963-971 969 Figure 2. Plot of Table 1 sorted by the exponent values of the Faraday constant term. A problem is that the right hand side of the equations are inherently more accurate than the left hand side of the equations; which means any exact answer found by my method is merely a good guess. On the other hand, these guesses appear to have over seven significant digits of accuracy. Practically speaking, the right hand sides of Eq.1 through Eq.4 are close enough to the “right answers” to solve most problems and if one wishes more accuracy one can always use the left hand side to directly compute a decimal value. 4. SUMMARY In some ways, this paper is mundane. We have a fam- ily of similar equations where any single equation can be proven with dimensional analysis to be unitless. Assuming that a suitable expression can be found for the right hand sides of the equations, then most of these equations could be used like a Swiss army knife to change from one physical constant to another. On the mundane side we basically have a relationship between nine constants that connects the constants like a key ring. On the other hand, one could argue that the relationships shown in this paper existed before any of the physical constants were measured. Obviously I can not address the range of philosophical issues that this paper may cause. To answer the reader’s unspoken question, I do not know why these relation- ships exist; I only know that each time that I check them they seem to be correct. I invite other papers to address the deeper issues and physical interpretations of my equa- tions. A database of over 17,000 equations is available for download; the reader is encouraged to download the da- tabase and verify my work. By definition the terms of these equations tend to be self canceling, meaning if you make the wrong substitution, the whole left hand side can disappear and just leave a number. This has hap- pened to me quite a few times in the last few months, which leads me to my final statement of the paper: “I claim nothing.” REFERENCES [1] Rømer, O. (1677) Lettre No 2104. In: J. Bosscha, Ed., Oeuvres Complètes de Christiaan Huygens, M. Nijhoff, La Haye, 1888-1950. [2] Planck, M. (1920) The genesis and present state of de- velopment of the quantum theory. Nobel Lecture, El- sevier Publishing, Amsterdam. [3] Feynman, R., Leighton, R. and Sands, M. (1989) The Feynman lectures on physics, vol. 1. Addison Wesley, Boston, 35-2-35-3. [4] Avogadro, A. (1811) Essai d’une maniere de determiner Copyright © 2013 SciRes. OPEN ACCESS  M. Snyder / Natural Science 5 (2013) 963-971 970 les masses relatives des molecules elementaires des corps, et les proportions selon lesquelles elles entrent dans ces combinaisons. Journal de Physique, 73, 58-76. [5] Newton, I. and Turnbull, H.W. (1960) The correspond- dence of Isaac Newton: Volume 2 (1676-1687). Cam- bridge University Press, Cambridge, 309. [6] Maxwell, J.C. (1904) Treatise on electricity and magnet- ism. Clarendon Press, Oxford, 173. [7] Faraday, M. (1859) Experimental researches in chemistry and Physics. Richard Taylor and William Francis, Cam- bridge. [8] Менделеев, Д.И. (1874) О сжимаемости газов (Из лаборатории С.-Петербургского Университета). Жу- рнал русского химического общ ес т ва и физического общес т ва . Том 6, 309-352. [9] Apéry, R. (1979) Irrationalité de ζ(2) et ζ(3). Astérisque, 61, 11-13. Copyright © 2013 SciRes. OPEN ACCESS  M. Snyder / Natural Science 5 (2013) 963-971 971 APPENDIX I ---------------------------------------------------------------- #include "stdio.h" #define searchsize 29 // Search Size Should be an Odd Interger Greater than 5 // nvcc helloworld08g29.cu -o world08g29 -arch=sm_21 -maxrregcount=24 -ccbin=gcc-4.4 // Note size 29 runs in about 15 seconds on a GTX560, size 79 runs in a few hours. // All rights reserved, M. Snyder June 18, 2013 // Looking for solutions of (x4-x5)^2+(x3+x8)^2+(x4+x7+x8)^2+(x2+x4-x6)^2+(-2 *(x4+x6)+x8-x1-x2)^2+(2*(x2+x4)+x1+x5+3*x6)^2 = 0 __global__ void helloworld() { int x1,x2,x3,x4,x5,x6,x7,x8,rlow,rhgh; rlow=-((gridDim.x-1)/2); rhgh=((gridDim.x-1)/2); x1=blockIdx.x+rlow; x2=blockIdx.y+rlow; x3=threadIdx.x+rlow; x4=rlow; x5=rlow; x6=rlow; x7=rlow; x8=rlow; while (x8<rhgh) { if (x4 + x7 == -x8){ if (x3 == -x8){ if ( (x2+x4) == x6){ if (2*(x2+x4) + x1 + x5 == -3*x6){ if (x4 == x5){ if (-2*( x4 + x6) + x8 == x1 + x2){ printf("%+4d,%+4d,%+4d,%+4d,%+4d,%+4d,%+4d,%+ 4d \n", x1,x2,x3,x4,x5,x6,x7,x8); } } } } } } x4=x4+1; if (x4>rhgh){x5=x5+1;x4=rlow; if (x5>rhgh){x6=x6+1;x5=rlow; if (x6>rhgh){x7=x7+1;x6=rlow; if (x7>rhgh){x8=x8+1;x7=rlow; } } } } } } int main() { int rangeofsearch(searchsize),seconds; dim3 grid,block; grid.x=rangeofsearch; grid.y=rangeofsearch; block.x=rangeofsearch; size_t buf=1e7; cudaFuncSetCacheCon- fig(helloworld,cudaFuncCachePreferL1); cudaDeviceSetLimit(cudaLimitPrintfFifoSize, buf); seconds = time(NULL); helloworld<<<grid,block>>>(); cudaDeviceSynchronize(); printf ("\n\n\nComplete CUDA Time: %i ", int(time(NULL))-seconds); return 0; ---------------------------------------------------------------- APPENDIX II A maple script one could use to check the program out- put. ---------------------------------------------------------------- with(ScientificConstants); c0 := evalf(Constant(c)); c0u := GetUnit(Constant(c)); h0 := evalf(Constant(Planck_constant)); h0u := GetUnit(Constant(Planck_constant)); G0 := evalf(Constant(Newtonian_constant_of_gravitation)); G0u := GetU- nit(Constant(Newtonian_constant_of_gravitation)); w0 := evalf(Constant(Wien_displacement_law_constant)); w0u := GetU- nit(Constant(Wien_displacement_law_constant)); R0 := evalf(Constant(R)); R0u := GetUnit(Constant(R)); N0 := evalf(Constant(Avogadro_constant)); N0u := GetUnit(Constant(Avogadro_constant)); A0 := 1; A0u := Unit('A'); F0 := 96485.3399; F0u := Unit('C')/Unit('mol'); Copyright © 2013 SciRes. OPEN ACCESS |

