Open Journal of Microphysics, 2013, 3, 85-105
http://dx.doi.org/10.4236/ojm.2013.33015 Published Online August 2013 (http://www.scirp.org/journal/ojm)
The Coulomb Resonances, the Quasi-Real Photons and
Electro-Disintegration of Nuclei by High-Energy Electrons
A. A. Pasichnyi1, O. A. Prygodiuk2
1Institute for Nuclear Research, Kyiv, Ukraine
2Taras Shevchenko Kyiv National University, Kyiv, Ukraine
Received October 3, 2012; revised November 5, 2012; accepted November 15, 2012
Copyright © 2013 A. A. Pasichnyi, O. A. Prygodiuk. This is an open access article distributed under the Creative Commons Attribu-
tion License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly
cited.
ABSTRACT
Various aspects of the influence of the quasi-real photons and the Coulomb resonances on the formation of the cross-
section of inelastic scattering of high energy electrons on atomic nuclei are investigated. Emiss is the energy that disap-
pears in the processes of knocking-on of protons in the reactions . A new hypothesis that interprets the
origin of the energy losses is proposed. Specific experiments that can confirm or refute this hypothesis are proposed as
well. The “regularized” cross-sections of electro-disintegration of nuclei by high-energy electrons are
calculated in the framework of the nuclear shell model. It is shown that for the experimental verification of the exis-
tence of Coulomb resonances, it is necessary to investigate the processes at relatively small angles of scattering.
The peculiarities of numerical methods that are crucial in the investigation of inelastic scattering of high-energy elec-
trons on nuclei in the framework of the nuclear shell model are analyzed in this work as well. The cross-sections of the
scattering of high-energy electrons on the angle are calculated. It is shown that the orthogonality of the wave
functions of a knocked-on proton in the initial and final states plays an important role in the interpretation of this proc-
ess.
()(
,Aeep A
′−
()
,ee
′
)
1
()
,
reg
σωθ

′


0 θ
′=
Keywords: Coulomb Resonance; Quasi-Real Photon; Inelastic Scattering; High-Energy Electron;
Electro-Disintegration; Nuclear Shell Model; Numerical Method; Inelastic Scattering; Quasi-Elastic Peak
1. Introduction: The Electro-Disintegration
of Atomic Nuclei by High-Energy
Electrons
Due to the relative weakness of the electromagnetic and
weak interactions of electrons, positrons, muons and neu-
trinos with nuclei, the structure investigation of atomic
nuclei in the processes of elastic and inelastic scattering
of these particles on nuclei [1-27] provides the most re-
liable information on various aspects of the structure of
atomic nuclei. The above statement is based on the rela-
tively high reliability of the information about the prop-
erties of electromagnetic and weak interactions, as well
as the relatively high accuracy of the perturbation theory,
in the framework of which (impulse approximation) we
interpret the inelastic scattering of high-energy leptons
by nuclei. The technical perfection reached at the mo-
ment in forming the monoenergetic high-energy elec-
trons beams, as well as in registering these particles in
nuclear experiment, played a decisive role in the choice
of particles-projectiles as means of external influence on
the atomic nucleus for studying the structure and proper-
ties of nuclei: they were certainly the high-energy elec-
trons.
It is important to note that the structure of nuclei is in-
vestigated in this paper in the framework of the nuclear
shell model (LS-coupling, independent particles). In the
framework of this nuclear shell model, we will study and
interpret the features of such unusual phenomena as the
Coulomb resonances and the quasi-real photons in the
aspect of their influence on the dynamics of electro-dis-
integration of nuclei. In other words, the aim of this pa-
per is the investigation of possibilities of visualization
and identification of Coulomb resonances in experimen-
tal studies of nuclear electro-disintegration.
C
opyright © 2013 SciRes. OJM

A. A. PASICHNYI, O. A. PRYGODIUK
86
It must be emphasized that the Coulomb resonances
are the something more than merely the Coulomb reso-
nances. First, the Coulomb resonances present a practi-
cally essential part of the quantum-mechanical theory of
quasi-discrete spectrum in non-relativistic quantum me-
chanics [12,25,27]. Second, the Coulomb resonances are,
first and foremost, a natural extension of the nuclear shell
model to the continuous spectrum region [12,25,27]. Third,
it is the Coulomb resonances that will provide additional
and very useful insight into our understanding of gigantic
dipole resonance phenomenon in the framework of the
shell model [12,25,27], etc. Finally, the reader may re-
member [12,25,27] that at this stage the Coulomb reso-
nances and the quasi-real photons are investigated exclu-
sively poorly. However, in both theory of inelastic high-
energy electron scattering and theory of atomic nuclei,
the Coulomb resonances and the quasi-real photons are
phenomena that can manifest itself in many phenomena
and experiments of nuclear physics [12,25,27].
We suppose that the study of the reactions of proton
knockout and neutron knockout
from various atomic nuclei presents a
particular interest just in the framework of the nuclear
shell model. From this point on, we shall assume that the
process of inelastic scattering of a high-energy electron at
a nucleus is accompanied by transfer of energy
(; and are the initial and final energies of
the scattered electron), and momentum to the
nucleus. and are the electron momenta before
and after the act of inelastic collision of the electron and
the nucleus. We also suppose that the process of inelastic
collision of the electron with the nucleus in the investi-
gated region of the kinematic variables is caused
mainly by a collision of the scattered electron with a
single nucleon of the nucleus.
()(
,Aeep A
′−
()
1A
−
ε
′
k′ k
)
1
()
,Aeen
′
>0 ωε
ωεε
′
=−
′ =− kqk
, ω q
As a result of this collision, one of the nucleons of
the atomic nucleus, having received the required energy
in this act, overcomes the action of attractive nuclear
forces and flies out from the atomic nucleus A with mo-
mentum
ω
x
≡
K
K (
x
p= and
x
n= in the cases of
knocking out of a proton and a neutron, respectively) and
energy
x
EE≡: 2
x
M
E=
x
K.
Note that according to the conservation laws of mo-
mentum and energy, the exact expression for the distri-
bution of the transferred electron energy between the
nucleus
ω
1
A
− and the knocked-out nucleon has the fol-
lowing form (here and in the following [28]):
1=c=
()
2
2
,1
.
22
xlxl ApA
p
A
ww
AM M
νν
ω
−

−


=+ +≡++
q
K
qTT
(1)
The new quantities appearing in Equation (1) are as
follows:
x
l
w
ν
is the energy required for ejection of nu-
cleons from the xvl-shell of an infinitely heavy nucleus
(the separation energy of the nuclear xvl-nucleon); A is
the energy of motion of the center of mass of the target
nucleus
T
A
after its collision with the scattering electron;
is the energy of relative motion of the knocked-
(
,1pA
T−
)
out proton and the residual nucleus 1
A
−; =
p
A1M
A
−
M
is the reduced mass of the proton.
We point out that Equation (1) could be written in the
following form as well:
2
,
2
eff
x
l
p
w
M
ν
ω =+
K (2)
where the effective separation energy eff
x
l
w
ν
is defined by
the following apparent formula:
22
2
22
p
p
eff
xl xlAM AM
AM
ww
νν


⋅
=+ +−





qq
Kq
(3)

It is important to point out that, according to Equation
(3), the effective separation energy eff
x
l
w
ν
of the xvl-
nucleon depends somewhat on the kinematics of experi-
ment. In the limit case of 1
A
 we have:
()
2
,1 ;
2
eff
p
xl xl pA
TE ww
M
ν
ν −== =
K. (4)
The effective separation energy eff
x
l
w
ν
in the approxi-
mation
(
1, p
)
A
MM= will be identified in the fu-
ture numerical calculations with the binding energy of
the nucleon
x
l
ν
ε in the nuclear shell. There is a good
reason to believe that the calculations of the cross sec-
tions of nuclear electro-disintegration of heavy, medium
and even light nuclei, which are performed in this ap-
proximation, will be quite acceptable for preliminary
conclusions.
A nucleon knocked out from a nucleus moves in the
average field of this nucleus in both the bound
state and the state of continuous spectrum. In the shell
model the knocked-out nucleon dynamics in the bound
state is presented by the wave functions
calculated in average field ; here
()
Ax
Vr
() )
ψϕ =
1,
(
xlm ν
rr
2,3,
()
Ax
Vr
ν
=
()
Ax
Vr
() )
ψϕ =
()
is the radial quantum number; l = 0(s), 1(p), 2(d), 3(f), ···
is the orbital quantum number. It is reasonable to calcu-
late the continuous spectrum wave functions
K in the same average field In this
case the bound state wave functions
and the continuous spectrum wave functions
are orthogonal to each other.
()
=
()
=
(
ψψ r
(
ψψ r
)
r
)
r
±
±
(
xlm ν
rr
<0E
K
Note that the wave functions of the discrete
and continuous spectra are solutions of the
Sturm-Liouville problem based on the non-relativistic
single-particle Schrödinger equation:
(
>0E
)
()()()
2
.
2Ax
Vr E
M

−Δ+ Ψ=Ψ


rr 5) (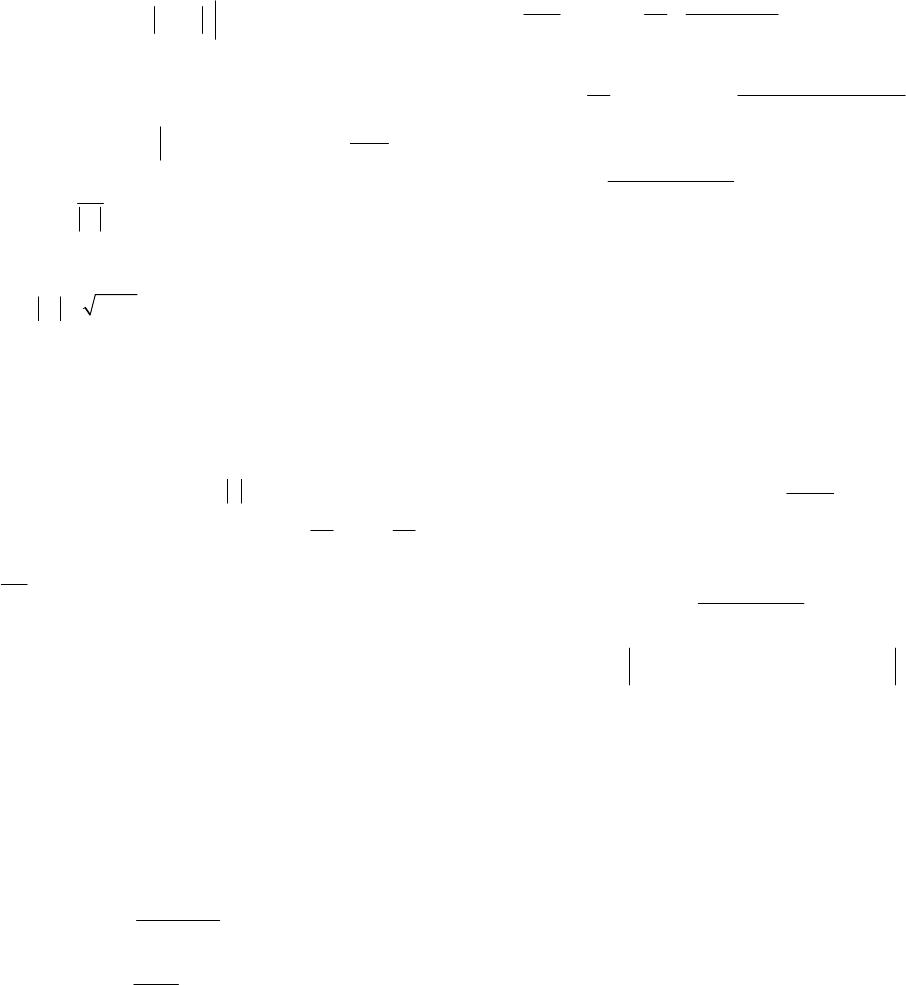

A. A. PASICHNYI, O. A. PRYGODIUK 87
The bound state solutions of Equation (5) must satisfy
the following integrability conditions:
()
2
20,> 0;
r
r
δ
δ
+
→∞
Ψ→r (6)
in the latter case, the condition (6) must be re
following condition:
placed by
()
()
() ()
e
e,
iKr
i
K
f
r
ψ
±
±
Ψ=→ +
Kr
K
rr n
.
K
r
→∞
=K nK
(7)
One can recall that the vector K appearing in Equation
(7) is the wave vector of the knocked-out nucleon:
2.
K
ME==K
2. The Cross Sections of the Nucleus
Electro-Disintegration
om the
In this paper we restrict ourselves to those processes in
which the knockout of protons and neutrons fr
nuclei is associated with relatively small transfers of
energy ω and momentum q from the scattered elec-
trons to the atomic nucleus
A
: 1
M
ω
; 1
q
M
;
1
x
K
M
; In the present approximonteraf
can be quite accurately described the quasi-rela-
ati the inction o
a relativistic electron with a non-point nucleon of the
nucleus
tivistic Hamiltonian of McVoy-Van Hove [1,2], which
takes into account empirically the electromagnetic struc-
ture of the knocking-out non-point nucleon in the form of
relativistic corrections. After carrying out simple calcula-
tions (perturbation theory, the impulse approximation),
the cross section
()
,,
xl ν
σ
′
kk K of knocking out of an
x
-nucleon from the
x
l
ν
-shell of the nucleus
A
by an
inelastically scattered ultra-relativistic electron is pre-
sented in the follow expression [5,7,21,25]:
()
ing factorized
()
()( )()
5
d
,, dd d
xl
xl
ν
ν
σ
σε
′′′
ΩΩ
≡kk K
42
2
2
4,,
, ,,
xl xx xl
MK
eN FqPSG
νμ ν
′′
=×kk kk KqK
k
(8)
where is the proton charge,e
x
l
N
ν
is the number of
x
-nucleons in the nuclear
x
l
ν
-shell,
, , 0, '0, π, θθθθθ
ϕϕ ϕ
′′ ′
′≡ ===
kKk q
(9)
1.791 ,
≡≡
k
1.9
x
xp xn
γ
δδ =− (10)
(11)
() ()
()
()
2
2
22 2
1 0.055;
x
Fq FqFmq
μμ μ
−
≡=+
()
()
()
() ()()
[]
()
2
2
22
2
2
22
2
2
,,
12
11
24
4
2
2
4
4
x
x
xp
x
S
kkM M
q
MM
q
M
μ
μ
γ
ω
δεε
εε
γ
′

−
′′
=++ + 

′




 ′
+
′′
−++






′+
+


kk K
qkk
KkKkK
Kk k
kk
(12)
is a dimensionless, positive definite and continuous
function of the vector arguments
is in this function that the structural features
of the interaction of the scattered relativistic electron and
ocked-out nucle
tonian o
tially di
()
()
,, 1||
x
S′kkK
,,
′
kk K. It
the knon in the quasi-relativistic Hamil-
f McVoy-Van Hove are reflected. Two essen-
fferent functions appearing in Equation (8), which
depend on kinematic variables of the process of the elec-
tro-disintegration of nuclei,
()()
()
22
2
2
,PP
q
μ
θ
′
′′
≡=
kk
kk (13)
and
()()
()
()()()
()
3
2
*3
1
(,)
212π
expd ,
xvl
ml
xlm
ml
G
l
i
ν
ψϕ
=−
=−
=×
+
K
qK
rqrrr
(14)
exert most comprehensive and determinative [25,2
fluence on the interpretation of various aspects
processes electro-disintegration of nuclei. The function
7] in-
of the
()
,qK
xl
G
ν
depending on the kinematic parameters
and
q
K
defines the distorted momentum distribution of
nucleons in the
x
l
ν
-shell of the atomic nucleus. It is
()
,
xl
G
ν
qK that contains the most complete information
abouynamics of the nucleon in the nucleus force
field
() ()
:
Axx l
Vr
ν
ϕ r appearing in Equation (14) are
the wave function of the nucleon in the bound state;
t the d
m
()
−
()
uous spectrum
field on
final state, the factorization of expression (8) for the cross
x
ψ
Kr is the wave function of the nucleon in the state
of contin.
If we take into account the influence of the nuclear
the motion of the knocked-on nucleon in the
section
()
,, σ
′
kk K is approxim
xl ν
ate. The factorized
expression (8) becomes exact only in the plane-wave
approximation, which is valid when the energy of the
knocking-out protons is quite large. In this case
()
()
ψ
±≈
KrKr
, and
()
,
xl
G
ν
qK transforms into
()
0
xl
G
ν
−qK, which determines the momentum distribu-
( )
exp i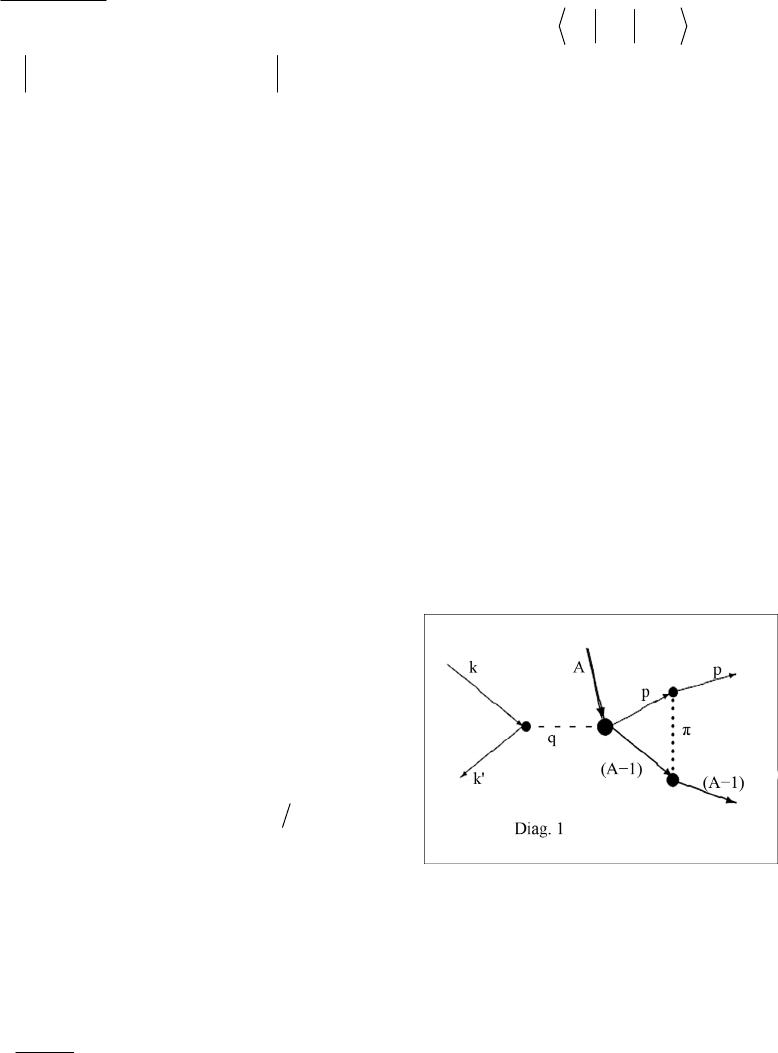

A. A. PASICHNYI, O. A. PRYGODIUK
88
tion of the nucleons in the xvl-shell:
()
()
()
() ( ( ) )
01
212π
exp
ml
G
l
i ϕ
=
+
⋅
x
(15)
3
2
3
d .
xl
ml xl
m
ν
ν
=−
−=
−
qK
qKxx
Here and below the exclusive and inclusive cross
tions of the nucleus electro-disintegration calculate
the plane-wave approximation will be labeled, if neces-
sary, in the graphs, tables and formulas by the symbol 0,
an
of
sec-
d in
d the similar values calculated with taking into account
the interaction of the knocked-out nucleon in the final
state will be labeled by the symbol d. Formula (8) speci-
fies the initial exclusive cross section of electro-disinte-
gration of the atomic nucleus. Experimental verification
of (8) requires fairly laborious experiments in which both
the inelastically scattered electron and the knocked-out
proton are simultaneously registered or identified. At the
moment, a large number of less laborious experiments
are realized. In these experiments one investigates the
energy distributions of inelastically scattered electrons at
certain scattering angles and initial energies of the scat-
tered electrons.
There are carefully developed methodologies taking
into account the inelastically scattered electrons that have
lost their energy in a variety of quantum-electro-dy-
namical [28,30] processes such as bremsstrahlung, birth
electron-positron pairs, etc. If we subtract these elec-
trons from other scattered ones, we obtain the inclusive
cross section
()
, σωθ
′ of inelastic scattering of high-
energy electrons in the process of collisions of ultra-
relativistic electrons and nuclei:
() ()()
,, ,,
u
xl xl
xl
N
νν
ν
σωθσ ωθσ ωθ
′′ ′
==
 (16)
where
xl
xl
ν
ν
x
l
N
ν
is the number of x-nucleons in xvl-nuclear
shell,
()
,
xl ν
σωθ
′ and
() ()
,,
u
x
lxlxl
N
ν
νν
θ σωθ
′′
=
are thlete and specific knock-out cross se
a x-nthe
σω
e comp
ucleon f
ctions of
rom
x
l
ν
-shell of the atomic nucle
partially, filled shells of the investigated
us,
respectively. The summation in Equation (9) is applied to
all, ful
nucleus, and
()
,
xl ν
σωθ
′ is calculated in 0- and d-ap-
proximations by direct numerical integration of the
differential cross section (8) over the total solid angle
Ω≡Ω
ly or
K
of propagation of the knocked-out nucleons:
() ()
d
,,,d.
dd
xl
xl xl
ν
νν
σ
σωθ σ
ε
Ω
′′ ≡= Ω

′′
ΩK
kk K (17)
ing the reaction
()()
,1Aeen A
′−, we can extract
3
Study
realistic information about tic nuclei
in the framework of an investigated model by co
the calculated and measured exclusive (8) and inclusive
(1 sections of t
shell model then the calculations of these cross sections
he structure of atom
mparing
7), (17) differential crosshe electro-disin-
tegration of nuclei. If we restrict ourselves to the nuclear
are associated with labor-intensive computing of the over-
lap integrals:
()
()
()
()()()
*3
,e
expd .
x
i
xlm xx
Ixlm
ixlm
ν
ν
ψϕ
ν
−
≡
=
 
−∞
qr
K
qK K
rqr rr
(18)
These integrals determine the distorted momentum
distributions (Equation (14)) of nucleons in the filled
xvl-shells of atomic nuclei. The deductions an
sions of this paper depend strongly on the numerical
values of the calculated electro-disintegration cross sec-
tio
of nuclear forces is re-
st
the knocked-out nucleon
m
d conclu-
ns of various nuclei. Because of this, the reliability and
correctness [33] of applied numerical methods of the
electro-disintegration cross-section calculation will be dis-
cussed in Appendix A in detail.
Note that the electro-disintegration processes of nuclei
are relatively easy interpreted in the approximation pre-
sented below by the quantum-electro-dynamical Feyn-
man diagram of second order.
If we suppose that the range
ricted then we can assert that the wave function of the
knocked-out
()
>0E nucleon [29] has the asymptotic
form given by Equation (7). The condition (7) mentioned
above once more affirms that
oving in the region of the residual nucleus
()
1A−
scatter itself elastically on this one.
These processes of the nucleus electro-disintegration
are presented on the above Feynman diagram. On this
diagram, we can distinguish the initial electron with 4-
momentum kk
μ
≡, which acquires the status of scat-
tered electron
a
()
kk
μ
′′
with the residua
rese
≡
ts
is p
after emission of a virtual pho-
ton. The virtual photon q is absorbed by one of the
nucleons of the target nucleus and provokes the ejection
of this nucleon from the nucleus. The knocked-out nu-
cleon interacl nucleus in the final state.
This interactionnted on the diagram by a hypo-
thetical exchange meson with 4-momentum π.
In this paper we estimate the dependence of the so-
called χ-sections (see Equation (35)) of nuclear electro-
disintegration from the processes represented below by
the sum of Feynman diagrams of higher order: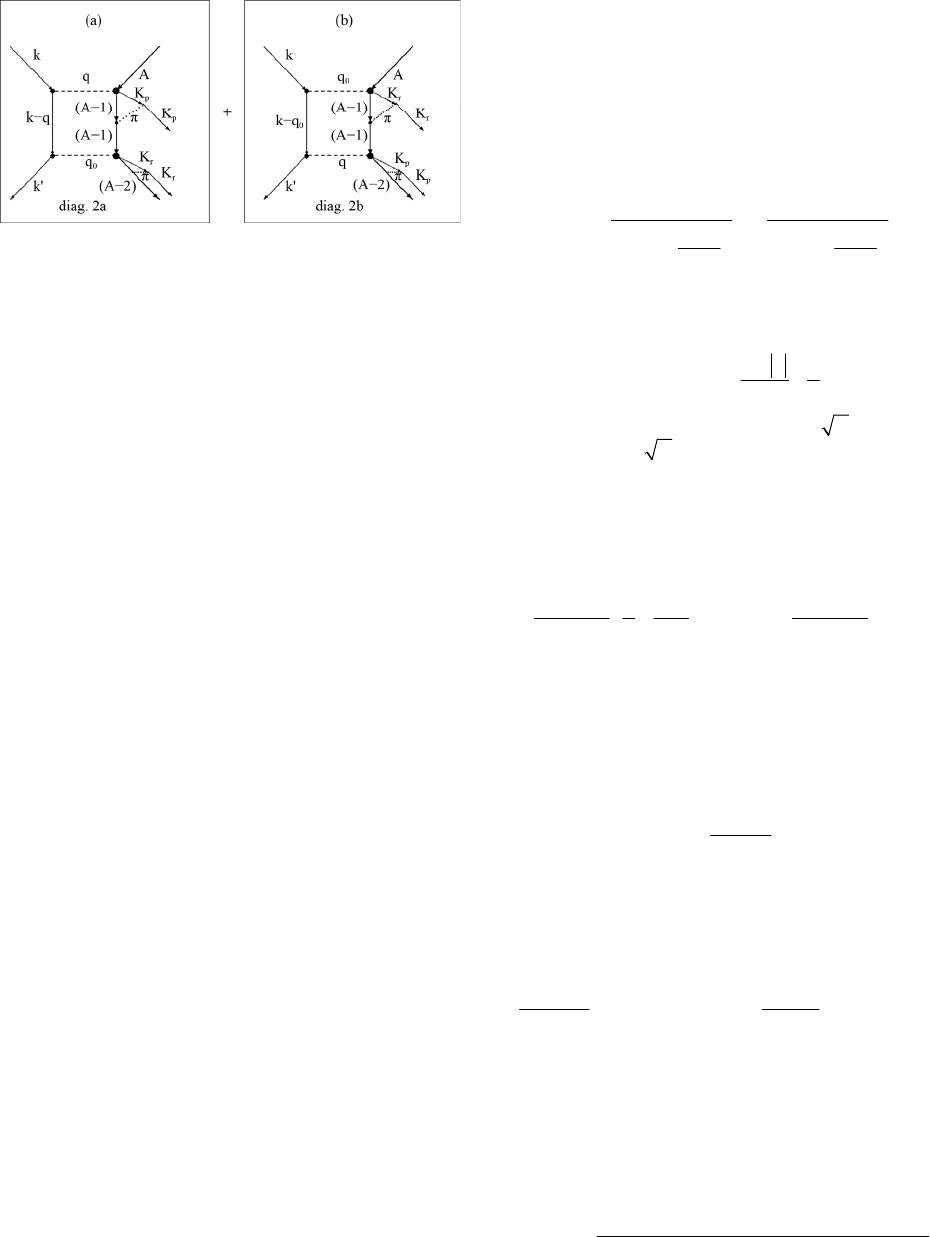

A. A. PASICHNYI, O. A. PRYGODIUK 89
In these diagrams we see new additional participants
of the more comprehensive theoretical interpretation of
the inelastic scattering of high-energy electrons on nuclei.
First and foremost, it is a quasi-real
()
00
qq
μ
≡
oton of the
virtual
photon [25], which is absorb by a prnucleus ed
A
and provokes the transition of this proton in the qua-
si-discrete state Kr of the nucleus
A
or 1
A
−. The
knocked-out protons
p
K
and r
K
interact in the final
state with the residual nucleus. This in shown
schematically in the diagrams by 4-momenta of ππ
teraction is
μ
=
hypothetical mesons. The knocked-out nucleons ex-
change by such a meson with the daughter nucleus A − 2.
The Feynman diagram(diag.2diag.2b) describe the
processes of the two-proton knockout from the atomic
nucleus, which are predicted by the nuclear shell
As we will see later, these processes are also capable to
provide a non-trivial impact on the results of experimen-
tal studies of reactions
()()
,1AeepA
′−.
It is well known that 4-vertex quantum-electro-dy-
namical processes (diag.2a, diag.2b) in general case (if
we substitute 000
,qqqqq
′
→≠ ≠ in diag.2a, diag.2b)
are weakly visible against the backgrounds of the 2-
vertex processes (diag
of
s a,
model.
.1). It is use
s (diag.2a and dia
ful to remind once
again that 4-vertex quantum-electro-dynamical processes
(diag.2a, diag.2b) become apparent only in the case when
in both diagramg.2b) and in, at least,
one of two left vertex of each diagram the electron emits
a quasi-real photon 0
q (0 θ
′=, “0-0”-scattering). It is
the quasi-real photon 0
q that, as we will see subse-
quently, is capable to excite with high probability the
Coulomb resonance in the atomic nucleus.
It is necessary to note that the nucleon knocked out
from the nucleus
A
an participate in the processes of
inelastic scattering on th residual
()
1A− nucleus. For
example, this nucleon can spend a part of its energy for
the excitation of the discrete state of the res
c
e
idual nucleus.
C
c
ng int
is
olliding with another nucleon of the residual nucleus,
the knocked-out nuleon is capable to increase the num-
ber of knocked-out nucleons. Takio account the
process of inelastic scattering of the knocked-out nucleon
on the residual nucleus can essentially complicate the
interpretation of the electro-disintegration processes in
the coincidence experiments.
3. Quasi-Discrete Spectra of Atomic Nuclei
Let us calculate the cross sections (8) and (16) of the
knockout of a nucleon (reactions
()()
,1AeepA
′−). In
the nuclear shell model (LS-coupling) we approximate
the potential
()
Ax
Vr by a sum of two terms:
() ()()
AxWSxpC
VrVr Vr δ =+ . The first term
()
WS
Vr
the short-range Woods-Saxon potential:
() ()
()
0
0
00
,
1exp
>0,
Ax
Ax
WS
Ax x
Vbr
V
Vr rR rR
VV
Θ−
=− ≈−
−−
 
 

≡
1e xpaa ++
 (19)
where:
() ()
00
1
122
x
x
xx
xx δ
+
Θ=− + δ
is the Heaviside unit function;
(20)
3
020br Aa≈⋅ +; 0Ax
V,
a and 3
o
Rr A=× are parameters of the
Saxon potential.
The second term is the lon
lomb potential:
Woods-
()
xp C
Vr δ
g-range Cou-
()
() () ()()
2.
22rrR
Rr
R
2
1
3
C
Vr
Ze 2
21
Ze
rR


− 
Θ−
− 
=− +Θ−








(21)
The wave functions of continuous spectrum can be
obtained in the form of the following series:
n. (22)
()
()
()
()( )()
111
1
11 11 1
111
*
0
4π
lml
l
lmrlmK Kl
lml
iR rYY ψ
=∞ =±
±
==−
=
Krn
()
() ()() 111 1
1
11 1
1
111
0
*
4π
lml Kl
l
lmr lm Kl
lml
Zr
iAY Y
r
=∞ =±
==−
= nn (23)
1K
The radial functions
the half-open space
real and bounded soer
wave equation with
() ()(
,
Kl Kl
ZrAZ rE
λ
=∀
0<r≤∞ in our model are always
tions of the radial Schröding
e real potential
()
Ax
Vr:
)
>0. in
lu
th
() ()
)
()
(
()
2
0 .
ll
rZ r
+
− =

pect (7) de-
termines the asymptotic behavior of the radial functions
22
d1
2
dAx
Zr mE V
rr
λ
λ

+−


(24)
It is useful to remind [31] that the asymptotic behavior
of the wave functions of continuous srum
()
Z
r
λ
:
()
()
() ()
()
() ()
()
()
() ()
() ()
()
;
2
Kl Kl
Kl llll
AZrrb
Zr Sg ifg if
i
λ
;rb Kr
ρρ ρρ
ρ
−
⋅∀ ≥=
−−
∀≤


=+−−



(25)

A. A. PASICHNYI, O. A. PRYGODIUK
90
()
l
g
ρ
and
()
l
f
ρ
()
K
r ρ =
oulomb funct
Here: in Equation (25)
are then [3ions well-know
()
0≠:
4,35] C
()
C
Vr
()() ()()
,, ,,
ll ll
gG fF
ρ
η
ρρ
η
ρ
==
(26)
where
()
2
12
M
ZeE η =− (27)
mb pais the Coulorameter. If , then
()
0
C
Vr=
()()( )
()()( )
0
0
,;
lim
,,
lim
ll l
ll
l
gnG
fj F
η
η
ρρρ
η
ρ
ρρρ ηρ
→
→
=− =
==
where
()
l
n
ρ
and
()
l
j
ρ
are the N
utions (25ion (24)
at the point , we find the coefficients
eumann and Bessel
spherical functions.
Tailoring [12,25,27] the sol) of Equat
rb=
()
() ()
KL L
A
AE:
()
−
−−
≡
()() ()
1,
LL
AE wEiwE
−

=+

LG ZFZ

where

(28)
()) () (() ()
dd,
dd
Kl l L
GZ Kl
Zr G
wE Zr
rr
ηρ
ρ

=−

,
l
G
rb
η
=
;


(29)
()( )() ()()
dd,
,
dd
Kll .
l Kl
Zr F
F Zr
rr
rb
ηρ
ηρ

=−


=
(30
Simple mathematical analysis of the amplitude expres-
sion
L
FZ
wE
)
()
()
l
A
E
−
ing conclusions.
omb reson
in Equation (28) [12] leads to the fol
One can determine the energies of the
Coulances
low-
r
p
NL
EE= from the condition [12]
()
()
()
()
dd,
dd
KL L
Zr G
rr
Z
ηρ 

,
KL L
rG
rb rb
ηρ
  
=
==
(31)
and the half-width r
N
Lp
γ
from the equality [12]
() ()
()
1
d.
2d
L
r
GZ
pNL L
FZ
r
N
L
wE
wE E
EE
γ
−


=

=
Direct mathematical analysis of the expression (28) for
(32)
the amplitude
()
L
()
A
E
reveals [1
magnitude
of the prot
− of the separate radial compo-
nent 2,25,27] the cause of the abrupt
increase of the cross section
in th on resonance energy
()
Kl
Rr
of the
e vicinity
()
, σωθ
′
r
p
NL
e in the
EE=.
We lities (31) and (32) are tru
case when the strong inequality
recall that the equa
() () () ()
22
22
d, d,
,,
dd
LL
GF
GF
ηρ ηρ
ηρ ηρ
ρρ
 
+>>>+
 
 
is valid. When the energy r
LL

p
NL
EE= of Coulo
nance approaches the Coulomb barrier height
()
mb reso-
2
3
C
r
pNL
Vb
E

≥


, the mentioned strong inequality re-
laxes to a more delicate inequality:
() () (() )
22
2
d, d,
,
L
GF
2
,
dd
LL
L
GF
ηρ ηρ
ηρ
 
he Coulhe status of
incipient resonanc
apparent when one calculates spectra of inelastically
peaks of resonances
have moderate heights and rather large half-widths
ηρ ρρ
++
 
 
.
In that case tomb resonances acquire t
es. Such Coulomb resonances become
scattered electrons. In this case the
r
p
l
ν
γ
.
)-(3As an example of application of Equations (24
we present the calculated main characteristics (the ener-
2),
gies
N
Lx
E, the half-widths
N
Lx
γ
and the wave function
amplitudes
N
Lx
A) of quasi-discrete levels of some
atomic nuclei in Table 1. It is important to keep in mind
that these characteristics can depend essentially [12,27]
on the parameters of the Woods-Saxon potential. Ne otic
th
the c
mental aical inv
ockout reac-
tio
9,25,27] that t
functions of transmitted energy
r shell
width)
changed due to the small
at the parameters r0 and a of the Woods-Saxon poten-
tial in the calculations of this article are kept invariable:
01.24r=Fm and 0.55a= Fm. This simplification does
not influenceonclusions of this paper.
Note also that the analysis of the quasi-discrete spectra
(jj-coupling) of the light, medium and heavy nuclei per-
mits to affirm that the nucleus quasi-discrete spectrum is
the natural extension of the nuclear shell structure to the
continuous spectrum region. For this reason, the experi-
nd theoretestigations of quasi-discrete
spectra properties in
()()
,1AeepA ′−-kn
ns of protons are, at the same time, investigations of
the nuclear shell model.
4. The Cross-Sections of Excitation of
Coulomb Resonances
It is well known [12,13,1heoretical inves-
tigations of the inelastic scattering of high-energy elec-
trons predict the resonance structure of inclusive (Equa-
tion (9)) cross-sections as
ω (50 ω ≤ MeV) in the framework of the nuclea
model. The dynamic characteristics (height, half-
resonance peaks substantiallyof
variations of the parameters of Woods-Saxon potential.
For instance, the maximum values of
()
,
lNL ν
σω θ
→′ and
the half-widths lNL
ν
γ
→ of resonance cross-sections
()
,
lNL ν
σω θ
→′ can undergo enormous quantitative
ang huge variations of characteristics of reso-
nance peaks undoubtedly require additional investiga-
tions of this phenomenon.
ches. Such

A. A. PASICHNYI, O. A. PRYGODIUK
91
Table 1. The principal physical characteristics of the quasi-discrete spectra of some atomic nuclei.
NL x ENLx NLx
A
γNLx NLx ENLx NLx
A
γNLx
56Fe; (0; 0)=(63.3 ; 50.55)
pn
VMeV 58Ni; (0; 0)= (62.0 ; 49.3415)
pn
VMeV
2
1.36 10− × 5 3.82 10× 12 3.05 10− × 13n 3 2.02 10− × 7 1.67 10× 14 N 16 6.06 10− ×
14 P 2
1.3 − × 6 1044 6.85 10× 90 1.071− × 014p 1 5.9 − × 7 106 7.151× 014 6.33 10− ×
22 P 15 p 1
81Y; MeV 119Sn;
2.78 15.43 2
1.48 10− × 3.350.76 0.47
()
()
0;0 =54.13 ;41.73V4 pn
()
0
()
;0 =63.3 ; 50.55 pn
VMeV
14 P 3 8.83 10− × 78 3.27 10× 158 3.5110− × 23p 2.26 3 6.0932 10× 7 1.06 10− ×
22 N 2
4.40 10− × 31.58
22 P 16p
3.99
10.31
27 MeV 40Ca;
4
3.15 10− × 31p 3.96 1 2.6415 10× 3 5.09 1× 0−
3.48 22.43 3 8.17 10− × 7.20 2
2.4490 10×4
1.82 10− ×
30 P 4.12 1
1.60 10− × 17n 11.48 5.961 3.34 10− ×
15 P 11.18 2
9.52 10− × 17p 17.64 9.98 1 1.60 10− ×
Al;
()
()
0;0 =63.5 ; 54. pn
V0
()
V
()
0;0 =53.9 ; 42.352 pn MeV
13 P 0.455 3
09.17 1× 8 3.3172 10− × 13n 3− 5.27 10× 4 03.79 1× 10 1.76 10− ×
13 N 0.748 31.20 3 3.2143 10− × 13p 3− 6.06 10× 51 3.93 10× 104 2.02 10− ×
21 P 21 p
208Pb; MeV 198Au; MeV
0.802 22.633
3.0319 10− × 1.56 1 1.77 10× 3 7.54 10− ×
()
()
0;0 =57.48 ;47.4125 pn
V
()
()
0=57.48 ;47.4125 pn
V;0
17 N 3− 8.17 10× 10 9.7110× 23 3.57 10− × 17- - - -
23 P 2
2.70 10− × 100 5.75 10× 202 1.31 10− × 23p 1 6.721 − × 015 3.09 10× 31 2.28 10− ×
16 P 17 n
1.98 9
1.30 10× 18 3.22 10− × 1.39 3 1.88 10× 6 1.25 10− ×
31 P 2.39 5 4.36 10× 11 1.66 10− × 16p 2.86 6 6.8210 ×13 1.41 0− × 1
24 P 7.74 77.53 3 1.16 10− × 31p 2.99 4 1.90 10× 9 9.65 10− ×
18 N 8.30 17.372
3.38 10− × 24p 8.49 1 3.67 10× 3 5.35 10− ×
32 P 9.83 5.001
2.12 10− × 18n 9.81 11.142 8.78 10− ×
17 P 10.06 2 3.7110× 5 8.92 10− × 17p 11.14 2 1.73 10× 4 4.3110− ×
18 P 18.53 22.39 2 3.23 10− × 18p 19.79 15.882 6.67 10− ×
te tht in this cas the location of peaks
re s [25,27] practically unchanged
thample, the microscopical mfica
MeV) of depth
lNL ν
ωω
→
=
gain
tions (4 10− ≤
No ae
main . Note once a
at, for exodi
0
p
V
f
of Woods-Saxon poten
to
tions of the nutial para
of Coulom
almost insurmountable difficulties in the inter-
pr
of thisonance does exist in the crtion given
Eat(16) [27]. Indeed, the predicted values of the
rnaross sectins (which are me s-
ured in experiment) prt depend on the
a nucleus wh
tial can lead
reso-
of varia-
an increase of the Coulomb resonance peak
() ()
,
lNL ν
σω θ
→′ of order of 100200
10 10− times and a
corresponding decrease of the half-width of this
nance of order o100 200
10 10
−−
− times. In this connec-
tion it is necessary to investigate the influence
clear shell potenmeters on the
theoretically predicted measurable values of cross-sec-
tions of excitationsb and centrifugal reso-
nances.
It is worth noting that the absence of inter-compensa-
tive relation between the increase of height of any peak
and the decrease of its half-width would mean the exis-
tence of
resoss secby
qu ion
esonce co
etation of processes of nuclei electro-disintegration in
the framework of the nuclear shell model. However, we
will see that a correlation of high order between the in-
crease (decrease) of the height of Coulomb resonance
and the “adequate” decrease (increase) of the half-width
height and half-width of Coulomb resonances, as we will
see below.
Let us consider an example of the influence of so-
called quasi-real photons [25,27] on the scattering of
()
,
lNL ν
σω θ
→
actically do no
′a
high energy electrons on nuclei. Let us recall that the
quasi-real photons are the result of such collision of a
high energy electron anden the direction of
movement of the electron is practically unchanged after
it (0 θ
′=, “0-0” - scattering): ′
≈
kk
. The energy ω
′
kk
transmitted at such a frontal collision and the value of the
transmitted momentum ′ =−qkk (the energy and mo-
mentum of the quasi-real photon 0 qq= on the Feyn-
man diagrams (the diag.2a and diag.2b)) are approxi-
mately equal. Let us recall also [25,27] that the cross
section
()
, σωθ
′ as a function of the electron scattering
angle sharp maximume point, θ ′ have a at th 0 θ ′=

A. A. PASICHNYI, O. A. PRYGODIUK
92
especially in the region where td energy ω is
not l
()
ωε
′
. Moreover, ry confirms [25,
ransmitte
arge our theo
retica
e
27] that it is the quasi-real photons that gives the main
contribution to the knockout of the protons in the reac-
tion
()()
,1AeepA
′− in the investigated kinematic re-
gion. Scattering of electrons to large angles is barely no-
ticeable in the proton knock-out mentioned above.
The theol interpretation of the inclusive cross-
section
()
, σωθ
′ as a function of ω allows us to
′
confirm that at arbitrary electron scattering angl
θ
()
0 θπ
′
≤≤ or some values of transmitted energy
lNL ν
ωω
→
= one can see sharp and high (10300 b/MeV/sr
and more) peaks on the plots of
()
, σωθ
′. The half-
width
and f
lNL ν
γ
→ of such peaks may be abnormally small
(300
10− MeV and less). These peaks correspond to the
excitation of so-called Coulomb
()
x
p= and centrifu-
gal
()
x
n= resonances in atomic nuclei. Note that the
excitation ef the resonances is equal to the sum of
the binding energy of the nucleon
nergy o
x
l
ν
ε in the nuclear
x
l
ν
-shel
resona
l an
nce
d the energy of the Coulomb (centrifugal)
x
NL
E: r
x
lxNLxlxNL
E
νν
ωε
→=+.
Taking into account properties of the funon
()
,
xl ν
σωθ
′ and properties of the inelastic electron scat-
tering with lNL
ν
ωω
→
= and 0 θ
′≈, one can conclude
that the integral
()
02π
00
,dd,
,
E
r
rur
plpNLpll NL
E
r
r
NL
N
θ
ωδ
ννν
ωδ
σσσωθω
γ
′
+
→→
−
′′
≡× =Ω


(33)
determines le
cti
E
δ
the lower limit of the compte
(
r
)
p
lpNL
σ
→ ν
fic
()
ur
and speci
p
lpNL ν
σ
→ cross-sections of excitation of
the pNL-Coulomb resonance of the investigated atomic
nucleus quite accurately. The limit of integration
over the angle,
upper
, appearing in Eq
is a small quwe restrict ou
value of
0
θθ
′′ =
antity. As a ru
1
le,
uation (33)
rselves to the
0
π
60
θ ≈ during the numerical integration.
The total cross-section of excitation of the Coulomb
NL -resonance r
N
L
σ is equal to the sum
r
N
LplNL
pl
ν
ν
σ
→
= (34)
In the case of low Coulomb NL-resonances this cross-
section is defined the only term corresponding
to the dipole transition: ,
σ
mainly by
L
l
N
ν
= 1Ll=+.
For instanceet us consider the process of inela
scattering the energy 500 ε = MeV
, lstic
of electrons with on
th
tion of the
Ca with the quantum num
d in Table 2. The prot
es of exciton of pNL-
C
f the in
on
e nucleus 40Ca. The results for specific cross-sections
N
L
of excita of the Coulomb reso
40
ur
l ν
σ
→
nucleus
are presente
from di
this nu
nances
bers 13,21NL =
ons are knocked out
fferent occupied shells
()
10,11,12, 20l ν = of
cleus. The dominant position in the excitation of
Table 2. The theoretical predictions of specific cross-sec-
tions →
ν
σ
ur
lNL
and energi ati →
ν
ω
r
lNL
oulomb resonances with quantum numbers NL = 13.21 in
the nucleus 40Ca. The initial energy oelastically
scattered electrons is ε = 500 MeV. The half-widths of that
resances are 13
γ
r
p
= 1.964 × 10−117 MeV and 21
γ
r
p
= 7.51
× 10−3 MeV. The depth parameter of the W
potential is V0p = 53.9020 MeV.
l
oods-Saxon
ν
13
ru
l ν
σ
→, b 13
r
l ν
ω
→, MeV 21l ν →,b 21l ν →, MeV
ru
σ
r
ω
10 2.288 10
× 33.59 8.414 10× 35.54
3−3−
11 1 10 − × 23.59 2 9.12 10− × 25.31
1215.19 12.20 2.19 13.96
20 5 7.55 10− × 9.57 17.98 11.29
1.265
Coulomb resones belongs to the dipole transitions: anc
[
]
[
]
[
]
[
]
1213 ,2021→→ , as follows from the results
given in Table 2.
In this case assumthe radiquantum-
bers are equal
e w
to each ot
e that al num
her: lL N
ν
=
resonance
. One can see
thexcitation oous cusedthe
qupole
that
by e f Clomb a
uadr
[
]
[
]
()
11 13→, octupole
[
]
[
]
()
10 1→
tion again
ike to
]
for the
3, etc.
trnfthe
background on,
for exam chosen
that the abov
ansitios is very diff
of dpole o
ple, that
[][
ur
e inequality
rbitrary
icult or obs
We wo
[][
ur
σσ
→→
1 .
ervast
ines.uld lmenti
]
θ
′
12 1310 13
parameters of the model. At the same time, it is possible
may be strongly weakened or
even violated for a

Let us assume that the radial quantum numbers are not
equal now: lL
N
ν
≠ (usually,1
l
L N
ν
=+). In this case
the magnitude of ur
lNL ν
σ
→ is significantly smaller as
compared wi lL
N
th the case of
ν
=.
The effect considered above may be a starting point
for the interpretation of the phenomenon of gigantic di-
pole resonance in the nuclear shell
model. Thus, the investigation of the inelastic scattering
of high-energy electrons in the region where the trans-
mitted energy is not large e
he framework of t
can bused for studying the
ph
that thelts have to
comm
nd on e choice of the nu-
cl
enomenon of gigantic dipole resonance. It is interest-
ing to note above resu some extent
general character andon quantum nature.
These results do not depeth
ear target and the energy of the scattered ultra-relativ-
istic electrons. For instance, let us consider the excitation
of the Coulomb resonance with the quantum numbers
[NL] = [12] in the nucleus 12C when a proton is knocked
out from one of two filled shells
[
]
[
]
[
]
()
10,11l ν =. The
initial energy of the scattered electrons is 2020 ε =
MeV. It follows from the data of Table 3 that the excita-
tion cross-section
[][]
11 12
ru
pp
σ
→ substantially exceeds the
cross-section
[][]
10 12
ru
pp
σ
→. Let us note that the cross -
se ctions of exitation of Coulomb resonances as well as
the role of quasi-real photons increase significantly with
an increase of the initial energee
ε
of the scattered

A. A. PASICHNYI, O. A. PRYGODIUK
93
Table 3. Main physical characteristics (energies 12
r
p
E
, maximum amplitudes 12palf-widths 12
r
A, h
γ
r
p
) of the Coulomb
resonance NL = 12, specific cross-sec energies→
ν
ω
lNL
of excitation of the Coulomb resonance NL = [12] in
the nucleus 12C versus the depth V0p of the Woods-teal. The initial energy of the inelastically sattered electrons is
ε = 2020 MeV.
12
r
p
E, MeV
tions
Saxon pontic
→ ν
σ
r
lNL
and
12
r
p
A
12
r
p
γ
, MeV 11
ru
σ
→1210 1211 12
, b , b , MeV
ru
σ
→
r
ω
→0MeV p
V
0.0062 13 6.85 10× 29 6.36 10− × 540.4 2.705 16.71 61.412
0.182 750.8 2.81 539.98 2.654 16.48 60.5
2.090 5.23 0.169 570.2 2.52 15.24 56.0
6
8 10− ×
electrons [25,27]. We note lso that the enon of
the aus increase of the scattering cross-section
caused an increase of the
initialy of the electroeam may have significan
influe the results oinvestigation ofrious as-
pects of nuclear structure. For instance, the results of
do not require additional comments.
i-
re
determin
aphenom
nomalo
by quasi-real photons with
energ t n b
nce onf va
experimental measurements of different cross-sections of
inelastic electron scattering can essentially depend on the
target thickness.
As an additional illustration of the above statements, in
the Table 4 we present the calculated values of specific
cross-sections of the Coulomb resonances excitation in
the heavy nucleus 198Au for two initial energies of scat-
tered electrons: ε = 2020 MeV and ε = 3365 MeV. The
results of Table 4
We would like to attract attention the fact that the
inclusive cross-sections
()
, σωθ
′ have the form of
sharp resonance peaks at certain values of the transmitted
energy r
lNL ν
ωω
→
=. Note that the theoretically predicted
enormous heights and insignificantly small half-widths
of
()
,
r
lNL ν
σω θ
→′ give no possibility to determine d
ctly the shape of the Coulomb resonances in experi-
ment. That is why we cane only integral char-
acteristics of the Coulomb resonances, such as the cross-
sections r
p
lpNL ν
σ
→
the physical experim
of excitation of these resonances, in
ent.
Let unce again [25,27] that the physical cha-
racteristics (the half-widths r
s recall o
N
Lp
γ
and the amplitudes
(
N
Lp
A) of the wave functions) of Coulomb resonances
can undergo essential changes. For example, the sharp
decrease of r
N
Lp
γ
and the equally drastic increase of
N
Lp
A) is possible even at nee changes of parame-
te
cr
on of
we
pende
gligibl
rs of nuclear shell model potential. This uncertainty
raises the question whether theoss-sections of excita-
ti Coulomb resonances undergo essential changes
too. Table 5 gives an answer to this question.
In Table 5 present the calculated functional de-
nce of the most important specific cross-sections
r
p
lpNL ν
σ
→ of excitation of resonances of nucleus 40Ca.
These cross-sections are interpreted as functions of the
half-width of Coulomb resonances, which varies with the
change of the depth 0
p
V of the Woods-Saxon potential.
used by the dle transition[13], [20] →21]
h, in tuused by ine-
astic scattef ultra-relac electronsnu-
leus 40Ca.
The resulted in ble 5 do quire
extensive comments as well. The specific cross-sections
ca ipos [12]→[
whic
l
rn, are ca
ring o
quasi-real pho
tivisti
tons in
on the
c
ts presenthe Ta not re
Note that the specific cross-sections mentioned above are
of the Coulomb resonance excitation ru
p
lpNL ν
σ
→ and the
n energies r
lNL ν
ω
→ are practically invariant
when the half-widths and the amplitudes of the wave
function of Coulomb resonances change substantially.
This result is very imrtant. It essentially increases the
chances of success for the nuclear shell model in the
excitatio
po
lusive Cross-Sections
lf-widths of the
b and cenifu-
ly less thahe
hac peaks. At the
scattered
el
recall that the cross-section at the arbitrary
interpretation of inelastic electron scattering experiments
aimed at studying the nuclear structure.
5. The Inc
()
,′ σωθ
and the Coulomb Resonances
One of the top-priority tasks of this paper is to study the
manifestation of Coulomb and centrifugal resonances in
experiments on inelastic scattering of high-energy elec-
trons. In particular, it is of interest to investigate the pos-
sibilities to disclose and identify Coulomb and centrifu-
gal resonances in the spectra of high-energy electrons
inelastically scattered on various atomic nuclei.
Comparing the Coulomb resonances and the quasi-
elastic peaks, one can state that the ha
theoretically calculated peaks of Coulomtr
gal resonances are, as a rule, considerabn t
lf-widths of the calculated quasi-elasti
same time, the height of a Coulomb resonance peak is
significantly larger than the height of a quasi-elastic peak.
For convenience, such peaks of
()
, σωθ
′ should be
“cut off” on the plots of
()
, σωθ ′ versus transmitted
energy ω. For this reason, we lose clarity and important
information about the observability of Coulomb reso-
nances in the measured spectra of inelastically
ectrons. Taking the logarithm of that function adds very
little information since the microscopical half-width of a
Coulomb resonance can hardly be represented on the
plot.
In order to investigate the possibility of detection of
Coulomb resonances in physical experiment, one should
()
, σωθ
′

A. A. PASICHNYI, O. A. PRYGODIUK
94
Table 4. Specific cross-sections
[][]
→ ν
σ
ru
lNL
of excitation of the pNL-Coulomb resonances with the quantum numbers NL in the
nucleus 198Au. The initial energiese inelastically scatteredectrons are ε = 2020 MeV and ε = 3595 MeV. The parameters
of the Woods-Saxon potential are V0p = 51.13 MeV and V0n = 41.734 MeV.
202 ε =
of th el
0 MeV
NL → 23 16 31 24 17 18
l ν  23
ru
l ν
σ
→, b 16
ru
l ν
σ
→, b ru l ν
σ
31→24 17 18
, b , b , b , b
ru
l ν
σ
→
ru
l ν
σ
→
ru
l ν
σ
→
10 2
2.42 10− × 6 1.28 10− × 2 1.97 10− × 3 1.89 10− × 6 3.73 10− × 4 1.45 10− ×
11 1 2.57 10− × 5 6.04 10− × 1 3.67 10− × 2 2.4110− × 6 5.97 10− × 5 4.28 10− ×
12 1.20 3 2.91 10− × 1 3.00 10− × 1 2.29 10− × 4 2.12 10− × 4 7.32 10− ×
20
13
21
6.
5.
8.
M
2
9.82 10− × 8 8.81 10− × 1.88 3 4.54 10− × 5 8.49 10− × 3 1.42 10− ×
3 .821
1.31− 10×1 3.10 − 10×1 7.22 − 10×3 6.50 − 10×3 2.620− 1×
4.08 6
0− 1.03 1× 5.71 1 0− 1.16 1× 4− 1.20 10× 3 0− 3.59 1×
14 45.3 733 3.19 10− × 4.49 1 2.21 10− × 2 1.49 10− ×
22 498.0 5 1.04 10− × 108.3 394 7.4110− × 3 7.67 10− ×
30 3 1.81 10− × 12 3.60 10− × 596.3 3 1.23 10− × 3 2.10 10− × 3 9.15 10− ×
15 1
2.02 10− × 665.5 7 5.22 10− × 43.53 891 3.57 10− ×
3595 ε = eV
10 0.077 6
4.07 10− × 2 6.27 1× 0−3 6.02 10− × 5 1.19 10− × 4 4.66 10− ×
11 0.817 4
1.92 1× 0−1.17 2 7.68 10− × 5 1.91 10− × 4 1.37 10− ×
12 3.81 3
9.22 10− × 1− 9.52 10× 1 7.27 10− × 4 6.75 10− × 3 2.34 10− ×
20 0.311 7 2.79 10− × 5.95 2 1.44 10− × 4 2.70 10− × 3 4.53 10− ×
13 12.1 1− 4.15 10× 1 9.81 10− × 2.29 2 2.06 10− × 3 8.36 10− ×
21
28
12.9 6 3.25 10− × 18.0 1 3.69 10− × 4 3.81 10− × 2 1.14 10− ×
14 143.0 21.2 2
1.00 10− × 14.2 1 7.00 10− × 2 4.75 10− ×
22 1566.0 5
3.28 10− × 341.1 17.03 2.34 10− × 2 2.43 10− ×
30 3 5.67 1× 0−11 1.13 10− × 1876.0 3 3.87 10− × 3 6.63 10− × 2 2.90 10− ×
15 0.636 2093.06 1.64 10− × 137.3.1 1.13
Table 5ecific cross-sections and enegies ocitation of the Coulomb resonans with the quaum
number3,21] in the nucleselascat electrons versus te resonance half-wth
. Sp →
ν
σ
ru
lNL
40Ca at in
r→
ν
ω
lNL
tering of
f excent
s [1utic shid
γ
r
NLp . The initial
energy e electrons is ε = 500 MeV. The angle of scattering is θ
, MeV
of th' = =0.
12
σ
13
ru
→, b12 13
r
ω
→ 13
r
p
γ
, MeV , Me
20 21
ru
σ
→, b 2021
r
ω
→V 21
r
p
γ
, MeV 0MeV
p
V
1 12.20 17.98 11.30 53.908 5.19 294
1.116 10− × 3 7.41 1× 0−4
15.19 12.20 53.9050
15.19 12.20 117
1.964 10− × .98 11.29 3 7.51 10− × 53.9020
15.20 12.19 38
2.935 10− × 17.98 11.27 3 8.46 10− × 53.8400
15.22 12.18 25
6.10510− × 17.97
151
4.688 10− × 17.98 11.29
17
11.48 53.7500
15.31 12.10 18.00 11.19 53.2000
3
7.46 10− ×
2
1.00 10− ×
11
10− ×3.392 2 10− × 2.41
15.52 11.87 6
3.680 10− × 18.47 10.65 2 9.22 10− × 52.0000
15.60 11.87 5
2.917 10− × 18.90 10.64 1 1.40 10− × 51.5000
point
)
is meaxperimentally by means
of ”av” proced
(
, ωθ
′sured e
eraging'ure:
() ()()
′
0E
ω +Δ
0E
x
ω
−Δ

1,dd
2
x
xx
x
E
σςωθσωθω
Ω
′′
=Ω

Δ⋅Ω
(35)
Here
,,
;
2
ωθ
′
x
E is the spectral widtof gap -
eter. Note that
Δh of the scat
tered electron spectrom
()
,
ς
ω
fficiency of registration
of sc
we su
assu
θ
′ is the
ctionat determines the eof
d electrons at various anles
ne . Hereinafter
in this papwe
fun
the scattere
th
rgie
)
1 =
g attering θ
′
that
the
and es ε
′=−
εω
her on
ppose
(
, ςωθ
′. Furter me that

A. A. PASICHNYI, O. A. PRYGODIUK 95
strong inequality 2
NLx x
E
γ
Δ
vy
stance is connected wi
t
(
0.5 MeV γ
h
2
is true.
worth n
nuclei in our model. This
circumth the existence [27] of the
so-called incipien
)
Coulomb
resonances. When tsible that
the inequality
It isoting that this inequality may be broken in
the case of medium and hea
2 MeV
NLx
≤≤
ey take place, it is quite pos
N
Lx x
E
γ
≈Δ mentioned above ma
brnd e
y be
oken aven inverted: 2
N
Lxx
E
γ
≥Δ . In the calcu-
lated cross-sections the parameters of Wxon po-
tential were chosen so that the inequality 2
oods-Sa
N
Lx x
E
γ
Δ
was true for the most of investigated cases.
Consequentlyrons losing their energy lNL
ν
ω
→
00
<
, the elect
()
<
x
lNL x
E
ν
ωω
→+Δ during the excitation of
a Coulomb resonagistered a
E
nce will be re
ω −Δ
the en
s electrons with
ergies in the interval
00
x
x
EE εωεεω
′
−−Δ≤≤−+Δ
. In this case the “regu-
larized” cross-section
()
,
reg
σωθ
′ can be theoretically
determined as
() ()
1
,,dd.
2
x
E
reg
xx
E
ω
ω
σωθ σωθω
+Δ
′′′
=Ω

Δ⋅Ω (36)
It is necessary to note that the proposed above regu-
larization practically does not change the fu
regions of its smooth variation. In this co
xx
E−Δ Ω
nctions in the
nnection, for
exam
nces and may have values
comparable with the height of th
be done i
solated Coulomb resonance in the
specified energy interval
ple, we have:
()
() ()
00
,,
reg
σωθσωθ
′′
≈;
>60MeV.
This “regularized” cross-section has resonant form in
the area of Coulomb resona
e quasi-elastic peak. Our
further conclusions willn the assumption that
we have only one i
()
()
,
dregd
σωθ
′
≈
()
,for: σωθω
′
2
x
EΔ
.0
r these co
. In the following
suppose that MeV for all experiment
various kinenditions we get pre-
di
es of inelastic scattering of
electrons. In this case photons emitted by
rel
pola
one studie
electrons is
is
the id
ented plot that
we
s with 21
x
EΔ=
matics. Unde
ctive plots of experimental cross-sections
()
,
reg
σωθ
′
of inelastic scattering of high-energy electrons on nuclei.
In the examples presented below we will investigate
relatively large angl
()
01
θ
′≈
the virtual
ativistic electrons have relatively large
()
22 2
m ω −q
imaginary masses. This fact manifest itself, first of all, in
reduction and disappearance of the dominant role of di-
pole transitions during the excitation of Coulomb reso-
nances. Dipole, quadrupole, octopole transitions and tran-
sitions of even higher multi-rity should be taken into
account whens the spectra of inelastic large-
angle scattering of high-energy electrons.
Very often the scattering of high-energy
investigated with a carbon (12C) target. This light nucleus
selected as standard for comparison of the efficiency of
different kinematics inentification of Coulomb
resonances in the spectra of inelastic scattered electrons
(Figure 1). One can see from the pres,
using the kinematics [15], one cannot observe the Cou-
Figure 1. The inclusive and “regularized” cross-sections
of inelastic scattering of electrons on nuclei 12C
initial energy of scattered electrons ε and the
scattering . The kinematics of scattering is
in fulfilledriments [15]: ε = 500 MeV, θ' =
MeV,' = 37˚ (b); ε = 730 MeV, θ' = 37˚
MeV, = 50.1˚ (d). The parameters of
Woods-Saxon potential are: V0p/MeV = 61.412, V0n/MeV =
55.684. Here and hereinafter the solid and the dashed
curves were calculated, respectively, with allowance for the
final-state interaction (regularized cross-sectins, [(14),(36)]),
and in the plane-wave approximation (15).
lomb resonance with quantum numbers , which
is theoretically predicted by the nul, in
be empha
corre-
sponds to the height of theperirmined
()
′
reg
σω,θ
versus the
angle of
selected as
60˚ (a); ε =
(c); ε =
′
θ
expe
θ
θ'
537
779.5
12NL =
clear shell mode
the spectra of inelastically scattered electrons. It should
sized that this conclusion is wrong in the case
of other kinematics presented on Figure 1. It is also
pertinent to note that for the disclosure and identification
of the resonances of the nucleus 12C with the quantum
numbers 12NLx p= and 12NLx n=, it is necessary to
carry out more thorough experimental measurements in
the spectral region of interest, having essentially reduced
the step of the argument ω Δ.
It is worth noting that the height of the regularized re-
sonance peak on the graphs of reg σ
()
, ωθ
′
mentally dete ex
cross-section if the energy gap width of the recording
device of scattering electrons is, as indicated above,
21
x
EΔ= MeV. At the same time, the width of the re-
sonance peak is equal to the theoretically calculated width
of the investigated resonance. It is necessary to empha-

A. A. PASICHNYI, O. A. PRYGODIUK
96
size that the height of the Coulomb resonance essentially
depends on the width of the energy gap of the recording
device of for instwidth of the energy
gap of spectrometer is equal to 5 MeV, then the possibil-
ity of manifestation of Coulomb resonances in the spec-
tra of inelastically scatterlec
electrons. If,ance, the
ed etrons strongly decreases.
tering
heights o
One can conclude from Figure 1 that decreasing the
initial energy ε and the angle of scatof elec-
trons improves the conditions for observation of Cou-
lomb resonances in the spectra of inelastically scattered
electrons. Let us remind that the theoretically predicted
f Coulomb and centrifugal resonances are com-
parable with the height of the quasi-elastic peak.
Note that the Woods-Saxon potential depth parameters
(0
θ
′
p
V and 0n V) giving the highest accuracy were used, as
a rule, in our calculations. The half-width γ12 of a Cou-
lomb resonance essentially increases (see Table 3) with a
decrease of the depth of the Woods-Saxon potential. In
this case the theoretically calculated Coulomb resonance
12NL = is widened so much that its half-width can
considerably exceed the spectral energy gap of the spec-
trometer 2
x
EΔ. In this case the height of inciient Cou-
lomb resonance decreases and this resonance can be iden-
tified directly in spectra of inelastically scattered electrons.
Figure 2 shows theoretically calculated regularized
cross-sections
()
,
reg
σωθ
′ of inelastical scattering of
electrons and experimentally measured cross-
p
sections
ne c
heavy nucle
()
, ωθ
′ of electro-disintegration on different nuclei
()
27 58198
,Al,i,Au. The kinematics of the experi-
ments is borrowed from [20].
Analysing the calculated
()
,
reg
σωθ
′ (solid line) and
()
0,
σωθ
′ (dashed line; plane wave approximation), we
can observe some peculiarities of identification of Cou-
onances in the spectra of inelastically scattered
electrons in the framework of nuclear shell model. For
example, an conclude that the Coulomb resonances
may be registered in all considered cases. But careful and
painstaking measurements in the kinematics region in-
σ
12 C N
lomb res
o
ter
width
ν
esting for us were not presented in [20]. Note also that
in the case of i we have a large number of
Coulomb, centrifugal, and incipient (with large half-
12
lNL
γ
→
the theoreti
≈÷ MeV) [27] resonances. In this case
of the full resonance picture of
cross-section
()
,
reg
σωθ
′ beco
cal analys
Figure 2. Regularized cross-section σreg(ω, θ') of inelastic
scattering of electrons on the nuclei 12C, 27Al, 56Fe, 198Au
versus the transmitted energy ω. The initial energy of the
scattered electrons is ε = 2020 MeV, the angle of scattering
is θ' = 15˚.
is
complex.
sections
mes more
presented Finally at the Figure 3 arecalculated cross-
()
0
,
reg
σωθ
′ for different nuclei (A1, Mg, Ca,
Ni) and for the different kinematics: the initial energies
of scattered electrons 779.5;500;545;500 ε = MeV and
the angles of scattering
θ
′ = 50.1˚; 60˚; 45˚; 60˚. The
results of calculations presented on Figure 3, in general,
do not contradict to the conclusions based on analysis of
results presented at Figures 1 and 2. We can, however,
state a fact that qualitative and quantitative comparisons
of theoretical calculations and experimental data and
Figure 3. The cross-sections σreg(ω, θ') of inelastic scattering
of high-energy electrons on nuclei 27Al, 24Mg, 40Ca, 58Ni as a
functions of the initial energy of scattered electrons ε and
angle of scattering θ'. Kinematics of scattering agrees with
kinematics of experiments [9,15,22]: MeV, θ' =
50.1˚ (Al), ε = 500 MeV, θ' = 60˚ (MgMeV, ε =
545 (Ca). The parameters of Woods-Saxon potential are: Al:
V0p,0n = 63.5; 54.0 (MeV); Mg: V0p,0n = 68.674; 60.1 (MeV);
Ca: V0p,0n = 53.9; 42.352 (MeV); Ni: V0p,0n = 62.85; 49.342
(MeV).
= 779.5 ε
,Ni); ε = 545

A. A. PASICHNYI, O. A. PRYGODIUK 97
moreover the conclusions from such comparison are im-
possible at the moment. The reason is that experimental
data and theoretical investigations are practically absent
for the declared above range of transmitted energies.
6. Quasielastic Peaks and Orthogonality of
Wave Functions
The interpretation of inelastic scattering of high-energy
electrons and the reaction
)
considered
here in the frames of nul, despite of
simplicity, remains self-consistent quantum-mechanical
problem in the theory of nuclei. The main reason and
decisive argument for this statement is such well-known
property as the mutual orthogonality of the wave func-
tions [7] of discrete and continuous, including the quasi-
discrete, spectra. Notice that the term “orthogonal func-
tions” in aspect of interpretation of processes of elec-
tro-disintegration of nuclei by the high-energy electrons
was unambiguously used in [7]. In addition to stated in [7]
one may note that it is very difficult to imagine quan-
tum-mechanical theory of quantum transitions as well as
based on it theory of inelastic scattering withoum-
()(
,1AeepA
′−
clear shell mode
t co
plete orthogonal basis of wave functions of investigated
quantum-mechanical system. We emphasize also that the
conclusions below are based only on the postulates of the
nuclear shell model and may be used for the investigation
of different aspects of this model.
In order to illustrate the role of orthogonality of wave
functions in the theory of electro-disintegration of nuclei,
let us consider the process of small-angle (θ' = 15˚) and
very small-angle scattering (quasi-real photons phenome-
non: 1
m ω
θεε
′′
). Let us now calculate the cross-
sections
()
,1 σωθθ
′′ of inelastic scattering of high-
12 al
at the dominant position in the
iables,
energy electrons on nucleus C for two values of initi
energy of electrons, ε = 500 MeV and ε = 2020 MeV.
First, let us remind th
expression for the exclusive cross section belongs to two
functions of kinematical var
)
(Equation
(13))) and
()
,
xl
G
ν
qK (Equation (14))). It is more than
appropriate mention here that the latter one is determined
by overlap integral:
()
()
()()
()
(
,P′
kk
()
*3
,expd
xlm xxlm
x
Ii
νν
ψφ
−
−∞
= qKrqrr r
K.
Taking into consideration the formula cited above, in
an early stage of our analysis let us suppose that 0=q.
Therefore,
()
exp 1i=qr . Then, due to the orthogonality
condition of the wave functions of discrete and continu-
ous spectra,
()
0
,0
xlm x
I
ν
== q
qK . It should be noted that
this case
()
0=q is unacceptable. If 0=q then ine-
lastic (and elastic) scattering is impossible.
Second, let us now suppose that 1 R− =q. In this case
()
exp 1iqR ≈ (R is the radius of the nucleus) and
()
32 ,1
xlm x
RI
ν
−qK . This latter case
()
0≠q is
possible. In this case the losses of momentum and energy
of the scattered electron must be minimal. If the value of
transmitted energy ω is fixed then the minimal value of
transmitted momentum takes place at the minimum angle
of scattering (0 θ
′=, quasi-real photons). As this is the
case, ω ≈q. And, as a rule, the inequality
22
1
ω

−q takes place as well [25,27].
2


The minime of the energy necessary for the
ofr
ω

excitationesonances is practically defined

al va
Coul
lu
omb
ω
by the minimal excitation energy of the lowest Coulomb
resonance, pNLx l
E
ν
ε +, where
x
l
ν
ε is the proton en-
ergy in the highest filled nuclear shell. Hence, the ine-
quality 1 R− q may be satisfied with reasonable ac-
curacy. The numerical estimates for ttigated nu-
clei lead to the fog result:
he inves
llowin 1
min 0.05
F
m− ≈q. So, it
is natural that the inequality 1 R− q, in turn, leads to
the inequality
()
32 ,1RI −qK , which has already
been ment
xl ν
g ou
f in
is ph
m x
ioned.
Thus, restrictinrselves only with the analysis of
ph
ease o
ction oe
d small scattering a
hat th
because the p
enomenon of orthogonality of wave functions of dis-
crete and continuous spectra, we may predict decrf
the cross-selastic scattering of high-energy
electrons. This decrease takes place at small transmitted
energies ω anngles
()
1 θ ′ of elec-
trons. Note tenomenon is cauecreasing
of distorted momentum distribution
)
xl
G
ν
. In the
case of plane-wave approximation this state
sed by d
()
(
,
dqK
ment is wrong
lane wave
()
exp i
K
r is essentially nonor-
function of bounded e
proton in the considered kinematical region.
Let us recall that the expression for the cross-section
()
, σωθ
′ has dimensionless factor
()
,P′ kk that, as it
well known [25,27], is large in the mentioned above
region. Just the function
()
,P′ kk due to nonorthogo-
nality of
()
exp i
thogonal to the w of thave state
K
r and
()
xlm ν
ϕ r will lead to unac-
ceptabl values of cross-section in plane-y hugewave ap-
proximation. A to draw an
unambiguous conclficance of
ta of
ulations
rons
ri (NL = 12
sually ob
ctions calculated in
fily exceed calculated
with taking into account of inknocked-
nd just this factor allows us
usion concerning the signi
king into account of orthogonality wave functions of
discrete and continuous spectra.
The phenomenon of orthogonality of wave functions
in our calcrepresented on Figure 4, where
plotted the cross-sections
()
, σωθ
′ of inelastic scatter-
ing of elect on nucleus 12C. The parameters of
Woods-Saxon potential were chosen in such way that the
Coulomb (NL = 20, 12) and centfugal ) reso-
nances have relatively large viserved half-width.
The cross-sethe plane-wave ap-
proximation signi
)
()
is
cant
(
,
d
σωθ
′
teraction of the

A. A. PASICHNYI, O. A. PRYGODIUK
98
Figure 4. The cross-sections σ(ω, θ') of inelastic scattering of electrons on the nucleus 12C versus the transmitted energy ω.
The parameters of the Woods-Saxon potential: V0p = 53.7 MeV, V0n = 51.0 MeV; the initial energies of the electrons: ε = 500
MeV (a, b); ε = 2020 MeV (c); the angles of scattering are: θ' = 15˚ (a); []
−
′′
9
310 mω
εε
θ =×  (b, c).

A. A. PASICHNYI, O. A. PRYGODIUK 99
out nucleon in the final state, see Figure 4. Note that
after some doubts and speculations the reader cannot
disturb himself and fear of unusual units (Gb, Tb) that
appear at the Figure 4. These units will be usual and
natural units in the near future.
The plane-wave cross-sections have huge, nonphysical
magnitudes in the region of the quasi-elastic peak. This
fact is a convincing proof of the necessity of taking into
account the interaction of the knocked-out nucleon with
the residual nucleus in the final state.
7. Coulomb Resonances, Quasi-Real Photons
and χ-Experiments
In this section we will attempt to interpret some new
aspects of experiments on investigation of exclusive cross-
sections [10,15,23] basing on the results above. These
new cross-sections
()
6
d
ddd d
miss
EE
σ
χε =′′
ΩΩ
(37)
depend on the energy lost in processes of scatter-
ing and re-scatteringinelastically scattered elec-
tron and the knocked-ough-energy proton in the initial
and final states. In sueriments one fixes the cases
of simultaneous regiof scattered electron with the
energy and knoc proton with the energy
MeV). As ts place, we can ea
perimente lost energy :
. Thes ofesented
weaknce pl
e nucle
mum
convenient interpretation of the minimal lost energy is
is the binding energy at the upper
s
miss
E
of the
t hi
ch exp
stration
ked-out
his take
ally th
plot
resona
us 12
at E
40 M
0
miss
rk of n
ε
′
0
ine ex
,23]
the case of t
har
mum a
()
s
in th
E
sily
in
e, in
()
miss
ooth
ost
(10E≈
determ
εε
′
=+
[10, 15
have a s
max i -
mis
χ
With
miss
E
()
pr
For exam
nction
MeV and a sm
same tim
.
ode
miss
EE +
have
h
p maxi
t E
0 <EE≈∀
e
miss E χ
nature.
the fu
17
At the
MeV


clear shell m
C
miss
eV.
17E≈
u
E χ
e,
l the m
≈
miss ≈
miss
framewo
11
h
miss
E ε =,
filled shell
If E
11 >0
h
ε
of nucleu
h
12 C.
>
miss l
ν
ε , then additional losses of energy
h
lmiss miss
EE
ν
ε Δ=
or several p
re: strong
he
−
one he
ena a in
with tresidual nucleus
h
miss missl
EE
ν
ε Δ= −
knocked-out proton
in strong interaction [15,16] of the
with the residual nucleus in the finite
state. Note that in this case we suppose that the probabil-
ity of inelastic re-scattering of the weakly interacting
high-energy electron on nucleons of the residual nucleus
or another nucleus of the target is negligible.
Let us suppose that one of the protons of an upper
shell of the nucleus receives the energy after
an act of collision with a high-energ This
proton with the energy
ωεε
′
=−
y electron.
h
p
l
E
ν
ωε =−
scattering on
ords, the knoc
t the part of acqu
ttering
s. The knockin
ent, for instan
-out nucleons i
cleons, etc. Let u
ering of knocki
portant role in
at these processe
retation of processe
c nuclei in co
propose anothe
ditional losses
can participate in
residual A
king-out stro
ired energy
on that 1A−
out strong
ce, the pa
residual nucleus or inc
the processes
s suppo
ng-out proto
our investig
s can esse
s of electro-
ncidence ex
r alternative in
of energy in
the processes of inelastic
nucleus too. In other w
interacting proton spen
processes of inelastic re-sca
other A atomic nucleug-
teracting proton may sp
energy for the excitation of
the number of knockingn
collisions with other nu
the processes of re-scatt
the finite state play an im
Then it is evident th
complicate the interp
disintegration of atomii
ments. We intend to
pretation of origin of ad
()
1−
ngly
in the
()
or
ly in-
rt of its
rease
of
se that
ns in
ation.
ntially
peri-
ter-
χ
-
anoma-
used
experiments [10,15,2proceed from
lously large values of thoss
by quasi-real photons (
We noticed above that in the analyzed experiments the
coincidence of two particles was recorded. These parti-
cles are: the inelastically scattered electron and
knocking-out (it is very desirable that just by t elec-
tron) proton Using simple empirical concept one
can state thatocking-out of proton from someeus
unambusly testify that the scattere
e insider in the immediate vicinity) of thnu-
s. It is nifficult estimate the length mean
path of istic electron inside ofleus
ing thoss-section of excitation of b re-
ce in s by electrons with trgy
As a sult of the estimate we can assert
hierg in the prollision
leus re or after of knockooton
te tb resonance is (or
another) nucleus with large probability.
Previously developed theory [12,25,27] of Coulomb
resonances and presented above estimates based on the
calculated data of cross-sections of excitation of Cou-
lomb resonances stimulate us to state such hypothesis in
contrary to primordially widespread opinion: the lost
energy in experiments [10,15,23] is the energy
that is u for the excitation of discrete, quasi-discrete
and continuous spectra of investigated nucleus but namely
3]. Let us
e scattering cr
0
′=, “0-0”
the
-sections ca
- scattering). θ
k′
his
ion
nucl
d electron
is
of
nuc
om
e ene
of pr
th
K.
kn
iguo
(o
ot d
relativ
e cr
nucleu
MeV.
gh-en
12C
he C
12 C
resid
cleu
free
know
sonan
ε =
that su
with
may
λ
this
Coul
h
cess of co
ut
in
12C
re
y electron
befo
om
779
ch
nuc
exci oul 12NL =
may be interpreted as the result of
nomena listed below. These phenom-
teraction of the knocked-out proton
1
A
− in the final state [15,16],
which is accompanied by excitation of this nucleus; the
knocking-out of protons out of deeper filled nuclear
shells; losses of energy of the scattered electron in initial
state; accidental coincidences that are caused by the
existence of intensive background of protons, the source
of which is [25] the scattering of high-energy electrons
caused by quasi-real photons; the dispersion of the initial
energies of scattered electrons in the incident beams; etc.
At the initial stage of investigations it is reasonable to
look for the cause of additional energy losses
miss
E
sed

A. A. PASICHNYI, O. A. PRYGODIUK
100
by the high-energy electrons. Note that in this case the
main role belongs to quasi-real photons (0 θ
′=, “0-0” -
scattering).
In connection with the hypothesis preseove we
ncesquasi-real
ceirmation.
ent [15] where the iusive cross-
section of electro-disintegratio
12C by hi (MeV) el
tigated. Tmeasuremrely the
ed n
ditiona
elimi-
nary estimate of tsed aux
e e = 100
get contai
22 nucleon are
protons. The Table 3 contains calculatsections
of
1p-shell of this nuc
MeV) electronse the
Cmb reso
nted ab
and
ncl
n of nu
ectr
is me
cross-
that excit
should say the following. Let us suppose for a while that
the results presented in Tables 1-5 are unknown. In this
case the hypothesis stated above is, at least, a striking
and very glaring example of absurdity, irresponsibility,
and nonsense.
The origin of the hypothesis stated above is in results
of works [12,25,27] and in above-presented calculations
of the cross-sections of the excitation of Coulomb reso-
nances. In other words, the hypothesis mentioned above
is undoubtedly based on the processes that are introduced
to our theory by the Coulomb resona
photons. It is worth noting that the experiment can verify
or refute this hypothesis, but in both cases we will re-
ve equally important info
In order to confirm or to refute the hypothesis pre-
sented above, we suggest the modification of experi-
ments [10,15,23] already mentioned above. Consider, for
instance, the experim
()
miss
E χ
gh-energy
he
cleus
ons is inves- 779.5 ε =
ent of
tende
()
E χ
miss
first stage of slightly exd experiment. The final stage
of suggested experiment is practically the same. The
physicist must measure the cross-section
()
miss
E χ in
slightly changed configuration.
The important but practically negligible and easily im-
plement modification of presented configuration is i
adl auxiliary carbonic target installed at the very
entry of spectrometer of scattered electrons. For pr
hickness of suppoiliary carbonic
target we may use the following speculations. Let we
have 1 cm2 of target of thtalon density (D
mg/cm2). This carbonic tarns 100 × 10−3/(1.66
× 10−24) ≈ 6 × 10s. A half of these nucleons
ed
excitation of Coulomb resonances of the nucleus 12C.
According to this Table, each of four protons of the
leus is an impermeable shield for the
high-energy (700 ε ≈
oulonce na
[
]
21NL = of the investigate
f this shield is 24 2 202010cmb− =× .
Thus the total impermeable shield of 1 cm2 of our etalon
target will be 242222 2010210cm0.4 cm
−
×××≈ . The
obtained result testifies tout 40% of electrons
moving through the target and having the direction of
movement unchanged will have the energy less by 17
MeV than in the incident beam. Thus, according to the
calculations, the density D of our additional target must
be 2 240260mg/cmD≈−.
If the hypothesis about the origin of energy losses
shifted to the right along the axis miss E by the value
17
miss
EΔ≈ MeV. Note that the simplest version of
d nu-
cleus. The are
cross-section he only difference be-
the two cros is that the latter will be
instance,
by varying the th
ion of ine-
la
nces and
ativistic me
arized
he
di
- i
h
resolutio
al state
f high energy
a o
hat ab
miss
E in our measurements is valid then in the modified
configuration we must obtain practically the same picture
of themiss E. T
()
χ
s-sectionstween
modification of experiment [15], which was proposed
above, may be diversified and complicated, for
ickness of the additional target on the
entry slit of the electron/proton spectrometer or by choos-
ing another sort of nuclei for the additional target. At the
moment, a more detailed analysis of such variations is, at
least, premature.
Finally, we can conclude that the investigat
stic scattering of high-energy electrons and, particularly,
the experimental study of Coulomb resonaquasi-
real photons is of general theoretical importance, espe-
cially, for quantum nonrelchanics.
8. Conclusions
The main results of present paper can be summand
briefly stated in the following way:
• Coulomb resonances are the direct theoretical pro-
longation of the nuclear shell structure to the conti-
nuous spectrum region. In the framework of the one-
particle(!) theory of Coulomb resonances one can
readily explain many features of such well-known
phenomenon as dipole (quadrupol, octopol,...) giant
resonance. It is a real possibility to interpret the phe-
nomenon of dipole giant resonance as real experi-
mental confirmation of existence of the Coulomb re-
sonances in the atomic nuclei. The brief theory of
Coulomb resonances and calculated quasi-discrete
spectra of some atomic nuclei are presented in Sec-
tions 2 and 3.
• The regularized cross sections calculated in this paper
convince of the theoretical possibility of direct mani-
festation of Coulomb resonances in the spectra of in-
elastically scattered high energy electrons. T pre-
sented calculations allow us to suggest the best kine-
matic contions for observation of such manifesta-
tion:
nitial energies of high energy electrons, ε ≈ 300 - 500
MeV;
- electron scattering angles, 1025 θ
′≈− degrees.
The necessary condition for such manifestation is sub-
stantially painstaking measurement of cross sections of
inelastic scattering ofigh energy electrons with high
n in the region of transmitted energy, 5 MeV ≤
ω ≤ 60 MeV (Section 3).
• To emphasize the significance of the wave functions
orthogonality (both initial and fins of nuclei)
one may investigate the scattering o

A. A. PASICHNYI, O. A. PRYGODIUK 101
electrons at very small angles 1 θ
′ (Section 4).
• The main kinematic peculiarity of virtual quasi-real
photons is the approximate equality of their quasi-
momentum q and energy ω : 22 q ω ≈. This ap-
proximate equality determines the effective capability
of queal photons for knocking-out of protons of
high nuclear shells into quasi-discrete states of nuclei.
In other words, quasi-real photons excite Coulomb
resonances of atomic nuclei with high efficiency. The
cross sections of such exciting processe result in
huge, alm
asi-r
an
ost tremendous val be equal to
dgements
.
s c
hat mayues t
hundreds and thousands of barns depending on the
initial value of energy
ε of scattering electrons. Such
processes can be discovered in experiments proposed
in this paper (Section 5).
9. Acknowle
Authors wish to thank Dr. V. V. Lutsenko and Dr. Yu. V.
Yakovenko for their sincere efforts in improvement of
the style of the language of submitted text of this article.
REFERENCES
[1] A. G. Sitenko and V. N. Gur’ev, “Inelastic Scattering of
High Energy Electrons on Nuclei,” Soviet Physics—JETP,
Vol. 12, No. 8, 1960, pp. 1228-1234
[2] K. W. McVoy and L. Van Hove, “Inelastic Electron-
Nucleus Scattering and Nucleon-Nucleon Correlations,”
Physical Review, Vol. 125, No. 3, 1962, pp. 1034-1043.
doi:10.1103/PhysRev.125.1034
[3] W. Czylastic Electron Scattering from Nuclei and
Single-Particle Ex Physical Review, Vol. 131,
No. 5, 1963, pp. 2141-2148.
doi:10.1103/PhysRev.131.2141
z, “Ine
citations,”
[4] V. Devanathan, “Quasi-Free Scattering of Electrons and
Nuclear Shell Structure,” Annals of Physics, No.
1, 1967, pp.74-90. doi:10.1016/0003-4916(67)90292-8
Vol. 43,
[5]
tney et a
, Vol. 9, No
V. K. Tartakovskii and A. A. Pasichnyi, “Inelastic Scat-
tering of High-Speed Electrons by Nuclei with Nucleon
Knockout,” Ukrainian Journal of Physics, Vol. 13, No. 8,
1968, pp. 1361-1368.
[6] A. A. Pasichnyi and V. K. Tartakovskii, “Coupled
One-Particle States of Nucleons in a Spherical Potential,”
Ukrainian Journal of Physics, Vol. 13, No. 12, 1968, pp.
2013-2019.
[7] A. G. Sitenko, A. A. Pasichnyi and V. K. Tartakovskii,
“On Electrodisintegration of Light Nuclei,” Soviet Jour-
nal of Nuclear Physics, Vol. 12, 1970, pp. 663-672.
[8] A. A. Pasichnyi, “Study of Nuclear Shell Structure in
Inelastic High Energy Electron Scattering,” Ukrainian
Journal of Physics, Vol. 17, No. 7, 1972, pp. 1130-1138.
[9] R. R. Whil., “Quasielastic Electron Scattering,”
Physical Review C. 6, 1974, pp. 2230-2235.
doi:10.1103/PhysRevC.9.2230
[10] J. Moygey, et al., “Quasi-Free (e, e’p) Scattering on 12C,
28Si, 40Ca and No. 3,
1976, pp. 461-492. doi:10.1016/0375-9474(76)90510-8
58Ni,” Nuclear Physics A, Vol. 262,
[11] J. S. O’Connell, et al., “Electromagnetic Excitation of the
Delta Resonance in Nuclei,” Physical Review C, Vol. ,
No. 3, 1987, pp. 1063-1071.
doi:10.1103/PhysRevC.35.1063
35
[12] ynamic s of Electrodisintegration A. A. Pasichnyi, “On D
Phy
Vol. 45
of Nuclei at Low Energies,” Soviet Journal of Nuclear
Physics, Vol. 54, No. 12, 1991, pp. 944-955.
[13] A. A. Pasichnyi, “Coulomb Resonances and Nuclear
Disintegration,” Ukrainian Journal of Physics, Vol. 37,
No. 4, 1992, pp. 487-497.
[14] M. Zhongyu and F. Dachun, “Quasielastic Electron Scat-
tering in Quasiparticle Approach,”sical Review C,
, No. 2, 1992, pp. 811-818.
doi:10.1103/PhysRevC.45.811
[15] G. Garino, et al., “Proton Propagation in Nuclei Studied
in the (e,e’p) Reaction, ” Physical Review C, Vol. 45, No.
2, 1992, pp. 780-790. doi:10.1103/PhysRevC.45.780
[16] V. R. Pandharipande and S. C. Pieper, “Nuclear Trans-
parency to Intermediate-Energy Nucleons from (e,e’p)
Reactions,” Physical Review C, Vol. 45, No. 2, 1992, pp.
791-798. doi:10.1103/PhysRevC.45.791
[17] Y. H. Jin, D. S. Onley and L. E. Wright, “Electron Cou-
lomb Effects in Quasielastic (e,e’p) Reactions,” Physical
Review C, Vol. 45, No. 3, 1992, pp. 1311-1320.
doi:10.1103/PhysRevC.45.1311
[18] A. A. Pasichnyi, “Dynamics of Electrodisintegration of
nergies,” Proceedings of the 8th Seminar
etic Nuclear Interactions at Low and In-
pectra of Atomic Nu-
Nuclei at Low E
on Electromagn
termediate Energies, Nauka, January 1992, pp. 296- 299.
[19] A. A. Pasichnyi, “Quasi-Discrete S
clei,” Ukrainian Journal of Physics, Vol. 38, No. 11,
1993, pp. 1619-1630.
[20] D. B. Day, et al., “Inclusive Electron-Nucleus Scattering
at High Momentum Transfer,” Physical Review C, Vol.
48, No. 4, 1993, 1849-1863.
doi:10.1103/PhysRevC.48.1849
[21] A. I. Akhiezer, A. G. Sitenko and V. K. Tartakovskii,
“Nuclear Electrodynamics,” Springer, Berlin, 1994.
[22] C. F. Williamson et al., “Quasielastic Electron Scattering
from 40Ca,” Physical Review C, Vol. 56, No. 6, 1997, pp.
3152-3172. doi:10.1103/PhysRevC.56.3152
[23] D. Dutta, et al., “Separated Spectral Functions for the
Quasifree 12C(e,e’p) Reaction,” Physical Review C, Vol.
61, No. 6, 2000, Article ID: 061602.
[24] A. Meucci, C. Giusti and F. D. Pacati, “Relativistic Cor-
rections in (e,e’p) Knockout Reactions,” Physical Review
C, Vol. 64, No. 1, 2001, Article ID: 014604.
doi:10.1103/PhysRevC.64.014604
[25] A. A. Pasichnyi and O. A. Prigodyuk, “On the Electro-
disintegration of Nuclei,” Physics of Atomic Nuclei, Vol.
68, No. 12, 2005, pp. 1988-2008.
on-Nucleus Scattering,” Reviews of Modern Physics,
9-
[2
Vol. 80, No. 1, 2008, pp. 18224.
6] O. Benhar, D. Day and I. Sick, “Inclusive Quasielastic
Electr

A. A. PASICHNYI, O. A. PRYGODIUK
102
doi:10.1103/RevModPhys.80.189
[27] A. A. Pasichnyi, “The Coulomb Resonances and Dynam-
ics of Electrodisintegration of Nuclei by High-Energy
Electrons,” Physics of Particles and Nuclei, Vol. 41, No.
1, 2010, pp. 108-148. doi:10.1134/S1063779610010065
[28] J. J. Sakurai, “Advanced Quantum Mechanics,” Addison
Wesley Publishing Company, Reading, 1967.
[29] V. V. Balashov, “Quantum Theory of Collisions,” Mos-
kow University, Moskow, 1985, in Russian.
[30] V. B. Berestetskii, E. M. Lifshitz and L. P. Pitaevskii,
“Course of Theoretical Physics, Quantum Electro-dyna-
mics,” Vol. 4, Pergamon, Oxford, 1982.
[31] A. S. Davydov, “Theory of the Atomic Nucleus,” Nauka,
Moscow, 1958 (in Russian).
[32] D. A. Varshalovich, A. N. Moskalev and V. K. Herson-
skiy, “Quantum Theory of Angular Momentum,” World
, 1963, pp. 31-44.
Scientific, Singapore, 1988.
[33] S. E. Koonin, “Computational Physics,” Addison Wesley
Publishing Company, London, 1986.
[34] H. F. Lutz and M. D. Karvelis, “Numerical Calculation of
Coulomb Wave Functions for Repulsive Coulomb Fields,”
Nuclear Physics, Vol. 43, No. 1
doi:10.1016/0029-5582(63)90325-0
[35] M. Abramowitz and I. A. Stegun, “Handbook of Mathe-
matical Functions,” National Bureau of Standarts: Appli-
ed Mathematics Series 55, 1964.

A. A. PASICHNYI, O. A. PRYGODIUK 103
Appendix
A. Calculation of the Electro-Disintegration
Cross Sections and Testing of Numerical
Programs
The accurate calculation of the cross sections of inelastic
electron scattering is connected with the accurate calcu-
lation of the overlap integrals (18), which are the most
important components of Equation (8). That problem
will be investigated in detail below. Note that the inte-
grand in Equation (18) is the product of the exponent
()
exp iqr , the bound-state wave function
()
xlm ν
ϕ r and
±
the wave function of continuous spectrum
()
ψ
Kr. For
the Woods-Saxon potential, the wave function of the
bound state
()
xlm ν
ϕ r is well known [6]. This function
an be written as c
()()( )()()
()
22
0
;
d1.
xl
xlmxllm rxllmr
xl xl
Zr
RrY AY
r
AZ rr
ν
νν ν
νν
ϕ
∞
=≡
=

rn n
(A1)
The form and the content of the expressions presented
bove for and together with the
quiremene crosations are of
igh precision predetermine the choice of the integration
ethod in Equation (18).
To calculate the overlap integral (18), we use the well-
nown plane-wave expansion [31,32]:
a
()
xlm ν
ϕ r
t that th
()
()
ψ
−
Kr
s-section calculre
h
m
k
() ()
()
222
2
22222
222
*
0
e4π,
r
lml
l
llmlmqq
lml
iij qrYY
=∞ =
==−
==
 q
qr nnn
q
(A2)
After putting Equations (22), (A1), and (A2), into
quation (18), we presentin the follow-
orm:
E
()
,.
xlm x
I
ν
qK
ing f
() () ()
()()
()
()
() ()() ()
11122 21
12
111222
12
12 12
2
00
2
21
1
22 11
,4π1
2121000
4π21
,,
lmllmll
ll
xlm xlmllml
ll
ll lmm
Ii
ll
lll
l
lmlmlmAqKYY
ν
ν
=∞ ==∞= +
==−==−
=−

++
×+
×Kq
qK
nn
(A3)
here w
()()( )()
121 2
2
0
,d
lllKllxl;
A
qKRrjqrRr rr
νν
∞
= (A4)
nd a
()
22 11
lmlmlm are the Clebsh-Gordon [31,32] coef-
cients.
The overlap integral is presented in Equation (A3) in
ector form, that is to say, Equation (A3) is valid in any
rbitrarily chosen reference frame. We can take advan-
fi
v
a
tage of this freedom of choice and simplify Equation
(A3). With this purpose, we recall that
()
0
21
4π
zm
l
m
Yl
δ
+
==
nne (A5)
If we superpose vector
z
e with vector q or
K
then, according to Equation (A5), the summa tion in
Equation (A3) is essentially simplified.
We restrict ourselves to the case ofz
eq
and make
use of well-known [32] properties of the Clebsh-Gordon
coefficients. After that, the overlap integral takes the
form
()
()
()
()
()
()
()
()()()
1
100 1
1
,4π21121
ljl j
l
xlm xlj
Iil l
ν
=∞ =
−
==
=+−
 +
qK
()
1
12
11 1 1
21
20 00 20
,:2 and
l
ll l mz
ll jllll jlmlm
AqKY lllj
ν
×− + ×−+
×∀=−+
K
ne q
(A6)
Notwithstanding the achieved facilitation, the overlap
integral (A6) remains a very complicated expression in
the form of a twofold series, the convergence of which
depends essentially on the kinematic parameters. It is
well known [33] that the computer programming of such
problems is always associated with a risk to receive an
erroneous result because of “natural” errors, which easily
and freely “penetrate” into initial formula and programs.
To avoid such errors, we propose a few tests [8], which
substantially raise the level of trust to the obtained results.
Note that it is the plane-wave approximation that pro-
vides useful and invaluable aid at this stage of investiga-
tions. Note also that the tests proposed below retain their
validity in the case of relativistic models as well.
Let us recall that the distorted momentum distributions
turn into plane-wave ones if we substitute
r . After that substitution the plane-
can be calculated with two differ-
rst method is to perform the limit
(18) → Equation(A6), using the
. According to Equation
()( )
exp i ψ →
KrK
wave overlap integral
ent methods. The fi
transition of Equation
substitution
()
Kl
Rr
(A6), we obtain:
( )
11
l
jKr→
()
()
i
lm r
003
,e eed
ii
xlm xxx
Ixlm
νν
νϕ
−
−∞
≡=

qrKr qr
qK K
()() ()()
()
r
7) (A
()() ()()
()
1112 221
12
1112 22
12
12 12
22
00 1
0
21 2211
2121
4π14π21
00 0,,
lmll mll
ll
lmll ml
ll
ll lmm
ll
il
llllmlmlmA qKYY
ν
=∞ ==∞=+
==−==−
++
−
 +
⋅× Kq nn

A. A. PASICHNYI, O. A. PRYGODIUK
104
(A8)
here
.
w
() ()()()
121 2
02
0
,d
lllllxl
A
qKjKrjqr Rr rr
νν
∞
= (A9)
d method is to calculate of the overlap
ion (A7) in another way:
The secon
integral Equat
() (
00
,e ee
iii
xlm xxxlm
Ixlm
νν
νϕ
−
−∞
≡=

qrKr qr
qK Kr
)
3
dr
(A10)
()
()
()
()
()
() ()
3
2
0
ed
4πd,
i
xlm
ll
mll
qK
iYsjsrRr rr
ν
ν
ϕ
−
−∞
∞
−
=
=×

qKr rr
(A11)
where =−sqK, =ss .
Note that the succession of operations Equations
11) can be continued. All one ha is to
remember that the plane-wave momentum diution
Equation (15) is proportional to the sum
(
(A10), (As to do
strib
)
2
00
,,
ml
lxlm
ml
SI
ν
=
=−
=qK . In this case one can as well as
x
to recall a well-known equality [32]:
()
221
4π
ml l
m
ml
l
Y
=
=−
+
=
ner m . After that, the summation ov
in can be performed analytically:
0
l
S
()( ) ()
()
()
2
0
0
4π21 d.
ll
SljsrRrrr
∞
→+
It is useful to note that for a large number 1 l
()
120l≥ the strong inequality
()
xl ν

(
(
)
)
2
11 12 Ax
llrMVr+ takes place in the region
at
for we
have the approxality h
is of high accreforthe
conditions of convergence of the plane-wave approxima-
tion series and those of the series with distorted ov
in
stablishe
o values of the plane-wave overlap integral
calculated with the two different methods. This means
that we have obtained a confirmation of reliable conver-
gence of both series Equation (A7) and Equation (18).
Note that in this way we can, at the same time, verify the
convergence of expansions of the plane wave in te
spherical functions [Equation (25)] and the distorted
wave function [Equation (A2)] in the investigated kin-
ematical region.
calculating the overlap integrals (one after an-
other) by two different (Equations (A8) and (A11)) meth-
ods and comparing the former and the latter resu
have established the following.
r small energ
≤ E ≤ 50 MeV, medium nuclei) it is relatively easy to
achieve agreement between the plane-wave cross sec-
tions calculated by the two mentioned above methods
with an accuracy ofsignificant figures in man-
tissa. Note that withosed comparison we achieve
also a reliableck of Equations (A3) and
check alsouracy of such special-func-
tio
)
the accuracy of calcu
[the parameters of
gration step, the n
(A
resul
rounds for the following assertions:
• The probability of errors and inaccuracies in our
programmes and transformations of formulas in the
investigated kinematic region is insignificant.
• The convergence of series in Equations (A3) and (A6
with empirically chosen boundaries of summation
over quantum numbers is quite sat-
isfactory for the investigate of ele
of
omic nucleus
()
rR≤. It is evident that when the
mentioned inequality takes place then1>20l
( )
Kr, whic
that
imate equ
uracy. The
()
11
Kll
Rr j≈
e, we can affirm
erlap
tegrals are identical.
Let us assume that we have ed the agreement
between tw
rms of
After
lts, we
Foies of the knocked-on protons (1 MeV
(A8); we
14 10÷
the prop
accuracy che
the acc
lations
he calcul
ber of ite
n subroutines as
() ()
,l
lm
jx Px, coefficients of Clebsh-
Gordon, as well as the accuracy of direct integration me-
thods in the overlap integrals, etc. When the transmit- ted
energy ω and, consequently, the energy E of the
knocked-out protons increase
(
E ω ≈,300450 MeV÷,
r invar
proce
in the sum in Equation
ults coin-
unde
tation
um ms
iable conditions
ss such as inte-
7), etc. do not change] decreases: the two res
cide only with an accuracy of 65÷ significant figures
in mantissa.
The good agreement between two ts obtained
with two different methods with high accuracy and in a
wide interval of variation of the kinematic parameters
gives g
)
ctro-
12
,ll
()
12
,50ll≤
d kinematics
disintegration of medium and heavy nuclei.
Let us consider one more test, which also essentially
raises the reliability of the calculated numerical values of
the nucleus electro-disintegration cross sections. In this
case we test the process of solution of the radial
Schrödinger equation [Equation (24)] and the process of
tailoring of the solutions
()
()
Kl
Rr
− at the point rb≈.
To do this test, we should implement the special case of
()()
0>0
Ax
Vr E=∀ in the subroutine solving the ra-
dial Schrödinger Equation (24). One way to do this is to
put 00
x
V= and 10Z−= for the potentials
()
WS
Vr
and
()
C
Vr) correspondingly. In this case, if the pro-
gram is correct, we must finally realize the conversions:
()( )
Kl l
Rr jKr=;
() ()
e
0
i
rVr
−
Ψ=
=
Ax
K
r
K. Hence, the
cide
plane-wave momentum distribution calculated so must
coin with two distributions [Equations (A3) and (A7)]
calculated by the traditional methods mentioned above.
In our tests we obtained agreement of all distributions
with an accuracy of 126÷ significant figures in man-
tissa in diverse reof kiatic parameters.
Therefore, we o suppose that the cross
sections of nuclea
gions nem
have a right t
r electro-disintegration in the approxi-
mation of distorted waves are calculated in our computer
program with sufficient accuracy.

A. A. PASICHNYI, O. A. PRYGODIUK
105
We have considered two tests that substantially raise
the reliability of final results of our computer program.
Let us suppose that we deal with large mass numbe r
A
and large energy of the knocked-on proton. It
structive to mention about one more mathematical trick
[8], which in this case improves the convergence of se-
ries appearing in calculations of the distorted momentum
distributions. One can represent the overlap integral Eq-
uation (11) in the following form:
d
ν




(A12)
Finally,
ν
ϕ




(A13)
We calculate the first term of Equation (A13) with a
e in Equation (A6) but with
su
ou ap
method as rational as possible, for instance, like in Equa-
tions (A3)-(A11). As to the second term, we calculate it
with the help of series lik
E is in- bstantially improved convergence. For this purpose,
one needs to perform the following substitution in Equa-
tion (A6):
[]
−
()
()
()()()
()
() () ()
*3
*
,exp
exp exp
xlm xxlm
i
ii
ν
ψϕ
ψ
−
−∞
−
=
 

=−−+−
 
K
K
qKrqrr r
rKrKr
() ()
()()( )()
12 12
112
2
0
,,
d.
ll lll l
Klllx l
AqK AqK
RrjKrjqrRrrr
νν
ν
∞
→

=−

This method gives a possibility to extend essentially
the possibilities of numerical simulation of electro-dis-
integration processes of heavy nuclei for large trans-
ferred energies ω. Note that all the tests described above
have been taken into accnt,proved and implemented
practically as early as in paper [7]. It is a cause for regret
that all these tests do not were published so far elsewhere.
I
() ()
3
exp d .
xl m
i
ν
ϕ
−∞
⋅

qr r r
() ()
()
()
()
()()()()
3
*3
,expd
exp expd
xlm xxlm
xlm
Ii
ii
ν
ν
ϕ
ψ
−∞
−
−∞

=−
 

+−− 
 

K
qKqKrrr
rKrqrrr