Circuits and Systems
Vol.07 No.11(2016), Article ID:71069,29 pages
10.4236/cs.2016.711327
A Novel Asymmetric Three-Phase Cascaded 21 Level Inverter Fed Induction Motor Using Multicarrier PWM with PI and Fuzzy Controller
A. Abdul Namith1, T. S. Sivakumaran2
1Anna University, Chennai, India
2Department of EEE, Arunai College of Engineering, Tiruvannamalai, India
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: May 6, 2016; Accepted: May 18, 2016; Published: September 30, 2016
ABSTRACT
Multilevel inverters are gaining popularity in high power applications. This paper proposes a new ladder type structure of cascaded three-phase multilevel inverter with reduced number of power semiconductor devices which is used to drive the induction motor. The ultimate aim of the paper is to produce multiple output levels with minimum number of semiconductor devices. This paper uses only 11 switches along with 3 diodes and 4 asymmetrical sources to produce an output voltage of 21 levels. The modulation technique plays a major role in commutation of the switches. Here we implement the multicarrier level shifting pulse width modulation technique to produce the commutation signals for the inverter. The proposed multilevel inverter is used to drive the three-phase induction motor. The mathematical modeling of three-phase induction motor is done using Simulink. Furthermore the PI and fuzzy logic controllers are also used to produce the reference waveform of the level shifting technique which in turn produces the commutation signals of the proposed multilevel converter. The controllers are used to control the speed of the induction motor. The effectiveness of the proposed system is proved with the help of simulation. The simulation is performed in MATLAB/Simulink. From the simulation results, it shows that the proposed multilevel inverter works properly to generate the multilevel output waveform with minimum number of semiconductor devices. The PI and fuzzy logic controller performances are evaluated using the results which indicate that with the help of controllers the harmonics has been reduced and the speed control of induction motor is achieved under different loading conditions.
Keywords:
Multilevel, Multicarrier Level Shifting Pulse Width Modulation MC-LS-PWM, Proportional Integral PI and Fuzzy Logic Controller

1. Introduction
In recent years the energy demand is moving on increasing toward generating power with renewable energy source that may be dispersed in a wide area, and most of them are renewable, as they have greater advantages due to their environmentally friendly nature. The solar can be used by all in universe which doesn’t need more investigations of producing electricity. This leads to research in multilevel inverters. The multilevel inverters are classified into three types namely:
・ Diode clamped multilevel inverters;
・ Flying capacitor multilevel inverter;
・ Cascaded H bridge multilevel inverter.
Of these the cascaded H bridge multilevel inverter topologies give better results. The research goes on increasing to propose a new structure of inverter with reduced semiconductor devices with increased multilevel at the output waveform. In [1] , Ruiz- Caballero et al. propose a symmetrical multilevel inverter with spwm technique. This system uses only switches and DC sources. The clamping diode and capacitor are avoided but here they have used 8 switches to produce an output of five-level which is same as that of the conventional one. Though the SPWM technique is implemented the THD is not reduced since the structure of the inverter remains same it fails to achieve the desired THD. Therefore the switching losses remain the same. In [2] , Xiaotian Zhang et al. propose the study of the multi sampled multilevel inverters and their control techniques to improve the performance of the multilevel inverters. This also deals with the different control techniques to be implemented in multilevel inverters in order to reduce the THD. But they don’t concentrate on the structure of the multilevel inverters. In [3] , Amin Ghazanfari et al. propose a way to balance the capacitor voltage to produce voltage levels of equal width. Therefore the THD is reduced. There is no change in the structure of the inverter. Only the technique has been implemented with conventional structure but they achieved better THD. In [4] , Ayoub Kavousi et al. come with the new algorithm for producing the switching signals. Here they propose BEE algorithm to produce the modulation signals; the algorithm works better than the other techniques but the structure of cascaded multilevel inverter remains same. Hence the switching loss is more and the number of switches used is same as that of the conventional one. Therefore it is necessary to find the new structural way of producing multilevel with reduced semiconductor devices. In [5] , Roshankumar et al. use the five-level inverter to drive the induction motor. They propose cascading of flying capacitors to produce five levels at the output. The circuit uses the capacitors; hence balancing of capacitor voltage becomes a great problem and also the capacitor usage makes the circuit big and more complex and the cost of the entire system increases.
In [6] , Paulson Samuel et al. propose the cascaded H bridge topology to be used with the wind energy conversion system for grid interface. The system works on grid interface but again the structure remains same as that of the conventional one. Hence the structural part of the multilevel inverter doesn’t improve the system performance. In [7] by Faete Filho et al., the experiment is done with the conventional structure with ANN control strategy. The THD is minimized by the control strategy but the number of semiconductor diodes remains same thereby increasing the switching loss of the entire system. In [8] , Quanrui Hao et al. introduce the current source multilevel inverter; the main drawback is it increases the number of diodes and capacitors; the circuit is complex; also the control circuitry is complex. In [9] Javier Pereda et al. introduce a new concept of using only one variable DC source in asymmetric multilevel inverter to produce multiple levels at their output. The only disappointment is that since the structure is very large it is complex to produce the commutation signals. The control circuit is also big which again increases the circuit complexity thus reducing the effectiveness of the proposed system. In [10] Liliang Gao et al. propose multilevel inverter fed multiphase induction motor; here they use diode clamped inverter to produce multiple levels at the output and they are used to drive the five phase motor. The performance analysis is done using this. Since they use diode clamped multilevel inverter the number of semiconductor devices is high and hence the losses are heavy. On replacing it with a new structure and by increasing the number of levels can improve the performance of the system.
From all the above analysis we conclude that the researches have been done on the control circuitry of the multilevel inverter. But the structure of inverter remains same. On increasing the levels the structure becomes more complex and bigger in size reducing the efficiency of the system.
Here we propose a new structural multilevel inverter to produce multiple levels at the output voltage with minimum number of power semiconductor devices. The proposed system is used to drive the induction motor and the performance of induction motor is analyzed. The PI and fuzzy controllers are also used to produce the modulation signals; also the controllers have been implemented for speed control of induction motor. The multi carrier level shifting PWM has also been implemented. Hence the THD is reduced lot with minimum number of devices with low switching noise.
2. Proposed Cascaded Multilevel Inverter
The proposed multilevel inverter uses the ladder type connection of switches and diodes along with the voltage sources. In this topology we use asymmetrical voltage sources which may obtained from battery or from renewable energy sources like biomass, solar etc. the asymmetric dc voltage sources are incrementing in nature in the order of n, 2n, 3n, 4n, ∙∙∙ Where n = lowest DC voltage source magnitude.
The structure of proposed multilevel inverter is shown in Figure 1 consisting of main and auxiliary inverter. Here we use the igbt as the switching device. The antiparallel diodes are used for the reverse current path so that the multiple levels can be obtained at the outputs. The proposed system uses less number of power semiconductor devices. The following table shows the switching sequence given to the proposed
Figure 1. Structure of proposed multilevel inverter.
topology to generate 21 level voltage output. The operation of the proposed asymmetric multilevel inverter is explained with the help of Table 1. The switch works on two states on and off. When the switch is on it is in saturation region and it starts conducting when the switch is off it is in cut off region hence it does not conduct. It has 11 modes of operation to produce 11 voltage levels from zero to 10Vdc. The relation between the number of output levels and number of semiconductor devices are calculated by using the formulae as shown below. Let “NDC” be the number of DC sources or stages and the associated number of output voltage level can be calculated by using the equation,
 . (1)
. (1)
The number of switches used in this topology is given by the equation,
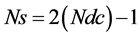 . (2)
. (2)
The number of bypassed diodes used in this topology is given by the equation,
 . (3)
. (3)
Therefore if we use 4 dc sources along with 3 diodes and seven semiconductor power switches we can capable of producing 21 voltage levels at the output. The proposed system consist of two parts namely main inverter and auxiliary inverter.
From Table 1 it is clear that the proposed multilevel inverter uses only minimum
Table 1. Comparison of Cascaded H-Bridge and Proposed MLI.
number of semiconductor devices when compared to the conventional one. Since the switching devices are reduced to a great extent the switching losses is also reduced which increases the effectiveness of the system.
Modes of Operation
MODE-1:
In mode the switch s1 alone conducts. The current flows through s1, the source V1, the diode d1, d2 and d3 to produce the voltage of 1Vdc. The circuit is shown in Figure 2(a) Mode-1. The red colour indicates the flow of current to produce the output voltage level.
MODE-2:
In mode the switch s3 alone conducts. The current flows through s3, the source V2, the diode d2 and d3 to produce the voltage of 2Vdc. The circuit is shown in Figure 2(b) Mode-2. The red colour indicates the flow of current to produce the output voltage level of 2Vdc.
MODE-3:
In mode the switch s5 alone conducts. The current flows through s5, the source V3, the diode d3 to produce the voltage of 3Vdc. The circuit is shown in Figure 2(c) Mode-3. The red colour indicates the flow of current to produce the output voltage level of 3Vdc.
MODE-4:
In mode the switch s7 alone conducts. The current flows through s7 and the source V4 to produce the voltage of 4Vdc. The circuit is shown in Figure 2(d) Mode-4. The red colour indicates the flow of current to produce the output voltage level of 4Vdc
MODE-5:
In mode the switch s1 and s6 conducts. The current flows through s1, the source Vdc, the diode d1 and d2, the switch S6 and the voltage source 4Vdc. Hence it produce the voltage level of 5Vdc (Vdc + 4Vdc = 5Vdc) at the output. The circuit is shown in Figure 3(a) Mode-5. The red colour indicates the flow of current to produce the output voltage level of 5Vdc.
MODE-6:
In mode the switch s3 and s6 conducts. The current flows through s3, the source 2Vdc, the diode d2, the switch S6 and the voltage source 4Vdc. Hence it produce the


Figure 2. (a) Mode-1, (b) Mode-2, (c) Mode-3, (d) Mode-4.



Figure 3. (a) Mode-5, (b) Mode-6, (c) Mode-7, (d) Mode-8, (e) Mode-9, (f) Mode-10.
voltage level of 6Vdc (2Vdc + 4Vdc = 6Vdc) at the output. The circuit is shown in Figure 3(b) Mode-6. The red colour indicates the flow of current to produce the output voltage level of 6Vdc.
MODE-7:
In mode the switch s5 and s6 conducts. The current flows through s5, the source 3Vdc, the switch S6 and the voltage source 4Vdc. Hence it produce the voltage level of 7Vdc (3Vdc + 4Vdc = 7Vdc) at the output. The circuit is shown in Figure 3(c) Mode-7. The red colour indicates the flow of current to produce the output voltage level of 7Vdc.
MODE-8:
In mode the switch s1, s4 and s6 conducts. The current flows through s1, the source 1Vdc, the diode D1, the switch S4, the voltage source 3Vdc, the switch s6 and the voltage source 4Vdc. Hence it produce the voltage level of 8Vdc (1Vdc + 3Vdc + 4Vdc = 8Vdc) at the output. The circuit is shown in Figure 3(d) Mode-8. The red colour indicates the flow of current to produce the output voltage level of 8Vdc.
MODE-9:
In mode the switch s3, s4 and s6 conducts. The current flows through s3, the source 2Vdc, the switch S4, the voltage source 3Vdc, the switch s6 and the voltage source 4Vdc. Hence it produce the voltage level of 9Vdc (2Vdc + 3Vdc + 4Vdc = 9Vdc) at the output. The circuit is shown in Figure 3(e) Mode-9. The red color indicates the flow of current to produce the output voltage level of 9Vdc.
MODE-10:
In mode the switch s1, s2, s4 and s6 conducts. The current flows through s1, the source 1Vdc, the switch S2, the voltage source 2Vdc, the switch S4, the voltage source 3Vdc, the switch s6 and the voltage source 4Vdc. Hence it produce the voltage level of 10Vdc (1Vdc + 2Vdc + 3Vdc + 4Vdc = 10Vdc) at the output. The circuit is shown in Figure 3(f) Mode-10. The red color indicates the flow of current to produce the output voltage level of 10Vdc.
MODE-11:
In this mode all the switches are in off state. Therefore the output voltage is zero.
The Main inverter can generate only zero and positive voltage levels as shown in Figure 4(b). The zero output voltage level is obtained when all the switches are turned OFF. The other voltage levels are obtained by proper switching between the switches. The switching is given in Table 2.
The output voltage of Main inverter is always zero and positive only. To operate as an inverter, it is necessary to change the voltage polarity in every half cycle. For this purpose, the output of the Main inverter is fed to the H-Bridge inverter circuit which is called as the auxiliary inverter. The auxiliary inverter converters the main inverter positive voltages into positive and negative outputs. The block diagram of the proposed inverter is shown in Figure 4(a). The switches s8 and s10 conducts to produce output voltage and the switches s9 and s11 conducts to produce the negative output voltages. When s8 to s11 are off it produce zero voltage. The main inverter switches s1 to s7


Figure 4. (a) Block diagram of proposed inverter; (b) Operation of proposed multilevel inverter.
Table 2. Switching states for the 11 modes of operation of 21 level main inverter circuit.
undergoes high switching frequency to produce multiple output voltage levels. The auxiliary inverter switches s8 to s11 uses fundamental switching frequency. The sample output waveform of the inverter is shown in Figure 4(b) which in turn explains the operation of the proposed system.
3. Modulation Techniques
Modulation is defined as a technique or methodology to produce the pulses for the semiconductor devices to operate them in ON and OFF states. During on state the device is in saturation region hence the switch starts conducting and during off state the switch is in cutoff region hence the switch stops conducting. Since the width of the pulse computes the width and level of the output voltage it is important to concentrate on the modulation technique. The PWM technique compares the reference and the carrier waveform to produce the switching pulse. The reference will be in line frequency whereas the frequency of carrier decides the switching frequency of the semiconductor device.
3.1. Classification of Modulation Techniques
The necessary of modulation technique is to produce the switching signals of the semiconductor device such that the output voltage waveform is nearest to the sinusoidal waveform. By achieving the output voltage shape as closest to that of the sinusoidal waveform the lower order harmonics will be reduced which in turn reduces the total harmonic distortion (THD) of the entire system. The modulation methods used in multilevel inverters can be classified according to switching frequency. Figure 5 shows the classification of modulation techniques. In this paper we have used level shifting PD modulation technique to produce multiple output levels.
Figure 5. Classification of modulation techniques.
3.2. Multicarrier Pulse Width Modulation Schemes
Mostly the Multilevel inverter uses the Multicarrier PWM technique to generate switching signals and also the output waveform appears as close as to the sinusoidal one. The multicarrier PWM uses N-1 carriers and the sine wave to produce the switching signals for the N level inverter. It compares the carrier along with the sinusoidal waveform in order to produce the switching signals of the inverter. Depending upon the physical structure of the carrier waveforms they are classified into two types namely:
1) Phase Shifting PWM;
2) Level shifting PWM.
In PS-PWM techniques the carriers are equal in amplitude and frequency but they have phase difference with each other.
In LS-PWM techniques the carriers are equal in amplitude (peak to peak amplitude), same frequency and phase but they differ in their levels of biasing.
3.3. Multicarrier Level Shifting PWM Technique
There are three alternative PWM strategies with different phase relationships for the level-shifted multicarrier modulation:
・ Phase disposition (PD), where all carrier waveforms are in phase.
・ Phase opposition disposition (POD), where all carrier waveforms above zero reference are in phase and are carrier waveforms below the zero reference are 180 degree out of phase.
・ Alternate phase disposition (APOD), where every carrier waveform both above and below zero reference are in out of phase with its neighboring carrier by 180 degree.
3.4. Phase Disposition Level Shifting PWM
In the present work, in the carrier-based implementation the phase disposition PWM scheme is used. Generally the sinusoidal reference signal is compared with the triangular carriers to produce switching signals to the circuit. In the carrier-based implementation, at every instant of time the modulation signals are compared with the carrier and depending on which is greater, the switching pulses are generated (Figure 6).
Usually for an N-level inverter, the system uses (N − 1) triangular carriers to produce the switching signals. But here our proposed system uses only (N − 1)/2 carriers to produce N level output voltages. Therefore in our system we have not only reduced the number of semiconductor devices but also we have reduced the number of carrier waveform by 50%. Hence the complexity of the control system is reduced which increases the performance of the entire system.
4. Controllers
The purpose of controllers is to have a wide range of control over the physical quantities of the system. Especially in industrial applications we use controllers such as speed controller and current controller in order to achieve constant speed and to reduce the harmonic content in the current. In our paper we use proportional Integral controller and Fuzzy Logic Controller to control the speed of the induction motor. Here we also compare the performance of both the controllers.
4.1. Proportional Integral Controller (PI Controller)
The Proportional Integral controller uses the Kp and Ki gain to control the system parameter. The proportional gain is used to increases the response of the system but it fails to meet the stability of the system. The Integral is used to have a better stability of the system with reduced speed of response. In general PI controller is used to have fast response with less noise and less disturbance there by reducing the system delays. The basic equation is
Figure 6. Multicarrier level shifting phase disposition pulse width modulation (MC-LS-PD- PWM).
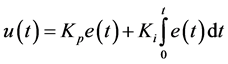 (4)
(4)
where u(t) is the output of the controller, e(t) is the error between the actual and the reference signal, Kp is the Proportional gain and Ki is the integral gain. He we use trial and error method to find the values of Kp and Ki. Therefore PI controller ids used to reduce the forced oscillations and steady state error. The structure of PI controller is shown in Figure 7 and the values of Kp and Ki are given in Table 3.
4.2. Fuzzy Logic Controller
A Fuzzy Logic Controller (FLC) is an extension of a logical system. It works based on the rules called as fuzzy sets. It is basically a rule based system which uses artificial intelligence to frame its fuzzy sets of rules. Fuzzy logic is flexible and it is easy to implement which can tolerate imprecise data and can used to model non linear functions. It comprises of four basic components: Fuzzification, rule-base, inference mechanism and defuzzification (Figure 8).
Figure 7. Structure of PI controller.
Figure 8. General structure of fuzzy logic controller.
Table 3. Values of proportional and integral gain.
Fuzzification
The membership function are assigned to the variables using seven fuzzy subset values called
・ negative big (nb),
・ negative medium (nm),
・ negative small (ns),
・ zero(zr),
・ positive small (ps),
・ positive medium (pm),
・ positive big (pb).
Variable e and ∆e are selected as the input variables, where e is the error and ∆e is the change in error. The output variable is the reference signal for PWM generator which is used to produce the switching signals of the inverter. In our paper we use Triangular membership function for process. Fuzzy associative memory for the proposed system is given in Table 4.
5. Simulation Results
5.1. Simulink Model of Multilevel Inverter Using MC-PD-LS-PWM
The proposed model uses only 11 switches and diodes with four asymmetrical voltage sources to 21 levels in the output voltage waveforms. The main inverter produces only positive voltage of levels 1 to 10. The auxiliary inverter converters it positive ten levels, negative ten levels along with one zero level to produce an output of 21 levels at their output voltage.
Figure 9 shows the simulation circuit of the proposed inverter. It has 11 switches numbered from S1 to S11. The Switches S1 to S7, along with three diodes D1, D2 and D3 with four asymmetric voltage sources Vdc, 2Vdc, 3Vdc, 4Vdc forms the main inverter whose output will be in positive regions only. It produces 11 levels of voltage from zero to 10Vdc. The switch S8 to S11 forms the auxiliary inverter which is a conventional h bridge inverter, when switch S8 and S11 is on it produce the positive voltage levels zero to 10Vdc. When S9 and S10 are on it produces the negative voltage
Table 4. Fuzzy associate memory for the proposed system.
Figure 9. Simulink model of proposed 21 level inverter.
levels zero to −10Vdc. Thus the proposed inverter produces 21 voltage levels with positive and negative levels of +10Vdc to −10Vdc. Here the Vdc used is 25 volts. Hence it is capable of producing amplitude of +250 to −250 volts.
The mathematical modeling of three-phase induction motor is shown in Figure 10. The output of the proposed three-phase asymmetric multilevel inverter is used to drive the induction motor. The parameters used for modeling of the three-phase induction motor is shown in Table 5.
The output voltage waveform with 21 voltage levels is shown in Figure 11. It indicates the single phase output voltage of proposed asymmetric cascaded multilevel inverter. The actual output of the inverter is +250 to −250 volts but due to some losses the output obtained is +240 to −240 volts.
Figure 12 shows the Multicarrier level shifting pulse width modulation signals. Here the sine wave acts as the reference signals, the carriers are triangular signals, here we use more than one carrier so it comes under multicarrier classification, the carrier signals are equal in amplitude and phase but they differ in their level of distribution.
Figure 13 indicates the three-phase output voltage of the proposed inverter, they have 21 levels in their outputs and each phase have phase shift of 120 degree. The magnitude is +250 volts to −250 volts this is used to drive the three-phase induction motor.
Figure 10. Modelling of three-phase induction motor.
Table 5. Machine parameters.
Figure 14 indicates the three-phase output current of the proposed multilevel inverter.
Figure 15 shows the three-phase stator current of the three-phase induction motor. The induction motor is run at different load condition. At 0.3 sec the load of the induction motor is increased and hence it shows the increase in current at 0.3 sec.
Figure 16 shows the electromagnetic torque of the three-phase induction motor, the initial starting torque of the induction motor is large after 0.1 sec it comes to normal condition and hence the torque is reduced, at 0.3 sec the load of the induction motor is increased to 5 N. This results in the increase in torque of the induction motor. Hence after 0.5 sec the electromagnetic torque is increased due to load disturbance.
Figure 11. Single phase 21 level output voltage waveform.
Figure 12. MC-PD-LS-PWM waveform.
Figure 13. Three-phase 21 level output voltage waveform.
Figure 14. Three-phase output current waveform.
Figure 15. Stator current of three-phase induction motor.
Figure 16. Electromagnetic torque of three-phase induction motor.
Figure 17 shows the speed of the three-phase induction motor, the rated speed of the induction motor is 1500 rpm. It settles at the rated speed at 0.2 sec. At 0.5 sec the load of the induction motor is increased to 5 N. This results in the increase in speed of the induction motor. Hence after 0.5 sec the speed is decreased due to load disturbance.
Figure 18 shows the total harmonic distortion present in the output voltage of the proposed multilelel inverter with level shifting pulse width modulation technique.
Figure 17. Speed of three-phase induction motor.
Figure 18. THD of voltage using MC-PD-LS-PWM.
5.2. Simulink Model of Multilevel Inverter Using PI Controller
Figure 19 shows the simulink model of proposed inverter with pi controller. The three- phase asymmetrical multilevel inverter output is used to drive the three-phase induction motor. Here mathematical modeling of three-phase induction motor is used. The speed control is achieved by using pi controller. The actual speed and the reference speed are compared and the error signal is produced. The error signal is processed by using the pi controller and it is used to produce the reference signal of the MC-LS- PWM technique. This reference signal is compared with the carrier signal to produce the commutation signals of the inverter.
Figure 20 indicates the three-phase output voltage and output current of the proposed inverter. The magnitude of the output voltage is 240 volts and the magnitude of the current is 2.2 ampere.
Figure 21 shows the three-phase stator current of the three-phase induction motor. The induction motor is run at different load condition. At 0.5 sec the load of the induction motor is increased to 5 N and hence it shows the increase in current at 0.5 sec.
Figure 22 shows the electromagnetic torque of the three-phase induction motor, the initial starting torque of the induction motor is large after 0.2 sec it comes to normal condition and hence the torque is small after 0.2 sec. At 0.5 sec the load of the induction motor is increased to 5 N. This results in the increase in torque of the induction motor. Hence after 0.5 sec the electromagnetic torque is increased due to load disturbance.
Figure 23 shows the speed of the three-phase induction motor, the rated speed of the induction motor is 1500 rpm. It settles at the rated speed at 0.15 sec. At 0.5 sec the load of the induction motor is increased to 5 N. This results in the increase in speed of the
Figure 19. Simulink model of multi level inverter using PI controller.
Figure 20. Three-phase output voltage and current using PI controller.
Figure 21. Three-phase stator current of induction motor using PI controller.
Figure 22. Electromagnetic torque of induction motor using PI controller.
Figure 23. Speed of three-phase induction motor using PI controller.
induction motor. Hence after 0.5 sec the speed is decreased due to load disturbance. Here the PI controller comes into action and hence the speed is retained after within 0.1 sec and therefore the speed is retained at 0.6 sec and it is maintained at the rated speed.
Figure 24 shows the total harmonic distortion present in the output voltage of the proposed multilevel inverter with PI controller. It reveals that THD has been reduced by using the PI controller.
5.3. Simulink Model of Multilevel Inverter Using FUZZY Logic Controller
Figure 25 shows the Simulink model of proposed inverter with pi controller. The three- phase asymmetrical multilevel inverter output is used to drive the three-phase induction motor. Here mathematical modeling of three-phase induction motor is used. The speed control is achieved by using fuzzy logic controller. The actual speed and the reference speed are compared and the error signal is produced. The error signal is processed by using the pi controller and it is used to produce the reference signal of the MC-LS-PWM technique. This reference signal is compared with the carrier signal to produce the commutation signals of the inverter.
Figure 26 shows the structure of the fuzzy logic controller with two inputs error and change in error and one output.
Figure 27 indicates the three-phase output voltage and output current of the proposed inverter. The magnitude of the output voltage is 240 volts and the magnitude of the current is 2.5 ampere.
Figure 28 shows the electromagnetic torque of three-phase induction motor with load variation at 0.5 sec.
Figure 29 shows the speed of the three-phase induction motor, the rated speed of the induction motor is 1500 rpm. It settles at the rated speed at 0.15 sec. At 0.5 sec the load
Figure 24. THD of voltage using PI controller.
Figure 25. Simulink model of multilevel inverter using fuzzy logic controller.
Figure 26. Structure of fuzzy logic controller.
Figure 27. Three-phase output voltage and current of proposed inverter using fuzzy controller.
Figure 28. Electromagnetic torque of induction motor using fuzzy controller.
Figure 29. Speed of three-phase induction motor using Fuzzy Logic controller.
of the induction motor is increased to 5 N. This results in the increase in speed of the induction motor. Hence after 0.5 sec the speed is decreased due to load disturbance. Here the PI controller comes into action and hence the speed is retained after within 0.07 sec and therefore the speed is retained at 0.57 sec and it is maintained at the rated speed.
Figure 30 shows the total harmonic distortion present in the output voltage of the proposed multilevel inverter with PI controller. It reveals that THD has been reduced by using the fuzzy logic controller.
Table 6 analyzes the performance of the PI and fuzzy logic controllers from Figure 23 and from Figure 29. We calculated the settling time rise time and overshoot time from the speed waveform. Using the table we understand that the fuzzy controller works better than the PI controller in terms of the settling and overshot time. Hence we conclude that fuzzy is better in this case.
Table 7 gives the comparison using the outputs from Figure 18, Figure 24 and Figure 30 which analyze that the THD of the proposed system with PWM technique along with PI and Fuzzy Logic controller.
6. Conclusion
The proposed asymmetric cascaded multilevel inverter produces multilevel output with minimum number of power semiconductor devices. The LS-PD-PWM technique involved to further improve the performance of the inverter by reduces the THD which was illustrated in the comparison tables. The simulation also proves that if any failure
Figure 30. THD of voltage using PI controller.
Table 6. Comparison of PI and FUZZY controller.
Table 7. Comparison of total harmonic distortion.
occurs in any one of the switches it is still capable of producing multiple voltage levels without shunt downing the entire systems. The multilevel inverter was successfully controlled by both PI and fuzzy logic controller and these were used to achieve control of multilevel output steps both in linear and nonlinear loads. From Table 6 and Table 7 we conclude that the fuzzy logic controller is the most efficient and effective than PI controller in our case. The simulation result also proves the effectiveness of the proposed multilevel inverter which uses less number of power semiconductor devices compared to the conventional one which is proved from using Table 5.
Cite this paper
Namith, A.A. and Sivakumaran, T.S. (2016) A Novel Asymmetric Three-Phase Cascaded 21 Level In- verter Fed Induction Motor Using Multicarrier PWM with PI and Fuzzy Controller. Circuits and Systems, 7, 3922-3950. http://dx.doi.org/10.4236/cs.2016.711327
References
- 1. Ruiz-Caballero, D.A., Ramos-Astudillo, R.M., Mussa, S.A. and Heldwein, M.L. (2010) Symmetrical Hybrid Multilevel DC-AC Converters with Reduced Number of Insulated DC Supplies. IEEE Transactions on Industrial Electronics, 57, 2307-2314.
http://dx.doi.org/10.1109/TIE.2009.2036636 - 2. Zhang, X.T. and Spencer, J.W. (2012) Study of Multisampled Multilevel Inverters to Improve Control Performance. IEEE Transactions on Power Electronics, 27, 4409-4416.
http://dx.doi.org/10.1109/TPEL.2012.2187313 - 3. Ghazanfari, A., Mokhtari, H. and Firouzi, M. (2012) Simple Voltage Balancing Approach for CHB Multilevel Inverter Considering Low Harmonic Content Based on a Hybrid Optimal Modulation Strategy. IEEE Transactions on Power Delivery, 27, 2150-2158.
http://dx.doi.org/10.1109/TPWRD.2012.2205277 - 4. Kavousi, A., Vahidi, B., Salehi, R., Bakhshizadeh, M.K., Farokhnia, N. and Fathi, S.H. (2012) Application of the Bee Algorithm for Selective Harmonic Elimination Strategy in Multilevel Inverters. IEEE Transactions on Power Electronics, 27, 1689-1696.
http://dx.doi.org/10.1109/TPEL.2011.2166124 - 5. Roshankumar, P., Rajeevan, P.P., Mathew, K., Gopakumar, K., Leon, J.I. and Franquelo, L.G. (2012) A Five-Level Inverter Topology with Single-DC Supply by Cascading a Flying Capacitor Inverter and an H-Bridge. IEEE Transactions on Power Electronics, 27, 3505.
http://dx.doi.org/10.1109/TPEL.2012.2185714 - 6. Samuel, P., Gupta, R. and Chandra, D. (2011) Grid Interface of Wind Power with Large Split-Winding Alternator Using Cascaded Multilevel Inverter. IEEE Transactions on Energy Conversion, 26, 299-309.
http://dx.doi.org/10.1109/TEC.2010.2096538 - 7. Filho, F., Tolbert, L.M., Cao, Y. and Ozpineci, B. (2011) Real-Time Selective Harmonic Minimization for Multilevel Inverters Connected to Solar Panels Using Arti?cial Neural Network Angle Generation. IEEE Transactions on Industry Applications, 47, 2117-2124.
http://dx.doi.org/10.1109/TIA.2011.2161533 - 8. Hao, Q.R. and Ooi, B.-T. (2010) Tap for Classical HVDC Based on Multilevel Current- Source Inverters. IEEE Transactions on Power Delivery, 25, 2626-2632.
http://dx.doi.org/10.1109/TPWRD.2010.2044895 - 9. Pereda, J. and Dixon, J. (2011) High-Frequency Link: A Solution for Using Only One DC Source in Asymmetric Cascaded Multilevel Inverters. IEEE Transactions on Industrial Electronics, 58, 3884-3892.
http://dx.doi.org/10.1109/TIE.2010.2103532 - 10. Gao, L.L. and Fletcher, J.E. (2010) A Space Vector Switching Strategy for Three-Level Five- Phase Inverter Drives. IEEE Transactions on Industrial Electronics, 57, 2332-2344.
http://dx.doi.org/10.1109/TIE.2009.2033087





























