Applied Mathematics
Vol.3 No.10A(2012), Article ID:24137,6 pages DOI:10.4236/am.2012.330212
Optimization of Geometry at Hartree-Fock Level Using the Generalized Simulated Annealing
1Instituto de Física, Universidade Federal da Bahia, Salvador, Brazil
2Instituto de Química, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil
Email: *micael@ufba.br
Received July 11, 2012; revised August 11, 2012; accepted August 17, 2012
Keywords: Geometry Optimization; Hartree-Fock Absolute Minimum; Generalized Simulated Annealing
ABSTRACT
This work presents a procedure to optimize the molecular geometry at the Hartree-Fock level, based on a global optimization method—the Generalized Simulated Annealing. The main characteristic of this methodology is that, at least in principle, it enables the mapping of the energy hypersurface as to guarantee the achievement of the absolute minimum. This method does not use expansions of the energy, nor of its derivates, in terms of the conformation variables. Distinctly, it performs a direct optimization of the total Hartree-Fock energy through a stochastic strategy. The algorithm was tested by determining the Hartree-Fock ground state and optimum geometries of the H2, LiH, BH, Li2, CH+, OH−, FH, CO, CH, NH, OH and O2 systems. The convergence of our algorithm is totally independent of the initial point and do not require any previous specification of the orbital occupancies.
1. Introduction
The global optimization problem is a subject of intense current interest. Stochastic optimization methods have been utilized to solve this kind of problem. Essentially these methods consist of performing a direct optimization of a given function, denominated cost function, E, within a determinated stochastic strategy. The Monte Carlo method (MC) is a well-known example of this kind of method. It has been proposed by Metropolis and Ulam [1] whose presented it as a general purpose tool1. In the stochastic strategy applied by Metropolis and Ulam, it is used a function, g, to calculate the visiting probability of the hypersurface definited by the cost function, 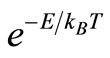 2. In the original concept of the MC method, the system configurations randomly chosen and used in the calculations of E, are supposed equiprobable. Metropolis [2] proposed a modification in the MC algorithm, i.e. he gave distinct weights to distinct configurations. This method is known in the literature concerned as the Metropolis method. Kirkpatrick et al. [3,4] proposed a new procedure denominated the Simulated Annealing (SA) method, which is a modification of the Metropolis method [2]. In the SA method, g is a gaussian function and the T parameter is no longer considered a constant and changes according to
2. In the original concept of the MC method, the system configurations randomly chosen and used in the calculations of E, are supposed equiprobable. Metropolis [2] proposed a modification in the MC algorithm, i.e. he gave distinct weights to distinct configurations. This method is known in the literature concerned as the Metropolis method. Kirkpatrick et al. [3,4] proposed a new procedure denominated the Simulated Annealing (SA) method, which is a modification of the Metropolis method [2]. In the SA method, g is a gaussian function and the T parameter is no longer considered a constant and changes according to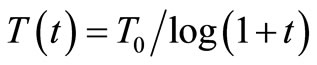 , where t enumerates the cycles of the process. In the literature this method is referred to as the Classical Simulated Annealing (CSA) method or Boltzmann Machine. Szu and Hartley [5] proposed a modification in the CSA method where the g function is a Cauchy-Lorentz function and T varies according to
, where t enumerates the cycles of the process. In the literature this method is referred to as the Classical Simulated Annealing (CSA) method or Boltzmann Machine. Szu and Hartley [5] proposed a modification in the CSA method where the g function is a Cauchy-Lorentz function and T varies according to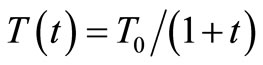 . The Szu and Hartley procedure became known in the literature as the Fast Simulated Annealing (FSA) method or Cauchy Machine. These SA methods have been applied in distinct situations such as restoration of degraded images [6] and microprocessor circuitry design [4].
. The Szu and Hartley procedure became known in the literature as the Fast Simulated Annealing (FSA) method or Cauchy Machine. These SA methods have been applied in distinct situations such as restoration of degraded images [6] and microprocessor circuitry design [4].
The Generalized Simulated Annealing method (GSA) [7], has been developed and includes both procedures, the FSA and CSA, as special cases. The GSA approach uses the Tsallis statistics [8,9] to define the visiting distribution function g and has been applied successfully in the description of a variety of global extremization problems. In the domain of the atomic and molecular aggregates, for example, the discovery of the lowest-energy conformations for biological macromolecules or crystal structures for systems with known composition is a frequent goal. In particular, the GSA approach has been used with success in the prediction of new three-dimensional protein structure and protein folding [10,11], fitting the potential energy surface for path reaction and chemical reaction dynamics [12,13], gravimetric problem [14], mechanical properties in alloys [15-17], in electronic structure problems [18-20], among others.
It is important to point out that those typical methodologies used to treat optimization problems based on solving nonlinear necessary-condition equations do not guarantee the achievement of the absolute minimum. This is the case with some variational electronic structure methods, for instance, the Hartree-Fock (HF), multiconfiguration selfconsistent field (MCSCF), molecular geometry determination problems and the correspondent methods in the scope of the Nuclear-Electronic Orbital theory (NEO) [21-26]. Moreover, it should be observed that the absolute minimum of the functional energy in a given class of functions is the best description of the ground state, as the energy is concerned, within that given class. These observations suggest the importance of developing direct optimization methods for studying these classes of extremal problems.
In previous works [18,19], the GSA algorithm was used to study the problem of determining the absolute minimum of the restricted Hartree-Fock-Roothaan (RHF) [27] and of the unrestricted Hartree-Fock-Pople-Nesbet (UHF) [28] functionals. In another work the GSA algorithm was applied to construct atomic bases [20]. The method presented in this work is also based on the GSA algorithm, and it is used to determine the absolute minimum and optimum geometry at the Hartree-Fock (HF) level. This geometry optimization method (hereafter referred to as HFg, RHFg or UHFg) was tested by determining the HF ground state and optimum geometries of the H2, LiH, BH, Li2, CH+, OH−, FH, CO, CH, NH, OH and O2 molecules, using minimal, double-zeta and double-zeta with polarization basis functions (d functions for Li, B, F and p functions for H). The main characteristic of this methodology is that it enables the mapping of the potential energy hypersurface in order to guarantee, at least in principle, that the absolute minimum of the functional in focus is achieved. This methodology does not use expansions of the energy, or of its derivatives, in terms of the conformation variables [29,30]. Distinctly, a direct optimization is performed of the total Hartree-Fock energy function through a stochastic strategy, the GSA method. A detailed discussion about the multiple HF extrema, the HF absolute minimum and the GSA algorithm can be found in [18,31-37].
2. The Real HFg Functional and the Constraint Equations
Since the Roothaan and Pople-Nesbet problems are very well known and documented in the literature, only the more general UHFg functional and constraint conditions will be presented. Consider a molecular system with nuclear coordinates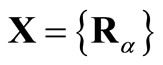 , n electrons, m atomic basis functions
, n electrons, m atomic basis functions 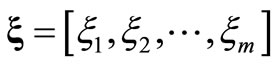 and
and  occupied LCAO3 molecular orbitals (MOs)
occupied LCAO3 molecular orbitals (MOs)
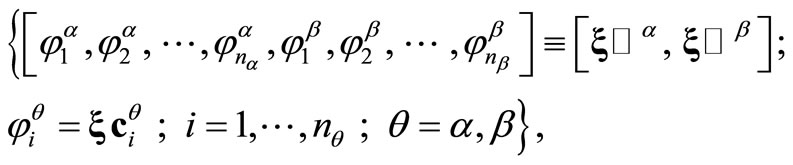
where  is a column vector with components
is a column vector with components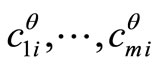 ,
,  is the matrix
is the matrix  formed by the
formed by the 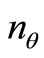 columns vectors
columns vectors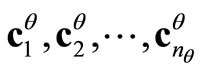 .
. 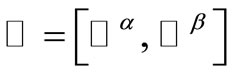 is the matrix
is the matrix 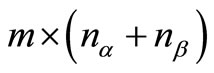 formed by the
formed by the 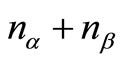 columns vectors
columns vectors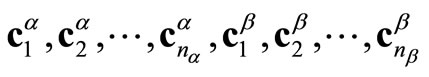 . The number m of atomic functions must satisfy the condition
. The number m of atomic functions must satisfy the condition 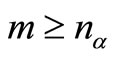 and
and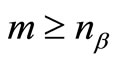 . The electronic energy functional (in atomic units), in the real UHF approximation, is given by,
. The electronic energy functional (in atomic units), in the real UHF approximation, is given by,
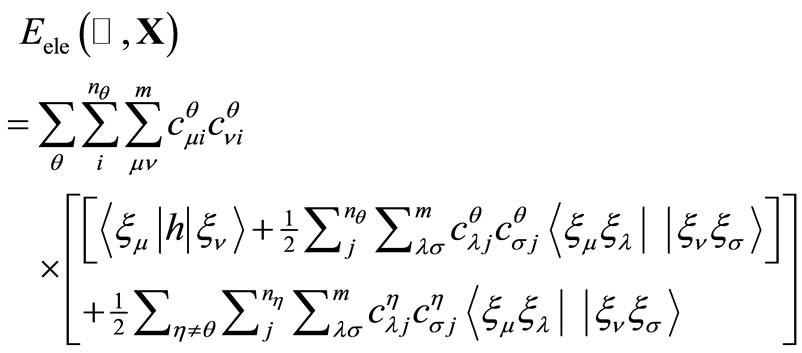
with the constraint conditions given by,
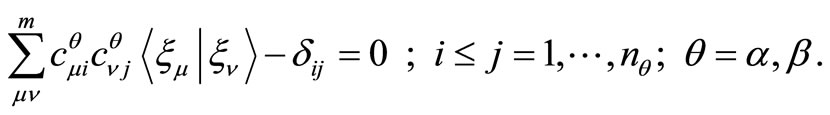 (1)
(1)
In the above equations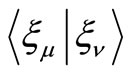 ,
, 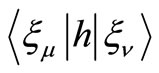 and
and 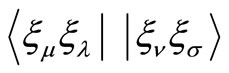 are the usual overlap, kinetic energy plus nuclear attraction, and electronic repulsion integrals, respectively, that depend of the nuclear coordinates
are the usual overlap, kinetic energy plus nuclear attraction, and electronic repulsion integrals, respectively, that depend of the nuclear coordinates . For the HFg functional, the total energy E, is given by,
. For the HFg functional, the total energy E, is given by,
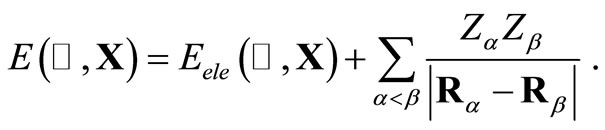 (2)
(2)
3. The HFg Algorithm
As in references [18-20], the GSA algorithm used here includes two additional modifications relative to the original version described in reference [7]. The first one is the introduction of constraint conditions in the structure of the algorithm (steps 4) and 9)) to treat our variational problem of constrained extrema. The second modification was the introduction of a new independent parameter, 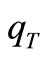 , to construct the temperature function defined in the step 6).
, to construct the temperature function defined in the step 6).
The procedure used to search for the global and local minima or to map the cost function hypersurface consists in comparing the total energy 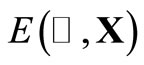 for two consecutive values of the
for two consecutive values of the  and X obtained with the GSA routine.
and X obtained with the GSA routine.  and X, for two consecutive GSA steps, are related to the previous ones via random perturbations on the LCAO-MOs coefficients and on the molecular conformation, respectively. In each cycle,
and X, for two consecutive GSA steps, are related to the previous ones via random perturbations on the LCAO-MOs coefficients and on the molecular conformation, respectively. In each cycle,  and X are simultaneous and independently generated.
and X are simultaneous and independently generated.
In summary, the whole UHFg algorithm for mapping and searching for the global minimum of the total energy surface is:
1) Fix the qA, qV and qT parameters relative to acceptance and visitation probability-distribution functions and temperature function, respectively;
2) Start at t = 1, the first step in the iterative process, with an arbitrary initial matrix guess , an arbitrary molecular conformation
, an arbitrary molecular conformation  and a high enough value for the “temperature”
and a high enough value for the “temperature”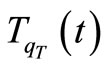 ;
;
3) Calculate the integrals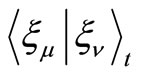 ,
, 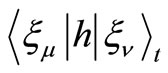 and
and 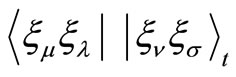 at
at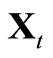 ;
;
4) Ortho-normalize the 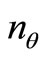 LCAO-MOs vectors
LCAO-MOs vectors 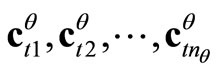 according to Equations 1;
according to Equations 1;
5) Calculate the total energy 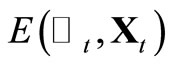 using Equation 2;
using Equation 2;
6) Calculate a new temperature as follows [7]:
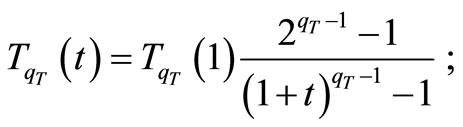
7) Generate randomly the increments 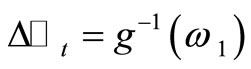 and
and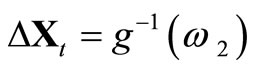 , where
, where 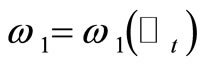 and
and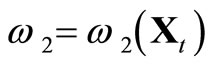 , are randomly generated by using the visiting probability distribution
, are randomly generated by using the visiting probability distribution 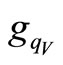 [7] to obtain the new matrix
[7] to obtain the new matrix 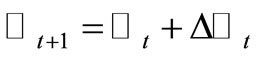 and the new molecular conformation
and the new molecular conformation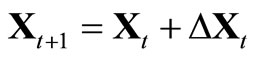 ;
;
8) Calculate the integrals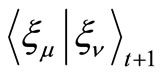 ,
, 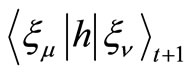 and
and 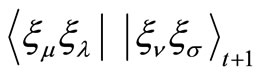 at
at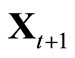 ;
;
9) Ortho-normalize the new LCAO-MOs vectors 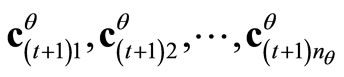 according to Equations 1;
according to Equations 1;
10) Calculate the total energy 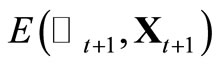 using Equation 2. The new energy value will be accepted or not according to the rule: if
using Equation 2. The new energy value will be accepted or not according to the rule: if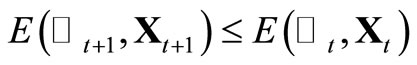 , replace
, replace  by
by 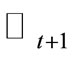 and
and 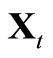 by
by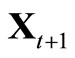 if
if 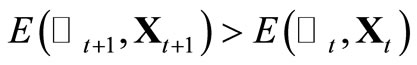 run a random number
run a random number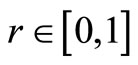 , if
, if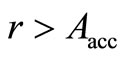 , the acceptance probability [7] defined by
, the acceptance probability [7] defined by
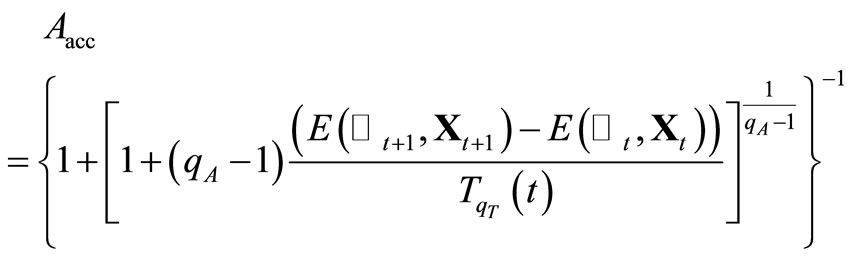
retain  and
and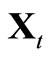 , otherwise, replace
, otherwise, replace 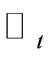 and
and 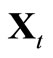 by
by 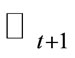 and
and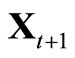 ;
;
11) Take 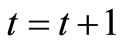 and return to 6) until the convergence of
and return to 6) until the convergence of 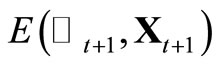 is reached within the desired criterion.
is reached within the desired criterion.
After convergence is achieved, the orbital energies 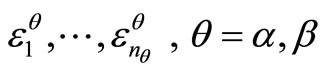 are obtained calculating
are obtained calculating 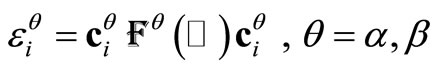 , where
, where 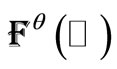 is the Fock’s matrix constructed with the converged UHFg occupied matrix
is the Fock’s matrix constructed with the converged UHFg occupied matrix . Also, it is always possible to obtain the virtual canonical vectors,
. Also, it is always possible to obtain the virtual canonical vectors, 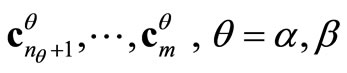 and the respective virtual orbital energies
and the respective virtual orbital energies 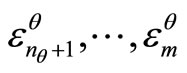 by diagonalization of the pseudo-eigenvalue equations
by diagonalization of the pseudo-eigenvalue equations  [28]. Note that, while for the standard RHF/UHF-SCF [27,28] calculations one needs to specify, a priory, the orbital occupancy, no ad hoc orbital occupation rule is needed for the RHFg and UHFg calculations The following stopping criterion was adopted for the HFg iterative process convergence was assumed if the difference between the current total energy value and the lowest total energy previously obtained during the process was less than a pre-established value
[28]. Note that, while for the standard RHF/UHF-SCF [27,28] calculations one needs to specify, a priory, the orbital occupancy, no ad hoc orbital occupation rule is needed for the RHFg and UHFg calculations The following stopping criterion was adopted for the HFg iterative process convergence was assumed if the difference between the current total energy value and the lowest total energy previously obtained during the process was less than a pre-established value 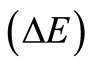 for a certain number of consecutive steps (nstop). The HFg calculations were performed in atomic units and was used
for a certain number of consecutive steps (nstop). The HFg calculations were performed in atomic units and was used 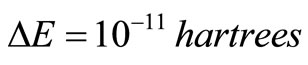 and
and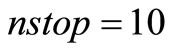 . The algorithm HFg described above is illustrated in the flowchart of Figure 1.
. The algorithm HFg described above is illustrated in the flowchart of Figure 1.
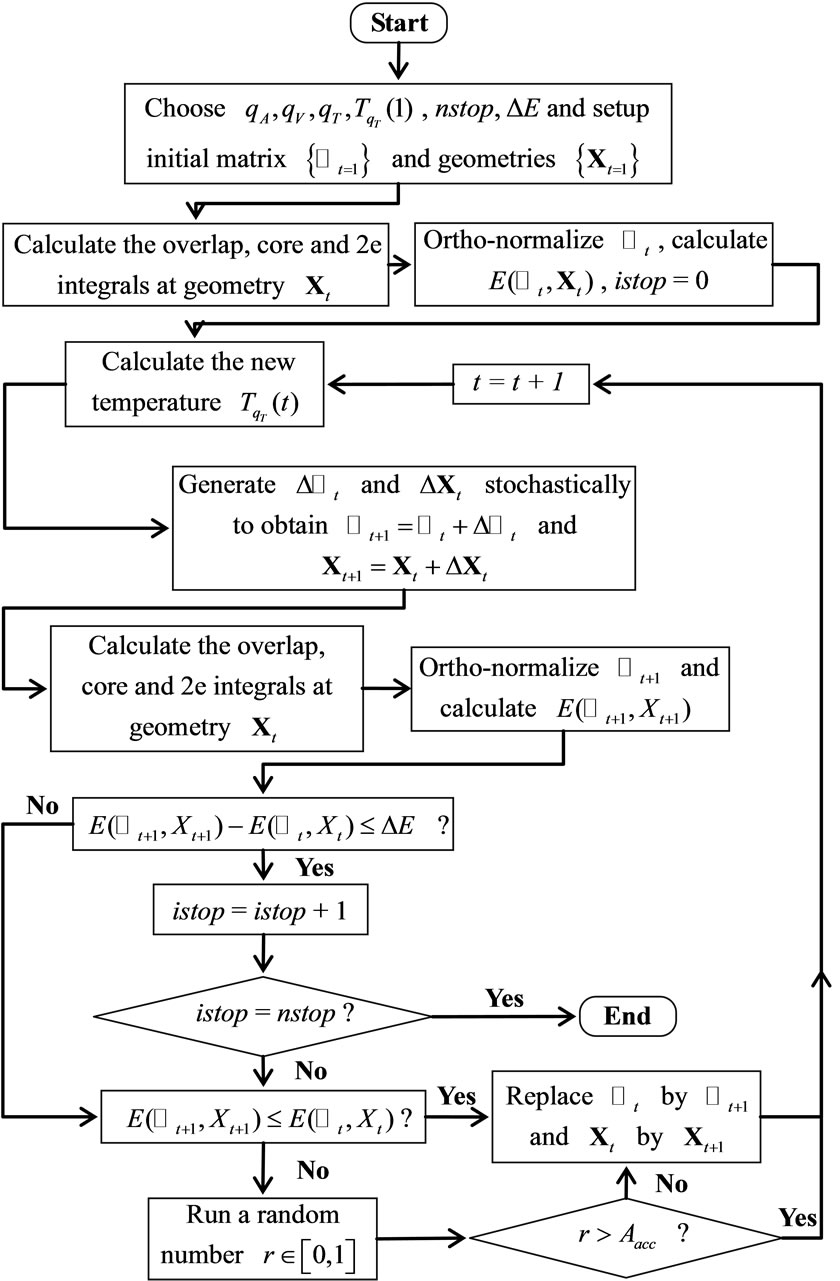
Figure 1. HFg-GSA Flowchart.
4. Discussion
To test the HFg method, we calculated the HF ground state energy and optimum geometry for the H2, LiH, BH, Li2, CH+, OH–, FH, CO, CH, NH, OH and O2 molecules. The calculations were carried out using minimal (STO- 6G), double-zeta, and double-zeta with polarization functions (d functions for Li, B, F and p functions for H) basis sets. Tables 1-3 show the point and spin symmetry classes of the ground state, the kind of calculations performed, the geometry and correspondent energy obtained and the experimental geometry extracted from the Herzberg book [38].
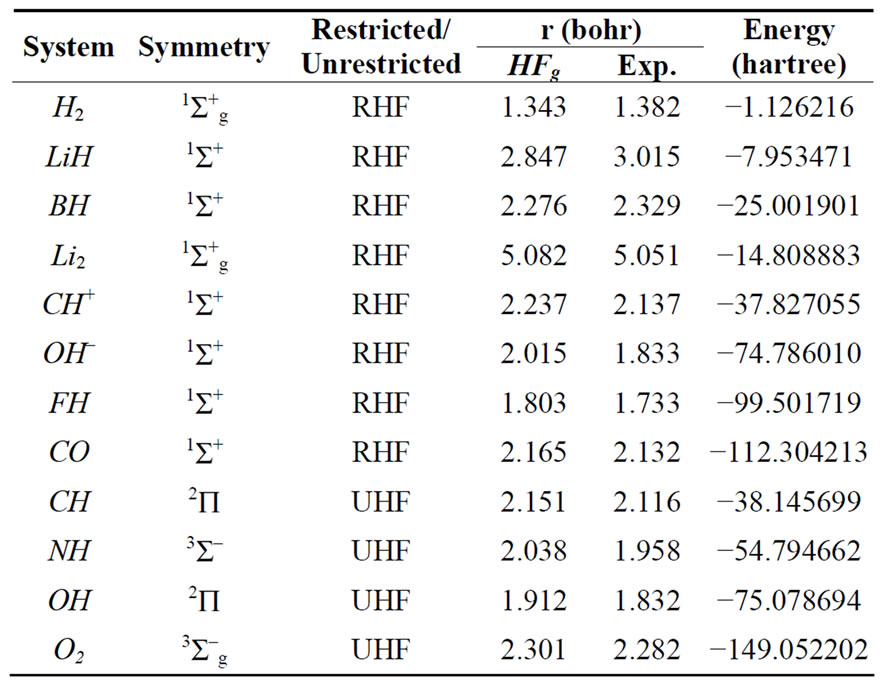
Table 1. Converged HFg energies and geometries using STO-6G basis.
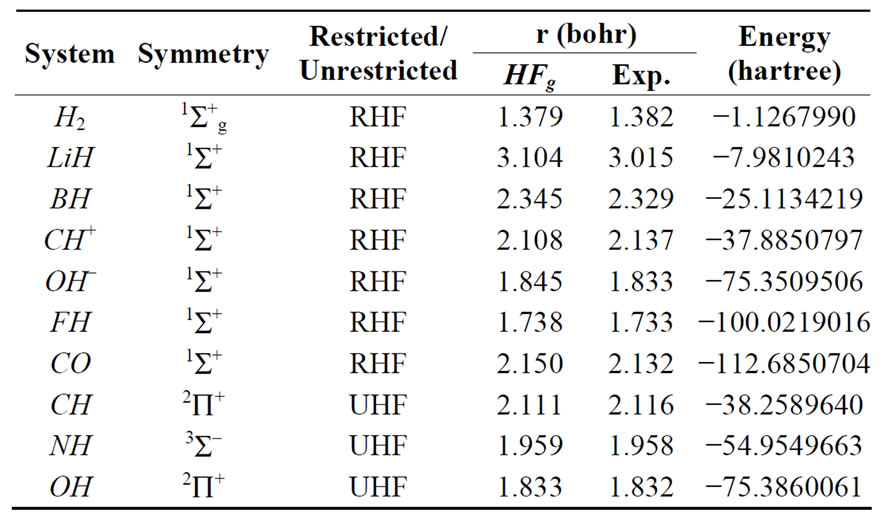
Table 2. Converged HFg energies and geometries using DZ basis.
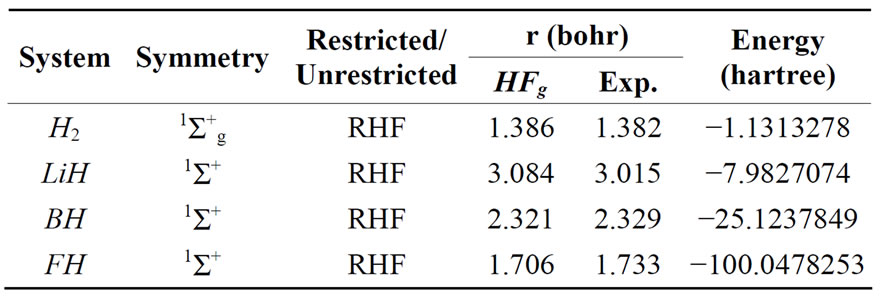
Table 3. Converged HFg energies and geometries using DZ polarized basis.
We performed several RHFg and UHFg calculations combining different initial values 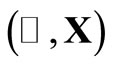 with distinct sets of the parameters qA, qV, qT and T0. We found that the narrow ranges of values of the parameters qV and qT, leading to a better convergence (smallest number of HFg cycles), namely,
with distinct sets of the parameters qA, qV, qT and T0. We found that the narrow ranges of values of the parameters qV and qT, leading to a better convergence (smallest number of HFg cycles), namely, 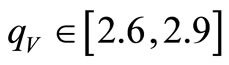 and
and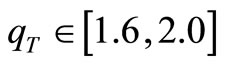 , are similar to those obtained in previous works [18,19]. In particular, for the minimal basis set, the best convergence is achieved for
, are similar to those obtained in previous works [18,19]. In particular, for the minimal basis set, the best convergence is achieved for 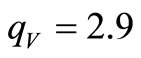 and
and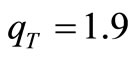 , which are quite close to the best values obtained for the RHF-GSA and UHF-GSA problems [18,19]. In addition, we performed several calculations using different values of qA, including
, which are quite close to the best values obtained for the RHF-GSA and UHF-GSA problems [18,19]. In addition, we performed several calculations using different values of qA, including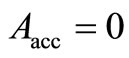 , which led to the convergence, therefore, been adopted in step 10) of the HFg algorithm, an acceptance probability,
, which led to the convergence, therefore, been adopted in step 10) of the HFg algorithm, an acceptance probability, 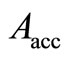 , equal to zero for all calculations.
, equal to zero for all calculations.
The general convergence behavior of the HFg algorithm is similar to that of the RHF-GSA and UHF-GSA methods [18,19]. For all systems and bases sets employed, it was always possible to obtain the global minimum, with several distinct combinations of these parameters, each set of parameters requiring a different number of HFg cycles. Also in all calculations, the HFg energies initially show a strong oscillatory behavior but soon afterwards the energy starts to smoothly converge towards the absolute minimum. Figures 2 and 3 present the RHFg and UHFg convergence profiles for the CH+ and OH molecules, indicating the values of the parameters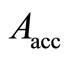 , qV, qT, T0, the atomic basis sets, the type of guess for the initial values of
, qV, qT, T0, the atomic basis sets, the type of guess for the initial values of 
 and X
and X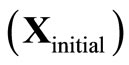 , and the number of the cycles for which convergence was achieved
, and the number of the cycles for which convergence was achieved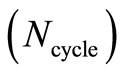 . Similar convergence profiles were obtained for all the others molecules.
. Similar convergence profiles were obtained for all the others molecules.
In order to verify the accuracy of the calculations, the RHFg and UHFg results were compared with those obtained by the standard gradient RHF/UHF geometry calculation method, for all molecules considered, using the
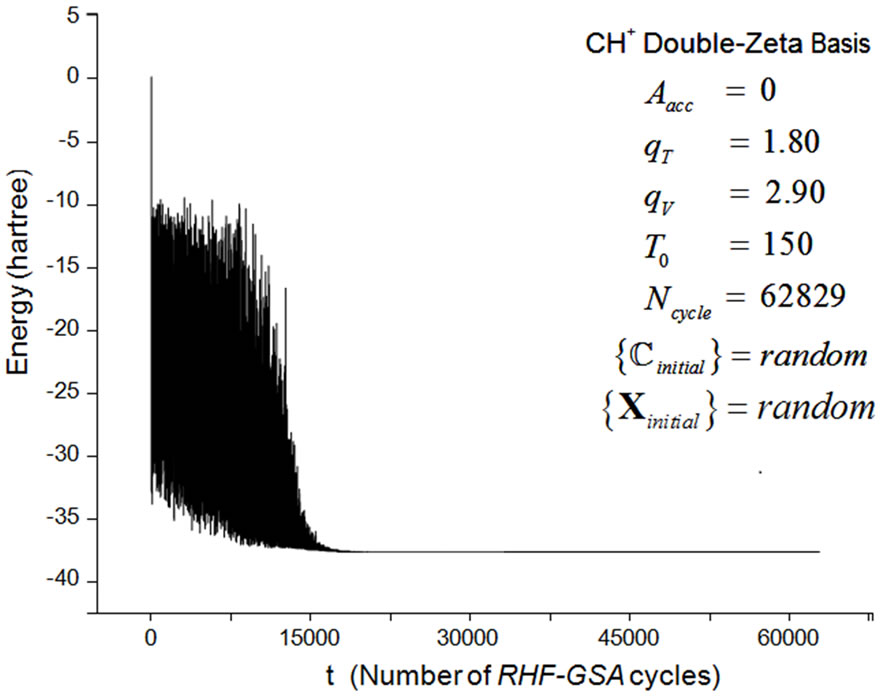
Figure 2. CH+ double-zeta basis HFg convergence process.
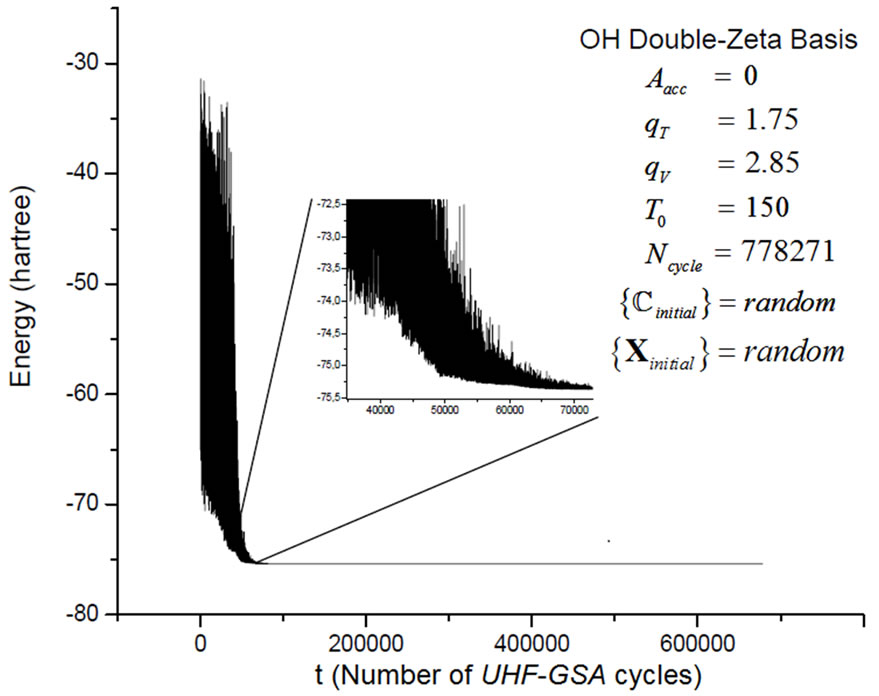
Figure 3. OH double-zeta basis HFg convergence process.
program GAMESS [39]. Three choices for the initial matrix  were considered when performing the RHF/ UHF-GAMESS calculations: the eigenvectors of core hamiltonian (Hcore)4, the eigenvectors of an extended Huckel calculations (Huckel)5, and the eigenvectors of a previous RHFg or UHFg calculation. Furthermore, whenever necessary, the Direct Inversion in the Iterative Subspace (DIIS) convergence acceleration technique [40,41] was also used for the RHF/UHF-GAMESS calculations.
were considered when performing the RHF/ UHF-GAMESS calculations: the eigenvectors of core hamiltonian (Hcore)4, the eigenvectors of an extended Huckel calculations (Huckel)5, and the eigenvectors of a previous RHFg or UHFg calculation. Furthermore, whenever necessary, the Direct Inversion in the Iterative Subspace (DIIS) convergence acceleration technique [40,41] was also used for the RHF/UHF-GAMESS calculations.
In all cases we examined, the RHFg and UHFg calculations converge to the global minimum with any randomly generated initial  and X values, what is not observed for the RHF/UHF-GAMESS calculations. Besides, the HFg method do not need any previous specification of the orbital occupancies.
and X values, what is not observed for the RHF/UHF-GAMESS calculations. Besides, the HFg method do not need any previous specification of the orbital occupancies.
The stochastic procedure GSA used in the previous works [18-20] and in this paper can be extended to other variational approaches, for instance, the Multi-Configuration Self-Consistent method [42] and in the NuclearElectronic Orbital theory [21-26]. Works in this direction are in progress.
5. Acknowledgements
M. A. C. Nascimento thanks financial support: FAPERJ (of Brazil); CAPES (of Brazil) and CNPq (of Brazil).
REFERENCES
- A N. Metropolis and S. Ulam, “The Monte Carlo Method,” Journal of the American Statistical Association, Vol. 44, No. 247, 1949, pp. 335-341. doi:10.1080/01621459.1949.10483310
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, “Equation of State Calculations by Fast Computing Machines,” Journal of Chemical Physics, Vol. 21, No. 6, 1953, pp. 1087-1092. doi:10.1063/1.1699114
- S. Kirkpatrick, C. D. Gelatt Jr. and M. P. Vecchi, “Optimization by Simulated Annealing,” Science, Vol. 220, No. 8, 1983, pp. 671-680. doi:10.1126/science.220.4598.671
- S. Kirkpatrick, “Optimization by Simulated Annealing: Quantitative Studies,” Journal of Statistical Physics, Vol. 34, No. 5-6, 1984, pp. 975-986. doi:10.1007/BF01009452
- H. Szu and R. Hartley, “Fast Simulated Annealing,” Physics Letters A, Vol. 122, No. 3-4, 1987, pp. 157-162. doi:10.1016/0375-9601(87)90796-1
- S. Geman and D. Geman, “Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images,” IEEE Transactions on Pattern Analysis Machine Intelligence, Vol. 6, 1984, pp. 721-741. doi:10.1109/TPAMI.1984.4767596
- C. Tsallis and D. A. Stariolo, “Generalized Simulated Annealing,” Physica A, Vol. 233, No. 1-2, 1996, pp. 395- 406. doi:10.1016/S0378-4371(96)00271-3
- C. Tsallis, “Possible Generalization of Boltzmann-Gibbs Statistics,” Journal of Statistical Physics, Vol. 52, 1988, pp. 479-487. doi:10.1007/BF01016429
- E. M. F. Curado and C. Tsallis, “Generalized Statistical Mechanics: Connection with Thermodynamics,” Journal of Physics A: Mathematical and General, Vol. 24, No. 2, 1991, p. L69; Journal of Physics A: Mathematical and General, Vol. 24, No. 4, 1992, p. 1019 (Corrigendum). doi:10.1088/0305-4470/25/4/038
- M. A. Moret, P. G. Pascutti, P. M. Bisch and K. C. Mundim, “Stochastic Molecular Optimization Using Generalized Simulated Annealing,” Journal of Computational Chemistry, Vol. 19, No. 6, 1998, pp. 647-657. doi:10.1002/(SICI)1096-987X(19980430)19:6<647::AID-JCC6>3.0.CO;2-R
- M. A. Moret, P. M. Bisch, K. C. Mundim and P. G. Pascutti, “New Stochastic Strategy to Analyze Helix Folding,” Biophysical Journal, Vol. 82, No. 3, 2002, pp. 1123-1132. doi:10.1016/S0006-3495(02)75471-4
- L. E. Espinola, R. Gargano, K. C. Mundim and J. J. Soares Neto, “The Na+ HF Reactive Probabilities Calculations Using Two Different Potential Energy Surfaces,” Chemical Physics Letters, Vol. 361, No. 3-4, 2002, pp. 271-276. doi:10.1016/S0009-2614(02)00924-7
- A. F. A. Vilela, J. J. Soares Neto, K. C. Mundim, M. S. P. Mundim and R. Gargano, “Fitting Potential Energy Surface for Reactive Scattering Dynamics through Generalized Simulated Annealing,” Chemical Physics Letters, Vol. 359, No. 5-6, 2002, pp. 420-427. doi:10.1016/S0009-2614(02)00597-3
- K. C. Mundim, T. J. Lemaire and A. Bassrei, “Optimization of Non-Linear Gravity Models through Generalized Simulated Annealing,” Physica A, Vol. 252, No. 3-4, 1998, pp. 405-416. doi:10.1016/S0378-4371(97)00634-1
- K. C. Mundim and D. E. Ellis, “Stochastic Classical Molecular Dynamics Coupled to Functional Density Theory: Applications to Large Molecular Systems,” Brazilian Journal of Physics, Vol. 29, No. 1, 1999, pp. 199-214. doi:10.1590/S0103-97331999000100018
- D. E. Ellis, K. C. Mundim, D. Fuks, S. Dorfman and A. Berner, “Interstitial Carbon in Copper: Electronic and Mechanical Properties,” Philosophical Magazine Part B, Vol. 79, No. 10, 1999, pp. 1615-1630.
- S. Dorfman, D. Fuks, L. A. C. Malbouisson, K. C. Mundim and D. E. Ellis, “Influence of Many-Body Interactions on Resistance of a Grain Boundary with Respect to a Sliding Shift,” International Journal of Quantum Chemistry, Vol. 90, No. 4-5, 2002, pp. 1448-1456. doi:10.1002/qua.10357
- M. D. de Andrade, K. C. Mundim and L. A. C. Malbouisson, “GSA Algorithm Applied to Electronic Structure: Hartree-Fock-GSA Method,” International Journal of Quantum Chemistry, Vol. 103, No. 5, 2005, pp. 493- 499. doi:10.1002/qua.20580
- M. D. de Andrade, K. C. Mundim, M. A. C. Nascimento and L. A. C. Malbouisson, “GSA Algorithm Applied to Electronic Structure II: UHF-GSA Method,” International Journal of Quantum Chemistry, Vol. 106, No. 13, 2006, pp. 2700-2705. doi:10.1002/qua.21080
- M. D. de Andrade, M. A. C. Nascimento, K. C. Mundim, A. M. C. SOBRINHO and L. A. C. Malbouisson, “Atomic Basis Sets Optimization Using the Generalized Simulated Annealing Approach: New Basis Sets for the First Row Elements,” International Journal of Quantum Chemistry, Vol. 108, No. 13, 2008, pp. 2486-2498. doi:10.1002/qua.21666
- S. P. Webb, T. Iordanov and S. Hammes-Shiffer, “Multiconfigurational Nuclearelectronic Orbital Approach: Incorporation of Nuclear Quantum Effects in Electronic Structure Calculations,” International Journal of Quantum Chemistry, Vol. 117, No. 9, 2002, pp. 4106-4118.
- M. V. Pak, C. Swalina, S. P. Webb and S. HammesShiffer, “Application of the Nuclear-Electronic Orbital Method to Hydrogen Transfer Systems: Multiple Centers and Multiconfigurational Wavefunctions,” Chemical Physics, Vol. 304, No. 1-2, 2004, pp. 227-236. doi:10.1016/j.chemphys.2004.06.009
- C. Swalina, M. V. Pak and S. Hammes-Shiffer. “Analysis of the Nuclear-Electronic Orbital Method for Model Hydrogen Transfer Systems,” Journal of Chemical Physics, Vol. 123, No. 1, 2005, p. 14303. doi:10.1063/1.1940634
- A. Reyes, M. V. Pak and S. Hammes-Shiffer, “Investigation of Isotope Effects with the Nuclear-Electronic Orbital Approach,” Journal of Chemical Physics, Vol. 123, No. 6, 2005, p. 64104. doi:10.1063/1.1990116
- J. H. Skone, M. V. Pak and S. Hammes-Shiffer, “Nuclear-Electronic Orbital Nonorthogonal Configuration Interaction Approach,” Journal of Chemical Physics, Vol. 123, No. 13, 2005, p. 134108. doi:10.1063/1.2039727
- C. Swalina, M. V. Pak, A. Chakraborty and S. HammesShiffer, “Explicit Dynamical Electron-Proton Correlation in the Nuclear-Electronic Orbital Framework,” Journal of Chemical Physics A, Vol. 110, No. 33, 2006, pp. 9983-9987. doi:10.1021/jp0634297
- C. C. J. Roothaan, “New Developments in Molecular Orbital Theory,” Reviews of Modern Physics, Vol. 23, No. 2, 1951, pp. 69-89. doi:10.1103/RevModPhys.23.69
- J. A. Pople and R. K. Nesbet, “Self-Consistent Orbitals for Radicals,” Journal of Chemical Physics, Vol. 22, No. 3, 1954, pp. 571-572. doi:10.1063/1.1740120
- D. B. Cook, “Handbook of Computational Chemistry,” Oxford University Press, Oxford, 1998, p. 671.
- A. Szabo and N. S. Ostlund, “Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory,” Dover Publications, New York, 1996, Appendix C, pp. 444.
- W. H. Adams, “Stability of Hartree-Fock States,” Physical Review, Vol. 127, No. 5, 1962, pp. 1650-1658. doi:10.1103/PhysRev.127.1650
- R. E. Stanton, “Multiple Solutions to the Hartree-Fock Problem I. General Treatment of Two-Electron ClosedShell Systems,” Journal of Chemical Physics, Vol. 48, No. 1, 1968, pp. 258-262. doi:10.1063/1.1667913
- J. C. Facelli and R. H. Contreras, “A General Relation between the Intrinsic Convergence Properties of SCF Hartree-Fock Calculations and the Stability Conditions of Their Solutions,” Journal of Chemical Physics, Vol. 79, No. 7, 1983, pp. 3421-3423. doi:10.1063/1.446190
- L. A. C. Malbouisson and J. D. M. Vianna, “An Algebraic Method for Solving Hartree-Fock-Roothaan Equations,” Journal of Chemical Physics, Vol. 87, 1990, pp. 2017-2025.
- R. M. Teixeira Filho, L. A. C. Malbouisson and J. D. M. Vianna, “An Algebraic Method for Solving Hartree-Fock Equations II. Open-Shell Molecular Systems,” Journal of Chemical Physics, Vol. 90, No. 10, 1993, pp. 1999-2005.
- L. E. Dardenne, N. Makiuchi, L. A. C. Malbouisson and J. D. M. Vianna, “Multiplicity, Instability, and SCF Convergence Problems in Hartree-Fock Solutions,” Journal of Quantum Chemistry, Vol. 76, No. 5, 2000, pp. 600-610. doi:10.1002/(SICI)1097-461X(2000)76:5<600::AID-QUA2>3.0.CO;2-3
- K. N. Kudin, G. E. Scuseria and E. Cancès, “A Black-Box Self-Consistent Field Convergence Algorithm: One Step Closer,” Journal of Chemical Physics, Vol. 116, No. 19, 2002, pp. 8255-8261. doi:10.1063/1.1470195
- K. P. Huber and G. Herzberg, “Constants of Diatomic Molecules,” Van Nostrand, New York, 1979.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, “General Atomic and Molecular Electronic Structure System,” Journal of Computational Chemistry, Vol. 14, No. 11, 1993, pp. 1347-1363. doi:10.1002/jcc.540141112
- P. Pulay, “Convergence Acceleration of Iterative Sequences. The Case of SCF Iteration,” Chemical Physics Letters, Vol. 73, No. 2, 1980, pp. 393-398. doi:10.1016/0009-2614(80)80396-4
- P. Pulay, “Improved SCF Convergence Acceleration,” Journal of Computational Chemistry, Vol. 3, No. 4, 1982, pp. 556-560. doi:10.1002/jcc.540030413
- R. McWeeny, “Methods of Molecular Quantum Mechanics,” 2nd Edition, Academic Press, London, 1978, p. 255.
NOTES
*Corresponding author.
1According to a citation in the article by Metropolis [2], this method was also proposed independently by J. E. Mayer in the study of liquids.
2kB it is the Boltzmann constant; T is a noise control parameter, usually denominated temperature, which is pre-established at the beginning of the process.
3Linear Combination of Atomic Orbitals.
4Input GAMESS “$GUESS” option “HCORE”.
5Input GAMESS “$GUESS” option “HUCKEL”.

