Paper Menu >>
Journal Menu >>
 Creative Education 2013. Vol.4, No.8A, 6-8 Published Online August 2013 in SciRes (http://www.scirp.org/journal/ce) http://dx.doi.org/10.4236/ce.2013.48A002 Copyright © 2013 SciRes. 6 Geometrical Approach to Kepler’s Laws of Planetary Motion Yusuke Yajima College of Education, Ibaraki University, Mito, Japan Email: yyjm@mx.ibaraki.ac.jp Received June 17th, 2013; revised July 17th, 2013; accepted July 25th, 2013 Copyright © 2013 Yusuke Yajima. This is an open access article distributed under the Creative Commons At- tribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. The elementary pen-and-string method to draw ellipsis has been devised to examine planetary orbits on the basis of the Kepler’s laws. Besides qualitative features of the orbits, quantitative dependence of the orbital shape on the quantities appearing in the Kepler’s laws can also be analyzed with simple geometri- cal procedures. The method thus provides a relevant intermediate step to students prior to the study of the rigorous theory of central force problems. Keywords: Kepler; Planet; Orbit; Ellipse Introduction Kepler’s laws of planetary motion are usually stated as (Fig- ure 1): 1) The planetary motion follows an elliptic orbit with the Sun at one of its two foci, 2) The area swept by a line joining a planet and the Sun dur- ing a unit time interval, areal velocity, is constant, and, 3) The cube of the semimajor axis of the elliptic orbit is pro- portional to the square of the orbital period, i.e. one year. Kepler’s laws are among the most well-known scientific laws that frequently appear in articles on popular sciences. Despite of their ubiquity, however, the laws require university level knowledge on analytical geometry to treat quadratic curves and some expertise on handling differential equations to solve physical problems if they are to be fully understood on the bases of more fundamental physical principles, i.e. Newtonian dynamics. This mathematical aloofness often discourages those, say secondary school students, who are not satisfied with knowing only what are stated in Kepler’s laws but interested further in how they work and why they stand. Therefore, it is of much pedagogic importance to provide some intermediate ap- proach that can turn Kepler’s laws into congenial working knowledge without recourse to university level mathematics. As a possible candidate for such approach, a method based solely on elementary geometry is discussed here. The method has been devised by noting that the key notion of the Kepler’s laws is the elliptic nature of planetary orbits, and, accordingly, any simple method to handle ellipses, if appropriately related to the principles of mechanics, could make the laws viable even without the knowledge on university level mathematics and physics. Motivated by R. P. Feynman’s solely geometric proof of Ke- pler’s first law (Goodstein & Goodstein, 1999), a non-mathematical scheme comprising a series of geometrical construction has been proposed to analyze major features of planetary orbits (Okabe & Yajima, 2004; Yajima & Okabe, 2006). Here an alternative but much simpler approach based on a familiar method to draw ellipses is discussed. Figure 1. Quantities appearing in Kepler’s laws of planetary motion. Method The most familiar and virtually unique elementary method to draw an ellipse is to use a pair of pins, a string, and a pen; also a paper is of course necessary on which the ellipse is drawn. The string is tied to the pins at each end and the pins are firmly pushed into the paper separately. The separation of the pins is thus shorter than the length of the string. The pen, when moved so as to keep pulling the string taut, traces an ellipse. By using 2a long string and setting the distance of pins to 2ae (e < 1: orbit’s eccentricity), one can draw an ellipse with its two foci on the pins and having semimajor and semiminor axes of a and 2 1ba e , respectively (Figure 2). This method to construct an ellipse is referred to as “pen-and-string” method hereafter. Next we summarize some important properties of the elliptic orbit of planets moving under the gravitational potential, Vr kr . (1) For details of the discussion to follow, any standard textbook on classical mechanics should be consulted (Goldstein, 1980). Semimajor axis a of the orbit becomes, 2 k aE (2) where E (<0) is the total mechanical energy. The angular mo- mentum vector L and the planet mass m determine semiminor axis b as,  Y. YAJIMA Figure 2. Pin-and-string method as applied to the drawing of pla- netary orbits under various conditions. 2 L bmE , (3) and semi latus rectum as, 2 1la e 2 L lmk , (4) where l = |L|. Quantities that appear in the Kepler’s laws, the orbital period, one year, 32 π2TkmE and the areal velocity 2 A Lm can then be expressed respectively by the above parameters characterizing the orbital shape, a, b, and l, as, 32 2πTmka , (5) and, 11 22 b Akmlkm a . (6) When the pen-and-string method is used to draw planetary orbits, the length of a string tied to pins, 2a, determines the orbital period (Equation (5)) and, though not appeared explic- itly in the Kepler’s laws, the total mechanical energy of the motion (Equation (2)). And orbits with various areal velocities can be drawn by changing the separation of the pins as in Fig- ure 2 (Equation (6)). For instance, one can draw orbits having the same areal ve- locity A but different orbital periods T, if one uses strings with different length and adjusts the pin separation so as to keep the semi latus rectum l constant. And in case one wants to see how the orbital having a definite one year period T, alters its shape when the areal velocity A is changed, one can use single string and draw orbits by changing either the semi latus rectum l or the semiminor axis b; the latter might be more convenient in this case since whilebAl A . Examples To see how this method works, Figure 3 shows orbits char- acterized by the same areal velocity but different one year pe- riod. The string used to draw the larger orbit is twice as long as the one used to draw the smaller orbit. The magnitude of the mechanical energy, |E| = −E, for the larger orbit is therefore one half of that for the smaller orbit (Equation (2)). Accordingly, the one year period on the larger orbit is about 2.8 times longer than that on the smaller orbit (Equation (5)). Despite the dif- ference in mechanical energy and one year period, they share the same areal velocity that leads to the equal length of semi latus rectum l. Figure 4 illustrates, on the other hand, orbits of a planet moving with the same one year period but with different areal velocity. Having the same orbital period, they can all be drawn with a string. Values of areal velocity for three orbits in the figure are in the ratio of 3:2:1, so are the lengths of semiminor axis (Equation (6)). Circles around the fixed pin that represents the sun in these figures have radii 2a, the length of the string used to draw each orbit. Any orbit having the particular one year period specified by the string used is drawn within the corresponding circle. It might merit attention that eccentricity of the orbits shown here is much exaggerated compared with that of actual planetary orbits in our solar system. For quantitative discussions, it is useful to prepare such graph data as those showing the relation between one year pe- riod T and the string length 2a: 32 2Ta (Figure 5), and Figure 3. Planetary orbits with the same areal velocity but different orbital period. See text for details. Figure 4. Planetary orbits with the same orbital period but different areal velocity. See text for details. Figure 5. Conversion graph assisting to draw orbits with various orbital period, i.e. one year period. Copyright © 2013 SciRes. 7 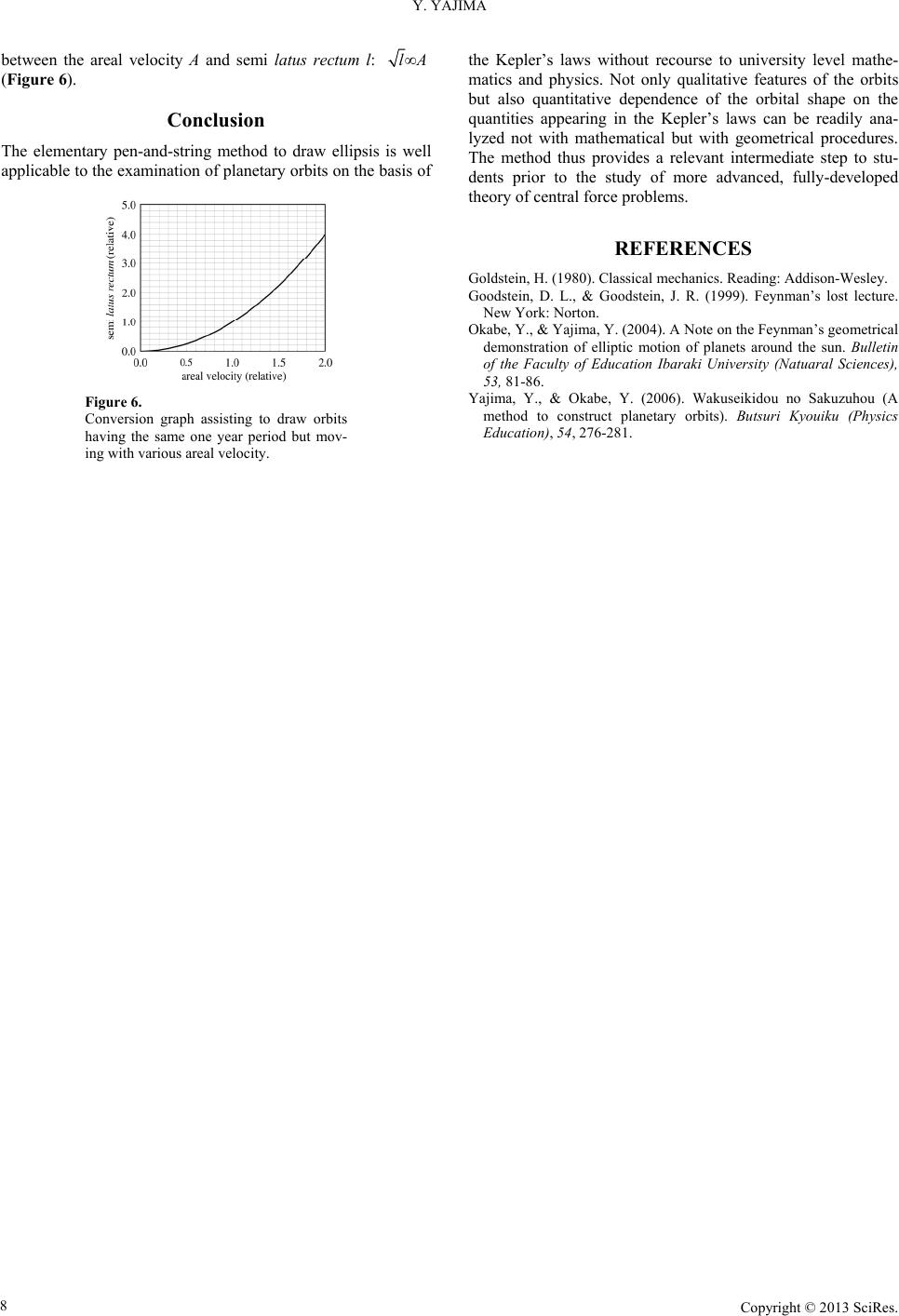 Y. YAJIMA Copyright © 2013 SciRes. 8 between the areal velocity A and semi latus rectum l: l A (Figure 6). the Kepler’s laws without recourse to university level mathe- matics and physics. Not only qualitative features of the orbits but also quantitative dependence of the orbital shape on the quantities appearing in the Kepler’s laws can be readily ana- lyzed not with mathematical but with geometrical procedures. The method thus provides a relevant intermediate step to stu- dents prior to the study of more advanced, fully-developed theory of central force problems. Conclusion The elementary pen-and-string method to draw ellipsis is well applicable to the examination of planetary orbits on the basis of REFERENCES Goldstein, H. (1980). Classical mechanics. Reading: Addison-Wesley. Goodstein, D. L., & Goodstein, J. R. (1999). Feynman’s lost lecture. New York: Norton. Okabe, Y., & Yajima, Y. (2004). A Note on the Feynman’s geometrical demonstration of elliptic motion of planets around the sun. Bulletin of the Faculty of Education Ibaraki University (Natuaral Sciences), 53, 81-86. Yajima, Y., & Okabe, Y. (2006). Wakuseikidou no Sakuzuhou (A method to construct planetary orbits). Butsuri Kyouiku (Physics Education), 54, 276-281. Figure 6. Conversion graph assisting to draw orbits having the same one year period but mov- ing with various areal velocity. |

