Journal of Environmental Protection, 2013, 4, 57-64
http://dx.doi.org/10.4236/jep.2013.48A1008 Published Online August 2013 (http://www.scirp.org/journal/jep)
57
An Analytical Formulation for Pollutant Dispersion
Simulation in the Atmospheric Boundary Layer
Glênio A. Gonçalves, Regis S. de Quadros, Daniela Buske*
Federal University of Pelotas (UFPel), Department of Mathematics and Statistics (IFM/DME), Pelotas, Brazil.
Received June 14th, 2013; revised July 16th, 2013; accepted August 3rd, 2013
Copyright © 2013 Glênio A. Gonçalves et al. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
In this work we present the solution of the two-dimensional advection-diffusion equation by the GILTT method. The
GILTT approach uses, in the series expansion, eigenfunctions given in terms of cosine functions. Here, a different ex-
pansion for the solution of the advection-diffusion equation will be explored. In other words, a Sturm-Liouville problem
carrying more information of the original problem is considered, given by Bessel functions. Numerical simulations and
comparisons with experimental data are presented.
Keywords: Analytical Solution; Advection-Diffusion Equation; Air Pollution Modeling; Integral Transform; Bessel
Functions
1. Introduction
The advection-diffusion equation has long been used to
describe the dispersion of contaminants in the atmos-
phere [1]. Efforts have been made over the years to ob-
tain analytical solutions of this equation in order to mod-
eling air pollution. According to [2,3], these solutions are
valid for very specialized practical situations, and in ma-
jority with restrictions on wind and eddy diffusivities
vertical profiles [4-18]. To solve the advection-diffusion
equation for more realistic physical scenario appeared in
the literature the ADMM (Advection Diffusion Multi-
layer Method) approach [19,20], valid for any eddy dif-
fusivity and wind profile depending on the height. The
main idea relies on the discretization of the Atmospheric
Boundary Layer (ABL) in a multilayer domain, assuming
in each layer that the eddy diffusivity and wind profile
take averaged values. The resulting advection-diffusion
equation in each layer is then solved by the Laplace
Transform technique. A more general methodology, which
skips the multilayer discretisation of the height z appear-
ing in the ADMM approach, is known in the literature as
GILTT (Generalized Integral Laplace Transform Tech-
nique) approach [2,3,21]. The main idea of this method-
ology relies on the expansion of the pollutant concentra-
tion in series of eigenfunctions attained from an auxiliary
Sturm-Liouville problem, replacement of this equation in
the advection-diffusion equation and taking moments.
The procedure results a matrix ordinary differential equa-
tion which is solved analytically by the Laplace Trans-
form technique. Similar solutions were proposed by [22,
23].
To reach our objective, we begin presenting the solu-
tion of the two-dimensional advection-diffusion equation
in Cartesian geometry by the GILTT approach [2], con-
sidering that the eddy diffusivity and the vertical wind
profile depend on the z variable. Traditionally, the
GILTT approach uses as basis eigenfunctions given in
terms of cosine functions. Here, another Sturm-Liouville
problem will be considered, carrying more information
of the original problem. In this case, the eigenfunctions
are given by Bessel functions. Once we construct the
general solution, numerical simulations and future per-
spectives of this methodology are presented.
2. The Advection-Diffusion Equation and the
GILTT Method
For a Cartesian coordinate system the advection-diffu-
sion equation, using first order closure of turbulence, is
written like [24]:
xyz
cccc
uvw
txyz
ccc
K
KK
xxyyzz


 
 
 
S



 

 
 
(1)
*Corresponding author.

An Analytical Formulation for Pollutant Dispersion Simulation in the Atmospheric Boundary Layer
58
where c denotes the average concentration of a passive
(g/m3), u, v, w are the mean wind (m/s) components
along the axis x, y and z, respectively and S is the source
term. Kx, Ky, Kz are the Cartesian components of eddy
diffusivity (m2/s) in the x, y and z directions, respectively.
In the first order closure all the information on the turbu-
lence complexity is contained in the eddy diffusivities.
Problem (1) is solved analytically by the 3D-GILTT
method [3,21,25]. Here, for comparison with experimen-
tal data we will assume for the advection-diffusion Equa-
tion (1): stationary conditions, crosswind integrated con-
centrations and that the advection is much higher than the
diffusion in the x-direction. After the simplifications, let
us consider the problem:
y
z
cc
uK
y
x
zz

 

 



(2)
for 0 < z < h and x > 0, subject to the boundary condi-
tions of zero flux at the ground and ABL top and a source
with emission Q at height Hs (
 
0,
ys
uczQz H   at
x = 0). Here
y
c represents the crosswind integrated
concentration, h is the ABL height,
z
K
is the eddy dif-
fusivity variable with the height z (

z
K
Kz), u is
the longitudinal wind speed (

zuu), and δ is the Di-
rac delta function.
Problem (2) has a well-known solution by the GILTT
method. Following the works of [2,25] we write the so-
lution of problem (2) as:
  
0
,
N
yn
n
cxzcx z


n
(3)
where are the eigenfunctions of an associated
Sturm-Liouville problem and

nz


n
cx is the transformed
concentration.
Traditionally, in the application of the GILTT method,
the following auxiliary Sturm-Liouville problem is cho-
sen:
 
20
nnn
zz 
 
at (4a) 0zh

0
nz

 at (4b) 0, ,zh
which has the solution


cos
nn
zz


 , where


nz
are the eigenfunctions and π
nnh


are the respective eigenvalues.

0,n

1, 2,
Here, a different expansion for the solution of the ad-
vection-diffusion equation will be explored. In other
words, we propose another Sturm-Liouville problem as
the basis generator. The idea of this proposal comes from
the fact that the auxiliary problem (4) has the same shape
of the ordinary differential equation (relative do z vari-
able) that appears in the solution of Equation (2) by the
method of separation of variables, when the vertical eddy
diffusivity is considered constant. This suggests the pos-
sibility of using an auxiliary problem that appears in the
solution of Equation (2) by the method of separation of
variables, considering linear vertical eddy diffusivity,
z
K
z

, given by:






20
nn nn
zz z 


 at 0 (5a) zh


0
nz


 at (5b) 0,zh
which has Bessel functions of first specie and order zero
as solution



0nn
zJ zh   , where n



0,1, 2,n are the positive roots of the Bessel func-
tion of first specie and order one, 1
J
. Problem (5) car-
ries more information from the original problem than the
previous one.
To determine the unknown coefficient


n
cx we re-
place Equation (3) in Equation (1). Applying the integral
operator , we come out with the result:

0
.
h
mzz d
 
00
00
dd
hh
NN
n
nnmnmz
nn
cxuz cxKz
zz

 
0

 





(6)
Using the integration parts technique, we can recast
the second integral in Equation (6) as:
00
dd
hh
nn
m zmzmz
n
K
zK K
zzz z
  
 


 


z
(6a)
and once 0
n
mz
Kz




, the Equation (6) is rewritten
as:
 
00
00
dd
hh
NN
n
nnmnmz
nn
cxuz cxKz
z




0

 



(7)
which in matrix form reads like:


0FY x


Yx (8)
Here



Yx is the vector whose components are


n
cx
and F = B−1. E;


,nm
Bb and are the ma-
trices whose entries are, respectively:

,nm
Ee
0
d
h
n,mn m
bu
z and
0
dd
d
h
n
n,mm z
eK
zz




.
Equation (8) is subject to the initial condition Y(0),
which is obtained from the source condition
(




0,
ys
uczQz H   at x = 0) by a similar proce-
dure leading to





1
00
nms
Yc QHB

 , B−1 being
the inverse of matrix B.
The transformed problem represented by the Equation
(8) is solved analytically following the work [2], by the
combined Laplace transform technique and diagonaliza-
tion of the matrix F


1
FXDX

. By this procedure
we come out with the result:




10Yx XGxXY 


, (9)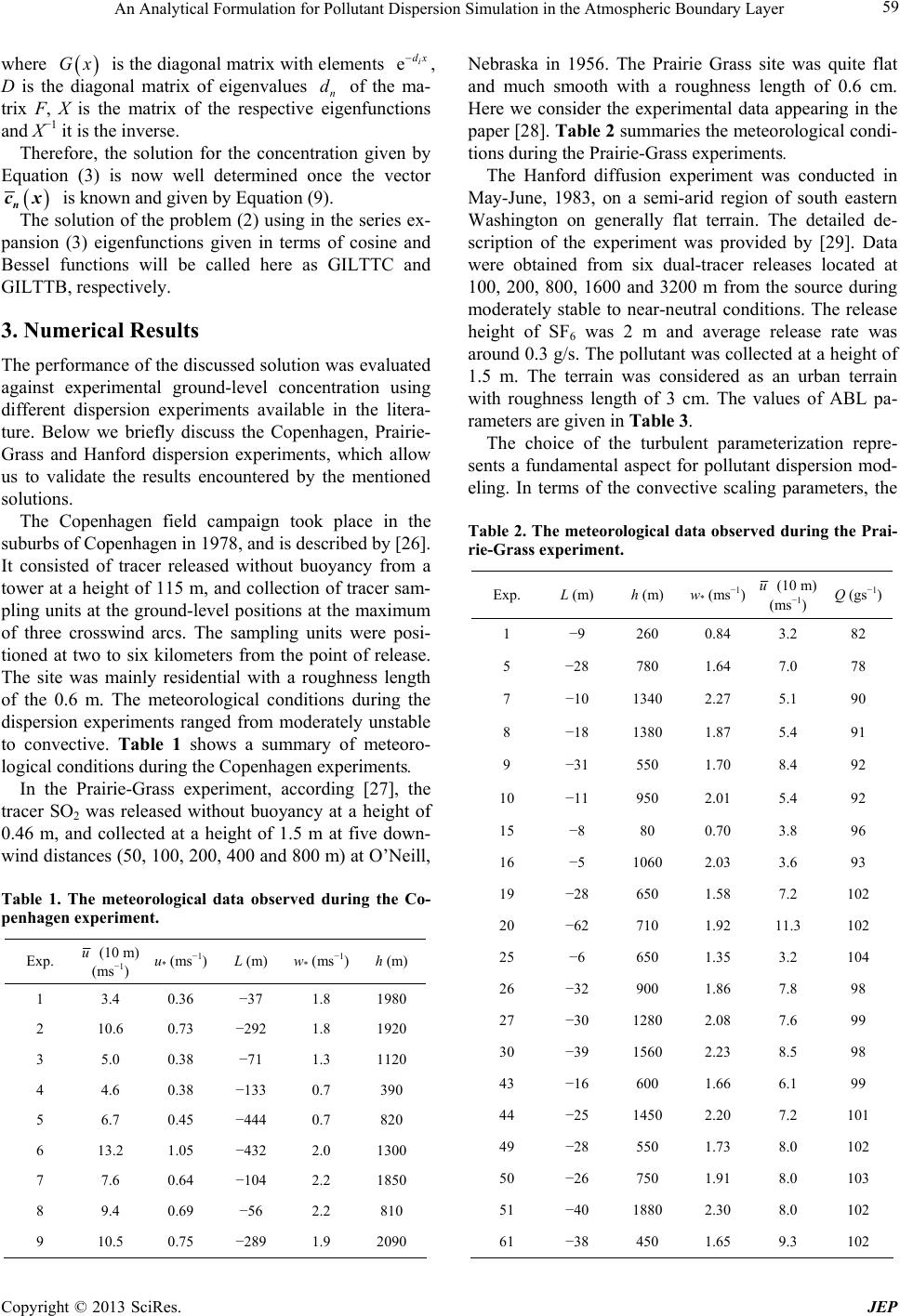

An Analytical Formulation for Pollutant Dispersion Simulation in the Atmospheric Boundary Layer 59
where is the diagonal matrix with elements ,
D is the diagonal matrix of eigenvalues n of the ma-
trix F, X is the matrix of the respective eigenfunctions
and X−1 it is the inverse.

Gx ei
dx
d
Therefore, the solution for the concentration given by
Equation (3) is now well determined once the vector

n
cx is known and given by Equation (9).
The solution of the problem (2) using in the series ex-
pansion (3) eigenfunctions given in terms of cosine and
Bessel functions will be called here as GILTTC and
GILTTB, respectively.
3. Numerical Results
The performance of the discussed solution was evaluated
against experimental ground-level concentration using
different dispersion experiments available in the litera-
ture. Below we briefly discuss the Copenhagen, Prairie-
Grass and Hanford dispersion experiments, which allow
us to validate the results encountered by the mentioned
solutions.
The Copenhagen field campaign took place in the
suburbs of Copenhagen in 1978, and is described by [26].
It consisted of tracer released without buoyancy from a
tower at a height of 115 m, and collection of tracer sam-
pling units at the ground-level positions at the maximum
of three crosswind arcs. The sampling units were posi-
tioned at two to six kilometers from the point of release.
The site was mainly residential with a roughness length
of the 0.6 m. The meteorological conditions during the
dispersion experiments ranged from moderately unstable
to convective. Table 1 shows a summary of meteoro-
logical conditions during the Copenhagen experiments.
In the Prairie-Grass experiment, according [27], the
tracer SO2 was released without buoyancy at a height of
0.46 m, and collected at a height of 1.5 m at five down-
wind distances (50, 100, 200, 400 and 800 m) at O’Neill,
Table 1. The meteorological data observed during the Co-
penhagen experiment.
Exp. u (10 m)
(ms−1) u* (ms−1) L (m) w* (ms−1) h (m)
1 3.4 0.36 −37 1.8 1980
2 10.6 0.73 −292 1.8 1920
3 5.0 0.38 −71 1.3 1120
4 4.6 0.38 −133 0.7 390
5 6.7 0.45 −444 0.7 820
6 13.2 1.05 −432 2.0 1300
7 7.6 0.64 −104 2.2 1850
8 9.4 0.69 −56 2.2 810
9 10.5 0.75 −289 1.9 2090
Nebraska in 1956. The Prairie Grass site was quite flat
and much smooth with a roughness length of 0.6 cm.
Here we consider the experimental data appearing in the
paper [28]. Table 2 summaries the meteorological condi-
tions during the Prairie-Grass experiments.
The Hanford diffusion experiment was conducted in
May-June, 1983, on a semi-arid region of south eastern
Washington on generally flat terrain. The detailed de-
scription of the experiment was provided by [29]. Data
were obtained from six dual-tracer releases located at
100, 200, 800, 1600 and 3200 m from the source during
moderately stable to near-neutral conditions. The release
height of SF6 was 2 m and average release rate was
around 0.3 g/s. The pollutant was collected at a height of
1.5 m. The terrain was considered as an urban terrain
with roughness length of 3 cm. The values of ABL pa-
rameters are given in Table 3.
The choice of the turbulent parameterization repre-
sents a fundamental aspect for pollutant dispersion mod-
eling. In terms of the convective scaling parameters, the
Table 2. The meteorological data observed during the Prai-
rie-Grass experiment.
Exp. L (m) h (m) w* (ms−1) u (10 m)
(ms−1) Q (gs−1)
1 −9 260 0.84 3.2 82
5 −28 780 1.64 7.0 78
7 −10 1340 2.27 5.1 90
8 −18 1380 1.87 5.4 91
9 −31 550 1.70 8.4 92
10 −11 950 2.01 5.4 92
15 −8 80 0.70 3.8 96
16 −5 1060 2.03 3.6 93
19 −28 650 1.58 7.2 102
20 −62 710 1.92 11.3 102
25 −6 650 1.35 3.2 104
26 −32 900 1.86 7.8 98
27 −30 1280 2.08 7.6 99
30 −39 1560 2.23 8.5 98
43 −16 600 1.66 6.1 99
44 −25 1450 2.20 7.2 101
49 −28 550 1.73 8.0 102
50 −26 750 1.91 8.0 103
51 −40 1880 2.30 8.0 102
61 −38 450 1.65 9.3 102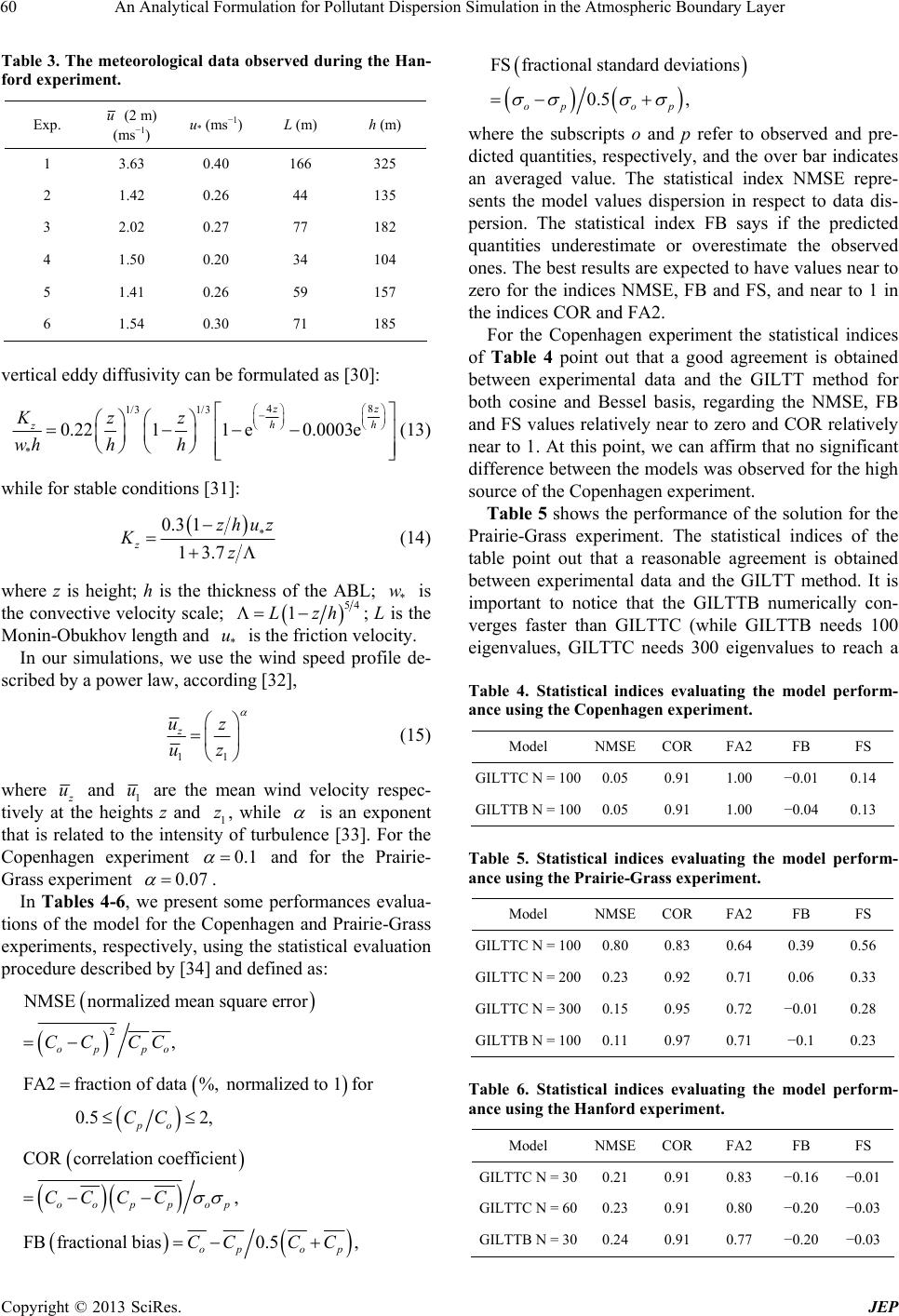

An Analytical Formulation for Pollutant Dispersion Simulation in the Atmospheric Boundary Layer
60
Table 3. The meteorological data observed during the Han-
ford experiment.
Exp. u (2 m)
(ms−1) u* (ms−1) L (m) h (m)
1 3.63 0.40 166 325
2 1.42 0.26 44 135
3 2.02 0.27 77 182
4 1.50 0.20 34 104
5 1.41 0.26 59 157
6 1.54 0.30 71 185
vertical eddy diffusivity can be formulated as [30]:
48 1/3 1/3
*
0.2211 e0.0003e
z
h z
Kzz
whh h
 

 
 

 


 
 

z
h




(13)
while for stable conditions [31]:

0.3 1
13.7
z
zhuz
Kz



(14)
where z is height; h is the thickness of the ABL; * is
the convective velocity scale;
w

54
1Lzh; L is the
Monin-Obukhov length and is the friction velocity.
*
In our simulations, we use the wind speed profile de-
scribed by a power law, according [32],
u
11
z
uz
uz




(15)
where
z
u and 1 u are the mean wind velocity respec-
tively at the heights z and 1, while z

is an exponent
that is related to the intensity of turbulence [33]. For the
Copenhagen experiment 0.1

 and for the Prairie-
Grass experiment 0.07

.
In Tables 4-6, we present some performances evalua-
tions of the model for the Copenhagen and Prairie-Grass
experiments, respectively, using the statistical evaluation
procedure described by [34] and defined as:



2
N
MSEnormalized mean square error
,
op po
CC CC


FA2fraction of data%, normalized to 1for
0.5 2,
po
CC




CORcorrelation coefficient
,
oo pp op
CCCC   


FBfractional bias0.5,
op op
CC CC



FSfractional standard deviations
0.5 ,
op op
   
where the subscripts o and p refer to observed and pre-
dicted quantities, respectively, and the over bar indicates
an averaged value. The statistical index NMSE repre-
sents the model values dispersion in respect to data dis-
persion. The statistical index FB says if the predicted
quantities underestimate or overestimate the observed
ones. The best results are expected to have values near to
zero for the indices NMSE, FB and FS, and near to 1 in
the indices COR and FA2.
For the Copenhagen experiment the statistical indices
of Table 4 point out that a good agreement is obtained
between experimental data and the GILTT method for
both cosine and Bessel basis, regarding the NMSE, FB
and FS values relatively near to zero and COR relatively
near to 1. At this point, we can affirm that no significant
difference between the models was observed for the high
source of the Copenhagen experiment.
Table 5 shows the performance of the solution for the
Prairie-Grass experiment. The statistical indices of the
table point out that a reasonable agreement is obtained
between experimental data and the GILTT method. It is
important to notice that the GILTTB numerically con-
verges faster than GILTTC (while GILTTB needs 100
eigenvalues, GILTTC needs 300 eigenvalues to reach a
Table 4. Statistical indices evaluating the model perform-
ance using the Copenhagen experiment.
Model NMSECOR FA2 FB FS
GILTTC N = 1000.05 0.91 1.00 −0.010.14
GILTTB N = 1000.05 0.91 1.00 −0.040.13
Table 5. Statistical indices evaluating the model perform-
ance using the Prairie-Grass experiment.
Model NMSECOR FA2 FB FS
GILTTC N = 1000.80 0.83 0.64 0.39 0.56
GILTTC N = 2000.23 0.92 0.71 0.06 0.33
GILTTC N = 3000.15 0.95 0.72 −0.010.28
GILTTB N = 100 0.11 0.97 0.71 −0.1 0.23
Table 6. Statistical indices evaluating the model perform-
ance using the Hanford experiment.
Model NMSECOR FA2 FB FS
GILTTC N = 300.21 0.91 0.83 −0.16 −0.01
GILTTC N = 600.23 0.91 0.80 −0.20 −0.03
GILTTB N = 300.24 0.91 0.77 −0.20 −0.03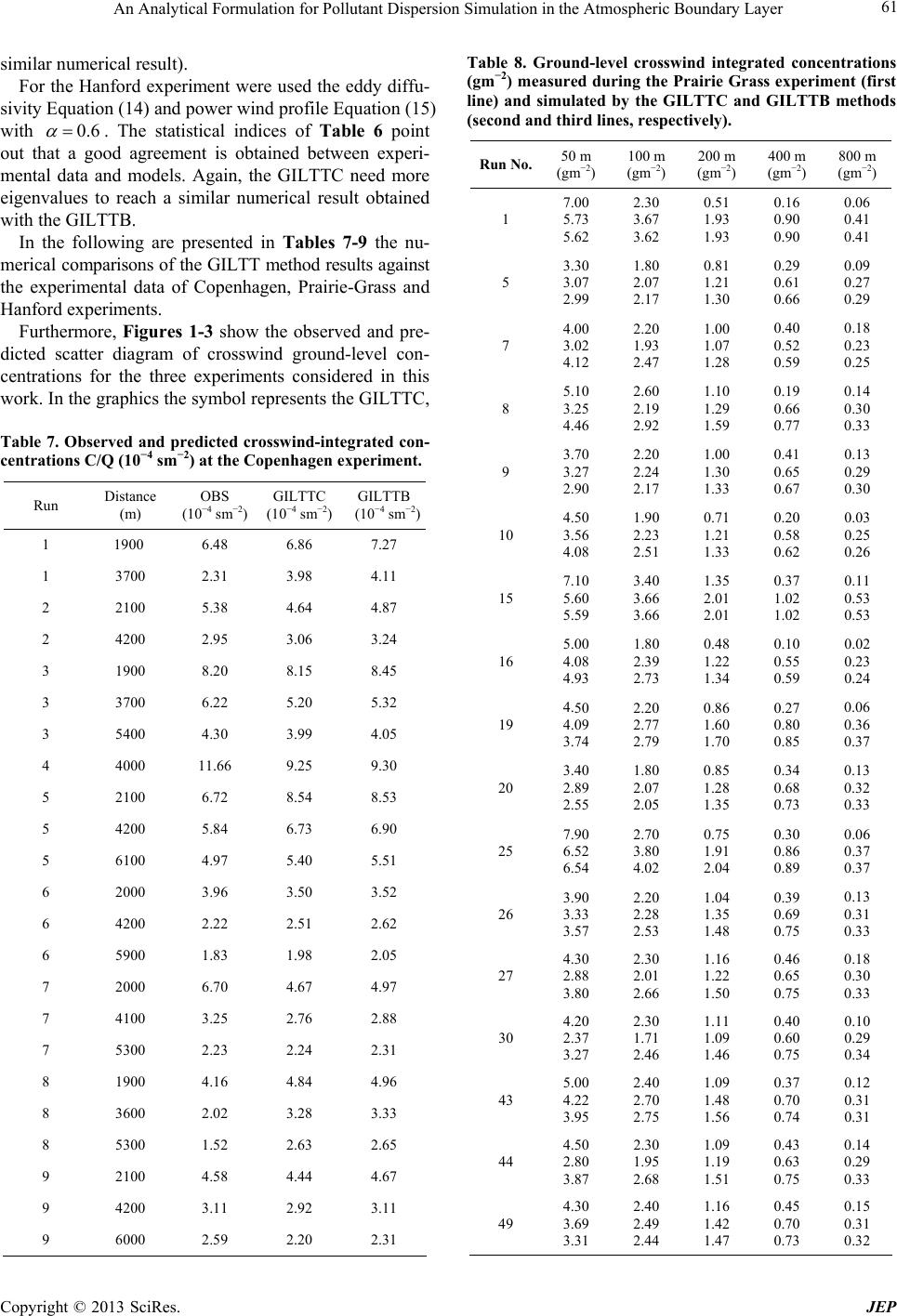

An Analytical Formulation for Pollutant Dispersion Simulation in the Atmospheric Boundary Layer 61
similar numerical result).
For the Hanford experiment were used the eddy diffu-
sivity Equation (14) and power wind profile Equation (15)
with 0.6

. The statistical indices of Table 6 point
out that a good agreement is obtained between experi-
mental data and models. Again, the GILTTC need more
eigenvalues to reach a similar numerical result obtained
with the GILTTB.
In the following are presented in Tables 7-9 the nu-
merical comparisons of the GILTT method results against
the experimental data of Copenhagen, Prairie-Grass and
Hanford experiments.
Furthermore, Figures 1-3 show the observed and pre-
dicted scatter diagram of crosswind ground-level con-
centrations for the three experiments considered in this
work. In the graphics the symbol represents the GILTTC,
Table 7. Observed and predicted crosswind-integrated con-
centrations C/Q (10−4 sm−2) at the Copenhagen experiment.
Run Distance
(m)
OBS
(10−4 sm−2)
GILTTC
(10−4 sm−2)
GILTTB
(10−4 sm−2)
1 1900 6.48 6.86 7.27
1 3700 2.31 3.98 4.11
2 2100 5.38 4.64 4.87
2 4200 2.95 3.06 3.24
3 1900 8.20 8.15 8.45
3 3700 6.22 5.20 5.32
3 5400 4.30 3.99 4.05
4 4000 11.66 9.25 9.30
5 2100 6.72 8.54 8.53
5 4200 5.84 6.73 6.90
5 6100 4.97 5.40 5.51
6 2000 3.96 3.50 3.52
6 4200 2.22 2.51 2.62
6 5900 1.83 1.98 2.05
7 2000 6.70 4.67 4.97
7 4100 3.25 2.76 2.88
7 5300 2.23 2.24 2.31
8 1900 4.16 4.84 4.96
8 3600 2.02 3.28 3.33
8 5300 1.52 2.63 2.65
9 2100 4.58 4.44 4.67
9 4200 3.11 2.92 3.11
9 6000 2.59 2.20 2.31
Table 8. Ground-level crosswind integrated concentrations
(gm−2) measured during the Prairie Grass experiment (first
line) and simulated by the GILTTC and GILTTB methods
(second and third lines, respectively).
Run No.50 m
(gm−2)
100 m
(gm−2)
200 m
(gm−2)
400 m
(gm−2)
800 m
(gm−2)
1
7.00
5.73
5.62
2.30
3.67
3.62
0.51
1.93
1.93
0.16
0.90
0.90
0.06
0.41
0.41
5
3.30
3.07
2.99
1.80
2.07
2.17
0.81
1.21
1.30
0.29
0.61
0.66
0.09
0.27
0.29
7
4.00
3.02
4.12
2.20
1.93
2.47
1.00
1.07
1.28
0.40
0.52
0.59
0.18
0.23
0.25
8
5.10
3.25
4.46
2.60
2.19
2.92
1.10
1.29
1.59
0.19
0.66
0.77
0.14
0.30
0.33
9
3.70
3.27
2.90
2.20
2.24
2.17
1.00
1.30
1.33
0.41
0.65
0.67
0.13
0.29
0.30
10
4.50
3.56
4.08
1.90
2.23
2.51
0.71
1.21
1.33
0.20
0.58
0.62
0.03
0.25
0.26
15
7.10
5.60
5.59
3.40
3.66
3.66
1.35
2.01
2.01
0.37
1.02
1.02
0.11
0.53
0.53
16
5.00
4.08
4.93
1.80
2.39
2.73
0.48
1.22
1.34
0.10
0.55
0.59
0.02
0.23
0.24
19
4.50
4.09
3.74
2.20
2.77
2.79
0.86
1.60
1.70
0.27
0.80
0.85
0.06
0.36
0.37
20
3.40
2.89
2.55
1.80
2.07
2.05
0.85
1.28
1.35
0.34
0.68
0.73
0.13
0.32
0.33
25
7.90
6.52
6.54
2.70
3.80
4.02
0.75
1.91
2.04
0.30
0.86
0.89
0.06
0.37
0.37
26
3.90
3.33
3.57
2.20
2.28
2.53
1.04
1.35
1.48
0.39
0.69
0.75
0.13
0.31
0.33
27
4.30
2.88
3.80
2.30
2.01
2.66
1.16
1.22
1.50
0.46
0.65
0.75
0.18
0.30
0.33
30
4.20
2.37
3.27
2.30
1.71
2.46
1.11
1.09
1.46
0.40
0.60
0.75
0.10
0.29
0.34
43
5.00
4.22
3.95
2.40
2.70
2.75
1.09
1.48
1.56
0.37
0.70
0.74
0.12
0.31
0.31
44
4.50
2.80
3.87
2.30
1.95
2.68
1.09
1.19
1.51
0.43
0.63
0.75
0.14
0.29
0.33
49
4.30
3.69
3.31
2.40
2.49
2.44
1.16
1.42
1.47
0.45
0.70
0.73
0.15
0.31
0.32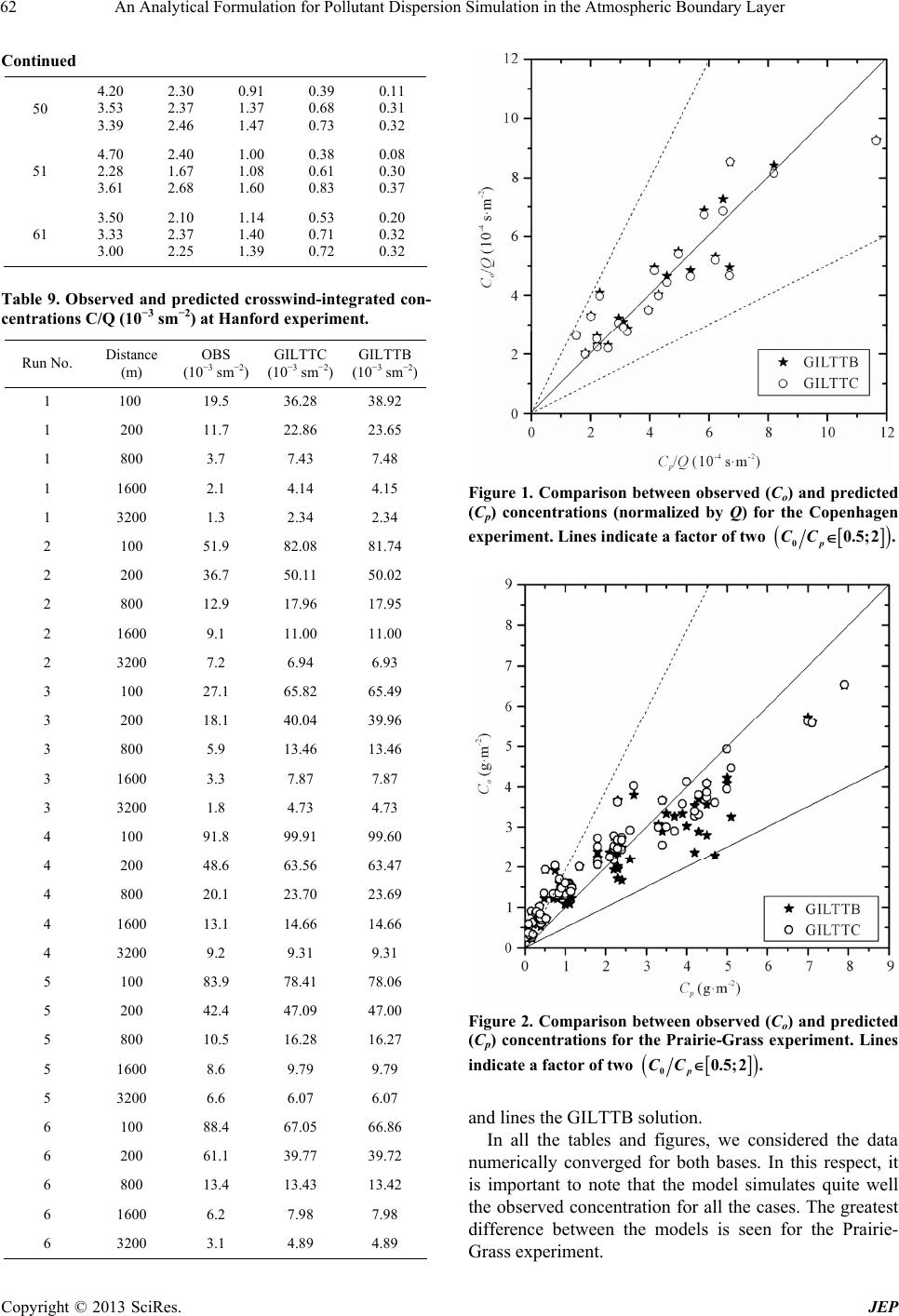

An Analytical Formulation for Pollutant Dispersion Simulation in the Atmospheric Boundary Layer
62
Continued
50
4.20
3.53
3.39
2.30
2.37
2.46
0.91
1.37
1.47
0.39
0.68
0.73
0.11
0.31
0.32
51
4.70
2.28
3.61
2.40
1.67
2.68
1.00
1.08
1.60
0.38
0.61
0.83
0.08
0.30
0.37
61
3.50
3.33
3.00
2.10
2.37
2.25
1.14
1.40
1.39
0.53
0.71
0.72
0.20
0.32
0.32
Table 9. Observed and predicted crosswind-integrated con-
centrations C/Q (10−3 sm−2) at Hanford experiment.
Run No. Distance
(m)
OBS
(10−3 sm−2)
GILTTC
(10−3 sm−2)
GILTTB
(10−3 sm−2)
1 100 19.5 36.28 38.92
1 200 11.7 22.86 23.65
1 800 3.7 7.43 7.48
1 1600 2.1 4.14 4.15
1 3200 1.3 2.34 2.34
2 100 51.9 82.08 81.74
2 200 36.7 50.11 50.02
2 800 12.9 17.96 17.95
2 1600 9.1 11.00 11.00
2 3200 7.2 6.94 6.93
3 100 27.1 65.82 65.49
3 200 18.1 40.04 39.96
3 800 5.9 13.46 13.46
3 1600 3.3 7.87 7.87
3 3200 1.8 4.73 4.73
4 100 91.8 99.91 99.60
4 200 48.6 63.56 63.47
4 800 20.1 23.70 23.69
4 1600 13.1 14.66 14.66
4 3200 9.2 9.31 9.31
5 100 83.9 78.41 78.06
5 200 42.4 47.09 47.00
5 800 10.5 16.28 16.27
5 1600 8.6 9.79 9.79
5 3200 6.6 6.07 6.07
6 100 88.4 67.05 66.86
6 200 61.1 39.77 39.72
6 800 13.4 13.43 13.42
6 1600 6.2 7.98 7.98
6 3200 3.1 4.89 4.89
Figure 1. Comparison between observed (Co) and predicted
(Cp) concentrations (normalized by Q) for the Copenhagen
experiment. Lines indicate a factor of two



00.5;2 p
CC .
Figure 2. Comparison between observed (Co) and predicted
(Cp) concentrations for the Prairie-Grass experiment. Lines
indicate a factor of two




00.5;2 p
CC .
and lines the GILTTB solution.
In all the tables and figures, we considered the data
numerically converged for both bases. In this respect, it
is important to note that the model simulates quite well
the observed concentration for all the cases. The greatest
difference between the models is seen for the Prairie-
Grass experiment.

An Analytical Formulation for Pollutant Dispersion Simulation in the Atmospheric Boundary Layer 63
Figure 3. Comparison between observed (Co) and predicted
(Cp) concentrations (normalized by Q) for the Hanford ex-
periment. Lines indicate a factor of two



00.5;2 p
CC .
4. Conclusions
Focusing our attention on the pollution dispersion simu-
lation in atmosphere, we present an analytical solution in
series expansion given by the well-known GILTT meth-
od to solve the two-dimensional advection-diffusion
equation by the GILTT approach. A Sturm-Liouville
problem carrying more information of the original prob-
lem, given by Bessel functions, was considered,
For the problems discussed, we promptly realize the
very good results achieved, under statistical point of view,
by the GILTT method when compared with the experi-
mental data for both cosine and Bessel basis used. For
the case of high source no significant difference was ob-
served between GILTTC and GILTTB. However, for the
low source, GILTTB numerically converges faster than
GILTTC. We focus our future attention on the direction
of the generalization of this solution considering an infi-
nite boundary layer.
5. Acknowledgements
The authors thank CNPq (Conselho Nacional de Desen-
volvimento Científico e Tecnológico) and FAPERGS
(Fundação de Amparo à Pesquisa do Estado do Rio
Grande do Sul) for the partial financial support of this
work.
REFERENCES
[1] J. H. Seinfeld and S. N. Pandis, “Atmospheric chemistry
and physics,” John Wiley & Sons, New York, 1998.
[2] D. M. Moreira, M. T. Vilhena, D. Buske and T. Tirabassi,
“The State-of-Art of the GILTT Method to Simulate Pol-
lutant Dispersion in the Atmosphere,” Atmospheric Re-
search, Vol. 92, No. 1, 2009, pp. 1-17.
doi:10.1016/j.atmosres.2008.07.004
[3] D. Buske, M. T. Vilhena, T. Tirabassi and B. Bodmann,
“Air Pollution Steady-State Advection Diffusion Equa-
tion: The General Three-Dimensional Solution,” Journal
of Environmental Protection, Vol. 3, No. 2, 2012, pp.
1124-1134. doi:10.4236/jep.2012.329131
[4] W. Rounds, “Solutions of the Two-Dimensional Diffu-
sion Equation,” Transactions of American Geophysical
Union, Vol. 36, 1955, pp. 395-405.
doi:10.1029/TR036i003p00395
[5] F. B. Smith, “The Diffusion of Smoke from a Continuous
Elevated Point Source into a Turbulent Atmosphere,”
Journal of Fluid Mechanics, Vol. 2, No. 1, 1957, pp. 49-
76. doi:10.1017/S0022112057000737
[6] R. A. Scriven and B. A. Fisher, “The Long Range Trans-
port of Airborne Material and Its Removal by Deposition
and Washout-II. The Effect of Turbulent Diffusion,” At-
mospheric Environment, Vol. 9, No. 1, 1975, pp. 59-69.
doi:10.1016/0004-6981(75)90054-2
[7] C. Demuth, “A Contribution to the Analytical Steady
Solution of the Diffusion Equation for Line Sources,”
Atmospheric Environment, Vol. 12, No. 5, 1978, pp.
1255-1258. doi:10.1016/0004-6981(78)90399-2
[8] A. P. van Ulden, “Simple Estimates for Vertical Diffusion
from Sources near the Ground,” Atmospheric Environ-
ment, Vol. 12, No. 11, 1978, pp. 2125-2129.
doi:10.1016/0004-6981(78)90167-1
[9] F. T. M. Nieuwstadt, “An Analytical Solution of the
Time-Dependent, One-Dimensional Diffusion Equation
in the Atmospheric Boundary Layer,” Atmospheric En-
vironment, Vol. 14, No. 12, 1980, pp. 1361-1364.
doi:10.1016/0004-6981(80)90154-7
[10] F. T. M. Nieuwstadt and B. J. de Haan, “An Analytical
Solution of One-Dimensional Diffusion Equation in a
Non-Stationary Boundary Layer with an Application to
Inversion Rise Fumigation,” Atmospheric Environment,
Vol. 15, No. 5, 1981, pp. 845-851.
doi:10.1016/0004-6981(81)90289-4
[11] M. Tagliazucca, T. Nanni and T. Tirabassi, “An Analyti-
cal Dispersion Model for Sources in the Surface Layer,”
Novembre-Dicembre, Vol. 8, No. 6, 1985, pp. 771-781.
[12] T. Tirabassi, “Analytical Air Pollution and Diffusion
Models,” Water, Air and Soil Pollution, Vol. 47, No. 1-2,
1989, pp. 19-24. doi:10.1007/BF00468993
[13] W. Koch, “A Solution of the Two-Dimensional Atmos-
pheric Diffusion Equation with Height-Dependent Diffu-
sion-Coefficient Including Ground-Level Absorption,”
Atmospheric Environment, Vol. 23, No. 8, 1989, pp.
1729-1732. doi:10.1016/0004-6981(89)90057-7
[14] T. Tirabassi and U. Rizza, “Applied Dispersion Modelling
for Ground-Level Concentrations from Elevated Sources,”
Atmospheric Environment, Vol. 28, No. 4, 1994, pp. 611-
615. doi:10.1016/1352-2310(94)90037-X
[15] M. Sharan, M. P. Singh and A. K. Yadav, “A Mathe-
matical Model for the Atmospheric Dispersion in Low

An Analytical Formulation for Pollutant Dispersion Simulation in the Atmospheric Boundary Layer
64
Winds with Eddy Diffusivities as Linear Function of
Downwind Distance,” Atmospheric Environment, Vol. 30,
No. 7, 1996, pp. 1137-1145.
doi:10.1016/1352-2310(95)00368-1
[16] J. S. Lin and L. M. Hildemann, “A Generalised Mathe-
matical Scheme to Analytically Solve the Atmospheric
Diffusion Equation with Dry Deposition,” Atmospheric
Environment, Vol. 31, No. 1, 1997, pp. 59-71.
doi:10.1016/S1352-2310(96)00148-3
[17] M. Sharan and M. Modani, “An Analytical Study for the
Dispersion of Pollutants in a Finite Layer under Low
Wind Conditions,” Pure and Applied Geophysics, Vol.
162, No. 10, 2005, pp. 1861-1892.
doi:10.1007/s00024-005-2696-5
[18] M. Sharan and M. Modani, “A Two-Dimensional Ana-
lytical Model for the Dispersion of Air-Pollutants in the
Atmosphere with a Capping Inversion,” Atmospheric En-
vironment, Vol. 40, No. 19, 2006, pp. 3469-3489.
doi:10.1016/j.atmosenv.2006.01.051
[19] D. M. Moreira, M. T. Vilhena, T. Tirabassi, C. Costa and
B. Bodmann, “Simulation of Pollutant Dispersion in At-
mosphere by the Laplace Transform: The ADMM Ap-
proach,” Water, Air and Soil Pollution, Vol. 177, No. 1-4,
2006, pp. 411-439. doi:10.1007/s11270-006-9182-2
[20] C. P. Costa, M. T. Vilhena, D. M. Moreira and T. Tira-
bassi, “Semi-Analytical Solution of the Steady Three-
Dimensional Advection-Diffusion Equation in the Plane-
tary Boundary Layer,” Atmospheric Environment, Vol. 40,
No. 29, 2006, pp. 5659-5669.
doi:10.1016/j.atmosenv.2006.04.054
[21] D. Buske, M. T. Vilhena, C. F. Segatto and R. S. Quadros,
“A General Analytical Solution of the Advection-Diffu-
sion Equation for Fickian Closure,” In: Integral Methods
in Science and Engineering: Computational and Analytic
Aspects, Birkhäuser, Boston, 2011, pp. 25-34.
doi:10.1007/978-0-8176-8238-5_4
[22] P. Kumar and M. Sharan, “An Analytical Model for Dis-
persion of Pollutants from a Continuous Source in the
Atmospheric Boundary Layer,” Proceedings of the Royal
Society A: Mathematical, Physical and Engineering Sci-
ences, Vol. 466, No. 2144, 2010, pp. 383-406.
doi:10.1098/rspa.2009.0394
[23] J. S. Perez Guerrero, L. C. G. Pimentel, J. F. Oliveira Jr.,
P. F. L. Heilbron Filho and A. G. Ulke, “A Unified Ana-
lytical Solution of the Steady-State Atmospheric Diffu-
sion Equation,” Atmospheric Environment, Vol. 55, 2012,
pp. 201-212. doi:10.1016/j.atmosenv.2012.03.015
[24] A. K. Blackadar, “Turbulence and Diffusion in the Atmos-
phere: Lectures in Environmental Sciences,” Springer-
Verlag, Berlin, 1997, 185p.
doi:10.1007/978-3-642-60481-2
[25] M. T. Vilhena, D. Buske, G. A. Degrazia and R. S. Qua-
dros, “An Analytical Model with Temporal Variable
Eddy Diffusivity Applied to Contaminant Dispersion in
the Atmospheric Boundary Layer,” Physica A: Statistical
Mechanics and Its Applications, Vol. 391, No. 8, 2012,
pp. 2576-2584. doi:10.1016/j.physa.2011.11.001
[26] S. E. Gryning and E. Lyck, “Atmospheric Dispersion from
Elevated Source in an Urban Area: Comparison between
Tracer Experiments and Model Calculations,” Journal of
Climate and Applied Meteorology, Vol. 23, No. 4, 1984,
pp. 651-654.
[27] M. L. Barad, “Project Prairie Grass: A Field Program in
Diffusion,” Geophysical Research Paper No. 59, Vols. I
and II, AFCRL-TR-58-235 (ASTIA Document No. AF-
152572), Air Force Cambridge Research Laboratories,
Bedford, 1958.
[28] F. T. M. Nieuwstadt, “An Analytical Solution of the
Time-Dependent, One-Dimensional Diffusion Equation
in the Atmospheric Boundary Layer,” Atmospheric En-
vironment, Vol. 14, No. 12, 1980, pp. 1361-1364.
doi:10.1016/0004-6981(80)90154-7
[29] J. C. Doran and T. W. Horst, “An Evaluation of Gaussian
Plume-Depletion Models with Dual-Tracer Field Meas-
urements,” Atmospheric Environment, Vol. 19, No. 6,
1985, pp. 939-951. doi:10.1016/0004-6981(85)90239-2
[30] G. A. Degrazia, H. F. Campos Velho and J. C. Carvalho,
“Nonlocal Exchange Coefficients for the Convective
Boundary Layer Derived from Spectral Properties,” Con-
tributions to Atmospheric Physics, Vol. 70, No. 1, 1997,
pp. 57-64.
[31] G. A. Degrazia, D. Anfossi, J. C. Carvalho, C. Mangia, T.
Tirabassi and H. F. Campos Velho, “Turbulence Parame-
terization for PBL Dispersion Models in All Stability
Conditions,” Atmospheric Environment, Vol. 34, No. 21,
2000, pp. 3575-3583.
doi:10.1016/S1352-2310(00)00116-3
[32] H. A. Panofsky and J. A. Dutton, “Atmospheric Turbu-
lence,” John Wiley & Sons, New York, 1984.
[33] J. S. Irwin, “A Theoretical Variation of the Wind Profile
Power-Low Exponent as a Function of Surface Rough-
ness and Stability,” Atmospheric Environment, Vol. 13,
No. 1, 1979, pp. 191-194.
doi:10.1016/0004-6981(79)90260-9
[34] S. R. Hanna, “Confidence Limit for Air Quality Models
as Estimated by Bootstrap and Jacknife Resampling
Methods,” Atmospheric Environment, Vol. 23, No. 6,
1989, pp. 1385-1395. doi:10.1016/0004-6981(89)90161-3