Paper Menu >>
Journal Menu >>
 J. Software Engineering & Applications, 2010, 3, 1155-1162 doi:10.4236/jsea.2010.312135 Published Online December 2010 (http://www.SciRP.org/journal/jsea) Copyright © 2010 SciRes. JSEA Representations in Genetic Algorithm for the Job Shop Scheduling Problem: A Computational Study Tamer F. Abdelmaguid Department of Mechanical Design and Production, Faculty of Engineering, Cairo University, Giza, Egypt Email: tabdelmaguid@alumni.usc.edu Received November 21st, 2010; revised November 29th, 2010; accepted December 12th, 2010. ABSTRACT Due to the NP-hardness of the job shop scheduling problem (JSP), many heuristic approaches have been proposed; among them is the genetic algorithm (GA). In the literature, there are eight different GA representations for the JSP; each one aims to provide subtle environment through which the GA’s reproduction and mutation operators would suc- ceed in finding near optimal solutions in small computational time. This paper provides a computational study to com- pare the performance of the GA und er six different representations. Keywords: Job Shop Scheduling, Genetic Algorithm, Mathematical Models, Genetic Representation 1. Introduction Genetic algorithm (GA) is a random search optimization technique that mimics the natural selection process [1]. Its approach is based on randomly generating a new set (generation) of solutions from an existing one, so that there is improvement in the quality of the solutions thr- oughout generations. In the simple GA implementation [2], this approach is conducted through three main oper- ators that are repeatedly applied to a given generation of solutions until a new child generation with a predeter- mined population size is obtained: 1) random selection of two solutions from the individuals in the parent genera- tion, 2) reproduction of two new child solutions by mat- ing the selected individuals. This mating process is con- ducted by randomly exchanging specific elements in the structures of the selected solutions in a manner similar to the crossover operation of chromosomes in natural ge- netics, and 3) mutation of some randomly selected ele- ments in the structures of the resultant child solutions to increase the capability of reaching further points in the search space. Different variations to the simple GA ap- proach, aiming to improve its search capabilities, can be found in the literature. The GA has proven to be a com- petitive random search technique for various types of optimi za ti on problems [3]. In order to apply GA to a specific optimization prob- lem, one has to decide first how to represent solutions of the problem in a suitable structure that can be dealt with through both the reproduction and the mutation operators. Such a structure, referred to as the genotype, needs to be easily interpretable to a feasible solution of the studied problem. The selection of a suitable represen tation is u s u a l - ly accompanied with, and sometimes affected by, the de- sign of suitable reproduction and mutation operators. In combinatorial optimization problems, the selection of a suitable GA representation is a challenging task. This class of problems is characterized by discrete decision variables that are usually interrelated through logical relationships. As a result, different mathematical models may exist for the same combinatorial optimization prob- lem, leading to the existence of different possible GA representations. The job shop scheduling problem (JSP) is a well known combinatorial optimization problem that arises i n low -volume production systems in which products are made to order [4]. It is concerned with sequencing a set of jobs on a set of technologically different machines; each is capable of processing at most one job at a time. Jobs follow dissimilar processing routes among the ma- chines and a job cannot be processed on more than one machine simultaneously. Furthermore, preemption is not allowed and a job is permitted to have multiple visits to any machine. The JSP with the objective of minimizing the makespan is known to be NP-h ard [5]. This complex - ity even exists in the small case of three jobs and three machines [6][6]. As a result, and due to its importance, there is an ever-growing literature of heuristic approach- es for that problem.  Representations in Genetic Algorithm for the Job Shop Scheduling Problem: A Computational Study Copyright © 2010 SciRes. JSEA 1156 Among all combinatorial optimization problems, the JSP is presumably the most frequently solved b y GA us- ing different GA representations. In their tutorial paper, Cheng, Gen and Tsujimura [7] provide a literature surv ey on the different GA representations used for the JSP. However, there is a gap in the literature regarding the co- mputational comparison of various representation schemes as only minor experimental comparison is reported by Gen and Cheng [3]. Anderson, Glass and Potts [8] report a computational study conducted with different metaheu- ristic approaches including four different GA implement- ations. However, their study falls short in the consisten- cy and coherence of the conducted experiments in terms of the number of runs and the number of tested problems. In this paper, six different representations are compared experimental ly to identify the most effective ones in t er ms of solution quality and co mputational time requirement. The rest of this paper is organized as follows. First, we illustrate the structure of the JSP and presen t the different mathematical models that have been used in Section 2. In Section 3, a classification and a literature review on the GA representations used for the JSP is presented. The different reproduction and mutation operators used for the GA representations are presented in Section 4. In Section 5, the experimental results are illustrated and discussed, a nd finally the c onclusion i s provided in Section 6. 2. Problem Structure and Mathematical Models Before discussing the available GA representations for the JSP, it is imperative to illustrate the structure of the problem and the different mathematical models that have been used in the literature. We denote J as th e set of jobs. Each job consists of an ordered list of operations that represents its processing route through a subset of ma- chines in the shop. We denote 1, 2 I v as the set of all operations’ indexes. The operations’ indexes are assigned such that for job kJ , the subset of consecu- tive indexes ,1,2,, kkk kk I I in- cludes the indexes of operations belonging to that job; where in the set Ik, the operation with the lower index is to be processed first. For operation i, the time needed to finish its processing is pi which is assumed to be integer without loss of generality, the job to which it belongs is denoted jb (i), and its processing machine is mc (i). The task of the scheduling process is to determine the start time si for every operation i I. There are two se ts of constraints in the JSP. The technological or prece- dence constraints define the mandatory processing se- quence of operations belonging to the same job. This set of constraints is represented by the following inequal ities. 1iii s sp ,1k iiI k J (1) The second set of constraints is in a disjunctive (ei- ther-or) form, and it represents the condition that opera- tions on the same machine must be processed in different time intervals. ij j s sp or ji i s sp i, j I, where mc (i) = mc (j) and jb(i)jb(j) (2) Different objective functions have been dealt with in the literature. In this paper, we concentrate on the objec- tive of minimizing the maximum completion time or the makespan. The makespan, denoted Cmax, is expressed as follows. Cmax = : max kii ikJ s p (3) Different mathematical models have been proposed for the JSP. The integer linear programming (ILP) models use different forms of binary variables. Table 1 summa- rizes the definitions of the binary variables used. Manne's model has gained larger interest in the research commu- nity due to its comparatively small number of variables and constraints. The precedence constraints (1) of the JSP can be viewed as a series of consecutive operations for each job, which is analogous to a series of consecu tive activities as found in project scheduling. This analogy motivated im- porting network models that are used in the project scheduling literature to th e JSP. To represent the disjun c- tive constraints (2), additional sets of arcs are required. This is achieved in the literature by two models, the dis- junctive graph model [9] and the permutation-induced acyclic network (PIAN) model [10]. In the disjunctive graph model, a disjunctive arc is de- fined between every pair of operations that share the same machine. Each disjunctive arc is associated with a binary decision variable similar to that of Manne’s model, such that a selection on the value of that variable defines the direction and the length of each disjunctive arc. Based on the disjunctive graph model, very efficient algorithmic techniques have been developed such as the immediate selections [11] and the shifting bottleneck heuristic [12]. Alternatively, in the PIAN model, permuta- tions are used to represent the processing sequence of all operations that share the same machine in a mannersimi- lar to the idea given in Wagner’s model. These per- Table 1. Binary variables used in the ILP models of the JSP. Reference Variable notation Definition Bowman [13] , m it x = 1 if operation i is processed on machine m in time unit t; = 0 otherwise. Wagner [14] , m il x = 1 if operation i takes the lt h position in the processing sequence on machine m; = 0 otherwise. Manne [15], m ij x = 1 if operation i is processed prior to operation j on machi ne m; = 0 otherwise.  Representations in Genetic Algorithm for the Job Shop Scheduling Problem: A Computational Study Copyright © 2010 SciRes. JSEA 1157 mutations are treated as decision variables and interpreted into directed arcs on the graph to provide a resolution for the disjunctive constraints (2). 3. GA Representations Cheng, Gen and Tsujimura [7] provide a survey on the different GA representations used for the JSP. They clas- sify them into two categories: direct and indirect. The distinction between direct and indirect representations depends on whether a solution is directly encoded into the genotype or not. Alternatively, in this paper we clas- sify the GA representations for the JSP into two main categories: model-based and algorithm-based. Figure 1 illustrates this classification and lists the available repre- sentations in the literature for each category. In model-based representations, the structure of the genotype is based on the definition of the decision va- riables of a specific JSP mathematical model, and a ge- notype can be directly interpreted to a feasible or infeasi- ble solution. A special algorithm may be needed to con- vert infeasible solutions into feasible ones. In mod- el-based representations, optimal solu tions are attainable. The existing model-based representations use three types of decision variables: 1) binary decision variables as found in the disjunctive graph model and the ILP model of Manne, 2) processing sequence decision variables as described in the PIAN model, and 3) integer variables representing the operations’ start or completion times. In the binary GA representation, the disjunctive graph- based representation [16] has a large chromosome size and many infeasible solu tions are encountered during the GA run, which requires extra computational effort to fix their infeasibilities. This GA representation is excluded from the computational comparison in this paper. In the processing sequence representations, there are three different forms that are based on the processing sequence decision variables as found in the PIAN model. The operation-based (OB) representation [17] uses a sin- gle string of genes, where each job is represented by a number of genes equals the number of operations it con- tains. Based on the order of the operations given in this representation, each operation is assigned the earliest start time permitted by considering the machine availa- bility constraints to generate feasible schedule. In this interpretation mechanism, the technological constraints are easily satisfied. The random keys (RK) representation [18] is very similar to the operation-based one, except that each gene is filled with a randomly generated number between 0 and 1. The random numbers in a given chromosome are sorted out and the resulting order is used to replace these numbers with an integer (the order). Each operation in the studied problem is assigned an integer value so that the resultant string of integers is equ ivalent to a string of operations. This string is then interpreted into feasible schedule using the same approach as in the operation- based representation with correcting any violation of the technological constraints. The pref erence list- based ( PL) representation, found in [19] and [20], uses a string of operations for each ma- chine instead of a single string for all the operations, which makes it a direct representation of the processing sequence decision variables of the PIAN model. Freq- uently, violations of the technological constraints are encountered, which requires additional computations to fix it during the interpretation phase. The completion time-based representation [21] uses a string of integer values having a length that equals the total number of operations. The integer value stored in a gene represents the completion time, which equals ii s p of its associated operation. This representation requires extra computational effort to fix an expectedly large number of infeasible representations. This repre- sentation has been excluded from the computational comparison in this paper. In the algorithm-based representations, the genotype is used to store guiding information to be used by an algo- rithm to generate feasible schedules, and there is no guarantee for obtaining optimal solutions. In the priority rule-based (PR) representation [22], the chromosome is a string of priority dispatching rules which are applied in sequence to schedule operations within an active sche- dule generator, namely Giffler and Thompson algorithm [23]. Consequently, the chromosome length equals th e total number of operations in a given problem. GA representations for the JSP Model-based Operation‐based(OB)[17] Randomkeys(RK)[18] Preferencelist‐based ( PL ) [ 19 ] [ 20 ] Binary Processing s e quence Disjunctivegraph‐based(job pairrelation‐based) representation[16] Algorithm-based Priorityrule‐based(PR)[22] Machine‐based(MB)[22] Job‐based(JB)[23] Integer Completiontime‐based[21] Figure 1. Types of GA representations for the JSP.  Representations in Genetic Algorithm for the Job Shop Scheduling Problem: A Computational Study Copyright © 2010 SciRes. JSEA 1158 In the machine-based (MB) representation [8], the chromosome is a string of machines with a total length equals the number of machines. The sequence of the machines in the chromosome represents the order by which a machine is treated as a bottleneck machine in th e shifting bottleneck algorithm [12]. In the job-based (JB) representation [24], the chromosome is a string of jobs with a total length equals the number of jobs. Using the order of the jobs given in the chromosome, a simple al- gorithm is used to schedule all the operations of the giv- en job in sequence on all the machines at once. To sche- dule an operation, this algorithm searches for an empty time slot on the assigned machine without violating the technological constraints. 4. Reproduction and Mutation Operators In GA, the reproduction operator can be seen as an ap- proach for conducting neighborhood search; while, mu- tation operator provides a mechanism to avoid being trapped in a local optima. The design of both operators is crucial for the success of GA. In the literature, the re- production and mutation operators applied to the JSP are mainly adopted from the literature of app lying GA to the traveling salesman problem (TSP). This adoption is mo- tivated by the similarity between the GA representations used for the JSP and the permutatio n representation used to encode the sequence of visited cities [3]. Among the reproduction operators used in the JSP li- terature are the partial-mapped crossover (PMX) [25], the order crossover (OX) [26] and the uniform or posi- tion-based crossover [27]. For both PMX and OX, there are two versions, one in which there are a single cros- sover point and another one in which there are two cros- sover points. The mutation operators used for the JSP implement different mechanisms to exchange the values assigned to randomly selected genes in a given chromosome. Swap mutation, also known as reciprocal exchange mutation, simply exchanges the values assigned to two different randomly selected genes. Inversion mutation, inverts the order of the values assigned to the set of genes located between two randomly selected positions in the chromo- some. Insertion or shift mutation selects a gene randomly and sets its value to another randomly selected gene, while the values of the genes between these randomly selected positions are shifted. The disp lacement mutation is another version of shift mutation in which a substring of genes, instead of a single gene, is moved to a random- ly selected new location. Gen and Cheng [3] provide a detailed description of the implementation of the repro- duction and mutation operators used in this study. 5. Experimentation, Results and Analysis The previously mentio n ed GA represen tations , ex cept the disjunctive graph-based and the completion time-based, are considered in the current computational study. A spe- cial computer program prepared in the C++ programming language is used to benchmark the performance of a simple GA implementation with elite preservation strat- egy. All chromosomes are initialized in a totally random fashion by selecting randomly the values assigned for each gene in the chromosome. In the cases of OB, PL and JB representations, a special attentio n has been made to avoid operation or job repetitions in the same chro- mosome. All experiments are conducted with a total number of generations of 300, a fixed population size of 40, a fixed elite size of 5, a fixed mutation probability of 0.1 and reproduction probability of 0.8. For the selection operato r, a tournament selector is used. In this selector, two can- didate solutions are drawn randomly with a probability proportional to their fitness values, and the one with the highest fitness (lowest makespan) is selected. For each GA representation, the reproduction and mu- tation operators described in the previous section have been programmed. Since studying the GA performance when different reproduction and mutation operators are used is outside the scope of this paper, we programmed the GA to randomly select an operator from the available list. All reproduction operator s have the same probab ility of being selected, and so the mutation operators. The benchmark problems used in the experimentations are selected 40 standard test problems reported in the literature and made available through the OR-Library in the World Wide Web [28]. All runs are conducted on a personal computer with Intel Pentium Core 2 Duo pro- cessor running with a clock speed of 2.67 GHz and RAM of 512 Mega Bytes. For each test problem and GA representation, five GA runs are conducted. The best and average makespan val- ues among the five runs are reported in Table 2. Based on these results, the optimality gap, which is defined as the difference between the best or average makespan value and the lower bound divided by the latter and mul- tiplied by 100, is evaluated for each test problem. Table 3 lists the average among all test problems for both the best and average op timality gaps. Fro m these results, it is clear that the MB representation gives the best quality solutions with a small optimality gap and it is relatively robust with minor variability in the final makespan value among the five runs. This is followed by the PR repre- sentation. The OB representation comes in the third place in terms of both the average and best optimality gaps; however its variability in the final makespan value is higher th an th at of MB an d PR rep re senta tions . The tr end of increasing variability is apparent for th e re maining GA representations, JB, RK and the worst PL. 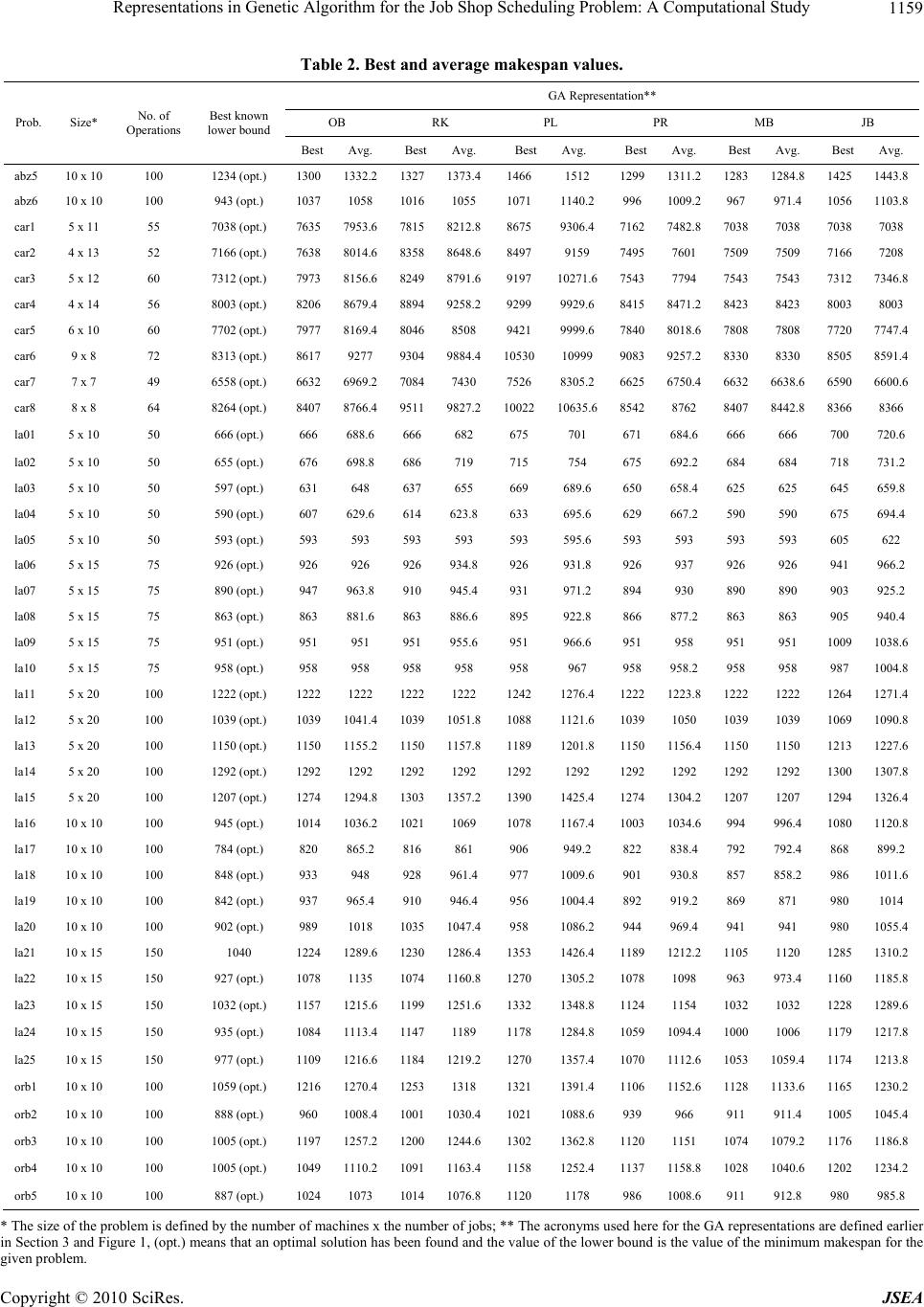 Representations in Genetic Algorithm for the Job Shop Scheduling Problem: A Computational Study Copyright © 2010 SciRes. JSEA 1159 Table 2. Best and average makespan values. Prob. Size* No. of Operations Best known lower bound GA Representation** OB RK PL PR MB JB Best Avg. Best Avg. Best Avg. Best Avg. Best Avg. Best Avg. abz5 10 x 10 100 1234 (opt.) 1300 1332.213271373.41466 1512 12991311.2 1283 1284.8 14251443.8 abz6 10 x 10 100 943 (opt.) 1037 1058 10161055 1071 1140.2 996 1009.2 967 971.4 10561103.8 car1 5 x 11 55 7038 (opt.) 7635 7953.678158212.88675 9306.4 71627482.8 7038 7038 70387038 car2 4 x 13 52 7166 (opt.) 7638 8014.683588648.68497 9159 74957601 7509 7509 71667208 car3 5 x 12 60 7312 (opt.) 7973 8156.682498791.69197 10271.675437794 7543 7543 73127346.8 car4 4 x 14 56 8003 (opt.) 8206 8679.488949258.29299 9929.6 84158471.2 8423 8423 80038003 car5 6 x 10 60 7702 (opt.) 7977 8169.480468508 9421 9999.6 78408018.6 7808 7808 77207747.4 car6 9 x 8 72 8313 (opt.) 8617 9277 93049884.41053010999 90839257.2 8330 8330 85058591.4 car7 7 x 7 49 6558 (opt.) 6632 6969.270847430 7526 8305.2 66256750.4 6632 6638.6 65906600.6 car8 8 x 8 64 8264 (opt.) 8407 8766.495119827.21002210635.685428762 8407 8442.8 83668366 la01 5 x 10 50 666 (opt.) 666 688.6 666 682 675 701 671 684.6 666 666 700 720.6 la02 5 x 10 50 655 (opt.) 676 698.8 686 719 715 754 675 692.2 684 684 718 731.2 la03 5 x 10 50 597 (opt.) 631 648 637 655 669 689.6 650 658.4 625 625 645 659.8 la04 5 x 10 50 590 (opt.) 607 629.6 614 623.8 633 695.6 629 667.2 590 590 675 694.4 la05 5 x 10 50 593 (opt.) 593 593 593 593 593 595.6 593 593 593 593 605 622 la06 5 x 15 75 926 (opt.) 926 926 926 934.8 926 931.8 926 937 926 926 941 966.2 la07 5 x 15 75 890 (opt.) 947 963.8 910 945.4 931 971.2 894 930 890 890 903 925.2 la08 5 x 15 75 863 (opt.) 863 881.6 863 886.6 895 922.8 866 877.2 863 863 905 940.4 la09 5 x 15 75 951 (opt.) 951 951 951 955.6 951 966.6 951 958 951 951 10091038.6 la10 5 x 15 75 958 (opt.) 958 958 958 958 958 967 958 958.2 958 958 987 1004.8 la11 5 x 20 100 1222 (opt.) 1222 1222 12221222 1242 1276.4 12221223.8 1222 1222 12641271.4 la12 5 x 20 100 1039 (opt.) 1039 1041.410391051.81088 1121.6 10391050 1039 1039 10691090.8 la13 5 x 20 100 1150 (opt.) 1150 1155.211501157.81189 1201.8 11501156.4 1150 1150 12131227.6 la14 5 x 20 100 1292 (opt.) 1292 1292 12921292 1292 1292 12921292 1292 1292 13001307.8 la15 5 x 20 100 1207 (opt.) 1274 1294.813031357.21390 1425.4 12741304.2 1207 1207 12941326.4 la16 10 x 10 100 945 (opt.) 1014 1036.210211069 1078 1167.4 10031034.6 994 996.4 10801120.8 la17 10 x 10 100 784 (opt.) 820 865.2 816 861 906 949.2 822 838.4 792 792.4 868 899.2 la18 10 x 10 100 848 (opt.) 933 948 928 961.4 977 1009.6 901 930.8 857 858.2 986 1011.6 la19 10 x 10 100 842 (opt.) 937 965.4 910 946.4 956 1004.4 892 919.2 869 871 980 1014 la20 10 x 10 100 902 (opt.) 989 1018 10351047.4958 1086.2 944 969.4 941 941 980 1055.4 la21 10 x 15 150 1040 1224 1289.612301286.41353 1426.4 11891212.2 1105 1120 12851310.2 la22 10 x 15 150 927 (opt.) 1078 1135 10741160.81270 1305.2 10781098 963 973.4 11601185.8 la23 10 x 15 150 1032 (opt.) 1157 1215.611991251.61332 1348.8 11241154 1032 1032 12281289.6 la24 10 x 15 150 935 (opt.) 1084 1113.411471189 1178 1284.8 10591094.4 1000 1006 11791217.8 la25 10 x 15 150 977 (opt.) 1109 1216.611841219.21270 1357.4 10701112.6 1053 1059.4 11741213.8 orb1 10 x 10 100 1059 (opt.) 1216 1270.412531318 1321 1391.4 11061152.6 1128 1133.6 11651230.2 orb2 10 x 10 100 888 (opt.) 960 1008.410011030.41021 1088.6 939 966 911 911.4 10051045.4 orb3 10 x 10 100 1005 (opt.) 1197 1257.212001244.61302 1362.8 11201151 1074 1079.2 11761186.8 orb4 10 x 10 100 1005 (opt.) 1049 1110.210911163.41158 1252.4 11371158.8 1028 1040.6 12021234.2 orb5 10 x 10 100 887 (opt.) 1024 1073 10141076.81120 1178 986 1008.6 911 912.8 980 985.8 * The size of the problem is defined by the number of machines x the number of jobs; ** The acronyms used here for the GA representations are defined earlier in Section 3 and Figure 1, (opt.) means that an optimal solution has been found and the value of the lower bound is the value of the mi ni mum mak esp an fo r th e given problem . 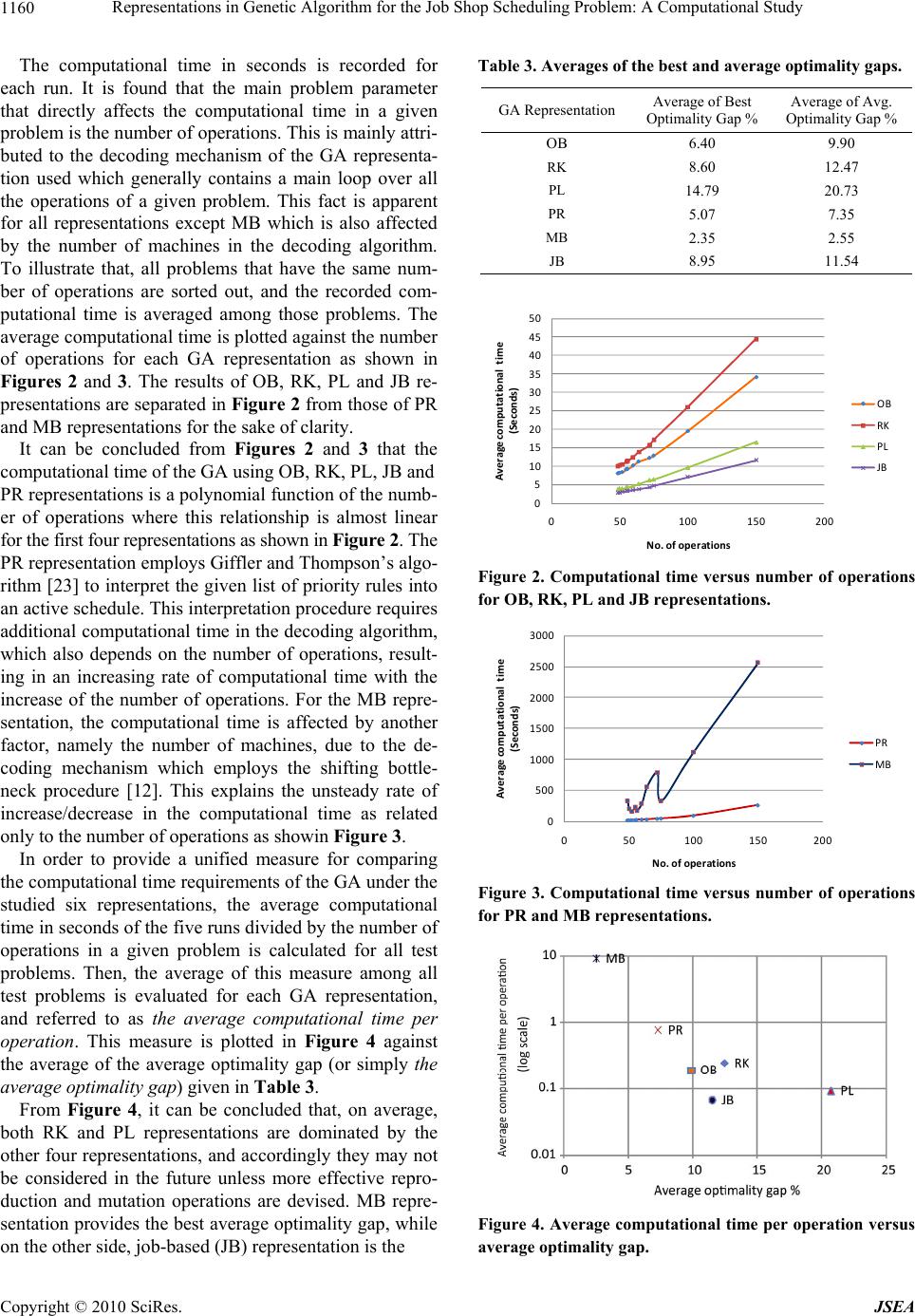 Representations in Genetic Algorithm for the Job Shop Scheduling Problem: A Computational Study Copyright © 2010 SciRes. JSEA 1160 The computational time in seconds is recorded for each run. It is found that the main problem parameter that directly affects the computational time in a given problem is the number of operations. This is mainly attri- buted to the decoding mechanism of the GA representa- tion used which generally contains a main loop over all the operations of a given problem. This fact is apparent for all representations except MB which is also affected by the number of machines in the decoding algorithm. To illustrate that, all problems that have the same num- ber of operations are sorted out, and the recorded com- putational time is averaged among those problems. The average computationa l time is plotted again st the number of operations for each GA representation as shown in Figures 2 and 3. The results of OB, RK, PL and JB re- presentations are separated in Figure 2 from those of PR and MB representations for the sake of clarity. It can be concluded from Figures 2 and 3 that the computational time of the GA using OB, RK, PL, JB and PR representations is a polynomial function of the numb- er of operations where this relationship is almost linear for the first four representations as shown in Figure 2. The PR representation employs Giffler and Thompson’s algo- rithm [23] to interpret the given list of priority rules into an active schedule. This interpretatio n procedu re requ ires additional co mputational time in the decoding algorith m, which also depends on the number of operations, result- ing in an increasing rate of computational time with the increase of the number of operations. For the MB repre- sentation, the computational time is affected by another factor, namely the number of machines, due to the de- coding mechanism which employs the shifting bottle- neck procedure [12]. This explains the unsteady rate of increase/decrease in the computational time as related only to the number of operations as showin Figure 3. In order to provide a unified measure for comparing the computational time requirements of th e GA under the studied six representations, the average computational time in seconds of the five runs divided by the number of operations in a given problem is calculated for all test problems. Then, the average of this measure among all test problems is evaluated for each GA representation, and referred to as the average computational time per operation. This measure is plotted in Figure 4 against the average of the average optimality gap (or simply the average optimality gap) given in Table 3. From Figure 4, it can be concluded that, on average, both RK and PL representations are dominated by the other four representations, and accordingly they may not be considered in the future unless more effective repro- duction and mutation operations are devised. MB repre- sentation provides th e best average optimality gap, while on the other side, job-based (JB) representation is the Table 3. Averages of the best and average optimality gaps. GA Representation Average of Best Optimality Gap % Average of Avg. Optimality Gap % OB 6.40 9.90 RK 8.60 12.47 PL 14.79 20.73 PR 5.07 7.35 MB 2.35 2.55 JB 8.95 11.54 0 5 10 15 20 25 30 35 40 45 50 050100 150 200 Averagecomputationaltime (Seconds) No.ofoperations OB RK PL JB Figure 2. Computational time versus number of operations for OB, RK, PL and JB representations. 0 500 1000 1500 2000 2500 3000 050100 150 200 Averagecomputationaltime (Seconds) No.ofoperations PR MB Figure 3. Computational time versus number of operations for PR and MB representations. Figure 4. Average computational time per operation versus average optimality gap.  Representations in Genetic Algorithm for the Job Shop Scheduling Problem: A Computational Study Copyright © 2010 SciRes. JSEA 1161 fastest. The four representations: MB, PR, OB and JB represent the Pareto front from which a software design- er may choose. 6. Conclusions In this paper, six different GA representations for the job shop scheduling problem (JSP) are compared. The main two factors that are used in the comparison are the aver- age optimality gap, and the average computational time in seconds divided by the number of operations of a giv- en problem. A set of 40 standard JSP benchmark prob- lems are solved using the GA under the studied six re- presentations, and the averages of both measures are calculated. It is found that the machine-based representa- tion is capable of achieving the lowest optimality gap of 2.55% on average with a small variability among the conducted runs, but with the highest co mputational ti me. Both the random keys and preferen ce-list representations are found to be incompetent compared to the other re- presentations. 7. Acknowledgements The author would like to thank an anonymous referee for his/her comments which helped to improve the presenta- tion of the results in this paper. REFERENCES [1] J. Holland, “Adaptation in Natural and Artificial Sys- tems,” University of Michigan Press, Ann Arbor, 1975. [2] D. E. Goldberg, “Genetic Algorithms in Search, Optimi- zation and Machine Learning,” Addison-Wesley, New York, 1989. [3] M. Gen and R. Cheng, “Genetic Algorithms and Engi- neering Design,” Wiley, New York, 1997. [4] M. Pinedo, “Scheduling-Theory, Algorithms, and Analy- sis,” Prentice-Hall, New Jersey, 2002. [5] M. R. Garey, D. S. Johnson and R. Sethi, “The Complex- ity of Flow Shop and Job-Shop Scheduling,” Mathematics of Operations Research, Vol. 1, No. 2, 1976, pp. 117-129. doi:10.1287/moor.1.2.117 [6] Y. N. Sotskov and N. V. Shakhlevich, “NP-Hardness of Shop Scheduling Problems with Three Jobs,” Discrete Applied Mathematics, Vol. 59, No. 3, 1995, pp. 237-266. doi:10.1016/0166-218X(93)E0169-Y [7] R. Cheng, M. Ge n and Y. Tsujimura, “A Tutoria l Survey of Job-Shop Scheduling Problems Using Genetic Algo- rithms-I. Representation,” Computers and Industrial En- gineering, Vol. 30, No. 4, 1996, pp. 983-997. doi:10.1016 /0360-8352(96)00047-2 [8] E. J. Anderson, C. A. Glass and C. N. Potts, “Local Search in Combinatorial Optimization,” Princeton Uni- versity Press, Princeton, 2003. [9] B. Roy and B. Sussmann, “Les Problemes d’ Ordon- nancement Avec Constraints Disjonctives,” SEMA, Note D.S., Paris, 1964. [10] T. F. Abdelmaguid, “Permutation-Induced Acyclic Net- works for the Job Shop Scheduling Problem,” Applied Mathematical Modeling, Vol. 33, No. 3, 2009, pp. 1560-1572. doi:10.1016/j.apm.2008.02.004 [11] J. Carlier and E. Pinson, “An Algorithm for Solving the Job-Shop Problem,” Management Science, Vol. 35, No. 2, 1989, pp. 164-176. doi:10.1287/mnsc.35.2.164 [12] J. Adams, E. Balas and D. Zawack, “The Shifting Bottle- neck Procedure for Job Shop Scheduling,” Management Science, Vol. 34, No. 3, 1988, pp. 391-401. doi:10.128 7/mnsc.34.3.391 [13] H. Bowman, “The Schedule-Sequencing Problem,” Op- erations Research, Vol. 7, No. 5, 1959, pp. 621-624. doi: 10.1287/opre.7.5.621 [14] H. M. Wagner, “An Integer Linear-Programming Model for Machine Scheduling,” Naval Research Logistics Quarterly, Vol. 6, No. 2, 1959, pp. 131-140. doi:10.1002 /nav.3800060205 [15] A. S. Manne, “On the Job-Shop Scheduling Problem,” Operations Research, Vol. 8, No. 2, 1960, pp. 219-223. doi:10.1287/opre.8.2.219 [16] H. Tamaki and Y. Nishikawa, “A Paralleled Genetic Al- gorithm Based on a Neighborhood Model and its Appli- cation to the Jobshop Scheduling, ” Proceedings Of the 2nd International Conference on P arallel P roblem Solving f rom Nature, Amsterdam, 28-30 September 1992, pp. 579-588. [17] M. Gen, Y. Tsujimura and E. Kubota, “Solving Job-Shop Scheduling Problems by Genetic Algorithm,” Proceed- ings of the IEEE International Conference on Systems, Man and Cybernetics, San Antonio, 2-5 October 1994, pp. 1577-1582. [18] J. Bean, “Genetic Algorithms and Random Keys for Se- quencing and Optimization,” ORSA Journal of Compu- ting, Vol. 6, No. 2, 1994, pp. 154-160. [19] L. Davis, “Job Shop Scheduling with Genetic Algo- rithm,” Proceedings Of the 1st International Conference on Genetic Algorithms, Pittsburgh, 24-26 July 1985, pp. 136-140. [20] F. D. Groce, R. Tadei and G. Volta, “A Genetic Algo- rithm for the Job Shop Problem,” Computers and Opera- tions Research, Vol. 22, No. 1, 1995, pp. 15-24. doi:10. 1016/0305-0548(93)E0015-L [21] T. Yamada and R. Nakano, “A Genetic Algorithm Ap- plicable to Large-Scale Job-Shop Problems,” Proceed- ings of the 2nd International Conference on Parallel Problem Solving from Nature, Amsterdam, 28-30 Sep- tember 1992, pp. 283-292. [22] U. Dorndorf and E. Pesch, “Evolution Based Learning in a Job Shop Scheduling Environment,” Computers and Operations Research, Vol. 22, No. 1, 1995, pp. 25-40. doi:10.1016/0305-0548(93)E0016-M [23] B. Giffler and G. L. Thompson, “Algorithms for Solving Production Scheduling Problems,” Operations Research, Vol. 8, No. 4, 1960, pp. 487-503.  Representations in Genetic Algorithm for the Job Shop Scheduling Problem: A Computational Study Copyright © 2010 SciRes. JSEA 1162 [24] C. W. Holsapple, V. S. Jacob, R. Pakath and J. S. Zaveri, “Genetics-Based Hybrid Scheduler for Generating Static Schedules in Flexible Manufacturing Contexts,” IEEE Trans. Systems, Man, and Cybernetics, Vol. 23, No. 4, 1993, pp. 953-971. doi:10.1109/21.247881 [25] D. Goldberg and R. Lingle, “Alleles, Loci and the Trav- eling Salesman Problem,” Proceedings of the 1st Interna- tional Conference on Genetic Algorithms and Their Ap- plications, Los Angeles, 1985, pp. 154-159. [26] L. Davis, “Applying Adaptive Algorithms to Epistatic Domains,” Proceedings of the 9th International Joint Conference on Artificial Intelligence, 1985, pp. 162-164. [27] G. Syswerda, “Uniform Crossover in Genetic Algo- rithms,” Proceedings of the 3rd International Conference on Genetic Algorithms, San Mateo, 1989, pp. 2-9. [28] J. E. Beasley, “Job Shop Scheduling,” 2008. http://people. brunel. ac.uk/~mastjjb/jeb/orlib/jobs hopinfo.html. |

