J. Software Engineering & Applications, 2010, 3, 1148-1154
doi:10.4236/jsea.2010.312134 Published Online December 2010 (http://www.scirp.org/journal/jsea)
Parametric Tolerance Analysis of Mechanical
Assembly Using FEA and Cost Competent
Tolerance Synthesis Using Neural Network
Govindarajalu Jayaprakash1, Karuppan Sivakumar2, Manoharan Thilak3
1Department of Mechanical Engineering, Shivani Engineering College, Tiruchirappalli, India; 2Department of Mechanical Engineer-
ing, Bannari Amman Institute of Technology, Sathyamangalam, Erode, India; 3Department of Mechanical Engineering, TRP Engi-
neering College, Tiruchirappalli, India.
Received November 24th, 2010; revised December 2nd, 2010; accepted December 13th, 2010.
ABSTRACT
Tolerance design plays an important role in the modern design process by introducing quality improvements and limit-
ing manufacturing costs. Tolerance synthesis is a procedure that distributes assembly tolerances between components
or distributes final part design tolerances between related tolerances. Traditional tolerance design assumes that all
objects have rigid geometry, overlooking the role of inertia effects on flexible components of assembly. The variance is
increasingly stacked up as components are assembled without considering deformation due to inertia effects. This study
deals with the optimal tolerance design for an assembly simultaneously considering manufacturing cost, quality loss
and deformation due to inertia effect. An application problem (motor assembly) is used to investigate the effectiveness
and efficiency of the proposed methodology.
Keywords: Compliant Assembly, Inertia Effects Quality, Loss Function, FEA
1. Introduction
Design procedure mainly includes two phases: functional
design (product design) and manufacturing design (process
design). The tolerance design directly influences the func-
tionality of parts and costs. Tolerance synthesis is an es-
sential step in both design phases to assure quality con-
formity and economic manufacturing. In order to make a
reliable trade-off between design tolerances and costs, it
is necessary to determine the cost-tolerance relationships.
Numerous cost-tolerance functions for manufacturing op-
erations are given in the literature. These functions are es-
tablished by regression analysis using empirical data from
the real manufacturing. In regression analysis, one must
make assumptions about the form of the regression equa-
tion or its parameters, which may not be valid in practice
and they are not suitable for considering the quality loss.
More recently, researchers adjusted the design tolerances
to reach an economic balance between manufacturing
cost and quality loss for product tolerance design. Loss
function is quadratic expression for measuring the cost of
the average value versus the target value and the variabil-
ity of the product characteristics in terms of monetary loss
due to product failure in the eyes of the consumers. The
total cost under the situation takes the form [1]
 
22
1
TC
qm
srr rMi
r1 i
kUT Ct 










(1)
Where m is the total number of components from q as-
sembly dimensions in a finished product,
K
j the cost coef-
ficient of the jth resultant dimension for quadratic loss
function, Uij the jth resultant dimension from the ith ex-
perimental results, ij

the jth resultant variance of sta-
tistical data from the ith experimental results, Tj the de-
sign nominal value for the jth assembly dimension, tik the
tolerance established in the ith experiment for the kth com-
ponent, and CM(tik) the manufacturing cost for the toler-
ance tik.
Aspects such as design for quality, quality improve-
ment and cost reduction, asymmetric quality losses, charts
for optimum quality and cost, minimum cost approach,
cost of assemblies, development of cost tolerance models
[2-7], have been explored in the quality area of tolerance
synthesis. Experiments (DOE) approach was used in ro-
bust tolerance design, where different cases like ‘nominal

Parametric Tolerance Analysis of Mechanical Assembly Using FEA and Cost Competent
Tolerance Synthesis Using Neural Network
1149
the best’, ‘smaller the better’, ‘larger the better’ were in-
vestigated [3] along with asymmetric loss function. The
allocation of tolerances of products with asymmetric qual-
ity loss was also investigated [4]. The combined effect of
manufacturing cost and quality loss was also investigated
under the restraints of process capability limits, design
functionality restriction and product quality requirements
by using tolerance chart optimization for quality and cost
[5]. Relationships between the product cost and toler-
ances have also been investigated. An analytical method
was proposed for determining tolerances for mechanical
parts with objectives of minimizing manufacturing costs
[8]. Investigation [9] is carried out to minimize the cost of
assembly where it is observed that widening the tolerance
of more expensive part and a tightening of tolerances on
cheaper parts could result in major reduction in cost of the
assembly. Exhaustive search, zero-one, SQP and Univa-
riate methods were evaluated for performing a combined
minimum cost tolerance allocation and process selection
[10]. The production cost tolerance and hybrid tolerance
models based on empirical cost tolerance data of manu-
facturing processes like punching, turning, milling, grind-
ing and casting were introduced [11]. Investigations [12,13]
were done to optimize tolerance allocation using robust
design approach considering quality and manufacturing
cost. Zhang and Huang [14] presented an extensive re-
view of neural network applications in manufacturing.
Neural networks are defined by Rumelhart and McClel-
land [15] as massively parallel interconnected networks
of simple (usually adaptive) elements and their hierar-
chical organizations which are intended to interact with
objects of the real world in the same way as biological
nervous systems do. The approach towards constructing
the cost}tolerance relationships is based on a supervised
back-propagation (BP) neural network. Among several
well-known supervised neural networks, the BP model is
the most extensively used and can provide good solutions
for many industrial applications [16]. In this paper a back
propagation neural network is used to develop cost-tolerance
model.In the optimization algorithm set, the Simulated
Annealing (SA) algorithm [17] and Genetic Algorithm (GA)
[18] have been reported to be reliable optimization me-
thods. An optimization method based on Non-dominated
Sorting Genetic Algorithm (NSGAII) is then used to lo-
cate the combination of controllable factors (tolerances)
to optimize the output response (manufacturing cost plus
quality loss) using the equations stemming from the trained
network.
A direct constraint model in CAD is developed and the
same is integrated to an optimal tolerance design problem
[19]. In the parametric approach, the analyzed dimension
is expressed as an algebraic function an equation, or a set
of equations that relates the analyzed dimension to those
on which it depends i.e., contributors. The function is
either linearized or directly used for the Monte Carlo si-
mulation in the nonlinear analysis. Results commonly
available are the lists of contributors, sensitivities, and
percentage contributions, and the tolerance accumulation
for worst-case and statistical cases.
Traditional tolerance analysis methods assume that all
objects have rigid geometry. The variance is increasingly
stacked up as components are assembled. The geometric
variation of assembly is always assumed to be larger than
those of its subassemblies and components. This rigid
body analysis overlooks the role of deformation of flexi-
ble parts of the assembly due to inertia effects like gravity,
angular velocity, etc. The conventional addition theorem
of tolerances has to be suitably modified to accommodate
deformation due to the inertia effects. Several studies
have been carried out to manage compliant structure
[20-23]. The Finite element (FE) simulation is used to
predict the influence of geometric tolerances on the part
distortions for complex part-forms and assembly design
[24]. Tolerance analysis of hull is done considering ther-
mo mechanical effect [25], where the effect of thermal
flux in modifying the contacts and distortion the geome-
try of parts are studied. Tolerance design of mechanical
assembly is done considering thermal impact [26], where
due to change in temperature causes the output variables
of interest to deviate from the design specifications due to
the sensitivity of the parameters and tolerance of compo-
nent to temperature changes. Tolerance allocation in as-
sembly design is performed using FE simulation as a vir-
tual tool [24].This article proposes a method by which the
deformation of the parts due to inertia effects are deter-
mined using FEA and by integrating the same in tolerance
design process.
2. Neural Network Based Cost—Tolerance
Functions
A major benefit of neural networks is the adaptive ability
of their generalization of data from the real world. Many
researchers apply neural network for nonlinear regression
analysis. A Back propagation (BP) network is a feed-
forward network with one or more layers of nodes be-
tween the input and output nodes (Figure 1).
The BP learning rule is as follows. The net input, the
weighed sum of activation values of the connected input
units plus a bias value and the activated values of the
middle processing nodes are calculated. Then they are
used to calculate the activation value of output processing
units, which are compared with the target value. In case
of any discrepancies, they are propagated backward. The

Parametric Tolerance Analysis of Mechanical Assembly Using FEA and Cost Competent
Tolerance Synthesis Using Neural Network
1150
detailed BP training algorithm can be found in Rumelhart
and McClelland [15].
2.1. Constructing Cost Tolerance Functions
The BP neural network is trained using experimental re-
sults by presenting them as the input-target pattern. If the
trained result is satisfactory, the cost-tolerance functions
can be generated. The results of BP neural network are
compared with that of regression analysis. The toler-
ance-cost pairs are used as training patterns for the BP
network. The architecture of this BP network is 1-3-1.
The BP specific parameters are learning rate = 0.6, mo-
mentum = 0.9 and training epochs = 2000 and the weights
are randomly initialized between –0.5 and 0.5. The BP
network is found to have better cost-tolerance fitting re-
sults than that of regression analysis (Figure 2).
3. The Optimization Approach
Kalyanmoy Deb proposed the NSGA-II algorithm [27].
Essentially, NSGA-II differs from non-dominated sorting
Genetic Algorithm (NSGA) implementation in a number
of ways. Firstly, NSGA-II uses an elite-preserving me-
chanism, thereby assuring preservation of previously
found good solutions. Secondly, NSGA-II uses a fast
non-dominated sorting procedure. Thirdly, NSGA-II does
not require any tunable parameter, thereby making the
algorithm independent of the user.
NSGA-II uses 1) a faster non-dominated sorting ap
Figure 1. Architecture of a three-layer BP network.
Figure 2. The cost-tolerance relationship.
proach, 2) an elitist strategy, and 3) no nicking parameter.
Diversity is preserved by the use of crowded comparison
criterion in the tournament selection and in the phase of
population reduction. NSGA-II has been shown to out-
perform other current elitist multi-objective EAs on a
number of difficult test problems.
4. Parametric Approach Using Direct CAD
In the parametric approach, the analyzed dimension is
expressed as an algebraic function an equation, or a set of
equations that relates the analyzed dimension to those on
which it depends i.e., contributors. The function is either
linearized or directly used for the Monte Carlo simulation
in the nonlinear analysis. Results commonly available are
the lists of contributors, sensitivities, and percentage con-
tributions, and the tolerance accumulation for worst-case
and statistical cases. In parametric CAD systems, con-
straint equations based on geometric and dimensional re-
lations are used to model a design. By perturbing the va-
riables in these equations, some kind of sensitivity and
tolerance analysis can be performed [28]. The design
process using such a system is as follows. First, create the
nominal topology to obtain a model exhibiting the desired
geometric elements and connectivity between the ele-
ments, but without the dimensions. Next, describe the re-
quired properties between the model entities in terms of
geometric constraints, which define the desired mathe-
matical relationships between the numerical variables of
the model entities. Third, the modeling system applies a
general solution procedure to the constraints, resulting in
an evaluated model where the declared constraints are
satisfied. Forth, create variants of the model by changing
the values of the constrained variables. After each change,
a new instance of the model is created by re-executing the
constraint solution procedure. As can be seen from the
earlier process, if the user specifies the dimension of in-
terest, the system solution procedure can also obtain that
value for a specific instance of the model. If one variable
is perturbed at a time, this variable’s sensitivity can be
studied by comparing this perturbation’s effect on the
dimension of interest. With the sensitivities of each varia-
ble and their perturbation ranges (tolerances), both linea-
rized and non-linearized analyses can be performed.
Therefore, tolerance analysis functionality is just an ex-
tension or by-product of parametric solid modeling.
5. The FEA Integration
The finite element analysis of the mechanical assembly is
carried out using commercial FEM code ANSYS 11.0
with solid 92. Solid 92 has quadratic displacement beha-
vior and is well suited to model irregular meshes such as
produced from CAD data. The element is defined by ten

Parametric Tolerance Analysis of Mechanical Assembly Using FEA and Cost Competent
Tolerance Synthesis Using Neural Network
1151
nodes having three degrees of freedom at each node. The
element has plasticity, creep, swelling, stress stiffening,
large deflection and large strain capabilities. The FEA of
the assembly is carried out to determine deformation due
to inertia effects like gravity, velocity, acceleration, etc.,
resulting in increase or decrease in the critical assembly
feature.
6. The Tolerance Design Example
A motor assembly consisting of an x-base, a motor, a shaft,
a motor base and a crank are investigated using the pro-
posed tolerance synthesis approach discussed previously
(Figure 3).
The four features of x-base flatness, motor base flat-
ness, motor shaft size, and the motor shaft perpendicular-
ity affect the clearance measurement and they are treated
as controllable factors. The dimensioning and tolerancing
schemes and tolerance levels are summarized in Table 1
and Table 2; shows the costs for each component toler-
ance at various levels [1]. The details of full factorial ex-
periment design and response data are obtained from ref-
erence paper [1].The output response in this example is
the total cost, consisting of manufacturing cost and quali-
ty loss as expressed in Equation(1).
The relationship between input factors X = (x1, x2, x3, x4)
= (x – base flatness, motor base flatness, motor shaft size,
motor shaft perpendicularity) and output response F (X)
(total cost defined by Equation(1) can be revealed from
the constructed neural network. To ensure efficient con-
vergence of network training and the desired performance
of the trained network, several network architectures are
investigated and the same is listed in Table 3. The solu-
tion of the motor assembly case can be found by solving
the following mathematical models:
Maximize F() F()
subject to 0.1 0.2,
0.05 0.1,
0.050.1,
0.040.08.
1234
1
2
3
4
X
x,x,x,x
x
x
x
x





(2)
A clearance of 8.9 cms has to be maintained between
motor base and crank. By integrating CAD, the Equation
(3) is obtained. In Equation (3) the value of , is deforma-
tion due to inertia effect and it is obtained by Equation
(4).
Figure 3. The motor assembly [1].
Table 1. Summary of the contr o llab le factors [1].
x1 x2 x3 x4
component x -base Motor base Motor shaft Motor shaft
Illustration Surface on Surface on Size of shaft Perpendicularity of
x-base the bottom (target value 20mm) shaft
of motor base
Tolerance feature Flatness Flatness Size Perpendicularity
Tolerance Levels 0.100 0.050 0.050 0.040
0.150 0.075 0.075 0.060
0.200 0.100 0.100 0.080
Table 2. Tolerance costs for each factor at various levels [1].
Lower le ve l Middle l e ve l Upper le ve l
x1 $18.07 $13.63 $12.82
x2 $35.18 $24.68 $21.90
x3 $279.61 $170.39 $108.57
x4 $29.87 $19.62 $17.98

22 2
2sin(56.9343) cos(56.9343)
sin(33.0657)
sin(33.0657) 0.116084
222
34 2
1
xx x
x

 
  

 
 

 
 
  
 
(3)

Parametric Tolerance Analysis of Mechanical Assembly Using FEA and Cost Competent
Tolerance Synthesis Using Neural Network
1152
Table 3. R2 Value for each network architecture.
NETWORK ARCHITECTURE R2
4-4-1 0.9926
4-5-1 0.9993
4-6-1 0.9997
4-7-1 0.9991
4-8-1 0.9985
4-9-1 0.9983
Table 4. The NSGA II specific da ta.
Variable type Real variable
Population size 100
Cross over probability 0.7
Real parameter mutation probability 0.2155
Real parameter SBX parameter 10
Real parameter mutation parameter 100
Total no of generation 100
230
230.5
231
231.5
232
232.5
233
233.5
234
234.5
235
1 10192837465564738291100
Generation no
cost in $
Figure 4. NSGA II solution history.
Figure 5. Direct constraint parametric model in CAD.
Figure 6. The assembly model.
Figure 7. The motor assembly (exploded view).
1
X
Y
Z
ELEMENTS
Figure 8. FE model of the motor assembly.
gv
δδ δ

 (4)
The value of g δ, deformation due to gravity and v δ,
deformation due to velocity effect are obtained by FEA
and it is equal to 0.153206 cms. The value of

, angular
velocity required for FE simulation is obtained using the
following equations.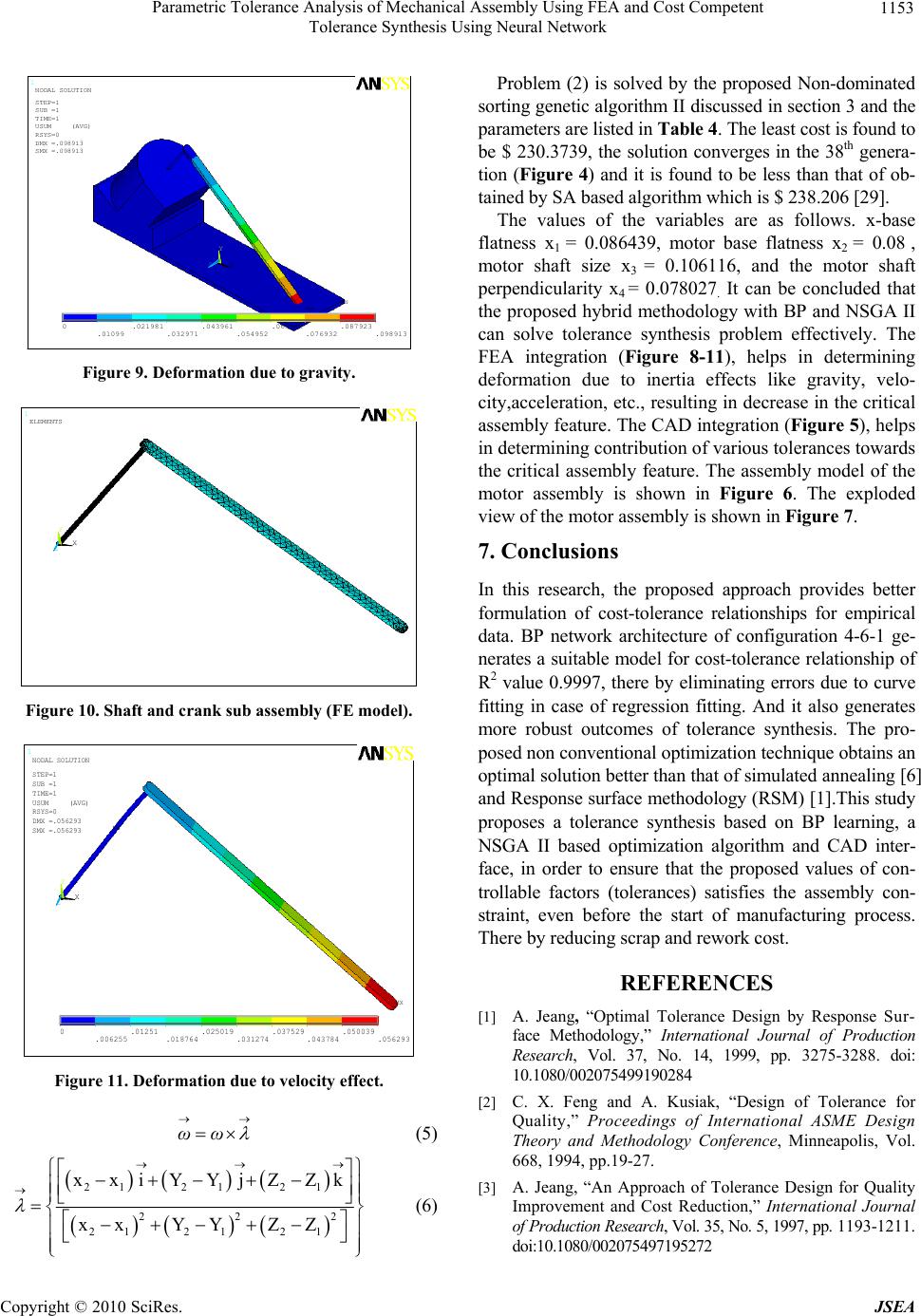

Parametric Tolerance Analysis of Mechanical Assembly Using FEA and Cost Competent
Tolerance Synthesis Using Neural Network
1153
1
MN
MX
X
Y
Z
0.01099 .021981 .032971.043961 .054952 .065942 .076932.087923 .098913
NODAL SOLUTION
STEP=1
SUB =1
TIME=1
USUM (AVG)
RSYS=0
DMX =.098913
SMX =.098913
Figure 9. Deformation due to gravity.
1
X
Y
Z
ELEMENTS
Figure 10. Shaft and crank sub assembly (F E model).
1
MN
MX
X
Y
Z
0.006255.01251 .018764.025019 .031274 .037529.043784.050039 .056293
NODAL SOLUTION
STEP=1
SUB =1
TIME=1
USUM (A VG)
RSYS=0
DMX =.05629 3
SMX =.05629 3
Figure 11. Deformation due to velocity effect.
ωω


 (5)


21 2121
222
21 2121
xxiYYjZZk
xxYY ZZ

















(6)
Problem (2) is solved by the proposed Non-dominated
sorting genetic algorithm II discussed in section 3 and the
parameters are listed in Table 4. The least cost is found to
be $ 230.3739, the solution converges in the 38th genera-
tion (Figure 4) and it is found to be less than that of ob-
tained by SA based algorithm which is $ 238.206 [29].
The values of the variables are as follows. x-base
flatness x1 = 0.086439, motor base flatness x2 = 0.08 ,
motor shaft size x3 = 0.106116, and the motor shaft
perpendicularity x4 = 0.078027. It can be concluded that
the proposed hybrid methodology with BP and NSGA II
can solve tolerance synthesis problem effectively. The
FEA integration (Figure 8-11), helps in determining
deformation due to inertia effects like gravity, velo-
city,acceleration, etc., resulting in decrease in the critical
assembly feature. The CAD integration (Figure 5), helps
in determining contribution of various tolerances towards
the critical assembly feature. The assembly model of the
motor assembly is shown in Figure 6. The exploded
view of the motor assembly is shown in Figure 7.
7. Conclusions
In this research, the proposed approach provides better
formulation of cost-tolerance relationships for empirical
data. BP network architecture of configuration 4-6-1 ge-
nerates a suitable model for cost-tolerance relationship of
R2 value 0.9997, there by eliminating errors due to curve
fitting in case of regression fitting. And it also generates
more robust outcomes of tolerance synthesis. The pro-
posed non conventional optimization technique obtains an
optimal solution better than that of simulated annealing [6]
and Response surface methodology (RSM) [1].This study
proposes a tolerance synthesis based on BP learning, a
NSGA II based optimization algorithm and CAD inter-
face, in order to ensure that the proposed values of con-
trollable factors (tolerances) satisfies the assembly con-
straint, even before the start of manufacturing process.
There by reducing scrap and rework cost.
REFERENCES
[1] A. Jeang, “Optimal Tolerance Design by Response Sur-
face Methodology,” International Journal of Production
Research, Vol. 37, No. 14, 1999, pp. 3275-3288. doi:
10.1080/002075499190284
[2] C. X. Feng and A. Kusiak, “Design of Tolerance for
Quality,” Proceedings of International ASME Design
Theory and Methodology Conference, Minneapolis, Vol.
668, 1994, pp.19-27.
[3] A. Jeang, “An Approach of Tolerance Design for Quality
Improvement and Cost Reduction,” International Journal
of Production Research, Vol. 35, No. 5, 1997, pp. 1193-1211.
doi:10.1080/002075497195272

Parametric Tolerance Analysis of Mechanical Assembly Using FEA and Cost Competent
Tolerance Synthesis Using Neural Network
1154
[4] C. C. Wu and G. R. Tang, “Tolerance Design for Products
with Asymmetric Quality Losses,” International Journal
of Production Research, Vol. 36, No. 9, 1998, pp. 2529-2541.
doi:10.1080/002075498192670
[5] A. Jeang, “Tolerance Chart Optimization for Quality and
Cost,” International Journal of Production Research, Vol. 36,
No. 11, 1998, pp. 2969-2983. doi:10.1080/002075498192238
[6] A. Jeang, “Optimal Tolerance Design by Response
Surface Methodology,” International Journal of Produc-
tion Research, Vol. 37, No. 14, 1999, pp. 3275-3288. doi:
10.1080/002075499190284
[7] S. C. Diplaris and M. M. Sfantsikopoulos, “Tolerancing
for Enhanced Quality and Optimum Cost,” Proceedings of
the 33rd International MATADOR Conference, Manche-
ster, 1999, pp. 539-544.
[8] F. H. Speckhart, “Calculation of Tolerance Based on
Minimum Cost Approach,” Journal of Engineering for
Industry-Transactions of the ASME, Vol. 94, No. 2, 1972,
pp. 447-453. doi:10.1115/1.3428175
[9] M. F. Spotts, “Allocation of Tolerances to Minimize Cost
of Assembly,” Journal of Engineering for Industry-Trans-
actions of the ASME, Vol. 95, No. 3, 1973, pp. 762-764.
[10] K. W. Chase, W. H. Greenwood, B. G. Loosli and L. F.
Hauglund, “Least Cost Tolerance Allocation for Me-
chanical Assemblies with Automated Process Selection,”
Manufacturing Review, Vol. 3, No. 1, 1990, pp. 49-59.
[11] Z. Dong, W. Hu and D. Xue, “New Production Cost-Tolerance
Models for Tolerance Synthesis,” Journal of Engineering
for Industry, Vol. 116, No. 116, 1994, pp. 199-205. doi:
10.1115/1.2901931
[12] R. S. Robust, “Design by Tolerance Allocation Con-
sidering Quality and Manufacturing Cost,” International
Advances in Design Automation, Vol. 69, No. 1, 1994,
pp. 219-226.
[13] M. Krishnasawamy and R. W. Mayne, “Optimizing Tole-
rance Allocation Based on Manufacturing Cost,” Inter-
national Advances in Design Automation, Vol. 69, No. 1,
1994, pp. 211-217.
[14] H.-C. Zhang and H. Huang, “Applications of Neural
Networks in Manufacturing: A-State-of-the-Art Survey,”
International Journal of Production Research, Vol. 33, No.
3, 1995, pp. 705-728. doi:10.1080/00207549508930175
[15] D. E. Rumelhart and J. L. McClelland, “Parallel Distributed
Processing Exploration in the Microstructure of Cognition,”
2nd Edition, Cambridge MA, USA, 1986.
[16] R. P. Lippmann, “An Introduction to Computing with
Neural Nets,” IEEE ASSP Magazine, Vol. 3, No. 4, 1987,
pp. 4-22. doi:10.1109/MASSP.1987.1165576
[17] C. Zhang and B. Wang, “Robust Design of Assembly
Design and Machining Tolerance Allocations,” IIE Trans-
actions, Vol. 30, No. 1, 1998, pp. 17-29. doi:10.1080/0
7408179808966434
[18] M. D. Al-Ansary and I. M.Deiab, “Concurrent Opti-
mization of Design and Machining Tolerance Using the
Genetic Algorithm Method,” International Journal of
Machine Tools and Manufacture, Vol. 37, No. 12, 1997,
pp.1721-1731. doi:10.1016/S0890-6955(97)00033-3
[19] G. Jayaprakash, K. Sivakumar and M. Thilak, “Parametric
Tolerance Analysis of Mechanical Assembly by Developing
Direct Constraint Model in Cad and Cost Competent To-
lerance Synthesis,” Intelligent Control and Automation,
Vol 1, No. 1, 2010, pp. 1-14. doi:10.4236/ica.2010.11001
[20] S. J. Hu. and J. Camelio, “Modeling and Control of Com-
pliant Assembly Systems.” CIRP Annals-Manufacturing
Technology, Vol. 55, No.1, 2006, pp.19-22. doi:10.1016/S
0007-8506(07)60357-6
[21] M. L. Stewart and K. W. Chase, “Variation Simulation of
Fixture Assembly for Compliant Structures Using Piece
Wise-Linear Analysis,” American Society of Mechanical
Engineers, Vol. 16, No. 1, 2005, pp. 591-600.
[22] R. Soderberg, L. Lindkvist, S. Dahlstrom, “Compu-
ter-Aided Robustness Analysis for Compliant Assemblies,”
Journal of Engineering Design, Vol. 17, No. 5, 2006,
pp. 411-428. doi:10.1080/09544820500275800
[23] K. Xie, L. Wells, J. A. Camelio and B. D. Youn,
“Variation Propagation Analysis of Compliant Assemblies
Considering Contact Interaction,” Journal of Manu-
facturing Science and Engineering, Vol. 129, No. 5, 2007,
pp. 934-942. doi:10.1115/1.2752829
[24] A. M. Irfan and P. J. Neal, “Framework of an Integrated
Tolerance Synthesis Model and Using FE Simulation as a
Virtual Tool for Tolerance Allocation in Assembly
Design,” Journal of Material Processing Technology, Vol.
150, No. 1-2, 2004, pp. 182-193. doi:10.1016/j.jmatprotec.
2004.01.036
[25] L. Pierre, D. Teissandier and J. P. Nadeau, “Integration of
Thermomechanical Strains into Tolerancing Analysis,”
International Journal on Interactive Design and Manu-
facturing, Vol. 3, No. 4, 2009, pp. 247-263.
[26] A. Jeang, T. K. Cheng and C. L.Chang, “A Statistical
Dimension and Tolerance Design for Mechanical Assembly
under Thermal Impact,” The International Journal of Ad-
vanced Manufacturing Technology, Vol. 20, No. 12. 2002,
pp. 907-915. doi:10.1007/s001700200214
[27] D. Kalyanmoy, “Optimization for Engineering Design:
Algorithms and Examples,” Prentice-Hall of India Pvt.Ltd,
India, 1995.
[28] J. J. Shah and M. Mantyka, “Parametric and Feature-based
CAD/CAM-Concepts, Techniques and Applications,” Wi-
ley, New York, 1994.
[29] M.-C. Chen, “Tolerance Synthesis by Neural Learning and
Nonlinear Programming,” International Journal of Pro-
duction Research, Vol. 70, No. 1, 2001, pp. 55-65.