International Journal of Medical Physics, Clinical Engineering and Radiation Oncology, 2013, 2, 76-87
http://dx.doi.org/10.4236/ijmpcero.2013.23011 Published Online August 2013 (http://www.scirp.org/journal/ijmpcero)
A Practical Method to Evaluate and Verify Dose
Calculation Algorithms in the Treatment
Planning System of Radiation Therapy
Lanchun Lu1*, Guy Yembi-Goma1, Jian Z. Wang1, Nilendu Gupta1,
Zhibin Huang2, Simon S. Lo3, Douglas Martin1, Nina Mayr1
1Department of Radiation Oncology, Ohio State University, Columbus, USA
2Department of Radiation Oncology, East Carolina University, Greenville, USA
3Department of Radiation Oncology, Case Western Reserve University, Cleveland, USA
Received January 10, 2013; revised February 5, 2013; accepted March 2, 2013
Copyright © 2013 Lanchun Lu et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
Purpose: To introduce a practical method of using an Electron Density Phantom (EDP) to evaluate different dose cal-
culation algorithms for photon beams in a treatment planning system (TPS) and to commission the Anisotropic Ana-
lytical Algorithm (AAA) with inhomogeneity correction in Varian Eclipse TPS. Methods and Materials: The same
EDP with various tissue-equivalent plugs (water, lung exhale, lung inhale, liver, breast, muscle, adipose, dense bone,
trabecular bone) used to calibrate the computed tomography (CT) simulator was adopted to evaluate different dose cal-
culation algorithms in a TPS by measuring the actual dose delivered to the EDP. The treatment plans with a 6-Megavolt
(MV) single field of 20 × 20, 10 × 10, and 4 × 4 cm2 field sizes were created based on the CT images of the EDP. A
dose of 200 cGy was prescribed to the exhale-lung insert. Dose calculations were performed with AAA with inhomo-
geneity correction, Pencil Beam Convolution (PBC), and AAA without inhomogeneity correction. The plans were de-
livered and the actual doses were measured using radiation dosimetry devices MapCheck, EDR2-film, and ionization
chamber respectively. Measured doses were compared with the calculated doses from the treatment plans. Results: The
calculated dose using the AAA with inhomogeneity correction was most consistent with the measured dose. The dose
discrepancy for all types of tissues covered by beam fields is at the level of 2%. The effect of AAA inhomogeneity cor-
rection for lung tissues is over 14%. Conclusions: The use of EDP and Map Check to evaluate and commission the
dose calculation algorithms in a TPS is practical. In Varian Eclipse TPS, the AAA with inhomogeneity correction
should be used for treatment planning especially when lung tissues are involved in a small radiation field.
Keywords: Electron Density Phantom; Treatment Planning System; Anisotropic Analytical Algorithm; Pencil Beam
Convolution; Inhomogeneity Correction
1. Introduction
The accuracy of dose calculation directly impacts radia-
tion treatment efficacy. The complexity of human anat-
omy and the heterogeneous components of the body’s
tissues require the sophisticated dose calculation algo-
rithm of a treatment planning system (TPS) to precisely
calculate the dose prescribed to targets as well as to or-
gans at risk, for which electron density may vary from
low, as in the lungs, to high, as in dense bones. Various
dose calculation algorithms have been developed to in-
corporate inhomogeneity correction [1-25], and some of
them have been integrated into commercial TPS, such as
the Monte-Carlo-based collapsed cone convolution algo-
rithm in Pinnacle3 TPS and Pencil Beam Convolution
algorithm (PBC) and Anisotropic Analytical Algorithm
(AAA) in Varian Eclipse TPS. PBC and AAA have often
been described in literature [26,27]. The dose calculation
with inhomogeneity correction has greatly improved the
accuracy of dose calculation, especially when low-den-
sity tissues such as lung tissues are involved in the treat-
ment. However, from a clinical medical physicist’s point
of view, there has not been a simple and practical way to
evaluate, verify, and commission different dose calcula-
tion algorithms embedded in a TPS before they are used
*Corresponding author.
C
opyright © 2013 SciRes. IJMPCERO

L. C. LU ET AL. 77
for patients’ treatment planning. Despite this lack of vali-
dation in the clinic, these dose calculation algorithms are
generally accepted in various TPS. Although some tech-
niques for testing inhomogeneity correction are available,
they are highly cumbersome and require specifically de-
signed lung phantoms [28-30], and most of them are lim-
ited to point dose measurements. A good dose calculation
algorithm should be able to calculate dose accurately not
only at the prescription point and the tumor volume, but
also at the organs at risk. Therefore dose calculation al-
gorithms should be highly accurate universally through-
out the entire treatment area. Task Group 65 of the Am-
erican Association of Physicists in Medicine (AAPM
TG65) suggested that the accuracy in tissue inhomogene-
ity correction should reach a level of 2%, although this
goal may be difficult to achieve with many currently ex-
isting algorithms [25]. TG65 recommends that heteroge-
neity corrections be applied to treatment plans and dose
prescriptions and strongly advises physicists test the
planning systems using some of the benchmark data pre-
sented in Tables 10 to 12 of Ref. [25]. The current avail-
ability of only the point dose measurement makes this
process highly cumbersome and difficult to be imple-
mented. Furthermore, no evaluation method was pre-
sented in that report. A recent inhomogeneity correction
study on the AAA in Varian Eclipse TPS by Robinson
[29] shows that the discrepancy between his measure-
ments and the AAA calculation exceeds 2% at low-den-
sity tissues, and the discrepancy is greater for 6 MV than
that for 15 MV photon beams.
Another important issue is that more and more clinical
trial protocols have been proposed and carried out for
finding the optimum treatment strategy in radiation ther-
apy. Many of these clinical trial protocols involve differ-
ent institutions which may use different TPS and hence
dose calculation algorithms. The accuracy of these dif-
ferent dose calculation algorithms associated with the
protocol certainly affects the result of the clinical trial.
Therefore, it is also crucial to evaluate different dose
calculation algorithms when a clinical trial protocol is
proposed while different TPS or dose calculation algo-
rithms are correlated with this protocol.
In this paper, we present a practical method to measure
and evaluate dose calculation algorithms and to commis-
sion dose calculation models in a TPS. For example, in
our study, the Anisotropic Analytical Algorithm (Version
8.1.17, AAA_8117) with inhomogeneity correction, the
PBC algorithm, and the AAA without inhomogeneity
correction for treatment planning in Varian Eclipse TPS
were tested and evaluated using the Electron Density
Phantom (EDP) with different tissue-equivalent inserts.
As the tools used in this method are routinely used for
QA checks at many radiation oncology centers, the me-
thod may be applied generally to commission and evalu-
ate a dose calculation algorithm for any treatment plan-
ning system.
2. Methods and Materials
The CIRS Model 062 Electron Density Phantom (EDP)
(Computerized Imaging Reference Systems, Inc., Vir-
ginia, USA) was employed to calibrate the CT simulator
(Siemens Somatom Sensation Open-Somaris/5 SYNGO)
for the dose calculation in Varian Eclipse TPS. The EDP
has 17 holes to hold different types of tissue-equivalent
inserts. Each cylinder-like (they are not exactly cylinders
—the diameter on one side is slightly smaller than the
other side) insert is about 3 cm in diameter and about 8
cm in length. Nine inserts are in the small inner ring sec-
tion and the other 8 inserts are in the outer ring section as
shown in Figure 1(a). Only the 9 inserts on the inner
section were investigated in this work (see Figure 1(b)).
For the calibration of CT and TPS, CT images for this
phantom were taken using the Siemens CT simulator and
imported into the Varian Eclipse TPS. Then the CT
Hounsfield units corresponding to the regions of interest
(ROIs) for different tissue inserts were entered into the
TPS and the data conversion to electron density factor
was established.
The same EDP with tissue-equivalent inserts was
adopted to evaluate different dose calculation algorithms
in the Varian Eclipse TPS by measuring the actual dose
delivered to the EDP prescribed by treatment plans. To
take CT images with the Siemens Somatom Sensation
Open CT simulator, a 1-cm-thick bolus was placed over
the 9 inserts within the small inner section of the EDP
and 4 blocks of solid water phantom (thickness of each
block varies from 1 cm to 5 cm) were put under the EDP.
The images were exported to the Varian Eclipse TPS for
planning. Single open field treatment plans with different
field sizes (20 × 20, 10 × 10, and 4 × 4 cm2) were gener-
ated and different dose calculation algorithms were as-
signed to these plans and doses were computed respec-
tively with a grid size of 0.25 cm. The 6 MV photon
beam was investigated in this study since higher energy
photon beams have a less inhomogeneity correction ef-
fect [25]. The gantry angle and the collimator angle were
both set to 0. A dose of 200 cGy was prescribed to a
point 4 cm behind the 8.2 cm long exhale-lung tissue-
equivalent plug (which is the isocenter in the treatment
plan) to investigate the effect of different dose calcula-
tion algorithms on the lung tissue. For each field size,
dose calculations were performed using different calcula-
tion models: 1) AAA_8117 with inhomogeneity correc-
tion (the correction switch was turned on); 2) Pencil
Beam Convolution (Version 8.1.1.17, PBC_8117); and 3)
Anisotropic Analytical Algorithm (Version 8.1.17,
AAA_8117) without inhomogeneity correction (the cor-
ection switch was turned off), respectively. Figure 2 r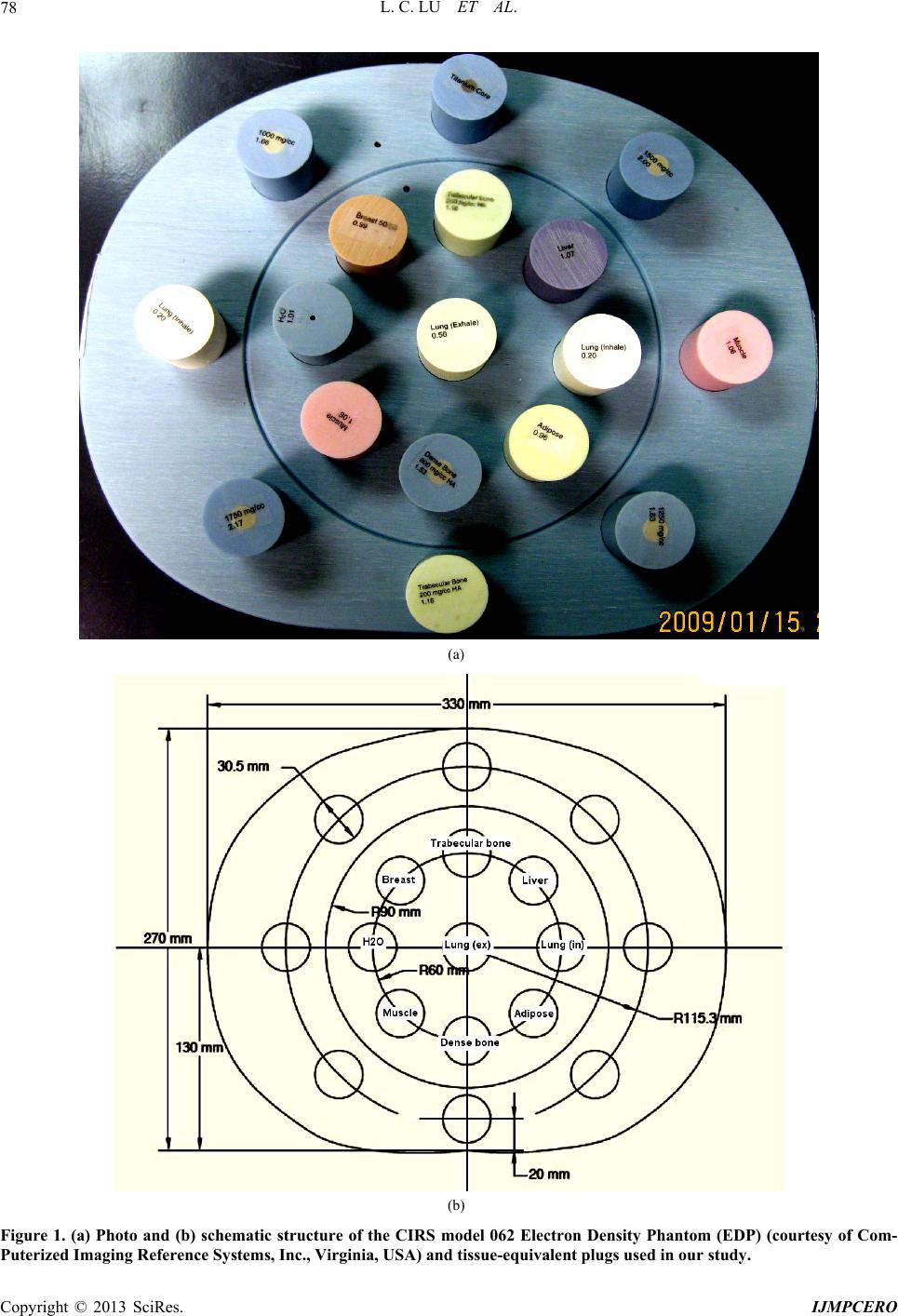

L. C. LU ET AL. 78
(a)
(b)
Figure 1. (a) Photo and (b) schematic structure of the CIRS model 062 Electron Density Phantom (EDP) (courtesy of Com-
Puterized Imaging Reference Systems, Inc., Virginia, USA) and tissue-equivalent plugs used in our study.

L. C. LU ET AL. 79
Figure 2. The treatment plan using the AAA inhomogeneity correction algorithm with the field size of 20 × 20 cm2.
shows a treatment plan for the field size of 20 × 20 cm2
with AAA inhomogeneity correction algorithm for dose
calculation. To measure the actual dose delivered to the
prescription point, the individual plans were delivered to
“treat” the EDP. The MUs delivered were defined by the
related treatment plans. The dose at a defined plane was
measured by MapCheck (Sun Nuclear Corporation
Model 1175, software version 3.05.02, 445 diode detec-
tors).
The setup of MapCheck is shown in Figure 3. A 2 cm
thick solid water phantom was placed on top of the
MapCheck to measure the 2-D dose distribution at a
depth of 4 cm below the EPD as shown in the bottom left
plot of Figure 2 created from Varian Eclipse TPS. As the
intrinsic depth from the surface of MapCheck to the de-
tector plane (the physical thickness is 1.35 cm) is 2 cm
water-equivalent thick, the depth to the measured 2-D
dose plane (coronal) in solid water blocks is 4 cm with
the isocenter in the detector plane. The source-axis dis-
tance (SAD) setup was used in the measurement so that
the inverse-square factor due to the difference between
the physical thickness (1.35 cm) and the water-equivalent
thickness (2 cm) does not need to be included. The
MapCheck was calibrated by running a 10 × 10 cm2 6
MV beam with a known dose at 5 cm depth before it was
used to measure the dose. We performed the measure-
ments for all the field sizes mentioned above (20 × 20, 10
× 10, and 4 × 4 cm2) with different dose calculation mod-
els, and compared the measured results with calculation
Figure 3. The setup for MapCheck measurement.
results from related treatment plans. Similar procedures
but independent measurements were carried out using
EDR-2 films with the RIT VXR-16 Dosimetry Vidar
System. The setup is similar to Figure 3 but the Map-
Check was replaced by an EDR-2 film placed at a depth
of 4 cm in the solid water. We compared not only the
measured dose with the calculated dose by different dose
calculation algorithms, but also compared the results
from MapCheck method with EDR-2 film method to
make sure the results from these two methods were mu-
tually consistent. To further verify our results, we also
measured the 2-D dose distributions at a different depth
(i.e. 3 cm) using the film method and compared the re-

L. C. LU ET AL. 80
sults with calculations. In addition to measuring 2-D dose
distributions, the prescribed point dose was measured
using an ion chamber. All the measured doses were com-
pared with the calculated doses from the respective asso-
ciated treatment plans. While we focused on the dose
accuracy for lung tissues, we have also evaluated the
accuracy of each dose calculation algorithm on different
types of tissues. This was carried out by comparing the
calculated dose with the corresponding measured dose on
different tissue-equivalent inserts inside the EDP regions
covered by the 20 × 20 cm2 field, such as the inserts of
inhale-lung, exhale-lung, breast, muscle, dense bone, liv-
er, adipose, trabecular bone, and H2O.
3. Results
3.1. MapCheck Measurements for AAA with
Inhomogeneity
We first studied the consistency between measurements
and calculations on different types of tissues for AAA
with inhomogeneity correction. Figure 4 shows the com-
parison of MapCheck measured dose with the calculated
dose using AAA with inhomogeneity correction for field
size 20 × 20 cm2. The top left is the measurement and the
top right is the calculation. The bottom left is the overlay
of isodose lines from measurements and calculations.
The bottom right plot shows the comparison between
measurements and calculations in the X-direction, which
ran from left to right through H2O insert, EDP body, lung
(exhale) insert, EDP body, Lung (inhale) insert. The cir-
cle points are the measurements and the smooth curve is
from calculations. The blue curve is the difference in
percentage (%) between measurements and calculations.
The difference between the calculated and the measured
dose is less than 2% for most of the compared points,
except for a few points, where the difference is slightly
larger than 2%. These points with higher discrepancies
are all located at the edge of inserts where there are tiny
air gaps between these inserts and the EDP body. The
positions of these air gaps might be different from where
they were in the CT image when the EDP was set up in
the treatment room. Figure 5 shows the comparisons
between measurements and calculations for the following
regions:
Y direction (−10 to 10 cm): dense bone, EDP body,
lung (exhale), EDP body, trabecular bone;
Negative Slope Diagonal ((−10, 10) to (10, −10)):
breast, EDP body, lung (exhale), EDP body, adipose;
Positive Slope Diagonal ((−10, −10) to (10, 10)): mus-
cle, EDP body, lung (exhale), EDP body, liver.
The above studies indicate that using the AAA inho-
mogeneity correction algorithm, the dose discrepancy
between measurement and calculation is about 2% for all
types of tissues. For the dose prescribed region (lung
exhale), the discrepancy is about 1%.
Figure 4. Comparison of measured dose with calculated
dose using AAA inhomogeneity correction, field si ze 20 × 20
cm2, with MapCheck method. Top left: measurement; Top
right: calculated dose; Bottom left: overlay of measured and
calculated isodoses; Bottom right: comparison betwee n me a s -
ured and calculated doses for X-direction: H 2O insert, EDP
body, lung (exhale) inser t, EDP body, lung (inhale) insert.
Figure 5. Comparison of measured dose with calculated
dose using AAA inhomogeneity correction, field si ze 20 × 20
cm2, with MapCheck method. Top for Y-direction: dense
bone, lung (exhale), trabecular bone inserts; Middle for
Negative slope: breast, lung (exhale), adipose inserts; and
Bottom for Positive slope: muscle, lung (exhale), liver in-
serts.
3.2. EDR-2 Film Measurements
Figure 6 shows the comparison of EDR-2 film meas-
urement with the calculation using AAA inhomogeneity
correction for the field size of 20 × 20 cm2. In the figure,

L. C. LU ET AL. 81
Figure 6. Comparison of measured dose with calculated dose of AAA inhomogeneity correction, field size 20 × 20 cm2 with
EDR2-film method. Target: calculated dose from treatment plan; Reference: film measurement. Green curve for X-direction:
H2O, lung (exhale), and lung (inhale) inserts; Red curve for Y-direction: trabecular bone, lung (exhale), and dense bone in-
serts.
“target image” is for the 2-D dose distribution from the
treatment plan, and “reference image” is for the one from
the film measurement. The 3-D gamma surface in Figure
6 represents the difference between measurement and
dose calculation in the 3-D format. Similar to the Map-
Check study, the large discrepancy between measure-
ments and calculations again were at the edge of inserts
—air gap. However, the overall discrepancy between
measurements and calculations for all tissue plugs is still
about 2%, which is consistent with the results from the
MapCheck study.
3.3. Point Dose Measurement
Table 1 gives the results of dose measurements at the
prescribed dose point using an ion chamber (model:
PTW TN30013, inner diameter 6.3 mm) and their com-
parisons with calculated results from different dose cal-
culation algorithms. The calculation from AAA without
inhomogeneity correction underestimates the dose to
lung-tissue by about 14%, and the discrepancy increases
when field size decreases due to increasing deviation
from nonequilibrium conditions and the ion chamber-
induced perturbing level of disequilibrium for smaller
field size. For the small field size 4 × 4 cm2, the AAA
with inhomogeneity correction provides a more accurate
result compared with the PBC calculation, although the
difference is not significant for larger field sizes such as
10 × 10 and 20 × 20 cm2.
3.4. Comparison of AAA Inhomogeneity
Correction, PBC Inhomogeneity Correction,
and AAA without Inhomogeneity Correction
The dose calculation accuracy within different tissues
using the AAA with inhomogeneity correction was com-
pared with 1) PBC and 2) AAA without inhomogeneity
correction by evaluating the difference between meas-
urements and calculations in X-direction, Y-direction,
Negative-Slope diagonal direction, and Positive-Slope
diagonal direction. Figures 7 and S1-S3 show those
comparisons for these plans with field size 20 × 20 cm2

L. C. LU ET AL. 82
Table 1. Prescribed point dose measurements using an ion
chamber and the comparison with calculated doses for dif-
ferent dose calculation models. Prescription dose: 200 cGy.
Field Size
20 × 20 (cm2) 10 × 10 (cm2) 4 × 4 (cm2)
Calculation Models
meas.
(cGy)
Diff
(%)
meas.
(cGy)
Diff
(%)
meas.
(cGy)
Diff
(%)
AAA Inhomogeneity
Correction 201 0.5 200.5 0.3 201.1 0.6
PBC Inhomogeneity
Correction 201 0.5 199 −0.5 195.5 −2.3
AAA No Inhomogeneity
Correction 227.5 13.8 229.5 14.8 234.4 17.2
Figure 7. Comparison of measured dose with calculated
dose for all three dose calculation models in X-direction:
H2O insert, EDP body, lung (exhale) insert, EDP body, lung
(inhale) insert. Top: AAA with inhomogeneity correction;
Middle: PBC; Bottom: AAA without inhomogeneity correc-
tion.
for various tissues respectively. Figures S1-S3 can be
found under “Supplementary Material” for this article.
For all types of tissues except lung tissues, both AAA
with inhomogeneity correction and PBC can reach the
accuracy of 2% if the air gap effect was excluded, and
there were no significant differences between the two
calculation models. Figure 8 shows the histogram dis-
tributions of the difference between measurement and
calculation for all the MapCheck measured points on
different types of tissues for both AAA inhomogeneity
correction and PBC methods with the field size of 20 ×
20 cm2. There were a small number of points where the
difference between measurement and calculation was
larger than 2%. These points were at the air gap region of
inserts. For the low-density tissues (lung tissues), AAA
with inhomogeneity correction had a much better corre-
lation with the measured dose than PBC, as shown in
Figures 7 and 9 and Table 1. For AAA without inho-
mogeneity correction, the discrepancy between meas-
urement and calculation was smaller for non-lung tissues
than for the low electron density tissues, such as lung.
For the field size of 4 × 4 cm2, which covered only the
lung-exhale insert, the AAA with inhomogeneity correc-
tion was much more accurate compared with PBC and
the AAA without inhomogeneity correction as shown in
Figure 9, where dose points at four directions—X, Y,
Negative-Slope diagonal, and Positive-Slope diagonal
were measured. Studies using an ion chamber (as in Ta-
ble 1) and using EDR-2 films for all the field sizes gave
consistent results with the MapCheck analysis.
4. Discussion
We have tested and verified different dose calculation
A AA I n hom ogenei ty Cor r ec t i on
0
10
20
30
40
50
60
-17.38
-14.594 -11.808
-9.022 -6.23 6
-3.45
-0.664
2.122 4.908 7.694
More
Measurement - Calculation (%)
Frequency
PBC
0
10
20
30
40
50
60
-21.66
-18.298 -14.936 -11.574
-8.212
-4.85
-1.488
1.874
5.236
8.598
More
Measurement - Calculation (%)
Frequency
Figure 8. Histogram of difference between measured dose
and calculated dose in percentage for all the measurement
directions: (X-direction, Y-direction, Negative-Slope direc-
tion, and Positive-Slope direction) corresponding to tissue-
equivalent inserts of H2O, lung (exhale), lung (inhale), dense
bone, trabecular bone, breast, adipose, muscle, liver. Top:
AAA with inhomogeneity correction; Bottom: PBC. Field
2
size: 20 × 20 cm.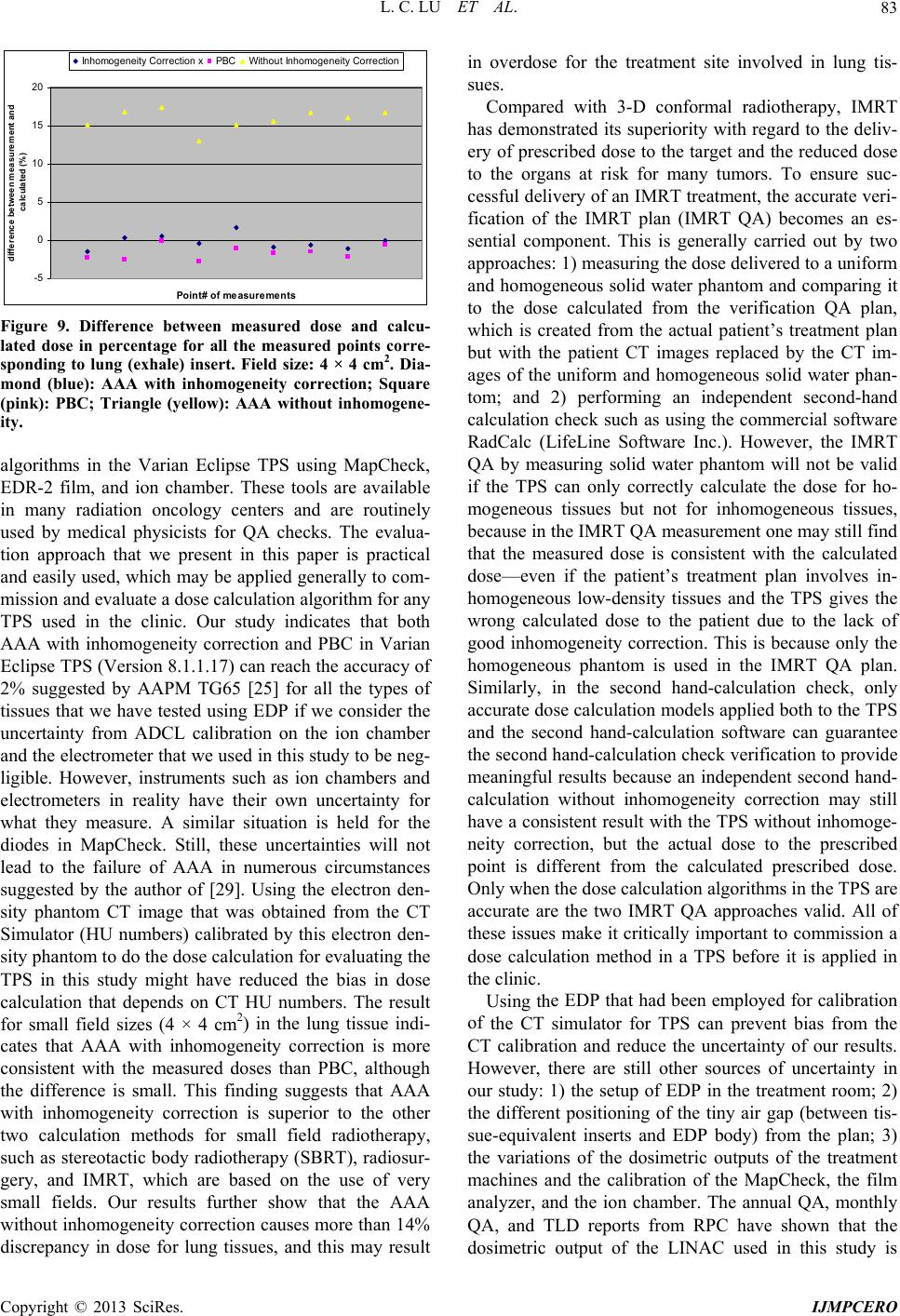

L. C. LU ET AL. 83
-5
0
5
10
15
20
Point# o f me asur ements
difference between measurement and
calculat ed ( %)
Inhomogeneity Correction xPBC Without Inhomogeneity Correction
Figure 9. Difference between measured dose and calcu
lgorithms in the Varian Eclipse TPS using MapCheck,
pared with 3-D conformal radiotherapy, IMRT
ha
e EDP that had been employed for calibration
of
-
lated dose in percentage for all the measured points corre-
sponding to lung (exhale) insert. Field size: 4 × 4 cm2. Dia-
mond (blue): AAA with inhomogeneity correction; Square
(pink): PBC; Triangle (yellow): AAA without inhomogene-
ity.
a
EDR-2 film, and ion chamber. These tools are available
in many radiation oncology centers and are routinely
used by medical physicists for QA checks. The evalua-
tion approach that we present in this paper is practical
and easily used, which may be applied generally to com-
mission and evaluate a dose calculation algorithm for any
TPS used in the clinic. Our study indicates that both
AAA with inhomogeneity correction and PBC in Varian
Eclipse TPS (Version 8.1.1.17) can reach the accuracy of
2% suggested by AAPM TG65 [25] for all the types of
tissues that we have tested using EDP if we consider the
uncertainty from ADCL calibration on the ion chamber
and the electrometer that we used in this study to be neg-
ligible. However, instruments such as ion chambers and
electrometers in reality have their own uncertainty for
what they measure. A similar situation is held for the
diodes in MapCheck. Still, these uncertainties will not
lead to the failure of AAA in numerous circumstances
suggested by the author of [29]. Using the electron den-
sity phantom CT image that was obtained from the CT
Simulator (HU numbers) calibrated by this electron den-
sity phantom to do the dose calculation for evaluating the
TPS in this study might have reduced the bias in dose
calculation that depends on CT HU numbers. The result
for small field sizes (4 × 4 cm2) in the lung tissue indi-
cates that AAA with inhomogeneity correction is more
consistent with the measured doses than PBC, although
the difference is small. This finding suggests that AAA
with inhomogeneity correction is superior to the other
two calculation methods for small field radiotherapy,
such as stereotactic body radiotherapy (SBRT), radiosur-
gery, and IMRT, which are based on the use of very
small fields. Our results further show that the AAA
without inhomogeneity correction causes more than 14%
discrepancy in dose for lung tissues, and this may result
in overdose for the treatment site involved in lung tis-
sues.
Com
s demonstrated its superiority with regard to the deliv-
ery of prescribed dose to the target and the reduced dose
to the organs at risk for many tumors. To ensure suc-
cessful delivery of an IMRT treatment, the accurate veri-
fication of the IMRT plan (IMRT QA) becomes an es-
sential component. This is generally carried out by two
approaches: 1) measuring the dose delivered to a uniform
and homogeneous solid water phantom and comparing it
to the dose calculated from the verification QA plan,
which is created from the actual patient’s treatment plan
but with the patient CT images replaced by the CT im-
ages of the uniform and homogeneous solid water phan-
tom; and 2) performing an independent second-hand
calculation check such as using the commercial software
RadCalc (LifeLine Software Inc.). However, the IMRT
QA by measuring solid water phantom will not be valid
if the TPS can only correctly calculate the dose for ho-
mogeneous tissues but not for inhomogeneous tissues,
because in the IMRT QA measurement one may still find
that the measured dose is consistent with the calculated
dose—even if the patient’s treatment plan involves in-
homogeneous low-density tissues and the TPS gives the
wrong calculated dose to the patient due to the lack of
good inhomogeneity correction. This is because only the
homogeneous phantom is used in the IMRT QA plan.
Similarly, in the second hand-calculation check, only
accurate dose calculation models applied both to the TPS
and the second hand-calculation software can guarantee
the second hand-calculation check verification to provide
meaningful results because an independent second hand-
calculation without inhomogeneity correction may still
have a consistent result with the TPS without inhomoge-
neity correction, but the actual dose to the prescribed
point is different from the calculated prescribed dose.
Only when the dose calculation algorithms in the TPS are
accurate are the two IMRT QA approaches valid. All of
these issues make it critically important to commission a
dose calculation method in a TPS before it is applied in
the clinic.
Using th
the CT simulator for TPS can prevent bias from the
CT calibration and reduce the uncertainty of our results.
However, there are still other sources of uncertainty in
our study: 1) the setup of EDP in the treatment room; 2)
the different positioning of the tiny air gap (between tis-
sue-equivalent inserts and EDP body) from the plan; 3)
the variations of the dosimetric outputs of the treatment
machines and the calibration of the MapCheck, the film
analyzer, and the ion chamber. The annual QA, monthly
QA, and TLD reports from RPC have shown that the
dosimetric output of the LINAC used in this study is

L. C. LU ET AL. 84
consistent with each other within 1%. Further study is
needed to perform with different beam energy although it
is expected that higher energy will have a less inhomoge-
neity correction effect.
In conclusion, we have proposed a practical m
w
5. Acknowledgements
Yanzhen Lu (Amherst Col-
REFERENCES
[1] N. Papanikola. Hendee, “Hetero-
ethod
hich may be applied universally to evaluate and verify
the dose calculation algorithms used in various clinical
treatment planning systems. For Varian Eclipse TPS used
in this study, our results have shown that AAA with tis-
sue inhomogeneity correction should be used for treat-
ment planning, especially when the lung tissue was in-
volved in a small radiation field. It should be pointed out
that the work presented in this study is based on Version
8.1 of Varian Eclipse TPS which was available at the
time. The new dose calculation algorithms thereafter im-
planted in the new versions of Eclipse in principle could
still be evaluated using the method proposed in this pa-
per.
The authors sincerely thank
lege) for the proofreading and editing of this manuscript.
ou, E. E. Klein and W.R
geneity Corrections Should Be Used in Treatment Plan-
ning for Lung Cancer?” Medical Physics, Vol. 27, No. 8,
2000, pp. 1702-1704. doi:10.1118/1.1287645
[2] N. Papanikolaou and T.R. Mackie, “Extension of the
. A. Shiu, S. W. Bujnowski, et al., “Ef-
6
Convolution/Superposition Based Algorithms to Include
Atomic Number Effects,” Medical Physics, Vol. 22, No.
6, 1995, p. 977.
[3] G. Starkschall, A
fect of Dimensionality of Heterogeneity Correction on the
Implementation of a Three-Dimensional Electron Pencil-
Beam Algorithm,” Physics in Medicine and Biology, Vol.
36, No. 2, 1991, pp. 207-227.
doi:10.1088/0031-9155/36/2/00
, “The Regional Monte [4] M. K. Woo, D. Scora and E. Webb
Carlo Method: A Dose Calculation Method Based on
Accuracy Requirement,” Medical Physics, Vol. 25, No.
10, 1998, pp. 1866-1871. doi:10.1118/1.598366
[5] I. Kawrakow, “VMC++, Electron and Photon Monte
rs and J. J. Bat-
Carlo Calculations Optimized for Radiation Treatment
Planning,” In: A. Kling, F. Barao, M. Nakagawa, L.
Tavora and P. Vaz, Eds., Advanced Monte Carlo for Ra-
diation Physics, Particle Transport Simulation and Ap-
plications: Proceedings of the Monte Carlo 2000 Meet-
ing, Springer, Berlin, 2001, pp. 229-236.
[6] T. R. Mackie, A. F. Bielajew, D. W. Roge
tista, “Generation of Photon Energy Deposition Kernels
Using the EGS Monte Carlo Code,” Physics in Medicine
and Biology, Vol. 33, No. 1, 1988, pp. 1-20.
doi:10.1118/1.598366
[7] A. Ahnesjo and M.-M
for External Photon Beams in Radiotherapy (Topical Re-
view),” P hys ics in Medicine and Biology, Vol. 44, No. 11,
1999, pp. 99-155. doi:10.1088/0031-9155/44/11/201
[8] M. Nilsson and T. Knoos, “Application of the Fano Theo-
rem in Inhomogeneous Media Using a Convolution Algo-
rithm,” Physics in Medicine and Biology, Vol. 37, No. 1,
pp. 1992, 69-83. doi:10.1088/0031-9155/37/1/005
[9] A. Ahnesjo, “Collapsed Cone Convolution of Radiant En-
ergy for Photon Dose Calculation in Heterogeneous Me-
dia,” Medical Physics, Vol. 16, No. 4, 1989, pp. 577-592.
doi:10.1118/1.596360
[10] R. Mohan, C.-S. Chui and L. Lidofsky, “Differential Pen-
cil Beam Dose Computation Model for Photons,” Medi-
cal Physics, Vol. 13, No. 1, 1986, pp. 64-73.
doi:10.1118/1.595924
[11] M. R. Sontag, “Photon Beam Dose Calculations in Re-
ong and R. M. Henkelman, “A New Approach to
gions of Tissue Heterogeneity Using Computed Tomo-
graphy,” Ph.D. Thesis, University of Toronto, Toronto,
1979.
[12] J. W. W
CT Pixel-Based Photon Dose Calculations in Heteroge-
neous Media,” Medical Physics, Vol. 10, No. 2, 1983, pp.
199-208. doi:10.1118/1.595294
[13] J. J. Battista, M. B. Sharpe, E. Webb and J. Van Dyk, “A
of Photon
new Classification Scheme for Photon Beam Dose Algo-
rithms,” In: D. D. Leavitt and G. Starkschall, Eds., Inter-
national Conference on the Use of Computers in Radia-
tion Therapy, XII ICCR, Salt Lake City, Medical Physics
Physics Publishing, Madison, 1997, pp. 39-42.
[14] A. L. Boyer, “Shortening the Calculation Time
Dose Distributions in an Inhomogeneous Medium,” Med-
ical Physics, Vol. 11, No. 4, 1984, pp. 552-554.
doi:10.1118/1.595526
[15] A. Ahnesjo, M. Saxner and A. Trepp, “A Pencil Beam
Model for Photon Dose Calculation,” Medical Physics,
Vol. 19, No. 2, 1992, pp. 263-273. doi:10.1118/1.595526
[16] N. Papanikolaou, T. R. Mackie, C. Meger-Wells, et al.,
nd and E. L. Chaney, “A Finite-Size Pencil
“Investigation of the Convolution Method for Polyener-
getic Spectra,” Medical Physics, Vol. 20, No. 5, 1993, pp.
1327-1336.
[17] J. D. Bourla
Beam Model for Photon Dose Calculations in Three Di-
mensions,” Medical Physics, Vol. 19, No. 6, 1992, pp.
1401-1412. doi:10.1118/1.596772
[18] M. B. Sharpe and J. J. Battista, “Dose Calculations Using
Convolution and Superposition Principles: The Orienta-
tion of Dose Spread Kernals in Divergent X-Ray Beams,”
Medical Physics, Vol. 20, No. 6, 1993, pp. 1685-1694.
doi:10.1118/1.596955
[19] J. R. Cunningham, “Tissue Inhomogeneity Corrections in
Photon Beam Treatment Planning,” Progress in Medical
Radiation Physics, Vol. 1, 1982, pp. 103-131.
doi:10.1118/1.596955
[20] J. W. Wong and J. A. Purdy, “Review of Methods of
Inhomogeneity Corrections,” Advances in Radiation On-
cology Physics: Dosimetry, treatment Planning and Bra-
chytherapy, American Institute of Physics, New York,
1992, pp. 887-899. . Aspradakis, “Dose Calculations

L. C. LU ET AL. 85
Wong, “Implementation of the ETAR [21] C. X. Yu and J. W.
Method for 3D Inhomogeneity Corrections Using FFT,”
Medical Physics, Vol. 20, No. 3, 1993, pp. 627-632.
doi:10.1118/1.597010
[22] C.-M. Ma, J. S. Li, T. Pawlicki, et al., “A Monte Carlo
Dose Calculation Tool for Radiotherapy Treatment Plan-
ning,” Physics in Medicine and Biology, Vol. 47, No. 10,
2002, pp. 1671-1689. doi:10.1118/1.597010
[23] S. Webb and R. P. Parker, “A Monte Carlo Study of the
Interaction of External Beam X-Radiation with Inhomo-
geneous Media,” Physics in Medicine and Biology, Vol.
23, No. 6, 1978, pp. 1043-1059. doi:10.1118/1.597010
[24] N. Papanikolaou, “Dose Calculation Algorithms in the
ou, J. J. Battista, A. L. Boyer, et al., “Tis-
cy
IMRT Era, Radiother,” Oncology, Vol. 61, Supplement 1,
2001, p. S12.
[25] N. Papanikola
sue Inhomogeneity Corrections for Megavoltage Photon
Beams,” AAPM Report No. 85, AAPM TG65, 2004.
[26] A. Gray, L. D. Oliver and P. N. Johnston, “The Accura
of the Pencil Beam Convolution and Anisotropic Ana-
lytical Algorithms in Predicting the Dose Effects Due to
Attenuation from Immobilization Devices and Large Air
Gaps,” Medical Physics, Vol. 36, No. 7, 2009, pp. 3181-
3191. doi:10.1118/1.3147204
[27] A. V. Esch, L. Tillikainen, J. Pyykkonen, et al., “Testing
of the Analytical Anisotropic Algorithm for Photon Dose
Calculation,” Medical Physics, Vol. 33, No. 11, 2006, pp.
4130-4148. doi:10.1118/1.3147204
[28] B. Kavanagh, M. S. Ding, T. Schefter, et al., “The Do-
simetric Effect of Inhomogeneity Correction in Dynamic
Conformal ARC Stereotactic Body Radiation Therapy for
Lung Tumors,” Journal of Applied Clinical Medical Phy-
sics, Vol. 7, No. 2, 2006, pp. 58-63.
doi:10.1118/1.3147204
[29] D. Robinson, “Inhomogeneity Correction and the Ana-
lytic Anisotropic Algorithm,” Journal of Applied Clinical
Medical Physics, Vol. 9, No. 2, 2008, p. 2786.
doi:10.1088/0031-9155/51/21/002
[30] T. Nishio, E. Kunieda, H. Shirato, et al., “Dosimetric
Verification in Participating Institutions in a Stereotactic
Body Radiotherapy Trial for Stage I Non-Small Cell Lung
Cancer: Japan Clinical Oncology Group Trial (JCOG-
0403),” Physi cs in M edi c ine and Biology , Vol. 51, No. 21,
2006, 5409-5417.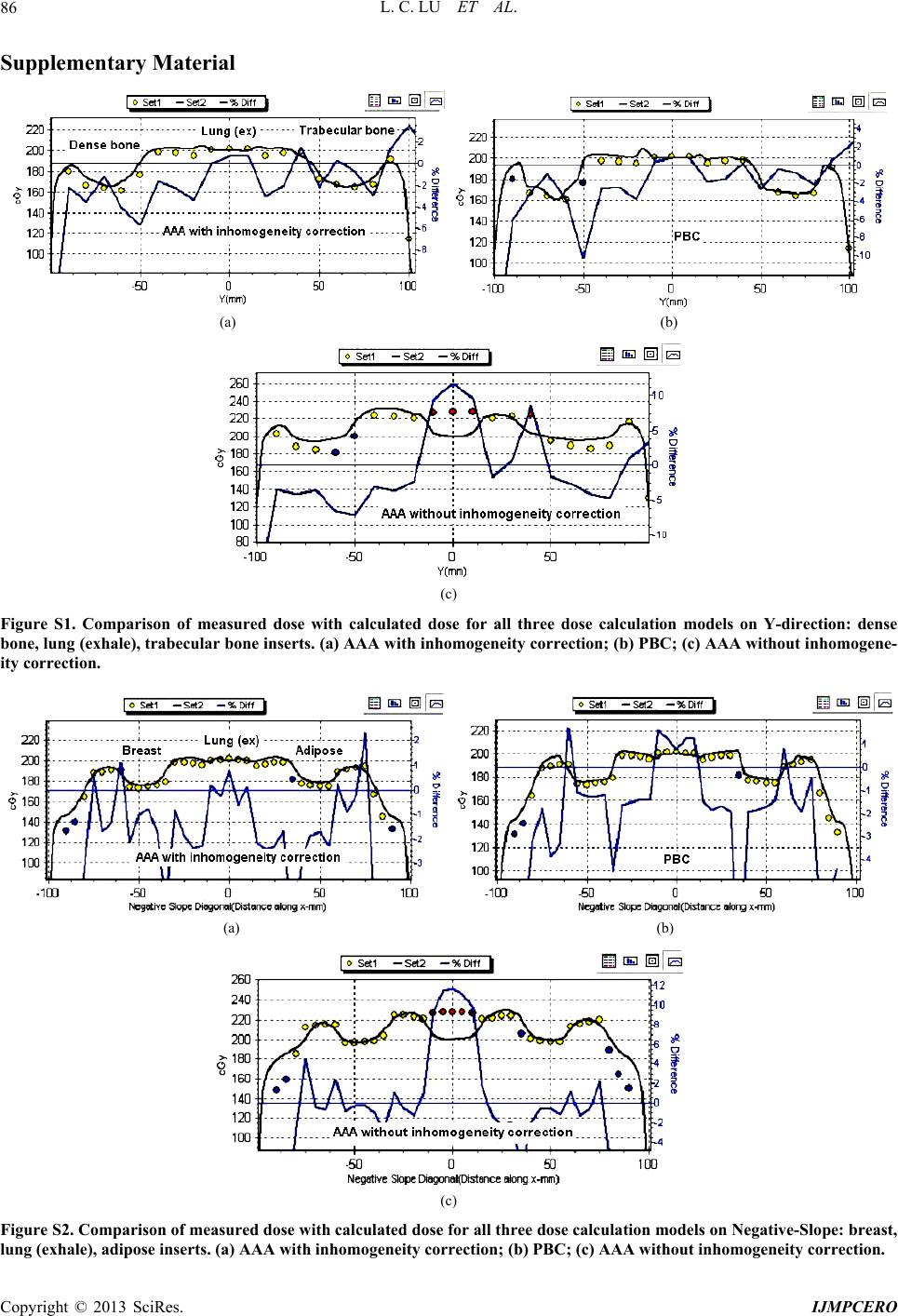

L. C. LU ET AL. 86
Supplementary Material
(a) (b)
(c)
Figure S1. Comparison of measured dose with calculated dose for all three dose calculation models on Y-direction: dense
bone, lung (exhale), trabecular bone inserts. (a) AAA with inhomogeneity correction; (b) PBC; (c) AAA without inhomogene-
ity correction.
(a) (b)
(c)
Figure S2. Comparison of measured dose with calculated dose for all three dose calculation models on Negative-Slope: breast,
lung (exhale), adipose inserts. (a) AAA with inhomogeneity correction; (b) PBC; (c) AAA without inhomogeneity correction.

L. C. LU ET AL. 87
(a) (b)
(c)
Figure S3. Comparison of measured dose with calculated dose for all three dose calculation models on Positive-Slope: muscle,
lung (exhale), liver inserts. (a) AAA with inhomogeneity correction; (b) PBC; (c) AAA without inhomogeneity correction.