Modeling perisaccadic time perception

doi:10.4236/jbise.2010.312147

Paper Menu >>

Journal Menu >>

J. Biomedical Science and Engineering, 2010, 3, 1133-1142

doi:10.4236/jbise.2010.312147 Published Online December 2010 (http://www.SciRP.org/journal/jbise/

JBiSE

Published Online December 2010 in SciRes. http://www.scirp.org/journal/JBiSE

Modeling perisaccadic time perception

Andrea Guazzini1, Pietro Liò2, Andrea Passarella1, Marco Conti1

1Institute of Informatics and Telematics-IIT-CNR, Pisa, Italy;

2Computer Laboratory, University of Cambridge, Cambridge, UK

Email: andrea.guazzini@gmail.com

Received 29 July 2010; revised 15 August 2010; accepted 18 August 2010.

ABSTRACT

There is an impressive scarcity of quantitative models

of the clock patterns in the brain. We propose a me-

soscopic approach, i.e. neither a description at single

neuron level, nor at systemic level/too coarse granu-

larity, of the time perception at the time of the sac-

cade. This model uses functional pathway knowledge

and is inspired by, and integrates, recent findings in

both psychophysics and neurophysiology. Perceived

time delays in the perisaccadic window are shown

numerically consistent with recent experimental mea-

sures. Our model provides explanation for several

experimental outcomes on saccades, estimates popu-

lation variance of the error in time perception and

represent a meaningful example for bridging psy-

chophysics and neurophysiology. Finally we found

that the insights into information processing during

saccadic events lead to considerations on engineering

exploitation of the underlying phenomena.

Keywords: Brain Clock; Saccades; Time Compression;

Time Perception; Craniotopiccoordinates

1. INTRODUCTION

One of the most important research areas in neurosci-

ence focuses on the neural mechanisms of time percep-

tion and in particular on the link between visual percep-

tion and the brain clock(s); for sake of simplicity, we

will call this visual timing. In the last decade important

evidences of a strong distortion of the time perception

during saccadic eye movements have been attracted the

most the attention of researchers. Saccades represents

probably the perfect process to study ”visual timing”

both for the changing of external space mapping onto

retina and for the brain pathways alterations caused by

the saccadic neural correlates [1-6]. The numerical

simulation of the known saccadic effects by a model

which integrates the insights coming from psychophys-

ics and neurophysiology appear today to be a promising

scenario to extend the discussion on the brain clock(s)

problem. One interesting question is whether temporal

judgments is distributed or centralized [7]. The time

perception in the range of milliseconds to minutes in-

volves variety of neural population located in the frontal

cortex, hippocampus, basal ganglia and cerebellum.

Nowadays it is well known that the “internal” represen-

tation of time depends on the integration of multiple

neural systems. While there is good evidence about dif-

ferent clocks for different interval lengths, some recent

evidences point clearly to the existence of visually based

timing mechanisms. Researchers from psychophysics

and neurophysiology have approached this topic from

different sides, both leading to experimental evidences

that can be now merged together to obtain a more com-

plete perspective for visual timing processes than in the

past. The description of the neurological structures can

be performed at different scales. At the lower level of

description, the micro-scale is represented by single

neurons as nodes. Using a complex network framework,

we can assign certain properties of individual nodes (de-

gree, centrality, clustering, etc.); in order to model the

dynamical process each node is performing in process-

ing the signal. This level of description is unfortunately

computationally very expensive nowadays and very pre-

cise only for small networks; therefore it does not allow

a generic analysis of the global properties of the system.

At the other extreme, we have the higher level of de-

scription, the macro-scale, represented by the psycho-

physics where statistical properties of the network as a

whole. In the middle of these descriptions still remains a

huge space for different scales of descriptions that are

termed mesoscales, or intermediate scales. These scales

are understood as substructures (eventually sub graphs)

that have topological entity compared to the whole net-

work, e.g. populations/communities of neurons which

are functionally and/or structurally homogeneous. In

particular, the community detection problem concerning

the determination of mesoscopic structures that have

functional, relational or even social entity is still contro-

A. Guazzini et al. / J. Biomedical Science and Engineering 3 (2010) 1133-1142

1134

versial, starting from the a priori definition of what a

community is. The correct determination of the meso-

scale in complex networks is a major challenge. On the

mesoscopic level, researchers have examined neural

activity as measured by means of local field potentials or

dense intracranial electrode arrays in human and

non-human subjects. These approaches have stimulated

models of neuronal communication between nearby re-

gions. By contrast, macroscopic parameters of neural

activity have been used to assess the characteristics of

large neuronal assemblies that fire in synchrony and thus

generate detectable voltage or magnetic gradients on the

surface of the scalp. This paper originates from our par-

ticipation in the three years EU project MEMORY in

which large amount of data has been collected. On the

light of the MEMORY project and discussions with ex-

perimentalist we aim at devicing the model that could

answer the question of time perception during the sac-

cadic events.

1.1. Combining Neurophysiological and

Psychophysical Evidencies

The psychophysical studies of the relationship between a

visual stimulus (say a dot moving etc) and the perception

of the elapsed time between the start and end of the sti-

mulus (which is subjective) have produced important

results. The finding that perceived duration of a dynamic

stimulus can be manipulated in a local region of visual

space has confirmed that the visual perception of time is

processed directly by superior visual areas at least in its

early stages [8]. An interesting experiment has recently

shown that the existence of a large contrast effects in the

discrimination of short temporal intervals during fixation

events [9]. Della Rocca et al. examined the effect of

temporal distractors on interval discrimination and

showed that the perception of the time driven by visual

events is affected by early past experiences, as it hap-

pens for others characteristics related to the visual stim-

uli such as the shape, color or movement of objects. An

important finding comes from the studies of Morrone

and Burr about time perception during saccades [4].

Their major results has been that perceived time is com-

pressed when stimuli are ashed shortly before or after

the onset of a saccadic eye movement [1,2,10]. More-

over time and space perception seem to follow the same

compression pattern during saccades both for timescale

and magnitude of the effects. This evidence suggests that

time information is embedded with other characteristics

in the same neural representation of stimuli. The neuro-

physiological approach to the visual timing has revealed

neural correlates of visual experience which could ac-

count for the psychophysical findings [11-13]. The

hypothesis of an explicit neural representation of tem-

poral attributes of visual stimuli has a wide acceptance

[14]. From this point of view the fundamental represen-

tation of visual information should be able to encode

temporal information similarly to the other characteris-

tics of the perceived matter (color, frequency, bright-

ness). Previous studies have drawn the hypothesis that

cerebral circuits are inherently able to rescale durations

in a proportional manner and compensate for the error

differences generated by the cerebellum. Following such

assumption, to explain visual timing failures during sac-

cades an explicit model has to consider at least those

neural areas and pathways by which visual experience is

represented, filtered and analyzed [15]. In a recent paper,

Buonomano proposed that short-term plasticity and dy-

namic changes in the balance of excitatory-inhibitory

interactions may underlie the decoding of temporal in-

formation, that is, the generation of temporally selective

neurons [16]. He first showed that it is possible to tune

cells to respond selectively to different intervals by

changing the synaptic weights of different synapses in

parallel. Short-term plasticity is a usage-dependent

change in synaptic strength on the time scale of milli-

second to seconds and is observed in almost every syn-

apse types of the central nervous system. Each type of

synapse has its own specificity with respect to this prop-

erty. When stimulated a few times within a second, some

synapses show facilitation, others depression or else

complex sequences of facilitatory and depressing changes

[16]. According with the previous claim, recent results

show that for visual perception the timing attributes of

visual experience and the temporal tuning properties of

certain visual neurons are linked. Moreover neurons in

visual areas of primate parietal cortex have reduced la-

tencies to visual stimulation at the time of a saccade [3].

Several hypotheses of time measuring systems, peculiar

to neural circuits, demonstrates synchronization enables

both the evaluation of different time scales and the

binding between different sensorial/cognitive modalities.

Lesion and functional imaging studies have identified

frontal, temporal, and parietal areas as playing a major

role in the control of visual timing processing, but very

little is known about these areas interact to form a dy-

namic attentional network. We know that the fronto-

parieto-temporal (FPT) network communicates by means

of neural phase synchronization. Results reveal that

communication within FPT proceeds via transient long-

range phase synchronization in the beta bend [17]. Re-

cent results concern the high-frequency long range cou-

pling between prefrontal and visual cortex. Desimone et al.

used paired recordings in the frontal eye field (FEF) and

area V4, they found that attention to a stimulus in their

joint receptive fields leads to enhanced oscillatory cou-

A. Guazzini et al. / J. Biomedical Science and Engineering 3 (2010) 1133-1142 1135

pling between the two areas, particularly at gamma fre-

quencies [18]. This coupling appeared to be initiated by

FEF and was time-shifted by about 8 to 10 ms across a

range of frequencies. Considering the expected conduc-

tion and synaptic delays between the areas, this

time-shifted coupling at gamma frequencies may affect

the postsynaptic impact of spikes from one area upon the

other, consequently affecting visual timing [18]. This

long-range synchronization mechanism could be crucial

especially during saccades, where we know those 100

ms before the saccade onset the FEF releases a corollary

discharge signal towards the lateral intraparietal cortex

LIP, where a craniotopical representation of the envi-

ronment is implemented. The receptive fields of visual

neurons are known to be retinotopically arranged, and in

awake animals they move with gaze, maintaining the

same retinotopic location regardless of eye position.

Nevertheless the existence in the monkey parietal cortex

of cells (called “real-position” cells) whose receptive

field does not systematically move with gaze has been

proven [19]. These cells respond to the visual stimula-

tion of the same spatial location regardless of eye posi-

tion and therefore directly encode visual space in crani-

otopic instead of retinotopic coordinates [20]. The de-

synchronization due to the long-range coupling between

FEF and V4 tell us that the remapping process act ini-

tially on the older visual signal, while the present one

will be encoded later. Finally at least two considerations

have to be taken into account in order to elucidate the

neurophysiological implications on the visual timing

during saccades. As shown in Figure 1, the former is a

delay between the stimulus administration and its en-

coding into the craniotopical representation of the world

allocated in LIP, and the latter is that this delay is in-

creased at the time of saccades because of the different

neural networks involved in the fixation and the saccadic

state.

1.2. Communication Network Approach

In modern neuroscience, computational methods occupy

an important niche. Neuroscience computing is con-

cerned with building mathematical and statistical models

to address a wide range of questions originated from

experimental neurobiology and related medical fields.

Typically, these models involve massive, hard-

ware-demanding amounts of calculations performed on

last-generation computers. However, the complexity of

real-life biological systems is indeed overwhelming, far

outreaching the abilities of modern computing systems.

This creates a considerable demand for parsimonious

models which capture main driving forces of biological

processes elucidating the mechanisms behind the ob-

served phenomena. The search for a model which is

(a)

(b)

Figure 1. Schematic representations of the neural cir-

cuits of early stage of vision process, respectively in-

volved in the fixation condition (a-simplified neural

network of vision during fixation) and during a sac-

cadic onset (b-neural network during saccades). From

a to g are indicated the links among the vertex which

form the pathway.

complex enough to be a reasonable approximation of the

biological reality and at the same time simple enough to

be manageable by available mathematical techniques is

some sort of an art. The task requires the researcher not

only to have a thorough understanding of the relevant

biology and mathematics but sometimes a great deal of

luck to have the predictions of the model to be consistent

with the natural phenomena. Computational neurosci-

ence focuses on two distinct levels of description: ‘sim-

ple models’ and ‘detailed models’. While detailed mod-

els focus on the measurement and description of com-

plex systems through using certain building blocks, their

interactions and dynamic properties, such as kinetic pa-

rameters, binding constants etc. Simple models aim at

capturing the behavior of the few most relevant compo-

nents of the system. This implies that such models are

also intrinsically more abstract than detailed models

their components and parameters often do not corre-

spond directly to well-defined physical quantities, such

as measured binding constants or chemical reaction rates.

A. Guazzini et al. / J. Biomedical Science and Engineering 3 (2010) 1133-1142

1136

Nonetheless, simple models can provide insights into the

behavior of a system and drive experimental and detailed

modeling efforts by suggesting further more detailed

experiments or models. Moreover such modeling frame-

work could allow easier predictive multi-scale descrip-

tions of the system under study than detailed models.

Current detailed models are based on two different ap-

proaches: a bottom-up approach which focuses on the

measurement and description of complex systems using

the building blocks their interactions and dynamic prop-

erties, a top-down modeling approach attempts to de-

velop integrative and predictive multi-scale models of

the system under study. Our goal is to develop a hybrid

strategy between the two frameworks, focusing on spe-

cific problems at particular scales using a simple model-

ing and then expand on other scales. A main target of

using such combination of modeling approaches is to get

deeper understanding of the system without suffering

from sudden growth of degrees of freedom. A coherent

approach to study visual timing should take into account

the neurophysiological knowledge about the fronto-pa-

rieto-temporal network, providing for first a simplified

model of its functional structures. Afterwards throughout

a reverse engineering process would be possible to vali-

date the model fitting the psychophysical data. Such

approach can provides insights about the way by which

the brain has optimized its “software” to measure the

time in the absence of clock, with respect to its own bi-

ological constraints. In order to represent the complexity

of the visual timing processing, it seems to be essential

to define at least three computational objects. The first

object is an appropriate structure of the neural represen-

tation for the visual information. From psychophysics

we know mainly that visual information preserves a cra-

niotopic structure from early to late stages of brain anal-

ysis. From these evidences the system seems to be char-

acterizable by coupling neural pathways, where the neu-

ral signal coming from visual ganglion cells propagates.

Moreover real neural structures are able to embed spatial

and temporal information about visual stimuli in the

same neural representation, and by a phase of synchro-

nization dynamics among FPT, are able to represent di-

rectly the time information. The second aspect that is

necessary to manage relies on the signal propagation

dynamics along the structures defined above. As shown

by recent experiments the dynamics of signal propaga-

tion could have a role in the visual timing, and to repro-

duce their peculiarity both the synchronization of the

neurons’ activity and the dynamics of synapses have to

be taken into account. An appropriate representation of

the synaptic learning parameters is to incorporate in the

model the insights of Buonomano about the relation be-

tween synapses short term dynamics and the capacity of

neural structure to represent the timing aspects of a per-

ceived stimulus. The last behavior which has to be cap-

tured is the phase synchronization dynamics which cha-

racterized the FPT network. To face this challenge a

phase dynamics of the neural signal is explicitly mod-

eled, and a correlation between this parameter and signal

propagation is shaped by the equations of the model.

Finally the main attempt of this paper will be to high-

light the interplay between the signal diffusion and the

information diffusion. The paper proceeds as follows, in

the Section 2 the computational model is presented and

their component is elucidated. Section 3 describes the

numerical simulations of the psychophysical experi-

ments taken into account, and in Section 4 the results are

presented. Finally in the Section 5 numerical results and

insights are discussed and next steps and conclusion are

outlined.

2. THE MODEL

2.1. The FEF-LIP-V4 Network

The cerebral network FEF-LIP-V4 is represented by a

cellular automata composed by interconnected elements

labeled as nodes, where the retinotopic input propagates

and that allocate the spatiotopic layer. The cellular au-

tomata can be seen as having one ’space dimension’

which are nodes describing clustered or homogeneous

populations (e.g. column), and one orthogonal ’time di-

mension’ which encode the duration of the stimuli and

the interval among them (Figure 2). Our aim is to inves-

tigate the visual timing related aspects without introduc-

ing particular topology. As a consequence we image to

have a neurons lattice where the distances among nodes

are related to the transfer of the stimulus information,

from one node ito the next one i + 1, and are assumed to

be equivalent. The purpose of this equivalence of time

transfer is to avoid explaining time space aberration

through the introduction of a bias or fictitious, ad hoc

mechanisms. Cerebral pathways connecting V4 with LIP

and FEF are approximated by parallel neural delay chains

Figure 2. Schema of two signals moving from left to right,

which are identified by their phases (arrow) and its intensity

(arrow’s length). See legend on the left.

A. Guazzini et al. / J. Biomedical Science and Engineering 3 (2010) 1133-1142

1137

of nodes, where the signal propagates synchronizing

subsequent nodes’ phase within a column, and modify-

ing the weight of synapses among nodes. The cellular

automata can be seen as having one ’space dimension’

which are nodes describing clustered or homogeneous

populations (e.g. column), and one orthogonal ’time di-

mension’ which encode the duration of the stimuli and

the interval among them.

Each node represents a homogeneous population of

neurons; nodes are spatially organized in parallel col-

umns to reproduce the pathway followed by the neural

signal coming from visual area V4. Neurons inside a

node are assumed to synchronize their activity whenever

a signal arrives, e.g. to fire simultaneously, and are

linked together by synapses with a long term dynamics

[21]. The node is assumed as the “atomic” component of

the system and its behavior is explicitly modeled by the

definition of an activation state Si,j

t within the interval (0,

1). Given the physiological constraints three different

contributions to the signal have to be taken into account.

Besides the contribution of the direct synapses it is

needed to consider the lateral connections (transcolum-

nar contribution) and the respective signals’ phases in

order to calculate the resulting signal which is summed

to the target node. The synaptic weights inside a column

are indicated as (Wdi,j

t) while the transcolumnar synaptic

weights are indicated as (Wli,j

t).Using the trigonometric

formulas one can write the contributions as follows:













1,12

2 2

1, 11, 11,1, 11, 1

tanh 1

Tijij ijijij

IS WlSS Wl





  



 



(1)













11,11,1,1 ,11,1,1

2cos

ij ijijijijij

ISWl SWd



 

 (2)











21, 11, 11, 11, 11, 11, 1

2cos

ij ijijijijij

ISWl SWd



 



(3)











3,1 ,11,11,1,11,1

2cos

ijijiji jiji j

ISWdSWl



 



(4)

JBiSE

The incoming signals are consequently computed us-

ing the Eq.5 and the activation state of each node are

finally updated according with the Eq.6.

,12

ˆt

ij T

SIII



t1

(5)

them a value φij

t within (-π, +π). Therefore the incoming

signals have to be described as having their own magni-

tude and phase. To estimate the resulting phase we use

again the trigonometric formulas:

11,11,

tt t

ij ij

SS Wl





 (7)

ijij ij

SSS



 (6)

2,1,

tt t

ij ij

SSWd



1

(8)

In order to introduce the long range synchronization

effects within the V4-LIP-FEF network the phase of

each node is explicitly considered assigning to each of 31,11,

tt t

ij ij

SS Wl





 (9)













 

11,12,131,1

sinsin sin

ˆarctan coscos cos

tttt tt

ijij ij

ij tttt tt

ijij ij

SSS





 



 













(10)

Then the phase dynamics of a node has been coupled

with the magnitude of the signal coming from the con-

nected nodes and the state of the node itself, as follows:

 

,,,,

ˆˆˆ

sin sin

arctan ˆˆˆ

cos cos

tttt

ij ijij ij

ij tttt

ij ijij ij























(11)

A way for the brain to encode in the same neural sig-

nal both time and space information about a stimulus,

could be to exploit the network V4-LIP as a sort of neu-

ral buffer. Assuming linked nodes which evolve ”rap-

idly” their connections weight according with the in-

coming signal features (e.g. activation and phase agree-

ment), it is possible to equip an artificial system with a

sort of embedded short memory of past signals or in

another words with a state dependent response behavior

to the signal. Such hypothesis has led Buonomano to

explore the role of synapses characterized by a short

term dynamics [16], demonstrating how a neural net-

work equipped with such synapses can represent both

spacial and temporal information about the stimulus by

the same neural correlates on a spatiotopic map. In order

to take into account the role of the synapses’ dynamics

on both the signal dynamics and the node’s synchroniza-

tion the equation for the synaptic enforcement has been

shaped including this features, according with the bio-

logical constraints. The synaptic weight (Wi,j

t) is defined

as a variable of the model belonging to the interval (0, 1).

A. Guazzini et al. / J. Biomedical Science and Engineering 3 (2010) 1133-1142

1138

To design the complex dynamics of the synapses two

ad-hoc parameters are designed and labeled respectively

learning factor (γ) and decay factor (δ), both defined

within (0, 1). Since the physiological characteristics of

the ocular dominance columns we introduced two dif-

ferent values to distinguish between the signals’ dynam-

ics inside and outside the column. Consequently we in-

dicate the intracolumnar and the transcolumnar learning

and decay factor respectively as γd and δd for the intra-

columnar synapses and γl and δl for the transcolumnar

(e.g lateral) synapses. Moreover two thresholds con-

stants are introduced to indicate the resting values for the

synaptic weight (Kw) and the nodes’ activity (Ks), both

within the interval (0, 1). The synaptic weight is finally

updated at each time step using the following recipe. If

the activity of the precedent node is greater than the ac-

tivity resting threshold (Ks), according to Hebb’s theory

[22], the synaptic weight increases with the signal mag-

nitude and the phase synchronization between the two

connected nodes. Otherwise the synapses would decay

proportionally with the distance between phases of con-

nected nodes and as a function of their activity (Eqs.13,

14).





,,1

,:, 1

min tt

ij ij

ijij









 (12)





,, ,:,1,

,:, 1,,

ttt t

ijij dijijijs

tt t

dijijij wij w

WdWdS K

Wd KWd K









 

  



(13)







,, ,:1,1,

,: 1,1,,

ttt t

ijijliji jijs

tt t

lijijij wij w

WlWlS K

Wl KWl K













 

 (14)

Finally the main assumption relies on the different

learning and decay functions for intracolumnar and ex-

tracolumnar synapses dynamics. In the Eqs.13 and 14

the parameters γd and γl rule the learning rate respec-

tively for intracolumnar and transcolumnar synapses.

2.2. Numerical Simulations

In order to study the phenomenology of the computa-

tional model we started grounding on few basic assump-

tions the design of the control parameters under consid-

eration. The decay dynamics is controlled by the pa-

rameters δd and δl. The different nature of intracolumnar

and transcolumnar connections is expressed also in terms

of signal propagation effciency. While the slow dynam-

ics of the transcolumnar synapses is coupled with a lin-

ear function of signal magnitude transmission [1,20,23],

the faster dynamics of the intracolumnar synapses has

been shaped by a sigmoidal behavior [24,25]. Another

fundamental assumption relies on the spatiotemporal

transformation at the neural level, here proposed as the

fundamental key-mechanism for the visual time percep-

tion. Our approach is based on a fundamental symmetry

between the neural buffer and the phases based theories

for the neural activities. Whether we assume the neural

propagation of the signal as a phase dynamics of differ-

ent neuronal populations the equations get biological

sense. Consequently the more computationally light ap-

proach has been adopted, implementing the time related

phase dynamics of a node as the degree of diffusion of

the signal along a neural delay chain. The retinotopic

input of a real stimulus is simulated by the imposition of

a pick of activation in those nodes of the first layer of the

automata, corresponding to the spatiotopic representa-

tion of the stimulus. The activation of the local popula-

tions of nodes is maintained for the entire duration of the

encoded stimulus. The nodes which encode the stimulus

are assumed as synchronized and characterized by the

same phase for the entire duration of the stimulus. At the

end of the stimulus the synchronization inside and within

the nodes decreases following the Eq.11. Among the

peculiarities of the saccades, there is the recalibration of

the spatiotopicityin the encoding stage of visual proc-

essing (LIP) which anticipate them. This recalibration is

reached by the FEF-LIP-V4 network by mean of an in-

ternal signal representing the eye position defined cor-

ollary discharge [26]. The corollary discharge (CD)

starts 60 ms before the saccade from the FEF and is

complete at saccadic offset producing an apparent en-

largement of the visual receptive fields, and a fast re-

mapping of the visual environment, biasing both time

and space detection ability. In order to simulate the CD

effects on the craniotopical representation of the visual

stimuli, in the remapping phase simply we shift the sig-

nal parallel to the direction of the saccade. In this way

while a stimulus temporally distant from a saccade (i.e.

long after or before) produces the same response in the

craniotopic map, during or in the temporal proximity

(50-100 ms) at the saccadic event the activation and

synchronization pattern of the map appear as altered

with respect to the fixation condition. As a consequence

of this alteration in the read out stage the system could

fail to estimate the time features of the stimuli. In hu-

mans the ”readout” task has to operate on the cranio-

topic representation of the early visual history, in order

to reveal both topological distances between stimuli and

timing features as duration of an interval between two

visual events. The model we have defined operates a

temporal to spatial transformation of the neural signal,

producing a representation of the craniotopic map allo-

cated in (LIP). The state of this map has been analyzed

by a two step procedure: for first the state of synchroni-

zation of the map were detected by a kohonen neural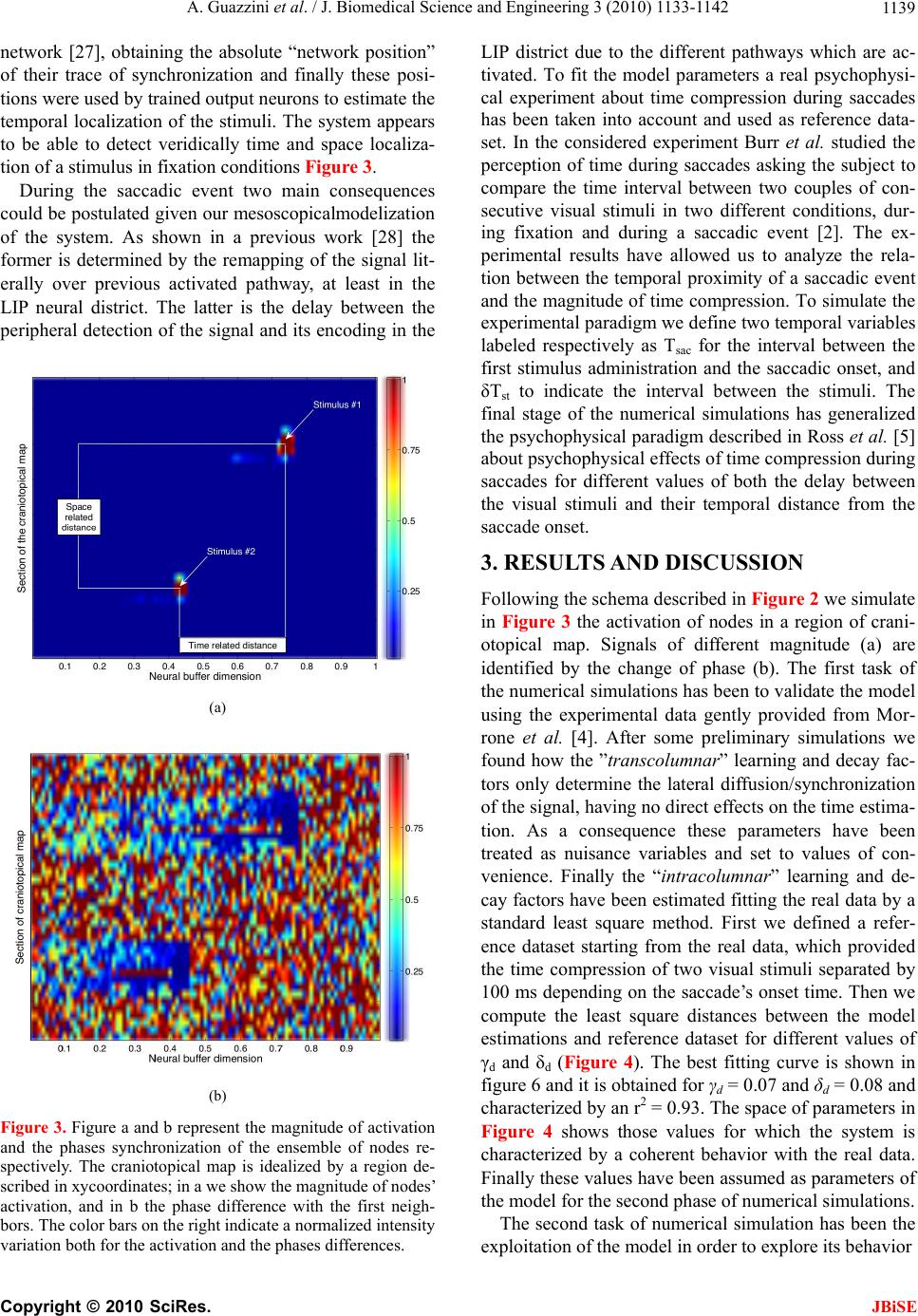

A. Guazzini et al. / J. Biomedical Science and Engineering 3 (2010) 1133-1142 1139

network [27], obtaining the absolute “network position”

of their trace of synchronization and finally these posi-

tions were used by trained output neurons to estimate the

temporal localization of the stimuli. The system appears

to be able to detect veridically time and space localiza-

tion of a stimulus in fixation conditions Figure 3.

During the saccadic event two main consequences

could be postulated given our mesoscopicalmodelization

of the system. As shown in a previous work [28] the

former is determined by the remapping of the signal lit-

erally over previous activated pathway, at least in the

LIP neural district. The latter is the delay between the

peripheral detection of the signal and its encoding in the

(a)

(b)

Figure 3. Figure a and b represent the magnitude of activation

and the phases synchronization of the ensemble of nodes re-

spectively. The craniotopical map is idealized by a region de-

scribed in xycoordinates; in a we show the magnitude of nodes’

activation, and in b the phase difference with the first neigh-

bors. The color bars on the right indicate a normalized intensity

variation both for the activation and the phases differences.

LIP district due to the different pathways which are ac-

tivated. To fit the model parameters a real psychophysi-

cal experiment about time compression during saccades

has been taken into account and used as reference data-

set. In the considered experiment Burr et al. studied the

perception of time during saccades asking the subject to

compare the time interval between two couples of con-

secutive visual stimuli in two different conditions, dur-

ing fixation and during a saccadic event [2]. The ex-

perimental results have allowed us to analyze the rela-

tion between the temporal proximity of a saccadic event

and the magnitude of time compression. To simulate the

experimental paradigm we define two temporal variables

labeled respectively as Tsac for the interval between the

first stimulus administration and the saccadic onset, and

δTst to indicate the interval between the stimuli. The

final stage of the numerical simulations has generalized

the psychophysical paradigm described in Ross et al. [5]

about psychophysical effects of time compression during

saccades for different values of both the delay between

the visual stimuli and their temporal distance from the

saccade onset.

3. RESULTS AND DISCUSSION

Following the schema described in Figure 2 we simulate

in Figure 3 the activation of nodes in a region of crani-

otopical map. Signals of different magnitude (a) are

identified by the change of phase (b). The first task of

the numerical simulations has been to validate the model

using the experimental data gently provided from Mor-

rone et al. [4]. After some preliminary simulations we

found how the ”transcolumnar” learning and decay fac-

tors only determine the lateral diffusion/synchronization

of the signal, having no direct effects on the time estima-

tion. As a consequence these parameters have been

treated as nuisance variables and set to values of con-

venience. Finally the “intracolumnar” learning and de-

cay factors have been estimated fitting the real data by a

standard least square method. First we defined a refer-

ence dataset starting from the real data, which provided

the time compression of two visual stimuli separated by

100 ms depending on the saccade’s onset time. Then we

compute the least square distances between the model

estimations and reference dataset for different values of

γd and δd (Figure 4). The best fitting curve is shown in

figure 6 and it is obtained for γd = 0.07 and δd = 0.08 and

characterized by an r2 = 0.93. The space of parameters in

Figure 4 shows those values for which the system is

characterized by a coherent behavior with the real data.

Finally these values have been assumed as parameters of

the model for the second phase of numerical simulations.

The second task of numerical simulation has been the

exploitation of the model in order to explore its behavior

A. Guazzini et al. / J. Biomedical Science and Engineering 3 (2010) 1133-1142

1140

Figure 4. Space of parameters for γd and δd respectively on the

X and Y axes. The color (see legend) indicates the normalized

least square distance between the model estimation and the real

data. The best fitting value is obtained for γd = 0.07 and δd =

0.08.

for different values of delay between the visual stimuli.

The estimation of the delay between two subsequent

stimuli separated by an interval of ΔTst is considered

both for different values of the saccadic onset Tsac, and

for different values of ΔTst. The percentage of time

compression is computed comparing the model’s interval

estimations in the fixation condition with those near the

saccade, and it was assumed as order parameter.

The normalized time compression among the two

conditions is reported using colors, with red for large

values of compression and blue for compression near to

0. The y axis indicates the delay between the time of the

saccade onset and the time of the first administered sti-

mulus while the x axis indicates the delay between the

couple of stimuli. Since the available experimental data

about this paradigm are only estimated for a delay

among the stimuli of 100 ms these results provide some

predictions/forecasting which would be interesting to

verify.

The Figure 5 shows how the maximum of compres-

sion is obtained always around the saccadic onset. Pairs

of stimuli separated by a little delay appear as more

compressed when administered largely before the sac-

cadic onset, and exists a critical values of 200 ms for

which no significant compression is revealed.

4. CONCLUSION

We have developed a model that provides a fit of experi-

mental data concerning time compression during saccades.

With this work we suggest a way to couple the cranio-

topical representation of space-time attributes of a visual

stimulus with the neurophysiological structure of the brain.

The model has been tested through using two parame-

Figure 5. Time compression (see legend) is indicated as the

normalized difference between the time estimation in the fixa-

tion condition and in the saccadic condition. In y axis we show

the delay between saccade onset and the first administered

stimulus. In x axis the delay between the stimuli is represented.

Figure 6. A cross-section of Figure 5 is shown for ΔTs = 100

ms. The vertical dashed line indicates the time of the saccadic

onset and the values on the x axis indicates the time delay of

the second stimulus administration. In the Y axis the percent-

age of compression is reported. Red dots indicate the experi-

mental observations and the continuous line represents the

model estimation.

ters which ruled the synaptic dynamics. Finally a fun-

damental mechanism for the process under scrutiny has

been identified as the interplay between the phase dy-

namics which characterize the neurons’ activity and the

synaptic dynamics. This model highlights how psycho-

physical and neurophysiological recent findings can

drive interesting explanations for time and space percep-

tion at the saccadic time and for the visual perception in

general. The simple implementation we propose for the

data analysis can be exploited in two main directions.

The former is the prediction of “new” and “unknown”

A. Guazzini et al. / J. Biomedical Science and Engineering 3 (2010) 1133-1142 1141

visual effects during saccade, by the numerical simula-

tion of arbitrary extreme setting conditions. Subsequent

experimental inspections would drive to important re-

finements for the model and to new theoretical questions

about the neural alghoritms used by the brain. The latter

is represented by a clinical exploitation of the model,

considering the evidences of the saccadic relate visual

behaviors in neuropathological conditions as a reference

dataset to be fitted [23,29]. We stress here that the mod-

eling of time perception at perisaccadic events is a

thriving field of research. It has two immediate and im-

portant benefits: the improved understanding of the

processes that shape saccadic events and our improved

ability to combine psychophysics and neuroscience to

address research on clocks in the brain. Multiple Sclero-

sis, Hungtington’s disease and Parkinson illness are only

three of the multitude of clinical pathologies which af-

fect both the neural phase dynamics and the synapses’

behavior [30,31,32]. Describing the different pathologies

in terms of their peculiar set of pathological effects al-

lows us to easily map them into the model. This last cru-

cial step would make of it a useful tool both to investi-

gate the expected time and space visual perception im-

pairment in those contexts and to explore new neu-

ral-related hypothesis for their explanation.

5. ACKNOWLEDGEMENTS

This work is financed by the EU 6 Framework Programme Project:

Measuring and Modeling Relativistic-Like Effects in Brain and NCSs’.

We thank David Burr, ConcettaMorrone, Marco Cicchini and Paola

Binda of Pisa Vision Lab for suggestions.

REFERENCES

[1] Binda, P., Cicchini, G.M., Burr, D.C., and Morrone, M.C.

(2009) Spatiotemporal distortions of visual perception at

the time of saccades. Journal of Neuroscience, 29,

13147-13157.

[2] Burr, D. and Morrone, C. (2006) Perception: Transient

disruptions to neural space time. Current Biology, 16, 848.

[3] Ibbotson, M., Crowder, N. and Price, N. (2005) Neural

basis of time changes during saccades. Current Biology,

16, 834-836.

[4] Morrone, C., Ross, J. and Burr, D. (2005) Saccades cause

compression of time as well as space. Nature Neurosci-

ence, 8, 950-954.

[5] Ross, J., Morrone, C., Goldberg, E. and Burr, D. (2001)

Changes in visualperception at the time of saccades.

TRENDS in Neurosciences, 16, 472-479.

[6] Ross, J., Burr, D. and Morrone, C. (1996) Suppression of

the magnocellular pathway during saccades. Behavioural

Brain Research, 80, 1-8.

[7] Abeles, M. (1982) Local cortical circuits: An electro-

physiological study. Springer, Berlin.

[8] Johnston, A., Arnold, D.H. and Nishida, S. (2006) Spa-

tially localized distortions of event time. Current Biology,

16, 472-479.

[9] Rocca, E.D. and Burr, D.C. (2007) Large contrast effects

in the discrimination of short temporal intervals. Percep-

tion 36 ECVP.

[10] Burr, D. and Morrone, C. (2006) Time perception: Space

time in the brain. Current Biology, 16, 171-173.

[11] Lewis, P.A. and Walsh, V. (2005) Time perception: com-

ponents of the brain’s clock. Current Biology, 15,

389-391.

[12] Meck, W.H. (2005) Neuropsychology of timing and time

perception. Brain Cognition, 58, 1-8.

[13] Ullner, E., Vicente, R., Pipa, G. and Garca-Ojalvo, J.

(2008) Contour integration and synchronization in neu-

ronal networks of the visual cortex. ICANN, Lecture

Notes in Computer Science, 5164, 703-712.

[14] Orban, G.A., Van Essen, D. and Vanduffel, W. (2004)

Comparative mapping of higher visual areas in monkeys

and humans. Trends in Cognitive Sciences, 8, 315-324.

[15] Karmarkar, U. and Buonomano, D. (2007) Timing in the

absence of clocks: Encoding time in neural network

states. Neuron, 53, 427-438.

[16] Buonomano, D.V. (2000) Decoding temporal information:

A model based on short-term synaptic plasticity. The

Journal of Neuroscience, 20, 1129-1141.

[17] Gross, J., Schmitz. F., Schnitzler, I., Kessler, K., Shapiro,

K., Hommel, B. and Schnitzler, A. (2004) Modulation of

long-range neural synchrony reflects temporal limitations

of visual attention in humans. Proceedings of the Na-

tional Academy Sciences, 101, 13050-13055.

[18] Gregoriou, G.G., Gotts, S.J., Zhou, H. and Desimone, R.

(2009) High-frequency, long-range coupling between

prefrontal and visual cortex during attention. Science,

324, 1207-1210.

[19] Mark, J. and Morrow, M.D. (1996) Craniotopic defects

of smooth pursuit and saccadic eye movement. Neurol-

ogy, 46, 514-521.

[20] Galletti, C., Battaglini, P. and Fattori, P. (1993) Parietal

neurons encoding spatial locations in craniotopic coordi-

nates. Experimental Brain Research, 96, 221-229.

[21] Graham, B.P

. and Stricker, C. (2008) Short term plastic-

ity provides temporal filtering at chemical synapses.

ICANN, Lecture Notes in Computer Science, 5164,

268-276.

[22] Hebb, D.O. (1949) The organization of behavior. Wily,

New York.

[23] Btzel, K., Rottach, K. and Bttner, U. (1993) Normal and

pathological saccadic dysmetria. Brain, 116, 337-353.

[24] Abarbanel, H., Gibb, L., Huerta, R., and Rabinovich, M.

(2003) Biophysical model of synaptic plasticity dynam-

ics. Biological Cybernetics, 89, 214-226.

[25] Dittman, J.S., Kreitzer, A.C. and Regehr, W.G. (2007)

Interplay between facilitation, depression, and residual

calcium at three presynaptic terminals, Journal of Neu-

roscience, 20, 1374-1385.

[26] Ford, J.M., Brian, J.R. and Mathalon, D.H. (2010) As-

sessing corollary discharge in humans using noninvasive

neuron physiological methods. Nature Protocols, 5, 1160

-1168.

[27] Kohonen, T. (1982) Self-organized formation of topo-

logically correct feature maps. Biological Cybernetics,

43, 59-69.

[28] Guazzini, A., Lio, P., Conti, M. and Passarella, A. (2009)

A. Guazzini et al. / J. Biomedical Science and Engineering 3 (2010) 1133-1142

1142

JBiSE

Information processing and timing mechanisms in vision.

ICANN, Lecture Notes in Computer Science, 1, 325-334.

[29] McGivern, R., Gibson, J., Jwnnings, D., Lavery, K. and

Montgomery,C. (2006) Normal and abnormal slowing of

saccades: are they one and the same phenomenon? An-

nals of the New York Academy of Sciences, Neurobiology

of eye movements: from molecules to behaviour, 956,

421-425.

[30] Huygena, P., Verhagenb, W., Hommesc, O. and Nico-

lasena, M. (1990) Short vestibule-ocular reflex time con-

stants associated with oculomotor pathology in multiple

sclerosis. Acta Oto-Laryngologica, 109, 25-33.

[31] Leigh, R. J., Parhad, I.M., Clark, A.W., Buettner-Ennever,

J.A. and Folstein, S.E. (1985) Brainstem findings in

Huntington’s disease: Possible mechanisms for slow ver-

tical saccades. Journal of the Neurological Sciences, 71,

247-256.

[32] Mosimann, U.P., Müri, R.M., Burn, D.J., Felblinger, J.,

O’Brien, J.T. and McKeith, I.G. (2005) Saccadic eye

movement changes in Parkinson’s disease dementia and

dementia with Lewy bodies. Brain, 128, 1267-1276.