American Journal of Industrial and Business Management, 2013, 3, 395-417
http://dx.doi.org/10.4236/ajibm.2013.34047 Published Online August 2013 (http://www.scirp.org/journal/ajibm)
395
An Experimental Analysis of Over-Confidence
Saoussen Jemaiel1, Chokri Mamoghli2, Mohamed Walid Seddiki3
1The Higher Institute of Management, DEFI Unit, Tunis, Tunisia; 2The Institute of High Commercial Studies, DEFI Unit, Tunis,
Tunisia; 3The Faculty of Legal Sciences, Economic and Management of Jendouba, DEFI Unit, Tunis, Tunisia.
Received November 27th, 2012; revised January 12th, 2013; accepted February 12th, 2013
Copyright © 2013 Saoussen Jemaiel et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
The purpose of this paper is to experimentally demonstrate the existence of the bias of over-confidence as a human
psychological bias. This bias was measured by three methods: the estimation interval, the frequency estimation method
and the method of question with two answer choices. The estimation interval method finds a very wide bias compared
to the other two methods, but overconfidence persists in the other two methods at lower levels. In the first experiment,
monetary incentives have exacerbated the over-confidence because of the given compensation. This system has demon-
strated that there is a strong link between over-confidence and risk taking. The second experiment that used the method
of question with two answer choices was given a different pay system and it was expected that overconfidence will be
reduced by monetary incentives but the results show that the bias is not significantly reduced by these new monetary
incentives. Similarly, the iteration that was made during the first experiment did not significantly reduce the bias.
Keywords: Over-Confidence; Uncertainty; Monetary Incentives; Experiments
1. Introduction
The behavior of financial markets is at the heart of be-
havioral finance. The experiments of psychologists con-
tinue to show that the investor is far from being placid
and intellectually powerful relied on by financial and
classical economic theory. Indeed, several scholar be-
haviors were identified by the followers of the behavioral
paradigm: among others, the behavior of loss aversion,
the behavior of over-confidence, availability behavior,
representation behavior, mimetic or follower behavior,
the behavior of mental accounting and the behavior of
mental anchor. However, there are other behaviors that
are cited by proponents of this paradigm, but their impor-
tance is minimal.
The term over-confidence, for example, has been used
to describe two distinct phenomena. The first is the ten-
dency of individuals to express an excessive belief in
their own abilities: for example the ability to drive
peacefully [1]. The second phenomenon is the tendency
of individuals to overestimate the precision of their
knowledge [2].
If the over-confidence is a characteristic of invasive
behavior, it will have profound implications for financial
markets. Recently, quite a number of theoretical models
of financial markets have incorporated on-confident
judgments [3-5].
Recently, several models of behavioral finance based
on overconfidence hypothesis have been proposed to
explain abnormal results of return, such as momentum
effect and reversal effect. This explanation represents a
challenge for financial economists. We characterize the
overconfidence hypothesis by four implications; firstly, if
the investors are overconfident they over react to private
information and under react to public information. Sec-
ondly, the profit of market causes the excessive trading
volume by overconfident investors. Thirdly, the exces-
sive trading volume of overconfident investors contrib-
utes at the excessive volatility. Fourthly, overconfident
investors under estimate risk and exchange more in risk-
ier securities. These hypotheses are empirically evaluated
by using econometric models in order to proof the exis-
tence of overconfidence in financial market.
Daniel et al. [6] demonstrate that if investors are
overconfident, they over react to private information and
under react to public information. By consequence this
asymmetric response of overconfident investors induces
the short term momentum effect and the long term re-
versal effect of return. Besides the overconfidence bias
causes financial fraud in financial market.

An Experimental Analysis of Over-Confidence 396
One part of literature stipulates that trading volume is
induced by informed investors who exchange actively in
their private information [7-11]. In addition, a grand part
of theoretical work in finance stipulates that private in-
formation has a more important effect on trading volume
than public information.
Overconfident investors attribute market gain to their
own capacities and exchange more aggressively, in the
subsequent periods. Losses are attributed to bad chance.
There is a causality bond between return and trading vol-
ume. The affirmation that overconfidence induces inves-
tors to exchange more aggressively, was also confirmed
by many experimental studies [12,13].
Several authors (e.g., [5,14]) demonstrated that volatil-
ity of risky securities increases with investors’ overcon-
fidence. The excessive trading volume of overconfident
investors contributes to excessive volatility. Chuang and
Lee [15] provided an empirical structure to identify if
excessive volatility is caused by overconfidence of in-
vestors.
Financial economists have modeled overconfidence as
an over estimation of private information precision. Their
theoretical models stipulate that if investors are overcon-
fident, they take more risky positions than they were ra-
tional. Chuang and Lee [15] found that if investors are
overconfident they exchange in more risky securities
following market gain.
Therefore, we can say that overconfidence is a very
important psychological bias. It has been proposed as an
explanation of many anomalies of return observed in
financial market. So, because of the economic impor-
tance of the subject, we have to verify experimental evi-
dence of overconfidence.
The main objective of this paper is to experimentally
analyze this behavior. The interval estimation method
and the frequency estimation method will be used in the
first part of the experiment. The method of question with
two alternative responses will be used in the second part
of the experiment. The purpose of using three different
methods is to check through the comparison of results if
overconfidence will be affected by the measurement
method used.
From the beginning of the 70s to the 90s, there was a
general consensus that judgments or responses in tests of
the interval estimation method and the method of ques-
tion with two alternative responses, showing a substantial
and consistent over-confidence. In a review of previous
studies of the method of two choices, Lichtenstein et al.
[16] reported that when participants state that they are
70% sure they have correctly answered, they are correct
in less than 60% of time. Overconfidence measured by
the method of interval or trusted domain is stronger.
Russo and Schoemaker [17] found that business manag-
ers are being asked of the confidence intervals of 90%,
have the right answer in the area said between 42% and
62% of times. Confidence intervals 50% do contain the
correct answer in only 20% of times.
This paper is organized as follows: Section 1 intro-
duces this research. Section 2 concerns measure of over-
confidence using the method of estimation interval and
the method of estimation frequency. The Section 3 pre-
sents the measure of over-confidence using the method
of question with two answer choices. The Section 4 con-
cludes the paper.
2. Method of Estimation Interval and
Method of Estimation Frequency
The objective of this experiment is to experimentally test
the stability of the results in the work of interval estima-
tion and frequency estimation.
In the first stage of the experiment, subjects are given
10 questions. Subjects must provide for each question, a
lower and an upper limit so that the subjective confi-
dence that the interval contains the correct answer is 90%.
In the second stage, each subject was asked to estimate
the number of intervals proposed in step 1 that contain
the exact answer. In stage 3, they are asked to estimate
the number of correct responses (number of intervals
containing the correct answer) given by their colleagues.
The estimates given by subjects in stage 2 and stage 3 are
respectively the frequency estimation and the frequency
estimation of others.
Stage 3 once completed, subjects are asked to, in a
fourth stage to review the responses in stage 1. Thus the
stage 4 is an iteration of stage 1. It is the same for stage 5
which is an iteration of stage 2. Stage 6 is an iteration of
stage 3.
2.1. Models of Experience and Assumptions
2.1.1. Participants and Procedures
Our first experiment involves 45 students in accounting
at the ISG (Institut Supérieur de Gestion) of Tunis. They
are recruited following an announcement that invites
students to participate in an experiment. These students
are informed that the experiment consists of two sessions
the first is free, the second is paid off.
In the paid session, participants will receive compen-
sation in proportion to the correct answers. R is the total
compensation received in the first experiment:
()
R0.55/ba=+ − (1)
0.5 TND be earned by any participant that provides an
interval [a,b] containing the correct answer regardless of
the width of the interval.
5 TND/(b − a) is the variable part of remuneration de-
pends on the precision, that is to say, the width of the

An Experimental Analysis of Over-Confidence 397
interval. A participant may gain accurate up to 5 dinars,
the more the width increases the more variable pay de-
creases.
In the second and third step, a correct answer will be
paid by 0.5 TND. Steps 4, 5 and 6 concern the iteration
and are similar to steps 1, 2 and 3.
The experiment involves six steps outlined below:
Step 1
Participants are asked to answer ten general knowl-
edge questions. It should be noted that these issues are
not selected for the difficulty. Since the set is heteroge-
neous, the level of difficulty varies from one subject to
another, a question may be considered difficult for a
subject and easy for another. Subjects must answer these
questions by an interval, providing its lower limit and
upper limit so that their subjective confidence that the
interval contains the true value is 90%. This step is called
the interval estimate.
Step 2
After answering the ten questions in the first stage,
participants are asked to estimate how many of their own
answers have contained the true value, that is to say, to
give a rating out of ten. This is called frequency estima-
tion or self-validation.
Step 3
We ask each participant to estimate the average num-
ber of correct responses made by these colleagues (other
participants). We mean by a correct response interval
containing the true value regardless of accuracy. This is
called frequency estimation of others.
Steps 4, 5 and 6
They are similar to steps 1, 2 and 3. They concern it-
eration in the sense of giving a second chance for those
who want to make adjustments to their ranges in step 4
by changing the lower bound, upper bound or both. Par-
ticipants who do not want to make adjustments may
mention that by confirming their answers. If a participant
has made some adjustment in step 4, then he/she should
provide a second frequency to estimate their own answer
in step 5, and estimate a second frequency of the other in
step 6.
As previously mentioned, this experiment has two ses-
sions, the first is free, the second is paid off. Each session
consists of six steps described above. The questions in
both sessions are different but of the same type, that is to
say that the sample is heterogeneous and is not selected
for difficulty. The purpose of this change is to avoid the
effect of learning that can bias the analysis.
2.1.2. Hypotheses and Tests
Let θ1, θ2.... θ6 be the population mean in each of the six
steps in the free session and β1, β2.... β6 denote the popu-
lation mean in each of the six steps in the paid session.
So θ1 [β1] refers to the average number that includes
the true value in step 1 for the free session [pay]. θ2 [β2]
refers to the estimated average frequency in Step 2 for
the free session [pay]. θ3 [β3] refers to the estimated av-
erage frequency of the other session for free [pay]. θ4 [β4]
θ5 [β5] and θ6 [β6] are strictly analogous to θ1 [β1] θ2 [β2]
and θ3 [β3] on the iteration in the free session and pay
respectively. Assumptions can be organized around four
central points:
• The comparison of over-confidence as measured by
the method of estimation interval and the method of
estimation frequency;
• Check if participants anticipate the over-confidence
of others through the estimation of the frequency of
others;
• Capture the effect of iteration on the results;
• Determine the impact of monetary incentives on the
behavior of individuals by comparing the free session
and the session fee.
1) Comparison of over-confidence as measured by
the method of confidence interval and the method of
frequency estimation
In our experiment, we measure the over-confidence by
two methods. The first one is the method of the confi-
dence interval or interval estimation used in step 1 and 4.
The second one is the method of estimating frequency
used in step 2 and 5.
Hypothesis 1: the range of over-confidence is
greater than the frequency of over-confidence
Free Session
(θ2 − θ1) < (9 − θ1) before iteration
(θ5 − θ4) < (9 − θ4) after iteration
Paid session
(β2 − β1) < (9 − β1) before iteration
(β5 − β4) < (9 − β4) after iteration.
In the first case, we will see if the over-confidence as
measured by the method of estimation interval is higher
than that measured by the method of estimation fre-
quency in the free session and the session fee, before and
after iteration.
2) Estimated frequency of other
By examining the frequency estimation of others
through step 3 and before step 6 iteration after iteration,
it is expected that participants expect the over-confidence
of others.
Hypothesis 2: Participants anticipate the over-con-
fidence of others
θn < 9 for n = 3, 6 free session
βn < 9 for n = 3, 6 paid session.
3) Iteration
Participants can give an inconsistent answer, they are
then asked to repeat the work of the estimate of the range
they want. The iteration is not required, because a subject
satisfied with his first answer may keep mentioning that.

An Experimental Analysis of Over-Confidence 398
In step 4, we recall about his answer by showing the
lower and upper bound of the interval he has chosen. He
then four choices:
Enter 0 for nothing fit
Type 1 only has to adjust, that is to say, the lower
bound.
Type 2 to adjust only b, that is to say, the upper bound.
Type 3 to adjust a and b, that is to say, the two termi-
nals.
In step 5, which is the iteration of step 2, the subject
has the choice of adjustment or maintenance of their re-
sponse. Recall that in step 3, each subject was asked to
estimate the average number of correct answers that his
colleagues have conducted on the ten questions. In step 6,
the subject has two choices:
Enter 0 for nothing fit
Type 1 to adjust the d, the average number of correct
answers of other participants estimated in step 3.
But it should be noted that the iteration will have the
effect of anchor the concept that an interval of 90% con-
fidence that actually involves 9 questions can be an-
swered correctly on average. There is an element of
learning for two reasons. First, the instructions are read
and the other participants are to a degree aware of their
failure to comply with the instructions.
Hypothesis 3: The iteration will reduce the range of
over-confidence that is overconfidence as measured
by the method of estimating the range will be reduced
by iteration
(9 − θ4) for the free session <(9 − θ1)
(9 − β4) for the paid session <(9 − β1).
4) Monetary incentives
Our experience consists of two sessions, one is free
and the other is paid for. To prevent participants from
giving too wide intervals in the paid session in order to
earn more money, we set a compensation system in a
step that takes into account both accuracy and precision.
We recall the compensation system in step 1:
R = 0.5 + 5/(b − a)
0.5 TND will be won by any participant who provides
an interval [a, b] containing the correct answer regardless
of the width of the interval.
5 TND/(b − a) is the variable part of remuneration de-
pends on the precision, that is to say, the width of the
interval to ensure the 0.5 TND, or they provide narrow
intervals to minimize (b − a) and maximize their profits.
This arbitration depends on the psychology of it is
risk-averse and under-confident, it will expand the range.
But his aversion to risk decreases and confidence in-
creases, the width of the interval that will supply de-
creases.
Previous research [5,18,19] believe that monetary in-
centives will align declaratory judgments and judgments
true. One simple reason is that subjects spend more cog-
nitive resources in the work where good performance is
rewarded financially. The second reason for providing
monetary incentives is that subjects may be reluctant to
admit they have not followed the instructions in the work
of estimating the range and thus exaggerates the esti-
mated frequency to align with the estimate of the interval.
This trend can be offset through monetary incentives as
the self-validation is not without cost. Self-validation is
manifested in steps 2 and 5 before and after iteration.
Previous researches also state that the subjects may be
more predisposed to recognize the over-confidence of
non-confidence on their own. This is the effect “above
average”. Since the estimated frequency of the other will
be paid in the session fee, we will check whether the ef-
fect “above average” will be reduced by monetary incen-
tives. Our goal in this section is to study the impact of
monetary incentives on responses. If the over-confidence
dominates the population of participants, it is expected
that the range of over-confidence in the session fee will
be greater than that of the free session. The study will be
made also by topic, to see the change in this way from
one person to another.
Hypothesis 4-a: The interval of over-confidence in
the session fee is larger than that of the session
(9 − β1) > (9 − θ1) before iteration and (9 − β4) > (9 −
θ4) after iteration.
Our second objective in this section is to study the
impact of monetary incentives on the estimated fre-
quency. Since self-validation is paid, participants will try
not to exaggerate.
Hypothesis 4-b: The monetary incentives will de-
crease the over-confidence as measured by the
method of frequency estimation
(θ2 − θ1) > (β2 − β1) before iteration and (θ5 − θ4) > (β5
− β4) after iteration.
Our third objective in this section is to study the im-
pact of monetary incentives on estimating the frequency
of others. Since this estimate is paid in steps 3 and 6. As
we have already declared the subjects may be more pre-
disposed to accept the over-confidence of other than their
own over-confidence.
Hypothesis 4-c: The monetary incentives will re-
duce the effect “above average”
(θ2 − θ3) > (β2 − β3) before iteration and (θ5 − θ6) > (β5
− β6) after iteration.
2.2. Results
Figure 1 below shows the average results in the six
stages of the experiment for the free session and the ses-
sion fee. For the free session, the average number of cor-
rect answers in the work of estimating the range in step 1
(before iteration) is θ1 = 4.555 and in step 4 (after itera-
tion) θ4 = 4.644. As for the session, the average number
of correct answers before iteration β1 goes up to 2.111,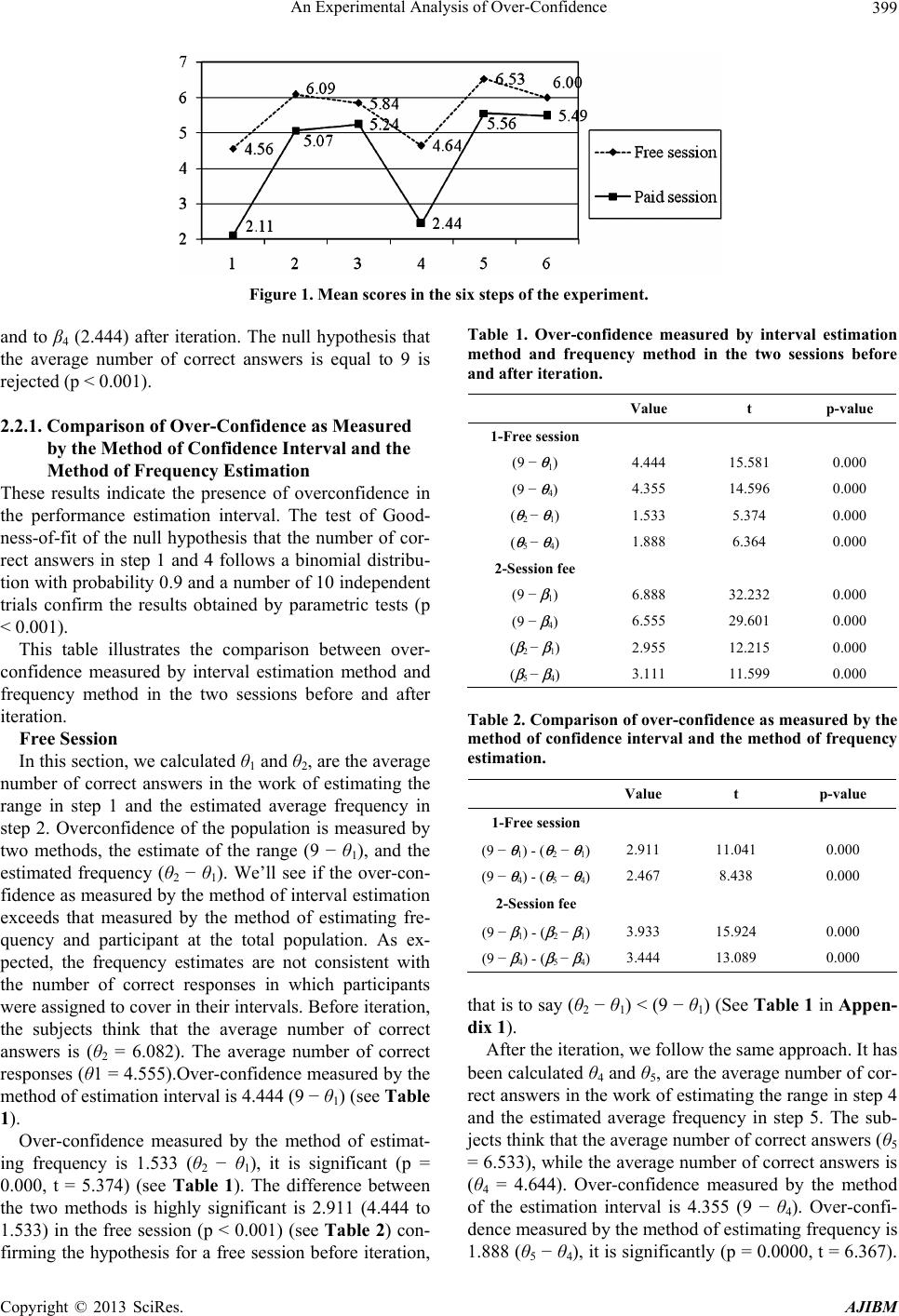

An Experimental Analysis of Over-Confidence 399
Figure 1. Mean scores in the six steps of the experiment.
and to β4 (2.444) after iteration. The null hypothesis that
the average number of correct answers is equal to 9 is
rejected (p < 0.001).
2.2.1. Comparison of Over-Confidence as Measured
by the Method of Confidence Interval and the
Method of Frequency Estimation
These results indicate the presence of overconfidence in
the performance estimation interval. The test of Good-
ness-of-fit of the null hypothesis that the number of cor-
rect answers in step 1 and 4 follows a binomial distribu-
tion with probability 0.9 and a number of 10 independent
trials confirm the results obtained by parametric tests (p
< 0.001).
This table illustrates the comparison between over-
confidence measured by interval estimation method and
frequency method in the two sessions before and after
iteration.
Free Session
In this section, we calculated θ1 and θ2, are the average
number of correct answers in the work of estimating the
range in step 1 and the estimated average frequency in
step 2. Overconfidence of the population is measured by
two methods, the estimate of the range (9 − θ1), and the
estimated frequency (θ2 − θ1). We’ll see if the over-con-
fidence as measured by the method of interval estimation
exceeds that measured by the method of estimating fre-
quency and participant at the total population. As ex-
pected, the frequency estimates are not consistent with
the number of correct responses in which participants
were assigned to cover in their intervals. Before iteration,
the subjects think that the average number of correct
answers is (θ2 = 6.082). The average number of correct
responses (θ1 = 4.555).Over-confidence measured by the
method of estimation interval is 4.444 (9 − θ1) (see Table
1).
Over-confidence measured by the method of estimat-
ing frequency is 1.533 (θ2 − θ1), it is significant (p =
0.000, t = 5.374) (see Table 1). The difference between
the two methods is highly significant is 2.911 (4.444 to
1.533) in the free session (p < 0.001) (see Table 2) con-
firming the hypothesis for a free session before iteration,
Table 1. Over-confidence measured by interval estimation
method and frequency method in the two sessions before
and after iteration.
Value t p-value
1-Free session
(9 − θ
1) 4.444 15.581 0.000
(9 − θ
4) 4.355 14.596 0.000
( θ
2 −
θ
1) 1.533 5.374 0.000
( θ
5 −
θ
4) 1.888 6.364 0.000
2-Session fee
(9 − β
1) 6.888 32.232 0.000
(9 − β
4) 6.555 29.601 0.000
( β
2 −
β
1) 2.955 12.215 0.000
( β
5 −
β
4) 3.111 11.599 0.000
Table 2. Comparison of over-confidence as measured by the
method of confidence interval and the method of frequency
estimation.
Value t p-value
1-Free session
(9 − θ
1) - (
θ
2 −
θ
1)2.911 11.041 0.000
(9 − θ
4) - (
θ
5 −
θ
4)2.467 8.438 0.000
2-Session fee
(9 − β
1) - (
β
2 −
β
1)3.933 15.924 0.000
(9 − β
4) - (
β
5 −
β
4)3.444 13.089 0.000
that is to say (θ2 − θ1) < (9 − θ1) (See Table 1 in Appen-
dix 1).
After the iteration, we follow the same approach. It has
been calculated θ4 and θ5, are the average number of cor-
rect answers in the work of estimating the range in step 4
and the estimated average frequency in step 5. The sub-
jects think that the average number of correct answers (θ5
= 6.533), while the average number of correct answers is
(θ4 = 4.644). Over-confidence measured by the method
of the estimation interval is 4.355 (9 − θ4). Over-confi-
dence measured by the method of estimating frequency is
1.888 (θ5 − θ4), it is significantly (p = 0.0000, t = 6.367).

An Experimental Analysis of Over-Confidence 400
The difference between the two methods is highly sig-
nificant is 2.467 in the free session (p < 0.001) (see Ta-
ble 2) confirming the hypothesis for a free session after
iteration (θ5 − θ4) < (9 − θ4) (See Table 2 in Appendix 1).
Session fee
We will repeat the same work to verify if the results
obtained for the free session are confirmed for the ses-
sion fee. It has been calculated β1 and β2 which represent
the average number of correct answers in step 1 and the
estimated average frequency in step 2 (See Table 3 in
Appendix 1).
Frequency estimates are not consistent with the num-
ber of correct responses in which participants were as-
signed to cover in their intervals. The subjects think that
the average number of correct answers β2 is 5.066. The
average number of correct answers β1 amounts to 2.111.
Over-confidence measured by the method of the estima-
tion interval is 6.888 (9 − β1). On the confidence meas-
ured by the method of estimating frequency is 2.955 (β2
− β1), it is significant is 3.933 (p < 0.001) confirming the
hypothesis for a session fee prior iteration (β2 − β1) < (9 −
β1) (See Table 3 in Appendix 1).
After iteration, we calculated that β5 and β4 represent
the average number of correct answers in step 4 and the
estimated mean frequency in step 5 (See Table 4 in Ap-
pendix 1).
Frequency estimates are not consistent with the num-
ber of correct responses in which participants were as-
signed to cover in their intervals. Participants felt that the
average number of correct answers β5 is 5.555. The av-
erage number of correct answers β4 equals 2.444. On the
confidence measured by the method of interval estima-
tion (9 − β4) is 6.555. Over-confidence measured by the
method of estimating frequency (β5 − β4), amounts on
average to 3.111 and is significant (p = 0.0000, t =
11.599). The mean difference between the two methods,
which is equal to 3.444, is highly significant either (p <
0.001) confirming the hypothesis after iteration 1.
2.2.2. Frequency Estimates of Others
In the free session, the estimated average frequency of
others (θ3 = 5.844) and (θ6 = 6) respectively before and
after iteration. In the session fee, the estimated average
frequency of others before β3 iteration is 5.244 (see Ta-
ble 3).
After the iteration, the estimated average frequency of
other β6 amounts to 5.488 (See Figure 1). In addition,
these estimates differ significantly from 9 (p < 0.001)
confirming hypothesis 2 (See Table 5 in Appendix 1).
2.2.3. Iteration
The opportunity to review the subjective confidence in-
tervals in step 4 was operated by 91% of participants in
the free session, and 93% of participants in the session
fee. The effect of using the iteration defined as the dif-
ference between the number of correct answers in steps 4
and 1 is 0.089 (θ1 = 4.555; θ4 = 4.644) in the free session
and 0.333 (β1 = 2.111; β4 = 2.444) in the session fee. The
over-confidence interval decreases with the iteration (see
Table 4), but this decrease is not significant for the free
session (p = 0.253, t = 1.151). By cons, it is significant
for the session fee (p = 0.01, t = 2.708) which is consis-
tent with the hypothesis 3. (9 − β1) > (9 − β4) for the paid
session.
2.2.4. Monetary Incentives
The effect of monetary incentives will be considered at
each step before and after iteration, since the pricing is
different from one stage to another. Recall that in step 1,
the compensation system is R = 0.5 + 5/(b − a). In step 2,
if the participant correctly estimates the number of cor-
rect responses it has made in the first stage, he won 0.5
TND. In step 3, if the participant correctly estimates the
average number of correct responses made by his col-
leagues, he earns 0.5 TND. The same principle is
adopted for the iteration.
Participants in overconfidence resulted intervals are
too narrow to maximize their gain, so (β1 = 2.111), which
represents the average number of correct answers is sig-
nificantly lower (θ1 = 4.555). So, over-confidence as
measured by the interval estimation in the session fee is
higher than that measured in the free session. Overconfi-
dence measured by the method of the estimation interval
is 6.888 in the session fee prior iteration, and 4.444 in the
free session before iteration. The difference is significant
(p = 0, t = 7.558). After iteration (β4 = 2.444) is signifi-
cantly lower (θ4 = 4.644).
Table 3. Estimated average frequency of others in the two
sessions before and after iteration.
Value t p-value
1-Free session
(9 − θ
3) 3.156 17.845 0.000
(9 − θ
6) 3.000 15.732 0.000
2-Session fee
(9 − β
3) 3.756 17.783 0.000
(9 − β
6) 3.511 16.009 0.000
Table 4. Impact of iteration on overconfidence measured by
the interval estimation method in the two sessions.
Value T p-value
1-Free session
(9 − θ
1) - (9 −
θ
4)0.089 1.151 0.253
2-Session fee
(9 − β
1) - (9 −
β
4)0.333 2.708 0.010

An Experimental Analysis of Over-Confidence 401
Therefore, the overconfidence as measured by the in-
terval estimation in the paid session (6.555) is higher
than that measured in the free session (4.355). The dif-
ference is significant (p = 0.000). These results confirm
the hypothesis 4-a:
(9 − β1) > (9 − θ1) before iteration
(9 − β4) > (9 − θ4) after iteration.
In addition, we measured overconfidence per partici-
pant for this psychological bias varies from person to
person. For example, we see over-confidence is highest
among participants 13, 24, 28, 31, 32 and 34 and lowest
among participants 3, 21 and 17 in the session fee prior
iteration. Those for which it is discovered through a
broad over-confidence intervals are given too narrow to
maximize their gains, many of them were too close to the
answer that is to say if they have just expanded their
ranges they would have answered correctly, and that's
what we are trying to demonstrate. People overestimate
the precision of their knowledge by giving intervals too
narrow. Monetary motivation, which involves the accu-
racy of the interval, caused the bias in over-confident
participants (see Table 5). They are fans of the risk and
want to maximize their gains. Plus this bias decreases as
the data is less close intervals.
In step 2, self-validation is paid, so (β2 = 5.066) and
(θ2 = 6.088). The difference is significant (p = 0.00, t =
3.804). Results in Table 6 show that monetary incentives
encourage participants to think before giving their esti-
mates and reduce the exaggeration of the estimates. After
iteration (β5 = 5.555) is less than (θ5 = 6.533). The dif-
ference is significant (p = 0.002, t = 3.367). Before itera-
tion, over-confidence measured by the method of esti-
mating frequency is 1.533 in the free session, and 2.955
in the session fee (see Table 1). After iteration, overcon-
fidence is 1.888 in the free session, and 3.111 in the ses-
sion fee (see Table 1). It is clear that the hypothesis is
rejected 4-b. That is to say, over-confidence as measured
by the estimated frequency is not reduced by monetary
incentives (see Table 6). On the contrary, it increased by
iteration of 1.422 (p = 0.007, t = 3.660), and after itera-
tion of 1.223 (p = 0.060, t = 2.908). This increase is due
to the fact that the average number of correct responses
in the session fee (β1 = 2.111) was significantly lower
than the average number of correct answers in the free
session (θ1 = 4.555) before iteration. The same results are
confirmed after iteration (β4 = 2.444) is significantly
lower (θ4 = 4.644). This is due to monetary incentives
that led to the existence of the intervals are too narrow
for lack of precision, thus the increase in number of
wrong answers.
We can conclude that monetary incentives have caused
an increase in overconfidence as measured by the inter-
val estimate and the estimate of frequency.
In step 3, the estimated frequency of the other is paid.
Before iteration, the effect “above average” is 0.244 (p =
0.36) for the free session, and −0.177 (p = 0.460) for the
session fee. Effect “above average” is not significant in
the session free of charge and pay before iteration. This
effect decreased with monetary incentives, but this de-
crease was not significant (p = 0.11) (See Table 6 in
Appendix 1). After iteration, the effect of “above aver-
age” is 0.533 (p = 0.058) for the free session and 0.066 (p
= 0.79) for the session fee. Effect “above average” is
significant at 10% in the free session, but not significant
in the session fee after iteration. This effect also de-
creased after iteration (p = 0.098). This decrease is sig-
nificant at 10% (See Table 7 in Appendix 1).
3. Method of Question with Two Answer
Choices
The objective of this experiment is to measure overcon-
fidence by a third method, called method of question
with two answer choices. Subjects were two response
alternatives, they must choose one to answer each ques-
tion by giving a certain percentage of the response cho-
sen on the scale [50% 100%]. We then studied the effects
of monetary incentives on outcomes. This will be
achieved by comparing the results of the free session and
the session fee. The main objective of this third method
is to compare the over-confidence as measured by three
methods and see if the choice of scale measure may ag-
gravate or alleviate this bias.
Table 5. Impact of monetary incentives on overconfidence
measured by the interval estimation method before and
after iteration.
Value t p-value
(9 − β
1) - (9 −
θ
1)2.444 7.558 0.000
(9 − β
4) - (9 −
θ
4)2.200 6.383 0.000
Table 6. Impact of monetary incentives on overconfidence
measured by frequency estimation method before and after
iteration.
Value t p-value Interpretation
θ
2 −
β
2 1.0223.804 0.000
θ
5 −
β
5 0.9783.367 0.002
The monetary
incentives incite
participants to reflect
before giving the
estimation and reduce
exaggeration of
estimation
( β
2 −
β
1) - (
θ
2 −
θ
1)1.4223.660 0.001
( β
5 −
β
4) - (
θ
5 −
θ
4)1.2232.908 0.006
Over-confidence
measured by
frequency estimation
do not reduce with
monetary incentives
Reject of hypothesis
5

An Experimental Analysis of Over-Confidence 402
3.1. Models of the Experience and Assumptions
3.1.1. Participants and Procedures
The experiment will involve 45 students at the ISG of
Tunis. In fact, the same students who participated in the
first experiment participated also in the second and for
having an adequate basis for comparison between the
three methods. This experience is also composed of two
sessions, one is free the other is paying.
In the session fee, participants will be paid in propor-
tion of correct responses they made. We follow the com-
pensation system as follows:
• In step 1, a correct answer is remunerated by 1 TND.
• In step 2, a self-validation is properly remunerated by
0.5 TND.
• In step 3, the estimated frequency of correct answer
of others is paid by 0.5 TND.
The experiment has three steps described below (no
iteration):
Step 1
Participants must answer ten questions, choosing an
alternative among the two alternatives proposed. Then
they give a certain percentage of this response on the
scale [50% 100%]. The percentage cannot be less than
50% because it implies the choice of alternative.
Step 2
We asked each subject to estimate the number of cor-
rect answers that he made in the ten questions. This is the
stage of self-validation.
Step 3
We asked each subject to estimate the average number
of correct answers that these colleagues have conducted
on the ten questions.
As mentioned earlier, this experience also includes
two sessions: the first is free and the second is paid off.
Each session consists of three steps described above. The
questions in both sessions are different but the same type
that is to say that the sample is heterogeneous and is not
selected for the difficulty. The purpose of this change is
to avoid the effect of learning that can bias the analysis.
It should be noted that the questions asked in the session
free of the first experiment are identical to those raised in
the free session of the second experiment. The questions
asked in the session fee of the first experiment are iden-
tical to those asked in the session fee in the second ex-
periment.
3.1.2. Assumptions and Tests
Let αi the population mean in step i (i = 1, 2 and 3) for
the free session, and λi the population mean in step i (i =
1, 2 and 3) for the session fee.
So α1 [λ1] refers to the average number of correct an-
swers in step 1 for the free session [paid]. α2 [λ2] refers to
the estimated average frequency in Step 2 for the free
session [pay]. α3 [λ3] refers to the estimate of the average
frequency of the other session for free [pay]. α4 is me-
dium confidence of participants in step 1 for the entire
issue of the free session, λ4 is medium confidence of par-
ticipants in step 1 for the entire question of the session
fee.
Comparison of over-confidence as measured by the
method of confidence interval and the method of ques-
tion two answer choices:
1) Comparison of over-confidence as measured by
the method of confidence interval and the method of
question with two answer choices
In our experiment, we measured the over-confidence
by the method of question two answer choices per par-
ticipant for the entire population (see Tables 1 and 2 in
Appendix 2) to compare it with that measured by the
method of confidence interval used in step 1 and 4 of the
first experiment.
Hypothesis 1: over-confidence as measured by the
method of the confidence interval is greater than that
measured by the method of question two answer
choices:
For the free session, this hypothesis implies that (9 −
θ1) > (α4 − α1) and (9 − θ4) > (α4 − α1). For paid session,
this hypothesis implies that (9 − β1) > (λ4 − λ1) and (9 −
β4) > (λ4 − λ1).
In the first case, we will see if the over-confidence
measured by the method of estimating the interval is
greater than that measured by the method of question two
answer choices in both free and paid sessions.
2) Frequency estimation of others
By examining the frequency estimation of others
through step 3, it is expected that participants expect the
over-confidence of others.
Hypothesis 2: Participants anticipate the confi-
dence of others:
α3 < α4 for free session
λ3 < λ4 for the paid session.
3) Monetary incentives
Our experiment consists of two sessions, the first is
free and the second is paid off. It should be noted that the
sample of questions is not the same for both sessions so
as not to bias the results by the effect of learning. How-
ever, both samples include questions of general knowl-
edge in much the same type.
In the session fee, participants are paid for each correct
answer of a dinar. So we expected to exert more effort
and thought to respond appropriately. Therefore, the
overconfidence as measured by the method of question
two answer choices will usually be reduced by monetary
incentives.
In step 2, self-validation is paid to 0.5 dinar. It is ex-
pected that overconfidence as measured by the estimated
frequency is reduced in this experiment.
In step 3, the estimated frequency of the other is paid

An Experimental Analysis of Over-Confidence 403
to 0.5 dinar. It is expected that the effect ‘above average’
is reduced.
Hypothesis 3-a: The over- confidence measured by
the method of question two answer choices will be
reduced by the monetary incentives
(λ4 − λ1) < (α4 − α1).
Hypothesis 3-b: The monetary incentives will de-
crease the over-confidence as measured by the fre-
quency estimation
(λ2 − λ1) < (α2 − α1).
Hypothesis 3-c: The monetary incentives will re-
duce the effect “above average”
(λ2 − λ3) < (α2 − α3).
3.2. Results
Figure 2 shows the mean scores in the three stages of the
experiment for the free session and the session fee.
The average number of correct answers in the work of
Open and answer choices in step 1 is (α1 = 6.022) in the
free session, and (λ1 = 5.644) in the session fee. Trust
average (α4 = 8.042), and (λ4 = 7.467) in the session fee.
The null hypothesis that the number of correct answer is
equal to the average confidence (α1 = α4) is released to
the free session (p = 0.000, t = 8.699). This same hy-
pothesis is rejected in the session fee (p = 0.000, t =
6.433). Therefore, the method of question two alternative
responses is also evidence of the bias of over-confidence.
The nonparametric Wilcoxon Mann-Whitney equality
of medians between the number of correct answers and
medium confidence confirms the results from the t-test
for both free session (p = 0.000; value = 6.202) pay for
the session (p = 0.000 value = 5.181).
3.2.1. Comparison of the Overconfidence as Measured
by the Method of Confidence Interval and the
Method of Question Two Answer Choices
1) Free Session
Our goal is to test the hypothesis that over-confidence
as measured by the method of interval estimation is
higher than that measured by the method of question two
answer choices. Overconfidence measured by the method
of choice is Open and 2.02 in the free session (See Table
1 in Appendix 2).
Overconfidence measured by the method of the esti-
mation interval is 4.444 in the free session before itera-
tion after iteration and 4.355.
The difference between the two methods is 2.242 (p =
0.000, t = 6.277) before iteration after iteration and 2.335
(p = 0.000, t = 6.124). This difference is highly signifi-
cant confirming the hypothesis for a free session.
The test of equal median Wilcoxon Mann-Whitney
confirmed the superiority of overconfidence as measured
by the interval estimation method that measured by the
method of Open and free choice in the session before
iteration (p = 0.000; value = 5.399) and after iteration (p
= 0.000; value = 5.221).
(9 − θ1) > (α4 − α1);
(9 − θ4) > (α4 − α1).
2) Paid Session
Our goal is to calculate λ1 and λ4 to determine the
over-confidence as measured by the method of question
two answer choices (see Table 2 in Appendix 2).
Overconfidence measured by the method of choice is
Open and 1.823 in the session fee. Overconfidence meas-
ured by the method of the estimation interval is 6.888 in
the session fee prior iteration and 6.555 after iteration.
The difference between the two methods is 5.065 before
iteration (p = 0.000, t = 15.387) and 4.732 (p = 0.000, t =
14.365) after iteration. This difference is highly signifi-
cant confirming the hypothesis for a session fee.
The test of equal median Wilcoxon Mann-Whitney
(Table 7) confirmed the superiority of overconfidence as
measured by the interval estimation method that meas-
ured by the method of choice in Open and before the
session fee iteration (p = 0.000; value = 7.7791) and after
iteration (p = 0.000; value = 7.8663).
(9 − β1) > (λ4 − λ1);
(9 − β4) > (λ4 − λ1).
3.2.2. Estimates of Frequency of Others
Estimates of average frequency of others (α3 = 6.911) in
the free session and (λ3 = 6.288) in the session fee as
shown in Figure 2. We tested whether these estimates
6,91
6,29
7,18
6,02
6,13
5,64
4
5
6
7
8
123
Session gratuite
Session payante
7.18
6.02
5.64 6.13
6.29
.
Figure 2. Mean scores in the three stages of the experiment.

An Experimental Analysis of Over-Confidence 404
Table 7. Comparison of the overconfidence as measured by
the method of confidence interval and the method of ques-
tion two answer choices.
Value t p-value Wilcoxon
Mann-Whitney
(9 − θ
1) - (
α
4 −
α
1) 2.424 6.2770.000 5.399
(9 − θ
4) - (
α
4 −
α
1) 2.335 6.1240.000 5.221
(9 − β
1) - (
λ
4 −
λ
1) 5.065 15.3870.000 7.7791
(9 − β
4) - (
λ
4 −
λ
1) 4.732 14.3650.000 7.866
differ significantly from the α4 or medium confidence in
the free session, and λ4 in the session fee. α4 = 8.042 and
λ4 = 7.467 (see Tables 3 and 4 in Appendix 2).
α3 < α4 and (p = 0.000, t = 5.717), the difference is sig-
nificant. The hypothesis is confirmed in the free session.
λ3 < λ4 and (p = 0.000, t = 5.799) the difference is sig-
nificant. So the hypothesis is confirmed in the session
fee.
The test of equal median Wilcoxon Mann-Whitney
confirmed these results both for the free session (p =
0.000; value = 4.027) than pay for the session (p = 0.000;
value = 4.580). Therefore, we can conclude that the par-
ticipants expect the over-confidence of others.
3.2.3. Monetary Incentives
Overconfidence measured by the method of choice is
Open and 2.02 in the free session and 1.823 in the ses-
sion fee. We tested whether overconfidence decreases by
monetary incentives. The difference is 0.197 (p = 0.577)
(Table 8). It is no longer significant, 3-a hypothesis is
rejected. In addition, the test of equal median shows that
overconfidence is not reduced by the monetary incentives
(p = 0.358).
The estimated frequency is α2 = 7.177 for the free ses-
sion, and λ2 = 6.133 for the session fee. Overconfidence
measured by estimated frequency is 1.155 in the free
session, and 0.489 in the session fee. It was verified that
overconfidence decreases by monetary incentives but this
decrease was not significant (p = 0.137 for the t-test, p =
0.089) led to the dismissal of the case 3-b.
The rejection of hypotheses 3-a and 3-b reflects the
persistence of overconfidence. Indeed, this bias is not
weakened by monetary incentives.
The estimate of the average frequency of others is α3 =
6.911 in the free session and λ3 = 6.288 in the session fee.
Effect “above average” is 0.266 (α2 − α3) in the free ses-
sion and −0.155 (λ2 − λ3) in the session fee. This effect
decreased with monetary incentives (p = 0.053). The
decrease is significant at 10% assuming 3-c is checked
(See Tables 3 and 4 in Appendix 2).
Table 8. Impact of monetary incentives on overconfidence
measured by the method of question with two answer
choices.
Value t p-value Wilcoxon
Mann-Whitney
( α
4 −
α
1) - (
λ
4 −
λ
1)0.1970.562 0.577 0.919946
4. Conclusions
We tried to measure and test the existence of the bias of
over-confidence and to examine the sensitivity of this
bias with respect to several factors. These factors are the
method of measurement, monetary incentives and itera-
tion.
The review of the literature tells us that overconfi-
dence can be measured by three methods namely; the
interval estimation method, the method of estimating
frequency and method of question two choices. We have
conducted an experiment involving students from the
ISG Tunis in order to measure overconfidence through
these three methods. The results of this experiment show
the existence of this bias for the three methods and thus
support the empirical evidence of Russo and Schoemaker
[17], Justin et al. [20], Cesarini et al. [21] and Klyaman
et al. [22].
At the sensitivity analysis of this bias, the tests show
that the method of interval leads to higher steps in com-
parison with other methods. These results confirm the
empirical evidence observed by Cesarini et al. [21].
The study of the effect of monetary incentives on the
level of overconfidence revealed conflicting results.
First, monetary incentives boost the level of overcon-
fidence for the method of estimating the range as well as
the estimation method of frequency. On the other hand,
overconfidence is not significantly sensitive to monetary
incentives when measured by the method of question two
choices. In our view, this discrepancy is explained by the
form of compensation issues. Indeed, the level of ex-
perience with the first two methods, the existence of a
variable component of compensation depending on the
accuracy of answers prompted the subjects to take more
risk by opting for more precise answers and less accurate
in the session fee in the free session. So the number of
correct responses decreased, and therefore, over-confi-
dence has increased. As regards the method of question
two choices, the form of total compensation fixed and
independent of the accuracy of answers does not lead
subjects to make a trade-off between accuracy and preci-
sion of the responses to the extent that it does not matter.
As a result, the number of correct answers, and overcon-
fidence was not significantly affected by monetary in-
centives. Regarding the impact of iteration on overconfi-
dence, the tests indicate the significance of it depends on

An Experimental Analysis of Over-Confidence 405
the motivation of money. In the session fee, one observes
that the subjects offered by reviewing their responses,
wider intervals reflect better understanding of the con-
cept of the range of 90%. So with the iteration, the num-
ber of intervals containing the correct answer has in-
creased and overconfidence is significantly reduced. In
the absence of monetary incentives, these mechanisms
did not function properly and over-confidence is not af-
fected by the iteration.
REFERENCES
[1] O. Svenson, “Are We All Less Risky and More Skillful
than Our Fellow Driver,” Acta Psychologia, Vol. 47, No.
2, 1981, pp. 143-148. doi:10.1016/0001-6918(81)90005-6
[2] M. Alpert and H. Raiffa, “A Progress Report on the
Training of Probability Assessors,” In D. Kahneman, P.
Slovic and A. Tversky, Ed., Judgment Under Uncertainty:
Heuristics and Biases, Cambridge University Press,
Cambridge, 1982, pp. 294-305.
doi:10.1017/CBO9780511809477.022
[3] J. B. De Long, A. Shleifer, S. Lawrence and R. J.
Waldmann, “The Survival of Noise Traders in Financial
Markets,” Journal of Business, Vol. 64, No. 1, 1991, pp.
1-19. doi:10.1086/296523
[4] A. Kyle and F. A. Wang, “Speculation Duopoly with
Agreement to Disagree: Can Overconfidence Survive the
Market Test?” Journal of Finance, Vol. 52, No. 5, 1997,
pp. 2073-2090. doi:10.1111/j.1540-6261.1997.tb02751.x
[5] T. Odean, “Volume, Volatility, Price and Profit when all
Traders are above Average,” Journal of Finance, Vol. 53,
No.6, 1998, pp. 1887-1934.
doi:10.1111/0022-1082.00078
[6] K. D. Daniel, D. Hirshleifer and A. Subrahmanyam, “In-
vestor Psychology and Security Market Under- and Over-
reactions,” Journal of Finance, Vol. 53, No. 6, 1998, pp.
1839-1885. doi:10.1111/0022-1082.00077
[7] A. Admati and P. Pfleiderer, “A Theory of Intraday Pat-
terns: Volume and Price Variability,” Review of Financial
Studies, Vol. 1, No. 1, 1988, pp. 3-40.
doi:10.1093/rfs/1.1.3
[8] F. D. Foster and S. Viswanathan, “A Theory of Interday
Variations in Volumes, Variances and Trading Costs,”
Review of Financial Studies, Vol. 3, No. 4, 1990, pp.
593-624. doi:10.1093/rfs/3.4.593
[9] A. Kyle, “Continuous Auctions and Insider Trading,”
Econometrica, Vol. 53, No. 6, 1985, pp. 1315-1336.
doi:10.2307/1913210
[10] G. Llorente, R. Michaely, G. Saar and J. Wang, “Dy-
namic Volume-Return Relation of Individual Stocks,”
Review of Financial Studies, Vol. 15, No. 4, 2002, pp.
1005-1047. doi:10.1093/rfs/15.4.1005
[11] J. Wang, “A Model of Competitive Stock Trading Vol-
ume,” Journal of Political Economy, Vol. 102, 1994, No.
1, pp. 127-168.
[12] B. Biais, D. Hilton, K. Mazurier and S. Pouget, “Judg-
mental Overconfidence, Self-Monitoring and Trading
Performance in an Experimental Financial Market,” Re-
view of Economic Studies, Vol. 72, No. 2, 2005, pp.
287-312. doi:10.1111/j.1467-937X.2005.00333.x
[13] M. Glaser and M. Weber, “Overconfidence and Trading
Volume,” Geneva Risk and Insurance Review, Vol. 32,
No. 1, 2007, pp. 1-36. doi:10.1007/s10713-007-0003-3
[14] S. Gervais and T. Odean, “Learning to be Overconfident,”
Review of Financial Studies, Vol. 14, No. 1, 2001, pp.
1-27. doi:10.1093/rfs/14.1.1
[15] W. Chuang and B. Lee, “An Empirical Evaluation of the
Overconfidence Hypothesis,” Journal of Banking and
Finance, Vol. 30, No. 9, 2006, pp. 2489-2515.
doi:10.1016/j.jbankfin.2005.08.007
[16] S. Lichtenstein, B. Fischhoff and L. D. Phillips, “Calibra-
tion of Probabilities: The State of the Art to 1980,” In: D.
Kahneman, P. Solvic and A. Tversky, Eds., Judgment
under Uncertainty: Heuristics and Biases, Cambridge
University Press, Cambridge, New York, 1982.
doi:10.1017/CBO9780511809477.023
[17] J. E. Russo and P. J. H. Schoemaker, “Managing Over-
confidence,” Sloan Management Review, Vol. 33, No. 2,
1992, pp. 7-17
[18] D. Davis and C. Holt, “Experimental Economics,”
Princeton University Press, Princeton, 1993.
[19] V. Smith and J. Walker, “Monetary Rewards and Deci-
sion Cost in Experimental Economics,” Economic Inquiry,
Vol. 31, No. 2, 1993, pp. 245-261.
doi:10.1111/j.1465-7295.1993.tb00881.x
[20] P. Juslin, P. Wennerholm and H. Olsson, “Format De-
pendence in Subjective Probability Calibration,” Journal
of Experimental Psychology: Learning, Memory, and
Cognition, Vol. 25, No. 4, 1999, pp. 1038-1052.
doi:10.1037/0278-7393.25.4.1038
[21] D. Cesarini, O. Sandewall and M. Johannesson, “Confi-
dence Interval Estimation Tasks and the Economics of
Overconfidence,” Journal of Economic Behavior and
Organization, Vol. 61, No. 3, 2006, pp. 453-470.
doi:10.1016/j.jebo.2004.10.010
[22] J. Klayman, J. B. Soll, C. Gonzalez-Vallejo and C. Barlas,
“Overconfidence: It Depends on How, What and Whom
You Ask,” Organizational Behavior and Human Decision
Processes, Vol. 79, No. 3, 1999, pp. 216-247.
doi:10.1006/obhd.1999.2847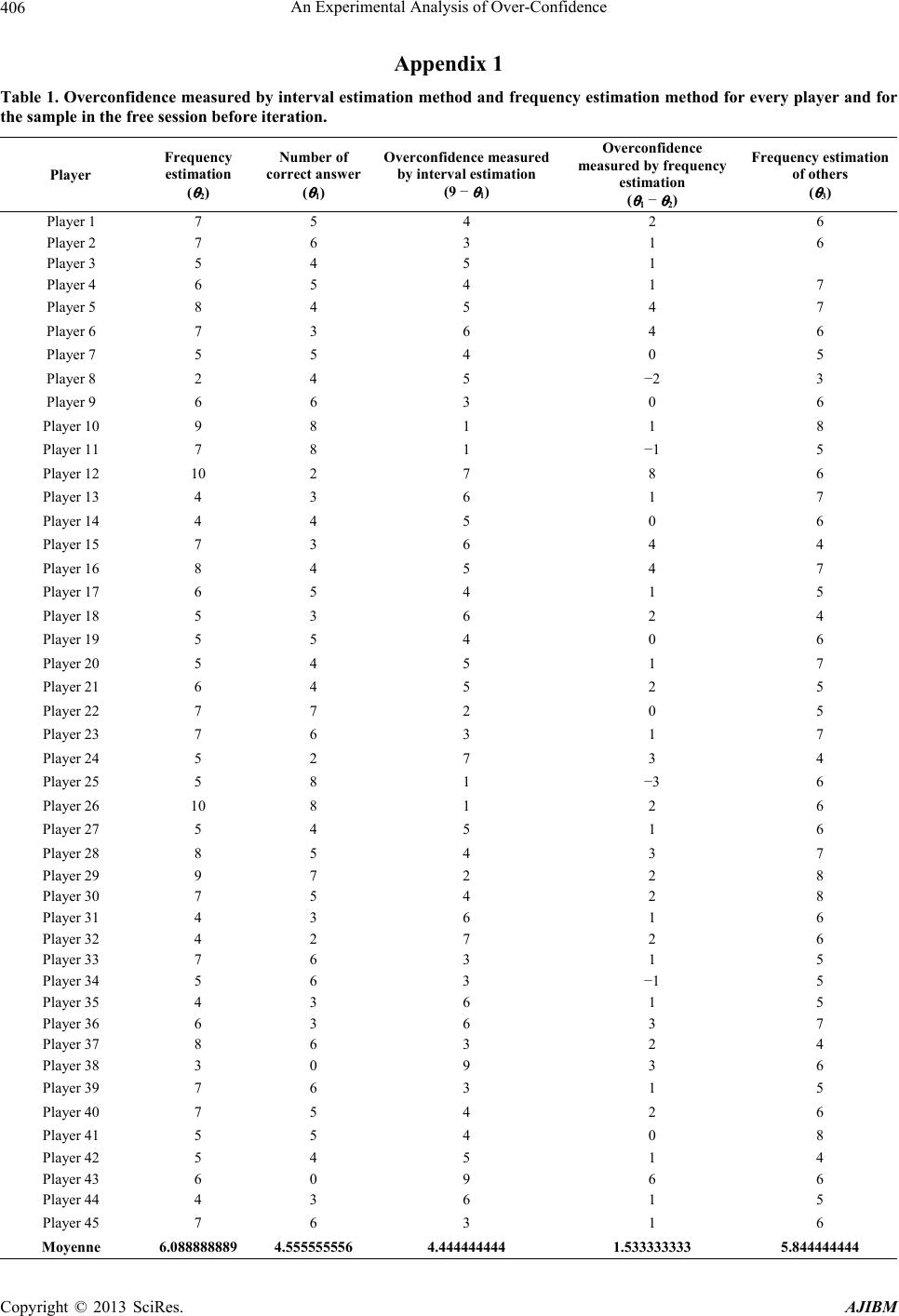

An Experimental Analysis of Over-Confidence 406
Appendix 1
Table 1. Overconfidence measured by interval estimation method and frequency estimation method for every player and for
the sample in the free session before iteration.
Player
Frequency
estimation
(
θ
2)
Number of
correct answer
( θ
1)
Overconfidence measured
by interval estimation
(9 − θ
1)
Overconfidence
measured by frequency
estimation
( θ
1 −
θ
2)
Frequency estimation
of others
(
θ
3)
Player 1 7 5 4 2 6
Player 2 7 6 3 1 6
Player 3 5 4 5 1
Player 4 6 5 4 1 7
Player 5 8 4 5 4 7
Player 6 7 3 6 4 6
Player 7 5 5 4 0 5
Player 8 2 4 5 −2 3
Player 9 6 6 3 0 6
Player 10 9 8 1 1 8
Player 11 7 8 1 −1 5
Player 12 10 2 7 8 6
Player 13 4 3 6 1 7
Player 14 4 4 5 0 6
Player 15 7 3 6 4 4
Player 16 8 4 5 4 7
Player 17 6 5 4 1 5
Player 18 5 3 6 2 4
Player 19 5 5 4 0 6
Player 20 5 4 5 1 7
Player 21 6 4 5 2 5
Player 22 7 7 2 0 5
Player 23 7 6 3 1 7
Player 24 5 2 7 3 4
Player 25 5 8 1 −3 6
Player 26 10 8 1 2 6
Player 27 5 4 5 1 6
Player 28 8 5 4 3 7
Player 29 9 7 2 2 8
Player 30 7 5 4 2 8
Player 31 4 3 6 1 6
Player 32 4 2 7 2 6
Player 33 7 6 3 1 5
Player 34 5 6 3 −1 5
Player 35 4 3 6 1 5
Player 36 6 3 6 3 7
Player 37 8 6 3 2 4
Player 38 3 0 9 3 6
Player 39 7 6 3 1 5
Player 40 7 5 4 2 6
Player 41 5 5 4 0 8
Player 42 5 4 5 1 4
Player 43 6 0 9 6 6
Player 44 4 3 6 1 5
Player 45 7 6 3 1 6
Moyenne 6.088888889 4.555555556 4.444444444 1.533333333 5.844444444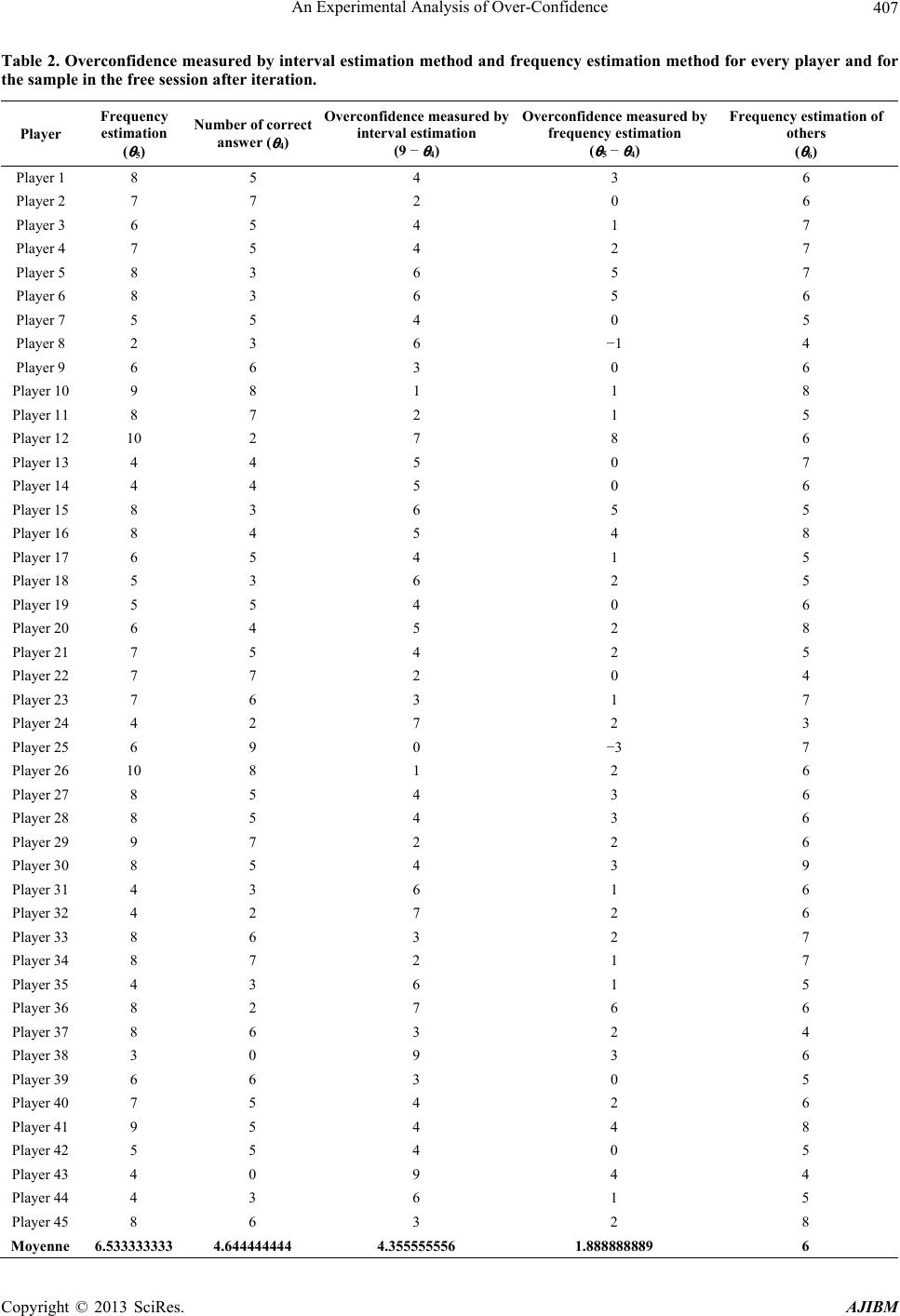

An Experimental Analysis of Over-Confidence 407
Table 2. Overconfidence measured by interval estimation method and frequency estimation method for every player and for
the sample in the free session after iteration.
Player
Frequency
estimation
( θ
5)
Number of correct
answer (
θ
4)
Overconfidence measured by
interval estimation
(9 − θ
4)
Overconfidence measured by
frequency estimation
( θ
5 −
θ
4)
Frequency estimation of
others
( θ
6)
Player 1 8 5 4 3 6
Player 2 7 7 2 0 6
Player 3 6 5 4 1 7
Player 4 7 5 4 2 7
Player 5 8 3 6 5 7
Player 6 8 3 6 5 6
Player 7 5 5 4 0 5
Player 8 2 3 6 −1 4
Player 9 6 6 3 0 6
Player 10 9 8 1 1 8
Player 11 8 7 2 1 5
Player 12 10 2 7 8 6
Player 13 4 4 5 0 7
Player 14 4 4 5 0 6
Player 15 8 3 6 5 5
Player 16 8 4 5 4 8
Player 17 6 5 4 1 5
Player 18 5 3 6 2 5
Player 19 5 5 4 0 6
Player 20 6 4 5 2 8
Player 21 7 5 4 2 5
Player 22 7 7 2 0 4
Player 23 7 6 3 1 7
Player 24 4 2 7 2 3
Player 25 6 9 0 −3 7
Player 26 10 8 1 2 6
Player 27 8 5 4 3 6
Player 28 8 5 4 3 6
Player 29 9 7 2 2 6
Player 30 8 5 4 3 9
Player 31 4 3 6 1 6
Player 32 4 2 7 2 6
Player 33 8 6 3 2 7
Player 34 8 7 2 1 7
Player 35 4 3 6 1 5
Player 36 8 2 7 6 6
Player 37 8 6 3 2 4
Player 38 3 0 9 3 6
Player 39 6 6 3 0 5
Player 40 7 5 4 2 6
Player 41 9 5 4 4 8
Player 42 5 5 4 0 5
Player 43 4 0 9 4 4
Player 44 4 3 6 1 5
Player 45 8 6 3 2 8
Moyenne 6.533333333 4.644444444 4.355555556 1.888888889 6

An Experimental Analysis of Over-Confidence 408
Table 3. Overconfidence measured by interval estimation method and frequency estimation method for every player and for
the sample in the session fee before iteration.
Player
Frequency
estimation
(β2)
Number of correct
answer
(β1)
Overconfidence measured
by interval estimation
(9 − β1)
Overconfidence measured by
frequency estimation
(β2 − β1)
Frequency estimation
of others
(β3)
Player 1 6 3 6 3 5
Player 2 4 3 6 1 5
Player 3 5 5 4 0 5
Player 4 6 2 7 4 7
Player 5 6 3 6 3 8
Player 6 6 3 6 3 6
Player 7 3 2 7 1 3
Player 8 4 1 8 3 7
Player 9 4 1 8 3 6
Player 10 9 3 6 6 8
Player 11 5 2 7 3 4
Player 12 4 2 7 2 4
Player 13 6 0 9 6 6
Player 14 2 1 8 1 4
Player 15 7 4 5 3 3
Player 16 6 4 5 2 6
Player 17 5 5 4 0 7
Player 18 6 1 8 5 5
Player 19 5 1 8 4 7
Player 20 4 1 8 3 7
Player 21 8 5 4 3 5
Player 22 9 4 5 5 6
Player 23 6 2 7 4 5
Player 24 2 0 9 2 2
Player 25 7 3 6 4 7
Player 26 7 4 5 3 6
Player 27 3 2 7 1 5
Player 28 6 0 9 6 7
Player 29 6 2 7 4 4
Player 30 6 1 8 5 8
Player 31 4 0 9 4 6
Player 32 3 0 9 3 5
Player 33 4 3 6 1 7
Player 34 4 0 9 4 5
Player 35 4 3 6 1 6
Player 36 4 1 8 3 5
Player 37 3 1 8 2 4
Player 38 5 3 6 2 4
Player 39 6 1 8 5 7
Player 40 6 3 6 3 4
Player 41 4 3 6 1 7
Player 42 6 2 7 4 6
Player 43 3 1 8 2 3
Player 44 3 3 6 0 4
Player 45 6 1 8 5 6
Moyenne 5.066666667 2.111111111 6.888888889 2.955555556 5.488888889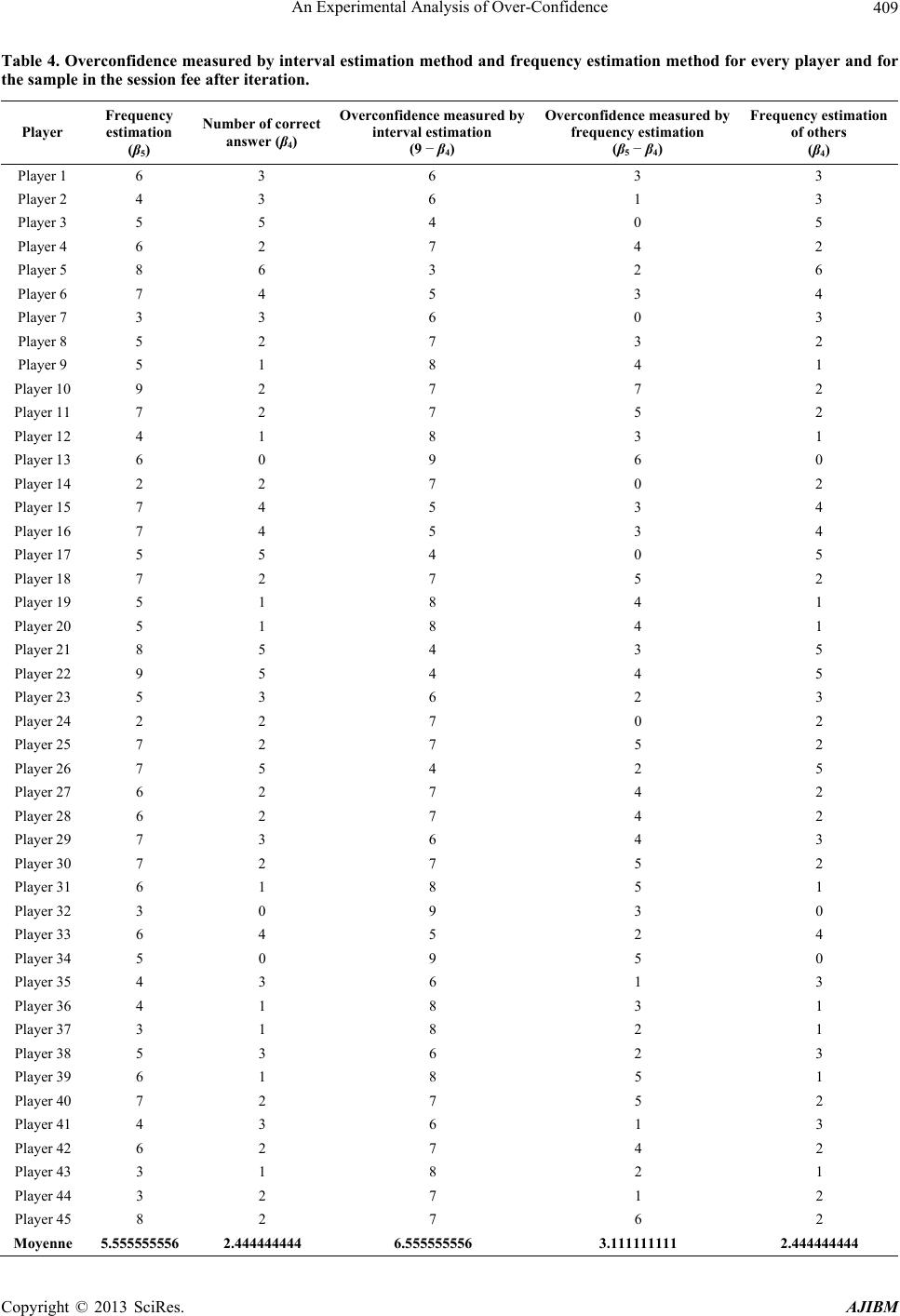

An Experimental Analysis of Over-Confidence 409
Table 4. Overconfidence measured by interval estimation method and frequency estimation method for every player and for
the sample in the session fee after iteration.
Player
Frequency
estimation
(β5)
Number of correct
answer (β4)
Overconfidence measured by
interval estimation
(9 − β4)
Overconfidence measured by
frequency estimation
(β5 − β4)
Frequency estimation
of others
(β4)
Player 1 6 3 6 3 3
Player 2 4 3 6 1 3
Player 3 5 5 4 0 5
Player 4 6 2 7 4 2
Player 5 8 6 3 2 6
Player 6 7 4 5 3 4
Player 7 3 3 6 0 3
Player 8 5 2 7 3 2
Player 9 5 1 8 4 1
Player 10 9 2 7 7 2
Player 11 7 2 7 5 2
Player 12 4 1 8 3 1
Player 13 6 0 9 6 0
Player 14 2 2 7 0 2
Player 15 7 4 5 3 4
Player 16 7 4 5 3 4
Player 17 5 5 4 0 5
Player 18 7 2 7 5 2
Player 19 5 1 8 4 1
Player 20 5 1 8 4 1
Player 21 8 5 4 3 5
Player 22 9 5 4 4 5
Player 23 5 3 6 2 3
Player 24 2 2 7 0 2
Player 25 7 2 7 5 2
Player 26 7 5 4 2 5
Player 27 6 2 7 4 2
Player 28 6 2 7 4 2
Player 29 7 3 6 4 3
Player 30 7 2 7 5 2
Player 31 6 1 8 5 1
Player 32 3 0 9 3 0
Player 33 6 4 5 2 4
Player 34 5 0 9 5 0
Player 35 4 3 6 1 3
Player 36 4 1 8 3 1
Player 37 3 1 8 2 1
Player 38 5 3 6 2 3
Player 39 6 1 8 5 1
Player 40 7 2 7 5 2
Player 41 4 3 6 1 3
Player 42 6 2 7 4 2
Player 43 3 1 8 2 1
Player 44 3 2 7 1 2
Player 45 8 2 7 6 2
Moyenne 5.555555556 2.444444444 6.555555556 3.111111111 2.444444444

An Experimental Analysis of Over-Confidence 410
Table 5. Frequency estimation of others in the free session and in the session fee.
Free session Session fee
Player Before iteration
(
θ
3)
After iteration
( θ
6)
Before iteration
(β3)
After iteration
(β6)
Player 1 6 6 5 5
Player 2 6 6 5 5
Player 3 6 7 5 5
Player 4 7 7 7 7
Player 5 7 7 7 8
Player 6 6 6 6 6
Player 7 5 5 3 3
Player 8 3 4 6 7
Player 9 6 6 6 6
Player 10 8 8 8 8
Player 11 5 5 4 4
Player 12 6 6 5 4
Player 13 7 7 8 6
Player 14 6 6 4 4
Player 15 4 5 3 3
Player 16 7 8 6 6
Player 17 5 5 7 7
Player 18 4 5 5 5
Player 19 6 6 7 7
Player 20 7 8 7 7
Player 21 5 5 5 5
Player 22 5 4 6 6
Player 23 7 7 6 5
Player 24 4 3 2 2
Player 25 6 7 6 7
Player 26 6 6 6 6
Player 27 6 6 3 5
Player 28 7 6 5 7
Player 29 8 6 4 4
Player 30 8 9 6 8
Player 31 6 6 6 6
Player 32 6 6 5 5
Player 33 5 7 5 7
Player 34 5 7 5 5
Player 35 5 5 4 6
Player 36 7 6 5 5
Player 37 4 4 4 4
Player 38 6 6 4 4
Player 39 5 5 7 7
Player 40 6 6 4 4
Player 41 8 8 7 7
Player 42 4 5 6 6
Player 43 6 4 3 3
Player 44 5 5 4 4
Player 45 6 8 4 6
Moyenne 5.844444444 6 5.244444444 5.488888889

An Experimental Analysis of Over-Confidence 411
Table 6. Effet “Above Average” mesuré dans les deux sessions avant iteration.
Player Free session
( θ
2 −
θ
3)
Session fee
(β2 − β3) Difference
Player 1 1 1 0
Player 2 1 −1 2
Player 3 −1 0 −1
Player 4 −1 −1 0
Player 5 1 −1 2
Player 6 1 0 1
Player 7 0 0 0
Player 8 −1 −2 1
Player 9 0 −2 2
Player 10 1 1 0
Player 11 2 1 1
Player 12 4 −1 5
Player 13 −3 −2 −1
Player 14 −2 −2 0
Player 15 3 4 −1
Player 16 1 0 1
Player 17 1 −2 3
Player 18 1 1 0
Player 19 −1 −2 1
Player 20 −2 −3 1
Player 21 1 3 −2
Player 22 2 3 −1
Player 23 0 0 0
Player 24 1 0 1
Player 25 −1 1 −2
Player 26 4 1 3
Player 27 −1 0 −1
Player 28 1 1 0
Player 29 1 2 −1
Player 30 −1 0 −1
Player 31 −2 −2 0
Player 32 −2 −2 0
Player 33 2 −1 3
Player 34 0 −1 1
Player 35 −1 0 −1
Player 36 −1 −1 0
Player 37 4 −1 5
Player 38 −3 1 −4
Player 39 2 −1 3
Player 40 1 2 −1
Player 41 −3 −3 0
Player 42 1 0 1
Player 43 0 0 0
Player 44 −1 −1 0
Player 45 1 2 −1
Moyenne 0.244444444 −0.177777778 0.422222222

An Experimental Analysis of Over-Confidence 412
Table 7. Effet “Above Average” measured in the two session after iteration.
Player Free session
( θ
5 −
θ
6)
Session fee
(β5 − β6) Difference
Player 1 2 1 1
Player 2 1 −1 2
Player 3 −1 0 −1
Player 4 0 −1 1
Player 5 1 0 1
Player 6 2 1 1
Player 7 0 0 0
Player 8 −2 −2 0
Player 9 0 −1 1
Player 10 1 1 0
Player 11 3 3 0
Player 12 4 0 4
Player 13 −3 0 −3
Player 14 −2 −2 0
Player 15 3 4 −1
Player 16 0 1 −1
Player 17 1 −2 3
Player 18 0 2 −2
Player 19 −1 −2 1
Player 20 −2 −2 0
Player 21 2 3 −1
Player 22 3 3 0
Player 23 0 0 0
Player 24 1 0 1
Player 25 −1 0 −1
Player 26 4 1 3
Player 27 2 1 1
Player 28 2 −1 3
Player 29 3 3 0
Player 30 −1 −1 0
Player 31 −2 0 −2
Player 32 −2 −2 0
Player 33 1 −1 2
Player 34 1 0 1
Player 35 −1 −2 1
Player 36 2 −1 3
Player 37 4 −1 5
Player 38 −3 1 −4
Player 39 1 −1 2
Player 40 1 3 −2
Player 41 1 −3 4
Player 42 0 0 0
Player 43 0 0 0
Player 44 −1 −1 0
Player 45 0 2 −2
Moyenne 0.533333333 0.066666667 0.466666667

An Experimental Analysis of Over-Confidence 413
Appendix 2
Table 1. Overconfidence measured by the method of question two answer choices for every player and for the sample in the
free session.
Player Number of correct answer
( α
1)
Average confidence
( α
4)
Overconfidence
( α
4 −
α
1)
Player 1 6 7.85 1.85
Player 2 8 7 −1
Player 3 7 8.5 1.5
Player 4 7 6.95 −0.05
Player 5 6 9.1 3.1
Player 6 5 8.74 3.74
Player 7 6 7.8 1.8
Player 8 4 7.3 3.3
Player 9 7 7.4 0.4
Player 10 5 8.35 3.35
Player 11 5 8.4 3.4
Player 12 6 6.75 0.75
Player 13 7 8.14 1.14
Player 14 3 6 3
Player 15 5 9 4
Player 16 7 7.9 0.9
Player 17 7 8.5 1.5
Player 18 5 8.2 3.2
Player 19 4 8.15 4.15
Player 20 5 7.4 2.4
Player 21 6 8 2
Player 22 5 7.5 2.5
Player 23 4 8.1 4.1
Player 24 4 7.55 3.55
Player 25 7 9.52 2.52
Player 26 7 8.7 1.7
Player 27 6 7.49 1.49
Player 28 6 9.1 3.1
Player 29 6 9.14 3.14
Player 30 6 8.3 2.3
Player 31 8 7.6 −0.4
Player 32 5 9 4
Player 33 6 8.75 2.75
Player 34 3 6.65 3.65
Player 35 9 8.1 −0.9
Player 36 5 8.9 3.9
Player 37 8 8.1 0.1
Player 38 6 8 2
Player 39 9 9.6 0.6
Player 40 7 8.7 1.7
Player 41 5 7.4 2.4
Player 42 8 7.15 −0.85
Player 43 6 7.5 1.5
Player 44 9 7.2 −1.8
Player 45 5 8.45 3.45
Moyenne 6.022222222 8.042888889 2.020666667

An Experimental Analysis of Over-Confidence 414
Table 2. Overconfidence measured by the method of question two answer choices for every player and for the sample in the
session fee.
Player Number of correct answer
( λ
1)
Average confidence
( λ
4)
Overconfidence
( λ
4 −
λ
1)
Player 1 6 8.6 2.6
Player 2 4 5.7 1.7
Player 3 8 8.3 0.3
Player 4 7 6.3 −0.7
Player 5 8 7.6 −0.4
Player 6 5 8.9 3.9
Player 7 8 6.1 −1.9
Player 8 3 6.7 3.7
Player 9 3 6.4 3.4
Player 10 6 9 3
Player 11 6 6.7 0.7
Player 12 6 8.34 2.34
Player 13 7 7.35 0.35
Player 14 4 6.1 2.1
Player 15 5 8.12 3.12
Player 16 6 6 0
Player 17 8 8 0
Player 18 6 7.75 1.75
Player 19 7 7.6 0.6
Player 20 7 7.75 0.75
Player 21 7 9.1 2.1
Player 22 8 8.4 0.4
Player 23 6 6.8 0.8
Player 24 4 6.3 2.3
Player 25 7 8.4 1.4
Player 26 8 8.7 0.7
Player 27 4 6.55 2.55
Player 28 8 6.9 −1.1
Player 29 7 8.24 1.24
Player 30 5 8.6 3.6
Player 31 5 7.7 2.7
Player 32 4 7.2 3.2
Player 33 4 8.25 4.25
Player 34 6 6.4 0.4
Player 35 2 7.59 5.59
Player 36 2 8.55 6.55
Player 37 5 7.1 2.1
Player 38 5 7.8 2.8
Player 39 6 9.1 3.1
Player 40 10 7.6 −2.4
Player 41 4 6.1 2.1
Player 42 5 6.1 1.1
Player 43 5 6.1 1.1
Player 44 5 7.05 2.05
Player 45 2 8.1 6.1
Moyenne 5.644444444 7.467555556 1.823111111

An Experimental Analysis of Over-Confidence 415
Table 3. Average number of correct answer, average confidence, frequency estimation and frequency estimation of others for
every player and for the sample in the free session.
Player
Number of correct
answer
( α
1)
Average
confidence
( α
4)
Frequency
estimation
( α
2)
Frequency estimation
of others
( α
3)
Effet above
average
Overconfidence
measured by frequency
estimation
Player 1 6 7.85 7 6 1 1
Player 2 8 7 7 6 1 −1
Player 3 7 8.5 7 7 0 0
Player 4 7 6.95 6 8 −2 −1
Player 5 6 9.1 10 9 1 4
Player 6 5 8.74 8 8 0 3
Player 7 6 7.8 5 4 1 −1
Player 8 4 7.3 7 8 −1 3
Player 9 7 7.4 6 5 1 −1
Player 10 5 8.35 7 8 −1 2
Player 11 5 8.4 8 7 1 3
Player 12 6 6.75 7 4 3 1
Player 13 7 8.14 8 9 −1 1
Player 14 3 6 6 6 0 3
Player 15 5 9 8 6 2 3
Player 16 7 7.9 7 6 1 0
Player 17 7 8.5 8 8 0 1
Player 18 5 8.2 8 6 2 3
Player 19 4 8.15 7 9 −2 3
Player 20 5 7.4 7 7 0 2
Player 21 6 8 8 7 1 2
Player 22 5 7.5 8 8 0 3
Player 23 4 8.1 7 7 0 3
Player 24 4 7.55 5 5 0 1
Player 25 7 9.52 8 8 0 1
Player 26 7 8.7 8 6 2 1
Player 27 6 7.49 5 5 0 −1
Player 28 6 9.1 9 8 1 3
Player 29 6 9.14 9 8 1 3
Player 30 6 8.3 8 9 −1 2
Player 31 8 7.6 7 8 −1 −1
Player 32 5 9 6 8 −2 1
Player 33 6 8.75 9 8 1 3
Player 34 3 6.65 7 8 −1 4
Player 35 9 8.1 7 8 −1 −2
Player 36 5 8.9 8 7 1 3
Player 37 8 8.1 6 5 1 −2
Player 38 6 8 7 6 1 1
Player 39 9 9.6 8 8 0 −1
Player 40 7 8.7 8 6 2 1
Player 41 5 7.4 7 8 −1 2
Player 42 8 7.15 7 7 0 −1
Player 43 6 7.5 6 6 0 0
Player 44 9 7.2 4 4 0 −5
Player 45 5 8.45 7 6 1 2
Moyenne 6.022222222 8.042888889 7.177777778 6.911111111 0.26666667 1.155555556

An Experimental Analysis of Over-Confidence 416
Continued
Free session Session fee
1 6.022222222 5.644444444
2 7.177777778 6.133333333
3 6.911111111 6.288888889
Table 4. Average number of correct answer, average confidence, frequency estimation and frequency estimation of others for
every player and for the sample in the session fee.
Player
Number of correct
answer
( λ
1)
Average
confidence
(
λ
4)
Frequency
estimation
(
λ
2)
Frequency estimation
of others
(
λ
3)
Effet above
average
Overconfidence
measured by frequency
estimation
Player 1 6 8.6 6 5 1 0
Player 2 4 5.7 4 5 −1 0
Player 3 8 8.3 5 6 −1 −3
Player 4 7 6.3 5 7 −2 −2
Player 5 8 7.6 7 8 −1 −1
Player 6 5 8.9 7 7 0 2
Player 7 8 6.1 3 3 0 −5
Player 8 3 6.7 7 8 −1 4
Player 9 3 6.4 5 5 0 2
Player 10 6 9 7 7 0 1
Player 11 6 6.7 6 6 0 0
Player 12 6 8.34 7 7 0 1
Player 13 7 7.35 8 9 −1 1
Player 14 4 6.1 3 5 −2 −1
Player 15 5 8.12 6 6 0 1
Player 16 6 6 6 5 1 0
Player 17 8 8 7 7 0 −1
Player 18 6 7.75 8 6 2 2
Player 19 7 7.6 6 8 −2 −1
Player 20 7 7.75 5 6 −1 −2
Player 21 7 9.1 7 7 0 0
Player 22 8 8.4 7 6 1 −1
Player 23 6 6.8 5 5 0 −1
Player 24 4 6.3 2 5 −3 −2

An Experimental Analysis of Over-Confidence 417
Continued
Player 25 7 8.4 9 4 5 2
Player 26 8 8.7 7 6 1 −1
Player 27 4 6.55 6 6 0 2
Player 28 8 6.9 6 7 −1 −2
Player 29 7 8.24 7 7 0 0
Player 30 5 8.6 8 7 1 3
Player 31 5 7.7 7 7 0 2
Player 32 4 7.2 5 7 −2 1
Player 33 4 8.25 7 8 −1 3
Player 34 6 6.4 6 6 0 0
Player 35 2 7.59 8 8 0 6
Player 36 2 8.55 6 6 0 4
Player 37 5 7.1 7 6 1 2
Player 38 5 7.8 7 7 0 2
Player 39 6 9.1 7 7 0 1
Player 40 10 7.6 6 6 0 −4
Player 41 4 6.1 4 7 −3 0
Player 42 5 6.1 5 6 −1 0
Player 43 5 6.1 8 7 1 3
Player 44 5 7.05 5 5 0 0
Player 45 2 8.1 6 4 2 4
Moyenne 5.644444444 7.46755556 6.1333333336.288888889 −0.15555556 0.488888889