 Optics and Photonics Journal, 2013, 3, 293-297 doi:10.4236/opj.2013.32B069 Published Online June 2013 (http://www.scirp.org/journal/opj) Intracavity Tunneling Intr oduced Transpar ency in Ultrastrong-coupling Regime Tao Wang, Rui Zhang, Chunxiao Zhou, Xuemei Su Physics College, Jilin University Changchun 130012, People’s Republic of China Email: suxm@jlu.edu.cn Received 2013 ABSTRACT Intracavity tunneling induced transparency in asymmetric double-quantum wells embedded in a microcavity in the ul- trastrong-coupling regime is investigated by the input-output theory developed by Ciuti and Carusotto. In this system a narrow spectra can be realized under anti-resonant terms of the external dissipation. Fano-interference asymmetric line profile is found in the absorption spectr a . Keywords: Ultrastrong Coupling; Spectra Narrowing; Anti-resonant Terms; Fano-interferences 1. Introduction Intersubband electronic transitions in doped semicon- ductor quantum wells play an important role in many re- markable devices, such as quantum cascade lasers, quan- tum-well infrared photodetectors and ultrafast optical modulators [1]. If semiconductor quantum wells in a mi- crocavity were explored by using the intersubband tran- sitions, it can achieve an ultrastrong light-matter cou- pling regime where vacuum Rabi frequency becomes comparable to the intersubband electronic transitions [2]. In the ultrastrong coupling regime, the usual rotating- wave approximation is not exact enough to explain the experimental data and the antiresonant terms should be considered. The contribution of antiresonant terms can create many new effects such as back-reaction, photon blocked and two-mode squeezed vacuum [3]. Quantum coherence is a fundamental problem in quantum mechanics and has been investigated for a long time in atom physics and optics physics. Strong cou pling is necessary for quantum coherence, but we still do not understand what will happen when the coupling strength reaches the ultrastrong-coupling region. The intersubband electronic transition in doped semiconductor quantum wells embedded in a microcavity provide a chance to discuss and test the problem. A full quantum descriptio n of the ultrastrong-coupling regime in doped semiconductor quantum wells microcavity has been developed by Ciuti and Carusotto [4] which can explicitly include the coupling to external dissipation baths including probe photons and injection electrons. The dissipation baths are not only responsible for damping rates but also provide a way of exciting and observing the cavity dynamics. The photonic mode is coupled to the external world mostly because of the finite reflectivity of the cavity mirrors, while the intersubband transition is coupled to other excitations in the semiconductor material-e.g., acoustic and optical phonons and free carriers in levels other than the ones involved in the considered transition. In particular, the coupling to this electronic bath allows one to electrically excite the intersubband transitions and induce electroluminescence. In the theory cavity field and electronic transition are treated as two oscillators . The vacuum Rabi splitting of a collection of oscillators in a single-mode cavity is proportional to the square root of their number. So the control of polariton coupling can be realized through the variatio n o f c arrier dens ity. In this paper we investigate quantum coherence in a multiple asymmetric double-well structure embedded in macrocavities. The cavity mode and the electronic excita- tions in each qu antum well interact strongly in the u ltras- trong-coupling regime and the in tersubb and transitio ns of each quantum well are coupled by quantum tunneling which can be tuned using bias voltage. Asymmetric semicon- ductor double quantum well structure has been studied for many interesting phenomena such as lasers without population inversion, tunneling induced transparency (TIT) [5] and opt i ca l swi tc h i ng [6]. TIT is a typical interesting quantum coherence pheno- mena similar as those of the idea of Electromagnetically induced transparency (EIT) [7]. Recent years intracavity EIT has attracted much attentions and has been studied experimentally in the multiatoms-cavity systems [8,9]. It has been shown that intracavity EIT results in an ultra- narrow spectral linewidth which may be used for Copyright © 2013 SciRes. OPJ  T. WANG ET AL. 294 frequency stabilization and high-resolution spectroscopic measurements. When the intracavity dark state is induced by a coupling laser in the cavity and -type atomic system , the cavity transmission spectrum exhibits three peaks: two side-bands associated with the multiatom vacuum Rabi splitting and a narrow central peak representing the cavity dark-state resonance of the two-photon Raman transition. Ulike atomic systems, semiconductor quantum well embedded in a microcavity is easily use to realize the ultrastrong coupling due to very large subband transition matrix elements [6]. In the asymmetric quantum wells microcavity, the transmission spectrum is similar with the multilevels atom-cavity system but is not symmetric and the narrow peak is not in the central position in the ultrastrong-coupling regime. Intuitively the antiresonant terms reduce the simultaneous creation and annihilation of the cavity photon and the electronic transition so the dark state must be destroyed. However the zero-absorp- tion at resonance is not changed by the aniresonant terms in the ideal condition and can be used to reduce the ab- sorption induced by the aniresonant terms to zero. The results mean that the intracavity TIT still hold even in the ultrastrong-coupling regime. 2. Model Figure 1 is the energy level diagram of the double qu an- tum wells separated by a thin tunneling barrier. The deep quantum well populates two-dimensional electron gas density (2DEG) in the first subband 1 at low tempera- tures with gas density. The energy sp litting of the energy subband 2 and 3 is caused by resonant tunneling. 12 , 13 are corresponding energies of the two in- tersubband transition energy from 1 to 2 and 3. If we denote with z the growth direction of the multiple quantum well structure, then the dipole moment of the transition is aligned along z, i.e., 12 12 ˆ , 13 13 ˆ ˆ ddzz ˆ dd . The in-plane wave vector is a conserved quantity. k 3 2 1 2DE G continuum Figure 1. Subband energy level diagram for double quan- tum wells separated by a thin tunneling barrier. The deep quantum well contains a two-dimensional electron gas in the lowest subband. The photons mode is chosen to be resonant to the fun- damental cavity photon mode, whose frequency disper- sion is given by 22 ,z cav k ckk , where is the dielectric constant of the cavity spacer and k s the quantized photon wav e vector along the growth direction, which depends on the boundary conditions imposed by the specific mirror structures. In the simplest case of me- llic mirrors, z cav π kL , with he cavity thickness. cav L The Hamiltonian of the present system is †† 12 , †† 13 12, †† †† 13, †† 12, † 13, cavkkk kk kk kkk kkkk kk kkk kkkkkkk kkk kk k kkk k Haabb ddiab ab iadadD aaaa iabab iadad † ††† kkkkkk Daa aa (1) The first three terms describe the energy of the cavity mode and the two intersunbband electronic transitions. The fouth term describe the resonant interactions be- tween the cavity photons and the electronic transitions and the fifth terms is the antiresonant interactions be- tween them. † k a is the creation operators of the cavity with in-plane wave vector and energy ,cav k k and † k b , † k d are respectively the creation operatrs of the electronic excitation mode of wave vector o k and en- ergy 12 , 13 . 12,k , 13,k are the vacuum Rabi frequency of the cavity photon and the two electronic excitation which quantifies the strength of the light-matter dipole coupling and it can become a significant fraction of the intersubband transition. The explicit expression is 12 221 12 3 12 3,0 2sin el QW eff k cav eNf mL (2) where QW is the number of quantum wells present in the cavity, N el el NS is the electron density per unit area in the deep quantum wells, el is the number of the electron in deep well and S is the quantization area. is the effective length of the cavity mode, N eff cav L is the cavity dielectric constant, and 1 is the intracavity probe photon propagation angle. are bilinear in the field operators and can be di- agonalized through a Bogoliubov transformation. Three intersubband polariton annihilation operators can be in- troduced as following † ,, , ,, †† ,, kjkkjkkjkkjk jk kjkk cwaxbydza pb qd k (3) Copyright © 2013 SciRes. OPJ  T. WANG ET AL. 295 where . The Hamiltonian of the system can be written as {1,2,3}j 3† ,,, 1 G kjkjk jk Ec c (4) where the constant term G is the vacuum energy and not considered here. The vectors E ,,,,,,, ,,,,, T jkjk jkjkjkjkjk vwxyzpq (5) Inserting expression (5) into (1) and notes the Bose commutation rule †, ,, , ,jj kjk kk cc (6) imposes the normalization condition **** ,,,,,, ,, ** , ,, ,, kjkjkjkjkjk jkjk jj jkjkjkj k wwxxyyzz pp qq (7) We found five excitations shou ld be taken into accoun t which are related with the cavity mode and the two elec- tronic transitions and treated as ensembles of quantum oscillators. In the double-sided cavity the cavity mode is coupled to two external electromagnetic field reservoirs through the front and back mirrors which are described by ph and ph . where , ph qk (, ph qk ) is the frequency of an extra-cavity photon with in-plane wave vector k and wave vector q in the orthogonal direction and † ,qk († ,qk ) is the corresponding creation operator, obeying the commutation rule † ,, , ,- qkq kkk qq ( † ,, , ,- qkq kkk qq ). The coupling between the cavity and extracavity radia- tion fields is quantified by the tunneling matrix element , h qk (, h qk ) through the cavity mirror. The damping and decoherence of the electronic transition is due to the in- terplay of different processes, such as the interaction with crystal phonons (optical and acoustical) and the scatter- ing with impurities and with free carriers in levels other than the ones involved in the considered electronic tran- sition. In the TIT media there is a shared continuum res- ervoir so the two electronic excitations are coupled by three baths which are 2 el , 3 el and el . Here, the bath operators () is only coupled to elec- tronic transition from 2, ,qk 3, , qk 1 to 2 (3) and ,qk is coupled to both. The operators satisfy the harmonic oscill- ator commutation rule and has frequency 2, , el qk (3, , el qk ). are the matrix elements quantifying the coupling 2, , el qk to the electronic polarization. † ,,, †† ,,, , † ,,, †† ,,,, 22, 1 2 1 2 ph ph qkqk qk k ph ph qkqk kqkqk k k ph ph qkqkqk k ph ph qkqk kqkqkk k el Hdq idqa a Hdq idqa a Hdq † ,2,,2,, †† 2, ,2, ,2, ,2, , † 33, ,3, ,3, , †† 3,, 3,,3,, 3,, 1 2 1 2 el qkqk qk k el el qkqk kqkqk k k el el qkqk qk k el el qkqk kqkqk k k idqb b Hdq idqdd † ,,, †† ,, ,,,, †† ,, ,,,, 1 2 el el qkqk qk k el el bqk qkkbqk qkk k el el dqkqk kdqkqk k k Hdq idqb b idqd d (8) 3. Results In the multiatoms-cavity system when the intracavity dark state is induced b y a couplin g laser in the cavity and multiple -type atomic system, the cavity transmission spectrum exhibits three peaks shown in (a): two side- bands associated with the multiatom vacuum Rabi split- ting and an ultranarrow central peak representing the cavity dark-state resonance of the two-photon Raman transition. In the quantum wells microcavity the ul- tranarrow polariton is a dark state which results from the coherent superposition of the cavity photons and the electronic transition. This is quantum interference phe- nomenon induced by multiple energy transfer pathways. In order to show intracavity TIT characteristics we use the input-output theory to solve equation (1) and obtain the spectra of reflectivity (a), transmission (b) and ab- sorption (c) spectra as functions of the incident photon energy E with (solid line) and without (dashed line) the antiresonant terms of the syste m and the external dissipa- tion bath. The calculations have been performed for a symmetric double-sided cav ity with doub le quantu m well structure in Ref. [6]. The parameters are 12 90 meV, 1312 17.6 meV, 25.6 meV, 3 meV . The parameters related with the cavity mode are chosen as 12,k 7.0 meV and 6 2 meV where is the loss of the cavity mode and and are decay rates of the 3 h sitions. Ottwo intersubband traner pare de- arameters Copyright © 2013 SciRes. OPJ 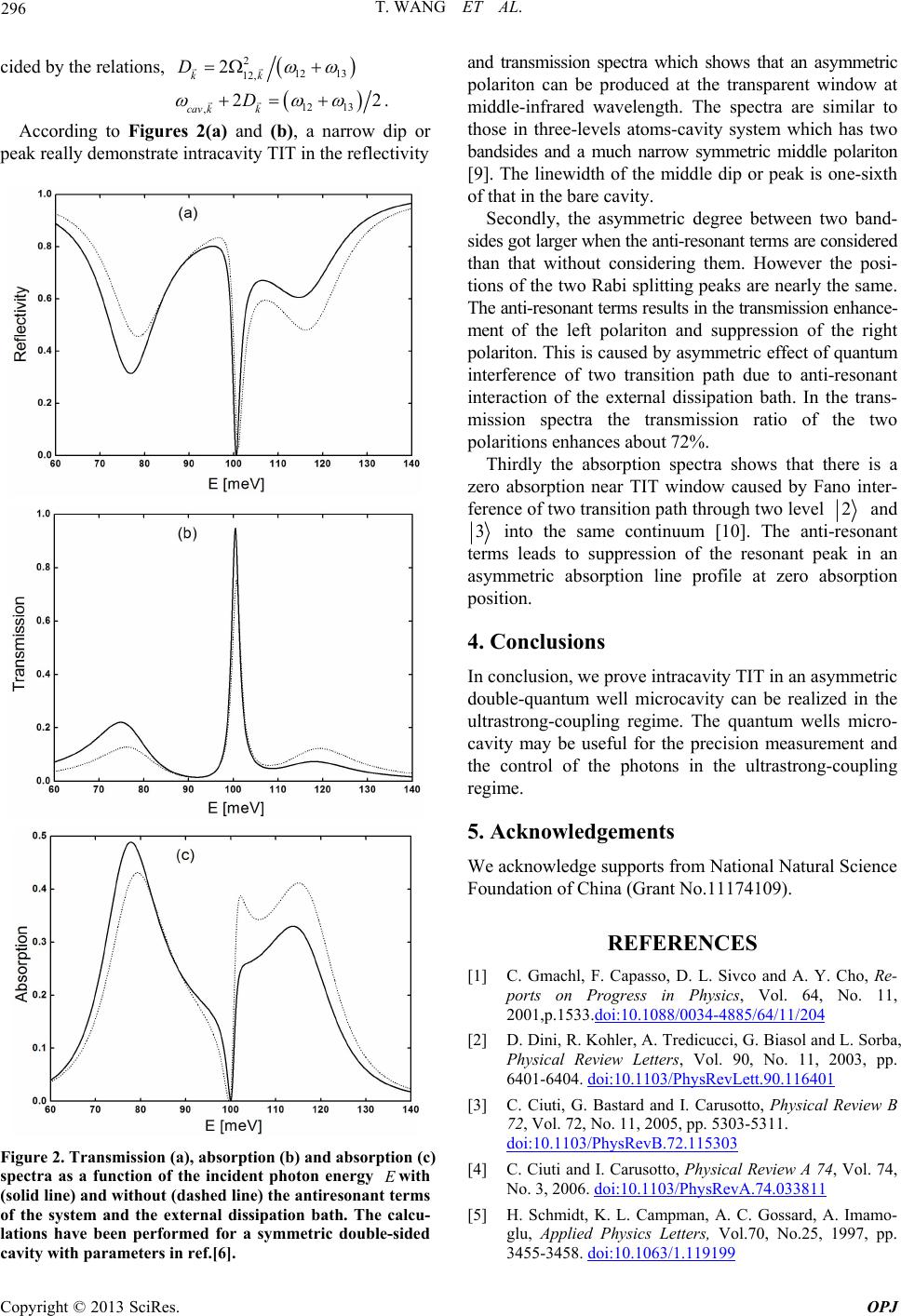 T. WANG ET AL. 296 cided by the relations, 212 13 12, 2 kk D 12 13 ,2 cav kk D . 2 Ac s 2(a) and (b), a narrow dip or pe cording to Figure ak really demonstrate intracavity TIT in the reflectivity Figure 2. Transmission (a), absorption (b) and absorption (c) cavity with parameters in ref.[6]. spectra as a function of the incident photon energy Ewith (solid line) and without (dashed line) the antiresonant terms of the system and the external dissipation bath. The calcu- lations have been performed for a symmetric double-sided and transmission spectra which shows that an asymmetric polariton can be produced at the transparent window at middle-infrared wavelength. The spectra are similar to those in three-levels atoms-cavity system which has two bandsides and a much narrow symmetric middle polariton [9]. The linewidth of the middle dip or peak is one-sixth of that in the bare cavity. Secondly, the asymmetric degree between two band- sides got larger when th e anti-reson ant terms ar e consider ed than that without considering them. However the posi- tions of the two Rabi splitting peaks are nearly the same. The anti-reson ant ter ms results in the trans mission enhance- ment of the left polariton and suppression of the right polariton. This is caused by asymmetric effect of quantum interference of two transition path due to anti-resonant interaction of the external dissipation bath. In the trans- mission spectra the transmission ratio of the two polaritions enhances about 72 %. Thirdly the absorption spectra shows that there is a zero absorption near TIT window caused by Fano inter- ference of two transition path through two level 2 and 3 into the same continuum [10]. The anti-resonant terms leads to suppression of the resonant peak in an asymmetric absorption line profile at zero absorption position. 4. Conclusions rove intracavity TIT in an asymmetric owledgements m National Natural Science [1] C. Gmachl, F.nd A. Y. Cho, Re- ports on Prol. 64, No. 11, In conclusion , we p double-quantum well microcavity can be realized in the ultrastrong-coupling regime. The quantum wells micro- cavity may be useful for the precision measurement and the control of the photons in the ultrastrong-coupling regime. 5. Ackn We acknowledge suppor ts fro Foundat i on of C h i na ( Grant N o.1117 4109). REFERENCES Capasso, D. L. Sivco a ogress in Physics, V 2001,p.1533.doi:10.1088/0034-4885/64/11/204 [2] D. Dini, R. Kohler, A. Tredicucci, G. Biasol and L. Sorba, Physical Review Letters, Vol. 90, No. 11, 2003, pp. 6401-6404. doi:10.1103/PhysRevLett.90.116401 [3] C. Ciuti, G. Bastard and I. Carusotto, Physical Review B 72, Vol. 72, No. 11, 2005, pp. 5303-5311. doi:10.1103/PhysRevB.72.115303 [4] C. Ciuti and I. Carusotto, Physical Review No. 3, 2006. A 74, Vol. 74, .74.033811doi:10.1103/PhysRevA 997, pp. [5] H. Schmidt, K. L. Campman, A. C. Gossard, A. Imamo- glu, Applied Physics Letters, Vol.70, No.25, 1 3455-3458. doi:10.1063/1.119199 Copyright © 2013 SciRes. OPJ  T. WANG ET AL. Copyright © 2013 SciRes. OPJ 297 [6] X.-M. Su and J.-Y. Gao, Physics Letters A, Vol. 264, 2000, pp.346-349. doi:10.1016/S0375-9601(99)00831-2 [7] M. Fleischhauer, A views of Modern Physics, Vol. 77, 200 . Imamoglu and J. P. Marangos, 5, pp. 633-673. Re- doi:10.1103/RevModPhys.77.633 [8] M. D. Lukin, M. Fleischhauer, M. O. Scully and V. L Velichansky, Optics Letters, Vol. 23. , No.4, 1998, pp. 4/OL.23.000295 295-297. doi:10.136 ang and Y. F. Zhu, Physical [9] Gessler Hernandez, J. P. Zh Review A 76, Vol. 76, No. 5, 2007, pp. 3814-3817. doi:10.1103/PhysRevA.76.053814 [10] A. E. Miroshnichenko, S. Flach and Y. S. Kivshar, Re- views of Modern Physics, Vol. 82, 2010, pp. 2257-2298. doi:10.1103/RevModPhys.82.2257
|