Optics and Photonics Journal, 2013, 3, 243-247
doi:10.4236/opj.2013.32B057 Published Online June 2013 (http://www.scirp.org/journal/opj)
A Theoretical Study of Light Absorption in Self
Assembled Quantum Dots
Tarek A. Ameen, Yasser M. El-Batawy, A. A. Abouelsaood
Department of Engineering Physics and Mathematics, Faculty of Engineering, Cairo University, Giza 12613, Egypt
Received 2013
ABSTRACT
Self assembled quantum dots have shown a great promise as a leading candidate for infrared detection at room tem-
perature. In this paper, a theoretical model of the absorption coefficient of quantum dot devices is presented. Both of
bound to bound absorption and bound to continuum absorption are taken into consideration in this model. This model is
based on the effective mass theory and the Non Equilibrium Greens Function (NEGF) formalism. NEGF formalism is
used to calculate the bound to continuum absorption coefficient. The results of the model have been compared with a
published experimental work and a good agreement is obtained. Based on the presented model, the bound to bound ab-
sorption coefficient component is compared to the bound to continuum absorption coefficient component. In addition,
the effects of the dot dimensions and electron filling on the bound to continuum absorption coefficient are also investi-
gated. In general, increasing the dot filling increases the absorption and decreasing the dots dimensions will increase the
absorption and move the absorption peak towards longer wavelengths.
Keywords: Absorption Coefficients; Non Equilibrium Greens Function; Self Assembled Quantum Dots
1. Introduction
Self assembled quantum dots have attracted the attention
due to the promise to improve the performance of many
applications, like quantum dot infrared photodetectors
(QDIP) [1], [2], and intermediate band solar cells (IBSC)
[3]. For the QDIPs, it is reported that due to 3-dimen-
sional confinement of the electrons in the quantum dots,
QDIPs should have lower dark current than the conven-
tional photodetectors at the same operating temperature,
thus QDIPs can operate at higher temperature with the
same signal to noise ratio [1]. Also QDIPs are very sen-
sitive to the normal incidence unlike the QWIP [1].
While for the IBSC it should have higher efficiency than
the conventional solar cell [4]. The proposed model is
based on the non equilibrium Green’s function formula-
tion (NEGF). NEGF formalism provides an approach to
study the transport in quantum systems in the presence of
open boundary conditions via the concept of self energy
[5]. The NEGF formalism was used before for modeling
the quantum dot-in-a-well (DWELL) structure [6-8].
This model calculated the responsivity not the absorption
coefficient of DWELL structure and in arbitrary units.
For calculating the bound to bound absorption coefficient
of a self assembled quantum dot, a model was presented
for the InAS/GaAs QDIP [9]. This model has led to an
important result: for QDIP the in-plane polarized absorp-
tion is dominant as long as the dot height is not very
small compared to its base radius. This result was con-
firmed experimentally [10]. There are many models that
calculate the bound to bound absorption [9,11], but very
little work has been done for the bound to continuum
absorption. The intraband absorption coefficient α is an
important parameter for the design of different quantum
dot applications.
In our model, the effective mass theory is used to build
a hermitian Hamiltonian matrix for an isolated self as-
sembled quantum dot. Diagonalizing this matrix gives
the bound states and energies. Then, this Hamiltonian
matrix with a nonhermitian self energy matrix are used to
get the NEGF. Using the NEGF, the continuum states of
the system have been calculated. Then, the bound to
bound and bound to continuum absorption coefficients
are both calculated. A comparison of our model and ex-
perimental data of [12] has been done, showing a good
agreement.
2. Theoretical Model
A schematic of self assembled quantum dot islands is
shown in Figure 1. The following assumptions are made:
● The self assembled quantum dot islands are as-
sumed to have ideal conical shape with uniform
size.
● Both the effects of the wetting layer and the cou-
pling between neighboring dots are neglected.

T. A. AMEEN ET AL.
244
These assumptions are justified from the scanning
probe microscopy done to the self assembled dots [13].
Modeling the absorption coefficient α for quantum dots
in previous models [9,11] considered only the bound to
bound absorption, where the ground state is the one filled
with electrons and the excited states are weakly bound
and unoccupied by electrons. These models do not in-
clude the bound to continuum absorption. For an efficient
and accurate model for α, both the bound to bound and
the bound to continuum absorption must be considered.
The absorption coefficient α can be expressed as
2
,
0
2ˆ
()( )
(),
dots if fifi
if
if
nNN deEE
nC
FF


 



 (1)
where

is the photon angular frequency, dots is the
number of dots per unit volume, the refractive index of
the material is , the speed of light in free space is C,
the free space permittivity is 0, where and
n
i
n

f
stand for initial and final states of possible transitions.
For the degeneracy of the initial states we multiply by
i, and for the degeneracy of the final states we multi-
ply by
N
f
N.
F is the probability of having an electron in an energy
state, ˆ
e is the polarization of the incident light, and
f
i
d is the first order dipole moment and is given by
.
fif i
V
dqr rdrddz  

 (2)
For the bound to continuum absorption, the initial
states i

are the bound states of the dots, and the final
states
f

are the continuum states in the conduction
band.
For the bound to bound absorption, the initial states
are the filled bound states of the dot, and the final states
are the empty bound states in the dot. The density of
states at
f
E is taken to be Gaussian function to add the
effect of inhomogeneous broadening resulting from the
variation in the dot dimensions, and the bound to bound
α can be expressed as
2
2
()
2
2
,
0
21
ˆ () 2*
(),
f
EE
dots if fi
if
if
nNN dee
nC
FF


 





(3)
this is equivalent to the expressions in [9], [11].
As shown in Figure 1, the potentialUof the dot in the
sample has cylindrical symmetry inside the
dot and outside the dot in the barrier region.
The effective mass Hamiltoniantakes the following
form in the cylindrical coordinates
(, )Urz 0
ˆ
H
(, )b Urz V
(,rr , )z

[7]:
22
2
11
ˆ ()()(,
2rz
r
rn
Figure 1. A schematic of the self assembled quantum dot
structure.
where r m is the effective mass in the lateral direction,
and
z
m is the effective mass in the growth direction,
nd e an is th

quantum number. The discretization of
Equatio4) gives the hermitian Hamiltonian matrix n (
H
.
Diaglizing this matrix gives the bound state wave
functions and energies. For the Continuum states, NEGF
is used to include the effects of open boundary conditio.
The retarded Green’s function
ona
ns
R
G of the Hamiltonian
operator ˆ
H
is given by [5]
1
() ,
RR
GEiIH






 (5)

add positive infinites asimal imaginary part to the
energy [14]. The self energy matrix
R
 is given by [5]
2
22
2
(,)(), 2
RR
lij b
avg
tgpp rt m


 


 (6)
where t is the coupling coefficient between an elem
the basic cell on the boundary and the adjacent el
in the lead as shown in Figure 2. is the average of
ent in
ement
)
H
Urz
rrm rzmz
rm




 





(4)
avg
the lateral effective mass of electrons between the two
materials. (, )
R
lij
m
g
pp is a matrix that contains zeros
except at the matrix elements be the points i
p,
tween
j
p at boundary b
rr

where it equals the retarded
Green’s funct just inside the lead. R
lead
G is
calculated for an isolated lead. A closed form solution for
retarded Green’ction in the semi-infinite lead is
obtained by solvinguation (5) assuming zerond-
ary conditions. The result is a series of harmonics and
Bessel functions,
ion R
lead
G
thes fun
Eq bou

T. A. AMEEN ET AL. 245
Figure 2. Discretization of the basic cell in the cylindrical
coordinates.
(1) (( ))
sin( )sin()
Renrlb
lead l
mHkr
Gkzkz

2( 1)
()
()() ()
()if ,
(( )
())
zl zl
bnrlb
nrlbnrlb nrlb
nrlb l
hH kr
JkrYkr Jkr
YkrE E




 
 

2
2(
sin( )sin()
if
()
()()(
,
)
()
(( )
())
Renr
leadzl zl
lnrlb
b
n rlbnrlbnrlb
nr llb
mKk
Gkzkz
Kkr h
KkrIkr Kkr
IEEkr








())
lb
r
(7)
where l is an integer,
22
2
2( )
,.,
lel
b rl
e
kmEE
l
kE Vk
m





The continuum wave function of the device is,
(8)
at dis-
n points that are adjacent to t
e lead. points, is the ex
fu
2
zl l
b
h
1
[], [][()].
RLi
GSStp  


 

[]S is the source vector which is zeros except
cretizatio
with th
nctio
i
p
At these
he interface
isting wave []S
n
L

in the lead close to the interface points i p
[5]. The wave function
L

is obtained analytically in
the isolated lead with zero bouny conditions. For the
infinite eof the lead at (r), another bounda
point L
r is added ad ()0
lL
rr
dar
nd ry
n

.
L

is ob-
tained by solving Equation (4) using the eigenfunction
expansion technique and applyese boundary condi-
tions.
ing th

2sin()( )( ),
r
Lzlnrnr
kkzJkrCYkr
 
 (1 )
bL
hr C
2
2
()2( )
, ,
()
nrbe b
z
lr
nrb b
JkrmEV
l
Ckk
Ykrh




zl
k 9)
For each mode, the number of continuum states in the
mode is determined from the density of states (D
Th
(
OS).
e DOS in the continuum spectrum have negligible
dependence on the quantum dot. Thus, the number of
states
f
N with energy
f
E in the mode l is calcu-
lated in the absence of the dot potential. The device
shape becomes a solid disk made from the barrier mate-
rial with radius
L
r and height b h.
f
N is obtained
using ordinary DOS calculations,
2
2
f
eL
f
dE
mr
Nm

 (10)
2
2()
efb b
l
EV h






Substituting Equation (10) into Equation (1), the inte-
gration
()1,
fi f
f
EE dE 



 as .
fi
EE


3. Results and Conclusion
The model can be used to calculate α for any self assem-
its band parameters,
s
bled quantum dot structure given
doping, dot dimensions d r, d h, and the polarization of
the incident light ˆ
e. The ability to absorb normally in-
cident radiation is an important property to the quantum
dot structure, unlike the quantum well structure that is
insensitive to the in-plane polarized light. Experimental
results have indicated that the normal incidence absorp-
tion is more dominant in the quantum dot, unless its
height is very small compared to the lateral dimension
[10]. So, we will make the calculations for the normally
incidence case in this paper.
Calculations have been done for InAs/GaAs quantum
dot with dimensions of 9.8
d
r

nm and 6.3
d
h

nm,
where the conduction band offset (CBO) 0.321
b
V eV
[15]. Figure 3 shows the calculated α for the system of
InAs/GaAs material with the number of dot unit
volume 2-31
1.25 m*10
dots
n at different values of filling.
As shown in this figure, the bound to continuum absorp-
tion increases when the excited states are not empty, as
the dipole moment from excited states is much greater
than the dipole moment from the ground state. Also the
bound to bound absorption has greater peak and smaller
band width than the bound to continuum absorption. The
greater the variations in the dot dimensions, the greater
the broadening in the bound to bound absorption. For the
bound to bound absorption to occur the dot dimensions
must be large enough to have at least one excited state.
To see the effect of changing the dot dimensions, calcu-
lations are made for different dot dimensions with 2
electrons per dot. Figure 4 shows the effect of changing
the dot radius d
r on the bound to continuum absorption
coefficient at 6.3
d
h
s per

nm. As shown in this figure,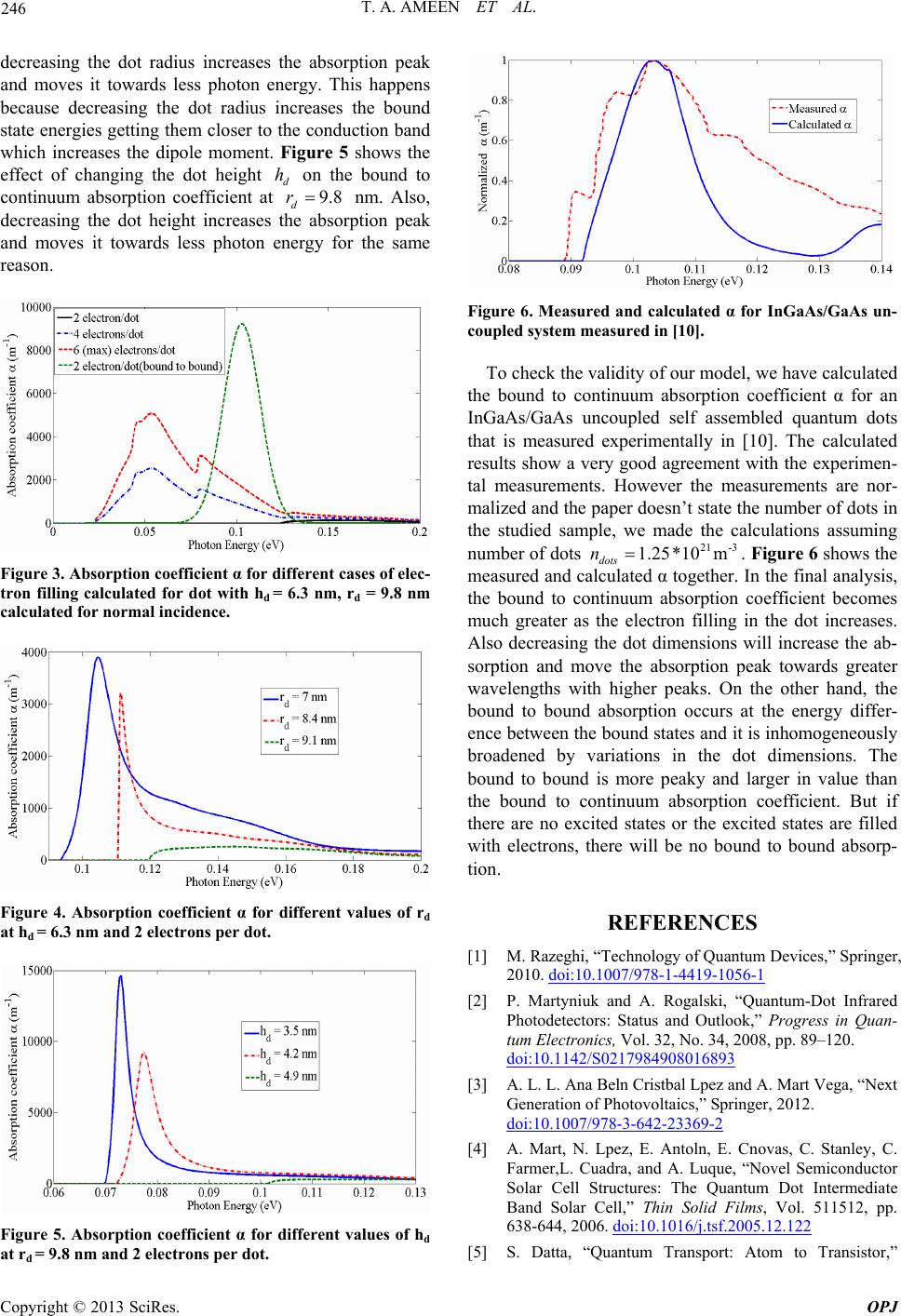

T. A. AMEEN ET AL.
246
decreasing the dot radius increases the absorption peak
and moves it tards less photon energy. This happens
because decrea dot radius increases the bound
state energies getting them closer to the conduction band
which increases the dipole moment. Figure 5 shows the
effect of changing the dot height d h on the bound to
continuum absorption coefficient at 9.8
d
r nm. Also,
decreasing the dot height increases the absorption peak
and moves it towards less photon energy for the same
reason.
ow
sing the
Figure 3. Absorption coefficient α fores of elec-
tron filling calculated for dot with hd = 9.8 nm
calculated for normal incidence.
diffe
d = 6.
rent cas
3 nm, r
Figure 4. Absorption coefficient α fornt values of rd
at hd = 6.3 nm and 2 electrons per dot.
differ e
Figure 5. Absorption coefficient α fornt values of hd
at rd = 9.8 nm and 2 electrons per dot.
differ e
Figure 6. Measured and calculated α for InGaAs/GaAs un-
coupled system measured in [10].
To check the validity of our model, we have calculated
the bound to continuum absorption coefficient α for an
InGaAs/GaAs uncoupled self assembled quantum dots
that is measured experimentally in [10]. The calculated
results show a very good agreement with the experimen-
tal measurements. However the measurements are nor-
malized and the paper doesn’t state the number of dots in
the studied sample, we made the calculations assuming
number of dotsFigure 6 shows the
measured and the final analysis
s will increase the ab-
o
hwill be no bou
2-31 1.25 m*10
dots
n.
calculated α together. In,
the bound to continuum absorption coefficient becomes
much greater as the electron filling in the dot increases.
lso decreasing the dot dimensionA
srption and move the absorption peak towards greater
wavelengths with higher peaks. On the other hand, the
bound to bound absorption occurs at the energy differ-
ence between the bound states and it is inhomogeneously
broadened by variations in the dot dimensions. The
bound to bound is more peaky and larger in value than
the bound to continuum absorption coefficient. But if
there are no excited states or the excited states are filled
with electrons, tere nd to bound absorp-
tion.
REFERENCES
[1] M. Razeghi, “Technology of Quantum Devices,” Springer,
2010. doi:10.1007/978-1-4419-1056-1
[2] P. Martyniuk and A. Rogalski, “Quantum-Dot Infrared
Photodetectors: Status and Outlook,” Progress in Quan-
tum Electronics, Vol. 32, No. 34, 2008, pp. 89–120.
doi:10.1142/S0217984908016893
[3] A. L. L. Ana Beln Cristbal Lpez and A. Mart Vega, “Next
Generation of Photovoltaics,” Springer, 2012.
doi:10.1007/978-3-642-23369-2
[4] A. Mart, N. Lpez, E. Antoln, E. Cnovas, C. Stanley, C.
Farmer,L. Cuadra, and A. Luque, “Novel Semiconductor
Solar Cell Structures: The Quantum Dot Intermediate
Band Solar Cell,” , Vol. 511512, pp.
638-644, 20062.122
Thin Solid Films
. doi:10.1016/j.tsf.2005.1
[5] S. Datta, “Quantum Transport: Atom to Transistor,”

T. A. AMEEN ET AL.
247
Cambridge University Press, 2005.
doi:10.1017/CBO9781139164313
[6] M. A. Naser, M. J. Deen and D. A. Thompson, “Spectral
Function of InAs/InGaAs Quantum Dots in A Well De-
tector Using Green’s Function,” Journal of Applied Ph
ics, Vol. 100, No. 9, 2006, p. 09310
ys-
2.
doi:10.1063/1.2372572
[7] M. A. Naser, M. J. Deen and D. A. Thompson
Function and Responsivity of Resonant Tunn
, “Spectra
eling and
l
Superlattice Quantum Dot Infrared Photodetectors Using
Green’s Function,” Journal of Applied Physics, Vol. 102,
No. 8, 2007, p. 083108. doi:10.1063/1.2799075
[8] M. A. Naser, M. J. Deen and D. A. Thompson, “Theo-
retical Modeling of Dark Current in Quantum Dot Infra-
red Photodetectors Using Nonequilibrium Green’s Func-
tions,” Journal of Applied Physics, Vol. 104, No. 1, 2008,
p. 014511. doi:10.1063/1.2952014
[9] B. Kochman, A. Stiff-Roberts, S. Chakrabarti, J. Phillips,
S. Krishna, J. Singh and P. Bhattacharya, “Absorption,
Carrier Lifetime, and Gain in InAs-GaAs Quantum-Dot
Infrared Photodetectors,” IEEE Journal of Quantum Elec-
tronics, Vol. 39, 2003, pp. 459-467.
doi:10.1109/JQE.2002.808169
[10] A. M. Adawi, E. A. Zibik, L. R. Wilson, A. Lemaˆıtre, J.
W. Cockburn, M. S. Skolnick, M. Hopkinson, G. Hill, S.
L. Liew and A. G. Cullis, “Strong In-Plane Polarized In-
Traband Absorption in Vertically Aligned Ingaas/gaas
Quantum Dots,” Applied Physics Letters, Vol. 82, No. 20,
2003, pp. 3415–3417. doi:10.1063/1.1575931
[11] K. Lantz and A. Stiff-Roberts, “Calcu
Absorption Coefficients in Org
lation of Intraband
anic/Inorganic Nanocom-
posites: Effects of Colloidal Quantum Dot Surface Ligand
and Dot Size,” IEEE Journal of Quantum Electronics,
Vol. 47, 2011, pp. 1420-1427.
doi:10.1109/JQE.2011.2169235
[12] B. Aslan, H. C. Liu, M. Korkusinski, S.-J. Cheng and P.
Hawrylak, “Response Spectra from Mid- to Far-Infrared,
Polarization Behaviors, and Effects of Electron Numbers
in Quantum-Dot Photodetectors,” Applied Physics Letters,
Vol. 82, No. 4, 2003, pp. 630-632.
doi:10.1063/1.1540728
[13] H. Lee, H. Park and T. Kim
Self-Assembled CdTe Quantum
, “Formation Mode of
Dots Directly Grown on
Gaas Substrates,” Journal of Crystal Growth, Vol. 291,
No. 2, 2006, pp. 442–447.
doi:10.1016/j.jcrysgro.2006.03.018
[14] S. Datta, “Electronic Transport in Mesoscopic Systems,”
Cambridge University Press, 1996.
doi:10.1063/1.2807624
[15] I. Vurgaftman, J. R. Meyer and L. R. Ram-Mohan, “Band
Parameters for iii–v Compound Semiconductors and
Their Alloys,” Journal of Applied Physics, Vol. 89, No.
11, 2001, pp. 5815–5875. doi:10.1063/1.1368156