Paper Menu >>
Journal Menu >>
 Optics and Photonics Journal, 2013, 3, 197-201 doi:10.4236/opj.2013.32B047 Published Online June 2013 (http://www.scirp.org/journal/opj) Design of Seven-core Photonic Crystal Fiber with Flat In-phase Mode for Yb: Fiber Laser Pumping Ruijuan Dong1, Peiguang Yan1*, Gelin Zhang1, Huiquan Li1, Shuangchen Ruan1, Huifeng Wei2, Jie Luo2 1Shenzhen key laboratory of laser engineering, Shenzhen University, College of Electronic Science and Technology,ShenZhen, China 2State Key Laboratory of Optical Fiber and Cable Manufacture Technology, Yangtze Optical Fiber and Cable Company Ltd. R&D center, Wuhan, China Email: *yanpg@szu.edu.cn Received 2013 ABSTRACT We numerically investigate the seven-core photonic crystal fiber (PCF) with the zero dispersion wavelength designed in the range of 1000 - 1080 nm, particularly suitable for the ytterbium-doped fiber laser pumping. Also, the PCFs are well designed for obtaining a flat in-phase mode by carefully adjusting the diameter of inner layer six holes, and the corre- sponding empirical values of fiber structure are summarized and listed. The variations of inner six holes to the ampli- tude of in-phase mode are further investigated, and our results show that a better tolerance can be achieved in the fiber structures with lower filling ratio configuration. Keywords: Photonic Crystal Fiber (PCF); In-phase Mode (IPM); Supercontinuum Generation (SCG) 1. Introduction The supercontinuum generation (SCG) in photonic crys- tal fiber (PCF) is an intensively research topic in optical and photonic science in the last decade [1-4]. Along with the research of SCG, the corresponding SC sources have already found their applications in optical coherence to- mography (OCT), pump-probe spectroscopy, metrology or non-linear microscopy. Recently, high power SC source becomes a new research trend and exhibits strong attraction because of the high spectral power density. The ytterbium fiber (Yb:fiber) laser system has the merits of high efficiency, reliability and compatibility with PCF, rendering them almost ideal candidates for compact sources of SC radiation [5-8]. H. Chen [7] reported a 35 W high power all fiber SC source based on PCF with picosecond laser, and X. Hu [8] reported a 50W strictly single mode all-fiber SC source spanning from 500 nm to over 1700 nm by using a 5-m-long commercially PCF. However, it is particularly challenging to further improve the SC power that limited by the low coupling efficiency from the large mode area Yb:fiber into the highly nonlinear PCF. The mismatch between their core diame- ters causes a high splicing loss, and the leaked power is enough to destroy the splicing point at high pump power. Simply increasing the core size of PCF would cause the zero dispersion wavelength (ZDW) shift to longer wave- length, hence unfavorable for spectral broadening ac- cording to the soliton mechanism. A feasible method is the PCF mode-field expanders [9], but the fabrication process is complicated and the large convert ratio of mode field is more challenging in itself. Several recent researches focused on the high pulse energy phase-locking multicore Yb-doped PCF laser [10-12], and SC genera- tion has reported with 5.4 W output power in a seven- ore PCF with femtosecond Yb:fiber laser system [13], but the fundamental supermode is not optimal in that fiber design. Among all supermodes, only the in-phase mode (IPM) where all cores have the same phase has the best Gaus- sian-like far field intensity distribution resulting in good beam quality [14-17]. A. Mafi [14-15] has presented a recipe for constructing custom-shaped modes based on perturbation theory of coupled modes, but the recipe is not intuitive. In this paper, our aim is to design the seven- ore PCFs with well flat IPM while keeping the ZDW in 1000 - 1080 nm for Yb:fiber laser pumping. The corre- sponding empirical values of fiber structure are summa- rized and listed. The variations of inner six holes to the amplitude of IPM are further investigated, and our results show that a better tolerance can be achieved in the fiber structures with lower filling ratio configuration. *Corresponding author. Copyright © 2013 SciRes. OPJ  R. J. DONG ET AL. 198 2. The Fiber Structure Figure 1 is the cross section of seven-core PCF with the enlarged microstructure region. The air holes are ar- ranged in a hexagonal pattern. Around the central core, the adjacent six air holes are missed to form a seven-core PCF, and each core is marked out with number. The lat- tice constant is set to Λ, the inner six air holes around central core have a diameter of d1 and air filling ratio of F1, while the other air holes have a diameter of d2 and filling ratio of F2. We utilize the full-vectorial finite ele- ment method to simulate the mode field distribution and fiber parameters of the seven-core PCF e.g. dispersion parameter D, nonlinear coefficient γ and effective mode area Aeff. Material dispersion of silica is included in our simulation [18]. 3. Results and Discussion In our calculation, the filling ratio F2 is set in the range of 0.45 - 0.55. These F2 values are slightly higher than the single mode condition [19], but can also achieve a high beam quality as has been proved in single core PCFs [20]. Also, a slightly higher F2 has the merits of mode con- finement. We check the lattice constant Λ from 2.8μm to 3.4μm, and adjust the filling ratio F1 to get the flat IPM. The corresponding values are organized in Table 1. It can be seen the F1 are 0.497, 0.577 for F2 = 0.45, 0.55 at Λ = 2.8 μm, while the corresponding value of F1 are 0.4928, 0.5728 at Λ = 3.4 μm. We notice that the F1 in- creases by ~0.008 when the F2 increases by 0.01 for a fixed Λ value in concerned range. Furthermore, the F1 decreases by ~0.0007 when the Λ increases by 0.1μm for a fixed F2. We then test the other Λ and F2 in the con- cerned range, and find that good flat IPM can be achieved based on the above mentioned empirical rela- tion. Figure 2 shows the 3-D flattened IPM distribution for Λ = 2.8 μm, 3.4 μm and F2 = 0.45, 0.55, respectively. It is evidently that all the lobes of the IPMs are of equal amplitude. Figure 1. The fiber structure. Table 1. The calculated F1 for flattened IPMs in the concerned range of Λ and F2. Λ F1 F2 2.8 2.9 3.0 3.1 3.2 3.3 3.4 F2=0.45 0.497 0.49630.49560.49490.49420.4935 0.4928 F2=0.46 0.505 0.50430.50360.50290.50220.5015 0.5008 F2=0.47 0.513 0.51230.51160.51090.51020.5095 0.5088 F2=0.48 0.521 0.52030.51960.51890.51820.5175 0.5168 F2=0.49 0.529 0.52830.52760.52690.52620.5255 0.5248 F2=0.50 0.537 0.53630.53560.53490.53420.5335 0.5328 F2=0.51 0.545 0.54430.54360.54290.54220.5415 0.5408 F2=0.52 0.553 0.55230.55160.55090.55020.5495 0.5488 F2=0.53 0.561 0.56030.55960.55890.55820.5575 0.5568 F2=0.54 0.569 0.56830.56760.56690.56620.5655 0.5648 F2=0.55 0.577 0.57630.57560.57490.57420.5735 0.5728 (a) (b) (c) (d) Figure 2. The flattened 3-D IPMs, here, (a) is for Λ = 2.8 μm and F2 = 0.45, (b) is for Λ = 2.8 μm and F2 = 0.55; (c) is for Λ=3.4 μm and F2 = 0.45, while (d) is for Λ = 3.4 μm and F2 = 0.55. Copyright © 2013 SciRes. OPJ 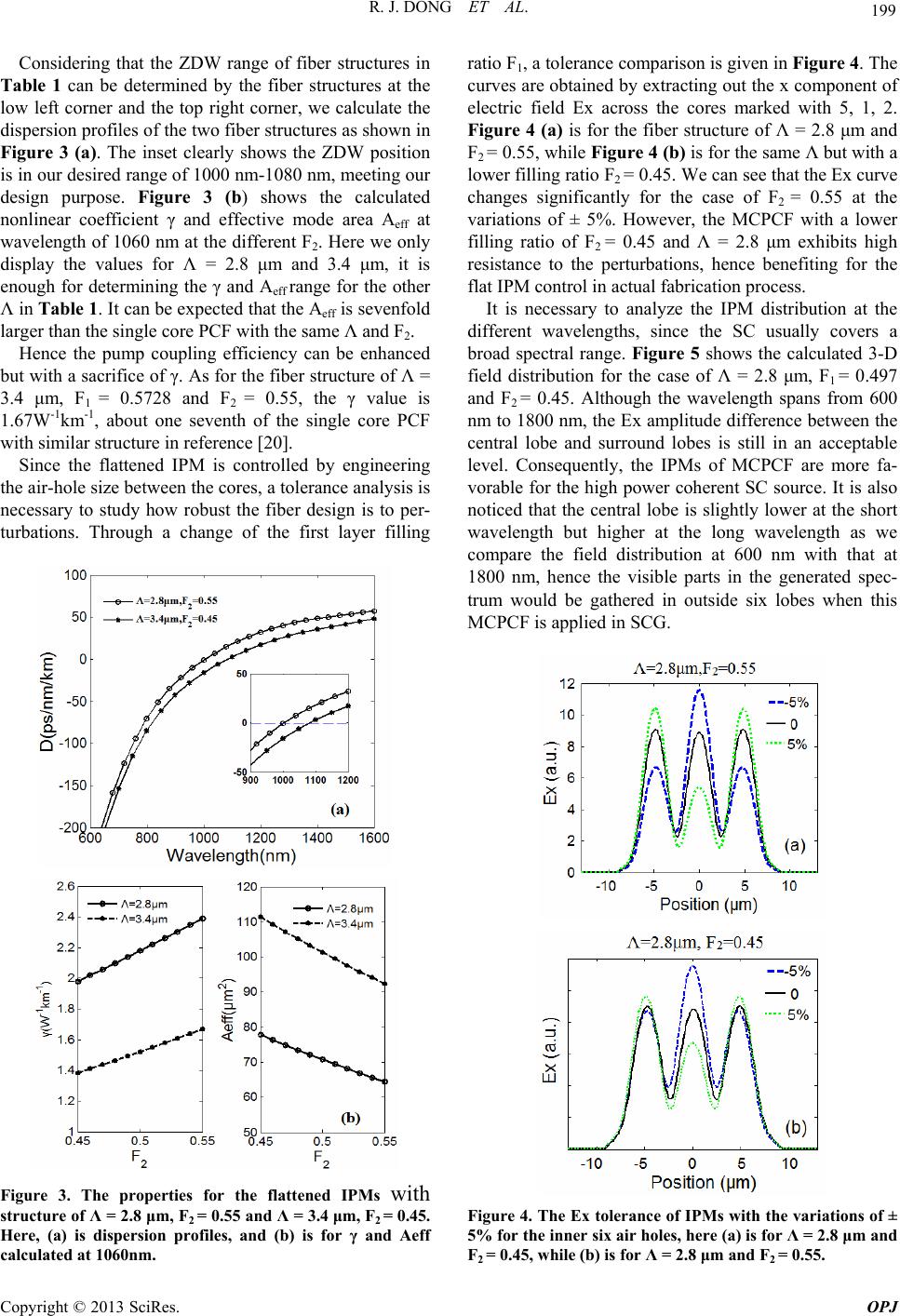 R. J. DONG ET AL. 199 Considering that the ZDW range of fiber structures in Table 1 can be determined by the fiber structures at the low left corner and the top right corner, we calculate the dispersion profiles of the two fiber structures as shown in Figure 3 (a). The inset clearly shows the ZDW position is in our desired range of 1000 nm-1080 nm, meeting our design purpose. Figure 3 (b) shows the calculated nonlinear coefficient γ and effective mode area Aeff at wavelength of 1060 nm at the different F2. Here we only display the values for Λ = 2.8 μm and 3.4 μm, it is enough for determining the γ and Aeff range for the other Λ in Table 1. It can be expected that the Aeff is sevenfold larger than the single core PCF with the same Λ and F2. Hence the pump coupling efficiency can be enhanced but with a sacrifice of γ. As for the fiber structure of Λ = 3.4 μm, F1 = 0.5728 and F2 = 0.55, the γ value is 1.67W-1km-1, about one seventh of the single core PCF with similar structure in reference [20]. Since the flattened IPM is controlled by engineering the air-hole size between the cores, a tolerance analysis is necessary to study how robust the fiber design is to per- turbations. Through a change of the first layer filling Figure 3. The properties for the flattened IPMs with structure of Λ = 2.8 μm, F2 = 0.55 and Λ = 3.4 μm, F2 = 0.45. Here, (a) is dispersion profiles, and (b) is for γ and Aeff calculated at 1060nm. ratio F1, a tolerance comparison is given in Figure 4. The curves are obtained by extracting out the x component of electric field Ex across the cores marked with 5, 1, 2. Figure 4 (a) is for the fiber structure of Λ = 2.8 μm and F2 = 0.55, while Figure 4 (b) is for the same Λ but with a lower filling ratio F2 = 0.45. We can see that the Ex curve changes significantly for the case of F2 = 0.55 at the variations of ± 5%. However, the MCPCF with a lower filling ratio of F2 = 0.45 and Λ = 2.8 μm exhibits high resistance to the perturbations, hence benefiting for the flat IPM control in actual fabrication process. It is necessary to analyze the IPM distribution at the different wavelengths, since the SC usually covers a broad spectral range. Figure 5 shows the calculated 3-D field distribution for the case of Λ = 2.8 μm, F1 = 0.497 and F2 = 0.45. Although the wavelength spans from 600 nm to 1800 nm, the Ex amplitude difference between the central lobe and surround lobes is still in an acceptable level. Consequently, the IPMs of MCPCF are more fa- vorable for the high power coherent SC source. It is also noticed that the central lobe is slightly lower at the short wavelength but higher at the long wavelength as we compare the field distribution at 600 nm with that at 1800 nm, hence the visible parts in the generated spec- trum would be gathered in outside six lobes when this MCPCF is applied in SCG. Figure 4. The Ex tolerance of IPMs with the variations of ± 5% for the inner six air holes, here (a) is for Λ = 2.8 μm and F2 = 0.45, while (b) is for Λ = 2.8 μm and F2 = 0.55. Copyright © 2013 SciRes. OPJ  R. J. DONG ET AL. 200 (a) (b) (c) (d) Figure 5. The 3-D IPMs at wavelength 600 nm, 1060 nm, 1400, 1800 nm from (a) to (b), respectively. The fiber has a structure of Λ = 2.8 μm, F1 = 0.497 and F2 = 0.45. 4. Conclusions In conclusion, we firstly numerically investigate the seven-core PCF with the ZDW designed in the range of 1000 - 1080 nm for the purpose of high power SC source pumped by the Yb: fiber laser. Also, the PCFs are well designed for obtaining a flat in-phase mode by carefully adjusting the diameter of inner layer six holes, and the corresponding empirical values of fiber structure are summarized and listed. The variations of inner six holes to the amplitude of in-phase mode are further investi- gated, and our results show that a better tolerance can be achieved in the fiber structures with lower filling ratio configuration. These results are helpful for design of seven-core PCF for high power SCG. 5. Acknowledgements Supported by NSFC (Nos.61007054, 61275144), Doctoral Program of Higher Education Research Fund (No.2010 408110002), the Improvement and Development Project of Shenzhen Key Lab (Nos.CXB201005240014A, ZDSY 0120612094924467), the Science and technology project of Shenzhen City (No. JC201105170693A), the Science and technology project of Shenzhen University (No.2012 1) and the Science and technology project of Shenzhen City (Nos.ZYC20100690103A, 2011PTZZ0125). REFERENCES [1] J. M. Dudley, G. Genty and S. Coen, “Supercontinuum Generation in Photonic Crystal Fiber,” Reviews of Modern Physics, Vol. 78, No. 4, 2006, pp. 1135-1184. doi:10.1103/RevModPhys.78.1135 [2] J. M. Dudley and J. Roy Taylor, “Ten Years of Nonlinear Optics in Photonic Crystal Fibre,” Nature Photonics 3, 2009, pp. 85-90. doi:10.1038/nphoton.2008.285 [3] L. Zheng, X. Zhang, X. M. Ren, H. F. Ma, L. Shi, Y. M. Wang and Y. Q. Huang, “ Dispersion Flattened Photonic Crystal Fiber with High Nonlinearity for Supercontinuum Generation at 1.55 \mum,” Chinese Optics Letters, Vol. 9, No.4, 2011, p. 040601. doi:10.3788/COL201109.040601 [4] L. Fang, J. L. Zhao and X. T. Gan, Chin. “Ultra Broad- Band-Flattened Dispersion Photonic Crystal Fiber for Supercontinuum Generation,” Optics Letters, Vol. 8, No. 11, 2010, pp.1028-1031. doi: 10.3788/COL20100811.1028 [5] S. P. Chen, H. W. Chen, J. Hou and Z. J. Liu, “100 W All Fiber Picosecond MOPA Laser,” Optics Express, Vol. 17, No. 26, 2009, pp. 24008-24012. doi.org/10.1364/OE.17.024008 [6] K. K. Chen, J. H. V. Price, S. Alam, J. R. Hayes, D. J. Lin, A. Malinowski and D. J. Richardson, “Polarisation Main- taining 100W Yb-Fiber MOPA Producing µJ Pulses Tunable in Duration from 1 to 21 ps,” Optics Express, Vol. 18, No.14, 2010, pp.14385-14394. doi.org/10.1364/OE.18.014385 [7] H. W. Chen, S. P. Chen, J. H. Wang, Z. L. Chen and J. Hou, “35 W High Power All Fiber Supercontinuum Gen- eration in PCF with Picosecond MOPALaser,” Optics Communications,Vol.284,No.23,2011, pp. 5484-5487. doi:10.1016/j.optcom.2011.08.024 [8] X. H. Hu, W. Zhang, Z. Yang, Y. S Wang, W. Zhao, X. H. Li, H. S. Wang, C. Li and D.Y. Shen, “ High Average Power, Strictly All-Fiber Supercontinuum Source with Good Beam Quality,” Optics Letters, Vol. 36, No. 14, 2011, pp. 2659-2661. doi.org/10.1364/OL.36.002659 [9] X. M. Xi, Z. L. Chen, G. L. Sun, and J. Hou, “Mode-Field Expansion in Photonic Crystal Fibers,” Applied Optics, Vol. 50, No. 25, 2011, pp. E50-E54. doi.org/10.1364/AO.50.000E50 [10] L. Michaille, D. M. Taylor, C. R. Bennett, T. J. Shepherd and B. G. Ward, “Characteristics of A Q-Switched Mul- ticore Photonic Crystal Fiber Laser with A Very Large Mode Field Area,” Optics Letters, Vol. 33, No. 1, 2008, pp.71-73. doi.org/10.1364/OL.33.000071 [11] X. H. Fang, M. L. Hu, C. Xie, Y. J. Song, L. Chai and C. Y. Wang, “High Pulse Energy Mode-Locked Multicore Photonic Crystal Fiber Laser,” Optics Letters, Vol. 36, No. 6, 2011, pp.1005-1007. doi.org/10.1364/OL.36.001005 [12] M. L. Hu, X. H. Fang and B. W. Liu, “Multicore Photonic- Crystal-Fiber Platform for High-Power All-Fiber Ultrashort-Pulse Sources,” Journal of Modern Optics, Vol.58, No. 21, 2011, pp.1966-1970. doi.10.1080/09500340.2011.597521 [13] X. H. Fang, M. L. Hu, L. L. Huang, L. Chai, N. L. Dai, J. Y. Li, A. Y. Tashchilina, A. M. Zheltikov and C. Y. Wang, “Multiwatt Octave-Spanning Supercontinuum Generation in Multicore Photonic-Crystal Fiber,” Optics Copyright © 2013 SciRes. OPJ  R. J. DONG ET AL. Copyright © 2013 SciRes. OPJ 201 Letters, Vol. 37, No.12, 2012, pp. 2292-2294. doi.org/10.1364/OL.37.002292 [14] A. Mafi and J. V. Moloney, “Phase Locking in A Passive Multicore Photonic Crystal Fiber,” Journal of the Optical Society of America B, Vol. 21, No. 5, 2004, pp. 897-902. [15] A. Mafi and J. V. Moloney, “Shaping Modes in Multicore Photonic Crystal Fibers,” Photonics Technology Letters, IEEE, 2005, pp. 348-350. [16] L. Li, A. Schülzgen, S. Chen, V. L. Temyanko, J. V. Moloney and N. Peyghambarian, “Phase Locking and In-Phase Supermode Selection in Monolithic Multicore Fiber Lasers,” Optics Letters, Vol.31, No. 17, 2006, pp. 2577-2579. doi.org/10.1364/OL.31.002577 [17] K. M. Gundu, M. Kolesik and J. V. Moloney, “Mode Shaping in Multicore Fibers,” Optics Letters, Vol. 32, No. 7, 2007, pp. 763-765.doi.org/10.1364/OL.32.000763 [18] G. P. Agrawal, “Nonlinear Fiber Optics,” 4th Edition, Academic Press, 2009. [19] T. A. Birks, J. C. Knight and P. S. J. Russell, “Endlessly Single-Mode Photonic Crystal Fiber,” Optics Letters, Vol. 22, No.13, 1997, pp. 961-963. doi.org/10.1364/OL.22.000961 [20] C. Y. Guo, S. C. Ruan, P.G. Yan, E. Pan and H. F. Wei, “Flat Supercontinuum Generation in Cascaded Fibers Pumped by A Continuous Wave Laser,” Optics Express, Vol. 18, No. 11, 2010, pp. 11046-11051. doi.org/10.1364/OE.18.011046 |

