 Optics and Photonics Journal, 2013, 3, 143-147 doi:10.4236/opj.2013.32B035 Published Online June 2013 (http://www.scirp.org/journal/opj) Study on Turbulence Effects for Beam Propagation in Turbulent Atmosphere Pingping Pan College of physics and communication electronics, Jiangxi normal university, Nanchang, 330022 Received 2013 ABSTRACT Based on the theory for the turbulence and the Rytov method, the propagation formulas of the scintillation index and the mean square angle-of-arrival fluctuation for the beam propagation in atmospheric turbulence have been derived respec- tively. The propagation properties of the two turbulence effects have been investigated, and the effects of the character- istic parameters of turbulence and the beam parameters have been discussed. The results show that the variation of the two turbulence effects depends on the structure constant of the refractive index fluctuations Cn2, the inner scale of the turbulence l0, the waist width of source beam w0 and the wave length λ. Moreover, there are two parameters including Cn2 and l0 which show more significant effects in atmosphere. Consequently, a new method for determining the char- acteristics parameters of the turbulence by using the measurement of the scintillation index and the angle-of-arrival fluctuation has been proposed. Keywords: Atmospheric Turbulence; Rytov Method; Scintillation Index, Mean Square Angle-of-Arrival Fluctuations; Constant of the Refractive Index Fluctuations 1. Introduction The study on the propagation of laser beams through turbulence is of great importance for many practical ap- plications, such as the remote sensing, atmospheric opti- cal communications, and track system [1-5]. There are a few affecting factors on the beam propagation in atmos- phere, such as atmosphere attenuation, atmospheric ab- sorption, scattering, and atmospheric turbulence effect etc. The atmospheric turbulence effects include the beam spreading, the angle-of-arrival fluctuations, the scintilla- tion index and the bit error rate, and they have more ob- vious influence on the performance of a communication system. [6-10]. The scintillations and the angle-of-arrival fluctuations are more significant effects of atmospheric turbulence on the beam propagation. The effect of the angle of arrival may increase the field-of-view requirements in a di- rect-detection optical receiver and degrade the perform- ance a heterodyne system [11-13]. It is well known that the atmospheric turbulence affects the received intensity, resulting in the intensity fluctuations at the receiver plane. Consequently, the optical scintillation take place in at- mospheric optic links [14-15]. In this paper, the propaga- tion properties of the scintillations and the angle-of-ar- rival fluctuations have been investigated, the effects of the turbulent parameters and the beam parameters have been discussed, and a method for estimating the charac- teristics parameters of the turbulence has been proposed. 2. Turbulence Effects for Beam Propagation in Atmosphere 2.1. Mean Square Angle-of-Arrival Fluctuations When light travels through the atmosphere, it experiences phase fluctuations due to turbulence. The mean square angle-of-arrival fluctuation is related to the phase struc- ture function through the expression below [14], 12 2 2 (0, , () s a DR kR pp )L (1) Here the mean square angle-of-arrival fluctuations are evaluated at a radial distance R, L is the path length, i.e., the length of the atmospheric link, and k = 2π/λ is the wave number, λ is wavelength. The second phase point lies at 22 11 221 (,), , (,)(0,0) xy xy ppR ppppp (2) The phase structure function described as 2 121 2 ( ,,)[( ,)(,)] s DLSLSLPPPP (3) where <> denotes the ensemble average over the medium statistics, 1 (, )[ (, )*(, )] 2 SLL L j ppp (4) the asterisk represents the complex conjugate. In Rytov method, ψ denotes the fluctuations of the complex am- Copyright © 2013 SciRes. OPJ  P. P. PAN ET AL. 144 plitude in turbulence [4], 1 2 3FS FS ' (,)'(,') (,') 2(,) exp(' ) ' V k LdrnzE EL ik pp' p rr rr zp' z (5) EFS (P, z) is the field in free space and '(',')(',','), '''' xyx y zppzddpdpd rPr (6) 11 (,')(',',') xy nznppzp' (7) expresses the random part of the refractive index, which can be written in the form of a Fourier–Stieltjes repre- sentation [5] for a statistically homogeneous and iso- tropic medium. The field distribution of Gaussian beam can be written as, '2 '2 '' 11 11 2 0 ( ,,0)exp() y Ex yw (8) where w0 is the waist width and (x1 ′, y1 ′) is the transversal coordinates at the z=0 plane. Then, by using the paraxial form of the extended Huygens-Fresnel principle, the field distribution of Gaussian beam through free space can be obtained, 2 22 0 111 1 2 0 22 22 01 1 22 0 (,, )exp[() 2 2 () ] 42 FS kw ik Exyzikz xy z kw iz kw xy zikzw (9) Assume that the turbulent atmosphere is statistically homogenous and isotropic, the source and the medium statistics are independent. The mean square angle-of- arrival fluctuation of Gaussian beam in turbulence can be derived, 221/3 0 0 11/62 22 2 0 1 1/62 2 0.1628( 14.45.5663() 1 Re{[] 1(1) []}) (1 ) m an m m CL dt Lt k kj L t 1/3 (10) Re means the real part, Cn 2 is the structure constant of the refractive index fluctuations of the turbulence. κm =5.92/l0, l0 is the inner scale of turbulence; κ0=1/L0, L0 is the outer scale of turbulence. And 2 0 1222 2 00 0 1, (/ ) kw jLt kwL wkwjL (11) 2.2. Scintillation Index The scintillation index in atmospheric turbulence at the L receiver plane is given by [8-10] 24(,,B 12 ) Iz pp (12) 121 2 (, ,)(,)(BzL L ,)L pppp (13) is the correlation function of the log-amplitude L fluctua- tions at the receiver plane z =L, (,) 0.5[(,LL) *(,)] ppp (14) and Bχ can be written as y * 0 [Re()Re()]( ) nx Bd dd z (15) Φn (κ) denotes the spatial power spectra of the refractive index fluctuations of the turbulent atmosphere, Φn(κ) =0 in free space, and κ= (κx 2+κy 2)1/2. 2 0 2 0 22 0 2 0 exp( ) (0, )2 ()(2 ) exp[] 2(2 ) FS kw ikikz Ez izkw zLt Ltikw kizkw (16) Letting x=0 and y=0 in EFS(x, y, z), the on-axis field distribution E FS (0, z) can be obtained. Tatarskii power spectra is represented as 2 2 11/3 2 ( )0.033exp() nn m C (17) After some tedious integral calculation, the scintilla- tion index of Gaussian beam in turbulence can be de- rived, 22 1 2222 0 22 2 00 5/6 0 2 0 2(1) 1 0.8816Re {[] (1 4) (1)(12)1 []} (1 2) In m m wL t CkLkLwk L tiLtwdt ik iLwk (18) 3. Numerical Examples and Analysis f-arrival fluc- wave propagation through at RMS-AOA is zero in the initial plane, and it increases 3.1. Angle-of-Arrival Fluctuations In this section, the variation of the angle-o tuations have been studied, and the effects of the turbu- lent parameters and the beam parameters have been dis- cussed. Eq. (10) is numerically evaluated and used in plotting the root mean square of the angle-of-arrival (RMS-AOA) fluctuations. Figure 1 gives the variation of the angle-of-arrival fluctuations, and the calculation pa- rameters are Cn 2 = 10-14 m-2/3, w0 = 30 mm, λ = 1.55 μm, L = 3 km, l0 = 10 mm, L0 = 25 m. The wave front tilt of optical mospheric turbulence gives rise to an angle-of-arrival fluctuation. Figure 1(a) shows the effects of constant of the refractive index fluctuations, C = Cn 2/10-15 m-2/3. The Copyright © 2013 SciRes. OPJ 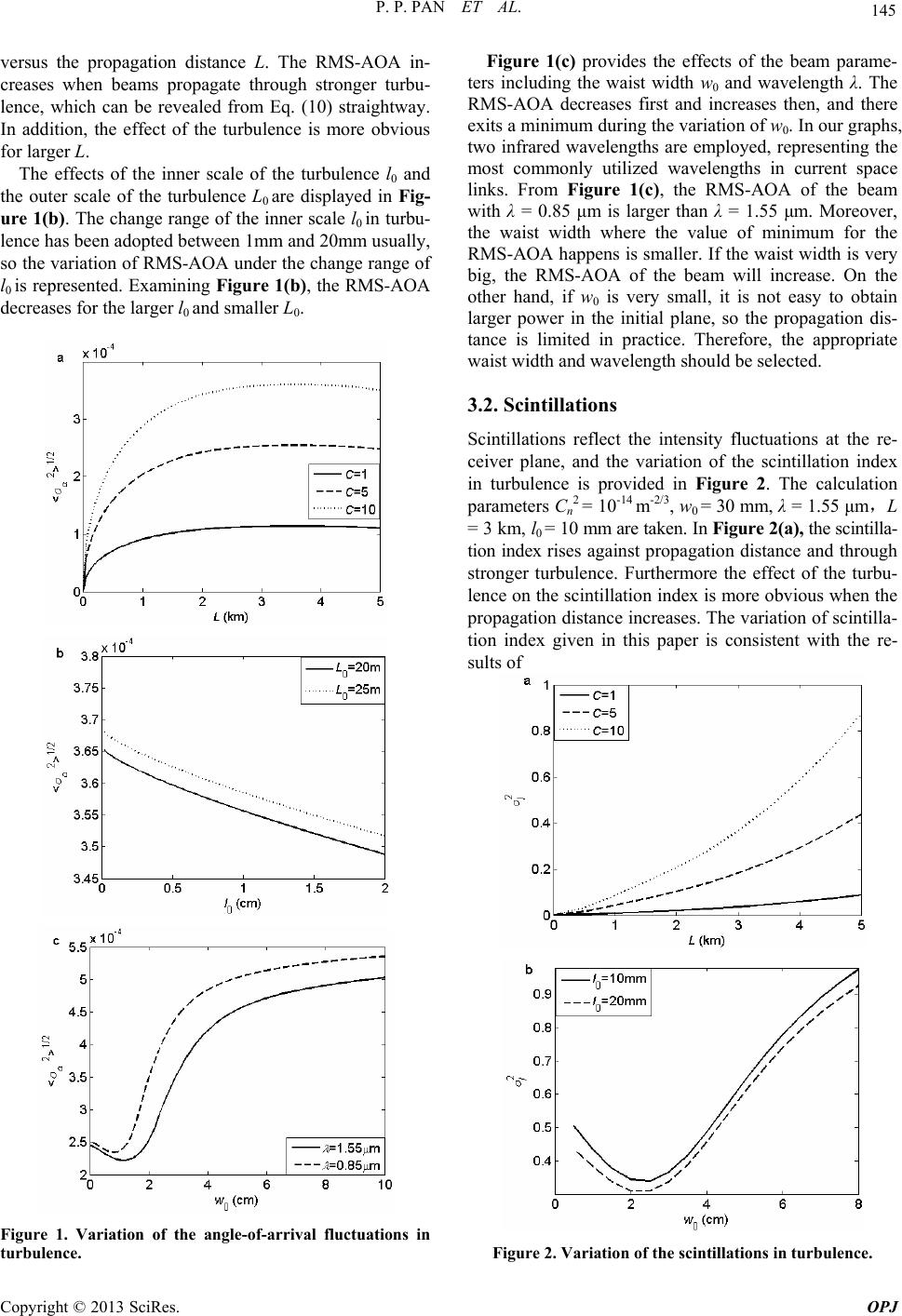 P. P. PAN ET AL. 145 versus the propagation distance L. The RMS-AOA in- creases when beams propagate through stronger turbu- lence, which can be revealed from Eq. (10) straightway. In addition, the effect of the turbulence is more obvious for larger L. The effects of the inner scale of the turbulence l0 and the outer scale of the turbulence Lare displayed in Fig- ur 0 e 1(b). The change range of the inner scale l0 in turbu- lence has been adopted between 1mm and 20mm usually, so the variation of RMS-AOA under the change range of l0 is represented. Examining Figure 1(b), the RMS-AOA decreases for the larger l0 and smaller L0. Figure 1. Variation of the angle-of-arrival fluctuations in turbulence. R the intensity fluctuations at the re- Figure 1(c) provides the effects of the beam parame- ters including the waist width w0 and wavelength λ. The MS-AOA decreases first and increases then, and there exits a minimum during the variation of w0. In our graphs, two infrared wavelengths are employed, representing the most commonly utilized wavelengths in current space links. From Figure 1(c), the RMS-AOA of the beam with λ = 0.85 μm is larger than λ = 1.55 μm. Moreover, the waist width where the value of minimum for the RMS-AOA happens is smaller. If the waist width is very big, the RMS-AOA of the beam will increase. On the other hand, if w0 is very small, it is not easy to obtain larger power in the initial plane, so the propagation dis- tance is limited in practice. Therefore, the appropriate waist width and wavelength should be selected. 3.2. Scintillations Scintillations reflect ceiver plane, and the variation of the scintillation index in turbulence is provided in Figure 2. The calculation parameters Cn 2 = 10-14 m-2/3, w0 = 30 mm, λ = 1.55 μm,L = 3 km, l0 = 10 mm are taken. In Figure 2(a), the scintilla- tion index rises against propagation distance and through stronger turbulence. Furthermore the effect of the turbu- lence on the scintillation index is more obvious when the propagation distance increases. The variation of scintilla- tion index given in this paper is consistent with the re- sults of Figure 2. Variation of the scintillations in turbulence. Copyright © 2013 SciRes. OPJ  P. P. PAN ET AL. 146 related literature [13]. As observed from Figure 2(b), there exits a minimum for the scintillation index during the variation of w0, and both the scintillation index and the corresponding minimum are larger for the smaller l0. In a word, the effect of the turbulence on beam propa- gating in turbulence is very obvious, so the beam quality may be affected, and especially the effect of the constant of the refractive index fluctuations is not neglected. Consequently, it is significative to estimate the structure constant of the turbulence. 3.3. Estimation of the Structure Constant of the Turbulence so stant of the turbulence can be estimated roughly. Secondly, if the scintillation index is scintnd turbulent parameters (see Figure The relations of the turbulence effects and turbulent pa- rameters are illustrated in Figure 3 and Figure 4 respec- tively, which implies a method for the estimation of the structure constant of the turbulence. We noted that in our lution, the change range of the inner scale l0 is adopted between 1 mm and 20 mm, whereas the range of the structure constant spans several magnitudes. Firstly, if the RMS-AOA is measured by experiments, by using the relation of the RMS-AOA and turbulent parameters (see Figure 3), the structure con measured by experiments, by using the relation of the illation index a 2 4), C n can be estimated once again. Applying the two change ranges, we can estimate the range of the structure constant of the turbulence more accurately. 4. Conclusions In this paper, the propagation formulas of the angle-of- arrival fluctuation and the scintillation index for the beam propagation in atmospheric turbulence have been obtained respectively, indicating that there are similarities in the derivation of the RMS-AOA and the scintillation Figure 3. Relation of the RMS-AOA and turbulent parame- ters. Figure 4. Relation of the scintillation index and turbulent parameters. index. The effects of the turbulent parameters and the beam parameters have been analyzed quantitatively. The angle-of-arrival fluctuation and the scintillation index rise with the increasing propagation distance and the structure constant of the turbulence, and the decreasing inner scale, moreover there exits a minimum for them during the variation of waist width. Finally, the range of the structure constant of the turbulence can be estimated from the RMS-AOA and the scintillation index measured by experiments. REFERENCES s of anomalous hollow beams in a turbulent at- mosphere,” Optics Communications, Vol. 281, No. 21, [1] Y. Cai, H. T. Eyyuboğlu and Y. Baykal, “Propagation propertie 2008, pp. 5291-5297 doi:10.1016/j.op tcom.2008.07.080 [2] Y. Dan, B. Zhang and P. pan, “Propagation of Partially Coherent Flat-Topped Beams Through A Turbulent At- mosphere,” Journal of Optical Society of America A, Vol. 25, No.9, 2008, pp. 2223-2231. doi:10.1364 /JOSAA.25.0022 23 [3] P. Pan, Y. Dan, B. Zhang, N. Qiao and Y. Lei, “Propaga- tion Properties of Flat-Topped Beams in A Turbulent Atmosphere,” Journal of Modern Optics, Vol. 56, No. 12, 2009,pp.1375-1382.doi:10.1080/09500340903 145049 [4] A. Ishimaru, “Fluctuations meters of Spherical Waves Propagtmosphere,” Radio Partially Coherent in the Para ating in A Turbulent A Science, Vol. 4, 1969, pp. 209-305. [5] A. Ishimaru, Wave Propagation and Scattering in Ran- dom Media, New York San Francisco, London, 1978, pp. 93-101. [6] G. Gbur and E. Wolf, “Spreading of Beams in Random Media,” Journal of the Optical Society of America A, Vol. 19, No.8, 2002, pp. 1592-1598. doi:10.1364 /JOSAA.19.0015 92 [7] X. Ji, X. Li, S. Chen, E. Zhang and B. Lü, “Spatial Cor- Copyright © 2013 SciRes. OPJ  P. P. PAN ET AL. Copyright © 2013 SciRes. OPJ 147 chell Model Beamsrelation Properties of Gaussian-S Propagating through Atmospheric Turbulence,” Journal of Modern Optics, Vol. 55, 2008, pp. 877-891. doi:10.1080 /095003407015 04314 [8] H.T. Eyyuboğlu, Y. Baykal and X. Ji, “Scintillations of Laguerre Gaussian beams,” Applied Physics B, Vol. 98, No. 4, 2009, pp. 857-863. doi:10.1007 /s00340-009- 3702-x [9] Y. Cai, Y. Chen, H. T. Eyyuboğlu and Y. Baykal, “Scin- tillation Index of Elliptical Gaussian Beam in Turbulent Atmosphere,” Optics Letters, Vol. 32, 2007, pp. 2405-2407. doi:10.1364/OL.32.00240 5 [10] Y. Chen, Y. Cai, H. T. Eyyuboğlu and Y. Baykal, “Scin- tillation Properties of Dark Hollow Beams in A Weak Turbulent Atmosphere,” Applied Physics B, Vol. 90, 2008, pp. 87-92. doi:10.1007/s003 40-007-2 825-1 [11] Y. Baykal and H. T. Eyyuboğlu, “Scintillation Index of Flat-Topped Gaussian Beams,” Applied Optics, Vol.45, No.16, 2006, pp. 3793-3797. doi:10.1364 /AO.45.003793 [12] P. Pan, B. Zhang, N. Qiao and Y. Dan, “Characteristics of Scintillations and Bit Error Rate of Partially Coherent Rectangular Array Beams in Turbulence,” Optics Com- munications, Vol.284, 2011, pp. 1019-1025. doi:10.1016/j.op tcom.2010.10.053 [13] Y. Chen, Y. Cai, H. T. Eyyuboğlu, Y. Baykal, “Scintilla- tion Properties of Dark Hollow lent Atmosphere,” Applied Phy Beams in A Weak Turbu- sics B, Vol. 90, 2008, pp. 87-92. doi:10.1007/s00340- 007-2825-1 [14] Y. Zhang and C. Tao, “Angle-of-arrival of Gaussian Schell Beam Propagation in Atmospheric Turbulence,” Acta Photonica Sinica, Vol. 34, 2005, pp. 424 [15] J. Ma, C. Gao and L. Tan, “Angle-of-a -427. rrival Fluctuations in Moderate to Strong Turbulence,” Chinese Physics, Vol. 16, 2007, pp. 1327-1333. doi:10.1088 /1009-1963/16 /5/027
|