Optics and Photonics Journal, 2013, 3, 131-135
doi:10.4236/opj.2013.32B032 Published Online June 2013 (http://www.scirp.org/journal/opj)
Photonic Communications and Quantum Information
Storage Capacities
William C. Lindsey
University of Southern California, Department of Electrical Engineering, Los Angeles, CA, USA
Received 2013
ABSTRACT
This paper presents photonic communications and data storage capacitates for classical and quantum communications
over a quantum chan nel. These capacities repr esent a generalization of Sh annon’s classical chan nel cap acity and co ding
theorem in two ways. First, it extends classical results for bit communicatio n transport to all frequencies in the electro-
magnetic spectrum. Second, it extends the results to quantum bit (qubit) transport as well as a hybrid of classical and
quantum communications. Nature’s limits on the rate at which classical and/or quantum information can be sent er-
ror-free over a quantum channel using classical and/or quantum error-correcting codes are presented as a function of the
thermal background light level and Einstein zero-point energy. Graphical results are given as well as numerical results
regarding communication rate limits using Planck’s natural frequency and time-interval units!
Keywords: Quantum Communications; Quantum Information Storage; Quantum Error-correcting Coding; Nature’s
Photonic Limits
1. Introduction
Photonic modulation can be used, respectively, to relia-
bly transport classical information bits as well as quan-
tum information qubits, see Figure 1. Using the “second-
quantization” of the electromagnetic field, quantum me-
chanical models for coherent photonic states and Shan-
non’s sphere-packing argument, the quantized analog of
Shannon’s classical channel capacity and coding theorem
is derived when classical or quantum information bits are
transported over a quantum channel. Using this result,
the unit information metric between a classical bit and a
quantum bit, the qubit, is established from which the
quantum channel capacity and spectral efficiency, quan-
tum information storage density and quantum informa-
tion storage capacity are developed. It is shown that the
quantized capacities (signal energy discrete) reduces to
Shannon’s classical results when the energy in the field is
assumed to be continuous and the channel center fre-
quency c

 Hz/°K is less than the partitioning frequency
p

 Hz/°K, i.e., Hz/°K, where k is
Boltzman’s and h is Planck’s consta nt.
0.4 /
cp kh
 

Nature’s limits on the rate at which classical and
quantum information can be sent error-free over a quan-
tum channel using classical and/or quantum error-cor-
recting codes are presented as functions of the thermal
background light level and Einstein’s zero-point energy
(ZPE). For system engineering design, num e rous graphical
results are plotted for both the quantized and quantum
channel capacities, spectral efficiencies and the informa-
tion storage capacities. Th e results demonstrate the feasi-
bility of Terabit per sec to Petabit per sec data rates and
Petabyte information storage capacities of 2/ln2 bits/
photon or one qubit per photon. In this regard, it is shown
that the qubit information unit equals two nats/qubit or
2/ln 2 bits/qubit, i.e., 1 qubit = 2 nats = 2/ln 2 bits! Fi-
nally, it is shown that error-free quantum communica-
tions can be asymptotically approached in a wideband
pristine environment using a minimum of 0.345 photons
per bit or one photon per qubit. In a low temperature en-
vironment, it is shown that classical or quantum informa-
tion, storage density and communications capacity do not
depend upon energy but upon the ratio of two integers,
viz., the ratio of the number of photons per message,
s
N
to the number of dimension per message, N, or equiva-
lently, the interialess photon‐time bandwidth product
p
BT . By setting a fundamental bandwidth limitation on
the quantum channel bandwid th B using Planck’s natural
frequency and time‐interval units at boundary p1BT

,
it is shown that Planck’s quantum communications ca-
pacity approximately equ als 1043 qubits/sec or (2 .9)1043
bits/sec.
It is further shown that there exists a quantum error
correcting code that achieves zero MEP if and only if the
code rate 0
s
Nqb
where 0
2ln2 ln2EZR/2Zh


is Einstein’s zero-point energy level. From th is we obtain

W. C. LINDSEY
132
the energy per bit to noise condition 0, or
equivalently, bit rate 0b for all
/ln
qb
EZ
2[,B
2
/lnSZR]


.
This compares with the classical results of Shannon
where 0qb and 0b for /EZln2SNR/ln2
p



.
Finally, information quanta are identified and related to
Planck‐Einstein energy quanta.
2. System Functional Architectures
In this section, functional architectures for quantized-
classical and quantum communication systems are pre-
sented along with system parameters and performance
metrics. System parameters include: time intervals,
channel bandwidth, bit and qubit signal energies and as-
sociated thermal background light levels. Performance
metrics include: channel capacities, information storage
densities and information storage capabilities. Relation-
ships connecting these performance metrics are estab-
lished together with those that relate quantum assets to
their classical counterparts.
2.1 Classical-Quantum Communication System
Models
For transmission, classical bits are encoded into coded-
digits using a classical [, error-correcting code;
see Figure 1. ]NK
More specifically, assume Mequiprobable messages
containing 2
log
K
M
T
bits per message, see Figure 1.
Each message is assumed to last for 2 sec
per message; b is the time per bit. Each K-tuple is en-
coded into N coded-digits using a classical [N, K] error-
correcting code of code rate
(log) b TMT
2
(log )
N
RKNMN
bits per dimension. Each coded digit lasts for
N
T sec
such that
N
TNT

seconds per message are used to
modulate the polarization of a coherent photon source of
rate 1
p
p
T

 photons per second and center frequency


,B
c


 Hz at code rate 2 log
s
N
s bits per
photon; here RMN
s
N is the average number of signal pho-
tons in each message. Thus every T sec an N-dimensional
photonic signal containing energy
s
qb
ENE h
s
Nc


.
qb c
Eh

is transmitted with energy per qubit

 Here h
is Planck’s constant.
Consider now the extended classical-quantum system
shown in Figure 1. Here a classical error-correcting code
[N, K] is concatenated with a quantum error-correcting
⌊⌊ ⌋⌋ code containing ,qb NK qb
K
qubits per message
with quantum code rate h
N
qb
QNK
,qb NK
dimensions per
qubit. The notation ⌊⌊ ⌋⌋ implies an N-dimen-
sional quantum code protecting qb
K
-qubits. Since the
systems in Figure 1 contain both classical and quantum
subsystems, we refer to this system as a hybrid system.
In this regard, we can write the time interval-coding
equation for Figure 1, viz.,
22
(log log)
bbNqbqb
TKTMT NTKTNT
sp

 (1)
where qb is the time per qubit and qb s T
K
NK N

.
Dividng both sides of (1) by 2

log
p
M
T/
q
, the bit rate
can be related to the quantum code rate
N
qb
RNK
dimensions per qubit, the quantum-modulator rate
h
M
qb s
QKN qubits per photon. The combined trans-
mit code rate s
qh
N
NNM
RRRQ is related to the channel
photon rate
p
 and bit rate , i.e.,
b
its / sec.
s
hh
bNpNNMp
RRQQ (2)
Figure 1. Quantum communication system functional architecture with concatenated classical and quantum error correcting
codes.

W. C. LINDSEY 133
Furthermore, (1) and (2) allow us to connect all rates
to the number of classical messages
22 222
s
NN
bN ss
p
N
RR
TNR
KT
M
 
 (3)
in the hybrid system transmit alphabet. The various
energy packages are related to the energy per message E
to the energy per photonic qubit qb c Eh

 through
2
(log)bNsqbs EMENENEN
c
h

 (4)
where Eb is the energy per bit and EN is the energy per
dimension. The corresponding power-energy relationship
is

2
log bNqbs ESTMSTNSTKSNSTp (5)
where S watts is the average power per message. From
(5), we note that the number of photons per bit (qubits/bit)
is given by the ratio 1
s
bbqbN
P
EE R

 which may be
used as a measure of the energy efficiency of a quantum
communication system to transport classical information.
The time interval-coding equations, code rates, en-
ergy-power relationships and the alphabet sizes will be
useful when the performance metrics of the quantized-
classical systems are compared to their quantum coun-
terparts of Figure 1. In particular, the quantized channel
capacity C bits per sec and
N
C bits per dimension
(spectral efficiency in (bits/sec)/Hz) and the quantized
information storage capacity
s
N
C bits per photon are
related to the average information stored in bandwidth W
Hz through
b
its /message.
s
NsN
ICTNC NC  (6)
The quantum counterparts are the quantum channel
capacity of Q qubits per second and
N
Q qubits per di-
mension and the quantum information storage density
s
N
Q qubits per sec are related to the average quantum
information Q
I
storage in bandwidth W Hz throug h
qubits / message.
s
QNsN
IQTNQNQ  (7)
With all parameters of our system models defined and
connecting relationships introduced, we are in a position
to present the quantized classical capacities, the quantum
capacities, their connections and nature’s limits regarding
error-free transmission. Before doing so, we present the
quantum channel model.
3. Quantum Communications Channel
Model
From elementary quantum mechanics, the vibrational
states of an atomic harmonic oscillator have energies that
depend on frequency

 
1/2En nh

 , 0,1,2n


and the probability of finding the “oscillator” in vibra-
tional state n is




00
expexp[1 exp()]Pn n

   (8)
where 0/kT h


 is the “natural frequency” of the
quantum channel, k is Boltzmann’s constant and is
the background temperature in degrees Kelvin. T
Thus using this notation one can show that [3]

 

000
00 00
2coth2
coth
EN
ZN ZN
0

 
 (9)
where 0
NkT

 eJoules characterizes the energy level of
thermal noise defined in classical systems and 0/2Zh


.
In limit as ν/ν0 approaches zero, 0
while
limit as ν/ν0 approaches infinity, Z
0 is Ein-
stein’s zero-point energy (ZPE) found in quantum me-
chanics where all thermal energy in the background light
vanishes. We will use this condition to partition the elec-
tromagnetic spectrum into a classical region and a quan-
tum region, see Figure 2.

0
E  

0;E
 
N
0
Z
In the classical region 00 //0
p.4

 
and
tanh
x
x

. In this region, and energy may
be treated as a continuous variable (photon energy levels
are small and infinitesimally close together) while for
00

00
EN  
//
p0.4



 we may consider this to be the
“quantum region.” For 0
/0.4

 
2WBp
, we will show that
all quantized capacity results reduce to Shannon’s clas-
sical results [1]. Figure 3 depicts the notion of our quan-
tum channel of bandwidth Hz, note 0
0.4



.
At room temperature, and
30 0TK2.5
p

 THz.
Further, as T approaches zero, 0


approaches zero
and all thermal energy vanishes. By letting h approach
Figure 2. Partitioning the classical and quantum r e gions.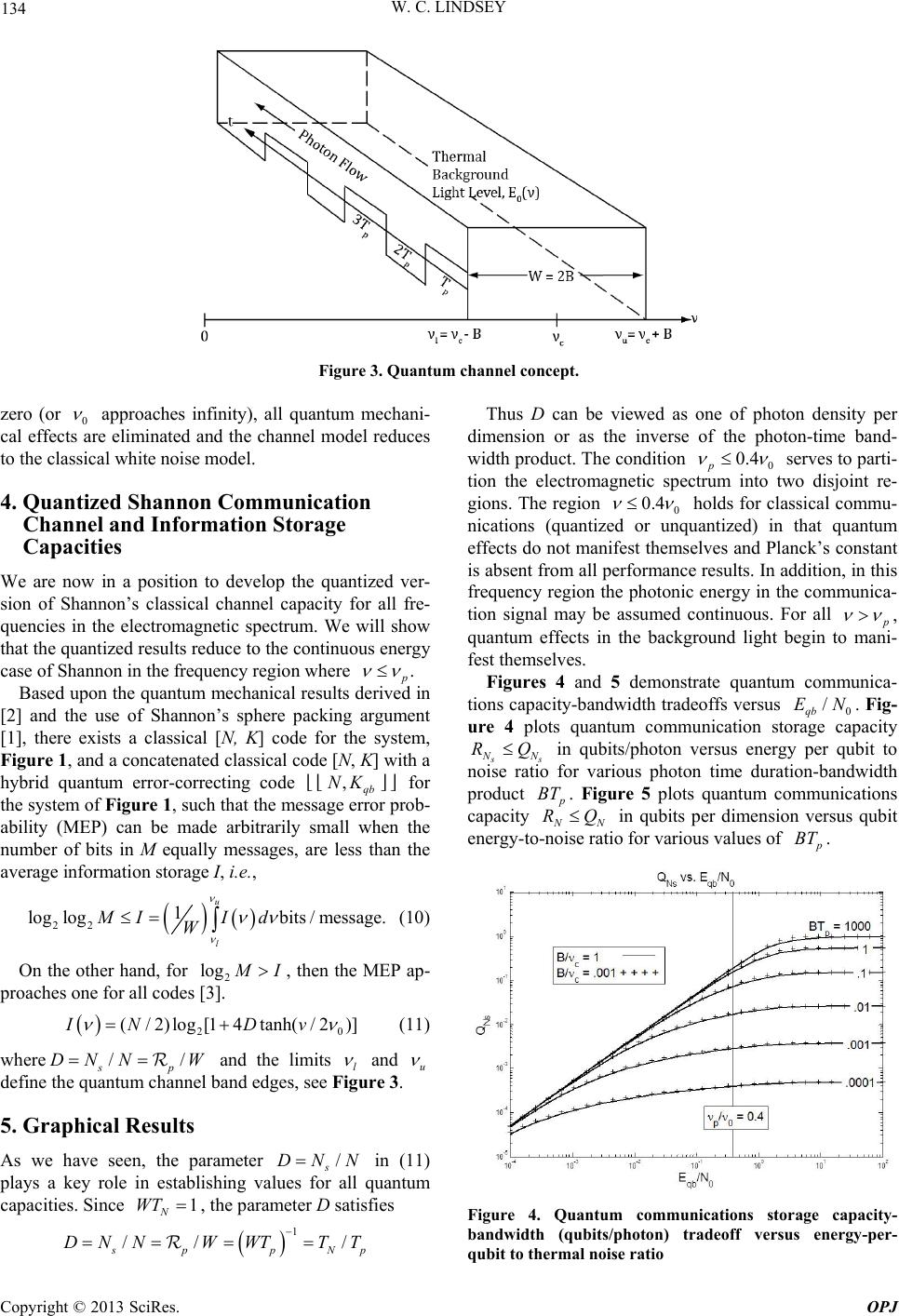

W. C. LINDSEY
134
Figure 3. Quantum channel concept.
zero (or 0

approaches infinity), all quantum mechani-
cal effects are eliminated and the channel model reduces
to the classical white noise model.
4. Quantized Shannon Communication
Channel and Information Storage
Capacities
We are now in a position to develop the quantized ver-
sion of Shannon’s classical channel capacity for all fre-
quencies in the electromagnetic spectrum. We will show
that the quantized results reduce to the continuous energy
case of Shannon in the frequency region where .
p



Based upon the quantum mechanical results derived in
[2] and the use of Shannon’s sphere packing argument
[1], there exists a classical [N, K] code for the system,
Figure 1, and a concatenated classical code [N, K] with a
hybrid quantum error-correcting code ⌊⌊ ⌋⌋ for
the system of Figure 1, such that the message error prob-
ability (MEP) can be made arbitrarily small when the
number of bits in M equally messages, are less than the
average information storage I, i.e.,
,qb NK


22 1
loglogbits / message.
u
l
MII d
W


   (10)
On the other hand, for 2 log
M
I, then the MEP ap-
proaches one for all codes [3].

20
(/ 2)log[14tanh(/)2]IN Dv

  (11)
where and the limits l /
sp
NDN W/

and u

define the quantum channel band edges, see Figure 3.
5. Graphical Results
As we have seen, the parameter in (11)
plays a key role in establishing values for all quantum
capacities. Since , the parameter D satisfies
/
s
DNN
1
N
WT 

1
//
Thus D can be viewed as one of photon density per
dimension or as the inverse of the photon-time band-
width product. The condition 0 0.4
p

  serves to parti-
tion the electromagnetic spectrum into two disjoint re-
gions. The region 0
0.4



holds for classical commu-
nications (quantized or unquantized) in that quantum
effects do not manifest themselves and Planck’s constant
is absent from all performance results. In additio n, in this
frequency region the photonic energy in the communica-
tion signal may be assumed continuous. For all
p

 ,
quantum effects in the background light begin to mani-
fest themselves.
Figures 4 and 5 demonstrate quantum communica-
tions capacity-bandwidth tradeo ffs versus 0. Fig-
ure 4 plots quantum communication storage capacity
/
qb
EN
s
s
N
N in qubits/photon versus energy per qubit to
noise ratio for various photon time duration-bandwidth
product
RQ
p
BT . Figure 5 plots quantum communications
capacity
N
N
RQ

in qubits per dimension versus qubit
energy-to-noise rati o for vario us values o f
p
BT .
Figure 4. Quantum communications storage capacity-
bandwidth (qubits/photon) tradeoff versus energy-per-
qubit to thermal noise ratio
/
s
ppN
WDNNWT TT

 p

W. C. LINDSEY 135
Figure 5. Quantum communications capacity in qubits
per dimension versus for various photon-time
bandwidth products, .
From these curves we see that performance is, for all
practical purposes, insensitivity to the normalized band-
width parameter /c B

. Figure 6 plots 1/
s
q
bN
PQ
which is the minimum number of photons per qubit to
achieve quantum communications capacity
s
N
Q. From
Figures 4 and 6 we observe the limit of one photon per
qubit is theoretically achievable.
6. Acknowledgements
The author wishes to thank Professor Debbie Van Al-
phen of Cal State Northridge for her diligent and untiring
Figure 6. Minimum number of photons per qubit required
to achieve capacity ; ( photons/qubit).
support in providing the graphical results and comments
on the manuscript.
REFERENCES
[1] C. E. Shannon, “A Mathematical Theory of Communica-
tions,” Bell System Technical Journal, Vol. 27, 1948, pp.
379-423.
[2] W. C. Lindsey, “On Quantum Information Storage Ca-
pacity,” submitted for publication IEEE Transations, 2012
[3] W. C. Lindsey, “Photonic Communications and Quantum
Information, Storage Capacities,” submitted for publica-
tion IEEE Transations, 2013.