Paper Menu >>
Journal Menu >>
 iBusiness, 2010, 2, 363-369 doi:10.4236/ib.2010.24047 Published Online December 2010 (http://www.scirp.org/journal/ib) Copyright © 2010 SciRes. iB The System Size Distribution for M/G/1 Queueing System under N-Policy with Startup/Closedown Mingwu Liu1, Yongkai Ma2, Bin Deng2 1School of Management, Chongqing Jiaotong University, Chongqing, China; 2School of Management and Economics, University of Electronic Science and Technology of China, Chengdu, China. E-mail: liumingwu2007@yahoo.cn Received June 4th, 2010; revised August 9th, 2010; accepted September 27th, 2010. ABSTRACT This paper develops a new method for calculating the system size distribution on two different M/G/1 queueing system under N-policy with general startup/closedown. Firstly, the stochastic decomposition property is used to derive the p.g.f. of the system size distribution. By the Leibniz formula of derivation, we investigate the additional system size distribu- tion, and then, we get the recursion expression of system sizes distribution. Finally, several examples are given for il- lustrating the application of the recursion expression and sensitivity analysis is also performed. Keywords: Queue-Length, N-Policy, Stochastic Decomposition, Recursion Expression, Leibniz Formula 1. Introduction This paper presents a new approach for study M/G/1 queueing system under N-policy with general startup/ closedown times. N-policy is an effective mechanism for cutting down operating cost, which has been widely ap- plied in modeling queue-like production system. As soon as each service is completed, the server will be turned off for a random closedown time and a random startup time is needed before commencing his service, which reflects more actual situation. Queueing system under N-policy first considered by Yadin and Naor [1] has been extensively expanded by many authors. Kella [2] discussed N-policy M/G/1 queueing system with server vacations. Bothakur et al. [3] extended Baker’s model [4] with exponential startup time to the general startup time. Lee et al. [5-7] investi- gated the batch arrival N-policy M/G/1 queueing system with a single vacation and multiple vacations. The p.g.f. (probability generating function) of the system size dis- tribution was derived, which shown the famous stochas- tic decomposition property proposed by Fuhrmann and Cooper [8] still came into existence. The concept of clo- sedown time was introduced by Takagi [9]. Ke [10] de- veloped an M/G/1 queueing system under varieties and extensions of NT queueing systems with breakdowns, startup and closedown. It is difficult to get the analytic steady-state system size distribution based on the p.g.f. under the general distribution of service time. Wang and his co-authors [11-14] derived the analytic steady-state solutions of the N-policy M/M/1 queueing system, the N-policy M/Hk/1, the N-policy M/Ek/1, and the M/H2/1 respectively. Re- cently, a maximum entropy approach was used to ana- lyze the steady-state characteristics of M/G/1 queueing system [15,16]. Based on this method, Wang et al. [17- 20] developed the approximate probability distribution of the system size for the N-policy M/G/1 queue with vari- ous cases. Also, the maximum entropy approach could be succeeded applied to batch arrival queueing system [21-23]. Tang [24] developed a total probability decom- position method for deriving the recursion expression of system size distribution in equilibrium. This method could be used to discuss batch arrival continuous-time or discrete-time queueing system [25,26], while the analysis procedure was very complicated. This paper will present a new method for analyzing the N-policy queueing system. Our method can derive the analytical expressions of system size distribution which is different from the maximum entropy approach. It is to be noted that the analytic system size distribution under N-policy is very difficult to be derived by Tang’s method. Our method is much simpler than Tang’s in analyzing the N-policy queueing system. The arrangement of this paper is as follows: First, we This work was supported by the New Century Excellent Talents in Min- istry of Education Support Program under Grant NCET-05-0811.  The System Size Distribution for M/G/1 Queueing System under N-Policy with Startup/Closedown Copyright © 2010 SciRes. iB 364 develop a new approach for derive the recursion expres- sion of system size distribution in equilibrium. Second, some special cases are presented in this paper for our new method. Finally numerical examples are given for illustrating the accurate calculation of the system size distribution and then sensitivity analysis is investigated. 2. Model Description and Assumption In this paper, we discuss two different kinds M/G/1 queueing system under N-policy with startup/closedown. The models are described in detailed as follows: Assumption of the model 1. 1) Customers arrive according to a Poisson process with rate . Arriving customers form a single waiting line and are served according to the order of his arrivals. The server can process only one customer at a time. 2) The service time provided by a single server is an independent and identically distributed random vari- able ()Gwith a general distribution function Gt . 3) Whenever the system becomes empty, the sever shuts down with a random closedown time()D. When the number of arrivals in the queue reaches a predeter- mined threshold N, the server immediately reactivates and performs a startup time with random length ()U before starting service. When the server completes his startup, he starts serving the waiting customers until the system becomes empty. 4) If a customer arrives during a closedown time, the server is immediately started without operating N-policy and without a startup time. Assumption of the model 2. The first three assump- tions are the same as those in model 1. However the fourth assumption now is that even if a customer arrives during a closedown time, the server still be shut down. As soon as the closedown is over, the server immediately reactivates. Before starting service, the server still need a random startup time()U, however without satisfying the conditions of N-policy. In many literatures [9,10], they suppose that the server will resume shutting down and offers service when a customer arrives during a close- down time. However, in some real-world, the server (machine) restarts until the closedown is finished for protecting the machine when a customer arrives during the closedown time. 3. Preliminary Formula for the System Size Distribution for M/G/1 Queueing System Before discussing our models, let us recall some results in the ordinary M/G/1 queueing system. For the sake of convenience, we define several items. We call a time interval when the server is working a busy period. A time interval when the server is unavailable (such as startup/ closedown, or idle) an idle period. Let 00,1, j pj be the probability distribution of the system size in equi- librium. From Tang [24], we have 0 01p (1) 0(1) ,1 jj pj (2) where 1 0 11 () 1! j t j t eGt dt gj 1 0 10 11,1. ! i jk t jk ki t edGtj gi 0 t g edGt , and if0j, 1 0 j k . We denote j by the probability distribution of system size during the busy period at stationary. Note that EG is traffic intensity and it should to be sup- posed to be less than unity, which ensures the system reaching at equilibrium. The p.g.f. of the queue size of the M/G/1 queueing system is given by 0 11 1 1 zg z zgzz (3) 4. Analysis of Model 1 4.1. The p.g.f. of the System Size In this section we derive the p.g.f. of the system size dis- tribution following the similar arguments as in [10]. Model 1 is as an extension of the M/G/1 queueing sys- tem given in Section 3. At the beginning of the busy pe- riod for Model 1 can be described by Case 1: no customers arrive when the server is shut- ting down, which occurs with probability D . For this system, the server will start up until the number of customer arrival reach N during the idle period. The p.g.f. of the system size at the beginning of the busy is given by N zU z , where Us is LST of U. Case 2: Some customers arrive when the server is shutting down, which occurs with probability 1D . In this case, the service is started immediately without a startup time and without N-policy. There is only one customer at the beginning of the busy period. By the stochastic decomposition results [8], the p.g.f of the number of customers found at the beginning of the busy period is give by 11 N zD zUzDz (4) where Uz denotes the p.g.f. of the number of customers arrive during the startup time. Following the result of Medhi and Templeton [27], the stochastic de-  The System Size Distribution for M/G/1 Queueing System under N-Policy with Startup/Closedown Copyright © 2010 SciRes. iB 365 composition of the p.g.f. of number of customers in the N policy M/G/1 queueing system with startup/closedown still comes into existence. We obtain 1 10 ' 1 1 11 z zz z (5) where ' 111DNEU D is the ex- pected number of customers that arrive during the idle period plus startup time. 4.2. Additional System Size Distribution From Equation (5) we see that the stationary system size is sum of two random variables, one of which is the sys- tem size of the general M/G/1queue. The other is the additional system size distribution due to N-policy and startup/closedown. The p.g.f. of additional system size distribution is give by 1 ' 1 1 11 a z zz (6) Following the definition of p.g.f., the probability of additional system size distribution can be written by can be written by 0 1| ! n a az n dz pn ndz , 0,1,n (7) Notice that, when iN, we have 1 0 1, 0 (()1)) |1(),1 0,2, ,1 i z i i dz Di dz iN , (8) And when iN, we have 1 0 1| i z i dz dz 0 0 | kN ik i z kik k dzd Uz i Dkdz dz 0 !! iN tt Die dUt iN (9) Substitute (8) and (9) into (7), we get the additional system size distribution 1 01 a pDNEU D (10) , 1 a D pn DNEUD 1, ,1nN (11) 0 0 1! , 1 m nN t m a t DedUt m pn DNEU D ,1,nNN (12) 4.3. System Size Distribution In this section we will derive the stationary-state system size distribution. The chain rule of differentiate is used as the main tool for calculation. Obviously, the probability of the number of customers in the queue which equals to zero is given by 01 0 1 |. 1 z pz DNEU D (13) When 1,,1nN , by the Leibniz formula, from (5), the probability of the number of customers is n in the queue is also given by 0 0 ' 0 1 11 | ! 1 knk n nz knk k dzd z k pn ndz dz 0 0 ' 0 1 1| ! 1 nk n k z nk k dz p nk dz (14) where, 0 k p is given by Formulas (1) and (2). We de- note ()z by 1() 1 1 z z , using the rule of chain of derivation again, conditioning on ,nk N thus we have 0 | nk z nk dz dz 1 0 1 0 1! 1|. 1 i nk nki z inki i dz nki i nk dz z !1 1!nk nkDnk !nk D (15) Substitute (15) into (14) and combing (2), we get the system size distribution 1 1 1 . 1 n nk k n DD pDNEU D 1, ,1nN (16) When nN, if ,nk N that is knN , we have  The System Size Distribution for M/G/1 Queueing System under N-Policy with Startup/Closedown Copyright © 2010 SciRes. iB 366 0 |!1, nk z nk dz nk DUk dz , (17) From the (15), (17) and combing (2), we obtain the system size distribution. * 11 110, 1, 1 nN n kk kknN n DU DUkD pDNEUD , nN (18) where 0 0 ,! m nk Nt m t Uke dUt m , 0 0 0, ! m nN t m t UedUt m . The recursion expressions of system size distribution are given by (13), (16) and (18), which can be used for cal- culating the probability of system size in equilibrium. Remark 4.1 If the startup time equals to zero, which implies 0EU and 0, 1,, 1UUk , model 1 can be reduced to the M/G/1 queueing system with delayed N-policy. In this case, these results coincide with those of Tang’s system [28]. The approach discussed in this paper is much easier than the total probability de- composition method for the system size distribution used in [28]. 5. Analysis of Model 2 5.1. The p.g.f. of the System Size In this section, we consider another N-policy for M/G/1 queueing system with startup/closedown. In this system, the only difference from the model 1 is that if some cus- tomers arrive during the closedown period, the server will still be shut down in order to protecting the server. After the closedown, the server immediately commences a startup with a random time. The server will offer ser- vice without operating N-policy until the startup is fin- ished. For this system, from the similar arguments as for mod- el 1, the p.g.f. for the number of customers found in the system at the beginning of the busy period is given by 2()( )() N zD zUz (1( ))()()DD zUz , (19) where Dz denotes the p.g.f. of the number of customers arrive during the closedown time. And the expected number of customers at the beginning of busy period is as follows ' 21DNEU 1DEDEU (20) From (19) and (20), we have the distribution for the system size at an arbitrary time 2 20 ' 2 1 11 z zz z . (21) 5.2. System Size Distribution In this section, we derive the system size distribution. Similarly, from (19), (20), we have the probability that the system is empty 0' 2 111 . 1 DDU p (22) As in Section 4, when 1,,1,nN the probability of the system size equals tonis given by 0 0 ' 0 1 1(()) | ()! (1) nk n k nz nk k pdz pnk dz ٛ , (23) where, we denote z by 21 1 z z . From (19), we get 2 0 1| i z i dz dz 0 11,0 , 1,,1,,1 i l DDU i l DiliN i (24) where 00 ,lil tt ile tdDte tdUt Thus, we get 0 |11 ! nk z nk dz DDU nk dz 10 !1, ! nk i il nk l Dil i i . (25) Take (25) into (23), we get ' 1 111 1 n pDDU  The System Size Distribution for M/G/1 Queueing System under N-Policy with Startup/Closedown Copyright © 2010 SciRes. iB 367 10 1 1, ! ni il l Dil i i 10 1 1, ! nk i il l Dil i i 1 11 n k k DDU , 1, ,1nN . (26) When nN, we analyze the following two cases. 1) If ,nk N that is knN , we have 0 |1 ,! nk z nk dz UkDn k dz 00 ! 1, ! nk i il nk l Dil i i , (27) 2) If ,nk N which implies knN , we get 0 00 ! |11, ! nk nk i z nk il dz nk l Dil i i dz (28) Substitute (27) and (28) into (23), we have 0 0 ' 0 1 1(()) | ()! (1) nk nN k nz nk k pdz pnk dz 0 0 ' 1 1 1| ! 1 nk n k z nk knN dz p nk dz ' 00 1 11 10, 1, ! 1 ni il l UD Dil i i 1 1, nN k k Uk D 00 1 1, ! nki il l Dil i i 100 1 11 , ! nnki k knNi l l Dil i i , nN (29) We get the recursion expressions of the system size distribution for the model 2, which are shown by (22), (26) and (29). Remark 5.1 Suppose that we let 01PU, which indicates 0EU and 1U . In this case, our model 1 can be simplified to M/G/1 queueing system with general closedown time. It is different from Tang’s system [28] because the server will be shut down, even if some customer arrives during the closedown time. We get the system size distribution as follows: 0 111 1 DD pDND ED (30) 1 1 n pDND ED 10 1 111 , ! ni il l DDD il i i 1 11 n k k DD 10 1 1, ! nk i il l Dil i i , 1, ,1nN (31) 1 1 n pDND ED 00 1 1, ! ni il l Dil i i 100 1 1, ! nN nki k kil l Dil i i 100 1 11 , ! nnki k knNi l l Dil i i ,nN (32) where 0 0, . ,,. l t il il etdDtil Remark 5.2 If we let the closedown time equal to zero, which implies 0ED and 1D . In this case, our model 1 and 2 can describe the N-policy M/G/1 queueing system with general startup time. The system size distribution can be simplified to the following ex- pressions: 0 1 pNEU (33) 1 11 n nk k pNEU , 1, ,1nN (34) 11 110,1 , nN n kk kknN n UUk pNEU nN. (35) 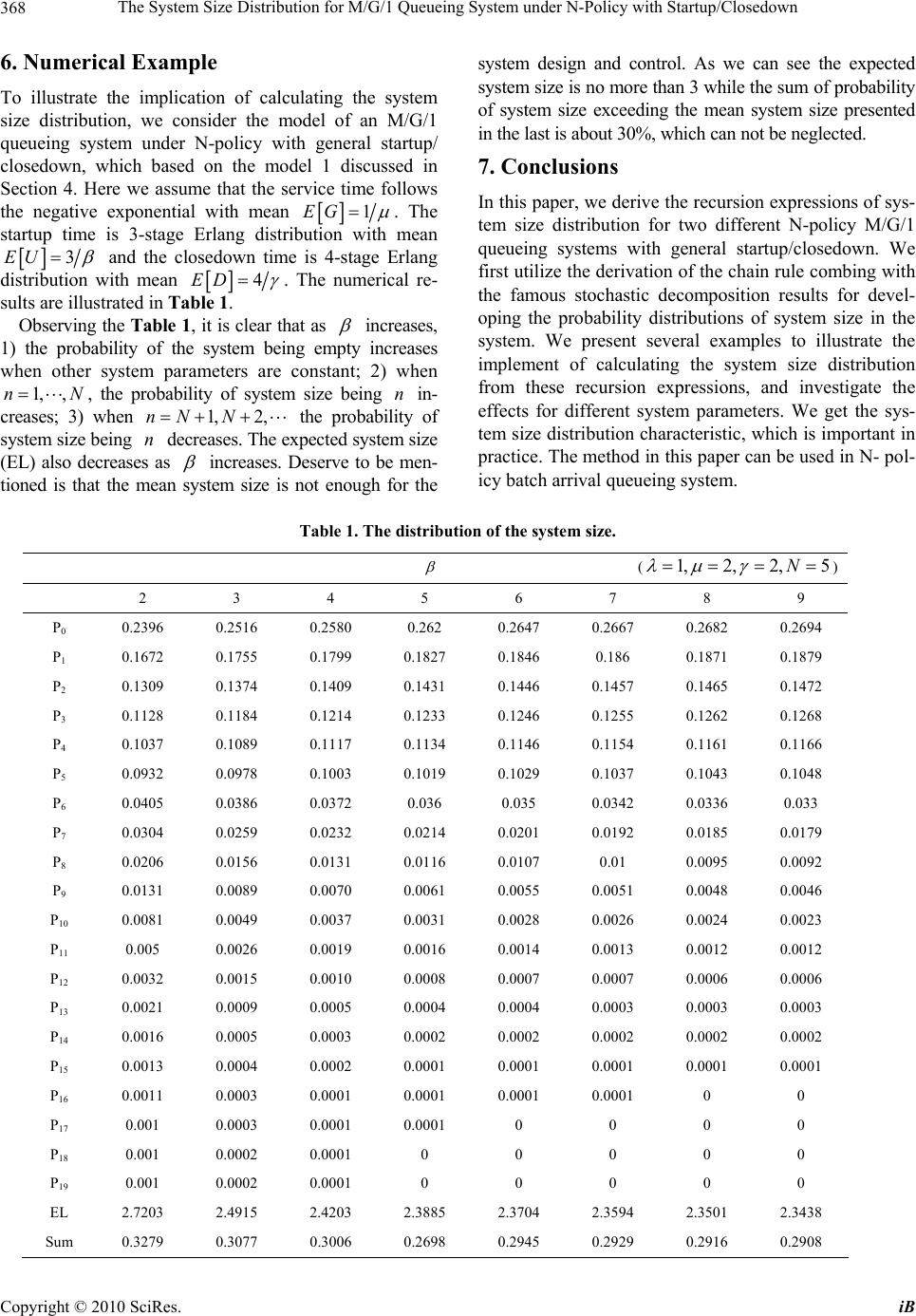 The System Size Distribution for M/G/1 Queueing System under N-Policy with Startup/Closedown Copyright © 2010 SciRes. iB 368 6. Numerical Example To illustrate the implication of calculating the system size distribution, we consider the model of an M/G/1 queueing system under N-policy with general startup/ closedown, which based on the model 1 discussed in Section 4. Here we assume that the service time follows the negative exponential with mean 1EG . The startup time is 3-stage Erlang distribution with mean 3EU and the closedown time is 4-stage Erlang distribution with mean 4ED . The numerical re- sults are illustrated in Table 1. Observing the Table 1, it is clear that as increases, 1) the probability of the system being empty increases when other system parameters are constant; 2) when 1, ,nN , the probability of system size being n in- creases; 3) when 1,2,nNN the probability of system size being n decreases. The expected system size (EL) also decreases as increases. Deserve to be men- tioned is that the mean system size is not enough for the system design and control. As we can see the expected system size is no more than 3 while the sum of probability of system size exceeding the mean system size presented in the last is about 30%, which can not be neglected. 7. Conclusions In this paper, we derive the recursion expressions of sys- tem size distribution for two different N-policy M/G/1 queueing systems with general startup/closedown. We first utilize the derivation of the chain rule combing with the famous stochastic decomposition results for devel- oping the probability distributions of system size in the system. We present several examples to illustrate the implement of calculating the system size distribution from these recursion expressions, and investigate the effects for different system parameters. We get the sys- tem size distribution characteristic, which is important in practice. The method in this paper can be used in N- pol- icy batch arrival queueing system. Table 1. The distribution of the system size. (1,2, 2,5N ) 2 3 4 5 6 7 8 9 P0 0.2396 0.2516 0.2580 0.262 0.2647 0.2667 0.2682 0.2694 P1 0.1672 0.1755 0.1799 0.1827 0.1846 0.186 0.1871 0.1879 P2 0.1309 0.1374 0.1409 0.1431 0.1446 0.1457 0.1465 0.1472 P3 0.1128 0.1184 0.1214 0.1233 0.1246 0.1255 0.1262 0.1268 P4 0.1037 0.1089 0.1117 0.1134 0.1146 0.1154 0.1161 0.1166 P5 0.0932 0.0978 0.1003 0.1019 0.1029 0.1037 0.1043 0.1048 P6 0.0405 0.0386 0.0372 0.036 0.035 0.0342 0.0336 0.033 P7 0.0304 0.0259 0.0232 0.0214 0.0201 0.0192 0.0185 0.0179 P8 0.0206 0.0156 0.0131 0.0116 0.0107 0.01 0.0095 0.0092 P9 0.0131 0.0089 0.0070 0.0061 0.0055 0.0051 0.0048 0.0046 P10 0.0081 0.0049 0.0037 0.0031 0.0028 0.0026 0.0024 0.0023 P11 0.005 0.0026 0.0019 0.0016 0.0014 0.0013 0.0012 0.0012 P12 0.0032 0.0015 0.0010 0.0008 0.0007 0.0007 0.0006 0.0006 P13 0.0021 0.0009 0.0005 0.0004 0.0004 0.0003 0.0003 0.0003 P14 0.0016 0.0005 0.0003 0.0002 0.0002 0.0002 0.0002 0.0002 P15 0.0013 0.0004 0.0002 0.0001 0.0001 0.0001 0.0001 0.0001 P16 0.0011 0.0003 0.0001 0.0001 0.0001 0.0001 0 0 P17 0.001 0.0003 0.0001 0.0001 0 0 0 0 P18 0.001 0.0002 0.0001 0 0 0 0 0 P19 0.001 0.0002 0.0001 0 0 0 0 0 EL 2.7203 2.4915 2.4203 2.3885 2.3704 2.3594 2.3501 2.3438 Sum 0.3279 0.3077 0.3006 0.2698 0.2945 0.2929 0.2916 0.2908  The System Size Distribution for M/G/1 Queueing System under N-Policy with Startup/Closedown Copyright © 2010 SciRes. iB 369 REFERENCES [1] M. Yadin and P. Naor, “Queueing Systems with a Re- movable Service Station,” Operational Research Quar- terly, Vol. 14, No. 4, 1963, pp. 393-405. [2] O. Kella, “The Threshold Policy in the M/G/1 Queue with Server Vacations,” Naval Research Logistics, Vol. 36, No. 2, 1989, pp. 111-123. [3] A. Borthakur, J. Medhi and R. Gohain, “Poisson Input Queueing Systems with Startup Time and under Control Operating Policy,” Computers and Operations Research, Vol. 14, No. 1, 1987, pp. 33-40. [4] K. R. Baker, “A Note on Operating Policies for the Queue M/M/1 with Exponential Startup,” INFOR, Vol. 11, No. 1, 1973, pp. 71-72. [5] H. W. Lee, S. S. Lee, J. O. Park and K. C. Chae, “Analy- sis of MX/G/1 Queue with N Policy and Multiple Vaca- tions,” Journal of Applied Probability, Vol. 31, No. 2, 1994, pp. 467-496. [6] S. S. Lee, H. W. Lee, S. H. Yoon and K. C. Chae, “Batch Arrival Queue with N Policy and Single Vacation,” Com- puters and Operations Research, Vol. 22, No. 1, 1995, pp. 173-189. [7] H. S. Lee and M. M. Srinivasan, “Control Policies for the MX/G/1 queueing System,” Management Science, Vol. 35, No. 6, 1989, pp. 708-721. [8] S. Fuhrmann and R. B. Cooper, “Stochastic Decomposi- tions in the M/G/1 Queue with Generalized Vacations,” Operations Research, Vol. 33, No. 5, 1985, pp. 1117- 1129. [9] H. Takagi, “Vacation and Priority Systems,” Part I. In: Queueing Analysis: A Foundation of Performance Eva- luation. Vol. I, Amsterdam, 1991. [10] J.-C. Ke, “On M/G/1 System under NT Policies with Breakdowns, Startup and Closedown,” Applied Mathe- matical Modelling, Vol. 30, No. 1, 2006, pp. 49-66. [11] K. H. Wang, “Optimal Control of a Removable and Non- Reliable Server in an M/M/1 Queueing System with Ex- ponential Startup Time,” Mathematical Methods of Op- erations Research, Vol. 58, No. 1, 2003, pp. 29-39. [12] K.-H. Wang and K.-L. Yen, “Optimal Control of an M/ Ek/1 Queueing System with a Removable Server,” Mathematical Methods of Operations Research, Vol. 57, No. 2, 2003, pp. 255-262. [13] K. H. Wang, “Optimal Control of an M/Ek/1 Queueing System with Removable Service Station Subject to Breakdowns,” Journal of the Operational Research Soci- ety, Vol. 48, No. 9, 1997, pp. 936-946. [14] K. H. Wang, K.-W. Chang and B. D. Sivazlian, “Optimal Control of a Removable and Non-Reliable Server in an Infinite and a Finite M/H2/1 Queueing System,” Applied Mathematical Modelling, Vol. 23, No. 8, 1999, pp. 651- 666. [15] J. E. Shore, “Information Theoretic Approximations for M/G/1 and G/G/1 Queueing Systems,” Acta Information, Vol. 17, No. 1, 1982, pp. 43-61. [16] M. A. El-Affendi and D. D. Kouvatsos, “A Maximum Entropy Analysis of the M/G/1 and G/M/1 Queueing Sys- tems at Equilibrium,” Acta Information, Vol. 19, No. 4, 1983, pp. 339-355. [17] K.-H. Wang, S.-L. Shuang and W. L. Pearn, “Maximum Entropy Analysis to the N Policy M/G/1 Queueing Sys- tem with a Removable Server,” Applied Mathematical Modelling, Vol. 26, No. 12, 2002, pp. 1151-1162. [18] K.-H. Wang, L.-P. Wang, J.-C. Ke and G. Chen, “Com- parative Analysis for the N Policy M/G/1 Queueing Sys- tem with a Removable and Unreliable Server,” Mathe- matical Methods of Operations Research, Vol. 61, No. 3, 2005, pp. 505-520. [19] K.-H. Wang, T.-Y. Wang and W. L. Pearn, “Maximum Entropy Analysis to the N Policy M/G/1 Queueing Sys- tem with Server Breakdowns and General Startup Times,” Applied Mathematics and Computation, Vol. 165, No. 1, 2005, pp. 45-61,. [20] K.-H. Wang and K.-B. Huang, “A Maximum Entropy Approach for the <p N>-Policy M/G/1 Queue with a Removable and Unreliable Server,” Applied Mathemati- cal Modelling, Vo1. 33, No. 4, 2009, pp. 2024-2034. [21] K.-H. Wang, M.-C. Chan and J.-C. Ke, “Maximum En- tropy Analysis of the Mx/M/1 Queueing System with Multiple Vacations and Server Breakdowns,” Computers & Industrial Engineering, Vol. 52, No. 2, 2007, pp. 192- 202. [22] J.-C. Ke and C.-H. Lin, “Maximum Entropy Solutions for Batch Arrival Queue with an Un-Reliable Server and De- laying Vacations,” Applied Mathematics and Computa- tion, Vol. 183, No. 2, 2006, pp. 1328-1340. [23] J.-C. Ke and C.-H. Lin, “Maximum Entropy Approach for Batch-Arrival Queue under N Policy with an Un-Re- liable Server and Single Vacation,” Journal of Computa- tional and Applied Mathematics, Vol. 221, No. 1, 2008, pp. 1-15. [24] Y. H. Tang, “The Transient Solution for M/G/1 Queue with Server Vacations,” Acta Math Scientia, Vol. 17(B), No. 3, 1997, pp. 276-282. [25] Y. H. Tang and X. W. Tang, “The Queue-Length Distri- bution for Mx/G/1 Queue with Single Server Vacation,” Acta Mathematical Scientia, Vol. 20(B), No.3, 2000, pp. 397-408. [26] Y.H. Tang, X. Yun and S. J. Huang, “Discrete-Time Geox/G/1 Queue with Unreliable Server and Multiple Adaptive Delayed Vacations,” Journal of Computational and Applied Mathematics, Vol. 220, No. 1-2, 2008, pp. 439-455. [27] J. Medhi and J. G. C. Templeton, “A Poisson Input Queue under N-Policy and with a General Start up Time,” Computers and Operations Research, Vol. 19, No. 1, 1992, pp. 35-41. [28] Y. H. Tang, “The Transient and Equilibrium Distribu- tions of the Queue-Length for M/G/1 Queue with De- layed N-Policy,” System Engineering - Theory & Prac- tice, Vol. 27, No. 11, 2007, pp. 130-134 (in Chinese). |

