Engineering, 2013, 5, 611-621
http://dx.doi.org/10.4236/eng.2013.57073 Published Online July 2013 (http://www.scirp.org/journal/eng)
Modelling Propagation of Stress Waves through Soil
Medium for Ground Response Analysis
Palaniyandi Kamatchi1*, Gunturi Venkata Ramana2, Ashok Kumar Nagpal2, Nagesh R. Iyer1
1CSIR-Structural Engineering Research Centre, Chennai, India
2Department of Civil Engineering, Indian Institute of Technology, Delhi, India
Received August 14, 2012; revised January 1, 2013; accepted January 8, 2013
Copyright © 2013 Palaniyandi Kamatchi et al. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
During past earthquakes, damages occurred to buildings located at soil sites are more compared to damages observed on
buildings located at rock sites. Modelling wave propagation through soil medium helps to derive the primary and sec-
ondary wave velocities. Most of the time soil mediums are heterogeneous, layered and undergoes nonlinear strains even
under weak excitation. The equivalent linear approximation with one dimensional wave propagation is widely adopted
for modeling earthquake excitation for layered soil. In this paper, importance of local soil effects, the process of wave
propagation through three dimensional elastic medium, layered medium situated on rigid rock, attenuation of stress
waves due to material damping, equivalent linear approximation, the concept of one dimensional wave propagation, and
a case study of one dimensional wave propagation as a part of site-specific ground response analyses for Delhi region
are included. The case study brings out the importance of carrying out site-specific ground response analyses of build-
ings considering the scenario earthquakes and actual soil conditions for Delhi region.
Keywords: Propagation of Stress Waves; Ground Response Analysis; Site-Specific Analysis; Delhi
1. Introduction
During many of the past earthquakes (Kachh, 1819,
Mexico City, 1985, Loma Prieta, 1989, Chi Chi, 1999,
Kobe, 1995) it has been observed that damages occurred
to buildings located at soil sites are more compared to
damages observed on buildings located at rock sites as
reported in literature [1-6]. Figure 1 shows the ground
motions recorded at two adjacent sites viz., a rock site
(UNAM) and a soil site (SCT) located 350 km away
from epicenter during 1985 Mexico city earthquake. The
response spectra of UNAM site and SCT site are shown
in Figure 2. The earthquake has caused only moderate
damage near the epicenter and caused severe damage in
the lake zone underlain by 38 to 50 m of soft soil (site
period was 1.9 to 2.8 sec). Most of the buildings in the 5
- 20 storey range got severely damaged and the buildings
of less than five stories or more than 30 stories suffered
lesser damage. This pattern of damage was partly attrib-
uted to the resonance effect of time period of soil deposit
and the time period of the building. Initially, it was felt
that soil amplification can be observed for week motions
only and for strong shaking there may not be consider-
able amplification due to damping of soil. Figure 3
shows the nonlinear relation of peak ground acceleration
(PGA) for weak and strong motion as observed in Mex-
ico City, Loma Prieta earthquake and numerical calcula-
tions. Adapting to the response spectra (Figure 4) of
Seed and Idriss [3] which depicted the variation of re-
sponse of different site conditions, building codes viz.,
Figure 1. Recorded time histories at rock (UNAM) and soil
sites (SCT) during Mexico City earthquake (1985) [15].
*Corresponding author.
C
opyright © 2013 SciRes. ENG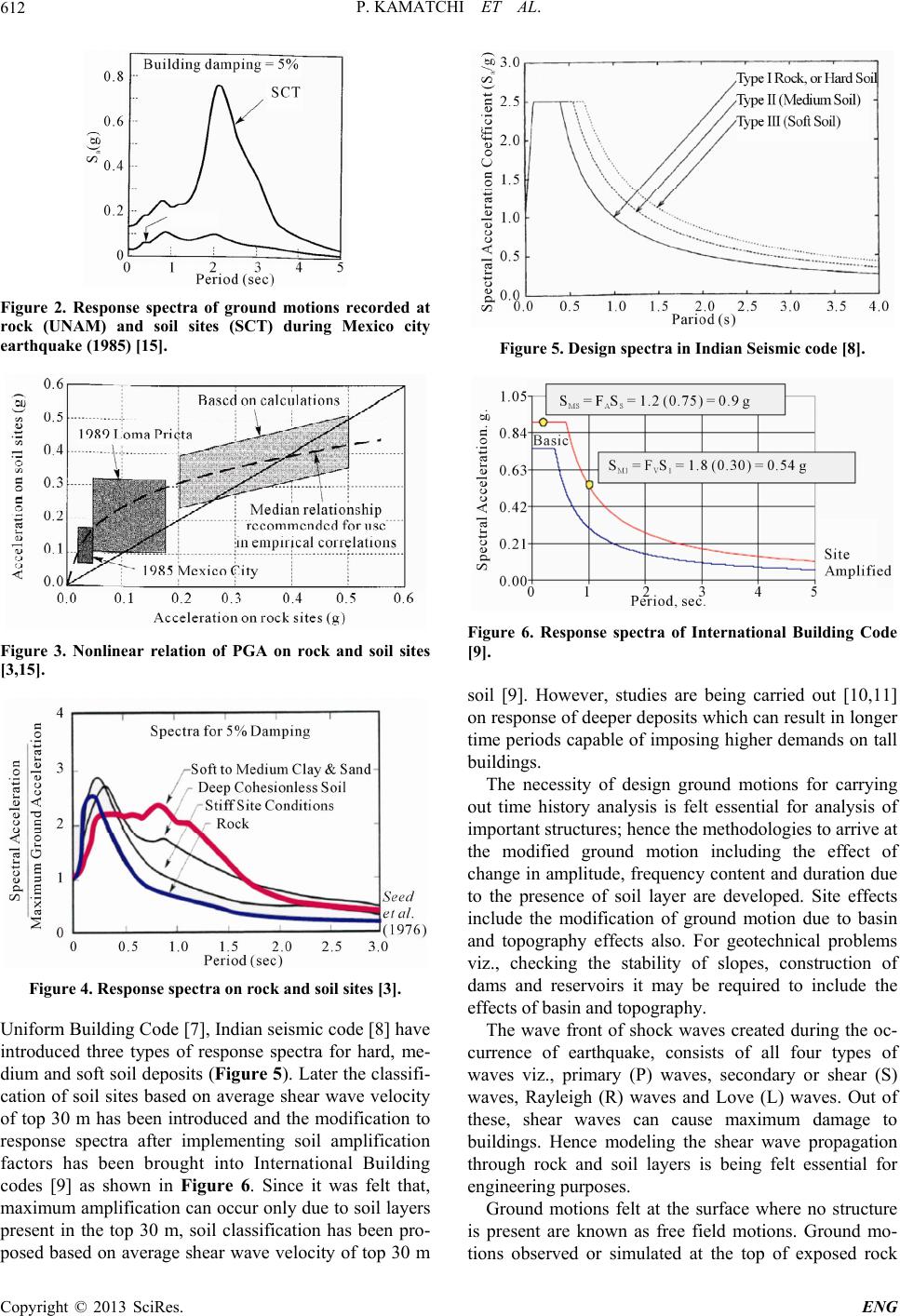

P. KAMATCHI ET AL. 612
Figure 2. Response spectra of ground motions recorded at
rock (UNAM) and soil sites (SCT) during Mexico city
earthquake (1985) [15].
Figure 3. Nonlinear relation of PGA on rock and soil sites
[3,15].
Figure 4. Response spectra on rock and soil sites [3].
Uniform Building Code [7], Indian seismic code [8] have
introduced three types of response spectra for hard, me-
dium and soft soil deposits (Figure 5). Later the classifi-
cation of soil sites based on average shear wave velocity
of top 30 m has been introduced and the modification to
response spectra after implementing soil amplification
factors has been brought into International Building
codes [9] as shown in Figure 6. Since it was felt that,
maximum amplification can occur only due to soil layers
present in the top 30 m, soil classification has been pro-
posed based on average shear wave velocity of top 30 m
Figure 5. Design spectra in Indian Seismic code [8].
Figure 6. Response spectra of International Building Code
[9].
soil [9]. However, studies are being carried out [10,11]
on response of deeper deposits which can result in longer
time periods capable of imposing higher demands on tall
buildings.
The necessity of design ground motions for carrying
out time history analysis is felt essential for analysis of
important structures; hence the methodologies to arrive at
the modified ground motion including the effect of
change in amplitude, frequency content and duration due
to the presence of soil layer are developed. Site effects
include the modification of ground motion due to basin
and topography effects also. For geotechnical problems
viz., checking the stability of slopes, construction of
dams and reservoirs it may be required to include the
effects of basin and topography.
The wave front of shock waves created during the oc-
currence of earthquake, consists of all four types of
waves viz., primary (P) waves, secondary or shear (S)
waves, Rayleigh (R) waves and Love (L) waves. Out of
these, shear waves can cause maximum damage to
buildings. Hence modeling the shear wave propagation
through rock and soil layers is being felt essential for
engineering purposes.
Ground motions felt at the surface where no structure
is present are known as free field motions. Ground mo-
tions observed or simulated at the top of exposed rock

P. KAMATCHI ET AL. 613
esponse analysis will include the
pr
are known as outcrop motions and the ground motions buildings and structures. In this paper, brief introduction
about wave propagation through soil medium and a case
study of site-specific ground response analysis for Delhi
region are included.
felt below the soil layer are denoted as bedrock motions.
There are different definitions for bedrock, seismic bed-
rock (shear wave velocity in the range of 3.2 km/sec) or
engineering bedrock (shear wave velocity more than 400
m/sec). When the foundation is proposed to be located
below the ground level for specific applications it is re-
quired to arrive at the ground motion at the base of the
soil layer using the surface level ground motions (simu-
lated or recorded design ground motion for a specified
risk level on surface). This process of obtaining the bed-
rock motion from free field motion is known as
de-convolution. Knowledge of propagation of horizontal
component of shear wave through soil medium located
on rigid or elastic rock is essential for carrying out soil
amplification studies.
A complete ground r
2. Wave Propagation through Soil Medium
For carrying out dynamic analysis, structural elements
made of materials viz., Reinforced Concrete (RC) and
steel can be idealized as discrete elements with quantifi-
able stiffness and mass. When the dynamic load is ap-
plied to continuous medium like soil, the deformation
that takes place in the soil medium causes stress waves.
Propagation of stress waves through soil can be modelled
by either of these three methods 1) stress waves in an
elastic unbounded medium 2) stress waves in a longitu-
dinal bar 3) stress waves in elastic half space.
ocess of modeling the rupture mechanism at the source
and the path attenuation and wave propagation through
soil medium. The response spectrum at the soil surface is
significantly different from that of bedrock response
spectrum due to the modification of ground motion as it
passes through the soil layers overlying the bedrock.
Building codes are simplified tools and do not adequately
represent any single earthquake event from a probable
source for the site under consideration. Recently, it has
been recommended [11-14] that in addition to the use of
seismic codes, site-specific analysis which includes gen-
eration of strong ground motion at bedrock level and
propagating it through soil layers and arriving at the de-
sign ground motions and response spectra at surface
should also be carried out in the design of important

2.1. Three Dimensional Modeling of Wave
Propagation through Soil Medium
Situated on Rigid Rock
To understand the propagation of stress waves in infinite
elastic medium and bounded elastic medium equations of
motion can be written in terms of stresses. Let the normal
and shear stresses acting on a soil element with sides dx,
dy and dz are

x,

y,

z and

xy,

yx,

yz,

zy,

zx, and

xz
respectively as shown in Figure 7. When u, v, and w are
the displacement components in x, y and z directions the
equation of equilibrium along x, y and z directions can be
written as given in Equations (1)-(3) [16,17] wherein the
unbalanced external forces are balanced by an inertial
force, where
 is the mass per unit volume or the density.
dx
x
xy
xy 

 
dx
x
x
x

 
dx
x
xz
xz 


z

zx

zy

dy
y
y
y


dy
y
yz
yz 

 
dy
y
yx
yx 



yx
σy
yz
dz
z
zy
zy 

 
dz
z
z
z


dz
z
zx
zx 

 
xz
xy
σx
d
y
d
x
d
z
z
Y
X
Figure 7. Stresses in an elastic solid.

P. KAMATCHI ET AL. 614
2
2
yx
xzx
u
x
yz t






 

(1)
2
2
yxyzy v
yxz t
   

 
(2)
2
2
yz
xz zw
zxy t

 



 
(3)
Referring to theory of elasticity [18] and writing the
eq
o
uations for normal, shearing strains in terms of partial
derivatives of displacements and linking the stresses and
strains by Hook’s law with material constants viz.,
young’s modulus (E), shear modulus (G), bulk modulus
(
 ) and poisson’s ratio (  ) and substituting 
xy =

yx;

yz =

zy and

xz =

zx the equation of motion for x component is
btained as given in Equation (4). Similarly by getting
the equation of motion in other components and differen-
tiating with respect to x, y and z and by adding Equation
(5) which relates volumetric strain (ε) and primary wave
velocity (vp) of soil medium is obtained.

2u
 
2
2GG
u
tx
  

(4)
222
2
222
x
yz

 

2
22
2p
v
t



 (5)
where,
uvw
x
yz





2
p
vG

 
The propagation of stress waves in a bounded elastic
medium is similar to Equation (5) and can be expressed
as
22
2
2
c
uu
v
t



2
x
(6a)
c
vE

 (6b)
For shear waves or S waves the equation of motion in
x direction reduces to the following form
2
2
x
wvG
tyz



 



 (7a)
2
22
2
x
s
x
v
t



 (7b)
where s
vG

, 1
2
x
wv
yz









rotational strain
in x-direction
ot cause any rotation and S-wave does
volume change. The ratio of P-wave ve-
lo
P waves do n
not cause any
city and S-wave velocity is given by
22
p
v
12
s
v



 where 0.3v1.87
ps
v


;
The body waves t hemispherical wa front
and Rayleigh waves travel with cylindrical wave front.
Th
ravel withve
e amplitude of body waves is proportional to 1/r and
amplitude of Rayleigh wave is proportional to 1r.
2.2. Wave Propagation in a Layered Med on ium
Rigid Rock
homoge halfspace and the softer surface
esses, the amplitudes and
st
To illustrate the wave propagation at the interface of
neous elastic
layers, the problem of harmonic stress wave travelling
along a constrained rod in the positive x-direction and
approaching an interface between two different materials
is often chosen (Figure 8).
Satisfying the compatibility conditions of displace-
ments and continuity of str
resses of incident, reflected and transmitted waves are
related by the following equations
22
11
1z
ri
AA

1where
2
1
z
z
ti
z
v
v
AA






; (8)


11
1
1where
2
1
z
ri
z
ii
z
ti
z
ivA









(9)
Impedance ratio of zero means free boundary condi-
tions (surface), amplitude of displacement at boundary is
twice as that of displacement of incident wave and the
stresses are equal with opposite sign. Impedance ratio of
infinity means (rigid rock) displacement is zero, ampli-
tude of incident and reflected waves are equal but with
opposite signs. Stress at this boundary is twice as that of
incident wave. Impedance ration of unity means, all the
incident waves are getting transmitted and no component
is reflected back.
Figure 8. One dimensional wave propagation at materia
interface. l

P. KAMATCHI ET AL. 615
Response of a dynamically loaded system can be
solved by making use of Fourier transforms and transfer
functions in frequency domain. This approach is widely
used for ground response analysis, wherein the applied
time history at rock level is converted to Fourier trans-
forms and multiplied with transfer functions of the soil
layer and converted back to time domain by inverse Fou-
rier transforms and the ground motion at surface is ob-
tained.
The problem is now to get the transfer functions of the
soil layers, which is the ratio of maximum displacement
of the topmost and bottommost point of the soil layer.
The modulus of transfer function gives the amplification
function. The soil layer is seldom homogeneous and the
heterogeneity of soil layers can be modeled by inclusion
of more number of soil layers. The response of layered
soil on elastic rock can be determined using the proce-
dure described in the following sections.
During earthquake shaking fault ruptures below the
earth surface and body waves travel away from the
source when met with boundaries between different geo-
logical materials they get reflected and refracted. Due to
the lesser velocity of materials present at shallower
depths inclined rays that strike horizontal layer bounda-
ries are usually reflected to a more vertical direction.
Assumption of one dimensional ground response analysis
is that soil boundaries are horizontal and the response of
a soil deposit is predominantly caused by SH-waves
propagating vertically from the underlying bedrock.
2.3. Attenuation of Stress Waves Due to Material
The )-(7) represent wave propagation with-
Damping
Equations (1
out change in amplitude, which cannot be practical. Dur-
ing the propagation of wave through soil medium, dissi-
pation of energy takes place which results in decrease in
amplitude. If the soil medium is idealized as visco elastic
material with spring stiffness G and viscous damping
constant
 the as shown in Figure 9, and the shear stress
(
 )-strain (  ) relationship is given by
Gt




 (10)
One dimensional equation of moti on for vertically pro-
Figure 9. Soil idealized as visco-elastic material [15].
pagating SH waves can be written as,
2
2
u
tz






 (11)
Substituting Equation (10) in Equation (11)
22 3
22
uu
G
tzz

2
u
t




 
(12
Considering soil as a visco-elastic m
N horizontal layers where Nth layer is bedrock (
10 expressed
as
)
2.4. Transfer Function
aterial consisting of
Figure
), the solution to the wave equation can be



,e e
itkzitk
uzt AB





z (13)


 
,
u
ztGG i 
12
u u
G i 
zz z





where A and B are the amplitudes of waves travelling in
the upward and downward direction, k* is the complex
wave number extending the results of Equations (8) and
(9),
(14)
the complex impedance ratio

m

 between layers
m and m+1 can be given by


11
ms
m
m
ms
m
v
v






 (15)
At ground surface, the shear stress must be equal to
zero and A1 = B1 the functions relating amplitudes at
layer m and layer 1 are given by
m

1m
A
aA (16a)
The transfer function relating the displacement ampli-
tude at lay

(16b)

1mm
Bb B  
er i to layer j is given by
  
 
ii
i
ij
jj
ab
u
Fua j
b




 
Since

 (17)
2
uu  
 ,u this tran
used for finding amplification of a
placements also. If the ground motion for a particula
sfer function can be
r
ccelerations and dis-
Figure 10. Layered soil deposit on elastic bedrock [15].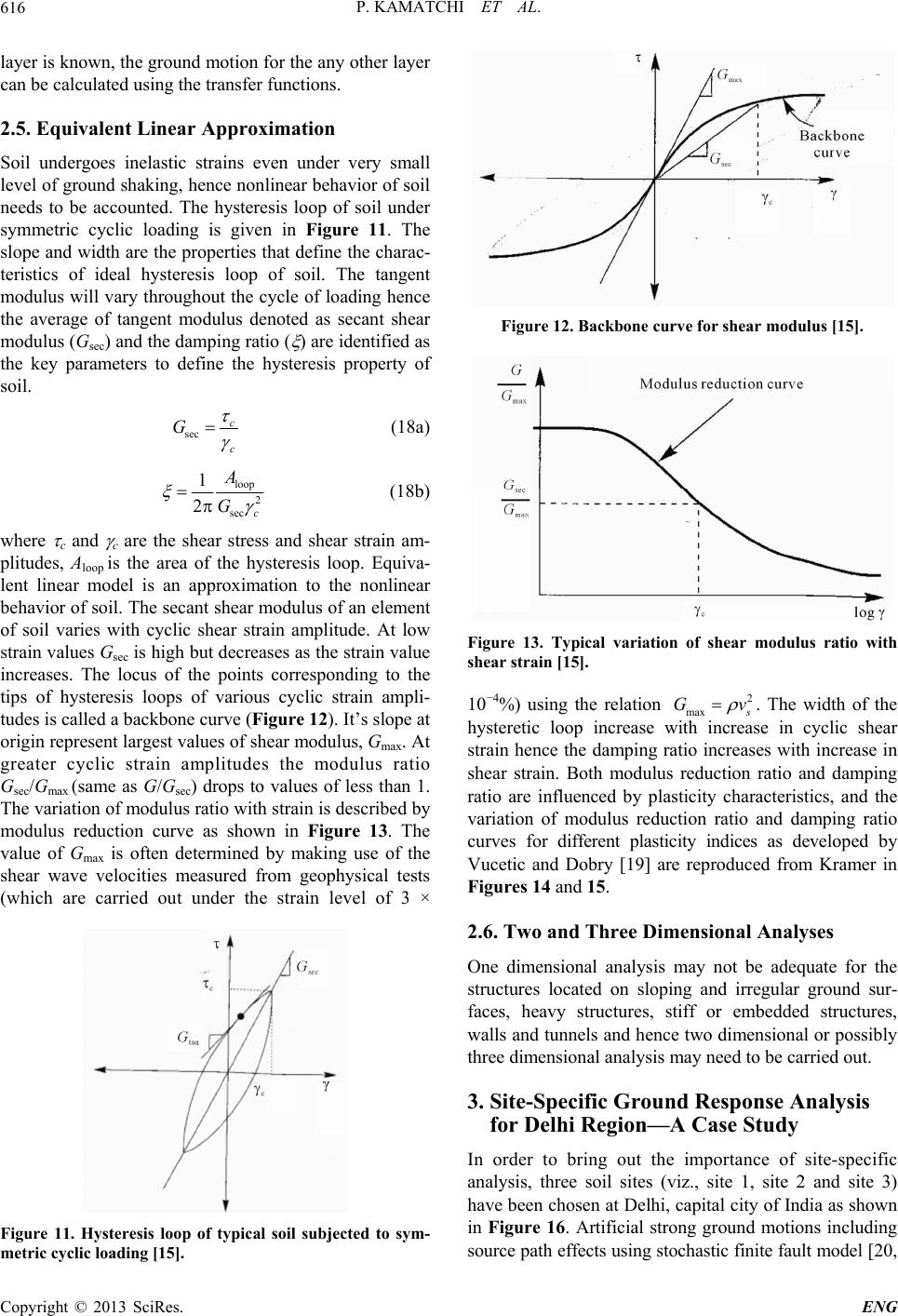

P. KAMATCHI ET AL. 616
layer is known, the ground motion for the any other layer
can be calculated using the transfer functions.
2.5. Equivalent Linear Approximation
Soil undergoes inelastic strains even under very small
level of ground shaking, hence nonlinear behavior of soil
needs to be accounted. The hysteresis loop of soil under
symmetric cyclic loading is given in Figure 11. The
slope and width are the properties that define the charac
cant shear
entified as
property of
-
ter t
modulus will vary throughout the cycle of loading hence
the average of tangent modulus denoted as se
istics of ideal hysteresis loop of soil. The tangen
modulus (Gsec) and the damping ratio (  ) are id
the key parameters to define the hysteresis
soil.
sec
c
c
G


 (18a)
loop
2
sec
1
2c
A
G


 (18b)
where

c and

c are the shear stress and shear strain am-
plitudes, Aloop is the area of the hysteresis loop. Equiva-
lent linear model is an approximation to the nonlinear
behavior of soil. The secant shear modulus of an element
of soil varies with cyclic shear strain amplitude. At low
strain values Gsec is high but de
increases. The locus of the points corresponding to the
tips of hysteresis loops of various cyclic strain ampli-
tudes is called a backbone curve (Fi
origin represent largest values of shear modulus, Gmax. At
creases as the strain value
gure 12). It’s slope at
greater cyclic strain amplitudes the modulus ratio
Gsec/Gmax (same as G/Gsec) drops to values of less than 1.
The variation of modulus ratio with strain is described by
modulus reduction curve as shown in Figure 13. The
value of Gmax is often determined by making use of the
shear wave velocities measured from geophysical tests
(which are carried out under the strain level of 3 ×
Figure 12. Backbone curve for shear modul [15]. us
Figure 13. Tit
shea
10−4%) using the relation
ypical variation of shear modulus ratio w
r strain [15]. h
2
max
s
Gv


th increase i
. The width of the
hysteretic loop increase win cyclic shear
strain hence the damping ratio increases with increase in
shear strain. Both modulus reduction ratio and damping
ratio are influenced by plasticity characteristics, and the
variation of modulus reduction ratio and damping ratio
curves for different plasticity indices as developed by
Vucetic and Dobry [19] are reproduced from Kramer in
Figures 14 and 15.
2.6. Two and Three Dimensional Analyses
ces, heavy structures, stiff or embedded structures,
e two dime
l strong ground motions including
source path effects using stochastic finite fault model [20,
One dimensional analysis may not be adequate for the
structures located on sloping and irregular ground sur-
fa
walls and tunnels and hencnsional or possibly
three dimensional analysis may need to be carried out.
3. Site-Specific Ground Response Analysis
for Delhi Region—A Case Study
In order to bring out the importance of site-specific
analysis, three soil sites (viz., site 1, site 2 and site 3)
have been chosen at Delhi, capital city of India as shown
in Figure 16. Artificia
Figure 11. Hysteresis loop of typical soil subjected to sym-
metric cyclic loading [15].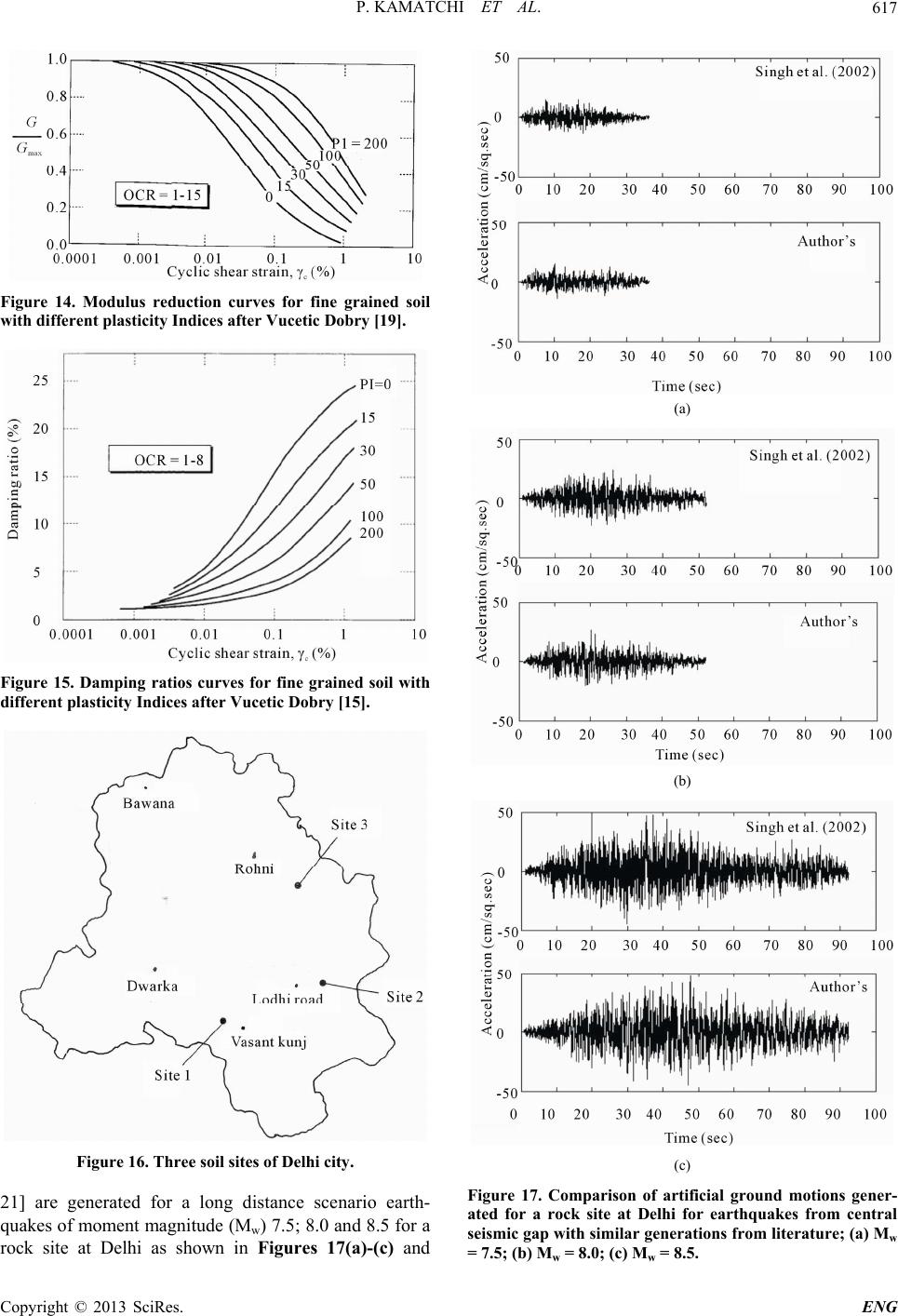

P. KAMATCHI ET AL. 617
Figure 14. Modulus reduction curves for fine grained soil
with different plasticity Indices after Vucetic Dobry [19].
Figure 15. Damping ratios curves for fine grained soil with
different plasticity Indices after Vucetic Dobry [15].
(a)
(b)
Figure 16. Three soil sites of Delhi city.
21] are generated for a long distance scenario earth-
quakes of moment magnitude (Mw) 7.5; 8.0 and 8.5 for a
rock site at Delhi as shown in Figures 17(a)-(c) and
(c)
Figure 17. Comparison of artificial ground motions gener-
ated for a rock site at Delhi for earthquakes from central
seismic gap with similar generations from literature; (a) Mw
= 7.5; (b) Mw = 8.0; (c) Mw = 8.5.

P. KAMATCHI ET AL. 618
compared with similar simulation from literature [22].
One dimensional equivalent linear vertical wave propa-
gation analysis is the widely used numerical procedure
for modeling soil amplification problem [2,23] as dis-
cussed in the earlier section. In one dimensional wave
propagation analysis, soil deposit is assumed to be hav-
ing number of horizontal layers with different shear
modulus (G), damping (
 ) and unit weight (  ) as shown
in Figure 10. Equivalent linear analysis program SHAKE
[24,25] is used in the present study. Equivalent linear
modulus reduction (G/Gmax) and damping ratio (  ) curves
generated from laboratory test results are adopted from
Vucetic and Dobry [19] depending on the plasticity index
of different soil layers.
Three actual soil sites designated as site 1, site 2 and
site 3 located in Delhi as shown in Figure 16 are chosen
in the present study. The layer wise soil characteristics
(medium type) and the depth to the base of the layer from
the surface is given elsewhere [10,26] The variation of
shear wave velocity along the depth in the present study
is obtained by using the correlations suggested for Delhi
region by Rao and Ramana [27] as given in Equation
(19).
(19a)
(19b)
From the ground response analyses results, it has been
observed that the PGA amplifications and the response
spectra of the three sites are quite different for the earth-
quakes considered.
Using the site-specific response spectra, storey shear
of three storey and fifteen storey building (Figure 18) are
estimated using response spm method. The com-
hree sites considered.
As per IBC [9] guidelines site-specific a
ommended for soil type F only for which a
wave velocity of top 30 m is less than 180 m/s. T
sites considered in the present study are moderate sites
an
damping, equivalent linear approximation, the concept of
one dimensional wave propagation analysis, and a case
study of site-specific ground response analyses for Delhi
region are presented.
In the case study, rock outcrop motions have been
generated for Delhi for the scenario earthquakes of mag-
nitude, Mw = 7.5, Mw = 8.0 and Mw = 8.5. Three actual
soil sites have been modeled and the free field surface
motions and the response spectra have been obtained
through one dimensional wave propagation analyses.
Further, the response of a three storey building and a
fifteen storey building are studied and it is observed that,
for the three sites considered the response of the building
varies significantly. The studies made, brings out the
importance of carrying out site-specific ground response
analyses of buildings considering the scenario earth-
varies significantly from the storey shear obtained using
Indian seismic code BIS 1893-2002 Part 1 [8] code. The
linear displacements for the two buildings are obtained
by linear static analyses program and the comparison has
been made for the three sites as shown in Figure 20. It is
seen that displacement response also varies significantly
for the t
nalysis is rec-
verage shear
he soil
d do not come under the category of F type. The stud-
ies made, bring out the importance of carrying out
site-specific ground response analyses of buildings con-
sidering the scenario earthquakes and actual soil condi-
tions for Delhi region.
4. Summary
In this paper, importance of local soil effects and proce-
dure for modeling wave propagation through three di-
mensional elastic medium, layered medium situated on
rigid rock, attenuation of stress waves due to material

0.43
79 sand
s
VN

0.42
86silty sandsandy silt
s
VN/
s
ectru
parisons of storey shears for the buildings on three sites
and storey shears obtained using Indian seismic code BIS
1893-2002 Part 1 [8] are shown in Figure 19. From the
comparison of storey shear values it can be seen that for
the three sites considered the response of the building
Figure 18. Plan of a three storey and a fifteen storey RC framed building.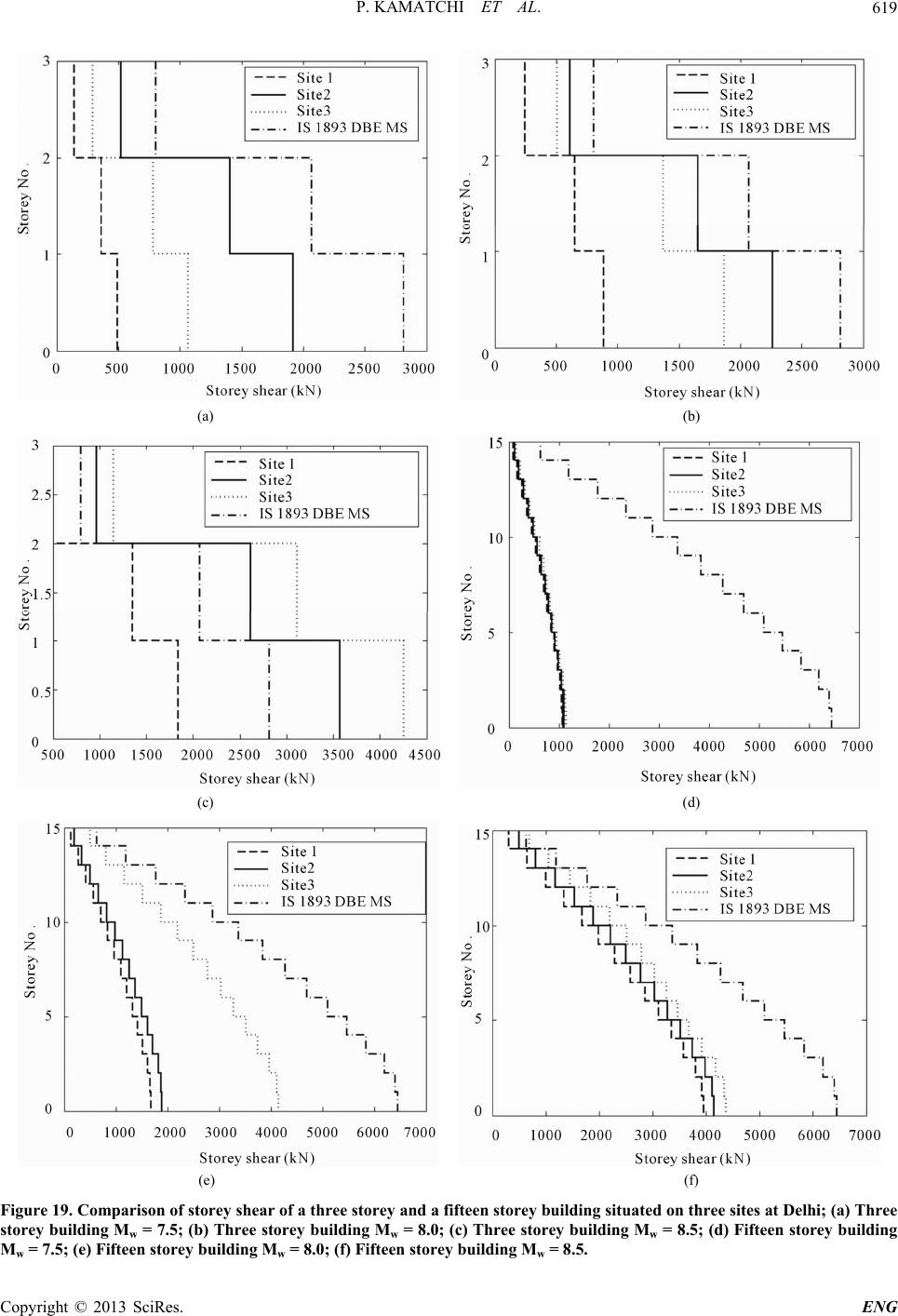

P. KAMATCHI ET AL. 619
(b) (a)
(c) (d)
(e) (f)
Figure 19. Comparison of storey shear of a three storey and a fifteen storey building situated on three sites at Delhi; (a) Three
storey building Mw = 7.5; (b) Three storey building Mw = 8.0; (c) Three storey building Mw = 8.5; (d) Fifteen storey building
Mw = 7.5; (e) Fifteen storey building Mw = 8.0; (f) Fifteen storey building Mw = 8.5.

P. KAMATCHI ET AL. 620
(a) (b)
Figure 20. Comparison of linea.0; Mw = 8.5; (b) Fifteen
storey building Mw = 7.5; M
quakes and actual soil conditions for Delhi region.
5. Acknowledgements
This paper is being published with the kind permission of
director CSIR-SERC.
REFERENCES
[1] I. M. Idriss and H. B. Seed, “Seismic Response of Soil
Deposits,” Journal of the Soil Mechanics and Founda-
tions Division, Vol. 96, No. 2, 1970, pp. 631-638.
[2] I. M. Idriss, “Response of Soft Soil Sites during Earth-
quakes,” Proceedings, Memorial Symposium to Honor
Professor H. B. Seed, Berkeley, 1990, pp. 273-289.
[3] B. H. Seed and I. M. Idriss, “Influence of
on Ground Motions du
“Re-Examination of Damage Distribution in Adapazari:
Geotechnical Considerations,” Engineering Structures,
Vol. 27, No. 7, 2005, pp. 1002-1013.
doi:10.1016/j.engstruct.2005.02.002
r displacement response; (a) ee storey building Mw = 7.5; Mw = 8
w = 8.0; Mw = 8.5. Thr
Soil Conditions
ring Earthquakes,” Journal of the
Soil Mechanics and Foundations Division, Vol. 95, No. 1,
1969, pp. 99-137.
[4] B. S. Bakir, M. T. Yilmaz, A. Yakut and P. Gulkan,
[5] D. M. Boore and W. B. Joyner, “Site Amplifications for
Generic Rock Sites,” Bulletin of the Seismological Soci-
ety of America, Vol. 87, No. 2, 1997, pp. 327-341.
[6] S. S. Tezcan, I. E. Kaya, E. Bal and Z. Ozdemir, “Seismic
Amplification at Avcilar, Istanbul,” Engineering Struc-
tures, Vol. 24, No.5, 2002, pp. 661-667.
doi:10.1016/S0141-0296(02)00002-0
[7] International Conference of Building Officials, “Uniform
Building Code 1997 Volume 2: Structural Engineering
Design and Provisions,” Uniform Building Code, 1997.
[8] IS 1893, “Criteria for Earthqu
Structures—Part 1: Gene
national Code
Council, 2003.
[10] D. Park and Y. M. A. Hashash, “Evaluation of Seismic
Site Factors in the Mississippi Embayment. I. Estimation
of Dynamic Properties,” Soil Dynamics and Earthquake
Engineering, Vol. 25, No. 2, 2005, pp. 133-144.
doi:10.1016/j.soildyn.2004.10.002
[11] P. Kamatchi, “Neural Network Models for Site-Specific
Seismic Analysis of Buildings,” Ph.D. Thesis, Depart-
ment of Civil Engineering, Indian Institute of Technology,
Delhi, 2008.
[12] T. Balendra, N. T. K. Lam, J. L. Wilson and K. H. Kong,
“Analysis of Long-Distance Earthquake Tremors and
Base Shear Demand for Buildings in Singapore,” Engi-
neering Structures, Vol. 24, No. 1, 2002, pp. 99-108.
doi:10.1016/S0141-0296(01)00065-7
[13] F. Heuze, R. Archuleta, F. Bonilla, S. Day, M. Doroudian,
oehler, T. Lai, D. Lavallee,
ic Strong Earthquake Motions,” Soil Dy-
namics and Earthquake Engineering, Vol. 24, No. 3,
2004, pp. 199-223. doi:10.1016/j.soildyn.2003.11.002
A. Elgamal, S. Gonzales, M. H
B. Lawrence, P. C. Liu, A. Martin, L. Matesic, B. Minster,
R. Mellors, D. Oglesby, S. Park, M. Riemer, J. Steidl, F.
Vernon, M. Vucetic, J. Wagoner and Z. Yang, “Estimat-
ing Site-Specif
[14] T. Mammo, “Site-Specific Ground Motion Simulation
and Seismic Response Analysis at the Proposed Bridge
Sites within the City of Addis Ababa, Ethiopia,” Engi-
neering Geology, Vol. 79, No. 3-4, 2005, pp. 127-150.
doi:10.1016/j.enggeo.2005.01.005
[15] S. L. Kramer, “Geotechnical Earthquake Engineering,”
Prentice Hall International Series, Upper Saddle River,
2003.
[16] B. M. Das, “Fundamentals of Soil Dynamics,” Elsevier
Science Publishing Co. Inc., Amsterdam, 1983.
[17] B. M. Das and G. V. Ramana, “Principles of Soil Dy-
namics,” Cengage Learning Publishers, Stamford, 2011
r, “Theory of Elasticity,”
[19] M. Vucetic and R. Dobry, “Effect of Soil Plasticity on
.
ake Resistant Design of
ral Provisions and Buildings,” [18] Timoshenko and Goodie
McGraw Hill, New York, 1970.
Bureau of Indian Standards, New Delhi, 2002.
[9] IBC, “International Building Code,” Inter

P. KAMATCHI ET AL. 621
pendent Characteristics of Stiffness and Damping,” Soil Cyclic Response,” Journal of Geotechnical Engineering,
Vol. 117, No. 1, 1991, pp. 89-107.
doi:10.1061/(ASCE)0733-9410(1991)117:1(89)
[20] I. A. Beresnev and G. M.
Fault Radiation from the
Atkinson, “Modeling Finite—
n Spectrum,” Bulletin of the
[21] I. A. Beresnev and G. M. Atkinson, “FINSIM—A FOR-
TRAN Prograastic Acceleration
Time HistorieSeismological Re-
Seismological Society of America, Vol. 87, No. 1, 1997,
pp. 67-84.
m for Simulating Stoch
s from Finite Faults,”
search Letters, Vol. 69, No. 1, 1998, pp. 27-32.
doi:10.1785/gssrl.69.1.27
[22] S. K. Singh, W. K. Mohanty, B. K. Bansal and G. S.
Roonwal, “Ground Motion in Delhi from Future
Large/Great Earthquakes in the Central Seismic Gap of
the Himalayan Arc,” Bulletin of the Seismological Society
of America, Vol. 92, No. 2, 2002, pp. 555-569.
doi:10.1785/0120010139
[23] N. Yoshida, S. Kobayashi, I. Suetomi and K. Miura,
“Equivalent Linear Method Considering Frequency De-
Dynamics and Earthquake Engineering, Vol. 22, No. 3,
2002, pp. 205-222. doi:10.1016/S0267-7261(02)00011-8
[24] P. B. Schnabel, J. Lysmer and H. B. Seed, “SHAKE, a
Computer Program for Earthquake Response Analysis of
Horizontally Layered Sites,” Report No. EERC 72-12,
io Earthquakes,” Proceedings of the 14th World
f
Earthquake Engineering Research Center, University of
California, Berkeley, 1972.
[25] G. A. Ordonez, “SHAKE 2000: A Computer Program for
the I-D Analysis of Geotechnical Earthquake Engineering
Problems,” 2000.
[26] P. Kamatchi, G. V. Ramana, A. K Nagpal and N.
Lakshmanan, “Site-Specific Analysis of Delhi Region for
Scenar
Conference on Earthquake Engineering, Beijing, 12-17
October 2008.
[27] H. Ch. Rao and G. V. Ramana, “Correlation between
Shear Wave Velocity and N Value for Yamuna Sand o
Delhi,” Proceedings of International Conference on Geo-
technical Engineering, UAE, 2004, pp. 262-268.