 Journal of Modern Physics, 2013, 4, 1027-1035 http://dx.doi.org/10.4236/jmp.2013.47138 Published Online July 2013 (http://www.scirp.org/journal/jmp) Gravitational Model of the Three Elements Theory: Mathematical Explanations Frederic Lassiaille University of Nice Sophia Antipolis, Nice, France Email: lumimi2003@hotmail.com Received January 19, 2013; revised February 21, 2013; accepted March 19, 2013 Copyright © 2013 Frederic Lassiaille. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT The aim is to parse the mathematical details related to the gravitational model of the three elements theory [1]. This model is proven to be coherent and really compatible with relativity. The Riemannian representation of space-time which is used in this model is proven to be legal. It allows to understand relativity in a more human sensitive manner than Minkowskian usual representation. Keywords: Relativity; Gravitation; Newton’s Law 1. Introduction The aim of this article is to depict the mathematical basis which supports the gravitational model of the three ele- ments theory [1]. The first analysis addresses the link between the two space-time representations. Those rep- resentations are Minkowskian usual representation and a Riemannian representation. The latter must be detailed, and usual relativity mechanisms like general relativity principles and Lorentz transformation are interpreted in this representation in a particular geometrical manner. Lorentz transformation is explained by postulate 1 of [1] which is interpreted geometrically in a wired manner. This must be explained here. Also, application of postu- late 3 of [1] uses a strange projection rule, which must be explained. The last analysis is checking that the “follow- ing geodesic principle” is still valid in this Riemannian representation, in a specific case. This is mandatory for the calculations which are done in [1]. 2. Comparison of the Two Metrics Let’s call the Minkowskian pseudo-Riemannian metric coefficients, and h ddd the corresponding Rieman- nian metric ones. As usual we have: 2 gxx (1) With 0 ct, and 123 ,, i xxx the three space co- ordinates. In this equation above variables are sup- posed to be space and time coordinates in some given 0 reference frame. Let’s choose a 0 base as part of this 0 reference frame. In other words, 0 is the reference frame at some given instant in time. R B RB 0 R B B 0g In each space-time point, a mathematical theorem states that, for the bilinear form associated with this ds2 quadratic form, it is always possible to find an orthogo- nal and normalizedbase with respect to some fixed 0 base, for which the metric local matrix is diagonal. In these orthogonal bases, the metric coefficients be- comes then such that if B B 222 122232 0011 2233 ddddd bb bb . That’s just a reminder. But let’s notice that time and space units in these bases are 0 base time and space units. In those bases, now the Minkowskian metric can be written: gc tgxgxgx 123 ,,,txxx B (2) bbbb are coordinates in the base. By defi- nition, the Riemannian coefficients are constructed the following way. 00 00 1,h (3) 1,0 ii ii hi g (4) Those equations are a consequence of the differences between Minkowskian representation and the Rieman- nian representation which is used in this model. The first one is of course the metric signature which is + + + + for the Riemannian one, in place of the + − − − Min- kowskian one. The second difference is that local time is inverted. In other words, the diagonal matrix coefficients C opyright © 2013 SciRes. JMP  F. LASSIAILLE 1028 are inverted when passing from one metric to another. This allows to apply the “following geodesics” principle in this Riemannian representation, as this will be shown in this document. The physics understanding of this sec- ond difference is the same as the general relativity ex- planation of the twin paradox. Let’s remind that this ex- planation is based upon the generation of a global vac- uum by the universe in the representation of the reference frame attached to the travelling twin. On the contrary the twin staying on earth is watching the vacuum generated by the travelling twin only locally and that’s the explana- tion of the asymmetrical roles of the twins. This is not a physical vacuum but a vacuum in the representation of space-time. Now in the Riemannian representation, with respect to 0 reference frame, this vacuum is supposed to be generated globally by the free falling particle (as if the free falling particle was not less than the universe itself!). On the contrary, in the Minkowskian representa- tion in 0 this vacuum is supposed to be generated only locally to the particle along its trajectory. Of course, only the latter version is the realistic one. But one may notice that the mathematical model do not prefer any physical configuration. R R An illustration of this relationship rule between those two metrics is given by the case of the Schwarzschild metric. 1 2 2 1 d bb M 22 d1 d M ct x xx 1 (5) Of course this is the Minkowskian metric usual ver- sion. M is supposed to be the Schwarzschild ray of the at- tracting object as usual. x is as usual in this metric the spatial physical distance from the attracting object (more usually written r). , and bb 0 bb ct x x BR B R RR 0 R R 222 2 00 11 ddd bb are, respec- tively, the time and space coordinates in the system of bases. ds is the infinitely small space-time length, calculated in some given space-time point. The 0 ref- erence frame which generated this system of bases gets on its origin its time axis parallel to local time axis in two cases. The first one is when the origin of 0 is located in the middle of the attracting object of this Schwarzschild metric. The second one is when the origin of 0 is located infinitely far from the attracting object. In the latter case, 0 time axis is tangent to the trajec- tory of a null mass free falling particle. Because of the equivalence principle, this free falling particle trajectory will coincide with a time coordinate curve in the system of bases. Because of the “following geodesics” prin- ciple, it will also be a geodesic in the Minkowskian met- ric. As usual this free falling particle gets a null mass, because we don’t want it to generate any space-time de- formations around it. Otherwise, this should modify the studied metric. And it gets a null speed when located infinitely far, because this means that its trajectory will always be perpendicular to space lines with respect to . In other words, this trajectory is a time curve in this 0 representation. In this document, the expression “free falling particle” will always means in fact this par- ticular case of free falling particle, and the expression “time line” will always means that specific kind of tra- jectory. The term “space line” will mean perpendicular curves to such time lines. B The corresponding Riemannian version of this Sch- warzschild metric is the following. hc thx d (6) Here, is also a function of space and time lengths with respect to the base. As it will be seen, Bd allows to draw space and time lines in the space-time Riemannian representation, with respect to 0. It is this drawing which will allow to measure space-time lengths in this representation. R Using Equations (3), (4), and (5) there is: 1 2222 d1d1 d bb MM ct x xx (7) and spherical coordinates are not written here. Their coefficients will get opposite sign when passing from one metric to the other, because their Euclidean associated local coordinates have their Minkowskian coefficients equal to −1. Therefore, they becomes equal to +1 during the metric transformation when applying Equations (3) and (4). Hence, the and coefficients get also their sign modified but that’s all. Distance no tations Affine distance generated by Euclidean canonical metric of :,RD . 0 Distance given by the Riemannian metric and Equa- tion (7): ,d. On Figure 1 are drawn qualitatively those space lines associated with this Schwarzschild Riemannian metric, with respect to 0. It is only after this drawing, that space-time lengths can be measured by evaluating the distances in 0between space lines (for measuring time) and between time lines (for measuring space). R R R On Figure 2 are firstly added two space-time points, A, and B. A and B are supposed to be infinitely close one to each other, and located on the same time line. It can be checked on Figure 2 that the space-time length between A and B correspond roughly to the number of space lines passed through when going from A to B. Therefore when space lines get close from each other, Riemannian local time is elapsing faster with respect to 0. This is the case as we get x weaker and weaker, that is, as we get closer to the attracting object. Of course, it goes reversely for space distances. That’s for a qualitative understand- ing. Copyright © 2013 SciRes. JMP  F. LASSIAILLE 1029 Figure 1. Space lines drawn with respect to R0 reference frame. Figure 2. Two couples of points, each of them aligned on their local time line, B and sharing the same space line, and such that B ,, ABD AB d . In a precise manner, the Riemannian metric distance between A and B is a value calculated by Equation (7). Let’s calculate this space-time length between A and B: 1 222 1 d b Mc t x d0 b x 2 ,ddA B s (8) because here , and then: 1 ,d 1 b ct M x dAB (9) Now let’s redo this calculation for B and points. Like A and B, they share the same time line, but they are located far from the attracting object. It is sup- posed: DAB ,,DAB R (10) In other words, those segment distances are equal with respect to the Euclidean canonical metric given by 0. If B is the distance of the point from the attracting object, we get: 1 ,d 1 b dAB ct M x (11) and B Because that’s Equation (9) applied to . Since is supposed to be far greater than M, then the following approximation can be done. ,d b dAB ct d,d b ct DABct (12) That’s because here the space-time deformations gen- erated by the attracting object are vanishing. It can be written by other means: BB (13) Indeed, here the base is the 0 base except for their origins. Back to B point, Equation (9) can be written the following way. 1 dd 1 t M x d (14) This equation gives the time ratio between , the local Riemannian time in B point, and its corresponding time in 0 reference frame. For yielding this equa- tion, it has been used Equation (9), dt R ,d, d, ,dd bb dAB c ctDABDABct ct dct . , time distance in 0, has been renamed because this distance can be also evaluated in B point. Now let’s calculate the local and physical time dilatation between x and Rdct distances from the attracting object. The same reasoning with Minkowskian metric yields relativity time dilatation: d1d Mt (15) Another way to understand the difference between Equation (14) and Equation (15) is the following. By construction, the physical local time ratio is growing in- versely as compared with the Riemannian metric local time ratio. In other words, ,,dABDAB ratio must be inverted in order to get the ddctc ratio. That’s because local times are inverted when passing from Min- kowskian to Riemannian representation. In geometric words: The Riemannian time distance is growing proportion- ally with the number of crossed space lines; Local time physical length is growing proportionally with Euclidean distance between two given space lines. Those values are inversely proportional to each other and Equation (15) could be retrieved this way starting from Equation (14). In other words, the relativistic coef- Copyright © 2013 SciRes. JMP  F. LASSIAILLE 1030 ficient 1 is equal to ddt , as seen projected along local tangent of space lines. It can be said that it is also projected along space lines. This rule is illustrated by Figure 3. cd represents, everywhere, the local physical dis- tance between a given couple of space lines. This dis- tance is measured with 0 Euclidean metric. When those lines get close to each other, this value decrease because it is measured with . R R d 0 Inversely, the Riemannian distance, B R , between those space lines remains the same everywhere. This dis- tance is calculated with Equation (7) in a covariant man- ner along space lines. 3. Covariance and Bases This covariance will be used for understanding this geo- metrical Riemannian mechanism. For this let’s go back to Figure 2. Let’s write m the base which is constructing, in B point, theinertial reference frame of the free falling particle. By construction, if uB m are base vectors, and if um B are base vectors, there is m g uu B B . In other words, this m base is orthogonal with its vectors normalized in the Minkowskian metric. This is not a new concept. It comes from general relativity in Minkowskian representation [2]. Now the same way, let’s write r the following base, in B point. If r u are the base vectors, there is r B r h u ur B d . In other words, this base is orthogo- nal with its vectors normalized in the Riemannian metric. 0 u R distance between two space lines is the Riemannian length of r vector. By construction this length stays constant along a given space line. Inversely, cdt represents the distance between space lines calculated along 0 time axis (not along local time axis). The cd vector is parallel transported along a Figure 3. Local time, and global time. “cd ” vector is paral- lel transported along space lines. given space line. The cdt vector is the projected vector of this cd vector. This projection is done along the local space line tangents. But evaluation of this cdt vector pro- jection can be done everywhere along the corresponding space lines, in a parallel transport manner. This is also illustrated by Figure 3. What about the space length ratio? The rule for the answer is the famous “constancy of metric determinant”, which is a classical rule of general relativity. Using it, of course the consequence is merely an inverted evolution of the space length ratio as compared to the time ratio. As an intermediate conclusion, the Riemannian dis- tance allows drawing space lines. When drawing those lines, it is supposed that this Riemannian metric distance, d , between two given space lines is always the same when measured everywhere along those lines. Those space and time lines are drawn in the 0 R reference frame. This representation is understandable with human senses. In [1], it allows to understand the relativistic en- ergy equation in the simple geometric manner of the Py- thagore theorem. Let’s remind that it is possible to de- scribe this Pythagore equation, using surfaces, as a func- tion of luminous points space-time deformation heights. This gives the determination of space-time shape in [1]. 4. How to Apply the Rules of the Postulate 3 [1] When applying the third postulate [1], the projection used for writing 2 dd 1, 1 soper LL R r B R was done along time axis, not along time lines. 0 On Figure 4 this postulate 3 application mode is shown. That’s because the determinant of the metric is sup- posed to be constant, as it was discussed above. Indeed, a geometrical property of this determinant is that it is the surface of the ABCD rectangle of Figure 5 which is de- scribed by the base (of course this surface is meas- ured in ). 0 But this surface is also the surface of the BDE F paral- lelogram of Figure 6 which vertical sides are given by the c dt vector. The other vector side of this parallelo- Figure 4. Application of Postulate 3 of [1]. C opyright © 2013 SciRes. JMP 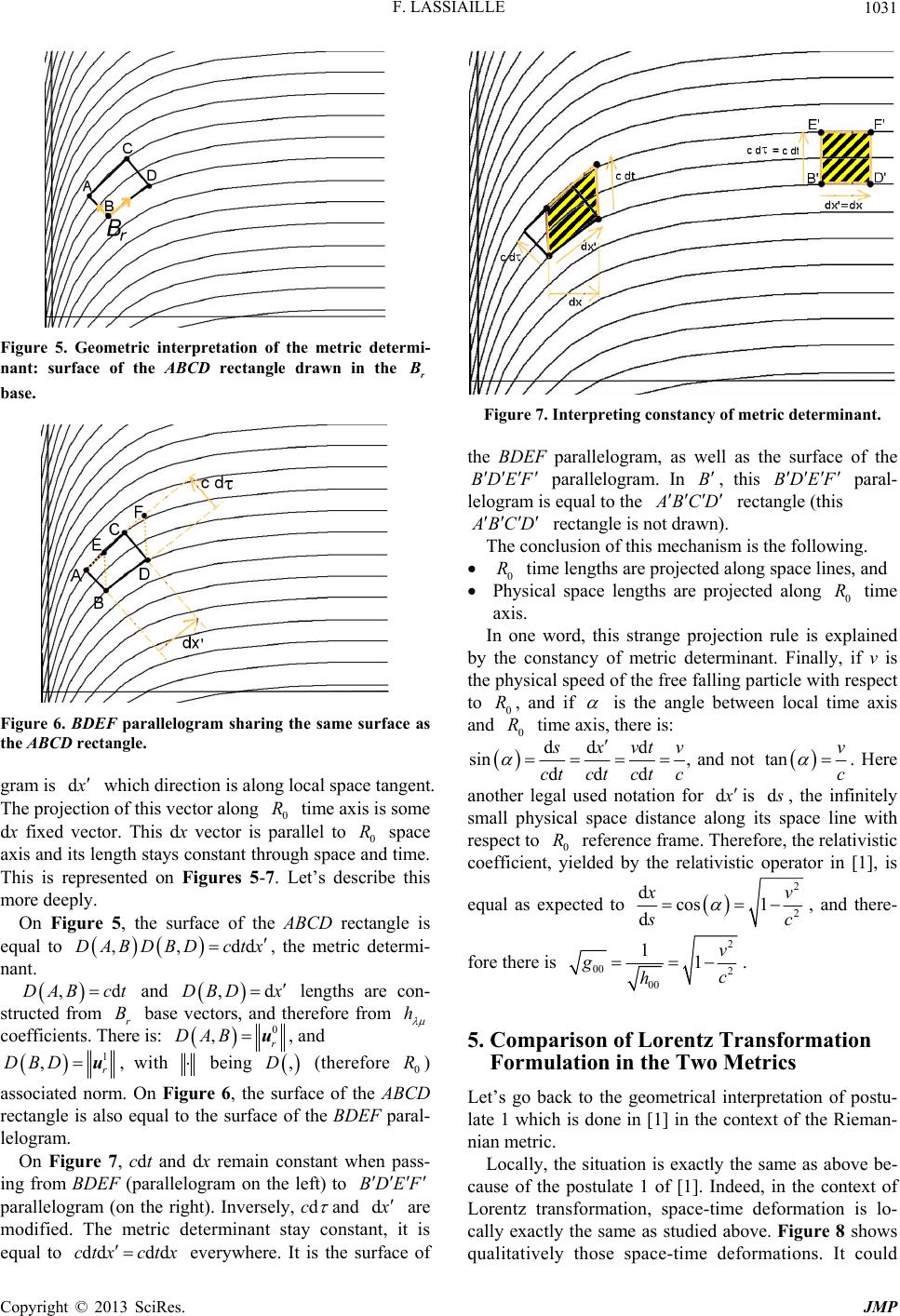 F. LASSIAILLE 1031 Figure 5. Geometric interpretation of the metric determi- nant: surface of the ABCD rectangle drawn in the base. r B Figure 6. BDEF parallelogram sharing the same surface as the ABCD rectangle. gram is d RR ,,ddBD ctx DA ,dDBD x h which direction is along local space tangent. The projection of this vector along 0 time axis is some dx fixed vector. This dx vector is parallel to 0 space axis and its length stays constant through space and time. This is represented on Figures 5-7. Let’s describe this more deeply. On Figure 5, the surface of the ABCD rectangle is equal to , the metric determi- nant. DABD ,dB ctB and lengths are con- structed from r base vectors, and therefore from coefficients. There is: 0 ,r DAB u, and 1 ,r DDB u, with being (therefore ) ,D0 R BDEF associated norm. On Figure 6, the surface of the ABCD rectangle is also equal to the surface of the BDEF paral- lelogram. On Figure 7, cdt and dx remain constant when pass- ing from BDEF (parallelogram on the left) to Figure 7. Interpreting constancy of metric determinant. the BDEF parallelogram, as well as the surface of the BDEF BBDEF parallelogram. In , this paral- lelogram is equal to the d parallelogram (on the right). Inversely, cd and are modified. The metric determinant stay constant, it is equal to everywhere. It is the surface of dd ddctx ctx BCD rectangle (this BCD 0 R rectangle is not drawn). The conclusion of this mechanism is the following. R time lengths are projected along space lines, and 0 Physical space lengths are projected along 0 R time axis. In one word, this strange projection rule is explained by the constancy of metric determinant. Finally, if v is the physical speed of the free falling particle with respect to , and if is the angle between local time axis and time axis, there is: 0 R dd d sin ddd xvtv ct ct ct c , and not tan v c . Here d is another legal used notation for d , the infinitely small physical space distance along its space line with respect to 0 reference frame. Therefore, the relativistic coefficient, yielded by the relativistic operator in [1], is R equal as expected to 2 2 dcos 1 d v sc , and there- 2 00 2 00 11v gc h fore there is . 5. Comparison of Lorentz Transformation Formulation in the Two Metrics Let’s go back to the geometrical interpretation of postu- late 1 which is done in [1] in the context of the Rieman- nian metric. Locally, the situation is exactly the same as above be- cause of the postulate 1 of [1]. Indeed, in the context of Lorentz transformation, space-time deformation is lo- cally exactly the same as studied above. Figure 8 shows qualitatively those space-time deformations. It could Copyright © 2013 SciRes. JMP  F. LASSIAILLE 1032 Figure 8. Space-time deformations in the case of Lorentz transformation, with respect to R frame. even be possible to write also metric equations for this case. Space line has rocked with an angle such as sin vc 00 ,, ,,, ,etc mr RRBBBB ;,ROct ;,,,ctxyz . Therefore, the same construction of vec- tors, bases and frames still applies. The usual and reference frames will be used as usual when writing Lorentz transformation: ,,xyzRO 22 2 22 1 1 1 1 xvt vc vx tt c vc R R (16) For the geometrical understanding of this transforma- tion in [1], a projection of space-time lengths along the time and space axis of referential frame is used. But the normal usage of a basis should dictate to project those lengths along the time and space axis of ref- erential frame. And in the Riemannian representation which has been seen above, those projections were even more different. They were done, for time lengths along space lines (therefore along space axis), and for physical space lengths alongtime axis. Indeed, corresponds to in the description above, and corresponds to R R RR 0 R RB (which is just a reduced version of ). B Let’s write Lorentz transformation in the context of the Riemannian metric. Using the strange projection rule of this representation, the space-time deformation of Fig- ure 8, which is the postulate 1 of [1] space-time defor- mation, yields the following equations. 22 22 2 1 1 1 b b xvt vc vx ct c O tv (17) Equations (17) are the result when applying the strange projection rule seen above, to the Figure 1 of [1] (or Figure 8). Let’s remind that the coordinates of the point are 2 ,, oo tvtvxc RR R , . Therefore the first equation is the projection of local space lengths along 0 time axis (and along Lorentzframe time axis). The second equation is the projection of time lengths along space lines and along Lorentz frame space axis. Let’s remind that the final bb tB RO OR variables of (17) are the coordinates of space-time events in thebase. Here, space lines where parallel to 0 space axis, before the deformation, which is only local to the point. There- fore the speed vector of the point is parallel to 0 space axis. This remark allows to write Equations (17). Now let’s write , rr t B the r base coordinates. This transformation becomes the following. 2 r r xvt vx tt c (18) These equations are obtained using rb hx O R and Equation (17). This is a Galilean transformation, which corresponds to the motion of the point which is the local point of the reference frame. But this motion is interpreted now with covariant space and time units. In- deed, those , rr t B O coordinates are those of the r base which is part of a space-time map. By construction, in this map the resulting metric is the Euclidean trivial tensor, constant everywhere in space-time. It is therefore coherent to find here a Galilean transformation. This last formulation of Lorentz transformation is the correspond- ing one in this Riemannian representation of space-time. Now (16) is derived from (18). First of all, (18) is similar to the affine transformation which is the identity linear application composed with the O to transla- tion. But it is noticed that the O point is moving and its coordinates are function of x and t. Therefore, (18) is in fact a linear transformation with respect to the x and t variables. As such, its determinant is no longer 1, which was the identity linear transformation determinant. Now its determinant is equal to 22 1vc. Therefore, compo- 22 vc sition of this transformation (18) with 11 which multiplies the Identity transformation yields (16), which is the same as (18) but with a determinant equal to 1. And of course this final (16) result is Lorentz transfor- mation. This correspondence between those different formula- tions of Lorentz transformation gives the explanation of the strange projection rule: the geometrical Euclidean interpretation is driven by Equation (18). But this equa- tion is another formulation of Lorentz transform. 6. Comparison of the Geodesics between the Two Metrics Now let’s compare the “following geodesics” principle in those two metrics. This comparison is mandatory be- C opyright © 2013 SciRes. JMP  F. LASSIAILLE 1033 cause this principle is used with the Riemannian metric when writing Equation (15) of [1]. The simplest way to express the “following geodesics” principle is the following. The free falling particle tra- jectory is a geodesic in the Riemannian metric. That’s the most natural and simple way to express the “following geodesics” principle. Of course, this is not the official one. The official one is the following. The free falling particle trajectory is an extremal trajectory in the Minkowskian metric. Now, the usual following reasoning must be done. It is always possible to construct a null trajectory close to any other trajectory. Since the free falling particle trajectory is a strictly positive one, and because of the signature + − − −, (which is not − + + + otherwise the trajectory would be- come a minimal one), therefore its extremal value cannot be a minimal one. Therefore this is a maximal one. This was a reminder. This complicated and mathematical rea- soning will be compared further with the one given by the gravitational model of the three elements theory. Now it must be checked that those two geodesic defi- nitions coincide. That is to say: 1) maximal trajectory in the Minkowskian metric, 2) minimal trajectory in the Riemannian metric, are exactly the same. This is false in the general case. But it is true for a time line and in the case of the weak space-time defor- mations. For proving this let’s compare the geodesic trajectories in the two metrics. Let’s remind usual equations of ex- tremal trajectories in some given metric: 2 2 xx i (19) being 0 for ct, or i for as usual, and being the Christoffel symbols. is the exponential map metric parameter. In the Minkowskian one, it is equal to the physical local time. In the Riemannian one, along a time line the ddh local time is different, related to the first one with 00 . Let’s remind that the difference be- tween those local times is driven by the importance of the space-time vacuum generated along time lines. The extremal (maximal) trajectory in the Minkowskian metric is the following. 20 21 2 200 00 20 2 00 21 2 2 xc g g xc x (20) It has been supposed 0011 for i = 2 and i = 3. Therefore, the corresponding equations for i = 2 and i = 3 become trivial and are not written here. It has been supposed also that 0 ii gxgx 1 1 0xx along the trajectory, meaning that this trajectory is a time line. Under those considerations, (20) equations are coming from (19) equations after calculations. The details of these calculations are available in [3]. Now the extremal (minimal) trajectory in the Riemannian metric is the fol- lowing (expressed with the Minkowskian coefficients and Minkowskian local time for comparison). 20 2 200 00 20 21 2 400 00 21 2 2 xc g xc g (21) It has been supposed also that the trajectory is a time line in the Riemannian metric. The difference between (20) and (21) trajectory equations is only occurring for their second equations and is summarized this way: 22 4 00 22 mr x g (22) 1 where m is the value of in the Minkowskian met- ric trajectory, and r its value in the Riemannian one. Therefore, it is impossible to detect this difference in the weak deformations case. For example, in the Schwarz- schild metric, there is 4 4 00 11 M gx for involved physical distances. (Of course, x is the distance from the attracting object, and M is the Schwarzschild ray). In a more convincing manner, the (20) second equation be- comes the following. 22 22 2 Mc (23) Which is Newton’s acceleration. Whereas the (21) sec- ond equation becomes the following. 4 22 2 22 2 1 22 Mc MMc x x (24) Which is an approximation of Newton’s acceleration. Therefore, those equations are approximately equal. Finally, the second equation of (20) can be written us- ing the angle of the space curve tangent in this space- time Riemannian representation. The result is that Equa- tion (15) of [1] is also a good approximation of the last equation of (20), in the weak space-time deformations case. Nevertheless, Equations (20) and (21) do not yield ex- actly the same trajectories. Of course, the question of which system equation is correct is easy to answer. The Minkowskian metric trajectory is the correct one. This choice can be argued with the help of the gravitational model of the three elements theory. Indeed, in this model the classical space-time distance 22 2 00 11 ddd gc tgx depends upon 00 ddgct c, Copyright © 2013 SciRes. JMP  F. LASSIAILLE Copyright © 2013 SciRes. JMP 1034 related to the total energy of the particle, and 11 dx, the height of the asymmetrical space-time vacuum gen- erated by the motion of this free falling particle. In this model, this vacuum has always a key importance. Therefore it is very coherent to have it minimized in the trajectories. This straightforward physical reasoning must be compared with the mathematical and compli- cated official one, which was reminded above. As a consequence the Minkowskian metric is still of extreme importance and can’t be replaced by the Rie- mannian one. 7. Conclusions The aim given in the introduction has been achieved in a coherent manner. This proves that the gravitational model of the three elements theory is coherent and therefore really compatible with relativity. The Riemannian repre- sentation of space-time which is used in this model is legal. It allows to understand relativity in a more human sensi- tive manner than Minkowskian usual representation. Postulate 1 of [1] geometrical interpretation and postulate 3 of [1] application rule has been explained. Equation (15) of [1] has been explained. It uses the “following ge- odesics” principle in the context of the Riemannian metric. And this has been proven to be a correct approximation for involved physical distances and for time line trajecto- ries. Moreover, this geometrical sensitive description of re- ality allows the construction of the three elements theory, a unifying theory [4]. This theory is fully understandable in this geometrical and deterministic manner. It gives a complete traceability of the mathematic models calcula- tions along their physical explanations. It indicates that a more intimate link might exist between classical physics theories and reality. REFERENCES [1] F. Lassiaille, Journal of Modern Physics, Vol. 3, 2012, pp. 388-397. doi:10.4236/jmp.2012.35054 [2] S. Carroll, “Space Time and Geometry, an Introduction to General Relativity,” Addison-Wesley, San Francisco, 2004. [3] F. Lassiaille, “Gravitational Model of the Three Elements Theory: Mathematical Detailed Calculations,” 2013. http://lumi.chez-alice.fr/anglais/MathDetailedCalc.pdf [4] F. Lassiaille, “Three Elements Theory,” 1999. http://lumi.chez-alice.fr/3elt.pdf  F. LASSIAILLE 1035 Glossary c: Speed of light. : Space-time coordinates. i : Space coordinates. t: Time variable with respect to reference frame. 0 x: Space physical distance between a space-time point and the center of the attracting object in the Schwarz- schild metric, with respect to 0. It is calculated with the help of an integral along a given space line. R R R 0 RB R R 0 R B R B R B B 0: Inertial reference frame “attached to” the universe. For example, in the case of the Schwarzschild metric, is also attached to the attracting object. 0: Base located along0trajectory. The set of those bases is thereference frame. 0 : Inertial reference frame of a “free falling particle” (see definition). This particle is supposed as usual as get- ting a null mass for avoiding modification of the space- time structure. It is located at rest with respect to when located infinitely far. R : Orthogonal and normalized base with respect to 0 Euclidean metric, in which the Minkowskian metric is diagonal. m: Normalized base with respect to the Minkows- kian metric. The set of those bases along a given “time line” (see definition) will construct the reference frame. This base is constructed from base. Its vec- tors are parallel tovectors. Their lengths are inverted from vectors lengths, with respect to the Minkowskian metric. In other words, we get B m g uu B R B B B r: Normalized base with respect to the Riemannian metric. In some way it explains time and space values in reference frame before space-time vacuum genera- tion by the free falling particle. This base is constructed from base. Its vectors are parallel to vectors. Their lengths are inverted from vectors lengths, with respect to the Riemannian metric. In other words, we get . r h uu B . : The vectors of this base are equal to 22 1vcB B R 0 R R which multiplies the vectors of . Free falling particle: in this document, this always means a special kind of free falling particle. Its trajectory coincides with a time coordinate curve in the system of bases. Because of the “following geodesics” princi- ple, it is a geodesic in the Minkowskian metric. As usual this free falling particle gets a null mass, because we don’t want it to generate any space-time deformations around it. Otherwise, this should modify the studied met- ric. And it gets a null speed when located infinitely far, because this means that its trajectory will always be per- pendicular to space lines with respect to 0. In other words, this trajectory is a time curve in this repre- sentation. Space line: a space curve, which is the space three di- mension manifold, represented by a curve after projec- tion on the two dimension figures of this document. But in this document, this curve is always perpendicular to any local time axis in the representation. 0 Time line: the trajectory of a free falling particle (refer to the above definition of “free falling particle”). uB m : base vectors. um B r : base vectors. uB: base vectors. r : Coefficients of the Minkowskian metric with re- spect to the base. B h : Coefficients of the Riemannian metric with re- spect to base. B Copyright © 2013 SciRes. JMP
|