Optics and Photonics Journal, 2013, 3, 29-33
doi:10.4236/opj.2013.32B007 Published Online June 2013 (http://www.scirp.org/journal/opj)
Electromagnetically Induced Transparency Using a
Artificial Molecule in Circuit Quantum Electrodynamics
Hai-Chao Li, Guo-Qin Ge
School of Physics, Huazhong University of Science and Technology, Wuhan, China
Received 2013
ABSTRACT
Electromagnetically induced transparency (EIT) having wide applications in quantum optics and nonlinear optics is
explored ordinarily in various atomic systems. In this paper we present a theoretical study of EIT using supercon- duct-
ing circuit with a V-type artificial molecule constructed by two Josephson charge qubits coupled each other through a
large capacitor. In our theoretical model we make a steady state approximation and obtain the analytical expressions of
the complex susceptibility for the artificial system via the density matrix formalism. The complex susceptibility has
additional dependence on the qubit parameters and hence can be tuned to a certain extent.
Keywords: EIT; Artificial Molecule; Complex Susceptibility
1. Introduction
Electromagnetically induced transparency (EIT) [1,2]
through quantum coherent effects has attracted consider-
able interest due to its extensive applications in quantum
optics and atomic physics. The first experimental dem-
onstration of EIT was based on a Λ-type atomic system
[3]. EIT has also been observed experimentally in the V-
type [4] and cascade-type [5] energy level configurations.
It’s of particular interest to indicate EIT how to appear
via quantum interference in a V-type system because
population trapping isn’t involved. In contrast to the usual
weak probe regime, EIT can be realized in the strong
probe regime [6], where population inversion is not cor-
related with optical gain and the traditional correspond-
dence between inversion and gain is not satisfied.
Circuit quantum electrodynamics(QED) [7,8], where
transmission line resonator plays the role of cavity and
superconducting qubit [9,10] behaves as artificial atom to
replace the natural atom, has recently become a new test-
bed for quantum optics. Compared with the conventional
cavity QED with atomic gases, superconducting circuits
as artificial quantum systems in solid-state devices have
significant advantages, such as offering long coherence
time to implement the quantum gate operations [11], huge
tunability and controllability by external electromagnetic
fields [12]. As an on-chip realization of cavity QED, circuit
QED has reproduced many quantum optical phenomena,
including Kerr and cross-Kerr nonlinearities [12,13], the
Mollow Triplet [14], Autler-Townes effect [15], EIT [16,
17]. Further- more, circuit QED can be used to realize
ultrastrong coupling regime [18] previously inaccessible
to atomic systems and explore novel optical phenomena
emerging only in this regime.
Although have being extensively studied in traditional
atomic systems, investigations of EIT phenomena in
superconducting circuits based on mesoscopic Josephson
junctions are still scarce. Recently experimental observa-
tion of EIT has been reported by using a single artificial
atom coupled to a 1D transmission line [16] and EIT can be
utilized as a sensitive probe of decoherence in superconduc-
ting circuits [19]. Besides, a nanomechanical resonator
can provide additional auxiliary energy levels to a
superconducting Cooper-pair box so that EIT can be
realized in the system [20].
Motivated by these investigations, we propose a scheme
to perform EIT employing V-type artificial molecule, which
is constructed by two superconducting charge qubits
coupled each other through a large capacitor. In our EIT
scheme, a weak probe field with Rabi frequency 1

and frequency ω1 couples the 13 transition while
a strong control field with Rabi frequency 2

and
frequency ω2 couples the 12 transition, as shown
in Figure 1.
This paper is organized as follows. We first describe
the theoretical model and gain the energy spectrum of the
V-type artificial system in Section 2. Then, we give
steady-state analysis of EIT by utilizing the density ma-
trix method and acquire the complex susceptibility for
the superconducting system in Section 3 and our con-
clusions are given in Section 4.

H.-C. LI, G.-Q. GE
30
Figure 1. Schematic illustration of EIT for the artificial
molecule.
2. The Model of Artificial Molecule
Let us consider two interacting superconducting charge
qubits which are electrostatically coupled to each other
by a large capacitor Cm. Each charge qubit has a super-
conducting quantum interference device (SQUID) ring
geometry biased by an external flux and so the effective
Josephson coupling energy can be varied from zero up to
its maximum value. The Hamiltonian of coupled qubits
reads
22
111112 22
22 1122
()cos (
cos( )()
cgJc g
Jmgg
HEnn EEnn
EEnnnn


 

)
(1)
The first four terms represent two independent qubits
and the last term describes the interaction between the
qubits due to the electrostatical coupling of the capacitor.
EJ1 and EJ2 are the effective Josephson coupling energy
for the corresponding SQUID; β1 and β2 are the phases of
the SQUID; Ec1 and Ec2 are the effective Cooper-pair
charging energies for the qubits; ni and ngi for I = 1,2 are
the number operator of excess Cooper-pairs on the island
and the normalized gate induced charge; Em is the capa-
citive coupling energy between the charge qubits.
Working in the vicinity of one degeneracy point (ngi∈
[0,1]), only two adjacent charge states 0 and 1 on
the island are relevant while all other charge states, hav-
ing a much higher energy, can be ignored [10]. In this
case the Hamiltonian can be written as
12
1,2
21 12
11 1
22 4
11
22
z
iziJiximz z
i
mz mz
HBEE
EE


 


 




(2)
where Bzi = Eci(1–2ngi) for I = 1,2 are the difference of
the electrostatic energy between the states 0 and 1,
z

and
x

are the Pauli matrices and δi = 1/2–ngi.
Switching to the eigenbasis e and
g
of the qubits
and exactly at the co-resonance point δi = 0, the Hamil-
tonian takes the form
112 21 2
11 1
22 4
J
zJzmx
HEEEx

    (3)
To avoid confusion we introduce a second set of Pauli
operator ρ acting on the eigenstates of qubits. Without
loss of generality, we assume that the two supercon-
ducting charge qubits are identical (i.e., Ec1 = Ec2 = Ec,
EJ1 = EJ2 = EJ). So the eigenvalues of coupled qubits are
readily written as
1
22
2
3
2
1
22
2
1
4
1(16)
4
1
4
1
4
1(16)
4
mJ
m
mJ
m
EEE
EE
EE
EEE



 
(4)
with the corresponding eigenstates being


4sin cos
1
32
1
22
1cos sin
g
ge
ge eg
ge eg
e
g
ge





e
(5)
Here the parameter α satisfies the following relations
22 2
4
sin2cos 2
16 16
mJ
mJ m
EE
EE EE
 

2
J
(6)
It is worthwhile to note that arbitrary transitions can
not be allowed in the above four states due to selection
rules for superconducting qubits. By calculating the ma-
trix elements of ρx1 and ρx2 between the eigenstates, we
find that the transitions 14 and 23 are
forbidden while the other transitions with nonzero matrix
elements are allowed. choosing the three levels with low-
est eigenenergies shown in Figure 1, we obtain the V-
type artificial system.
3. Complex Susceptibility
EIT phenomenon of a closed three level system inter-
acting with a weak probe field and a strong control field
can be demonstrated by adopting the density matrix for-
malism. In the eigenbasis of the qubits, the interaction
Hamiltonian between the three-level artificial molecule
and two semiclassical fields is expressed as (ħ = 1)
12
12
2211
1..
2
iti t
int
H
eeg egHce
  


  (7)
In the basis {1, 2and 3} of the V-type artificial
system and with the rotating-wave approximation, the
interaction Hamiltonian is given by
1
2
1
2
11
cos3 1
22
1
cos21..
2
(
)
it
int
it
He
eH






 
 c
(8)

H.-C. LI, G.-Q. GE 31
In the interaction picture, the Hamiltonian of the sys-
tem reads
12 12
1
33223121 ..
2()
I
H
Hc    (9)
where Δ1 = ω31ω1 is the detuning of the probe field, Δ2 =
ω21ω2 is the detuning of the control field,
11
cos 2   and 22 cos 2   .
We can select the frequencies of the fields so that the
probe field ω1 and the control field ω2 are near resonant
with the transitions 13 and 12, respectively.
In this case, other transitions can be ignored in our dis-
cussion. The evolution of the system is governed by the
set of density matrix equations of motion
1
2
*
333331 1331
*
222222 1221
3131131111332 32
2121 21211221 23
*
3232132231112
11 22 33
22
22
()()
22
()
22
()
22
1
ii
ii
ii
i
ii
ii
i



 
 
 






 
 
 
 
 







(10)
Here we further assume that the control field frequency
ωc matchs the level spacing between the states 2 and
1, i.e. Δ2 = 0. In these equations we have introduced
phenomenologically the relaxation rates Γi (I =1,2,3) for
the levels as well as the total dephasing rates γij =
(Γi+Γi)/2+τφ including the relaxation and pure dephasing
processes. Since we are interested in the dispersion and
absorption properties of the V-type artificial system, only
first-order perturbation expansion of the equations of
matrix elements are necessary. For the system we set[21]
(0)(0)(0) 2
33 2211
22
0
22
B
B
B
 

 
 B
(11)
where B is the rate of pumping by the control field
2
2
21
1
2
B


 (12)
Taking into account the steady-state solution (i.e., all
derivatives are set equal to zero), we have the first order
matrix element
2(0) (0)
211 22 (1) (0)
1
3111 321
21
1
2
2
311 321
()
=()
2
()()
4
ii
ii
 

 









  


Combining the relation
2
0 131 31
2
 
 (14)
with equation (12), we have the following expressions of
the complex susceptibility i
 
  :
2
2
31 12 (0)2 2
111 32
0
2
2(0) (0)
112231 32
21
cos [()
4
2
()()]
4
Z
 





 


(15)
2
2
31 2
(0) 2
11323132311
0
22
22
(0) (0)2
112231 321
21
cos {[() ]
4
2
()()}
44
Z
 



 





  
(16)
where 0

is the vacuum permittivity, μ31 is the transi-
tion dipole moment and

2
2
232
31 321311321
()
4
Z
 

  (17)
It seems that the above expressions are similar to the
susceptibilities of the conventional three level atomic
systems, but here the complex susceptibility of the
artificial molecule has additional dependence on the
tunable Josephson coupling energy EJ and the capacitive
coupling strength Em through the parameter α and hence
can be tuned to a certain extent.
Figures 2(a) and (b) plot both the real and imaginary
parts of the susceptibility χ as a function of the probe
detuning Δ1 and the dimensionless ratio of the Josephson
coupling energy EJ to the interaction energy Em acco-
rding to the equations (15) and (16). Figure 2 shows that
the absorption profile is even symmetric and the disper-
sion profile is odd about the zero probe detuning point Δ1
= 0. We can observe that the absorption is minimum at
the zero point Δ1 = 0 and increases with the growth of
the Josephson coupling energy EJ, but the absorption
value does not become large after the EJ is increased to a
cer- tain value, as can be seen from Figure 2(b).
4








(13)
Moreover, absorption coefficient can be dominated
greatly by the control field strength Ωc, as depicted in
Figure 3. From the drawing, we see that single absorp-
tion peak appears in the regime of weak control field and
indicates strong absorption to probe field. As the control
power is increased, the doublet spacing of absorption
curve increases and absorption value between the two
peaks gradually tends to zero EIT, i.e. EIT effect arises in
the higher control intensities.
4. Conclusions
In conclusion, we have theoretically investigated the EIT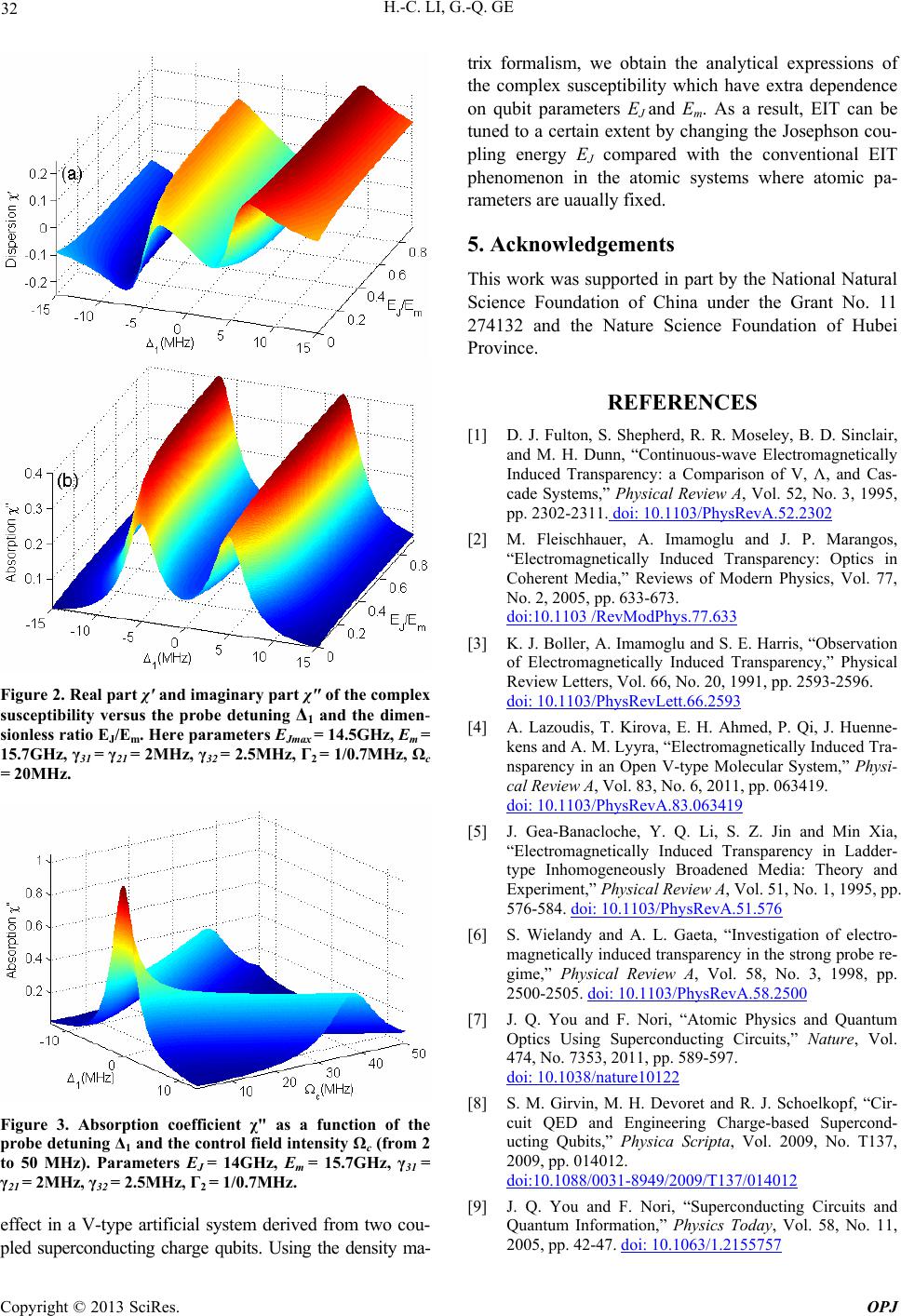

H.-C. LI, G.-Q. GE
32
Figure 2. Real part χ' and imaginary part χ" of the complex
susceptibility versus the probe detuning Δ1 and the dimen-
sionless ratio EJ/Em. Here parameters EJmax = 14.5GHz, Em =
15.7GHz, γ31 = γ21 = 2MHz, γ32 = 2.5MHz, Г2 = 1/0.7MHz, Ωc
= 20MHz.
Figure 3. Absorption coefficient χ" as a function of the
probe detuning Δ1 and the control field intensity Ωc (from 2
to 50 MHz). Parameters EJ = 14GHz, Em = 15.7GHz, γ31 =
γ21 = 2MHz, γ32 = 2.5MHz, Г2 = 1/0.7MHz.
effect in a V-type artificial system derived from two cou-
pled superconducting charge qubits. Using the density ma-
trix formalism, we obtain the analytical expressions of
the complex susceptibility which have extra dependence
on qubit parameters EJ and Em. As a result, EIT can be
tuned to a certain extent by changing the Josephson cou-
pling energy EJ compared with the conventional EIT
phenomenon in the atomic systems where atomic pa-
rameters are uaually fixed.
5. Acknowledgements
This work was supported in part by the National Natural
Science Foundation of China under the Grant No. 11
274132 and the Nature Science Foundation of Hubei
Province.
REFERENCES
[1] D. J. Fulton, S. Shepherd, R. R. Moseley, B. D. Sinclair,
and M. H. Dunn, “Continuous-wave Electromagnetically
Induced Transparency: a Comparison of V, Λ, and Cas-
cade Systems,” Physical Review A, Vol. 52, No. 3, 1995,
pp. 2302-2311. doi: 10.1103/PhysRevA.52.2302
[2] M. Fleischhauer, A. Imamoglu and J. P. Marangos,
“Electromagnetically Induced Transparency: Optics in
Coherent Media,” Reviews of Modern Physics, Vol. 77,
No. 2, 2005, pp. 633-673.
doi:10.1103 /RevModPhys.77.633
[3] K. J. Boller, A. Imamoglu and S. E. Harris, “Observation
of Electromagnetically Induced Transparency,” Physical
Review Letters, Vol. 66, No. 20, 1991, pp. 2593-2596.
doi: 10.1103/PhysRevLett.66.2593
[4] A. Lazoudis, T. Kirova, E. H. Ahmed, P. Qi, J. Huenne-
kens and A. M. Lyyra, “Electromagnetically Induced Tra-
nsparency in an Open V-type Molecular System,” Physi-
cal Review A, Vol. 83, No. 6, 2011, pp. 063419.
doi: 10.1103/PhysRevA.83.063419
[5] J. Gea-Banacloche, Y. Q. Li, S. Z. Jin and Min Xia,
“Electromagnetically Induced Transparency in Ladder-
type Inhomogeneously Broadened Media: Theory and
Experiment,” Physical Review A, Vol. 51, No. 1, 1995, pp.
576-584. doi: 10.1103/PhysRevA.51.576
[6] S. Wielandy and A. L. Gaeta, “Investigation of electro-
magnetically induced transparency in the strong probe re-
gime,” Physical Review A, Vol. 58, No. 3, 1998, pp.
2500-2505. doi: 10.1103/PhysRevA.58.2500
[7] J. Q. You and F. Nori, “Atomic Physics and Quantum
Optics Using Superconducting Circuits,” Nature, Vol.
474, No. 7353, 2011, pp. 589-597.
doi: 10.1038/nature10122
[8] S. M. Girvin, M. H. Devoret and R. J. Schoelkopf, “Cir-
cuit QED and Engineering Charge-based Supercond-
ucting Qubits,” Physica Scripta, Vol. 2009, No. T137,
2009, pp. 014012.
doi:10.1088/0031-8949/2009/T137/014012
[9] J. Q. You and F. Nori, “Superconducting Circuits and
Quantum Information,” Physics Today, Vol. 58, No. 11,
2005, pp. 42-47. doi: 10.1063/1.2155757

H.-C. LI, G.-Q. GE
33
[10] Y. A. Pashkin, O. Astafiev, T. Yamamoto, Y. Nakamura
and J. S. Tsai, “Josephson Charge Qubits: a Brief Re-
view,” Quantum Information Processing, Vol. 8, 2009,
pp. 55-80. doi: 10.1007/s11128-009-0101-5
[11] B. C. Sanders, “Quantum Optics in Superconducting
Circuits,” AIP Conference Proceedings, Vol. 1398, 2011,
pp. 46-49. doi: 10.1063/1.3644209
[12] Y. Hu, G. Q. Ge, S. Chen, X. F. Yang and Y. L. Chen,
“Cross-Kerr-effect Induced by Coupled Josephson Qubits
in Circuit Quantum Electrodynamics,” Physical Review A,
Vol. 84, No. 1, 2011, p. 012329.
doi: 10.1103/PhysRevA.84.012329
[13] S. Rebić, J. Twamley and G. J. Milburn, “Giant Kerr
Nonlinearities in Circuit Quantum Electrodynamics,”
Physical Review Letters, Vol. 103, No. 15, 2009, p.
150503. doi: 10.1103/PhysRevLett.103.150503
[14] O. Astafiev et al., “Resonance Fluorescence of a Single
Artificial Atom,” Science, Vol. 327, No. 5967, 2010, pp.
840-843. doi: 10.1126/science.1181918
[15] M. A. Sillanpää et al., “Autler-Townes Effect in a Super-
conducting Three-Level System,” Physical Review Let-
ters, Vol. 103, No. 19, 2009, p. 193601.
doi: 10.1103/PhysRevLett.103.193601
[16] A. A. Abdumalikov, Jr., O. Astafiev, A. M. Zagoskin, Yu.
A. Pashkin, Y. Nakamura and J. S. Tsai, “Electromag-
netically Induced Transparency on a Single Artificial
Atom,” Physical Review Letters, Vol. 104, No. 19, 2010,
p. 193601. doi: 10.1103/PhysRevLett.104.193601
[17] J. Joo, J. Bourassa, A. Blais and B. C. Sanders, “Electro-
magnetically Induced Transparency with Amplification in
Superconducting Circuits,” Physical Review Letters, Vol.
105, No. 7, 2010, p. 073601.
doi: 10.1103/PhysRevLett.105.073601
[18] T. Niemczyk et al., “Circuit Quantum Electrodynamics in
the Ultrastrong-coupling Regime,” Nature Physics, Vol. 6,
No. 10, 2010, pp. 772-776. doi: 10.1038/nphys1730
[19] K. V. R. M. Murali, Z. Dutton, W. D. Oliver, D. S.
Crankshaw and T. P. Orlando, “Probing Decoherence
with Electromagnetically Induced Transparency in Su-
perconductive Quantum Circuits,” Physical Review Let-
ters, Vol. 93, No. 8, 2004, pp. 087003.
doi: 10.1103/PhysRevLett.93.087003
[20] X. Z. Yuan, H. S. Goan, C. H. Lin, K. D. Zhu and Y. W.
Jiang, “Nanomechanical-resonator-assisted Induced Tra-
nsparency in a Cooper-pair Box System,” New Journal of
Physics, Vol. 10, 2008, p. 095016.
doi: 10.1088/1367-2630/10/9/095016
[21] G. R. Welch, “Observation of V-Type Electromag- neti-
cally Induced Transparency in a Sodium Atomic Beam,”
Foundations of Physics, Vol.28, No. 4, 1998, pp. 621-638.
doi: 10.1023/A:1018765706887