 Journal of Modern Physics, 2013, 4, 28-37 http://dx.doi.org/10.4236/jmp.2013.47A2005 Published Online July 2013 (http://www.scirp.org/journal/jmp) Thermophysical Characterization and Crystallization Kinetics of Semi-Crystalline Polymers Matthieu Zinet, Zakariaa Refaa, M’hamed Boutaous*, Shihe Xin, Patrick Bourgin Université de Lyon, CNRS, INSA-Lyon, CETHIL, UMR 5008, F-69621, Villeurbanne, France Email: *mhamed.boutaous@insa-lyon.fr Received April 15, 2012; revised May 18, 2013; accepted June 23, 2013 Copyright © 2013 Matthieu Zinet et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Final properties and behavior of polymer parts are known to be directly linked to the thermomechanical history experi- enced during their processing. Their quality depends on their structure, which is the result of the interactions between the process and the polymers in terms of thermomechanical kinetics. To study the actual behavior of a polymer during its transformation, it is necessary to take into account all the thermal dependencies of their thermophysical properties. In this paper, a complete experimental thermal characterization of a semi-crystalline polymer is performed. Thermal con- ductivity is measured using the hot wire method. The PVT diagram is obtained by means of an isobaric piston type di- latometer. Heat capacity is characterized versus temperature by differential scanning calorimetry (DSC). A modification of the Schneider rate crystallization equations is proposed, allowing to identify in a simple way all the crystallization kinetics parameters, using only DSC measurements. Finally, a multiphysical coupled model is built in order to numeri- cally simulate the cooling of a polypropylene plate, as in the cooling stage of the injection molding process. Calculated evolutions of temperature, crystallinity, pressure and specific volume across the plate thickness are presented and com- mented. Keywords: Thermophysical Characterization; Heat Transfer; Crystallization Kinetics; Polymer; Multiphysical Modeling 1. Introduction Polymers materials play an important role in the industry, especially polymer based composite materials, which are increasingly used in many industrial domains such as au- tomotive, aeronautics, building and civil engineering. They represent solutions for weight and cost reduction, energy saving, increasing safety and possibilities of innovation in design. Due to a lack of experimental data (characterization experiments are costly and difficult) and to the complex- ity of the multiphysical coupling involved in the numeri- cal simulation of the behavior of polymers in processing condition, only few complete parametric studies are avai- lable in the literature. The thermal and mechanical rates experienced by the polymer during processing determine, to a great extent, the final material structure which in turn governs its final thermomechanical behavior. In semi- crystalline polymers, the crystallization phenomenon plays a crucial role in the quality of industrial parts. It strongly affects rheological properties and influences mechanical and barrier properties of obtained objects [1]. Many efforts have been devoted to the characterization of these materials and to the understanding of the funda- mentals concerning their physical structure, their ther- momechanical behavior and the link between the struc- ture, the process and the final properties [2-5]. Neverthe- less, there are still many phenomena to investigate in order to master the polymer final behavior, to explain the mechanisms involved in polymer transformation and/or crystallization in real industrial cases and to propose in- novative industrial solutions. For instance, in the injec- tion molding process (one of the most used in polymer processing industry), crystallization kinetics directly in- fluences the part behavior regarding both its dimensional stability and its mechanical and thermal performances. Indeed, the different crystalline morphologies and sizes are responsible for the residual stresses within the parts, leading to shrinkage and deformation of the material. In other words, the final physical structure is responsible for the thermal and mechanical characteristics of the obtain- ed parts. For the modeling of such material transformation, *Corresponding author. C opyright © 2013 SciRes. JMP 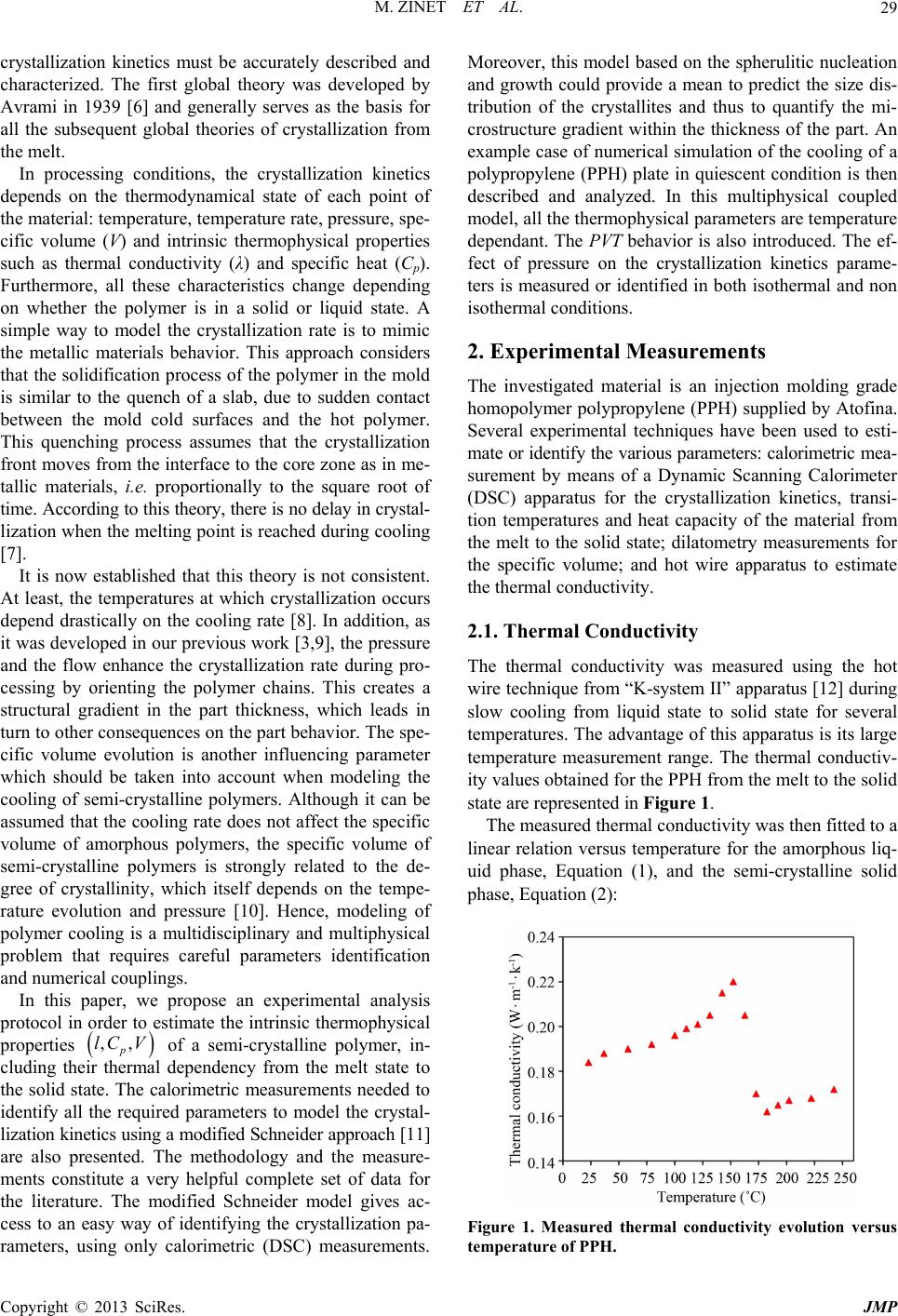 M. ZINET ET AL. 29 crystallization kinetics must be accurately described and characterized. The first global theory was developed by Avrami in 1939 [6] and generally serves as the basis for all the subsequent global theories of crystallization from the melt. In processing conditions, the crystallization kinetics depends on the thermodynamical state of each point of the material: temperature, temperature rate, pressure, spe- cific volume (V) and intrinsic thermophysical properties such as thermal conductivity (λ) and specific heat (Cp). Furthermore, all these characteristics change depending on whether the polymer is in a solid or liquid state. A simple way to model the crystallization rate is to mimic the metallic materials behavior. This approach considers that the solidification process of the polymer in the mold is similar to the quench of a slab, due to sudden contact between the mold cold surfaces and the hot polymer. This quenching process assumes that the crystallization front moves from the interface to the core zone as in me- tallic materials, i.e. proportionally to the square root of time. According to this theory, there is no delay in crystal- lization when the melting point is reached during cooling [7]. It is now established that this theory is not consistent. At least, the temperatures at which crystallization occurs depend drastically on the cooling rate [8]. In addition, as it was developed in our previous work [3,9], the pressure and the flow enhance the crystallization rate during pro- cessing by orienting the polymer chains. This creates a structural gradient in the part thickness, which leads in turn to other consequences on the part behavior. The spe- cific volume evolution is another influencing parameter which should be taken into account when modeling the cooling of semi-crystalline polymers. Although it can be assumed that the cooling rate does not affect the specific volume of amorphous polymers, the specific volume of semi-crystalline polymers is strongly related to the de- gree of crystallinity, which itself depends on the tempe- rature evolution and pressure [10]. Hence, modeling of polymer cooling is a multidisciplinary and multiphysical problem that requires careful parameters identification and numerical couplings. In this paper, we propose an experimental analysis protocol in order to estimate the intrinsic thermophysical properties p of a semi-crystalline polymer, in- cluding their thermal dependency from the melt state to the solid state. The calorimetric measurements needed to identify all the required parameters to model the crystal- lization kinetics using a modified Schneider approach [11] are also presented. The methodology and the measure- ments constitute a very helpful complete set of data for the literature. The modified Schneider model gives ac- cess to an easy way of identifying the crystallization pa- rameters, using only calorimetric (DSC) measurements. Moreover, this model based on the spherulitic nucleation and growth could provide a mean to predict the size dis- tribution of the crystallites and thus to quantify the mi- crostructure gradient within the thickness of the part. An example case of numerical simulation of the cooling of a polypropylene (PPH) plate in quiescent condition is then described and analyzed. In this multiphysical coupled model, all the thermophysical parameters are temperature dependant. The PVT behavior is also introduced. The ef- fect of pressure on the crystallization kinetics parame- ters is measured or identified in both isothermal and non isothermal conditions. 2. Experimental Measurements The investigated material is an injection molding grade homopolymer polypropylene (PPH) supplied by Atofina. Several experimental techniques have been used to esti- mate or identify the various parameters: calorimetric mea- surement by means of a Dynamic Scanning Calorimeter (DSC) apparatus for the crystallization kinetics, transi- tion temperatures and heat capacity of the material from the melt to the solid state; dilatometry measurements for the specific volume; and hot wire apparatus to estimate the thermal conductivity. 2.1. Thermal Conductivity The thermal conductivity was measured using the hot wire technique from “K-system II” apparatus [12] during slow cooling from liquid state to solid state for several temperatures. The advantage of this apparatus is its large temperature measurement range. The thermal conductiv- ity values obtained for the PPH from the melt to the solid state are represented in Figure 1. The measured thermal conductivity was then fitted to a linear relation versus temperature for the amorphous liq- uid phase, Equation (1), and the semi-crystalline solid phase, Equation (2): ,,lC V Figure 1. Measured thermal conductivity evolution versus temperature of PPH. Copyright © 2013 SciRes. JMP 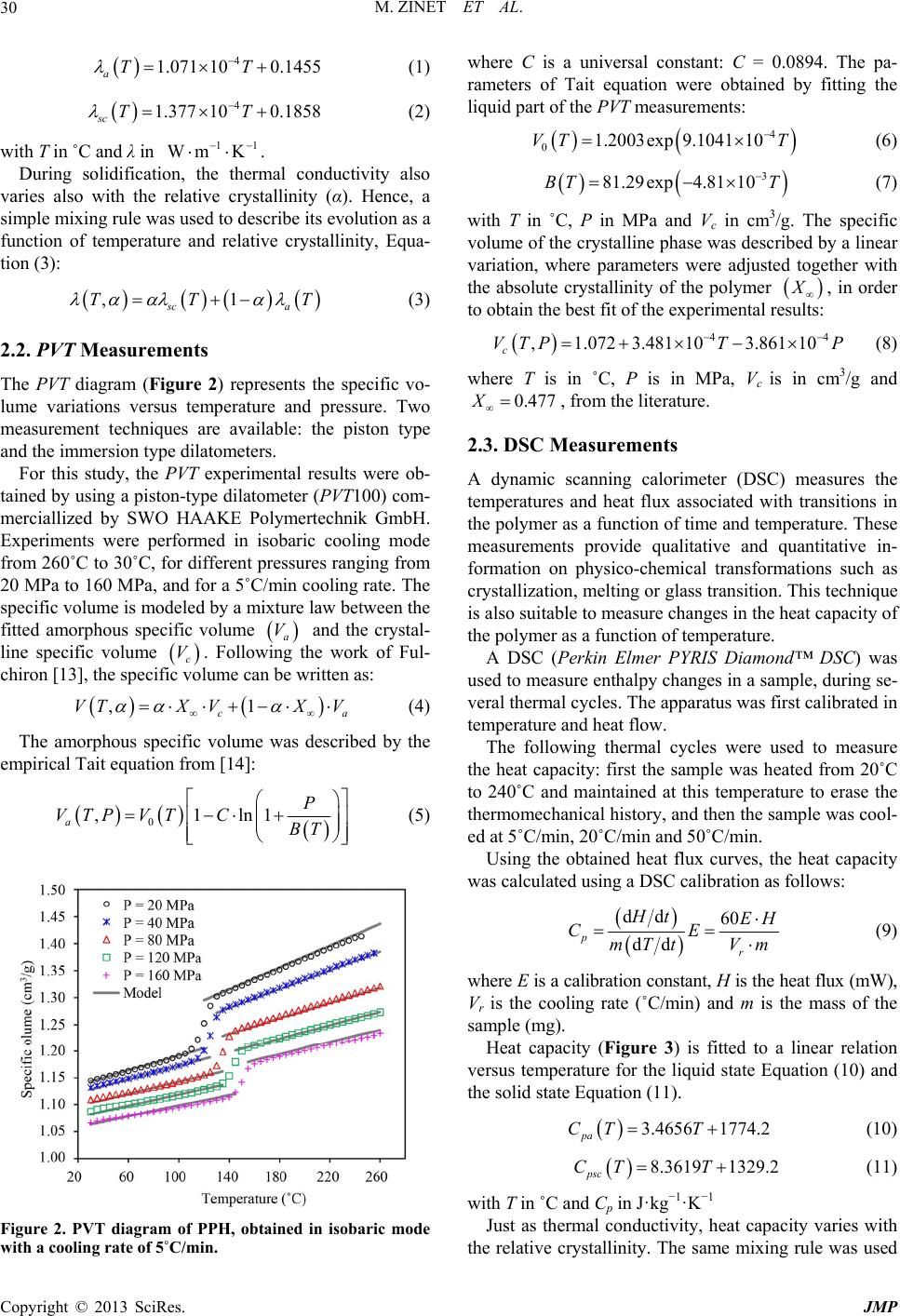 M. ZINET ET AL. 30 1.071 10 aT 40.1455T 40.1858T 11 K (1) 1.377 10 sc T Wm (2) with T in ˚C and λ in . During solidification, the thermal conductivity also varies also with the relative crystallinity (α). Hence, a simple mixing rule was used to describe its evolution as a function of temperature and relative crystallinity, Equa- tion (3): ,1 a TT T V 1 ca VX V sc (3) 2.2. PVT Measurements The PVT diagram (Figure 2) represents the specific vo- lume variations versus temperature and pressure. Two measurement techniques are available: the piston type and the immersion type dilatometers. For this study, the PVT experimental results were ob- tained by using a piston-type dilatometer (PVT100) com- merciallized by SWO HAAKE Polymertechnik GmbH. Experiments were performed in isobaric cooling mode from 260˚C to 30˚C, for different pressures ranging from 20 MPa to 160 MPa, and for a 5˚C/min cooling rate. The specific volume is modeled by a mixture law between the fitted amorphous specific volume a and the crystal- line specific volume . Following the work of Ful- chiron [13], the specific volume can be written as: c V ,X VT (4) The amorphous specific volume was described by the empirical Tait equation from [14]: 0 ,1 a VT P VTCln1 P BT (5) Figure 2. PVT diagram of PPH, obtained in isobaric mode with a cooling rate of 5˚C/min. where C is a universal constant: C = 0.0894. The pa- rameters of Tait equation were obtained by fitting the liquid part of the PVT measurements: 4 01.2003exp 9.104110VT T (6) 3 81.29exp4.81 10BT T (7) with T in ˚C, P in MPa and Vc in cm3/g. The specific volume of the crystalline phase was described by a linear variation, where parameters were adjusted together with the absolute crystallinity of the polymer , in order to obtain the best fit of the experimental results: 44 ,1.0723.481 103.861 10 c VTPT P 0.477X (8) where T is in ˚C, P is in MPa, Vc is in cm3/g and , from the literature. 2.3. DSC Measurements A dynamic scanning calorimeter (DSC) measures the temperatures and heat flux associated with transitions in the polymer as a function of time and temperature. These measurements provide qualitative and quantitative in- formation on physico-chemical transformations such as crystallization, melting or glass transition. This technique is also suitable to measure changes in the heat capacity of the polymer as a function of temperature. A DSC (Perkin Elmer PYRIS Diamond™ DSC) was used to measure enthalpy changes in a sample, during se- veral thermal cycles. The apparatus was first calibrated in temperature and heat flow. The following thermal cycles were used to measure the heat capacity: first the sample was heated from 20˚C to 240˚C and maintained at this temperature to erase the thermomechanical history, and then the sample was cool- ed at 5˚C/min, 20˚C/min and 50˚C/min. Using the obtained heat flux curves, the heat capacity was calculated using a DSC calibration as follows: dd 60 dd p r Ht EH CE mTt Vm (9) where E is a calibration constant, H is the heat flux (mW), Vr is the cooling rate (˚C/min) and m is the mass of the sample (mg). Heat capacity (Figure 3) is fitted to a linear relation versus temperature for the liquid state Equation (10) and the solid state Equation (11). 3.4656 1774.2 pa CT T (10) 8.3619 1329.2 psc CT T (11) with T in ˚C and Cp in J·kg−1·K−1 Just as thermal conductivity, heat capacity varies with the relative crystallinity. The same mixing rule was used Copyright © 2013 SciRes. JMP  M. ZINET ET AL. 31 to describe its evolution as a function of temperature and relative crystallinity, Equation (12). 1 pa CT 0 T cf TfT , ppsc CT CT (12) In order to study the crystallization kinetics, the same DSC apparatus was used to perform isothermal and non- isothermal crystallization measurements, for several tem- peratures and cooling rates. From the obtained heat flow curves Figures 4 and 5, the relative crystallinity was calculated from the partial area method (the area under the crystallization peak at in- stant t over the total area of the peak), see further in Fig- ures 6 and 7. The DSC measurements also give an estimation of the thermodynamic equilibrium melting temperature m of the polymer, using the Hoffman-Weeks method [5] and the analysis of isothermal measurements. In this approach, the equilibrium melting temperature is given by the intersection between the linear curve of the evolution of the crystallization temperature versus the melting temperature of the polymer and the curve of Tm = Tc. Figure 3. Heat capacity of PPH versus temperature. Figure 4. Measured heat flux for isothermal crystallizations. Figure 5. Measured heat flux for constant cooling rate crys- tallizations. Figure 6. Measured and simulated isothermal crystalliza- tion rates. Figure 7. Measured and simulated non isothermal crystal- lization rates. After summarizing all the DSC measurements, m T was found to be 200˚C as it is shown in Figure 8. The glass transition temperature Tg was found to be −10˚C. 0 Copyright © 2013 SciRes. JMP  M. ZINET ET AL. 32 Figure 8. Determination of the equilibrium melting tem- perature. 3. Crystallization Parameters 3.1. Crystallization Kinetics Model The evolution of the relative crystallinity t 1exptt Nt Gt as a function of time and temperature history is described by means of the quiescent crystallization kinetics theories. They generally belong to two types of approaches: the geometrical approach [6] expresses the volume occupied by the semi-crystalline part of the polymer, whereas the probabilistic approach expresses the probability that an element of volume crystallizes [15,16]. The mathemati- cal developments inferred by these approaches differ; nevertheless, they lead to identical results. In the geometrical approach, the free growth of sphere- ical crystalline entities (representing the spherulites) is modeled, then a correction is introduced to take into ac- count the fact that the growth is actually not free but lim- ited by the contact between adjacent entities (the socal- led impingement). This results in the following expres- sion: (13) where ’ is the extended crystalline fraction correspond- ing to the fictitious free growth of the crystallites. The set of equations developed by Schneider et al. [11] describes the evolution of the extended crystalline fraction on the basis of the spherulitic nucleation and growth process. According to these concepts, is the nuclei activa- tion rate (in s−1·m−3) and is the linear growth rate of the spherulites (m·s−1). Ri being the spherulite radius, the extended crystalline fraction (i.e. the crystalline vo- lume per material volume unit if impingement is disre- garded) is expressed as: 33 4 π 33 ii ii Rt 0 4 πt tRt (14) Successive time derivations of this expression lead to: 2 0 1 dd 4π dd i i R RGtt tt (15) 12 2 dd 4π dd i i tRtGt t tt (16) 2 3 dd 8π dd i i tRt Gtt tt (17) 3 d8π d tNt t (18) with the following intermediate variables: 3 14πitot i tRtSt (19) representing the total surface area of the spherulites Stot, 28π8π itot i tRtRt (20) 2 is proportional to the sum of the spherulites radii Rtot, and: 38πtNt (21) 3 is proportional to the number of spherulites per unit volume. The final set of these so-called rate equations reads: 3 23 12 01 8πtNt tGt t tGt t tGt t (22) and the relative crystallinity is ultimately given by: 0 1exptt (23) The main benefit of the Schneider modeling approach is that the simulated geometrical characteristics of the crystalline phase (number of spherulites, radii, surface area) can be retrieved thanks to the intermediate vari- ables of the system. 3.2. Modified Rate Equations For polypropylene, nucleation is known to be heteroge- neous: for a given supercooling, the activated nuclei ap- pear simultaneously; their number per unit volume is re- lated to temperature according to the following relation- ship [17]: 0 exp m NTtaT Ttb (24) 0 T where m is the equilibrium melting temperature, a and b are two parameters to be experimentally determined. The linear growth rate is temperature dependant and Copyright © 2013 SciRes. JMP  M. ZINET ET AL. 33 given by the Hoffman-Lauritzen model [18]: 0exp exp U GT GRT T 0 g m K TT T U 30 CTT 0 T (25) where is the activation energy, R is the gas constant, gis the temperature below which molecu- lar motion becomes impossible, Tg is the glass transition temperature, m is the equilibrium melting temperature, and G0 and Kg are two polymer parameter to be deter- mined. Thus, the time dependant growth rate appearing in Equation (22) can be written: 0 GGTt Gt (26) Insertion of Equations (24) and (25) in the set of rate equations, Equation (22) leads to: 0 3 20 02 2 10 2 2 01 3 00 1 3 00 d 8πexp exp d 8πexp exp 8πexp 8πexp 8πexp 8πexp 8πexp m taTT t tGbGTt Gbt tGbGTtt Gbt tGbGTt Gbt 0 m tb aTTt t i (27) A modified set of rate equations with new intermediate variables 0 m aTTt is thus obtained: 2 12 01 exptGTt tGTt t tGTt t 000 8πtCt 3 00 expCG b G 0 T 0 T 0 m T (28) and the link between this modified set of rate equation and the previously defined extended crystalline fraction is: (29) where C0 is a polymer parameter defined as: (30) Note that the parameter C0 is a combination of a growth related parameter 0 and a nucleation related parameter (b). On account of this, it has no strict physical meaning, but it allows the experimental characterization of the crystallization kinetics by means of differential scanning calorimetry only. Indeed, the nucleation rate effect and the growth rate effect on crystallinity evolu- tion measurements obtained from DSC experiments can- not be completely discriminated: G0 and exp b cannot be individually identified as they always appear together as a product in the rate equations. Thanks to this modified Schneider formalism, the cry- stallization kinetics of the polymer under quiescent con- ditions is completely described when the parameters m, Tg, U*, a, Kg and C0 are known. The equilibrium melting temperature m is determined by the Hoffman-Weeks method as shown in Section 2. The glass transition tem- perature Tg is known to be 0˚C for polypropylene. The activation energy U* can be assigned a universal value of 6270 J·mol−1. The parameters a, Kg and C0 are identified simultaneously from isothermal crystallization and con- stant cooling rate crystallization DSC experiments, as de- scribed in the next section. 3.3. Parameter Identification In isothermal crystallization experiments, the polymer is melted above the equilibrium melting temperature, then the temperature of the polymer is lowered as fast as pos- sible and maintained at the constant crystallization tem- perature T (lower than ). Consequently, the nuclea- 0 exp aTT m tion term and the growth term G* re- main at constant values during crystallization. Hence, integrating the set of rate equations, Equation (28) leads to: 3 30 0exp 6 m t GTaT T (31) 0t where t is the current time, corresponding to the instant at which the polymer melt reaches the crystalliza- tion temperature T. Using Equations (23) and (29), the evolution of the relative crystallinity is explicitly given as a function of time by: 303 0 4π 1exp exp 3m tCGTaTTt (32) In constant cooling rate crystallization experiments, the polymer is melted above the equilibrium melting tem- perature, and then the temperature of the polymer is de- creased at a controlled constant rate whereas crystalliza- tion occurs. Contrary to the isothermal case, the set of rate equations cannot be explicitly integrated to obtain the crystallinity evolution expression. Hence, the itera- tive identification procedure must be run in conjunction with a numerical time integration algorithm of the rate equations. The parameter identification procedure consists of finding a single set of values for parameters a, Kg and C0 that lead to the overall smaller deviation between the ex- perimental crystallinity evolutions and the calculated cry- Copyright © 2013 SciRes. JMP  M. ZINET ET AL. 34 stallinity evolutions given either by Equation (32) (iso- thermal cases) or by the numerical integration procedure (constant cooling rate case). The optimization algorithm used here is the Levenberg-Marquardt method [19,20]. Designed as an enhancement of the Gauss method, it is based on the minimization of a quadratic variance crite- rion (least square method). In the present application, the objective function is de- fined as the sum of the squared differences between the experimentally determined relative crystallinity values and the calculated ones. Since isothermal experiments at sev- eral temperatures and non-isothermal experiments at se- veral cooling rates are considered jointly in the identifi- cation procedure (care being taken that each single ex- periment has an equivalent weight in the objective func- tion), the resulting set of parameters is likely to yield the best overall description of the polymer crystallization ki- netics over the possible experimental range allowed by the DSC technique. After application of this procedure, the values obtained for the parameters are: 15 1 11 52 015 10s 13 10K 4.83610K 02. 1.1 g C a K Figures 6 and 7 show comparative curves of the mea- sured and modeled relative crystallinity evolution, under isothermal and constant cooling rate conditions. The mo- deled curves have been obtained using the identified set of parameters. The agreement between the modeled evolutions and the experimental ones is fairly good. The reduction of the crystallization half time as temperature decreases is well predicted by the model. Thanks to the simultaneous op- timization of the model against isothermal and constant cooling rate experiments, the validity range (in terms of crystallization temperature) of the identified parameters can be estimated to at least [90˚C - 140˚C]. 4. Application to the Cooling of a PPH Plate In this section, an example of simulation using the char- acterization data obtained in the previous section is pre- sented. The analyzed case is drawn from the injection molding process, and especially the cooling stage. Start- ing from a thermally homogeneous mold and polymer melt under high pressure, the isochoric cooling phase (i.e. constant material volume), which ends as soon as atmos- pheric pressure is reached and polymer shrinkage begins, is modeled and simulated. The model introduces a coupling between heat transfer, crystallization, compressibility and the temperature evolution of all the intrinsic thermophy- sical parameters. First, the equations describing pressure evolution, heat transfer and crystallization in the cavity are introduced. Then these equations are coupled together in order to si- mulate the isochoric cooling process. Note that in this work, the pressure history is not an input data, but a com- putational result. Indeed, pressure evolution is a direct consequence of the thermodynamical behavior of the po- lymer. The assumption of hydrostatic (i.e. homogeneous) pressure in the cavity is made. This is quite realistic as long as the polymer is in the melt state, but the reality is far more complex for the solidified state as physical pro- perties variations rapidly occur in the crystallizing mate- rial. Figure 9 shows the simulated geometrical configura- tion and the thermal boundary conditions. The cavity (thickness = 2ep = 3 mm) is filled with polypropylene (PPH) melt and surrounded by two steel blocks (thick- ness = e m). For symmetry reasons, only one half of the system is modeled. In addition, the lateral insulation boun- dary conditions account for an infinite length in the x di- rection. Although the model geometry is bidimensional, for the sake of simplicity, the boundary conditions are chosen such that the problem reduces to a 1D case. In the isochoric cooling phase, both total cavity vol- ume and total polymer mass present in the cavity are conserved. Consequently, there exists a coupling between pressure and specific volume, which is taken into account by considering mass and momentum conservation equa- tions: ,, ,, 0 PT PT t u (33) T ,, 2 11 3 PT t P uuu uu u (34) Figure 9. Geometry and boundary conditions of the thermal model. Copyright © 2013 SciRes. JMP  M. ZINET ET AL. 35 where the density is the inverse of the specific volume V, is a velocity vector, and is the dynamic viscosity. Note that the motion occurring in the polymer is only due to the local contraction and expansion caused by the evolution of the density gradients in the material. Con- sequently, the viscosity value (taken here as 106 Pa) has no effect on the calculation results. u It is assumed that the only heat transfer mode is con- duction, because no significant convective motion can occur in the packed polymer and the material is opaque to radiation. Furthermore, the thermal contact between the polymer and the mold is assumed to be perfect. Heat transfer in the polymer is modeled by the energy conser- vation equation in a compressible and phase-changing medium [21]: , ,, ,, p CT T VPT t VPT t ,TT HP TT (35) where the two right-hand source terms are respectively the latent heat of crystallization release and the compres- sibility heat release. In Equations (33) to (35), the ther- mophysical properties Cp, V, were specified in section 3. By analogy with polymer composites [22], the coeffi- cient of thermal expansion is approximated by: 11 a 1 c P a V X VT 11 W mKl c V X VT (36) The crystallization kinetics of the polymer is modeled by the Schneider modified rate equations, Equation (28) and the relative crystallinity is calculated according to Equations (23) and (29). Heat transfer in the metal is de- scribed by the heat conduction equation with constant thermophysical properties and no source term, since no phase change occurs and the material is assumed to be incompressible: 11 475 JkgK,45 p C 33 0.12710m /kgV and . In the present analysis, the ac- tual injection molding cooling stage have been somewhat simplified. At initial time t0, the temperature T0 is as- sumed to be homogeneous in the whole system, i.e. me- tallic block and polymer plate, and an initial pressure P0 is fixed. At temperature T0, the polymer is supposed to be fully amorphous. The thermal boundary conditions are presented on Figure 9. A convection boundary condition is applied outside the mold; the thermal exchange coeffi- cient h is set at 5000 W·m−²·K−1 and the fluid tempera- ture Tc = 20˚C (typical values for steel-water heat transfer in a mold cooling circuit). The whole set of equations is then solved over the considered geometry using the finite element method. At each time step, the thermal boundary condition and the heat source terms influence the tem- perature field. Crystallization progression is computed and thermophysical properties are updated (specific vo- lume in particular), such that the mass and momentum equations are satisfied and yield an updated pressure va- lue. This coupling is a strong one: the equations are not solved sequentially but together iteratively. When the pres- sure reaches the atmospheric value, convergence is no longer obtained as the mass conservation equation cannot be satisfied, and calculations are stopped. This is the end of the isochoric cooling stage. Since the following stage of the process does not take place at constant volume but at constant pressure, the pre- sent mathematical model is no longer relevant. In the actual process, if the temperature continues to decrease, an air gap between the polymer and the mold wall will appear because of the polymer shrinkage. A simulation with initial temperature: T0 = 220˚C and initial pressure: P0 = 200 MPa yields the temperature, relative crystallinity, pressure and specific volume evolu- tions. Figure 10 shows temperature evolutions across the polymer thickness YYe . Due to the thermal in- ertia of the mold, temperature starts to decrease at the wall/polymer interface after 20 s. At the core, the quasi- plateau of crystallization appears at 80 s, which corre- sponds to 158˚C. Figure 11 clearly shows that crystalli- zation near the mold wall (skin layer) is faster than at the center (core). After 140 s, the polymer is completely so- lidified. Pressure evolution is shown on Figure 12. The curve exhibits 4 distinct parts. In part one, the pressure remains constant: cooling has not yet started in the polymer due to the mold thermal inertia. In the second part, the poly- mer is in the amorphous state, its temperature decreases and pressure decreases in an almost linear way due to the isochoric cavity assumption. When crystallization occurs (third part), the specific volume strongly decreases and pressure falls faster. Finally, as crystallization is com- Figure 10. Temperature evolution at several locations across polymer thickness (T0 = 220˚C, P0 = 200 MPa). Copyright © 2013 SciRes. JMP  M. ZINET ET AL. 36 Figure 11. Evolution of relative crystallinity at several loca- tions across polymer thic kness (T0 = 220˚C, P0 = 200 MPa). Figure 12. Pressure evolution (T0 = 220˚C, P0 = 200 MPa). pleted, the polymer is entirely solidified, and temperature continues to drop while becoming more homogeneous across the thickness. Pressure still decreases until it reaches Patm, corresponding to the unsticking of the po- lymer from the mold. The evolution of the local specific volume (Figure 13) results from the interaction of two phenomena within the material: a contraction due to the temperature decrease, and an expansion due to the pres- sure drop. At the beginning of cooling, the skin tempera- ture decreases faster than at the core, so does the specific volume, which also implies a pressure drop in the cavity. For core locations, this relaxation first induces an in- crease in specific volume as pressure drops there faster than temperature, contrary to what occurs close to the metal/polymer interface. The phenomenon is even more noticeable during crystallization: the skin layers, whose temperatures are lower, are the first to crystallize and to contract. Pressure falls quickly, allowing polymer at the core (still in liquid phase) to dilate. When the core fi- Figure 13. Specific volume evolution at several locations across polymer thickne ss (T0 = 220˚C, P0 = 200 MPa). nally crystallizes, its specific volume decreases; there- fore, to compensate this, the volume of the cavity being constant, the crystallized skin layer dilates. After the end of the crystallization, the polymer is in semi-crystalline phase, pressure is stabilized, and the specific volume variations are mainly controlled by the temperature evo- lution. It is clear that under lower pressures, crystallization cannot be completed before the end of the isochoric phase: the lower the initial pressure, the sooner shrinkage begins. This is precisely the case in the actual injection molding process, for which the order of magnitude of pressure at the end of the packing phase is about 50 MPa. By the way, the end of the isochoric simulation is able to yield an initial state, in terms of temperature and density distributions, for a further simulation of the isobaric cooling stage and shrinkage development. 5. Conclusion After highlighting the importance of an accurate knowl- edge of the thermophysical characteristics of semi-crys- talline polymers and their role in the process-material in- teraction, a protocol for the determination of thermal conductivity, heat capacity, PVT diagram and crystalli- zation kinetics parameters is proposed. A modified Sch- neider model is developed in order to identify all the ne- cessary parameters for the crystallization kinetics, using only DSC measurements. Finally, a numerical simulation of the cooling of a polymer plate is carried out to illus- trate the interdependency of the thermophysical parame- ters and the importance of taking into account their evo- lution versus temperature and crystallinity. This work con- stitutes a complete dataset and a clear protocol for char- acterizing and modeling heat transfer in polymers sub- jected to phase change as usually encountered in Indus- trial processes. Copyright © 2013 SciRes. JMP  M. ZINET ET AL. Copyright © 2013 SciRes. JMP 37 REFERENCES [1] A. Sorrentino, F. De Santis and G. Titomanlio, Progress in Understanding of Polymer Crystallization, Lecture Notes in Physics, Vol. 714, 2007, pp. 329-344. doi:10.1007/3-540-47307-6_16 [2] R. Mendoza, G. Régnier, W. Seiler and J. L. Lebrun, Poly- mer, Vol. 44, 2003, pp. 3363-3373. doi:10.1016/S0032-3861(03)00253-2 [3] M. Zinet, R. El Otmani, M. Boutaous and P. Chantrenne, Polymer Engineering and Science, Vol. 50, 2010, pp. 2044-2059. doi:10.1002/pen.21733 [4] M. Boutaous, M. Zinet, Z. Refaa and P. Bourgin, Journal of Thermal Science and Technology, 2013, in press. [5] H. Zuidema, G. W. M. Peters and H. E. H. Meijer, Mac- romolecular Theory and Simulations, Vol. 10, 2001, pp. 447-460. doi:10.1002/1521-3919(20010601)10:5<447::AID-MAT S447>3.0.CO;2-C [6] M. Avrami, Journal of Chemical Physics, Vol. 7, 1939, pp. 1103-1112. doi:10.1063/1.1750380 [7] H. Janeschitz-Kriegl, “Crystallization under Process Con- ditions,” In: J. A. Covas, Ed., Rheological Fundamentals of Polymer Processing, NATO ASI Series, Vol. 302, 1995, pp. 423-436. doi:10.1007/978-94-015-8571-2_19 [8] G. Vanden Poel and V. B. F. Mathot, Thermochimica Acta, Vol. 446, 2006, pp. 41-54. doi:10.1016/j.tca.2006.02.022 [9] M. Boutaous, P. Bourgin and M. Zinet, Journal of Non- Newtonian Fluid Mechanics, Vol. 165, 2010, pp. 227- 237. doi:10.1016/j.jnnfm.2009.12.005 [10] H. Zuidema, G. W. M. Peters and H. E. H. Meijer, Jour- nal of Applied Polymer Science, Vol. 82, 2001, pp. 1170- 1186. doi:10.1002/app.1951 [11] W. Schneider, A. Köppl and J. Berger, International Po- lymer Processing, Vol. 2, 1988, pp. 151-154. [12] H. Lobo and C. Cohen, Polymer Engineering and Science, Vol. 30, 1990, pp. 65-70. doi:10.1002/pen.760300202 [13] R. Fulchiron, E. Koscher, G. Poutot, D. Delaunay and G. Régnier, Journal of Macromolecular Science-Physics B, Vol. 40, 2001, pp. 297-314. doi:10.1081/MB-100106159 [14] P. G. Tait, Physics and Chemistry of the Voyage of H.M.S. Challenger, Vol. 2, 1888, pp. 941-951. [15] A. N. Kolmogorov, “On the Statistical Theory of the Cry- stallization of Metals,” Bulletin of the Academy of Sci- ences of the USSR, Mathematics Series, Vol. 1, 1937, pp. 355-359. [16] U. R. Evans, “The Laws of Expanding Circles and Spheres in Relation to the Lateral Growth of Surface Films and the Grain-Size of Metals,” Transactions of the Faraday Society, Vol. 41, 1945, pp. 365-374. doi:10.1039/tf9454100365 [17] E. Koscher and R. Fulchiron, Polymer, Vol. 43, 2002, pp. 6931-6942. doi:10.1016/S0032-3861(02)00628-6 [18] J. D. Hoffman and R. L. Miller, Polymer, Vol. 38, 1997, pp. 3151-3212. doi:10.1016/S0032-3861(97)00071-2 [19] K. Levenberg, Quarterly of Applied Mathematics, Vol. 2, 1944, pp. 164-168. [20] D. W. Marquardt, SIAM Journal of Applied Mathematics, Vol. 11, 1963, pp. 431-441. doi:10.1137/0111030 [21] A. M. Bianchi, Y. Fautrelle and J. Etay, “Transferts Ther- miques,” Presses Polytechniques et Universitaires Roman- des, Lausanne, 2004, pp. 136-137. [22] C. P. Wong and R. S. Bollampally, Journal of Applied Po- lymer Science, Vol. 74, 1999, pp. 3396-3403. doi:10.1002/(SICI)1097-4628(19991227)74:14<3396::AI D-APP13>3.0.CO;2-3
|