Paper Menu >>
Journal Menu >>
 American Journal of Plant Sciences, 2010, 1, 106-112 doi:10.4236/ajps.2010.12014 Published Online December 2010 (http://www.SciRP.org/journal/ajps) Copyright © 2010 SciRes. AJPS The Multiplicative Analytic Hierarchy Process (MIAHP) as a Quality Criterion Determining the Technological Value of the Egyptian Cotton Varieties Khaled M. Hussein*, AbdElbaset A. Hassan, Mostafa M. Kamal Cotton Research Institute, Agricultural Research Center, Ministry of Agriculture and Land Reclamation, Gamaa street, Giza, Egypt. Email: *kkholio@hotmail.com Received August 10th, 2010; revised September 19th, 2010; accepted September 21st, 2010. ABSTRACT This study was undertaken to develop a numerical process that can be used as a quality criterion to determine the technological value of the Egyptian cotton varieties, which in turn would denote the end-use of their fibers. However the material used in the study comprised the 6 Egyptian cotton varieties Giza70, Giza80, Giza86, Giza88, Giza90 and Giza92. According to the local practice in Egypt, Giza70, Giza88 and Giza92 belong to the Extra-Long Staple (ELS) category, while Giza80, Giza86 and Giza90 are included under the Long Staple (LS) category. The regression analysis of the rela- tionships between fiber properties and yarn skein strength (lea product) of the 2 carded ring counts 40 and 50 Ne, was employed to drive an equation for calculating the Multiplicative Analytic Hierarchy Process (MIAHP) values. The values of the MIAHP have been used as numerical determinations of the technological values of the Egyptian cotton varieties. Nevertheless, the findings of this study clarified that with respect to the criteria weights, the pair-wise comparisons de- noted that fiber length properties of Egyptian cotton ranked first where they revealed the most dominant effect on yarn strength, while tensile properties ranked second with a relative weight close to that of fiber length. On the contrary, the relative weight of fiber fineness (micronaire reading) was found to be marginal. With regard to the relative weight of sub-criterion, the pair-wise comparisons indicated that the role of fiber tenacity as a determinant of yarn strength is much superior to that of fiber elongation. Further the global weights of the sub-criterion of fiber length pointed out that the UHML (upper half mean length) plays an important role in determining yarn strength of the Egyptian cotton com- paring with either the UI (uniformity index) or the SFC (short fiber content). In conformity with the values of the MIAHP, it was found that in the order of descending rank, Giza88 ranked first, followed by Giza92, Giza70, Giza86, Giza80 and finally Giza90. Keywords: Analytic Hierarchy Process, Cotton Fiber Quality, Technological Value 1. Introduction Cotton is a natural fiber having galore variability in its properties. Most of these properties play a decisive role in determining the tensile characteristics of yarns. Yarn strength, which is considered to be the most important property of spun yarns, is largely influenced by the te- nacity, length, length uniformity, short fiber content and fineness (micronaire reading) of the constituent cotton fibers [1]. In fact, the final overall quality of yarn is largely influenced (up to 80%) by the characteristics of raw cotton. However, the level to which various fiber properties influence yarn quality is diverse, and also changes depending on the yarn manufacturing technol- ogy. Besides, cotton may have conflicting standards in terms of different quality criteria. Therefore, the ranking or grading of cotton fibers in terms of different quality criteria will certainly not be the same and this will make the ranking of the quality of cotton fibers more complex [2]. The Analytic Hierarchy Process (AHP) is a multicrite- ria decision making describing which factors are ar- ranged in a hierarchic structure by using a multilevel hierarchical structure of objectives or goals, criteria, sub- criteria and alternatives. The principles and the philoso- phy of the theory give general background information of  The Multiplicative Analytic Hierarchy Process (MIAHP) as a Quality Criterion Determining the Technological Value of the Egyptian Cotton Varieties Copyright © 2010 SciRes. AJPS 107 the type of measurement utilized, its properties and ap- plications. The most creative task in making a decision is to choose the factors that are important for that decision. In the Analytic Hierarchy Process these factors, once selected are arranged in a hierarchic structure descending from an overall goal to criteria, sub criteria and alterna- tives in successive levels [3]. Analytic Hierarchy Process (AHP) is known to be the most appropriate for solving complicated problems. The AHP is a comprehensive framework that is designed to cope with the intuitive, the rational, and the irrational when making multi-objective, multi-criterion, and multi- actor decisions with and without certainty of any number of alternatives. The basic assumptions of AHP are that it can be used in functional independence of an upper part or cluster of the hierarchy from all its lower parts and the criteria or items in each level [4]. Hence, the AHP is a technique that represents a complex decision problem as a hierarchy with different levels and each level contains different elements with a relevant common characteristic. Using AHP, a cardinal measure of the importance or pri- ority of each element in a level is obtained by pair-wise comparisons of all elements in that level. Each element in level serves as the basis for effecting pair-wise com- parisons of the elements in the immediate lower level of the hierarchy. The final priorities of the elements in the lowest level (decision alternatives) are obtained using the principle of hierarchical composition. These lead to the overall ranking of alternatives [5]. Working on the Egyptian cotton Kamal et al., [6], pointed out that ranking of the Egyptian cotton varieties by virtue of Fiber Quality Index (FQI) and Staple Ratio (SR) indicated that, as concerns the Extra-Long Staple (ELS) category. Giza87 ranked first where it significantly excelled the other varieties of that category. As regards the Long-Staple (LS) category, Giza86 variety proved to have the best quality while Giza80 ranked last in this category and hence it represented the worst quality among the Egyptian varieties as a whole. The objective of this study was to ranking or grading the technological value of Egyptian cotton fibers by us- ing the analytic hierarchy process. 2. Material and Methods The Egyptian cotton varieties Giza70, Giza80, Giza86, Giza88, and Giza90, in addition to the promising hybrid Giza84 (Giza74 x Giza68) which is now known as Giza92, were used as a material in the present study. The samples of those varieties were taken from the two successive seasons 2008 and 2009. The lint cotton samples were spun into the two carded ring yarn counts 40 and 50 (Ne) using the 3.6 twist mul- tiplier. Fiber upper half mean length (UHML), uniformity in- dex (UI), micronaire reading (MIC), fiber strength (FS) and fiber elongation (FE %) were all determined on the High Volume Instrument (HVI) according to ASTM Designation [7]. Further the Sutter Web Comb Sorter was used to determine short fiber content by weight (SFC %) as directed in the ASTM Designation [7]. Yarn skein strength (lea product) was measured according to ASTM Designation [7]. All fiber and yarn tests were made at the laboratories of the Cotton Research Institute (CRI), Giza, Egypt un- der controlled atmospheric conditions. As for the statistical procedures, the correlation and regression analysis according to, Draper and Smith, [8], and the Multiplicative Analytic Hierarchy Process (MI- AHP) were used to deal with the data obtained. Since the Analytic Hierarchy Process is not commonly or widely used and since most of the researchers are not well acquainted with this process, hence, it seems con- venient to report on its details according to Majumdar et al. [2], as follows: Methodology of the Multiplicative Analytic Hierar- chy Process (MIAHP) Step 1: Develop the hierarchical structure of the problem. The overall objective or goal of the problem is positioned at the top of the hierarchy, and the decision alternatives are placed at the bottom. Between the top and bottom levels are found the relevant attributes of the decision problem such as criteria and sub-criteria. The number of levels in the hierarchy depends on the complexity of the problem [9-11]. Step 2: Generate relational data for comparing the alternatives. This requires the decision maker to formulate pair-wise comparison matrices of elements at each level in the hi- erarchy relative to each activity at the next higher level. In AHP if a problem involves M alternatives and N crite- ria, then the decision maker has to construct N judgment matrices of alternatives of M x M order and one judg- ment matrix of criteria of N x N order. Finally, the deci- sion matrix of M x N order is formed by using the rela- tive scores of the alternatives with respect to each crite- rion. In AHP, the relational scale of real numbers from (1 to 9) and their reciprocals are used to assign preferences in a systematic manner. When comparing two criteria (or alternatives) with respect to an attribute in a higher level, the relational scale proposed by Saaty [11] is used. The relational Satty’s scale is shown below which de- fines and explains the fundamental relational scale for pair-wise comparisons:  The Multiplicative Analytic Hierarchy Process (MIAHP) as a Quality Criterion Determining the Technological Value of the Egyptian Cotton Varieties Copyright © 2010 SciRes. AJPS 108 Intensity of importance on an absolute scale Definition Explanation 1 Equal importance Two activities contribute equally to the objective. 3 Moderate importance of one over anotherExperience and judgment slightly favour one activity over another. 5 Essential or strong importance Experience and judgment strongly favour one activity over another. 7 Very strong importance An activity is strongly favoured and its dominance is demonstrated in practice. 9 Extreme importance The evidence favoring one activity over another is of the highest possible order of affirmation. 2,4,6,8 Intermediate values between two adjacent judgment When compromise is needed. Reciprocals If activity p has one of the above numbers assigned to it when compared with activity q, then q has the reciprocal value when compared with p. Step 3: In this step, the relative importance of different criteria with respect to the goal of the problem and the alterna- tive scores with respect to each of the criteria is deter- mined. For N criteria, the size of the comparison matrix (C1) will be N × N, and the entry cij will denote the relative importance of criterion i with respect to the criterion j. n the matrix, cij = 1 if when i = j and ji ij 1 cc. 112 1N 21 12N 1 1 N1 N21 c...c c...c c ... ...... cc ... The importance (relative weight) of the i th criteria (Wi) is determined by calculating the geometric mean (GM) of the i th row, and then normalizing the geomet- ric means of the rows of the above matrix as follows: N j=1 cij GMi1N and N i=1 GMi GMi Wi Then, matrix C3 and C4 are calculated such that: C3 = C1 × C2 and C4 = C3/C2, where C2 = [W1 W2 …. WN]T. The principal eigen vector (λmax) of the original pair- wise comparison matrix (C1) is calculated from the aver- age of matrix C4. To check the consistency in a pair-wise comparison judgment, the consistency index (CI) and consistency ratio (CR) are calculated from the following equations λmax - N CI = N -1 and CI CR = RCI If the value of CR is 0.1 or less, then the judgment is consistent and acceptable. Otherwise the decision maker has to make some changes in the entry of the pair-wise comparison matrix. RCI is the random consistency index; its value could be obtained from the table below, RCI values for different numbers of alternative (M) M123 4 5 6 7 8 9 RCI000.580.901.12 1.24 1.32 1.411.45 [9]. Similarly, N numbers of pair-wise comparison matri- ces (one for each criterion) of M × M order are formed, where each alternative is pitted against all of its com- petitors, and pair-wise comparison is made with respect to each of the decision criterion. The eigen vector of each of these ‘N’ matrices represents the alternative perform- ance scores in the corresponding criterion and from a column of the final decision matrix. The decision matrix appears as follows: Criterion C1 C 2 C 3 … CN W1 W 2 W 3 … WN A1a11 a 12 a 13 … a1N A2a21 a 22 a 23 … a2N A3a31 a 32 a 33 … a3N …… … … … … Alternative AMaM1 a M2 a M3 … a MN 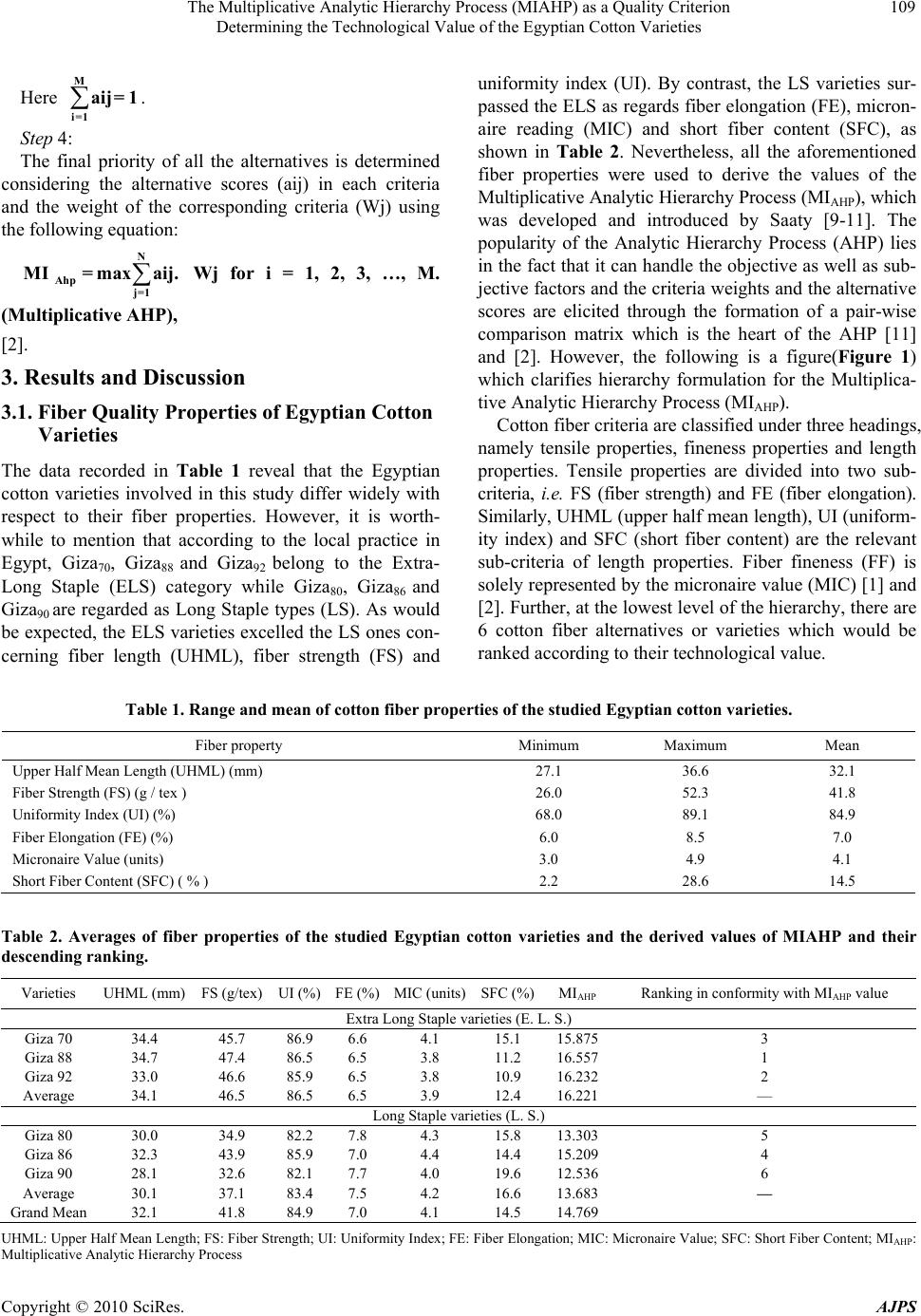 The Multiplicative Analytic Hierarchy Process (MIAHP) as a Quality Criterion Determining the Technological Value of the Egyptian Cotton Varieties Copyright © 2010 SciRes. AJPS 109 Here M i=1 aij= 1 . Step 4: The final priority of all the alternatives is determined considering the alternative scores (aij) in each criteria and the weight of the corresponding criteria (Wj) using the following equation: N Ahp j=1 MI = maxaij. Wj for i = 1, 2, 3, …, M. (Multiplicative AHP), [2]. 3. Results and Discussion 3.1. Fiber Quality Properties of Egyptian Cotton Varieties The data recorded in Table 1 reveal that the Egyptian cotton varieties involved in this study differ widely with respect to their fiber properties. However, it is worth- while to mention that according to the local practice in Egypt, Giza70, Giza88 and Giza92 belong to the Extra- Long Staple (ELS) category while Giza80, Giza86 and Giza90 are regarded as Long Staple types (LS). As would be expected, the ELS varieties excelled the LS ones con- cerning fiber length (UHML), fiber strength (FS) and uniformity index (UI). By contrast, the LS varieties sur- passed the ELS as regards fiber elongation (FE), micron- aire reading (MIC) and short fiber content (SFC), as shown in Table 2. Nevertheless, all the aforementioned fiber properties were used to derive the values of the Multiplicative Analytic Hierarchy Process (MIAHP), which was developed and introduced by Saaty [9-11]. The popularity of the Analytic Hierarchy Process (AHP) lies in the fact that it can handle the objective as well as sub- jective factors and the criteria weights and the alternative scores are elicited through the formation of a pair-wise comparison matrix which is the heart of the AHP [11] and [2]. However, the following is a figure(Figure 1) which clarifies hierarchy formulation for the Multiplica- tive Analytic Hierarchy Process (MIAHP). Cotton fiber criteria are classified under three headings, namely tensile properties, fineness properties and length properties. Tensile properties are divided into two sub- criteria, i.e. FS (fiber strength) and FE (fiber elongation). Similarly, UHML (upper half mean length), UI (uniform- ity index) and SFC (short fiber content) are the relevant sub-criteria of length properties. Fiber fineness (FF) is solely represented by the micronaire value (MIC) [1] and [2]. Further, at the lowest level of the hierarchy, there are 6 cotton fiber alternatives or varieties which would be ranked according to their technological value. Table 1. Range and mean of cotton fiber properties of the studied Egyptian cotton varieties. Fiber property Minimum Maximum Mean Upper Half Mean Length (UHML) (mm) 27.1 36.6 32.1 Fiber Strength (FS) (g / tex ) 26.0 52.3 41.8 Uniformity Index (UI) (%) 68.0 89.1 84.9 Fiber Elongation (FE) (%) 6.0 8.5 7.0 Micronaire Value (units) 3.0 4.9 4.1 Short Fiber Content (SFC) ( % ) 2.2 28.6 14.5 Table 2. Averages of fiber properties of the studied Egyptian cotton varieties and the derived values of MIAHP and their descending ranking. Varieties UHML (mm) FS (g/tex) UI (%) FE (%) MIC (units) SFC (%) MIAHP Ranking in conformity with MIAHP value Extra Long Staple varieties (E. L. S.) Giza 70 34.4 45.7 86.9 6.6 4.1 15.1 15.8753 Giza 88 34.7 47.4 86.5 6.5 3.8 11.2 16.5571 Giza 92 33.0 46.6 85.9 6.5 3.8 10.9 16.2322 Average 34.1 46.5 86.5 6.5 3.9 12.4 16.221–– Long Staple varieties (L. S.) Giza 80 30.0 34.9 82.2 7.8 4.3 15.8 13.3035 Giza 86 32.3 43.9 85.9 7.0 4.4 14.4 15.2094 Giza 90 28.1 32.6 82.1 7.7 4.0 19.6 12.5366 Average 30.1 37.1 83.4 7.5 4.2 16.6 13.683–– Grand Mean 32.1 41.8 84.9 7.0 4.1 14.5 14.769 UHML: Upper Half Mean Length; FS: Fiber Strength; UI: Uniformity Index; FE: Fiber Elongation; MIC: Micronaire Value; SFC: Short Fiber Content; MIAHP: Multiplicative Analytic Hierarchy Process  The Multiplicative Analytic Hierarchy Process (MIAHP) as a Quality Criterion Determining the Technological Value of the Egyptian Cotton Varieties Copyright © 2010 SciRes. AJPS 110 Figure 1. 3.2. Determination of Criteria Weights The comparisons between the three criteria (tensile properties, fineness properties and length properties) with respect to their relation to the technological value of the Egyptian cotton fibers (the goal) are shown in the pair- wise comparison matrix which is made according to Saaty’s scale (Table 3). The normalized geometric mean values (NGM) or weight vector denote that fiber length properties of Egyptian cotton rank first where they reveal the most dominant effect on yarn strength with a relative weight of about 0.489 (NGM). Fiber tensile properties rank second with a relative weight of 0.450, which doesn’t differ markedly from that of fiber length properties. On the contrary, fiber fineness relative weight is found to be marginal, i.e. 0.059. For the measurement of consistency of judgment, the original matrix is multiplied by the weight vector (NGM) to obtain the product as follows: 11 70.4501.356 11 90.4891.475 0.140.11 10.0590.178 1.356 1.4750.178 max3 3.007 0.450 0.489 0.059 3.007-3 Consistency Index CI==0.003 3-1 onsistency Ratio CR Consistency Index CI Random Consistency Index(RCI) 0.003 0.006 0.1 0.58 (acceptable). 3.3. The Relative Weights of Sub-Criteria with Respect to the Corresponding Criteria The pair-wise comparisons between the sub-criteria of tensile properties (FS, FE) and length properties (UHML, UI, SFC) and the derived weight vectors (global weight) are shown in Table 3. The global weights of sub-criteria are calculated by multiplying the relative weight of a sub-criterion (FS, FE, UHML, UI and SFC) with respect to the corresponding criterion (tensile properties and length properties) and the relative weight of that criterion with respect to the goal or objective (technological value of Egyptian cotton fibers). For instance, the global weight of fiber strength (FS) is 0.875 × 0.450= 0.394, and of elongation (FE) is 0.125 × 0.450= 0.056. Accordingly, it is quite apparent that the role of fiber tenacity as a deter- minant of yarn strength is much superior to that of fiber elongation. On the other hand, the global weights of the upper half mean length (UHML), uniformity index (UI) and short fiber content (SFC) were found to be 0.380, 0.054 and 0.054 respectively (Table 3). Thus, it is quite evident that the UHML plays an exceptionally important role in determining yarn strength of the Egyptian cotton in comparison with either UI or SFC. With respect to fiber fineness (FF) i.e. micronaire value, it is obvious that its role, as previously mentioned is marginal. 3.4. The Technological Value of the Egyptian Cotton Varieties The values of the Multiplicative Analytic Hierarchy Process (MIAHP) of the Egyptian cotton varieties are demonstrated in Table 2. Those values have been re- garded to be a quality criterion denoting the technologi- cal value of the Egyptian cotton. However, the values of MIAHP were correlated with yarn strength which is in fact the major yarn quality consideration. The values of cor- relation coefficients were found to be 0.93 and 0.94 for Technological value of cotton Tensile properties Fineness properties Length properties (FF)Fiber Fineness (MIC) (UHML) Upper Half Mean Length (SFC) Short Fiber Content (UI) Uniformity Index (FS) Fiber Strength (FE) Fiber Elongation Giza70 1 Giza80 2 Giza86 3 Giza88 4 Giza90 5 Giza92 6 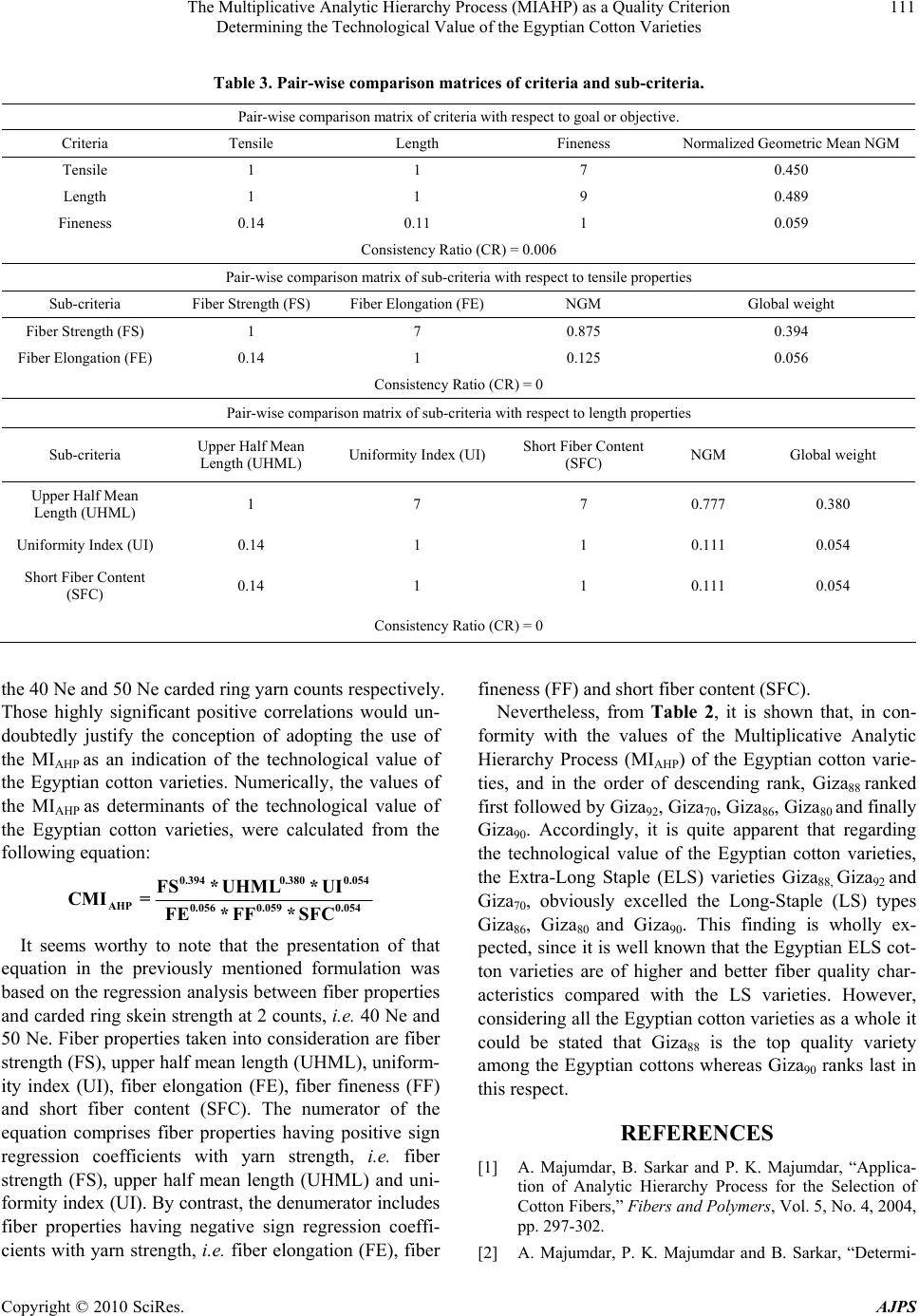 The Multiplicative Analytic Hierarchy Process (MIAHP) as a Quality Criterion Determining the Technological Value of the Egyptian Cotton Varieties Copyright © 2010 SciRes. AJPS 111 Table 3. Pair-wise comparison matrices of criteria and sub-criteria. Pair-wise comparison matrix of criteria with respect to goal or objective. Criteria Tensile Length Fineness Normalized Geometric Mean NGM Tensile 1 1 7 0.450 Length 1 1 9 0.489 Fineness 0.14 0.11 1 0.059 Consistency Ratio (CR) = 0.006 Pair-wise comparison matrix of sub-criteria with respect to tensile properties Sub-criteria Fiber Strength (FS) Fiber Elongation (FE) NGM Global weight Fiber Strength (FS) 1 7 0.875 0.394 Fiber Elongation (FE) 0.14 1 0.125 0.056 Consistency Ratio (CR) = 0 Pair-wise comparison matrix of sub-criteria with respect to length properties Sub-criteria Upper Half Mean Length (UHML) Uniformity Index (UI) Short Fiber Content (SFC) NGM Global weight Upper Half Mean Length (UHML) 1 7 7 0.777 0.380 Uniformity Index (UI) 0.14 1 1 0.111 0.054 Short Fiber Content (SFC) 0.14 1 1 0.111 0.054 Consistency Ratio (CR) = 0 the 40 Ne and 50 Ne carded ring yarn counts respectively. Those highly significant positive correlations would un- doubtedly justify the conception of adopting the use of the MIAHP as an indication of the technological value of the Egyptian cotton varieties. Numerically, the values of the MIAHP as determinants of the technological value of the Egyptian cotton varieties, were calculated from the following equation: 0.3940.380 0.054 AHP 0.056 0.0590.054 FS* UHML* UI CMI= FE* FF* SFC It seems worthy to note that the presentation of that equation in the previously mentioned formulation was based on the regression analysis between fiber properties and carded ring skein strength at 2 counts, i.e. 40 Ne and 50 Ne. Fiber properties taken into consideration are fiber strength (FS), upper half mean length (UHML), uniform- ity index (UI), fiber elongation (FE), fiber fineness (FF) and short fiber content (SFC). The numerator of the equation comprises fiber properties having positive sign regression coefficients with yarn strength, i.e. fiber strength (FS), upper half mean length (UHML) and uni- formity index (UI). By contrast, the denumerator includes fiber properties having negative sign regression coeffi- cients with yarn strength, i.e. fiber elongation (FE), fiber fineness (FF) and short fiber content (SFC). Nevertheless, from Table 2, it is shown that, in con- formity with the values of the Multiplicative Analytic Hierarchy Process (MIAHP) of the Egyptian cotton varie- ties, and in the order of descending rank, Giza88 ranked first followed by Giza92, Giza70, Giza86, Giza80 and finally Giza90. Accordingly, it is quite apparent that regarding the technological value of the Egyptian cotton varieties, the Extra-Long Staple (ELS) varieties Giza88, Giza92 and Giza70, obviously excelled the Long-Staple (LS) types Giza86, Giza80 and Giza90. This finding is wholly ex- pected, since it is well known that the Egyptian ELS cot- ton varieties are of higher and better fiber quality char- acteristics compared with the LS varieties. However, considering all the Egyptian cotton varieties as a whole it could be stated that Giza88 is the top quality variety among the Egyptian cottons whereas Giza90 ranks last in this respect. REFERENCES [1] A. Majumdar, B. Sarkar and P. K. Majumdar, “Applica- tion of Analytic Hierarchy Process for the Selection of Cotton Fibers,” Fibers and Polymers, Vol. 5, No. 4, 2004, pp. 297-302. [2] A. Majumdar, P. K. Majumdar and B. Sarkar, “Determi-  The Multiplicative Analytic Hierarchy Process (MIAHP) as a Quality Criterion Determining the Technological Value of the Egyptian Cotton Varieties Copyright © 2010 SciRes. AJPS 112 nation of the Technological Value of Cotton Fiber: A Comparative Study of the Traditional and Multi- ple-Criteria Decision-Making Approaches,” Autex Re- search Journal, Vol. 5, No. 2, 2005, pp. 71-80. [3] T. L.Saaty, “Highlights and Critical Points in the Theory and Application of the Analytic Hierarchy Process,” Euro- pean Journal of Operational Research, Vol. 74, 1994, pp. 426-447. [4] M. Dağdeviren and I. Yüksel, “Personnel Selection Using Analytic Network Process,” İstanbul ticaret üniversitesi fen bilimleri dergisi, Vol. l, No. 6, 2007, pp. 99-118. [5] R.M.Reddy; M.M. Naidu, and P. Govindarajulu, “An Integrated Approach of Analytical Hierarchy Process Model and Goal Model (AHP-GP Model) for Selection of Software Architecture,” International Journal of Com- puter Science and Network Security, Vol. 7, No. 10, 2007, pp. 101-112. [6] M. M. Kamal, M. T. Ragab, M. A. Mahgoub and M. R. Abd El-Malek, “Quality Valuation of Egyptian Cotton Varieties,” Egyptian Journal of Agricultural Research, Vol. 80, No. 3, 2002, pp. 1231-1247. [7] ASTM, “Test Method for Measurement of Cotton Fibers by High Volume Instruments (HVI),” American Society for Testing and Materials, Designation, Philadelphia, USA [8] N. R. Draper and H. Smith, “Applied Regression Analy- sis,” John Wiley and Sons, New York, 1966. [9] T. L. Saaty, “The Analytic Hierarchy Process,” McGraw- Hill International, New York, 1980. [10] T. L. Saaty, “Axiomatic Foundation of the Analytic Hier- archy Process,” Management Science, Vol. 32, No. 7, 1983, pp. 841-855. [11] T. L. Saaty, “How to Make a Decision: The Analytic Hierarchy Process,” European Journal of Operational Research, Vol. 48, No. 9, 1990, pp. 9-26. |

