American Journal of Plant Sciences, 2013, 4, 1466-1493
http://dx.doi.org/10.4236/ajps.2013.47180 Published Online July 2013 (http://www.scirp.org/journal/ajps)
Dynamic Monitoring of Plant Cover and Soil Erosion
Using Remote Sensing, Mathematical Modeling, Computer
Simulation and GIS Techniques
Z. Y. Zeng1*, J. Z. Cao2, Z. J. Gu3, Z. L. Zhang4, W. Zheng5, Y. Q. Cao6, H. Y. Peng7
1College of Geographical Science, Nanjing Normal University, Nanjing, China; 2Dandong Center for Oases Research, Dandong,
China; 3School of Bio-Chemical and Environmental Engineering, Nanjing Xiaozhuang University, Nanjing, China; 4School of Ar-
chitecture and Urban Planning, Suzhou University of Science and Technology, Suzhou, China; 5National Satellite Meteorological
Center, Meteorological Administration, Beijing, China; 6Dandong Bureau of Environment Protection, Dandong, China; 7Nanjing
Institute of Soil Science, Chinese Academy of Sciences, Nanjing, China.
Received April 24th, 2013; revised May 6th, 2013; accepted June 17th, 2013
Copyright © 2013 Z. Y. Zeng et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
Dynamic monitoring of plant cover and soil erosion often uses remote sensing data, especially for estimating the plant
cover rate (vegetation coverage) by vegetation index. However, the latter is influenced by atmospheric effects and
methods for correcting them are still imperfect and disputed. This research supposed and practiced an indirect, fast, and
operational method to conduct atmospheric correction of images for getting comparable vegetation index values in dif-
ferent times. It tries to find a variable free from atmospheric effects, e.g., the mean vegetation coverage value of the
whole study area, as a basis to reduce atmospheric correction parameters by establishing mathematical models and
conducting simulation calculations. Using these parameters, the images can be atmospherically corrected. And then, the
vegetation index and corresponding vegetation coverage values for all pixels, the vegetation coverage maps and cover-
age grade maps for different years were calculated, i.e., the plant cover monitoring was realized. Using the vegetation
coverage grade maps and the ground slope grade map from a DEM to generate soil erosion grade maps for different
years, the soil erosion monitoring was also realized. The results show that in the study area the vegetation coverage was
the lowest in 1976, much better in 1989, but a bit worse again in 2001. Towards the soil erosion, it had been mitigated
continuously from 1976 to 1989 and then to 2001. It is interesting that a little decrease of vegetation coverage from
1989 to 2001 did not lead to increase of soil erosion. The reason is that the decrease of vegetation coverage was chiefly
caused by urbanization and thus mainly occurred in very gentle terrains, where soil erosion was naturally slight. The
results clearly indicate the details of plant cover and soil erosion change in 25 years and also offer a scientific founda-
tion for plant and soil conservation.
Keywords: Atmospheric Correction; Field Measurement; Modeling; Regression; Simulation; Soil Erosion; Vegetation
Coverage; Vegetation Index
1. Introduction
Dynamic monitoring of plant cover and soil erosion is
very important for land use research and environment
management. Plant cover monitoring has been conducted
by using field observation, remote sensing, mathematic
modeling, simulation, GIS, and GPS techniques [1-7].
Remote sensing techniques usually comprise visual air-
photo or satellite image interpretation and digital image
classification [8,9]. Besides, various vegetation indices,
especially the Normalized Difference Vegetation Index
(NDVI) are also adopted and extensively used [10-15].
And for soil erosion monitoring as an application of
vegetation monitoring, GIS techniques and Universal
Soil Loss Equation (USLE) with its various versions are
often used too [16,17]. Gaffer et al. [17] indicated that a
geographical information system software package and a
modified Universal Soil Loss Equation were used to es-
timate erosion potential. Winchell et al. [18] also stated
that the GIS-based approach was shown to produce sta-
tistical distributions of the revised USLE length-slope
*Corresponding author.

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1467
factor values very similar to those described by the Na-
tional Resources Inventory database of field measure-
ments [16,19]. Some researchers also pointed out the
problems with the vegetation indices, e.g. their sensitiv-
ity to atmospheric conditions [13]; their variation due to
the sun angle [20]; their variability induced by the to-
pography [21]; etc. As Rundquist [13] indicated, “the
Normalized Difference Vegetation Index (NDVI) has
been criticized because of its sensitivity to atmospheric
conditions”. Some insufficiencies also exist with other
methods. For example, for the method of visual interpre-
tation and digital classification, the quantization level
and accuracy are still lower [22,23]. Some researchers
also pointed out the problems with the USLE method. As
Saha [19] pointed out, “the greatest criticism has been its
ineffectiveness in applications outside the range of con-
ditions for which it was developed”. And as Wang et al.
[16] stated clearly, “because of the multiple factors, their
interactions, and their spatial and temporal variability,
accurately mapping the factors and further soil loss is
very difficult”.
Let us return to the method of vegetation index. We
think that its main problem is the atmospheric effect. The
index values computed from original satellite images in
different times are incomparable because of the atmos-
pheric effects, so the monitoring results by using the
original vegetation index are generally far from the ob-
jective reality and unacceptable [23]. Consequently, the
atmospheric correction is needed [13,20]. Up to now
numerous methods of atmospheric correction have been
offered and applied and many useful results have been
obtained [24,25]. Generally speaking, these methods can
roughly be divided into two categories: 1) more accurate
methods such as the 6S model [26]; 2) simpler methods
such as the minimum value subtraction method [27].
However, more accurate methods generally demand
so-called synchronous meteorological parameters, even
through ground-measured reference data. But these data
are difficult to acquire, very costly or provided only
based on limited ground points. And especially for most
historical satellite scenes, such data are not available and
even for planned acquisitions, they may also be hard to
acquire [25,28]. Moreover, Mather [29] even indicated:
“Several methods for the atmospheric correction of re-
motely-sensed images have been reported in the literature;
none is universally applicable”. Singh et al. [14] also
mentioned: “Numerous algorithms have been developed
for correction of noise due to different sources, … how-
ever, complete physical ground corrections for all the
effects and for various land surfaces are not yet avail-
able.” As to the less accurate methods, their corrected
results do not have enough accuracy for our monitoring
task (Zeng, 2004) [23].
Since the late 1990s, along another train of thought,
we have been developing and testing a new practical and
fast method. It is another choice. In this method, the at-
mospheric correction of the vegetation index values is
conducted by an indirect way with the help of seeking for
one or more correct reference variables uninfluenced by
atmosphere, e.g. the mean vegetation coverage value of
whole study area. Based on the reference variable, the
atmospheric correction parameters can be deduced and
the images can be corrected. Then, using the corrected
vegetation indices and corresponding vegetation cover-
age values, the vegetation monitoring can be realized.
Vegetation coverage grade maps and ground slope grade
map (from DEM) can generate soil erosion grade maps
and so the soil erosion change in different years can be
judged. In fact, the method of using vegetation coverage
map and ground slope map to generate soil erosion map
has been adopted by some other researchers. For example,
Hazarika et al. [20] used to write: “A soil erosion model
was developed to integrate NDVI and land slope to esti-
mate the soil erosion rate and the vegetation cover is a
major factor of soil erosion. Therefore, a Normalized
Difference Vegetation Index derived from remote sens-
ing (LandsatTM) was used to assess the vegetation cover.”
Wang et al.[30] also described that “soil erosion was
classified and arranged based on slope and vegetation
coverage.” Consequently, we think that the vegetation
coverage and the ground slope are the two most impor-
tant factors for soil erosion, because in the factors influ-
encing soil erosion, the rain factor acts mainly through
the slope steepness and vegetation coverage, the C factor
is controlled mainly by the vegetation coverage, and even
the effects of the P factor follow the changes of slope
steepness and vegetation density.
To realize all the above tasks, a series of mathematic
modeling and computer simulation are needed. For ex-
ample, we should establish a relation between vegetation
coverage and vegetation index in a so-called reference
area by field measurement of vegetation coverage at nu-
merous distributed and accurately positioned quadrates
and then extend the relation to a study area by establish-
ing other models. And due to different effects of atmos-
phere on different image bands, some so-called differ-
ence coefficients of atmospheric effects on different
bands need to be estimated too.
This new method was originally and experimentally
used in a case study area, the Lianshui basin (579.26 km2)
of Ganjiang River in Jiangxi Province, China. The results
of soil erosion monitoring obtained by this method ac-
corded with those of other scientists obtained by satellite
image classification plus visual interpretation [31]. This
indicated the feasibility of the method [22,23]. However,
the original method was imperfect at that time. Since

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1468
then we have been continuing to improve it. Now all the
imperfections in the original version have been corrected
greatly. The improved method and its procedures are
presented in this paper.
2. Methodology
2.1. Study Area, Instruments and Materials
The study area is the city of Dandong and its suburbs,
Liaoning Province, China (40˚N, 125˚E), totaling 909.89
Km2. Its shape looks like a balloon or the map of Brazil
(refer to Figure 9). Along the eastern fringe of the area
runs the Yalujiang River. The area resembles the condi-
tions of humid temperate zone and is composed of in-
clining plains and undulating hills. These plains are oc-
cupied by agricultural land mainly composed of paddy
fields with a very few gently sloping corn farms. The
hills are covered by natural temperate forest, shrubs, and
grasses. The tree species in the forest are mainly locust,
white poplar, maple, oak, pine, China fir, etc. The city of
Dandong is on the west bank of the river (the pink area in
Figure 9(b)). It must be declared and emphasized here
that the study area comprises the Yalujiang River, which
is jointly owned by both China and Korea, i.e. some is-
lands belong to Korea and others belong to China. It
forms complicated situations and thus none of the maps
attached to this paper can be taken formally as the basis
of the national boundary between the two countries.
Besides the study area, we have yet a so-called refer-
ence area. It is for conducting field measurements to ob-
tain vegetation coverage data and using so-called refer-
ence images of ETM+ and SPOT of the area to establish
so-called reference relation equations between vegetation
coverage and vegetation index values. And in the area,
we also used several sets of TM, ETM+ and SPOT im-
ages and corresponding atmosphere observation data to
make atmospheric corrections with the TURNER model
[24] for testing the so-called difference coefficients of
atmospheric effects on different image bands, established
by the mountain shadow histogram method [22,23]. The
reference area is located in the city of Nanjing and its
surroundings, Jiangsu Province, China (32˚N, 119˚E)
(refer to Figure 3). It occupies an area of 3024 Km2 and
is composed of plains and undulating hills, which are
scattered with large quantity of small lakes and reservoirs.
Through the area run the Yangtze River and its small
tributary Qinhuai River. In the center of the area there is
the city of Nanjing. Around the city, there is vast land of
agricultural crops and bare fields on plains and natural
north-subtropical forest, shrubs and grasses on hills. The
tree species in the forest are mainly oriental plane
(sycamore), locust, poplar, maple, oak, ginkgo, pine,
cedar, China fir, etc.
The used instruments in this study comprise: Digital
camera, Canon Power Shot G5 (Canon inc. Japan); Star
link Invicta 210 DGPS (RAVEN Industries, INC. USA);
Digitizer: Size A0; Software: ENVI image processing
system; ArcGIS systems (including Arcmap); Microsoft
Excel 2003. The used images for the study area: 1) MSS
image, Landsat-2, WRS 127-32, Date: 09-15-1976; 2)
TM image, Landsat-5, WRS 118-32, Date: 09-12-1989; 3)
ETM+ image, Landsat-7, WRS 118-32, Date: 09-21-
2001. The used images for the reference area: 1) TM
images: Landsat-5, WRS 120-38, Dates: 07-05-1988 and
10-18-1997; 2) ETM+ images, Landsat-7, WRS 120-38,
Dates: 09-16-2000 and 11-06-2001; 3) SPOT image,
SPOT-5, K-J identification 290-286, Date: 11-09-2002.
The used topographic maps: for the study area: scale
1:50,000; for the reference area: scales 1:50,000 and
1:10,000.
2.2. A Variable Free from Atmospheric Effects:
The Mean Vegetation Coverage Value of the
Study Area and Its Estimation
As the key and first step of the method, we should esti-
mate the mean vegetation coverage value for the whole
study area. This value is not affected by atmospheric
effects, because it only refers to spatial distribution of
vegetation and is always the same in a short period de-
spite transparent or non-transparent atmosphere. Besides
the mean vegetation coverage, there are also other vari-
ables which are not affected by atmosphere, e.g. the soil
erosion amount or other ordinary geographic statistic for
an area within or outside the study area [22,23]. However,
the mean vegetation coverage value for the study area is
preferable, because it can be estimated directly from sat-
ellite image itself.
There are several methods for estimating the mean
vegetation coverage value. One is the method of visual
interpretation. In this case it is enough to only use a color
composite of very small scale and hence very small size.
Another one is the method of dynamic color composition.
This kind of composite is calculated by using the Heck-
bert Quantization Algorithm [32,33]. We used to apply
this kind of composites for determining vegetation cov-
erage values in Lianshui basin, Jiangxi Province, China
and found it having a very interesting and surprising
function for calculating vegetation coverage. Here we
only cite a figure of that research to show the potential of
this composite in this respect. Figure 1 shows the histo-
grams of ordinary (or standard) and dynamic color com-
posites.
We can see that the two kinds of histogram are very
different: for the standard color composites in different
years, there is neither obvious difference in the distribu-
tion of image pixels along the gray level axes nor other

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1469
(a) (b)
Figure 1. Comparison of the histograms between the standard color composites (a) and the dynamic color composites (b) for
different years in Lianshui basin, Jiangxi Province, China (cited from [23]).
significant difference; but for the dynamic color compos-
ites in different years, there is great difference in the dis-
tribution of image pixels along the gray level axes: more
image pixels concentrated in the range of lower gray
level values in 1987 when the vegetation coverage was
the lowest (36.83%); then the more pixels moved to-
wards the direction of higher gray level values in 1995
when the vegetation coverage became greater (54.87%);
and last, more pixels concentrated in the range of the
highest gray level values in 1996 when the vegetation
coverage was the highest (60.71%). By using some
specified threshold values in the histograms or using the
average values of gray level, the mean vegetation cover-
age values of the study area for different years could be
obtained and the results are almost the same as those
determined by image classifications [23]. The third
method is the classification. It is just what we choose of
use in this research.
We take the ETM+ image of September 21, 2001 as an
example for discussing the estimation. At first we used
the ISO data algorithm in ENVI system to conduct an
unsupervised classification for the images (geometrically
corrected, pixel size = 30 m × 30 m). One of the most
important classification tactics is to divide the classes as
many as possible (20 - 30 classes), because the discrimi-
nation of vegetation and non-vegetation is based upon
the resulting classes. If the number of classes is too small,
then the number of pixels in each class would be big.
This would lead to a discrimination error. We divided the
image into 21 classes. Table 1 lists the classification
statistics and Figure 2 shows the broken lines of mean
gray level values of each class in four classified bands
(TM2, 3, 4 and 5).
There are also several methods for differentiating
vegetation and non-vegetation according to the classifi-
cation results, e.g. using the 4-dimensional vegetation
index defined by Zeng [23] (refer to the last column of
Table 1). However, in this research we only present the
method of so-called class broken line analysis and dis-
crimination. Let us look closely at Figure 2. From it we
can clearly see that the broken lines of vegetation classes
are different from those of other kinds of classes. Classes
1-10 (solid and thick lines) are the dense, very dense, or
moderately dense vegetation and their broken lines are
prominently concave at the position of TM3 and convex
at the position of TM4; classes 13-18 (dotted and thick)
are the bare or very bare land and their broken lines are
prominently convex at the position of TM3 and concave
at the position of TM4, i.e. totally opposite in shape to
the dense, very dense, and moderately dense vegetation;
classes 19-21 (dotted and thin) are the water bodies and
their broken lines are inclined towards right and very low
in TM bands 4 and 5; finally classes 11-12 (solid and thin)
are the sparse vegetation and their broken lines are just
transitional ones between vegetation and bare land, i.e.
the r lines are almost straight, slightly concave or slightly i

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1470
Table 1. Gray level value in four ETM+ bands, NDVI value, 4-dimensional Vi value and area value (%) for the resulting
classes of the unsupervised classification in the study area (Dandong, China; ETM+ image of Sep. 21, 2001).
Mean gray level value for each of the TM bands
Class No
(NDVI order) Ground feature Area%
TM2 TM3 TM4 TM5
Vi (NDVI) Vi4d (4 dimen.)
1 Very dense vegetation 1 9.8130 45.97 35.86 76.61 78.82 0.3623 87.92
2 Very dense vegetation 2 6.4509 48.91 39.34 83.81 90.68 0.3611 92.86
3 Very dense vegetation 3 8.9049 43.56 33.24 67.81 67.98 0.3421 77.71
4 Dense vegetation 1 8.1539 42.21 32.63 57.20 59.36 0.2735 58.59
5 Dense vegetation 2 3.9837 39.37 27.47 47.75 46.36 0.2367 55.39
6 Dense vegetation 3 3.5271 62.68 55.84 88.91 75.34 0.2285 71.51
7 Mod. dense vegetation 1 8.7268 48.26 42.39 61.74 77.45 0.1858 41.21
8 Mod. dense vegetation 2 5.9217 54.74 51.53 74.60 106.26 0.1829 40.91
9 Mod. dense vegetation 3 12.9833 52.70 49.76 67.27 89.25 0.1496 32.20
10 Mod. dense vegetation 4 4.7148 58.43 54.70 69.11 71.33 0.1164 31.12
11 Sparse vegetation 1 8.7320 60.51 62.99 68.82 97.85 0.0442 1.67
12 Sparse vegetation 2 4.9395 66.24 73.34 71.45 116.17 −0.0131 −21.93
13 Bare land 6 2.4914 69.24 75.08 53.88 80.38 −0.1644 −51.01
14 Bare land 5 2.4113 61.97 63.35 44.29 63.85 −0.1771 −38.86
15 Bare land 4 1.5493 79.96 91.97 61.27 99.28 −0.2003 −79.62
16 Bare land 3 1.2174 91.22 110.13 71.79 127.90 −0.2108 −107.18
17 Bare land 2 1.5600 55.64 53.04 33.91 44.88 −0.2271 −33.84
18 Bare land 1 0.4172 116.18 147.17 83.53 157.62 −0.2759 −174.29
19 Water 3 1.0787 46.51 35.20 13.81 13.34 −0.4364 −19.06
20 Water 2 1.2110 56.32 55.13 20.89 15.52 −0.4504 −57.47
21 Water 1 1.2120 52.40 44.93 16.24 15.78 −0.4690 −38.19
total 100.0000
convex at the position of TM3. Consequently, we have
ascertained the classes designated by the solid and thick
lines, i.e. classes 1-10, as vegetation classes. And then
the overall area of the classes 1-10, i.e. 73.18% (see Ta-
ble 1) is the estimation of the mean vegetation coverage
value for the whole study area for year 2001. Taking the
dividing line between the sparse vegetation and the mod-
erately dense vegetation as the limit between vegetation
and non-vegetation only possesses correctness statisti-
cally, because the classes are statistical ones (classified
based on statistical theory), each of them inevitably con-
tains some pixels of other classes. For example, the
moderately dense vegetation might contain some pixels
of sparse vegetation; contrarily, the sparse vegetation
might contain some pixels of moderately dense vegeta-
tion. However, this kind of classification errors for the
sparse vegetation and the moderately dense vegetation
would be mutually compensated or set-off, as an ordinary
diagram of two adjacent Normal Distributions can show
[34].
We also conducted unsupervised classifications re-
spectively for the MSS image of bands 4, 5, 6, 7 on Sep-
tember 15, 1976 and the TM image of bands 2, 3, 4, 5 on
September 12, 1989. The MSS image was classified into
25 classes and the TM image 21 classes. And then fol-
lowing the same procedures as above, we obtained the
mean vegetation coverage values of the study area, i.e.
65.62% for 1976 and 75.07% for 1989 respectively. For
the convenience of the following calculations, we use
decimal digits to specify the mean vegetation coverage
values Vc, i.e. 0.6562, 0.7507 and 0.7318 for 1976, 1989
nd 2001 respectively. a

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1471
Figure 2. Gray level broken lines of the classes in four ETM+ bands, resulting from an unsupervised classification of ETM+
image of Sep. 21, 2001 in the study area, Dandong, China.
The vegetation coverage value above or other refer-
ence variable value here only refers to the mean value of
the whole study area and therefore there is only one
value for one date’s image of the study area and so it is
easier to acquire. As for all pixels of the image, vegeta-
tion coverage values cannot be obtained like this because
the above methods can not reach accuracy at the pixel
level. Nevertheless, the mean vegetation coverage value
for the whole area obtained like this is a good basis for
deducing pixels’ vegetation coverage values. How to
deduce them on this basis? This is a thorny problem. But
obviously, we need to use NDVI value as a bridge, be-
cause, just as Drake et al. [12] indicated, “NDVI is cur-
rently the only globally available remote sensing estima-
tion of vegetation cover”; Singh et al. (2003) also stated:
“NDVI has become the primary tool for mapping
changes in vegetation cover”.
A series of formulae, models, and simulation calcula-
tions are needed. We will talk about them next.
2.3. Specifying Expressions of NDVI and Other
Variables for NDVI Calculation and
Atmospheric Correction
For consistency of calculation, we need to fix the expres-
sions of NDVI and other variables in advance. And for
simplification of narration, we use Vi to specify the
NDVI. Suppose the atmospheric correctors for TM band
3 and TM band 4 are c3 and c4 respectively, then we have



 
i4
43
43
43
VTMcTMc
TMcTM c
3






  


(1)
Or

 
i43 43VTMTMaTMTMb

  (2)
We call a and b numerator corrector and denominator
corrector respectively. From Formulae (1) and (2) we
know:
3
ac c
4

 (3)


34
bcc  (4)
Also for convenience of calculation, we define C as
the mean corrector for visible band and infrared band, i.e.


34
2Ccc (5)
The C, c3, c4, a, and b are the atmospheric correction
parameters which we should solve.
2.4. Estimating the Difference Coefficients of
Atmospheric Effects on Different Image
Bands
The c3 and c4 in Formula (1) are different. This is due to

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1472
differences of atmospheric effects on visible and infrared
bands. Tarpley et al. [10] stated briefly: “Atmospheric
effects such as scattering by dust and aerosols, Rayleigh
scattering and sub pixel-sized clouds all act to increase
visible band values with respect to infrared band values
and to reduce the computed vegetation indices NDVI”. In
other conditions, as Townshend et al. [11] pointed out,
“reductions in irradiance due to atmospheric effects are
higher for shorter wavelengths and thus the NDVI tends
to be spuriously increased”. These differences mean that
we need to consider and estimate the so-called difference
coefficients of atmospheric effects on different image
bands, which are defined by us as the ratio of a band at-
mospheric corrector to the mean atmospheric corrector of
all the considered bands, i.e.
33
kcC (6)
44
kcC (7)
The values of k3 and k4 have been estimated by us in
consideration of the variation difference of gray level
values of mountain shadows from one year to another in
TM bands 3 and 4. They are respectively: k3 = 1.1394, k4
= 0.8606 (Zeng, 2001, 2004). In recent years, we have
used TM and ETM+ images to conduct more experi-
ments with the k3 and k4 estimation by the method of
mountain shadows histogram in two study areas of Dan-
jiangkou and Baihe, Hubei province, China (four ex-
periments: k3 = 1.1575, 1.1740, 1.0893, and 1.0840; k4 =
0.8425, 0.8260, 0.9107, and 0.9159) and also by the at-
mospheric correction model TURNER in the Nanjing
area (four experiments: k3 = 1.1842, 1.2768, 1.2886, and
1.1264; k4 = 0.8158, 0.7232, 0.7114, and 0.8736). The
resulting k3 and k4 values of the two methods are close to
each other, proving that both these methods can be used
to estimate the difference coefficients k3 and k4. Hereafter
we will adopt the overall average values, i.e. the mean
values of the methods of mountain shadows and the
TURNER model for further application. They are k3 =
1.1783 and k4 = 0.8217, i.e.
31.1783cC
C
(8)
40.8217c (9)
2.5. Modeling the Relationship between
Vegetation Coverage and Vegetation Index
The prerequisite of the modeling is having a fair amount
of data pairs of vegetation coverage and vegetation index.
We used to collect some vegetation coverage data of
Xianju County, Zhejiang Province, China, from literature,
calculate some corresponding vegetation index values
and establish a quadratic regression equation [22,23]. In
this study, we did some field measurements in the refer-
ence area to get vegetation coverage values. We took the
central reference area in Nanjing, China as our measure
area (Figure 3) and arranged more than forty measure
quadrates (the size is 30 m × 30 m) for ETM+ image and
over one hundred and forty quadrates (the size is 10 m ×
10 m) for SPOT image. At these quadrates we used
Canon Power Shot G5 camera and self-made special
stand, hanger rod and hanger cradle to measure the vege-
tation coverage. Simultaneously, a GPS receiver Starlink
Invicta 210 DGPS was used for accurate positioning [35,
36]. We chose two scenes of images on very clear days
for computing corresponding vegetation index values,
because the vegetation index values computed from this
sort of images are less influenced by atmospheric effects
and hence the established vegetation index-coverage re-
lation would be more reliable for reference. Among the
images in hand, which were received during the recent
15 years (1989~2004), the reception days of the ETM+
image on November 6, 2001 and the SPOT image on
November 9, 2002 have the best atmospheric conditions:
the visibility is higher, the atmosphere pressure is higher,
the air temperature is lower, the relative humidity is
lower and the vapor pressure is lower. So the sky is clear
and the weather is excellent; especially at 8 o’clock
which is very near the reception hour of images (Table
2). Thus, the two scenes of images were chosen as our
reference ones. They were geometrically corrected (the
pixel size is 30 m × 30 m for ETM+ image and 10 m ×
10 m for SPOT image).
According to the image reception times, our field
measurements of vegetation coverage were all planned to
be carried out in the same season (November 1-14, but
year 2004). The distribution of sample sites in the refer-
ence area is shown in Figure 3. After the measurements,
Figure 3. Distribution of the sampling sites in the central
reference area: F-Forest sites; S-Shrub sites; G-Grasses
ites; N-Non-vegetation sites. s

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1473
Table 2. Atmospheric conditions of reception days of some satellite images in the reference area (Nanjing City and its sur-
roundings, China) and in the study area (Dandong City and its suburbs).
Date hour Visibility, Km
Barometric
pressure, 1mb Air temperature, ˚CRelative humidity, %
Vapor pressure,
0.1mb
Reference area
10/18/1997 8 1.5 1019.5 15.3 85 14.7
14 10.0 1016.4 27.6 27 9.8
09/16/2000 8 7.0 1009.2 20.5 70 16.8
14 22.0 1007.5 29.2 26 10.6
11/06/2001 8 14.0 1032.7 8.4 70 2.7
14 24.0 1029.5 14.1 36 5.7
11/09/2002 8 11.0 1026.8 6.4 63 6.0
14 11.0 1020.8 14.9 32 5.4
Study area
09/15/1976 8 6 1012.9 14.2 80 13.0
14 8 1010.5 23.4 37 10.6
09/12/1989 8 20 1007.9 17.2 74 14.5
14 25 1007.2 23.6 38 11.1
09/21/2001 8 20 1028.3 12.4 30 4.3
14 30 1025.3 20.0 18 4.2
we designed a special method for processing photos in
laboratory [35,36]. Finally, the data pairs of the vegeta-
tion index and vegetation coverage for all quadrates were
obtained (Table 3, for ETM+ image). Note that the vege-
tation coverage values equaling 0 (entirely bare land or
open water surface) or 1 (100% vegetation cover) were
visually determined. We use the data pairs to establish
the relation model of vegetation coverage to index by
regression analysis. With Microsoft Excel, we estab-
lished a 4-order polynomial equation as follows and it
curve is shown in Figure 4.

4
ci
2
i
2
6.4870933608640 6.172463983663
1.14548311195 2.3151305575
0.492401042
R0.899607, data pairs40
VV
V




3
i
i
V
V
(10)
Figure 4. The 4-order polynomial regression curve and its
data points of vegetation coverage to vegetation index in the
reference area (Nanjing, China), established based on the
reference ETM+ image (November 6, 2001).
1.00726 is the significant local maximum of the curve;
the point of Vi = −0.22528 and Vc = 0.00000 is the sig-
nificant intersection point of the curve with the abscissa
axis; the point of Vi = 0.36572 and Vc = 1.00000 is the
significant intersection point of the curve with the line of
Vc = 1; and the the point of Vi = 0.05541 and Vc =
0.36171 is the significant point of inflexion (indicating
speed change of Vc increase with Vi).
The suitability of Equation (10) is in the range of Vi =
−0.22528 - 0.36572, i.e. Vc = 0.00000 - 1.00000 (in prac-
tice) or Vi = −0.33653 - 0.42218, i.e. Vc = −0.09798 -
1.00726 (theoretically). The foundation of the threshold
determination is the first and second derivatives of Equa-
tion (10) and its curve in Figure 4. From them we know
that The point of Vi = −0.33653, Vc = −0.09798 is the
minimum of the curve; the point of Vi = 0.42218, Vc = In consequence, we have to only use Vi = −0.22528 -

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1474
Table 3. Measured vegetation coverage values and their corresponding vegetation index values in the reference ETM+ image
for measurement quadrates of the reference area.
GPS positioning of the quadrate
Number of
quadrate
Type and status of vegetation
or ground feature
Vegetation coverage
value (Vc)
Vegetation Index
value (Vi) Latitude N Longitude E
1 Water (Yangtze river) 0 −0.3578 32.148551 118.797282
2 Water (lake) 0 −0.3645 32.037605 118.757994
3 Water (lake) 0 −0.3636 32.073481 118.798349
4 Water (lake) 0 −0.4727 32.030171 118.822036
5 Bare land (buildings) 0 −0.1359 32.076221 118.804170
6 Bare land (quarry) 0 −0.1880 32.137008 118.638511
7 Bare land (quarry) 0 −0.1795 32.166730 118.869477
8 Bare land (cropland) 0 −0.1954 32.119991 118.772371
9 Shrubs and grasses 0.2240 −0.1356 32.021047 118.763266
10 grasses 0.4383 −0.1282 32.060442 118.745227
11 Shrubs and grasses 0.2885 −0.1000 32.056527 118.627621
12 grasses 0.4534 −0.0787 32.058450 118.756310
13 grasses 0.3102 0.0710 31.998201 118.668948
14 grasses 0.1152 −0.0702 32.056234 118.628194
15 Shrubs and grasses 0.4596 −0.0278 32.175704 118.704355
16 Shrubs and grasses 0.2318 −0.0067 32.109713 118.905208
17 grasses 0.4514 0.0184 32.103149 118.905983
18 grasses 0.1330 0.0184 32.103269 118.905872
19 grasses 0.5671 0.0191 32.160044 118.783946
20 woodland 0.8778 0.0597 32.031586 118.779283
21 woodland 0.7200 0.0862 32.048129 118.778949
22 shrubs 0.6021 0.0651 32.108918 118.906333
23 woodland 0.9053 0.0959 32.033218 118.704289
24 Trees, shrubs and grasses 0.8676 0.1189 32.065556 118.616573
25 Shrubs and grasses 0.9163 0.1189 32.065375 118.616581
26 Trees, shrubs and grasses 0.8800 0.1636 32.047871 118.825891
27 Trees, shrubs and grasses 0.9206 0.2115 32.055195 118.764950
28 Shrubs and grasses 0.8889 0.2389 32.050896 118.756502
29 Shrubs and grasses 0.8757 0.2650 32.053248 118.755745
30 Trees and shrubs 0.9373 0.3000 32.051233 118.754455
31 Trees, shrubs and grasses 0.9704 0.3220 32.053147 118.825986
32 woodland 0.8980 0.3280 32.052790 118.754499
33 Broadleaf forest 1 0.3438 32.061181 118.835163
34 Broadleaf forest 1 0.6324 32.064705 118.835833
35 Broadleaf forest 1 0.4592 32.053581 118.831353
36 Broadleaf forest 1 0.4380 32.053166 118.827526
37 Broadleaf forest 1 0.4530 32.053262 118.831130
38 Broadleaf forest 1 0.3969 32.051084 118.754309
39 Coniferous forest 1 0.4861 32.064085 118.618000
40 Coniferous forest 1 0.4286 32.063893 118.618269

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1475
0.36572 for calculating Vc (Vc = 0 - 1) in practice. How-
ever, theoretically we can also use V
i = −0.33653 -
0.42218 for calculating Vc (Vc = −0.09798 - 1.00726).
We call the Vi = −0.22528 - 0.36572 practical thresholds
and the Vi = −0.33653 - 0.42218 theoretical thresholds.
The significance of the theoretical thresholds is: 1) The
water and the bare land can be separated from each other
and from other ground features as well in the vegetation
coverage map; 2) Part of vegetation coverage values
greater than 1 is still reserved, which might indicate bet-
ter vegetation status than that of Vc = 1; 3) Beyond these
two thresholds, the actually existing data are very few, so
only a few values will be cut off and assigned to corre-
sponding threshold values (Vc = −0.09798 or 1.00726).
Using the same procedures, the quantitative relation of
vegetation coverage to vegetation index for SPOT image
was also figured out based on 144 data pairs. The relation
is also a 4-order polynomial equation as follows and its
curve is similar to that of TM image (omitted).

4
ci
2
i
2
2.9052647822973 4.355348491887
0.000961875828 1.9591288370
0.440980513
R0.663543, data pairs144
VV
V





3
i
i
V
V
(11)
The suitability of Equation (11) is in the range of Vi =
−0.28946 - 0.37023, i.e., Vc = 0.00000 - 1.00000 in prac-
tice or Vi = −0.33932 - 0.53497, i.e., Vc = −0.01501 -
1.06048 theoretically.
Equations (10) and (11) can be called reference equa-
tions, because they were figured out based on the refer-
ence image in the reference area. With these two equa-
tions and by using so-called intermediate or transitional
equations relating the vegetation index values of the ref-
erence images in the reference area (Nanjing City area)
to those of other images in other area (e.g., the city of
Dandong and its suburbs), new relational equations be-
tween vegetation coverage and vegetation index, suitable
for the new area, can be obtained.
Generally speaking, for monitoring vegetation and soil
erosion change of an area in different periods, it is better
to use the same kind of image and the same vegetation
coverage-index relation. However, it is not easy for a
longer-period monitoring as in our case. The period ex-
tended over 25 years from 1976 to 2001; but available to
us, for 2001 there was only a scene of ETM+ images, for
1989 only a scene of TM images and for 1976 only MSS
images existed. So we have to use different types of im-
age simultaneously and the vegetation coverage-index
relation established by ETM+ image for all the years.
Nevertheless, the objective of using remote sensing im-
age and related models has been achieved, i.e., to assign
or “distribute” correct or rational vegetation coverage
values to all pixels and simultaneously keep the mean
vegetation coverage value of the study area unchanged
(equaling the result of classification). In our study area,
the Equation (11) for SPOT image was not used because
of lack of SPOT image. However, the equation may be
useful to users who have to use SPOT image for their
work.
2.6. Modeling the Relation of Vegetation Index
Values of the Reference Area and the Study
Area and the Relation of Vegetation
Coverage to Vegetation Index in the
Study Area
The relation of vegetation index values of the reference
area and the study area is an intermediate or transitional
equation for connecting these two areas and popularizing
and applying the reference Equation (10) or (11) to the
study area or any other new area. In our previous study,
we had established a linear equation to do this [22,23].
However, as revealed by recent research, this equation
should be a 3-order polynomial one. We may calculate
vegetation index maps or conduct unsupervised classifi-
cations of the original images both from the reference
area and the study area, respectively, and then seek cor-
responding data pairs to establish such a kind of regres-
sion equation. However, in the two cases, it is necessary
to get the reference images of ETM+, Nov. 6, 2001 or
SPOT, Nov. 9, 2002 in Nanjing as a reference area. It is
not convenient for other users. For simplification, we
propose to use a special data set of 12 vegetation index
values derived from the Nanjing reference ETM+ images,
i.e. the vegetation index values of image minimum, im-
age mean, image maximum, three water bodies, three
barest lands, and three densest vegetations.
Using the reference ETM+ images to compute vegeta-
tion index map (image) and simultaneously conduct un-
supervised classification, we obtained the special data set
of 12 values for the reference area: the minimum, mean,
and maximum vegetation index values came from the
statistics of vegetation index map; the vegetation index
values of three water bodies are the three smallest index
values in the classified classes; the vegetation index val-
ues of three barest lands are the smallest index values
except for the water bodies in the classified classes; and
the vegetation index values of three dense vegetations are
the three greatest index values in the classified classes
(Table 4, left column). This special data set can be used
to establish the relation of vegetation index values be-
tween the reference area and the study area or any other
new area. Using the same procedures for the images of
all the monitoring years in our study area respectively,
we obtained the special data set for each year (in the
middle and right columns of Table 4). For any other new

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1476
Table 4. Vegetation index values of 12 special objects for the reference area and the study area.
Special Object Reference area Nanjing,
ETM+ Nov. 6, 2001
Study area Dandong,
MSS Sep. 15, 1976
Study area Dandong, TM
Sep. 12, 1989
Study area Dandong,
ETM+ Sep. 21, 2001
Study area Dandong,
3-year mean values
Minimum −0.9429 −0.9231 −0.9630 −0.9512 −0.9458
Water 1 (clear & deep) −0.3674 −0.7918 −0.5495 −0.4690 −0.6034
Water 2 (clear & deep) −0.3607 −0.7340 −0.4319 −0.4504 −0.5388
Water 3 (clear & deep) −0.2295 −0.3006 −0.3470 −0.4364 −0.3613
Barest land 1 −0.1009 −0.2450 −0.0617 −0.2759 −0.1942
Barest land 2 −0.0853 −0.1359 −0.0483 −0.2271 −0.1371
Barest land 3 −0.0768 −0.0699 −0.0481 −0.2108 −0.1096
Mean 0.0690 0.4122 0.4096 0.1492 0.3237
Densest vegetation 3 0.2972 0.5366 0.5448 0.3421 0.4745
Densest vegetation 2 0.3176 0.5853 0.5777 0.3611 0.5080
Densest vegetation 1 0.4336 0.6069 0.6128 0.3623 0.5273
Maximum 0.9310 0.8286 0.9048 0.6441 0.7925
area, the 12 special data can be easily obtained too.
However, less specific data can also be accepted if it is
rather difficult to get 12 data.
By using the corresponding data pairs in Table 4, we
can figure out the relational regression equations of the
vegetation index values between our study area and the
reference area for different years. Generally speaking, the
3-order polynomial equations fit their data distribution
very well. Thus we have


3
inid76 id76
id76
2
1.30633645564 0.4111579885
0.0450594470.09233570year 1976
R0.9728528, data pairs12
VV
V




2
V

2
V

2
V

2
V
(12)


3
inid89 id89
id89
2
0.701896146217 0.17120203196
0.0403978160.09267900year 1989
R0.9931883, data pairs12
VV
V



(13)


3
inid01 id01
id01
2
0.939256816379 0.5444966933
0.6784680760.00306898year 2001
R0.9864059, data pairs12
VV
V



(14)


3
inidmean idmean
idmean
2
0.976796657728 0.3315327055
0.3788205380.0611651123-year mean
R0.9949500, data pairs12
VV V
V



(15)
In the equations above, V
in, V id76, V id89, Vid01, and
Vidmean are the NDVI values respectively for year 2001 of
Nanjing as the reference area and for years 1976, 1989,
2001, and the 3-year average of Dandong as the study
area. Figure 5 shows the curves of Equations (12)-(14)
only.
The next we would like to talk about is the relationship
of vegetation coverage to vegetation index in the study
area. Theoretically, we might substitute Vin of Equations
(12)-(14) respectively for Equation (10) to obtain the re-
lational equations. But in this case we will obtain three
7-order polynomial equations. The reduction will be a bit
troublesome. In addition, the 7-order is too high so that
the calculated values would be greatly varying and hence
erroneous at the two ends of the curve. By making ap-
propriate adaptation, we suppose the mean vegetation
index values of the study area Vid to be, for example,
−0.7, −0.6, ···, 0, ···, 0.6, 0.7 and substitute these Vid
values for Equations (12)-(14) respectively to obtain the
corresponding vegetation index values Vin. Then, by sub-
stituting the Vin values for Equation (10), we will obtain
the corresponding vegetation coverage Vc values. Finally,
we use the data pairs of Vid and Vc to structure regression
equations, which will be the relational equations of
vegetation coverage to vegetation index for the study
area. As an example, Table 5 lists the corresponding
values for year 1976. Its relational equation is a 5-order
polynomial one as follows:
54
cd76 d76
32
d76 d76
d76
6.1542529667859 1.851770749887
4.50069636461 1.2666003772
0.035544188 0.26889446
VV
VV
V
 


(16)
Figure 6 shows its curve. It should be noted that Equa-

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1477
(a)
(b)
(c)
Figure 5. Curves of the regression equations of the vegeta-
tion index values between the study area and the reference
area for different monitoring years: (a) 1976; (b) 1989; (c)
2001.
Table 5. Vegetation index values of the study area (sup-
posed), vegetation index values of the reference area (calcu-
lated by Equation (12)) and vegetation coverage values (cal-
culated by Equation (10)) for the year 1976.
Vegetation index for
study area, Vid76
Vegetation index for
reference area, Vin
Vegetation
coverage, Vc76
−0.7 −0.370483 −0.086447
−0.6 −0.253523 −0.040784
−0.5 −0.175368 0.090598
−0.4 −0.128180 0.191578
−0.3 −0.104120 0.246661
−0.2 −0.095352 0.267121
−0.1 −0.094036 0.270206
0 −0.092336 0.274196
0.1 −0.082412 0.297581
0.2 −0.056427 0.359293
0.3 −0.006543 0.477206
0.4 0.075079 0.657356
0.5 0.196276 0.865632
0.6 0.364886 0.999775
0.7 0.588774 0.978150
tion (16) and also the upcoming Equations (17) and (18)
were all structured by regression method in form but
mathematically in fact, because the data for structuring
these equations were all mathematically calculated by
Equations (12)-(14) and (10), respectively, and all the
equations are fixed when being used, despite of their
original regression property. Therefore, the correlation
coefficients of Equations (16)-(18) are insignificant and
not listed (the values of their correlation coefficients are
nearly 1.0), even though these equations are still used as
regression ones.
Theoretically, the suitability of Equation (16) is in the
range of Vid76 = −0.70204 - 0.64380, i.e. Vc = −0.089387
- 1.018948 (the lowest and the highest points of the curve
in Figure 6). But in practical use, the suitable Vid76 values
should be −0.57134 - 0.60024, i.e. Vc = 0.00000 -
1.00000.
Following the same procedures, the vegetation cover-
age-index relation equations for 1989 and 2001 were also
figured out. They are respectively shown as follows:
54
cd89 d89
32
d89 d89
d89
4.3147127293742 0.563786633935
1.26514392638 0.4048724515
0.958111039 0.27715437
VV
VV
V



V
(17)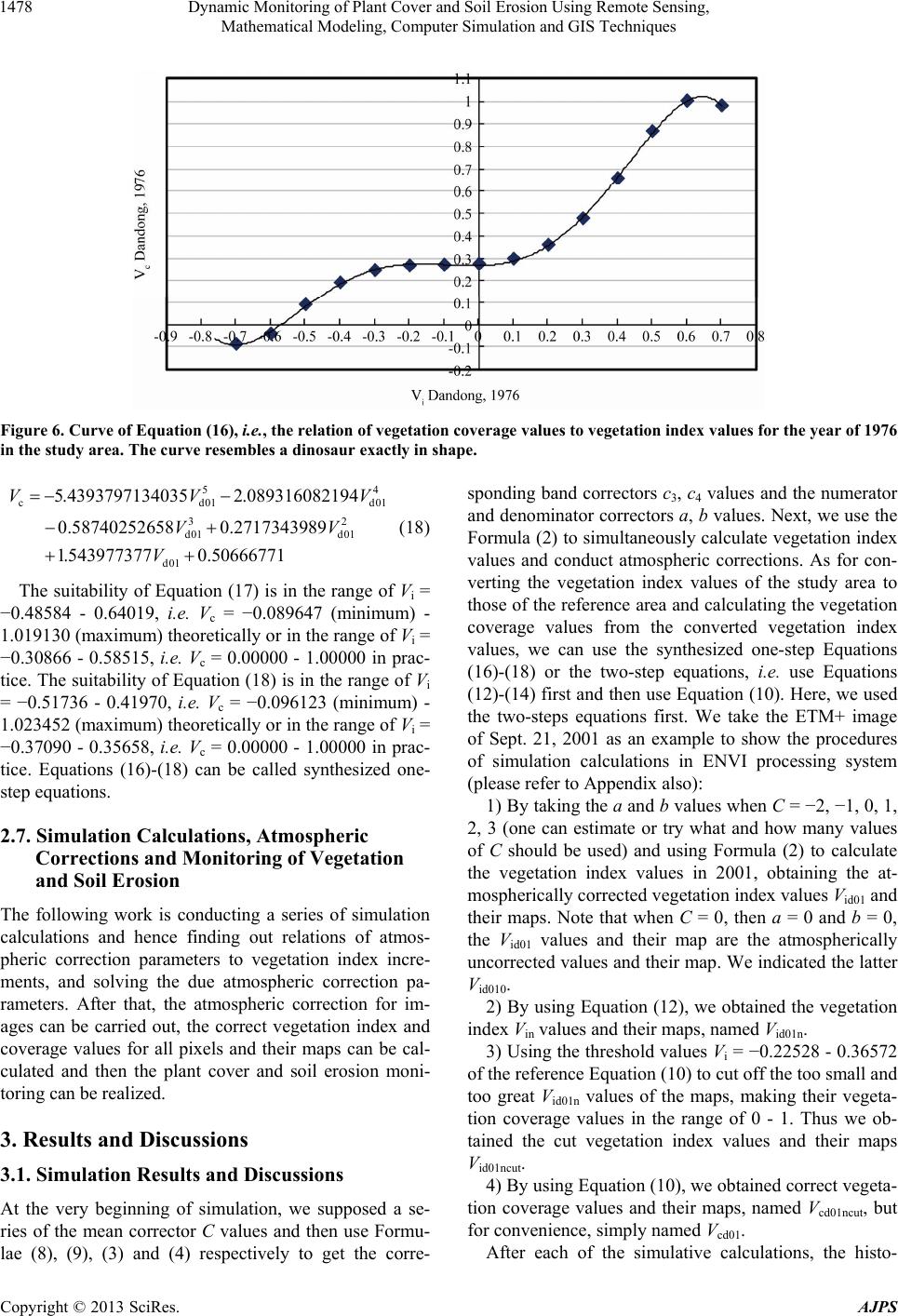

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1478
Figure 6. Curve of Equation (16), i.e., the relation of vegetation coverage values to vegetation index values for the year of 1976
in the study area. The curve resembles a dinosaur exactly in shape.
5
cd01
3
d01 d01
d01
5.4393797134035 2.089316082194
0.58740252658 0.2717343989
1.543977377 0.50666771
VV
V
V
 


4
d01
2
V
V (18)
The suitability of Equation (17) is in the range of Vi =
−0.48584 - 0.64019, i.e. Vc = −0.089647 (minimum) -
1.019130 (maximum) theoretically or in the range of Vi =
−0.30866 - 0.58515, i.e. Vc = 0.00000 - 1.00000 in prac-
tice. The suitability of Equation (18) is in the range of Vi
= −0.51736 - 0.41970, i.e. Vc = −0.096123 (minimum) -
1.023452 (maximum) theoretically or in the range of Vi =
−0.37090 - 0.35658, i.e. Vc = 0.00000 - 1.00000 in prac-
tice. Equations (16)-(18) can be called synthesized one-
step equations.
2.7. Simulation Calculations, Atmospheric
Corrections and Monitoring of Vegetation
and Soil Erosion
The following work is conducting a series of simulation
calculations and hence finding out relations of atmos-
pheric correction parameters to vegetation index incre-
ments, and solving the due atmospheric correction pa-
rameters. After that, the atmospheric correction for im-
ages can be carried out, the correct vegetation index and
coverage values for all pixels and their maps can be cal-
culated and then the plant cover and soil erosion moni-
toring can be realized.
3. Results and Discussions
3.1. Simulation Results and Discussions
At the very beginning of simulation, we supposed a se-
ries of the mean corrector C values and then use Formu-
lae (8), (9), (3) and (4) respectively to get the corre-
sponding band correctors c3, c4 values and the numerator
and denominator correctors a, b values. Next, we use the
Formula (2) to simultaneously calculate vegetation index
values and conduct atmospheric corrections. As for con-
verting the vegetation index values of the study area to
those of the reference area and calculating the vegetation
coverage values from the converted vegetation index
values, we can use the synthesized one-step Equations
(16)-(18) or the two-step equations, i.e. use Equations
(12)-(14) first and then use Equation (10). Here, we used
the two-steps equations first. We take the ETM+ image
of Sept. 21, 2001 as an example to show the procedures
of simulation calculations in ENVI processing system
(please refer to Appendix also):
1) By taking the a and b values when C = −2, −1, 0, 1,
2, 3 (one can estimate or try what and how many values
of C should be used) and using Formula (2) to calculate
the vegetation index values in 2001, obtaining the at-
mospherically corrected vegetation index values Vid01 and
their maps. Note that when C = 0, then a = 0 and b = 0,
the Vid01 values and their map are the atmospherically
uncorrected values and their map. We indicated the latter
Vid010.
2) By using Equation (12), we obtained the vegetation
index Vin values and their maps, named Vid01n.
3) Using the threshold values Vi = −0.22528 - 0.36572
of the reference Equation (10) to cut off the too small and
too great Vid01n values of the maps, making their vegeta-
tion coverage values in the range of 0 - 1. Thus we ob-
tained the cut vegetation index values and their maps
Vid01ncut.
4) By using Equation (10), we obtained correct vegeta-
tion coverage values and their maps, named Vcd01ncut, but
for convenience, simply named Vcd01.
After each of the simulative calculations, the histo-

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1479
gram for each resulting map should be calculated to get
necessary statistics, especially their mean values for the
whole study area. Through the simulative calculations,
we have finally obtained a series of simulated values and
maps of Vid01, Vid01n, Vid01ncut, and Vcd01. Then the vegeta-
tion index increment values ΔVid01 can also be calculated
by the following formula in general:
iii
VVV
0
V
V
V
V
V
V
(19)
In the formula, the Vi value which derived from the
simulation process is regarded by us as the atmospheri-
cally corrected mean vegetation index value and the Vi0 is
the Vi value when C = 0, i.e. the atmospherically uncor-
rected mean vegetation index value for the study area.
The Vid010 = 0.149239 (see Table 6). From Formula (19),
we know that ΔVid01= Vid01 − 0.149239 for the image of
2001. In Table 6, we only listed the simulated average
values for the whole study area. Obviously the magnitude
of ΔVi reflects the extent of atmospheric effects and
theoretically we can deduce the atmospheric correction
parameter from the ΔVi.
Using the same procedures and supposing C = 0, −1,
−2, −3, −4, −5, −6 and C = −1, −2, −3, −4, −5, −6, −7
respectively, the simulative calculations for 1976 and
1989 can be also carried out and their simulated values
and maps of Vid76, Vid76n, Vid76ncut, ΔVid76, Vcd76 and Vid89,
Vid89n, Vid89ncut, ΔVid89, Vcd89 can be also obtained (not
listed). It is necessary to mention that for the MSS image
of 1976, we used formula Vid76 = (MSS7 − MSS5 + a)/
(MSS7 + MSS5 + b) instead of formula (2).
Based on the simulation data pairs in Table 6, we fig-
ured out the following 2-order polynomial regression
equations for the year of 2001:
2
id01cd01 cd01
3.904254511 4.716306472
1.515224738
VV
 (20)


2
id01
id01
507.888822182
171.581092015 0.00092770624
CV
V
 
 (21)
2
cd01 cd01
170.498222689 84.4882934484
28.5622567074
CV
 (22)
Note that all these equations are regression equations
in form but almost mathematical equations in fact, be-
cause they were figured out based on the data calculated
by corresponding equations in simulation. Therefore, the
correlation coefficients of the Equations (20)-(22) are
insignificant and not listed (the values of their correlation
coefficients are nearly 1.0). The equation curves almost
pass through all data points exactly, as Figure 7 shows.
Among the equations above, equation (21) is the
so-called relation model of the atmospheric correction
parameter C to the vegetation index increment ΔVid01.
Similarly, from the supposed C values and corre-
sponding simulated data pairs for 1976 and 1989 (not
listed), we can also figure out the equations Vid = f(Vcd),
C = f(ΔVid) and C = f(Vcd) for the years 1976 and 1989
respectively:
2
id76cd76 cd76
0.0274492004137 0.486040822116
0.02948636616
VV
(23)


2
id76
id76
99.352058245426
49.91418527998 0.00678669882
CV
V
 

(24)
2
cd76 cd76
25.9571404450 65.4992299763
34.6714775372
CV 
 (25)
2
id89 cd89cd89
1.082756416921 0.843257649618
0.3920659730
VV
 (26)


2
id89
id89
177.50226229782
84.50953626216 0.00354815378
CV
V


(27)
2
cd89 cd89
5.98406989513 85.8549667258
64.7786479540
CV 
 (28)
Similarly, the correlation coefficients of Equations
Table 6. The supposed mean correctors C, the simulative area-averaged values of the corrected vegetation index, the con-
verted vegetation index, the cut converted vegetation index, the vegetation index increment, and the vegetation coverage for
the study area, i.e., the Vid01, Vid01n, Vid01ncut, ΔVid01, and Vcd01 (year 2001 and each-year model & two-step procedure).
C Numerator
corrector a
Denominator
corrector b Vid01 Vid01n Vid01ncut ΔVid01 Vcd01
−2 −0.7312 4.0000 0.137970 0.138875 0.135788 −0.011269 0.713806
−1 −0.3566 2.0000 0.143506 0.145415 0.141063 −0.005733 0.720033
0 0.0000 0.0000 0.149239* 0.152318 0.146374 0.000000 0.726208
1 0.3566 −2.0000 0.155181 0.159615 0.151693 0.005942 0.732315
2 0.7312 −4.0000 0.161343 0.167337 0.156989 0.012104 0.738335
3 1.0698 −6.0000 0.167736 0.175523 0.162236 0.018497 0.744254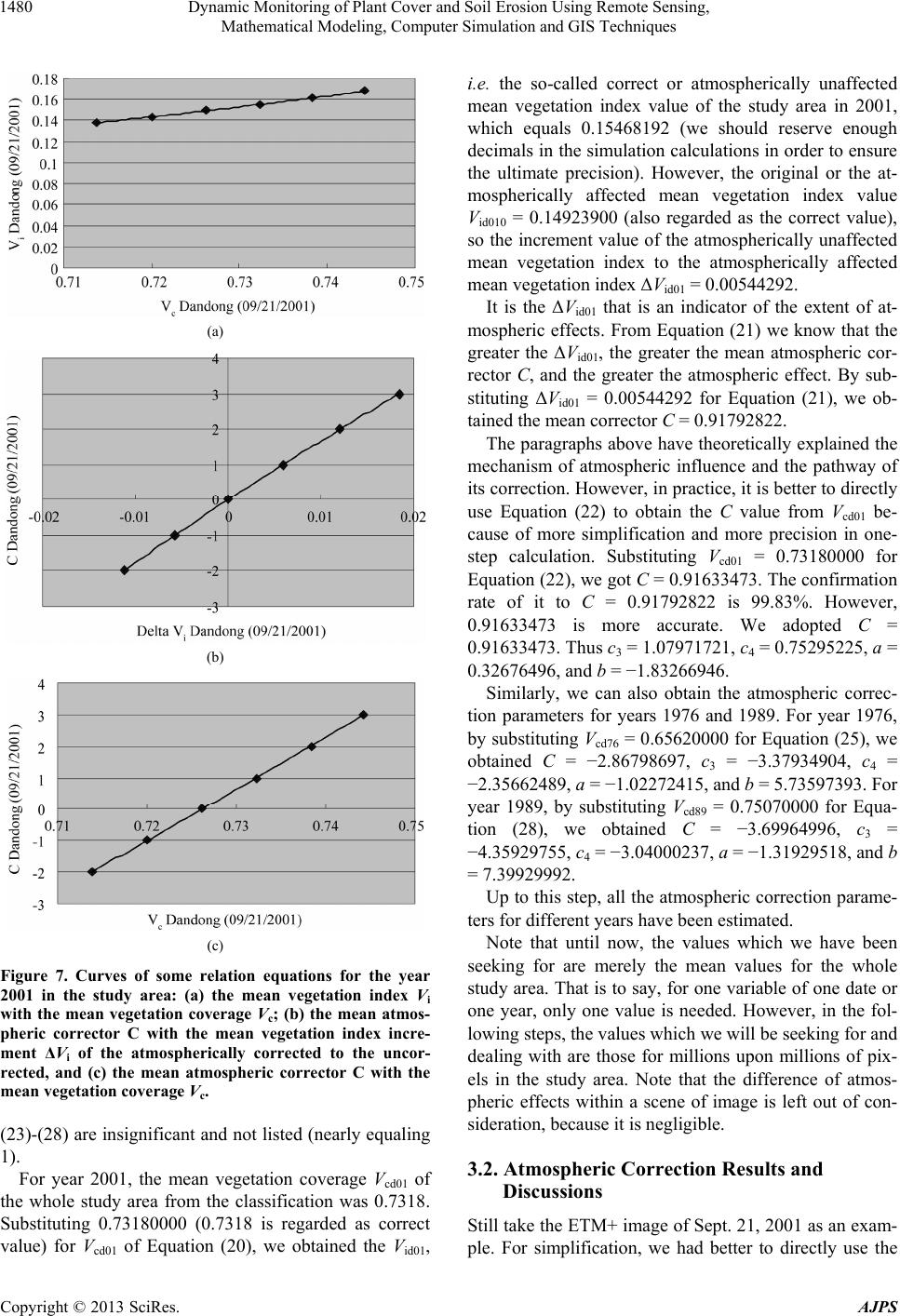

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1480
(a)
(b)
(c)
Figure 7. Curves of some relation equations for the year
2001 in the study area: (a) the mean vegetation index V
i
with the mean vegetation coverage Vc; (b) the mean atmos-
pheric corrector C with the mean vegetation index incre-
ment ΔVi of the atmospherically corrected to the uncor-
rected, and (c) the mean atmospheric corrector C with the
mean vegetation coverage Vc.
(23)-(28) are insignificant and not listed (nearly equaling
1).
For year 2001, the mean vegetation coverage Vcd01 of
the whole study area from the classification was 0.7318.
Substituting 0.73180000 (0.7318 is regarded as correct
value) for Vcd01 of Equation (20), we obtained the Vid01,
i.e. the so-called correct or atmospherically unaffected
mean vegetation index value of the study area in 2001,
which equals 0.15468192 (we should reserve enough
decimals in the simulation calculations in order to ensure
the ultimate precision). However, the original or the at-
mospherically affected mean vegetation index value
Vid010 = 0.14923900 (also regarded as the correct value),
so the increment value of the atmospherically unaffected
mean vegetation index to the atmospherically affected
mean vegetation index ΔVid01 = 0.00544292.
It is the ΔVid01 that is an indicator of the extent of at-
mospheric effects. From Equation (21) we know that the
greater the ΔVid01, the greater the mean atmospheric cor-
rector C, and the greater the atmospheric effect. By sub-
stituting ΔVid01 = 0.00544292 for Equation (21), we ob-
tained the mean corrector C = 0.91792822.
The paragraphs above have theoretically explained the
mechanism of atmospheric influence and the pathway of
its correction. However, in practice, it is better to directly
use Equation (22) to obtain the C value from Vcd01 be-
cause of more simplification and more precision in one-
step calculation. Substituting Vcd01 = 0.73180000 for
Equation (22), we got C = 0.91633473. The confirmation
rate of it to C = 0.91792822 is 99.83%. However,
0.91633473 is more accurate. We adopted C =
0.91633473. Thus c3 = 1.07971721, c4 = 0.75295225, a =
0.32676496, and b = −1.83266946.
Similarly, we can also obtain the atmospheric correc-
tion parameters for years 1976 and 1989. For year 1976,
by substituting Vcd76 = 0.65620000 for Equation (25), we
obtained C = −2.86798697, c3 = −3.37934904, c
4 =
−2.35662489, a = −1.02272415, and b = 5.73597393. For
year 1989, by substituting Vcd89 = 0.75070000 for Equa-
tion (28), we obtained C = −3.69964996, c3 =
−4.35929755, c4 = −3.04000237, a = −1.31929518, and b
= 7.39929992.
Up to this step, all the atmospheric correction parame-
ters for different years have been estimated.
Note that until now, the values which we have been
seeking for are merely the mean values for the whole
study area. That is to say, for one variable of one date or
one year, only one value is needed. However, in the fol-
lowing steps, the values which we will be seeking for and
dealing with are those for millions upon millions of pix-
els in the study area. Note that the difference of atmos-
pheric effects within a scene of image is left out of con-
sideration, because it is negligible.
3.2. Atmospheric Correction Results and
Discussions
Still take the ETM+ image of Sept. 21, 2001 as an exam-
ple. For simplification, we had better to directly use the

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1481
resulting numerator and denominator correctors a and b
to simultaneously correct images and calculate the vege-
tation index values and then calculate the vegetation
coverage values. By substituting the TM3 image, TM4
image and a = 0.32366496, b = −1.83266946 into for-
mula (2) to conduct so-called map calculation, the cor-
rected vegetation index values and their map Vid01 were
obtained. By substituting the map Vid01 in Equation (14),
we obtained the corrected vegetation index values and
their map Vind01. Then using the threshold values of Equa-
tion (10), i.e. Vi = −0.22528 - 0.36572 to cut the too
small and too big values in the Vind01 map for making the
calculated vegetation coverage values in the range of 0 ~
1. Thus we obtained the cut vegetation index values and
their map Vind01cut. The histogram of the map shows its
mean vegetation index value Vind01cut = 0.151248 for the
study area. By substituting Vind01cut map for Vi in equation
(10), the corrected vegetation coverage values and their
map Vcd01 were generated. The histogram of the map
shows its mean vegetation coverage value Vcd01 =
0.731807 for the whole study area, which exactly equals
that of the classification result (0.7318). Thereupon, we
have seen that the anticipated aim of correcting images
and assigning or “distributing” rational vegetation cov-
erage values to all pixels of the study area has been
achieved.
Following the same procedures, we corrected the TM
image of 1989 and the MSS image of 1976. For the im-
age of 1989, we used a = −1.31929518, b = 7.39929992,
and Equation (13); for the image of 1976, we used a =
−1.02272415, b = 5.73597393, and Equation (12). We
obtained their corrected vegetation index and coverage
values for all pixels and the resulting maps. The mean
values for the study area are respectively: Vind89cut =
0.145083, Vcd89 = 0.750659, V
ind76cut = 0.086276, and
Vcd76 = 0.656149. The pixels-statistical mean vegetation
coverage values equal those of the classification results.
Besides the above algorithm (including the model and
procedure), we have also tried some other algorithms.
We summarized them as follows.
Algorithm (1): Each-year model & two-step procedure,
i.e. the algorithm described as above and just what we
used as an example.
Algorithm (2): Each-year model & one-step procedure,
i.e. using the synthesized one-step Equations (16)-(18) to
directly convert the vegetation index values of the study
area into the vegetation coverage values.
Algorithm (3): 3-year-mean model & two-step proce-
dure, i.e. using Equations (15) and (10) for calculation.
Algorithm (4): One-year model & one-step procedure,
i.e. only using a selected synthesized one-step equation
of the years 1976, 1989 or 2001, i.e., Equations (16)-(18),
e.g. the Equation (18) of 2001, for all years.
Algorithm (5): no-transition model & one-step proce-
dure, i.e., directly using Equation (10) to convert the
vegetation index values of the study area to vegetation
coverage values for all years.
Algorithm (6): 3-order model & two-step procedure.
The 3-order model was established by the data pairs in
Table 3 except for those of water bodies and some other
features:

32
ci
i
2
0.502854541 2.76061717
2.2449857 0.512250579
R0.87365287, data pairs37
VV
V



i
V
(29)
Algorithm (7): 2-order model & two-step procedure.
The 2-order model was also established by the data pairs
in Table 3 except for those of water bodies and some
other features:

2
cii
2
2.47232832.2384756 0.5065307
R0.8733798, data pairs37
VVV 

(30)
Algorithm (8): no-error model & two-step procedure.
The no error-model is what was established by deleting
some data pairs in Table 3 to make its calculated mean
vegetation coverage value for the reference area equaling
the classification-determined value for the area:

43
cii
2
ii
2
2.4094382749 5.053033459
0.389735592.1073472 0.3578157
R0.95632924, data pairs26
VVV
VV



(31)
The results derived from the eight algorithms above
are very similar to each other. For simplification, Table 7
shows results of 6 algorithms only. Among the results, all
the mean vegetation coverage values for each year in the
study area (Vc) are exactly the same and equal those of
the classification results, i.e. 65.62% in 1976, 75.07% in
1989 and 73.18% in 2001.
To see the effect of atmospheric correction, let us have
a close look at the so-called atmospherically corrected
and converted mean vegetation index values Vincut (un-
derlined digits in Table 7). They are in the range of
0.0797 - 0.0951, averaged 0.0860 for the year 1976; in
the range of 0.1387 - 0.1589, averaged 0.1487 for the
year 1989; and in the range of 0.1512 - 0.1679 , averaged
0.1597 for the year 2001. However, for each algorithm,
they are all small for 1976, great for 1989 and further
great for 2001(only one exceptional value).
Comparing the mean vegetation index values of the
corrected images (0.0860, 0.1487 and 0.1597) with those
of the uncorrected images (0.4122, 0.4096 and 0.1492)
for the different years, we know that the atmospheric
effects were very great on the image of 1976 (absolute
ΔVi = 0.3262), great on the image of 1989 (absolute ΔVi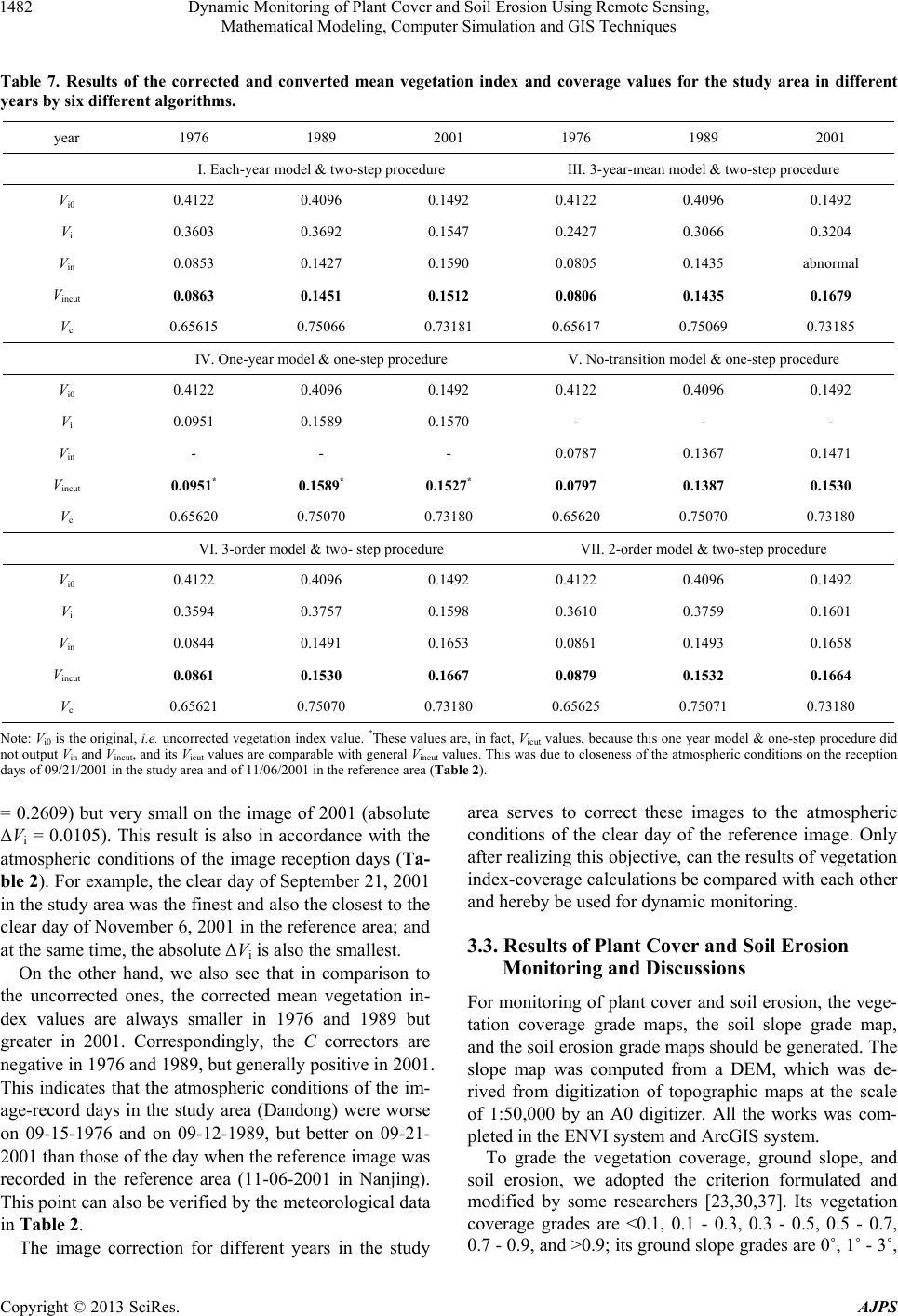

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1482
Table 7. Results of the corrected and converted mean vegetation index and coverage values for the study area in different
years by six different algorithms.
year 1976 1989 2001 1976 1989 2001
I. Each-year model & two-step procedure III. 3-year-mean model & two-step procedure
Vi0 0.4122 0.4096 0.1492 0.4122 0.4096 0.1492
Vi 0.3603 0.3692 0.1547 0.2427 0.3066 0.3204
Vin 0.0853 0.1427 0.1590 0.0805 0.1435 abnormal
Vincut 0.0863 0.1451 0.1512 0.0806 0.1435 0.1679
Vc 0.65615 0.75066 0.73181 0.65617 0.75069 0.73185
IV. One-year model & one-step procedure V. No-transition model & one-step procedure
Vi0 0.4122 0.4096 0.1492 0.4122 0.4096 0.1492
Vi 0.0951 0.1589 0.1570 - - -
Vin - - - 0.0787 0.1367 0.1471
Vincut 0.0951* 0.1589* 0.1527* 0.0797 0.1387 0.1530
Vc 0.65620 0.75070 0.73180 0.65620 0.75070 0.73180
VI. 3-order model & two- step procedure VII. 2-order model & two-step procedure
Vi0 0.4122 0.4096 0.1492 0.4122 0.4096 0.1492
Vi 0.3594 0.3757 0.1598 0.3610 0.3759 0.1601
Vin 0.0844 0.1491 0.1653 0.0861 0.1493 0.1658
Vincut 0.0861 0.1530 0.1667 0.0879 0.1532 0.1664
Vc 0.65621 0.75070 0.73180 0.65625 0.75071 0.73180
Note: Vi0 is the original, i.e. uncorrected vegetation index value. *These values are, in fact, Vicut values, because this one year model & one-step procedure did
not output Vin and Vincut, and its Vicut values are comparable with general Vincut values. This was due to closeness of the atmospheric conditions on the reception
days of 09/21/2001 in the study area and of 11/06/2001 in the reference area (Table 2).
= 0.2609) but very small on the image of 2001 (absolute
ΔVi = 0.0105). This result is also in accordance with the
atmospheric conditions of the image reception days (Ta-
ble 2). For example, the clear day of September 21, 2001
in the study area was the finest and also the closest to the
clear day of November 6, 2001 in the reference area; and
at the same time, the absolute ΔVi is also the smallest.
On the other hand, we also see that in comparison to
the uncorrected ones, the corrected mean vegetation in-
dex values are always smaller in 1976 and 1989 but
greater in 2001. Correspondingly, the C correctors are
negative in 1976 and 1989, but generally positive in 2001.
This indicates that the atmospheric conditions of the im-
age-record days in the study area (Dandong) were worse
on 09-15-1976 and on 09-12-1989, but better on 09-21-
2001 than those of the day when the reference image was
recorded in the reference area (11-06-2001 in Nanjing).
This point can also be verified by the meteorological data
in Table 2.
The image correction for different years in the study
area serves to correct these images to the atmospheric
conditions of the clear day of the reference image. Only
after realizing this objective, can the results of vegetation
index-coverage calculations be compared with each other
and hereby be used for dynamic monitoring.
3.3. Results of Plant Cover and Soil Erosion
Monitoring and Discussions
For monitoring of plant cover and soil erosion, the vege-
tation coverage grade maps, the soil slope grade map,
and the soil erosion grade maps should be generated. The
slope map was computed from a DEM, which was de-
rived from digitization of topographic maps at the scale
of 1:50,000 by an A0 digitizer. All the works was com-
pleted in the ENVI system and ArcGIS system.
To grade the vegetation coverage, ground slope, and
soil erosion, we adopted the criterion formulated and
modified by some researchers [23,30,37]. Its vegetation
coverage grades are <0.1, 0.1 - 0.3, 0.3 - 0.5, 0.5 - 0.7,
0.7 - 0.9, and >0.9; its ground slope grades are 0˚, 1˚ - 3˚,

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1483
3˚ - 5˚, 5˚ - 8˚, 8˚ - 15˚, 15˚ - 25˚, 25˚ - 35˚, and >35˚; its
soil erosion grades are: nearly none, slight, light, moder-
ate, great, very great, serious. The relation of the soil
erosion grades to the slope grades and the vegetation
coverage grades is described in Table 8.
Using the criteria of vegetation coverage grading and
the vegetation coverage maps (images) described in sec-
tion 3.2, the vegetation coverage grade maps for different
years can be generated. The working steps are as follows
(please refer to Appendix also):
1) Wiping off data outside the study area and convert-
ing the vegetation coverage image into a format accept-
able by Arcmap (in ENVI).
2) Generating the vegetation coverage grade map (im-
age) (in Arcmap).
3) Computing the histogram of vegetation coverage
grade map to obtain its statistics (in ENVI).
4) Assigning colors to the vegetation coverage grades
(in ENVI).
5) Output color vegetation coverage grade map (in
ENVI).
The results of various algorithms are all close to each
other. For simplification, Table 9 lists the results of three
algorithms only. From Tables 7 and 9, the process of
vegetation change during 25 years from 1976 to 2001 can
be seen clearly. The mean vegetation coverage values for
each year, averaged by the pixels-statistical results of the
3 algorithms, was 0.65620 for 1976, 0.75069 in 1989 and
0.73181 in 2001 respectively (Table 7). So the process of
change is that the mean vegetation coverage increased
from 1976 to 1989, i.e. from 0.6562 to 0.7507, increasing
by 14.40%; but decreased a little from 1989 to 2001, i.e.
from 0.7507 to 7318, decreasing by 2.52%.
Then we inspect the changes of different vegetation
coverage grades. For simplification, we only take the
results of the algorithm of the each-year model & two-
step procedure as an example. In Table 9 we can see that
from 1976 to 1989, the vegetation of coverage < 70%
decreased from 51.21% to 26.54%, decreasing by
48.17%; whereas the vegetation of coverage > 70% in-
creased from 48.79% to 73.46%, increasing by 50.56%.
This implies that the area of medium-low coverage of
vegetation decreased greatly and the area of high cover-
age of vegetation increased greatly, leading to improve-
ment of the plant cover status. However, from 1989 to
2001, the vegetation of coverage < 70% increased from
26.54% to 35.69%, increasing by 34.48%; while the
vegetation of coverage > 70% decreased from 73.46% to
64.31%, decreasing by 12.46%. But the vegetation of
coverage > 90% still increased from 27.65% to 37.58%,
increasing by 35.91%. This implies that the area of me-
dium-low coverage of vegetation increased to a great
extent and the area of high coverage of vegetation de-
creased to some extent, but the area of very high cover-
age of vegetation still increased to a great extent. That is
to say, the vegetation status became a little bit worse or
was basically stable or in a dynamic equilibrium from
1989 to 2001. With a closer look at the change of vegeta-
tion coverage < 70%, we will see that the vegetation of
coverage equaling 10% - 30%, 30% - 50%, and 50% -
70% all decreased from 1976 to 1989 and increased from
1989 to 2001. However, the vegetation of coverage <
10% increased continuously from 1976 through 2001, i.e.,
2.18% in 1976, 3.84% in 1989 and 5.29% in 2001.
The increase of vegetation coverage or the improve-
ment of environment in the period of 1976-1989 was
inconsistent with the general pattern in China. In the lat-
ter half of the 1970s, the ecological environment reached
its worst condition, then gradually taking a turn for the
better until now, as revealed by research works of us and
others in Jiangxi Province and Anhui Province of China
[22,23,31,38]. However, the decrease of vegetation cov-
erage in the period of 1989-2001 was somewhat abnor-
mal. The reason of the abnormality is that the study area
is a city with its suburbs and besides, the suburbs are not
large enough to attenuate the influences of urbanization.
It is the urbanization that causes the abnormality. Since
the 1980s, especially from the 1990s up to now, the city
of Dandong and its suburbs have been seeing a more
Table 8. The relation of soil erosion grades to the slope grades and the vegetation coverage grades.
Slope grade 0˚ 1˚ - 3˚ 3˚ - 5˚ 5˚ - 8˚ 8˚ - 15˚ 15˚ - 25˚ 25˚ - 35˚ >35˚
Vegetation
coverage grade Soil erosion grade
<0.1 Nearly none Slight Moderate Moderate Great Very great Serious Serious
0.1 - 0.3 Nearly none Slight Light Moderate Moderate Great Very great Serious
0.3 - 0.5 Nearly none Slight Light Light Moderate Moderate Great Very great
0.5 - 0.7 Nearly none Slight Light Light Moderate Moderate Moderate Great
0.7 - 0.9 Nearly none Slight Light Light Light Light Light Moderate
>0.9 Nearly none Slight Slight Slight Slight Slight Slight Light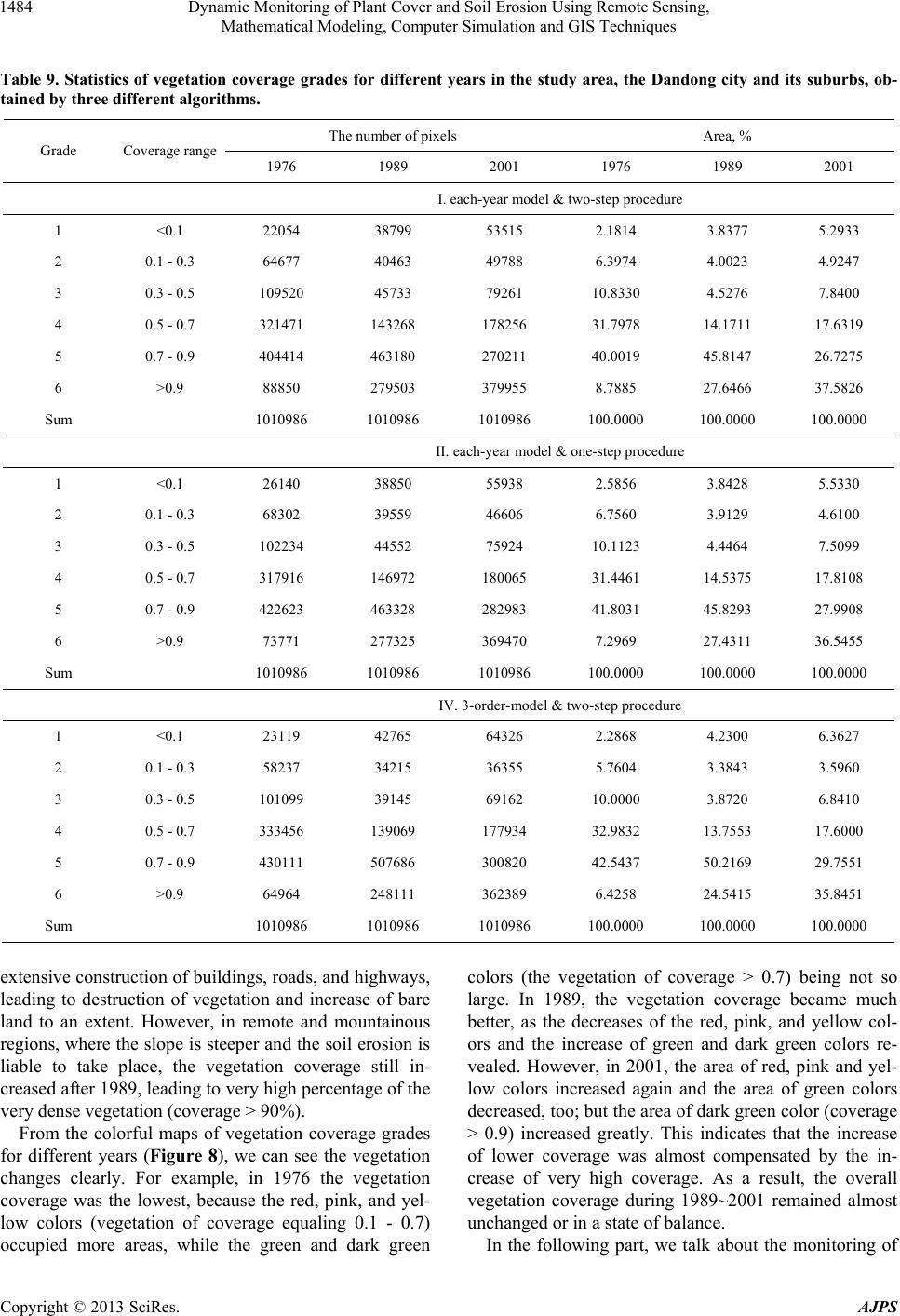

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1484
Table 9. Statistics of vegetation coverage grades for different years in the study area, the Dandong city and its suburbs, ob-
tained by three different algorithms.
The number of pixels Area, %
Grade Coverage range
1976 1989 2001 1976 1989 2001
I. each-year model & two-step procedure
1 <0.1 22054 38799 53515 2.1814 3.8377 5.2933
2 0.1 - 0.3 64677 40463 49788 6.3974 4.0023 4.9247
3 0.3 - 0.5 109520 45733 79261 10.8330 4.5276 7.8400
4 0.5 - 0.7 321471 143268 178256 31.7978 14.1711 17.6319
5 0.7 - 0.9 404414 463180 270211 40.0019 45.8147 26.7275
6 >0.9 88850 279503 379955 8.7885 27.6466 37.5826
Sum 1010986 1010986 1010986 100.0000 100.0000 100.0000
II. each-year model & one-step procedure
1 <0.1 26140 38850 55938 2.5856 3.8428 5.5330
2 0.1 - 0.3 68302 39559 46606 6.7560 3.9129 4.6100
3 0.3 - 0.5 102234 44552 75924 10.1123 4.4464 7.5099
4 0.5 - 0.7 317916 146972 180065 31.4461 14.5375 17.8108
5 0.7 - 0.9 422623 463328 282983 41.8031 45.8293 27.9908
6 >0.9 73771 277325 369470 7.2969 27.4311 36.5455
Sum 1010986 1010986 1010986 100.0000 100.0000 100.0000
IV. 3-order-model & two-step procedure
1 <0.1 23119 42765 64326 2.2868 4.2300 6.3627
2 0.1 - 0.3 58237 34215 36355 5.7604 3.3843 3.5960
3 0.3 - 0.5 101099 39145 69162 10.0000 3.8720 6.8410
4 0.5 - 0.7 333456 139069 177934 32.9832 13.7553 17.6000
5 0.7 - 0.9 430111 507686 300820 42.5437 50.2169 29.7551
6 >0.9 64964 248111 362389 6.4258 24.5415 35.8451
Sum 1010986 1010986 1010986 100.0000 100.0000 100.0000
extensive construction of buildings, roads, and highways,
leading to destruction of vegetation and increase of bare
land to an extent. However, in remote and mountainous
regions, where the slope is steeper and the soil erosion is
liable to take place, the vegetation coverage still in-
creased after 1989, leading to very high percentage of the
very dense vegetation (coverage > 90%).
From the colorful maps of vegetation coverage grades
for different years (Figure 8), we can see the vegetation
changes clearly. For example, in 1976 the vegetation
coverage was the lowest, because the red, pink, and yel-
low colors (vegetation of coverage equaling 0.1 - 0.7)
occupied more areas, while the green and dark green
colors (the vegetation of coverage > 0.7) being not so
large. In 1989, the vegetation coverage became much
better, as the decreases of the red, pink, and yellow col-
ors and the increase of green and dark green colors re-
vealed. However, in 2001, the area of red, pink and yel-
low colors increased again and the area of green colors
decreased, too; but the area of dark green color (coverage
> 0.9) increased greatly. This indicates that the increase
of lower coverage was almost compensated by the in-
crease of very high coverage. As a result, the overall
vegetation coverage during 1989~2001 remained almost
unchanged or in a state of balance.
In the following part, we talk about the monitoring of

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1485
(a)
(b)
(c)
Figure 8. Maps of vegetation coverage grades for different
years in the study area, the city of Dandong and its suburbs.
Note: None of the maps attached to this paper can be for-
mally taken as the basis of the national boundary between
China and Korea. Please see details in the section 2.1) (a)
1976; (b) 1989; (c) 2001.
soil erosion. Based on the DEM derived from topog-
raphic maps and the existing vegetation coverage grade
maps, we generated the slope map, slope grade map, and
soil erosion grade maps. The working steps in detail are
as follows (please refer to Appendix also):
1) Generating slope map from the DEM (in Arcmap);
2) Generating slope grade map from the slope map (in
Arcmap);
3) Computing histogram of the slope grade map to ob-
tain its statistics (in ENVI);
4) Changing the format of the vegetation coverage
grade maps into a format acceptable by Arcmap (in
ENIV);
5) Generating soil erosion grade maps from the slope
grade map and the vegetation grade maps (in Arcmap);
6) Computing the histograms of the soil erosion grade
maps to obtain their statistics (in ENVI);
7) Assigning colors to the soil erosion grade maps (in
ENVI).
8) Output the colorful soil erosion grade maps (in
ENVI).
Figure 9 shows the colorful slope grade map and col-
orful DEM concurrently. The statistics of the slope grade
map indicate that the study area is composed of flat land,
inclined hills, and steep mountains. The flat land of 0˚
(<0.5˚ in fact) occupies around one-half of the area, i.e.
49.0641%; the slightly inclined land (1˚ - 3˚) occupies
9.0593%; the lightly inclined land (3˚ - 5˚) occupies
5.8539%; the moderately inclined land (5˚ - 8˚) occupies
7.3014%; the very inclined slope land (8˚ - 15˚) occupies
14.1595%; the steep land (15˚ - 25˚) occupies 11.3512%;
the very steep land (25˚ - 35˚) occupies 2.8267%; and the
extremely steep land (>35˚) only occupies 0.3839%.
These terrain characteristics can be seen clearly on the
DEM, which was overlapped by a special color compos-
ite. The latter was derived from a special data transfor-
mation developed by Z. Y. Zeng [39,40]. On the com-
posite, the three primary colors, i.e. the red, green and
blue, denote the bare land, dense vegetation, and clear
and deep water respectively. In turn, the three transitional
colors, i.e. the yellow, pink and cyan, logically denote
the sparse vegetation; wetland, turbid water, or buildings
with shadows; and marsh, rice field, or other water sur-
face plus aquatic plant. It should be emphasized that the
relations of colors described here indicate those in optics
or in colored light, not in dyestuff or pigment. In the lat-
ter, the three primary colors are red, yellow and blue; the
three transitional colors are orange, purple, and green
respectively [41]. Thus the DEM clearly shows the to-
pography, terrain steepness, and ground cover of the
study area as follows: in the north-east and south-west of
the area, there are steeper mountains and hills covered by
dense vegetation (green color). Between the mountains
there is a river-let valley named Wulong, where gentle
slopes or flat land are situated and ground is bare or with
bright mature crops on it (red color). And at many places
of the mountains, hills, and valley, there is also scattered
sparse vegetation (yellow color) but its space extent is

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1486
(a)
(b)
Figure 9. Cross-reference of the color slope grade map (a)
and the color DEM (b) of the study area, city of Dandong
and its suburbs. DEM was overlapped with a color compos-
ite: Red—bare land or light matured crops; Green—dense
vegetation; Blue—water; Yellow—sparse vegetation; Cyan
—rice field; Pink—wet and low bare land, or buildings with
shadows. Urbanization (pink on DEM) occurred in the flat
area and dense vegetation (green on DEM) covered steep
terrain.
limited. Along the south-east edge of the area is the Ya-
lujiang River (blue color) and its low and flat valley,
where the city of Dandong and some towns are situated
(pink color). Finally, at the southern end of the area,
there is lower and flat land with vast paddy fields on it
(cyan color).
Table 10 lists the soil erosion grades for different
years, calculated by three algorithms only. We still take
the result of the each-year model & two-step procedure
as an example for discussing soil erosion change. Figure
10 shows the color maps of soil erosion grades for dif-
ferent years. Please note that 49.0641% of the study area
belongs to the grade of nearly-none erosion and it is al-
ways the same for all the monitoring years, because
49.0641% of the area lies in the flat land with slope of 0˚.
This kind of land has even turned into deposition areas in
(a)
(b)
(c)
Figure 10. Maps of soil erosion grades for different years in
the city of Dandong and its suburbs as a study area. (a)
1976; (b) 1989; (c) 2001.
many places, despite how the vegetation coverage is on
it.
In the period from 1976 to 1989 and then to 2001, the
overall area of erosion land, i.e. the sum of light, moder-
ate, great, very great, and severe erosions decreased from
35.36% to 25.43% and then to 18.53%. In other words,
the erosion land was reduced by 47.60% in the period of

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1487
Table 10. Statistics of soil erosion grades for different years in the study area, the city of Dandong and its suburbs, calculated
by three different algorithms.
The number of pixels %
Grade Erosion intensity
1976 1989 2001 1976 1989 2001
I. Each-year model & two-step procedure
1 Nearly none 496031 496031 496031 49.0641 49.0641 49.0641
2 Slight 157479 257912 327615 15.5768 25.5109 32.4055
3 Light 271952 228782 147287 26.8997 22.6296 14.5686
4 Moderate 82970 26264 36992 8.2068 2.5979 3.6590
5 Great 1844 1241 2247 0.1824 0.1228 0.2223
6 Very great 435 384 484 0.0430 0.0380 0.0479
7 Severe 275 372 330 0.0272 0.0368 0.0326
sum 1010986 1010986 1010986 100.0000 100.0000 100.0000
II. Each-year model & one-step procedure
1 Nearly none 496031 496031 496031 49.0641 49.0641 49.0641
2 Slight 146410 256693 322412 14.4819 25.3904 31.8908
3 Light 280292 229778 152809 27.4246 22.7281 15.1148
4 Moderate 82503 26500 36579 8.1606 2.6212 3.6182
5 Great 2365 1228 2315 0.2339 0.1215 0.2290
6 Very great 1990 386 506 0.1968 0.0382 0.0501
7 Severe 1395 370 334 0.1380 0.0366 0.0330
sum 1010986 1010986 1010986 100.0000 100.0000 100.0000
V. No transition model & one-step procedure
1 Nearly none 496031 496031 496031 49.0641 49.0641 49.0641
2 Slight 97010 194816 345712 9.5956 19.2699 34.1955
3 Light 310771 291018 131482 30.7394 28.7856 13.0053
4 Moderate 104251 26897 32433 10.3118 2.6605 3.2081
5 Great 2096 1398 3981 0.2073 0.1383 0.3938
6 Very great 460 840 893 0.0455 0.0435 0.0883
7 Severe 367 386 454 0.0363 0.0382 0.0449
sum 1010986 1010986 1010986 100.0000 100.0000 100.0000
25 years from 1976 to 2001. The decrease of soil erosion
area is contributed mainly by the decrease of the light
erosion grade, which occupied 26.90% in 1976, 22.63%
in 1989, and 14.57% in 2001. It is yet worth paying at-
tention to the fact that even from 1989 to 2001, the soil
erosion in the area was still lightened by 27.12%, al-
though in the same time the mean vegetation coverage
was slightly reduced, i.e. from 75.07% to 73.18%. This
implies that the slight decrease of the vegetation cover-
age did not lead to increase of soil erosion. The reason is
that the vegetation coverage decrease chiefly resulted
from urbanization and the latter mainly occurred on the
flatland or gently sloping land, which could not cause a
prominent increase of soil erosion due to the gentle
steepness. However, in the more greatly sloping or steep
regions, especially in the remote and mountainous areas,
where the land is apt to be eroded due to greater steep-
ness but rarely disturbed by urbanization, so the vegeta-

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1488
tion coverage was still magnified. As a synthetic result,
the area of soil erosion for the overall region tends to be
reduced.
From Figure 10 we can see clearly that the soil ero-
sion had been mitigated from 1976 to 1989 and then to
2001. This is revealed in the decrease of pink and red
colors, i.e. light and moderate erosion areas and in the
increase of the yellow colors, i.e. slight erosion area from
1976 to 1989 and then to 2001. Simultaneously, the areas
of cyan, blue, and maroon colors, i.e. great, very great,
and severe erosion grades have all changed but their
space extent is too small to be visualized in Figure 10
unless the figure is enlarged. Note that from 1989 to
2001, the increase of vegetation coverage 0.1 - 0.5 (the
red and pink colors in Figure 8) did not, by no means,
lead to the increase of light and moderate erosion (pink
and red colors in Figure 10). The reason for this has
been explained.
Finally, we say several words about credibility of the
method. The method was originally developed before the
year 2001. It has been used and tested in the Lianshui
basin of Jiangxi Province, China. Its monitoring results
were compared with those of other researchers [31] and
the comparison has proved that this method is correct,
reliable, and more precise [22,23]. And now the method
has been improving greatly in recent years. So the pre-
sent method should be more perfect and precise than its
original version and thus the present monitoring results
should suit the actual conditions all the more. However,
in the city of Dandong and its suburbs, there is no other
researcher’s result in the same space extent and same
time interval to be compared with our results. Neverthe-
less, fortunately, few existing unpublished data with the
whole Dandong Municipality (14685.2 Km2), a part of
which is our study area (909.9 Km2), can be used to be
compared with our results roughly. According to the un-
published reports of the Bureau of Soil and Water Con-
servation, Liaoning Province, September 29, 1997 and
the Bureau of Water Resource, Dandong Municipality,
January 11, 2000 and May 23, 2000, the soil erosion area,
i.e. the sum of light, moderate, great, very great, and se-
rious grade for the whole Dandong Municipality de-
creased from 33.4% in 1986 to 27.0% in 1996, and then
to <27.0% in 2000 (visual air-photo interpretation result).
According to our results, the soil erosion area for our
study area decreased from 35.4% in 1976 to 25.4% in
1989, and then to 18.5% in 2001. When we put the two
series of data together in an order, they were 35.4% in
1976, 33.4% in 1986, 25.4% in 1989, 27.0% in 1996,
<27.0 in 2000, and 18.5% in 2001. It is obvious that the
general trends and magnitudes of soil erosion change in
the whole region (Dandong Municipality) and in the par-
tial region (our study area) are consistent and almost fit
to each other, even though the two series of data came
from different space extent, different time interval, dif-
ferent researchers, and yet different methodology. We
have also noticed that a few of the data drift a bit off the
normal order of magnitude, i.e. the 27.0% in 1996 for
Dandong Municipality was a bit greater than the 25.4%
in 1989 for our study area. This may be caused by greater
erosion in some areas outside the city of Dandong and its
suburbs.
4. Summary and Conclusions
1) Traditional method of plant cover and soil erosion
monitoring is mainly the visual photo or image interpre-
tation or image classification. The accuracy of monitor-
ing is lower and the amount of work is great. One may
also adopt the USLE equation method. However, its in-
effectiveness in applications outside the range of condi-
tions for which it was developed and the hard evaluation
of its factors K, C, P and L restrict its application. It is
for these reasons that we suggested a new method as one
of choices. This method suggests finding one or more
variables free from atmospheric effects as a starting point
to reduce atmospheric correction parameters. This is an
indirect, fast and operational way, through a series of
modeling, simulation and correction, to obtain the due
atmospheric correction parameters and then correct im-
ages, calculate vegetation index and vegetation coverage
values for all pixels, so that the monitoring of vegetation
and soil erosion can be realized effectively.
2) We have already found some variables free from
atmospheric effects, e.g. the mean vegetation coverage
value of the whole study area. The latter is only the spa-
tial distribution of vegetation and can be obtained di-
rectly from the satellite image itself. For one-date image
of a study area, only one value of the mean vegetation
coverage is needed. So it is easier to acquire, e.g. in this
study it was acquired by unsupervised classification and
broken line analysis.
3) Using the mean vegetation coverage values for the
study area as a starting point, one can conduct a series of
simulative calculations, so that the corresponding correct
mean vegetation index values and the due atmospheric
correction parameters for the area can be deduced. How-
ever, to conduct the simulative calculations, one needs a
series of models in advance. All the needed models, e.g.
the models of relation between vegetation coverage and
vegetation index, the models of relation of vegetation
index values between the reference area and the study
area (or any other new area), the difference coefficients
of atmospheric effects on different bands, etc., have been
established in this research.
4) Supposing some mean atmospheric corrector C val-

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1489
ues, the simulative calculations can be carried out. Based
on the series of resulting simulated data pairs, a series of
new model can be structured. Among them, the impor-
tant ones are Vi = f(Vc), C = f(ΔVi), and C = f(Vc). By us-
ing these new models and the so-called correct mean
vegetation coverage values Vc obtained from classifica-
tion, one can compute out the due mean vegetation index
values and the due atmospheric correction parameters for
the study area and for different years.
5) By substituting the numerator and denominator cor-
rectors a and b values for the calculation formula of
NDVI, one can obtain the atmospherically corrected
vegetation index and coverage values for all pixels and
their maps for different years. Then the vegetation cov-
erage grade maps for different years can be obtained and
the vegetation monitoring was realized. Furthermore,
using the resulting vegetation grade maps and a slope
grade map from DEM, one can obtain the soil erosion
grade maps for different years and so the soil erosion
monitoring was also realized.
6) Our monitoring results, including the statistics of
vegetation index, vegetation coverage, and soil erosion as
well as the color maps of vegetation coverage and soil
erosion, are all reasonable and interesting, clearly and in
detail showing the change of vegetation and soil erosion
in the study area in the 25 years from 1976 to 2001. The
results also coincide with the existing other investigation
results and correspond to reality.
7) The essence of atmospheric correction in this
method is that using vegetation index values in a clear
day and corresponding vegetation coverage values to
establish a vegetation index-coverage relation, the rela-
tion can be regarded as a standard one in a clear day; and
then correcting vegetation index values of other area to
be appropriate for the standard relation, the corrected
vegetation index values can be regarded as ones of a
clear day.
8) For this method to be perfected and extensively ap-
plied, some research works are still needed. However, as
we have emphasized, the essence of this method is to
acquire the so-called correct mean vegetation coverage
value free from atmospheric effects for the study area
and then based on this value to rationally “assign” or
“distribute” appropriate vegetation coverage values to all
pixels. So the atmospheric correction and the vegetation
index calculation are merely a means or bridge for ful-
filling this task. Therefore, other things are not so impor-
tant, provided the more rational “distribution” work is
done. Even so, the atmospheric correction and vegetation
index calculation by this method are still credible.
5. Acknowledgements
We are grateful to the National Fund for Natural Sci-
ences of China, which sponsored our research (Project
numbers: 40071043, 40371053 & 41071281). We are
also grateful to Global Land Cover Facility, Institute for
Advanced Computer Studies, University of Maryland,
USA for offering some images via internet. We also ac-
knowledge the Bureau of Soil and Water Conservation,
Liaoning Province and the Bureau of Water Resource,
Dandong municipality for a few data cited. We are also
thankful to the anonymous reviewers for valuable sug-
gestions and comments.
REFERENCES
[1] J. R. Fan, J. H. Zhang, X. H. Zhong, S. Z. Liu and H. P.
Tao, “Monitoring of Soil Erosion and Assessment for
Contribution of Sediments to Rivers in a Typical Water-
shed of the Upper Yangtze River Basin,” Land Degrad &
Develop, Vol. 15, No. 4, 2004, pp. 411-421.
[2] O. Cerdan, N. Baghdadi, C. King and A. Couturier, “Soil
Erosion Modeling at the Catchment Scale Using Remote
Sensing,” Geophysical Research Abstracts, Vol. 7, 2005.
[3] Z. Y. Jiang, A. R. Huete, J. Chen, Y. H. Chen, J. Li, G. J.
Yan and X. Y. Zhang, “Analysis of NDVI and Scaled Di-
fference Vegetation Index Retrievals of Vegetation Frac-
tion,” Remote Sensing of Environment, Vol. 101, No. 3,
2006, pp. 366-378. doi:10.1016/j.rse.2006.01.003
[4] A. Goener, R. Gloaguen and F. Makeschin, “Monitoring
of the Ecuadorian Mountain Rainforest with Remote
Sensing,” Journal of Applied Remote Sensing, Vol. 1, No.
1, 2007.
[5] N. B. Chang, M. Han, W. Yao, L. C. Chen and S. G. Xu,
“Change Detection of Land Use and Land Cover in an
Urban Region with SPOT-5 Images and Partial Lanczos
Extreme Learning Machine,” Journal of Applied Remote
Sensing, Vol. 4, No. 1, 2010.
[6] C. G. Homer, C. L. Aldridge, D. K. Meyer and S. J.
Schell, “Multi-Scale Remote Sensing Sagebrush Charac-
terization with Regression Trees over Wyoming, USA:
Laying a Foundation for Monitoring,” International Jour-
nal of Applied Earth Observation and Geoinformation,
Vol. 14, No. 1, 2012, pp. 233-244.
doi:10.1016/j.jag.2011.09.012
[7] M. A. J. Wulder, C. White, S. Coggins, S. M. Ortlepp and
N. C. Coops, “Digital High Spatial Resolution Aerial
Imagery to Support Forest Health Monitoring: The Moun-
tain Pine Beetle Context,” Journal of Applied Remote
Sensing, Vol. 6, No. 1, 2012, Article ID: 062527.
[8] R. B. King, “Land Cover Mapping Principles: A Return
to Interpretation Fundamentals,” International Journal of
Remote Sensing, Vol. 23, No. 18, 2002, pp. 3525-3545.
doi:10.1080/01431160110109606
[9] G. Rees, M. Williams and P. Vitebsky, “Mapping Land
Cover Change in a Reindeer Herding Area of the Russian
Arctic Using Landsat TM and ETM+ Imagery and Indi-
genous Knowledge,” Remote Sensing of Environment,
Vol. 85, No. 4, 2003, pp. 441-452.
doi:10.1016/S0034-4257(03)00037-3

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1490
[10] J. D. Tarpley, S. R. Schneider and R. L. Money, “Global
Vegetation Indices from NOAA-7 Meteorological Satel-
lite,” Journal of Climate and Applied Meteorology, Vol.
23, No. 3, 1984, pp. 491-494.
doi:10.1175/1520-0450(1984)023<0491:GVIFTN>2.0.C
O;2
[11] J. R. G. Townshend, T. E. Goff and C. J. Tucker, “Mul-
titemporal Dimensionality of Images of Normalized Dif-
ference Vegetation Index at Continental Scales,” IEEE
Transactions on Geoscience and Remote Sensing, Vol. 23,
No. 6, 1985, pp. 888-895.
doi:10.1109/TGRS.1985.289474
[12] N. A. Drake, X. Y. Zhang, E. Berkhout, R. Bonifacio, D.
I. F. Grimes, J. Wainwright and M. Mulligan, “Modelling
Soil Erosion at Global and Regional Scales Using Remote
Sensing and GIS Techniques,” In: P. M. Atkinson and N.
J. Tale, Eds., Advances in Remote Sensing and GIS
Analysis, John & Sons, New York, 1999, pp. 241-261.
[13] B. C. Rundquist, “The Influence of Canopy Green Vege-
tation Fraction on Spectral Measurements over Native
Tall Grass Prairie,” Remote Sensing of Environment, Vol.
81, No. 1, 2002, pp. 129-135.
doi:10.1016/S0034-4257(01)00339-X
[14] P. P. Singh, S. Roy and F. N. Kogan, “Vegetation and
Temperature Condition Indices from NOAA AVHRR
Data for Drought Monitoring over India,” International
Journal of Remote Sensing, Vol. 24, No. 22, 2003, pp.
4393-4402. doi:10.1080/0143116031000084323
[15] P. Durante, C. Oyonarte and F. Valladares, “Influence of
Land-Use Types and Climatic Variables on Seasonal Pat-
terns of NDVI in Mediterranean Iberian Ecosystems,”
Journal of Applied Vegetation Science, Vol. 12, No. 2,
2009, pp. 177-185.
[16] G. X. Wang, G. Gertner, S. F. Fang and A. B. Anderson,
“Mapping Multiple Variables for Predicting Soil Loss by
Geostatistical Methods with TM Images and a Slope
Map,” Photogrammetric Engineering & Remote Sensing,
Vol. 69, No. 8, 2003, pp. 889-898.
[17] R. L. Gaffer, D. C. Flanagan, M. L. Denight and B. A.
Engl, “Geographical Information System Erosion Asses-
sment at a Military Training Site,” Journal of Soil and
Water Conservation, Vol. 63, No. 1, 2008, pp. 1-10.
doi:10.2489/jswc.63.1.1
[18] M. F. Winchell, S. H. Jackson, A. M. Wadley and R.
Srinivasan, “Extension and Validation of a Geographic
Information System-Based Method for Calculating the
Revised Universal Soil. Loss Equation Length-Slope Fac-
tor for Erosion Risk Assessments in Large Watershed,”
Journal of Soil and Water Conservation, Vol. 63, No. 3,
2008, pp. 105-111. doi:10.2489/jswc.63.3.105
[19] S. K. Saha, “Water and Wind Induced Soil Erosion Asse-
ssment and Monitoring Using Remote Sensing and GIS,”
In: M. V. K. Sivakumar, P. S. Roy, K. Harsen and S. K.
Saha, Eds., Satellite Remote Sensing and GIS Application
in Agricultural Meteorology, Dehra Dun, 2004, pp. 315-
330.
[20] M. K. Hazarika and K. Honda, “Estimation of Soil Ero-
sion Using Remote Sensing and GIS, Its Valuation and
Economic Implications on Agricultural Production,” In:
D. E. Stott, R. H. Mohtar and G. C. Steinhardt, Eds., Sus-
taining the Global Farm, 2001, pp. 1090-1093.
[21] R. Quiñonez-Piñón, A. Mendoza-Durán and C. Valeo,
“Design of an Environmental Monitoring Program Using
NDVI and Cumulative Effects Assessment,” Interna-
tional Journal of Remote Sensing, Vol. 28, No. 7, 2007,
pp. 1643-1644. doi:10.1080/01431160600887730
[22] Z. Y. Zeng, “Fully Automatic Mapping for Vegetation
and Soil Erosion Monitoring Using Remote Sensing,
Mathematical Modelling and GIS Techniques,” Pro-
ceedings of the 20th international cartographic confer-
ence: Mapping the 21st Century, Beijing, 6-10 August
2001, pp. 702-709.
[23] Z. Y. Zeng, “2004. Study on Computer Classification of
Satellite Images and Application in Geoscience,” Science
Press, Beijing, 2004. (In Chinese).
[24] R. E. Turner and M. M. Spencer, “Atmospheric Model for
Correction of Spacecraft Data,” Pro c e e dings of the Eighth
International Symposium on Remote Sensing of Environ-
ment, Ann Arbor, 2-6 October 1972.
[25] K. J. Thome, D. L. Helder, D. Aaron and J. D. Dewald,
“Landsat-5 TM and Landsat-7 ETM+ Absolute Radio-
metric Calibration Using the Reflectance-Based Method,”
IEEE Transactions on Geoscience and Remote Sensing,
Vol. 42, No. 12, 2004, pp. 2777-2785.
doi:10.1109/TGRS.2004.839085
[26] E. Vermote, D. Tanre, J. L. Deuze, M. Herman and J. J.
Morcette, “Second Simulation of the Satellite Signal in
the Solar Spectrum: An Overview,” IEEE Transactions
on Geoscience and Remote Sensing, Vol. 35, No. 3, 1997,
pp. 675-686. doi:10.1109/36.581987
[27] U. S. Geological Survey, “Landsat Data Users Hand-
book,” EROS Data Center, Sioux Falls, 1979, pp. 33-38.
[28] Y. Kaufman, “The Atmospheric Effect on Remote Sens-
ing and Its Correction,” In: G. Asrar, Ed., Theory and
Applications of Optical Remote Sensing, John Wiley,
New York, 1989, pp. 336-428.
[29] P. M. Mather, “Remote Sensing and Geographical Infor-
mation Systems,” In: P. M. Mather, Ed., TERRA-I: Un-
derstanding the Terrestrial Environment, Taylor & Fran-
cis, London-Washington DC, 1992, pp. 211-219.
[30] Z. G. Wang, Z. H. Hu, Z. Y. Wei, J. R. Xu, C. H. Wang
and Z. G. Ren, “Soil Erosion Control and Damland Sys-
tem Agriculture in Weijiayu Watershed,” In: J. M. Laflen,
J. L. Tian and C. H. Huang, Eds., Soil Erosion and Dry-
land Farming, CRC Press, Boca Raton, London, New
York, Washington DC, 2000, pp. 81-91.
[31] D. C. Li and D. M. Shi, “Application of Satellite Remote
Sensing Techniques for Monitoring Dynamic Change of
Soil Erosion in Xingguo County,” Soil and Water Con-
serv in China, Vol. 2, No. 1, 1998, pp. 29-32 (in Chi-
nese).
[32] P. Heckbert, “Color Image Quantization for Frame Buffer
Display,” Computer Graphics, Vol. 16, No. 3, 1982, pp.
297-307. doi:10.1145/965145.801294
[33] ILWIS Department, International Institute for Aerospace

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1491
Survey and Earth Sciences (ITC), “ILWIS 2.1 for Win-
dows, The Integrated Land and Water Information Sys-
tem,” User’s Guide, Enschede, 1997, pp. 213-216.
[34] D. S. Liu and Z. Y. Zeng, “Mathematic Method and Mo-
delling in the Research of Soil and Environment,” Agri-
culture Press, Beijing, 1987, pp. 197-202 (in Chinese).
[35] Z. J. Gu, Z. Y. Zeng, X. Z. Shi, D. S. Yu, W. Zheng, Z. L.
Zhang and Z. F. Hu, “A Model Calculating Vegetation
Fractional Coverage from ETM+ Imagery,” Frontiers in
Ecology and the Environment, Vol. 17, No. 2, 2008, pp.
771-776. (In Chinese)
[36] Z. J. Gu, Z. Y. Zeng, X. Z. Shi, D. S. Yu, W. Zheng, Z. L.
Zhang and Z. F. Hu, “Estimation Models of Vegetation
Fractional Coverage (VFC) Based on Remote Sensing
Image at Different Radiometric Correction Level,” Chi-
nese Journal of Applied Ecology, Vol. 19, No. 6, 2008, pp.
1296-1302 (in Chinese).
[37] Z. X. Zhang, X. L. Peng, X. F. Chen and J. Y. liu,
“Mountain Soil Erosion Mapping in Central Tibet Using
Remote Sensing and GIS,” The 4th International Sympo-
sium on High Mountain Remote Sensing Cartography,
Karlstad-Kirula-Troms, 19-29 August 1996, pp. 255-263.
http://www.kfunigrazac.at/geowww/hmrst/pdfs/hmvsc4/z
hEA.hm4.PDF
[38] D. C. Li, X. R. Shi and B. Zhou, “Dynamic Monitoring of
Soil Erosion in Mountains and Hills Area in the Southern
China Using Remote Sensing,” Proceedings of the 8th
National Symposium on Remote Sensing, Nanning, 19-25
December 1993, pp. 324-327 (in Chinese).
[39] Z. Y. Zeng, “A New Method of Data Transformation for
Satellite Images: I. Methodology and Transformation
Equations for TM Images,” International Journal of Re-
mote Sensing, Vol. 28, No. 18, 2007, pp. 4095-4124.
doi:10.1080/01431160601028912
[40] Z. Y. Zeng, “A New Method of Data Transformation for
Satellite Images: II. Transformation Equations for SPOT,
NOAA, IKONOS, Quick Bird, ASTER, MSS and Other
Images and Application,” International Journal of Remo-
te Sensing, Vol. 28, No. 18, 2007, pp. 4125-4155.
doi:10.1080/01431160601030082
[41] L. Zhang and Z. C. Li, “The English-Chinese Technical
and Scientific Dictionary,” Chemical Industry Press, Bei-
jing, 1997 (in Chinese).

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1492
Appendix
Our practical working procedures of using ENVI and
ArcGIS (Arcmap) systems for realizing the monitoring of
plant cover and soil erosion (At present, no software
package is offered for the algorithms)
Appendix A
Image correction and map calculation of vegetation index
and vegetation coverage in ENVI processing system
1) Image correction and map calculation of vegetation
index: taking C = 1 (a = 0.3566 and b = −2.0) and ETM+
image of Sept. 12, 2001 as an example
ENVI--basic tools--band math--enter an expression--
(float (b2)-b1-0.3566)/(float (b2) + b1 + 2.0)--input b1:
TM3--input b2:TM4--output file: vid01--ok
2) Calculation of histogram statistics
ENVI--basic tools—statistics--compute statistics--in-
put file:vid01--select mask band: ddbound (boundary fife
for the application area)--ok--calculate histogram--histo-
gram plot--text report--file--ok
3) Conversion of the vegetation index map from the
application area to that of the reference area
ENVI--basic tools--band math--enter an expression--
0.939256816379 * b0 * b0 * b0 + 0.5444966933 * b0 *
b0 + 0.678468076*b0 + 0.003068975--ok--inputb0:
vid01--output file: vid01n--ok--basic tools--… (compute
histogram, ditto)
4) Using relevant thresholds to cut the too small or too
great values in the map
ENVI--basic tools--band math--enter an expression--
(b0 LT (−0.22528)) * (−0.22528) + (b0 GT 0.36572) *
0.36572 + ((b0 GE (−0.22528) AND (b0 LE 0.36572)) *
b0--ok--inputb0: vid01 n--output file: vid01ncu t--basic
tools--… (compute histogram, ditto)
5) Calculation of vegetation coverage map from the
corrected and converted vegetation index map
ENVI--basic tools--band math--enter an expression--
6.487093360864 * b0 * b0 * b0 * b0 − 6.172463983663 *
b0 * b0 * b0 − 1.1454831195 * b0 * b0 + 2.3151305575
* b0 + 0.492401042--ok--inputb0:vd01ncut—outputfile:
vcd01—basic tools--… (compute histogram, ditto)
Appendix B
Generation of vegetation coverage grades map (image)
and slope grades map in ENVI system and ArcGIS sys-
tem: taking the vegetation coverage grades map as an
example
1) Wiping off data outside the area and changing the
vegetation coverage image into a format acceptable by
Arcmap in ENVI
ENVI--basic tools--band math--enter an expression--
b0 * b9--ok--input b0:vcd01--input b9: ddbound--output
file: vcd01a (a means area)--ok—file (in image frame)
--save file as--TIFF—vcd01at (t means tif)-ok
2) Generation of vegetation coverage grades image in
ArcGIS
Arcmap--ok (empty map)-- + (input map):vcd01at--
add-yes (create pyramid)--spatial analyst—reclassify--
classify--class: 6--break values (0~1): 0.1, 0.3, 0.5, 0.7,
0.9, 1.0--ok--save as type--TIFF--output raster--name:
vcd01atg (g means grade)--save--ok--x(exit)--no
3) Wiping off data outside the area and changing the
vegetation coverage grades image into a format accept-
able by Arcmap in ENVI
ENVI--basic tools--band math--enter an expression--
b0 * b9—ok--input b0: Vcd01atg--input b9: ddbound--
output file: vcd01atga (a means area)--ok--file (in image
frame)--save file as--TIFF—name: vcd01atgat--ok--basic
tools-(compute histogram, ditto)
Appendix C
Generation of soil erosion grades map (image) in ArcGIS
system and its color map in ENVI system
1) Generating all the possible combinations of vegeta-
tion coverage grades and slope grades for each erosion
grade
Arcmap--ok(empty map)-- + (input map): vcd01atgat
(1, 2, 3, 4, 5, 6)--Yes-- + (input map): ddslopeg (slope
grades map of the area: 1, 2, 3, 4, 5, 6, 7, 8)--confirm--
spatial analyst--raster calculator--vcd01atgat (double hit)
--*--10-- + --ddslopeg—evaluate − calculation (hit right
key)--data--export data--format: TIFF--name: erod01--
save--yes (add map as a layer) (Result: the combination
of 11, 21, 31, 41, 51 and 61 belong to the grade of
“Nearly none”; the combination of 12, 22, 32, 42, 52,
62, ···, 66 and 67 belong to the grade of “slight”; etc.)
2) Adding all combinations of each erosion grade to-
gether
All layers except erod01(hit right key for each)--re-
move--spatial analyst--raster calculator--erod01 (double
hit)-- = --11--or-- = -- 21 --or-- erod01… (until all num-
bers of the class “nearly none” are calculated)--evaluate
--calculation(double hit)--backspace or delete--rename:
none--spatial analyst--raster calculator--erod01-- = -- 12
--or--erod0… (until all numbers of the class “slight” are
calculated)—evaluate--calculation (double hit)--back-
space or delete--rename: slight--spatial analyst--raster
calculator--erod01-- = --23--or--erod01… (until all num-
bers of the class “light” are calculated)--evaluate--cal-
culation (hit two times)--backspace or delete--rename:
light--spatial analyst—raster calculator--erod01-- = --13
--or--erod01… (until all numbers of the class “moderate”
are calculated)--evaluate--calculation(double hit)--back-
space or delete--rename: moderate--spatial analyst--raster
calculator--erod01-- = --15--or--erod01… (until all num-

Dynamic Monitoring of Plant Cover and Soil Erosion Using Remote Sensing,
Mathematical Modeling, Computer Simulation and GIS Techniques
1493
bers of the class “great” are calculated)—evaluate--cal-
culation (double hit)--backspace or delete--rename: great
--spatial analyst--raster calculator-- = --16--or--erod01…
(until all numbers of the class “very great” are calcu-
lated)--evaluate—calculation (double hit)--backspace or
delete--rename: very great--spatial analyst--raster calcu-
lator--erod01-- = --17-- or—erod01… (until all numbers
of the class “extremely great” are calculated)--evaluate--
calculation(double hit)--backspace or delete--rename:
extremely great
3) Merging all the grades into a soil erosion grades
map
Spatial analyst--raster calculator—“none”-- + --
“slight”--*--2-- + “light”--*--3 + “moderate”--* --4-- +
“great”--*--5-- + “very great”--*--6-- + “extremely great”
--*--7--evaluate—calculation (hit right key)--data--export
data-format: TIFF--name: erod01g (g means grade)--
save--yes--no
Appendix D
Generation and output of color vegetation coverage
grades map or soil erosion grades map in ENVI system
1) Assign colors to vegetation coverage grades map
ENVI--file--new file--vcd01atgat--tools (in the image
frame)--color mapping--density slice--vcd01atgat 0 to o,1
to 1, 2 to 2, 3 to 3, 4 to 4, 5 to 5, 6 to 6--edit range
—white (red, green, blue)--ok--apply (ditto), blue, red,
magenta, yellow, green, dark green…
2) Assign colors to soil erosion grades map
ENVI--file--new file--erod01 g--tools (in the image
frame)--color mapping--density slice-erod01g--0 to o, 1
to 1, 2 to 2, 3 to 3, 4 to 4, 5 to 5, 6 to 6, 7 to 7--edit
range--white, green, yellow, magenta, red, cyan, maroo n
--ok--apply (ditto), …
3) Output their color maps and calculate their histo-
grams (omitted)