Materials Sciences and Applicatio ns, 2010, 1, 329-335
doi:10.4236/msa.2010.16048 Published Online December 2010 (http://www.scirp.org/journal/msa)
Variable Temperature Laser Light Scattering
Microscopy (VTLLSM) Studies on 10-100 μm
Size High Purity Gold and Commercial Grade
Zinc Grains*
P. Sita Rama Rao, P. B. V. Prasad, P. B. Shashikanth
S. R. Research Laboratory for Studies in Crystallization Phenomena, Khammam, India.
Received July 13th, 2010; revised October 28th, 2010; accepted November 26th, 2010.
ABSTRACT
The VTLLS microscopy studies were made on high purity gold and commercial grade zinc grains in a temperature
range of 30-230˚C. Differential area ω and surface activity Sa were estimated from photomicrographs. The ω vs dT/dt
(rate of heating) curve was seen to differ from those of silver and titanium. The nature of curve between normalized ω
and dT/dt was seen to be non-exponential. The characteristic relation between sectorized differential area ωsec and
mean temperature was examined. The present study further establishes the simplicity and versatility of the VTLLS tech-
nique, in studying the defect-sub-structure of metal particles such as Au and Zn in presence of an imposed temperature
gradient in a reasonable way. As such an attempt was made to connect the ω and defect-sub-structure related parame-
ters.
Keywords: Variable Temperature, Laser Light Scattering Microscopy, Au and Zn Grains, Defects
1. Introduction
Studies on defects in materials and metals have been a
fascinating subject and many techniques were developed
to support such investigations. Triftschauser and Kogel
[1] developed a positron annihilation technique to study
defect structure in metals in the vicinity of surfaces.
Recknagel and Wichert [2] reported a perturbed angular
correlation study on point defects in metals. NMR stud-
ies on point defects in Al and Cu were reported by
Minier and Minier [3]. Mossbauer studies of defectimpu-
rity interactions in metals were carried out by Vogl et al
[4]. Peisl [5] made X-ray scattering studies on defects in
metals. Earlier, the present authors [6] made variable
temperature laser light scattering microscopy (VTLLSM)
studies on relatively larger grains of aluminum, copper
and silver in a small temperature interval and established
the effectiveness of the technique. The technique was
similar to the variable oblique incidence reflection mi-
croscopy (OIRM) reported by the present authors [7].
Later on, the approaches were modified and the
VTLLSM was used to investigate structural variations of
high purity silver [8], titanium [8], gold [9] and (com-
mercial grade) Pb-Sn alloy [9] grains having sub-milli-
meter dimensions (within the range of 10-100 µm) as a
function of the temperature (in a wider temperature ran-
ge). The new technique consists of the Fourier space
interference images (resulted from light scattered by par-
ticles), which is the intermediate step in the formation of
a holographic image. Such an image is composed of
black and white contrast regions, which were attributed
to surface micro-facets of the particles. The present au-
thors used these contrasts and their variations with tem-
perature as the signature of particle’s structural changes
in terms of internal defects such as voids and disloca-
tions.
A large working distance (LWDO) optical microscope
with water cooled heat shield [10,11], a zero thermal
expansion (in upward direction) table (V+ZET) to func-
tion as sample holder [12] and a beam path cooler (BPC)
to stabilize image formed by scattered laser light at high
temperature [13] were developed for the VTLLSM stud-
*The study is part of a project funded by Defense Research and Devel-
opment Organization, Ministry of Defense, Government of India.

Variable Temperature Laser Light Scattering Microscopy (VTLLSM) Studies on 10-100 μm Size 330
High Purity Gold and Commercial Grade Zinc Grains
ies. Gold and zinc are too well known; a complete intro-
duction on them is therefore not attempted. Briefly,
Doremus [14] studied optical adsorption by gold parti-
cles. Granqvist and Hunderi [15] studied optical proper-
ties of ultra fine gold particles. Hassam et al. reported
[16,17] equilibrium phase diagram of some mixed sys-
tems, that contained gold as a component.
Investigations were made on 10-100 μm size gold and
zinc grains, by employing variable temperature laser
light scattering microscopy (VTLLSM). Results are pre-
sented in this report.
2. Experimental
As received Sigma-Aldrich (USA) made agglomerated
(+ 99.999% pure) 10-100 μm size gold grains and com-
mercial grade purity zinc grains (prepared one hour be-
fore the commencement of each experiment) were em-
ployed in the present study. The experimental procedure
and data analysis were almost identical to those reported
earlier [8,9,18]. A 10 mW, 670 nm laser, a zero thermal
expansion hot stage (V+ZET) coupled with a beam path
cooler (BPC), were employed [12,13]. Thermocouple
based thermometry was used to measure the tempera-
tures. Fused silica optical flat was used as sample holder;
linear thermal expansion coefficients [19,20] of fused
silica, gold and zinc are 0.4 × 10-6 k-1, 14 × 10-6 k-1 and
11.6 × 10-6 k
-1 (┴C axis) and 64.20 × 10-6 k -1 (║C axis)
respectively. In order to suppress the back ground scat-
tering, amorphous MnO2 was employed in the form of
thin layer. Reflection coefficients [21] of carbon black,
gold and zinc are 0.003, 0.75 and 0.45 respectively in the
visible spectrum. The coefficient of reflection of MnO2
may be equal or very close to that of carbon black. The
metal grains were heated on V+ZET and a series of pho-
tomicrographs were recorded at different temperatures.
Measurements were made from such photographs. The
same fused silica optical flat has been used in the studies
on Ag, Ti, Pb-Sn, Al, Zn and Au [8,9,18], in order to
eliminate the influence of substrate, if any, while com-
paring the results on grains of different metals.
3. Results
The VTLLS microscopy images of Au grains at three
different temperatures are shown in Figure 1. The im-
ages of zinc grains are similar to that of gold grains. The
areas of bright patches (BPs [13]) were measured from a
given photomicrograph and summed up, giving total area
(ATOT). Differential area ω, defined as 2(Amax – Amin)/
(Amax + Amin), where Amax and Amin were maximum ATOT
and minimum ATOT respectively in a heating-run, were
estimated. The ω values, obtained in five heating-runs vs
rate of heating (dT/dt) are shown in Figure 2. The curve
ω vs dT/dt of Au and Zn (Figures 2(a,b)) shows an ini-
tial increase and then a constant decrease in the average
value of ω of two grains, as the rate of heating was pro-
gressively increased. The relation between normalized
differential area ω/aI vs dT/dt of Au is shown in Figure
3(a). The curve joining most of the points (dashed line;
Figure 3(a)) has negative slope (similar to the curve in
Figure 2(a), between dT/dt = 0.26 and 0.66).
()
1
log tandT dt
ωϕ
−
= (1)
may describe the straight line (Figure 3(a)). It is a devia-
tion from earlier observations, that exponential curves
(connecting ω and dT/dt) with positive and negative
slopes were noticed in case of grains of silver [8] and tita-
nium [8]. In order to handle the experimental data, it may
therefore be useful to use a general equation, such as,
(
)
1
1x YKeKmx
φ ±
=−+ ± (2)
where Y
ω
=
,
x
dT dt
=
and
φ
is a constant. K is a
parameter that probably defines the state of a grain and
can assume a value 0 or 1. It is assumed that the value of
(a) (b) (c)
Figure 1. VTLLS microscopy images of Au grains. (a) 29˚C, (b) 130˚C, (c) 230˚C; dT/dt = 0.46˚C/min. 500X.

Variable Temperature Laser Light Scattering Microscopy (VTLLSM) Studies on 10-100 μm Size 331
High Purity Gold and Commercial Grade Zinc Grains
Figure 2. Differential area ω vs. dT/dt; (a) Case of Au and (b) Case of Zn.
Figure 3(a). Normalized ω (curve a) and normalized Sa (curve b) of Au grains. In the graph: p × logX = 10-3 × [log(Sa/aI)] and
q × logY = 10-5 × [log(ω/aI)].
Figure 3(b). Normalized Sa (curve a) and normalized ω (curve b) of Zn grains. In the graph: p × logX = 10-4 × [log(ω/aI)] and
q × logY = 10-3 [log(Sa/aI)].
The profile of distribution of bright patches (BPs) was
noticed to change with temperature [12]. A term surface
activity Sa was defined, while taking the decompositions
and recombinations of BPs into consideration. The sur-
face activity Sa was proposed to be given by an empirical
relation
()()(
21
11
aHBPs LBPsoTBPs
SN NNN
−−
⎡⎤
=− −−
⎣⎦
)
1
()
1
11 mh TT
−
⎡⎤
−+ −
⎣⎦
(3)
where NHBPs and NLBPs are highest and lowest number of
BPs respectively, found in photomicrographs of a heat-
ing-run; No and NTBPs are total number of (photomicro-
graph) frames and total number of bright patches respec-
tively. Tm and Th are melting temperature (of the metal)
and highest temperature reached (in a given heating-run)
respectively and expressed in ˚C.
It may be stated that Sa indicates the level of internal
and external activity promoted by thermal pressure. It is
known that atomic migration takes place at a much faster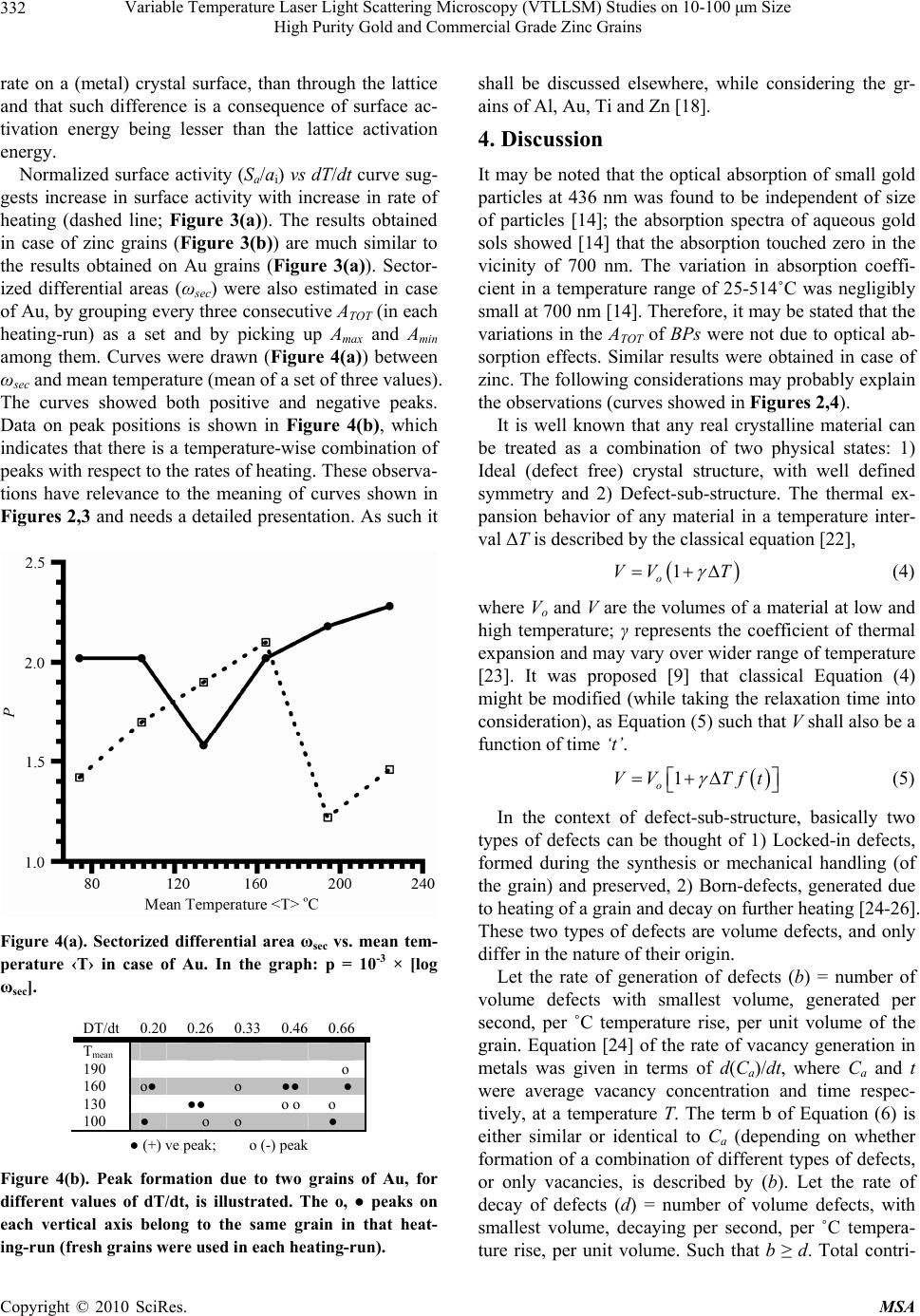

Variable Temperature Laser Light Scattering Microscopy (VTLLSM) Studies on 10-100 μm Size 332
High Purity Gold and Commercial Grade Zinc Grains
rate on a (metal) crystal surface, than through the lattice
and that such difference is a consequence of surface ac-
tivation energy being lesser than the lattice activation
energy.
Normalized surface activity (Sa/ai) vs dT/dt curve sug-
gests increase in surface activity with increase in rate of
heating (dashed line; Figure 3(a)). The results obtained
in case of zinc grains (Figure 3(b)) are much similar to
the results obtained on Au grains (Figure 3(a)). Sector-
ized differential areas (ωsec) were also estimated in case
of Au, by grouping every three consecutive ATOT (in each
heating-run) as a set and by picking up Amax and A
min
among them. Curves were drawn (Figure 4(a)) between
ωsec and mean temperature (mean of a set of three values).
The curves showed both positive and negative peaks.
Data on peak positions is shown in Figure 4(b), which
indicates that there is a temperature-wise combination of
peaks with respect to the rates of heating. These observa-
tions have relevance to the meaning of curves shown in
Figures 2,3 and needs a detailed presentation. As such it
Figure 4(a). Sectorized differential area ωsec vs. mean tem-
perature ‹T› in case of Au. In the graph: p = 10-3 × [log
ωsec].
DT/dt 0.20 0.26 0.33 0.46 0.66
Tmean
190 o
160 o● o ●● ●
130 ●● o o o
100 ● o o ●
● (+) ve peak; o (-) peak
Figure 4(b). Peak formation due to two grains of Au, for
different values of dT/dt, is illustrated. The o, ● peaks on
each vertical axis belong to the same grain in that heat-
ing-run (fresh grains were used in each heating-run).
shall be discussed elsewhere, while considering the gr-
ains of Al, Au, Ti and Zn [18].
4. Discussion
It may be noted that the optical absorption of small gold
particles at 436 nm was found to be independent of size
of particles [14]; the absorption spectra of aqueous gold
sols showed [14] that the absorption touched zero in the
vicinity of 700 nm. The variation in absorption coeffi-
cient in a temperature range of 25-514˚C was negligibly
small at 700 nm [14]. Therefore, it may be stated that the
variations in the ATOT of BPs were not due to optical ab-
sorption effects. Similar results were obtained in case of
zinc. The following considerations may probably explain
the observations (curves showed in Figures 2,4).
It is well known that any real crystalline material can
be treated as a combination of two physical states: 1)
Ideal (defect free) crystal structure, with well defined
symmetry and 2) Defect-sub-structure. The thermal ex-
pansion behavior of any material in a temperature inter-
val ΔT is described by the classical equation [22],
(
)
1
o
VV T γ
=
+Δ (4)
where Vo and V are the volumes of a material at low and
high temperature; γ represents the coefficient of thermal
expansion and may vary over wider range of temperature
[23]. It was proposed [9] that classical Equation (4)
might be modified (while taking the relaxation time into
consideration), as Equation (5) such that V shall also be a
function of time ‘t’.
()
1
o
VV Tft γ =+Δ
⎡
⎤
⎣
⎦ (5)
In the context of defect-sub-structure, basically two
types of defects can be thought of 1) Locked-in defects,
formed during the synthesis or mechanical handling (of
the grain) and preserved, 2) Born-defects, generated due
to heating of a grain and decay on further heating [24-26].
These two types of defects are volume defects, and only
differ in the nature of their origin.
Let the rate of generation of defects (b) = number of
volume defects with smallest volume, generated per
second, per ˚C temperature rise, per unit volume of the
grain. Equation [24] of the rate of vacancy generation in
metals was given in terms of d(Ca)/dt, where Ca and t
were average vacancy concentration and time respec-
tively, at a temperature T. The term b of Equation (6) is
either similar or identical to Ca (depending on whether
formation of a combination of different types of defects,
or only vacancies, is described by (b). Let the rate of
decay of defects (d) = number of volume defects, with
smallest volume, decaying per second, per ˚C tempera-
ture rise, per unit volume. Such that b ≥ d. Total contri-

Variable Temperature Laser Light Scattering Microscopy (VTLLSM) Studies on 10-100 μm Size 333
High Purity Gold and Commercial Grade Zinc Grains
T
)
bution to the volume (of defect free metal grain) due to
birth and decay of defects in a temperature interval (t – to
= ΔT) is,
()
()
1
o
VVbd=−Δ (6)
It is assumed logically that , where rm
is rate of migration of defects to surface, r
(
,,
mr
dfrrT=
r
)
}
⎤
⎦
is the rate of
recombination, and T is temperature. Let the concentra-
tion of locked-in defects (number of defects per unit
volume) = Г. Based on the fact that the physical proper-
ties of metals vary, depending on the nature of prepara-
tion [27], it may be stated that the value of Г depends on
the process of synthesis of grains. Decay of locked-in
defects due to rise of temperature may be represented by
a decay factor D (= number of defects decaying per unit
volume per ˚C rise of temperature). Therefore, total
change in excess initial volume due to decay of locked-in
defects is given by,
()
(
2
o
VV DT=Γ−Δ (7)
The real volume of grain is given by the sum of Equtions
(5-7) and may be written as:
()()( )
{
1
real o
VV TftbdD γ =+Γ+Δ+−−⎡
⎣ (8)
On differentiating Equation (8) with respect to time and
equating d(Vreal)/dt to zero (since expansion reaches
maximum after a certain length of time) it may be writ-
ten after simplification,
() []
{
12
1
real oder
dVVdT dtTF
−
=+Γ+ Δ
}
(9)
where derivative factor
(
)
(
)
der
F
dft bdDd
t
γ =+−− ⎡
⎣⎤ ⎦
)
.
It was shown [6] that the differential area ω, defined
as
()(
max minmax min
2AA AA−+, could give thermal
volume-strain variation
(
)( )
max minmaxmin
2VV VV ω =− +,
where Vmax and Vmin were maximum and minimum total
volumes respectively, exhibited by a grain, during a
heat-run. It may therefore be written that maxreal dV V
=
min and V−
()
maxmin 2 o
VV V≈+ , then Equation (9) may
be written as
() () []
{
12
25 der dT dtTF ω
−
=Γ+Δ
}
(10)
By using Equation (10), values of Fder were calculated
for a few assumed values of Г in case of the grains of
zinc; the results are shown in Figure 5. Expectedly, Fder
exhibits large variations, for relatively larger concentra-
tion of locked-in defects.
It may therefore be expected that, in case of small
metal grains, variations in the volume with systematic
changes in temperature, can be strongly influenced [28,29]
by the crystal-defects related parameters. It may be
Figure 5. Variation of Fder with dT/dt, for different values
of Г; case of Zn.
pointed out that, 1) Since no two metal grains (formed
under identical conditions) can have identical de-
fect-sub-structure, they exhibit non-identical response to
the injected heat energy. (It may be recalled that
non-uniform behavior is a frequent occurrence in crystal-
lization [30-32], when individual cases are considered);
and, 2) Yet, the defect-sub-structure parameters may
vary with in an upper and lower limits, permitted by the
parameters, controlling the nucleation and growth of
grains. These two factors coupled with the macroscopic
physical properties of a given material, lead to a sort of
uniformity in diversity-like condition. Individual metal
grains, studied by VTLLS microscopy, appear to have
anarchic behavior. But, when the behavior of a good
number of grains is considered, a systemization surpris-
ingly surfaces. Such diversity in the behavior should be-
come more dominant, with further reduction in the size
of metal grains. It can be pointed out that the observed
behavior of the grains is their intrinsic character and not
due to any secondary influences. Because, unlike the
conventional techniques, such as electron microscopy
and X-ray techniques (where the probing beam can in-
teract with the material and modify its state [33]),
VTLLS microscopy is powerful, yet passive. In the sense
that it does not modify the state of metal (or non-metal)
grain, if the beam energy is not too high (as in the pre-

Variable Temperature Laser Light Scattering Microscopy (VTLLSM) Studies on 10-100 μm Size 334
High Purity Gold and Commercial Grade Zinc Grains
sent case). The VTLLSM technique is most suited for
studies on surfaces and small grains.
5. Conclusions
The VTLLS microscopy technique can be effectively
employed to study the response of small metal grains (in
10-100 μm size range) to an imposed temperature gradi-
ent and the results can be interpreted in a reasonable way,
by taking the defect-sub-structure related parameters into
consideration.
6. Acknowledgements
PBSK and PSR are grateful to Prof. Prasad (deceased)
who lead the project.
REFERENCES
[1] W. Triftshauser and G. Kogel, In: J. I. Takamura, M.
Doyama and M. Kiritani, Eds., Point Defects and Defect
Interactions in Metals, University of Tokyo Press, North-
Holland Publishing Co., Amsterdam, 1982, p. 15.
[2] E. Recknagel and Th. Wichert, “Defects in Metals
Studied by Implanted Radioactve Atoms,” Nuclear
Instruments and Methods, Vol. 182, No. 1, 1981, pp. 439-
455.
[3] M. Minier and C. Minier, “Screeing Charge Density
around Several ΔZ = –1 Impurities in Copper: Nickel,
Palladium, Platinum, and Vacancy,” Physical Review B,
Vol. 22, No. 1, 1980, pp. 21-27.
[4] G. Vogl, W. Petry, K. Sassa and S. Mantl, In: J. I.
Takamura, M. Doyama and M. Kiritani, Eds., Point
Defects and Defect Interactions in Metals, University of
Tokyo Press, North-Holland Publishing Co., Amsterdam,
1982, p. 33.
[5] H. Peisl, “Diffuse X-Ray Scattering from the Displa-
cement Field of Point Defects and Defect Clusters,”
Journal of Applied Crystallography, Vol. 8, No. 2, 1975,
pp. 143-149.
[6] P. B. V. Prasad, K. R. Gopal and Ch. V. Gopal, “Laser
Light Scattering Studies on Small Metal Grains: Case of
Al, Cu and Ag,” Proceedings of Solid State Physics (In-
dia), Vol. 43, 2000, pp. 142-143.
[7] P. B. Shashikanth, P. B. V. Prasad and G. S. Rao,
“Oblique Incidence Reflection Microscopy (OIRM) on
Hydrocarbon Films,” Crystal Research Technology, Vol.
34, No. 10, 1999, pp. 1287-1292.
[8] P. B. V. Prasad and P. B. Shashikanth, “Variable
Temperature Laser Light Scattering Microscopy Studies
on High Purity 10-100 μm Ag and Ti Metal Particles,”
Materials Science and Technology, DOI: 10.1179/
026708310X12688283410361.
[9] P. Sita Rama Rao, P. B. V. Prasad and P. B. Shashikanth,
“On the Behaviour of Au and Pb-Sn Metal Grains
Subjected to Heat: A Variable Temperature Laser Light
Scattering Microscopy Study,” Materials Science: An
Indian Journal, Vol. 5, No. 4, 2009, pp. 428-432.
[10] P. B. V. Prasad and P. B. Shashikanth, “Design and Fab-
rication of a 20 cm2 Table Having Zero Thermal Expan-
sion in Positive Vertical Direction (V+ZET),” Proceed-
ings of National Conference on Current Trends in Con-
densed Matter Research, Warangal, 2004, p. 23.
[11] P. B. V. Prasad and P. B. Shashikanth, “A Large Working
Distance Microscope for High Temperature Studies,”
Proceedings of National Conference on Perspectives in
Engineering Optics & Spectroscopy, Meerut, 2004, p. 40.
[12] P. B. V. Prasad and P. B. Shashikanth, “Laser Light
Scattering Microscopy: Interpretation of Images,” Indian
Journal of Engineering & Materials Science, Vol. 12, No.
6, 2005, pp. 591-594.
[13] P. B. V. Prasad and P. B. Shashikanth, “On Imaging
Metal Grains at High Temperature: Laser Light Scat-
tering Microscopy,” Indian Journal of Engineering &
Materials Science, Vol. 13, No. 2, 2006, pp. 162-166.
[14] R. H. Doremus, “Optical Properties of Small Gold Parti-
cles,” Journal of Chemical Physics, Vol. 40, No. 8, 1964,
pp. 2389-2396.
[15] C. G. Granqvist and O. Hunderi, “Optical Properties of
Ultrafine Gold Particles,” Physical Review-B, Vol. 16, No.
8, 1977, pp. 3513-3534.
[16] S. Hassam, M. Gambino and J. P. Bros, “The Ag+Au+Pb
System: Determination of Liquidus Interface,” Thermo-
chimica Acta, Vol. 257, 1995, pp. 83-92.
[17] S. Hassam and Z. Bahari, “Equilibrium Phase Diagram of
the Ag-Au-Pb Ternary System,” Journal of Alloys and
Compounds, Vol. 392, No. 1-2, 2005, pp. 120-126.
[18] P. B. Shashikanth and P. Sita Rama Rao, “Variable
Temperature Laser Light Scattering Microscopy Studies
on 10-100 μm Size Grains of Gold, Aluminum, Zinc and
Titanium: Role of Relaxation Time in Thermally
Triggered Volume Changes,” Materials Science an
Indian Journal, Vol. 6, No. 1, 2010, pp. 68-70.
[19] K. Koopman, In: K. Koopman, Ed., Informatie Boek
Vwo-Havo Voor Het on Derwiji in De Natuurweten-
schappen, Wolters-Noordhoff, Groningen, 1986, p. 89.
[20] R. A. Walsh, “Machining and Metal Working Hand-
book,” McGraw-Hill, Inc., New York, 1994.
[21] R. C. Weast, “CRC Handbook of Chemistry and Phys-
ics,” CRC Press, Florida, 1988.
[22] D. Mckie and C. Mckie, “Crystalline Solids,” John Wiley
& Sons Inc., New York, 1974.
[23] V. E. Zinovev, “Handbook of Thermophysical Properties
of Metals at High Temperatures,” Nova Science Pub-
lishers, Inc., New York, 1996.
[24] T. Kino and K. Ono, In: J. I. Takamura, M. Doyama and
M. Kiritani, Eds., Point Defects and Defect Interactions
in Metals, University of Tokyo Press, North-Holland
Publishing Co., Amsterdam, 1982, p. 247.
[25] M. Kiritani and H. Takaka, “Dynamic Studies of Defect
Mobility Using High Voltage Electron Microscopy,” Jour-

Variable Temperature Laser Light Scattering Microscopy (VTLLSM) Studies on 10-100 μm Size
High Purity Gold and Commercial Grade Zinc Grains
335
nal of Nuclear Materials, Vol. 69-70, 1978, pp. 277-309.
[26] J. Takamura, In: J. I. Takamura, M. Doyama and M. Kiri-
tani, Eds., Point Defects and Defect Interactions in Met-
als, University of Tokyo Press, North-Holland Publishing
Co., Amsterdam, 1982, p. 431.
[27] E. Rose, “The Condensed Chemical Dictionary,” 7th
Edition. Reinhold Publishing Co., New York, 1961.
[28] J. P. Ganne and J. von Stebut, “Measurement of the
intrinsic Thermal Expansion of Irradiation Defects in
Aluminum at Low Temperatre,” Physical Review Letters,
Vol. 43, No. 9, 1979, pp. 634-636.
[29] R. W. Baluffi, “Vacancy Defect Mobilities and Binding
Energies Obtained from Annealing Studies,” Journal of
Nuclear Materials, Vol. 69-70, 1978, pp. 240-263.
[30] A. R. Konak, “Single Versus Suspension Growth,” Jour-
nal of Crystal Growth, Vol. 22, No. 1, 1974, pp. 67-68.
[31] P. Bennema, “The Rate of Growth of Crystals from
Slightly Supersaturated Solutions,” Ph.D. Thesis, Tech-
nical University of Delft, Delft, 1965.
[32] P. B. V. Prasad, “Dispersion in Crystal Growth Rates:
Palmiticacid-Xylene System,” Journal of Crystal Growth,
Vol. 102, No. 3, 1990, pp. 569-573.
[33] M. Chen, E. Ma and K. Hemker, “Mechanical Behavior
of Nanocrystalline Metals,” In: Y. Gogotsi, Ed., Nano-
materials Handbook, Taylor & Francis, Boca Raton,
2006, pp. 407-529.