Journal of Modern Physics, 2010, 1, 372-378
doi:10.4236/jmp.2010.16053 Published Online December 2010 (http://www.SciRP.org/journal/jmp)
Dynamics of Particle in a Box in Time Varying Potential
Due to Chirped Laser Pulse
Brijender Dahiya, Vinod Prasad
Department of Physics, Swami Shraddhanand College, University of Delhi, Delhi, India
Received August 13, 2010; revised October 15, 2010; accepted November 19, 2010
Abstract
We describe a computational method for simulating the time dependent quantum mechanical system inter-
acting with external field. In this method the Schrödinger equation is solved by expanding the wave function
in the basis set of unperturbed Hamiltonian. The expansion yields a set of coupled first order differential
equation. For expansion coefficients, the coupled channel method is applied to a particle in a box interacting
with external field in the form of chirped laser pulse. The pulse shape is taken as Gaussian. We study the ef-
fect of different pulse parameters i.e. chirp rate, intensity, center frequency, box length and laser duration on
the dynamics of the particle. Many interesting results are obtained and explained.
Keywords: Transition Probability, Chirp Rate, Box Length
1. Introduction
Quantum mechanics [1,2] is the fundamental base for sev-
eral branches in Physics and particle in a box is one of the
fundamental problems of quantum mechanics. In this paper,
we have studied dynamics of a particle in a box in time
varying external field/potential. This time varying field is
achieved using a chirped laser pulse. Wang and Cham-
pagne [3] have studied the interaction of Gaussian laser
pulse with the particle in a box. In their study they found
that by using laser centre frequency to be resonant with the
transition between first two states i.e. n = 1 and n = 2, tran-
sition probability of n = 2 state is appreciable and all other
higher state have non zero but negligible probability. Here,
we are presenting numerical simulation of the system. We
numerically solve the coupled differential equations ob-
tained for a particle in a box, in the presence of a chirped
laser pulse. It is shown that high-efficiency population
transfer is possible for several values of chirp rate and box
length. We also explore the dependence of population
transfer on chirp rate. The results indicate that we can have
large transition probabilities for higher states also with the
help of chirped laser pulse.
With the development in laser technology [4-6] in recent
years, various techniques have been developed to modulate
and even shape the laser pulse. The most exploited feature
of modulated pulse is the chirp which describes the varia-
tion of carrier frequency with time. If the frequency in-
creases with the time, the pulse is positively chirped and if
the frequency decreases with time, it is negatively chirped.
Ruhman and Kosloff [7] used negatively chirped pulse to
achieve large amplitude of vibrational motion in higher
vibrational states of the ground electronic surface of CsI
through an effective intra pulse pump dump mechanism.
Cao et al. [8] have studied that a positively chirped pulse is
very efficient in population inversion. So both positive and
negative chirps are important and can be used as per re-
quirement of the problem or the system. The selection also
depends on the system with which the laser pulse is inter-
acting and other parameters of pulse e.g. intensity, center
frequency, pulse width etc. No work for such type of prob-
lem has been published earlier. Recently coherent control
for box potential with laser fields has been studied by Imre
F. Barna and PéterDombi [9].
In this paper we have used numerical method and com-
puter simulation to express all results. In Section 2, we
have described a general coupled channel method to solve
the Schrödinger equation under time dependent perturba-
tion condition. The Schrödinger equation is reduced to a set
of first order coupled differential equations which are
solved using efficient and commonly used fourth order
Runge-Kutta method. Section 3 briefly describe particle in
a box and its interaction with chirped laser pulse. We apply
the coupled channel method to find the solution. In Section
4, we briefly describe the computer simulation work. Fi-
nally in Section 5, we describe the numerical results for the

B. DAHIYA ET AL.373
transition probabilities for different states as a function of
time, chirp rate, box length and laser center frequency. Par-
ticularly, effect of linear chirp is examined in detail. In
Section 6, we conclude the paper.
2. The Coupled Channel Method
The coupled channel method [10,11] is used to solve the
time dependent Schrödinger equation. Consider a quan-
tum mechanical system having unperturbed Hamiltonian
0
ˆ
H
for a eigen state n

with eigen energy values
which satisfy the equation
n
E
0
ˆnnn
HE

  (1)
Here n

forms a complete orthogonal set of eigen
vectors i.e.
|1,
nnn nmn

 

  (2)
Considering the wave function as
 


0exp
nn
n
ta iEt
n

 
 (3)
Without perturbation wave function will have usual
time dependence but coefficient n is independent of
time. Let us consider that perturbation is turned on in-
stantaneously at t = 0. Then the full Hamiltonian will be
described as
a

0
ˆˆ
H
HVt (4)


0
ˆˆ
n
HHVt
V(t) is the perturbation part (which is a function of
time) having condition
() 00
() 00
Vt t
Vt t



 (6)
Now the time dependent Schrödinger equation is (as
explained in Section 5, box units are used throughout the
paper)
 
ˆ
t
iH
t
 

t (7)
The solution of “(7)” can be written as
 

exp
nn
n
tatiEt
n



 (8)
Here n (probability amplitudes) acquire time de-
pendence. In the absence of external perturbation, if sys-
tem is in one of the eigen state of 0
a
ˆ
H
, then it will re-
main in that state forever. However by the presence of a
small perturbation, the system makes transition between
its unperturbed eigen states. So with the perturbation, the
probability of finding the system in nth state at any time t
will vary with time and Pn(t) is given by
 
2
nn
Pta t (9)
Using “(4)” in “(7)”
 


0
ˆ
t
iHVt
t
 

t (10)
Using “(1)” and “(8)” in “(10)”, we get the following
equation
n

 (5)








exp exp
exp exp
n
nnn nn
n
nnnnnn
nn
at
iiEtEatiEt
t
at iEtEat iEtV

n


 
 

 
 


 

(11)
Or





exp exp
n
nn nn
nn
at
iiEtatiEt
tn
V

 


  (12)
Operating it with k

from left, we get





exp |exp
n
nkn nnk
nn
at
iiEt atiEt
tn
V
 



  (13)





exp exp
k
nn nk
n
at
iiEtatiEt
tn
V

 

  (14)
Let the transition matrix element be
kn kn
VV

  (15)
The transition matrix element Vkn may be either zero or
non-zero depending upon the selection rules. Consider-
ing transition frequency as , Equation

knk n
EE  


B. DAHIYA ET AL. 374
(14) will become




exp
k
nkn
n
at
iati
t



kn
tV




(16)
Thus matrix differential equation for co-efficientsan is


11 1112 12
22 21 2122
exp
exp
nn nn
aa VVit
aa Vit V
i
aa V



 






 
  

  




(17)
And by solving this set of coupled differential equa-
tions we get value of an(t) for different states and hence
probability of finding the system in any particular state at
any time t. We can write
 
nnn
atRt iIt (18)
where Rn(t) and In(t) are real and imaginary part of an(t)
respectively. Using (18) in (16) we can have




 

 

cos sin
kk
nnknkn kn
n
Rt It
ii
tt
Rt iItt itV 
 







(19)
Separating real and imaginary parts of an(t) we get fol-
lowing equations






sin cos
k
nkn knnkn kn
n
Rt R ttVIttV
t




(20)






cos sin
k
nkn knnkn kn
n
It R ttVIttV
t

 

 
(21)
Equation (20) and (21) can be solved by using nu-
merical methods e.g. Runge-Kutta Method.
3. Particle in a Box in Chirped Laser Field
Consider a particle i.e. electron in a deep potential well
from which it cannot escape and loses no energy when it
collide with walls. So the potential is defined as
() 00
()0,
Vxx L
Vxxx L

 (22)
Now the Schrödinger equation becomes



22
2
2
xEx
mx
 


 (23)
By solving this equation, the unperturbed eigen func-
tion and the eigen energy value are
 
2sin /
n
and

222 2
2
n
Enm  L

0
(25)
where L is the length of the box and n = 1, 2, 3, , and
n ≠ 0 as it will give probability of finding the particle
everywhere equal to zero, which is not possible. Consider
that the system is interacted with chirped laser pulse [12].
Here the laser field is defined as

 

2
0
sin/ cosEt Ettt    (26)
Here E0, τ, ω0 and β are the amplitude, laser duration,
laser center frequency and the chirp rate respectively. The
laser interaction with the particle (i.e. electron) is defined
as




 ,. 2VxteEtx L  (27)
Here ‘e’ is electron charge and zero point potential is
chosen at L/2. Now the transition matrix Vkn can be writ-
ten as
 


 



*
*
2
2
kn kn
kn
kn
Vt eEtxxLxdx
eE txxLx dx
eE t D






 (28)
where
0
kn
D

if k = n or k + n is even,

2
22 2
nk
D8Lk nk n   if k + n is odd
Using this transition matrix Vkn in Equation (20) and
(21), we can find excitation/transition probability of any
state at any time t under chirped laser field. By using lin-
ear chirp, we will get some exciting new results which is
unexpected by simple laser pulse. These are described in
the results section.
4. Computational Analysis
The determination of coefficients an(t) of different states
allows us to calculate the transition probability for vari-
ous laser pulse parameters. For the present calculations,
we have studied the system with n = 10 levels. Further,
we have checked the convergence by variation in number
of levels, and have obtained excellent convergence with
n = 10 levels.
For making the calculations traceable we have sepa-
rated the real and imaginary parts of the coefficients an(t)
[see (18-21)]. Thus we obtain 20 real coupled differential
equations to be solved. Any time propagator scheme can
be used to solve these equations. For solving these equa-
tions we have used the efficient fourth order Runge-
Kutta method by assuming that the system is initially in
the ground state.

x
nx L
L
  (24) In next section, we discuss the results thus obtained.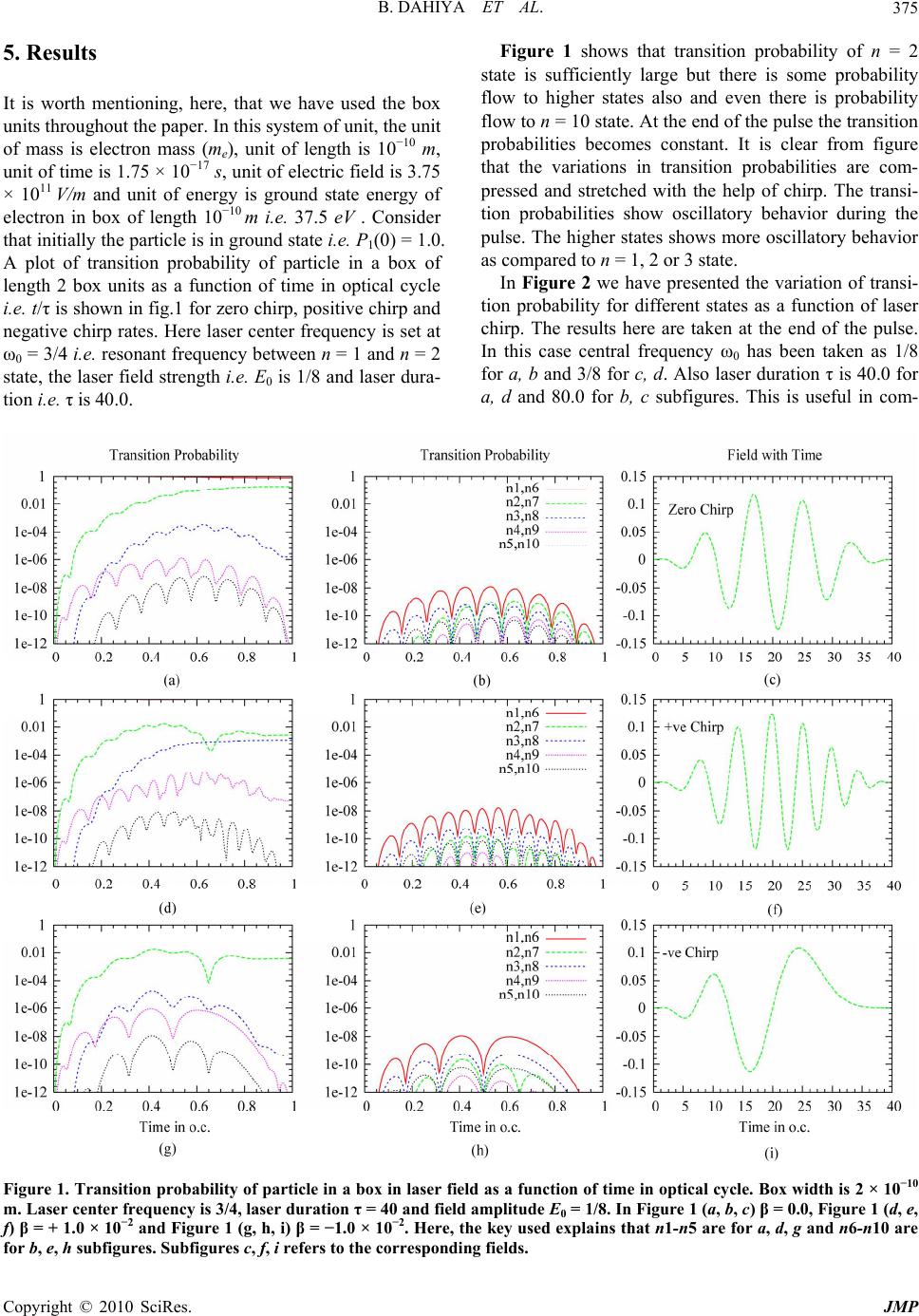

B. DAHIYA ET AL. 375
5. Results Figure 1 shows that transition probability of n = 2
state is sufficiently large but there is some probability
flow to higher states also and even there is probability
flow to n = 10 state. At the end of the pulse the transition
probabilities becomes constant. It is clear from figure
that the variations in transition probabilities are com-
pressed and stretched with the help of chirp. The transi-
tion probabilities show oscillatory behavior during the
pulse. The higher states shows more oscillatory behavior
as compared to n = 1, 2 or 3 state.
It is worth mentioning, here, that we have used the box
units throughout the paper. In this system of unit, the unit
of mass is electron mass (me), unit of length is 10−10 m,
unit of time is 1.75 × 10−17 s, unit of electric field is 3.75
× 1011 V/m and unit of energy is ground state energy of
electron in box of length 10−10 m i.e. 37.5 eV . Consider
that initially the particle is in ground state i.e. P1(0) = 1.0.
A plot of transition probability of particle in a box of
length 2 box units as a function of time in optical cycle
i.e. t/τ is shown in fig.1 for zero chirp, positive chirp and
negative chirp rates. Here laser center frequency is set at
ω0 = 3/4 i.e. resonant frequency between n = 1 and n = 2
state, the laser field strength i.e. E0 is 1/8 and laser dura-
tion i.e. τ is 40.0.
In Figure 2 we have presented the variation of transi-
tion probability for different states as a function of laser
chirp. The results here are taken at the end of the pulse.
In this case central frequency ω0 has been taken as 1/8
for a, b and 3/8 for c, d. Also laser duration τ is 40.0 for
a, d and 80.0 for b, c subfigures. This is useful in com-
Figure 1. Transition probability of particle in a box in laser field as a function of time in optical cycle. Box width is 2 × 10−10
m. Laser center frequency is 3/4, laser duration τ = 40 and field amplitude E0 = 1/8. In Figure 1 (a, b, c) β = 0.0, Figure 1 (d, e,
f) β = + 1.0 × 10−2 and Figure 1 (g, h, i) β = −1.0 × 10−2. Here, the key used explains that n1-n5 are for a, d, g and n6-n10 are
for b, e, h subfigures. Subfigures c, f, i refers to the corresponding fields.

B. DAHIYA ET AL. 376
Figure 2. Transition probability for a particle in a box in chirped laser field as a function of chirp rate. Field strength E0 =
1/2 and box length = 2.0. The centre frequency ω0 = 1/8 for a, b and ω0 = 3/8 for c, d subfigures. While the pulse width τ =
40.0 for a, d and τ = 80.0 for b, c subfigures. The results are taken at the end of the pulse.
paring the results for variation of transition probability of
different states as a function of chirp rate (β) for two
different frequencies and laser durations simultaneously.
As it can be seen from figure that transition probabilities
of n = 3 state is higher for negative chirp than positive
chirp for τ = 40.0 but it changes behviour for τ = 80.0,
although transition probability for n = 1 and n = 2 states
increases as frequency ω0 changes from 1/8 to 3/8 and
transition probability remains greater for positive chirp
than negative chirp. This change in probability shows
that probability also depends on exposer time. Further,
Figure 2 also shows that almost complete population
inversion can be achieved by chirped laser pulses. There
is substantial population transfer to higher states also.
Figure 3 represents the transition probability of 5
states as a function of box length. The results are taken at
the end of the pulse. It is clear from the figure that nega-
tively chirped pulse connects higher states more effect-
tively as compared to non-chirped pulse for the variation
in box length. Also (d) part shows that transition prob-
ability of different states changes drastically for the ex-
posed time.
In Figure 4, we compare the transition probability for
5 states as a function of laser frequency. The results are
taken at the end of the pulse. In part (b) the resonance
between n = 1 and n = 2 states occurs at their natural
frequency but in part (a) the chirp shifts the resonance
and also it connects the higher order terms more effi-
ciently.
6. Conclusions
The effect of chirped laser pulse on particle in a box has
been studied and we have come to the conclusion that
frequency modulated laser pulse is an effective approach
to get system in excited state. The transition probability
of different states as a function of different pulse pa-
rameters and the box length have been studied. The sys-

B. DAHIYA ET AL. 377
Figure 3. Transition probability of 5 states for particle in a box in chirped laser field as a function of box length. Chirp
rate β = −5.0 × 10−2 (except for (a) where β is zero), laser duration τ = 40 (except for (d) where τ is 80) and field ampli-
tude E0 = 1/2 (except for (b) where E0 is 1/4).The results are taken at the end of the pulse.
Figure 4. Transition probability of 5 states for particle in a box in chirped laser field as a function of central frequency.
Chirp rate in part (a) is β = −5.0 × 10−2 and zero in part (b). Laser duration is τ = 40, box length is 2.0 and field ampli-
tude E0 = 1/2.The results are taken at the end of the pulse.

B. DAHIYA ET AL. 378
tem is not merely two level shifting but with the help of
chirped laser pulse we can shift the system to higher
states, even n = 10 state has some transition probability
(whatever small, it may be). The main result of the study
is the variation in the dynamics due to time varying ex-
ternal potential and large transition probabilities for
higher states in the presence of chirped laser pulse which
can’t be achieved with non-chirped pulse. The system
remains in higher state for appreciable time that may
help in many physical and chemical aspects.
7. Acknowledgements
The authors are grateful to the unknown referee for
valuable suggestions for the improvement of the paper.
8. References
[1] D. Bouwmeester, A. K. Ekert and A. Zeilinger, “The
Physics of Quantum Information,” Springer Berlin, NY,
2000.
[2] D. J. Griffiths, “Introduction to Quantum Mechanics,”
2nd Edition, Pearson Prentice Hall, Upper Saddle River,
New Jersey, 2005.
[3] J. Wang and J. D. Champagne, “Simulation of Quantum
Systems with Coupled Channel Method,” American Jour-
nal of Physics, Vol. 76, No. 4-5, 2008, pp. 493-497.
[4] W. Koechner, “Solid State Laser Engineering,” 6th Edi-
tion, Springer, New York, 2006.
[5] H. Kawashima, M. M. Wefers and K. A. Nelson, “Fem-
tosecond Pulse Shaping, Multiple-Pulse Spectroscopy
and Optical Control,” Annual Review of Physical Chem-
istry, Vol. 46, October 1995, pp. 627-656.
[6] P. Krehlik, “Characterization of Semiconductor Laser
Frequency Chirp Based on Signal Distortion in Disper-
sive Optical Fiber,” Opto-Electronics Review, Vol. 14,
No. 2, June 2006, pp. 119-124.
[7] S. Ruhman and R. Kosloff, “Application of Chirped Ul-
trashort Pulses for Generating Large-Amplitude Ground-
State Vibrational Coherence: A Computer Simulation,”
Journal of the Optical Society of America B, Vol. 7, No. 8,
August 1990, pp. 1748-1751.
[8] J. S. Cao, C. J. Bardeen and K. R. Wilson, “Molecular _
pulses: Population Inversion with Positively Chirped
Short Pulses,” Journal of Chemical Physics, Vol. 113, No.
5, August 2000, pp. 1898-1909.
[9] I. F. Barna and P. Dombi, “Coherent Control for the
Spherical Symmetric Box Potential in Short and Intensive
XUV Laser Fields,” Central European Journal of Physics,
Vol. 6, No. 2, June 2008, pp. 205-210.
[10] J. P. Hansen and K. Taulbjerg, “Coupled-Channel Calcu-
lations of Partial Capture Cross Sections in Multiply
Charged Ion Collisions with Hydrogen,” Physical Review
A, Vol. 40, No. 7, October 1989, pp. 4082-4084.
[11] A. P. Hickman, “Coupled-Channel Calculations of Ex-
cited-Atom Collisions,” International Reviews in Physi-
cal Chemistry, Vol. 16, No. 2, 1997, pp. 177-199.
[12] M. H. Mitleman “Introduction to the Theory of Laser
Atom Interaction,” Plenum Press, New York, 1982.