Journal of Modern Physics, 2010, 1, 364-371
doi:10.4236/jmp.2010.16052 Published Online December 2010 (http://www.SciRP.org/journal/jmp)
Pinning Forces in Superconductors from Periodic
Ferromagnetic Dot Array
Wei Jiang Yeh, Bo Cheng, Tony Ragsdale
Department of Physics, University of Idaho, Moscow, USA
Received August 18, 2010; revised October 12, 2010; accepted October 25, 2010
Abstract
Using the London equation, we derive a formula by which the pinning force from magnetic dots can be cal-
culated. We numerically calculate the interaction between ferromagnetic dots and vortices in type II super-
conductors under various conditions. It is found that the pinning force of the magnetic dot with 50 nm thick-
ness reaches 3.5 × 10-11 N that is one order magnitude stronger than the intrinsic pinning force in cuprate at
77 K. We investigate various parameter dependences of the pinning force. It is found that the most effective
way to increase the pinning force is to increase the thickness of the dot. The pinning force is weakly de-
pendent on both the size and magnetic permeability of the dots. When temperature increases, the pinning
force linearly decreases. And when the magnetic field increases, the attraction force increases linearly in the
low field region.
Keywords: Pinning Force, Periodic Ferromagnetic Dot Array, Cuprate
1. Introduction
Because of the scientific interest and technological im-
portance, vortex pinning in superconductors has been the
subject of a large amount of theoretical and experimental
work. The introduction of external pinning centers has
attracted many interests. In general such approaches at-
tempt to create some artificial pinning centers to attract
vortices. Notably, irradiation by swift heavy ions such as
neutrons has been used to create columnar defects in
high-Tc superconductors [1-4]. Artificially introduced
regular arrays of holes (anti-dots) [5-8] and ferromag-
netic dots have been used for low-Tc and high-Tc super-
conductors [9-12]. Recently, triangular array of external
pinning centers without long-range order had been stud-
ied for Nb thin films [13]. In the last decade, the interac-
tions between the external pinning centers and flux lat-
tice in superconductors have been studied theoretically or
numerically by several groups [14-26]. A variety of pin-
ning behaviors have been found, and very rich dynamics
of vortex lattice and vortex motion have been discovered.
Milosevic et al. calculated the interaction between a
superconducting vortex with ferromagnets on top [14-18].
Multivortex states and vortex dynamics have been inves-
tigated by Reichardt et al. in the presence of the periodic
pinning arrays [19-22]. Pokrovsky et al. studied the in-
fluence of various magnetic structures on the underneath
superconducting films [23,24]. Vortex lattice structures
have been studied in presence of an artificial pinning
array by Pogosov et al. [25,26]. Magnetic pinning energy
has been estimated in superconductor-ferromagnet mul-
tilayer system [27].
In the present paper, we consider the interaction be-
tween superconducting vortices in a superconducting
thin film and a regular array of soft ferromagnetic dots
deposited on top of the superconducting film. Absolute
values of the pinning force on vortices from soft ferro-
magnetic dots were found for type II superconductors.
Numerical calculations show that the pinning force from
the magnetic dots can be orders of magnitude stronger
than the intrinsic pinning force in cuprate. We also stud-
ied the dependence of pinning force upon various pa-
rameters. In the calculation, we used the London equa-
tion to describe the vortex structure. Although most of
the parameters we used were similar to those of cuprate,
we believe that the majority of the conclusions obtained
from this paper could also be applied to other high-Tc
and low-Tc superconductors as long as the magnetic vor-
tex structure could be described by the London equation.
To make the problem simpler, we assume there is no
proximity effect between the superconducting materials
and the magnetic dots. This can be achieved experimen-

W. J. YEH ET AL.365
tally by inserting a thin insulating film between the su-
perconducting film and magnetic dots. This paper is or-
ganized as follows. In Section 2, the mathematical for-
mulas which were used to calculate the external pinning
due the magnetic dots are given. The general behaviors
of the pinning force are described in Section 3. In Sec-
tion 4, the dependences of the pinning force upon various
parameters are reported. And in Section 5, conclusions
are given.
2. Theoretical Formulas of the Pinning Force
In this paper we assume that the superconducting films
have large values of penetration length λ and very small
values of Ginzburg-Landau coherence length ξ, so that
the simple London equation can be used to describe the
magnetic field distribution of the vortex lattice. The
well-defined magnetic vortex structure coupled with the
regular (disc type) shape of the ferromagnetic dots al-
lows us to calculate the interaction between the dot and
the vortex within the electromagnetic context. The cal-
culation was carried out under the following conditions.
A magnetic field is applied perpendicularly to the surface
of the sample. A uniform array of soft ferromagnetic dots
with triangular pattern is on the surface of the sample.
The shape of the dots is a perfect disc. We only calculate
the pinning force created by the dots in a “matching”
field condition, which means the applied field has a
magnitude to create one flux quantum for each dot. Fig-
ure 1 shows the schematic drawing of the situation dis-
cussed above. If the distance between neighboring dots,
which we shall refer to as the lattice constant thereafter,
is C, the matching field strength is Φ0/[(3/2)1/2 C2] for a
triangle lattice, where Φ0 is the magnetic flux quantum.
For the typical C value of 625 nm that was used in most
of our calculations in Section 3, the corresponding field
is 4.32 mT. Since a magnetic field is applied perpen-
dicularly to the sample surface, the main component of
the magnetic field inside the dot and thin superconduct-
ing film is the z component. For simplicity, we assume
that the spreading of flux lines within the dot thickness is
negligible. Thus the magnetic field within the thickness
of the thin film sample and dots only has one component
perpendicular to the sample surface.
Since λ >> ξ, the magnetic field induction distribution
B around a single vortex can be described by the London
equation,
2
2
B
B




(1)
In cylindrical coordinates for the two-dimensional
case, this equation becomes:
Figure 1. The schematic drawing the condition used in this
paper.
2
0
dd
rBB
rdr dr






(2)
This equation has an exact solution [28]:

0
0
2
2
z
r
Br K








 (3)
where Bz(r) is the z-component of the magnetic field
induction (the only component inside of the supercon-
ductor) and K0(r/
 ) is the zeroth-order modified Bessel
function. Equation (3) is used to calculate the field dis-
tribution for a single vortex. Mathematically K0(r/
 ) di-
verges logarithmically as r approaches zero. In reality,
B(r) has a cutoff at r 
 as the density of the supercon-
ducting Cooper pair starts to drop to zero at this point.
The divergence of K0 at zero is removed by replacing the
values of K0(r/
 ) for r <  by the value obtained at r =  .
The real field is a collective one of all vortices surround-
ing it. In our numerical calculation, at each vortex side, a
total of 55 vortex sites around that one are included to
obtain a two-dimensional field distribution of the trian-
gular vortex lattice. Magnetic discs are magnetized in
this field. Since we consider the spreading of flux lines
within the disc thickness is negligible, magnetic induc-
tion (B), magnetic field (H), and magnetization (M)
within the disc and sample only have z component. Be-
cause the dot size is comparable with respect to the scale
of the field variation, the magnetization of the dot is not
uniform. To take the non-uniform magnetization into
consideration we divide each dot into 360 × 100 colum-
nar volume elements. The magnetic moment of each
element is found under local field strength and force act-
ing on it is then calculated. The total force on the dot is
obtained by summing up all volume elements. A volume
element dv of the dot with M in an external Bext experi-
ence a force [29]:



ext ext
dFdv MBdvMB


 
(4)
For simplicity, we assume a linear magnetization rela-
tion between M and H for the ferromagnetic dots:

1
M
H  H


(5)

W. J. YEH ET AL. 366
here H is the true magnetic field acting on dv and  is the
relative permeability of the dots. The demagnetization
effect needs to be considered to calculate H from the
external applied field Hext. In a magnetized object,
1
ext dext
M
HHH HNM




 
(6)
here Hd is the demagnetization field and N is the demag-
netization factor. For an object of disc shape with the
ratio of the diameter to the thickness r1 > 1, we have [30]
2
2
1 1
1
1
22
1 11
1
1
1sin ,
11
r
r
N
r
rr








1r





(7)
When the thickness of the disc is larger than the di-
ameter, we have [30]

2
2
22 2
22
22
1ln11, 1
11
r
Nrr
rr






r





(8)
Here r2 is the ratio of the thickness to the diameter of
the disc. The value of N changes from zero (for an infi-
nite long rod) to one (for an infinite thin disc). Solving
Equation (6), we obtain:
 
0
11
.
1111
ext
ext
B
MH
NN





 


(9)
In Equation (9) we use Bext/µ0 = Hext to replace Hext.
Since we assume that the spreading of flux lines within
the dot is negligible, both M and Bext within the dot have
z component only. Equation (4) reduces to:
2
z
ext
dFdvM B

(10)
here the direction of dF is perpendicular to the z direc-
tion, which is in the x-y plane. Combining Equation (9)
and Equation (10), the following equation is obtained:


0
21 .
11
ext ext
dF dvBB
N







(11)
Equation (11) allows us to calculate the force acting
on dv. The total force on the dot is obtained by the sum-
mation of all elements. Equation (11) shows that the at-
traction force is dependent upon dv, µ, N, Bext, and
ext . Since Bext, and ext are two important parame-
ters for the force, in Figure 2 we depict B and dB/dr ob-
tained from our calculation from Equation (3) under the
condition of ξ = 2 nm, λ = 150 nm, and C = 625 nm. The
horizontal axis in Figure 2 was along two nearest
neighbor vortex sites in a triangular lattice. In principle,
Equation (11) could be used to calculate the pinning
force from the magnetic dot for any type-II supercon-
ductors. However, the magnetic field distribution of a
vortex shown in Equation (3) is obtained from the Lon-
BB
Figure 2. Field and field gradient distribution of the trian-
gular vortex lattice for ξ = 2 nm, λ = 150 nm and C = 625
nm, and horizontal axis is along two nearest neighbor vor-
tex sites.
don equation that is only applicable in the condition of

>>
 . Restrictively speaking, the results of this paper
could only be valid to superconductors in this condition.
For arbitrary type-II superconductors (
 >  /21/2), the
more complicated Ginzburg-Landau equations have to be
used to calculate the magnetic field distribution of vor-
tices. On the other hand, although the magnetic field dis-
tributions of vortices obtained from these two models
defer in some fine details, the general shapes are similar.
We believe that the general trends obtained from this
paper could be applied to most type-II superconductors.
For ferromagnetic materials M is saturated in high
fields. For example, for nickel, M is saturated at about
200 Oe of H for bulk material. For a Ni dot of a disc
shape, due to the demagnetization effect M is saturated
in a higher field when it is magnetized in a vertical direc-
tion. When the demagnetization factor is included the
actual field (H) acting on the dots is always smaller than
the saturation field under the conditions discussed in this
paper. So the saturation will not play a role in our model.
3. The General Behaviors of Pinning from
Magnetic Dots
In the calculation, the parameters that can be changed
include λ, ξ, µ, C, dot orientation angle, dot thickness (d),
and dot radius (R). The dot orientation angle defines the
orientation of the triangular dot lattice relative to the
moving direction of vortices that is perpendicular to the
direction of the current flow in the superconductor. In
this paper, we only present the results from two different
orientation angles (30 degree and 15 degree). Their con-
figurations are shown in Figure 3. The arrows in Figure
3 represent our calculation paths. Figure 4 shows the
force acting on the vortex from the magnetic dots along
the arrow direction shown in Figure 3(a) under the fol-
lowing conditions: C = 625 nm, d = 50 nm, R = 94 nm
that is equal to 0.15 C, and µ = 75 (typical value for Co).

W. J. YEH ET AL.367
(a) (b)
Figure 3. The orientations of the periodic dot array relative
to the sample strip and calculation paths of two cases. (a) 30
degree; (b) 15 degree.
Figure 4. Pinning forces calculated along the path shown in
Figure 3(a) with C = 625 nm, d = 50 nm, R = 94 nm and µ =
75. The values of  and  were shown inside the figures.
The values of ξ and λ are displayed inside the figure. The
values of ξ = 2 nm and λ = 150 nm used in Figure 4(a)
are very close the accepted values of cuprate at zero de-
gree temperature [28]. The values of ξ and λ used in
Figure 4(b) are close the values of cuprate at 77 K.
Please note that the maximum force in Figure 4(a) is
about one order of magnitude larger than that in Figure
4(b), although the shapes of curves in these two figures
are similar. Figure 4(c) depicts the result of ξ = 30 nm
and λ = 150 nm. These values of ξ and λ resemble the
condition of low-Tc superconductors such as Pb/In alloy
[28]. In comparison with Figure 4(a), Figure 4(c) shows
that as ξ increases not only the maximum pinning
strength decrease, but also the curve becomes smooth
near the places where the pinning force is maximum.
These are due to the fact that as ξ increases, the magnetic
field intensity and gradient at and near the vortex core
region reduce, which result in a smoother and smaller
force.
The general behaviors of the pinning force under the
30˚ orientation angle configuration are as follows. The
vortex experiences no pinning force from the dot when
the centers of the two coincide. As the two shift apart
under the influence of the Lorentz force, there is an at-
tracting force pulling the vortex back. The force reaches
a maximum when the center the vortex being at the edge
of the dot. The maximum forces are in the range of 10-11
to 10-10 Newton depending upon the parameters. As the
vortex moves beyond the dot edge, the attracting force
decreases. When the vortex reaches the middle point
between two dots, the pinning is zero. The force direc-
tion is reversed when the vortex crosses the middle point,
as it is attracted by the other dot. The zero-force position
at the dot center is stable, whereas the one between two
dots is unstable.
We also calculated the pinning behaviors at other con-
figurations. Figure 5 shows the result from 15 degree of
the dot orientation angle. Other parameters are shown in
the figure caption. In this calculation, we assume that
initially the system is in a match condition, so that one
dot traps one vortex. We then pass a large current
through the superconductor so that vortices depin from
the dot pinning centers by a large Lorentz force that is
much stronger than the pinning force. In this case, the
vortices are moving along the path shown in Figure 3(b).
Also in the calculation, we only calculate the pinning
force along the path direction. The initial behavior of
the pinning force for the vortex is the same as the case
shown in Figure 4. When the vortex moves to the edge
of the trapping dot, it experiences a maximum pinning
force. After the vortex leaves that dot, the force de-
creases. Under this configuration shown in Figure 3(b),
the vortex glances through another dot after it leaves the
first dot. When the vortex at the position of C, it should
experience a strongest attraction force from the second
dot. However, at this point, the attraction force is per-
pendicular to the vortex path, the component of the force
along the path direction is very close to zero as shown in
Figure 5. Before and after the distance of C, the compo-
nent of the attraction force along the path from this dot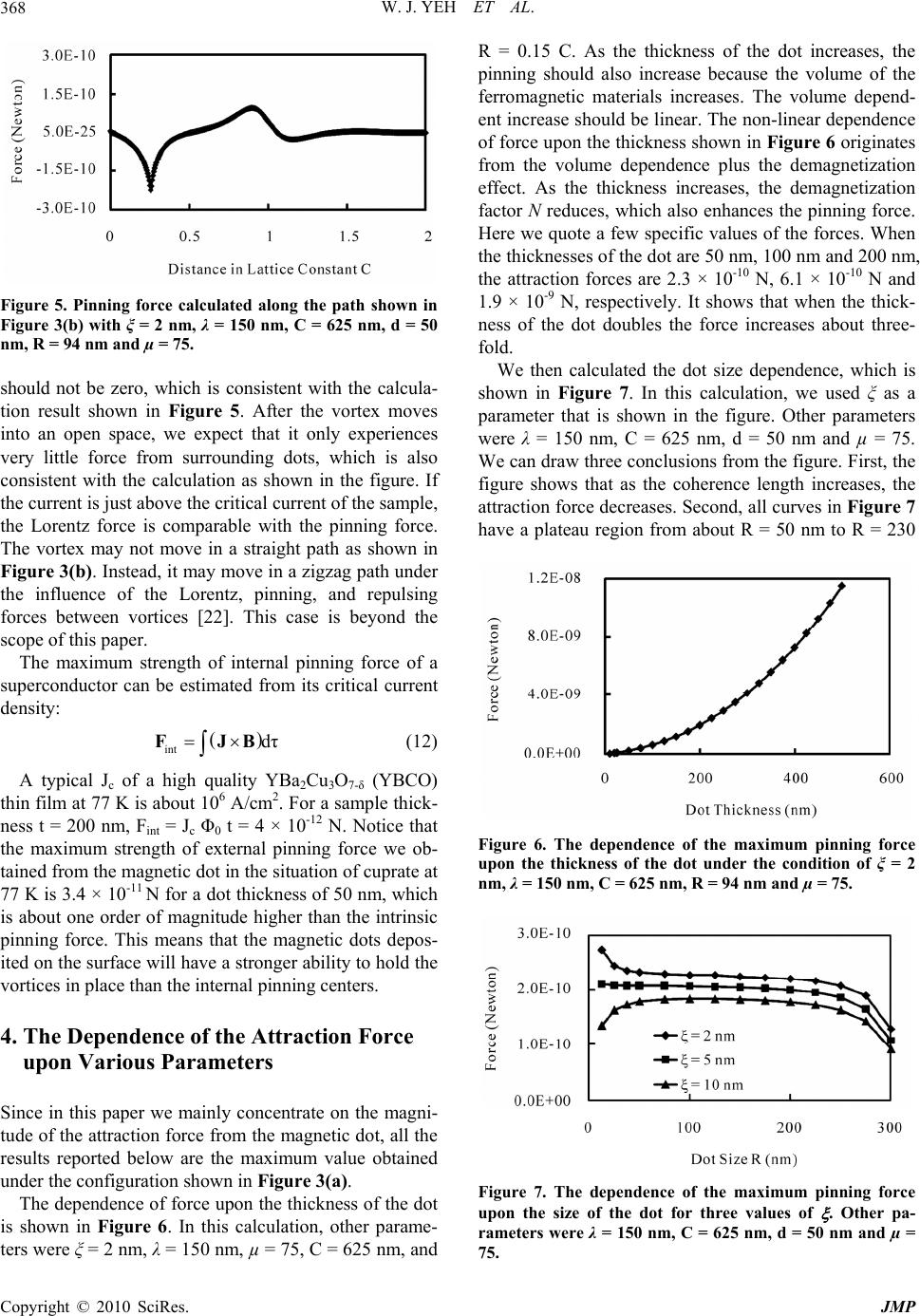

W. J. YEH ET AL. 368
Figure 5. Pinning force calculated along the path shown in
Figure 3(b) with ξ = 2 nm, λ = 150 nm, C = 625 nm, d = 50
nm, R = 94 nm and µ = 75.
should not be zero, which is consistent with the calcula-
tion result shown in Figure 5. After the vortex moves
into an open space, we expect that it only experiences
very little force from surrounding dots, which is also
consistent with the calculation as shown in the figure. If
the current is just above the critical current of the sample,
the Lorentz force is comparable with the pinning force.
The vortex may not move in a straight path as shown in
Figure 3(b). Instead, it may move in a zigzag path under
the influence of the Lorentz, pinning, and repulsing
forces between vortices [22]. This case is beyond the
scope of this paper.
The maximum strength of internal pinning force of a
superconductor can be estimated from its critical current
density:

int dτ 
FJB (12)
A typical Jc of a high quality YBa2Cu3O7-δ (YBCO)
thin film at 77 K is about 106 A/cm2. For a sample thick-
ness t = 200 nm, Fint = Jc Φ0 t = 4 × 10-12 N. Notice that
the maximum strength of external pinning force we ob-
tained from the magnetic dot in the situation of cuprate at
77 K is 3.4 × 10-11 N for a dot thickness of 50 nm, which
is about one order of magnitude higher than the intrinsic
pinning force. This means that the magnetic dots depos-
ited on the surface will have a stronger ability to hold the
vortices in place than the internal pinning centers.
4. The Dependence of the Attraction Force
upon Various Parameters
Since in this paper we mainly concentrate on the magni-
tude of the attraction force from the magnetic dot, all the
results reported below are the maximum value obtained
under the configuration shown in Figure 3(a) .
The dependence of force upon the thickness of the dot
is shown in Figure 6. In this calculation, other parame-
ters were ξ = 2 nm, λ = 150 nm, µ = 75, C = 625 nm, and
R = 0.15 C. As the thickness of the dot increases, the
pinning should also increase because the volume of the
ferromagnetic materials increases. The volume depend-
ent increase should be linear. The non-linear dependence
of force upon the thickness shown in Figure 6 originates
from the volume dependence plus the demagnetization
effect. As the thickness increases, the demagnetization
factor N reduces, which also enhances the pinning force.
Here we quote a few specific values of the forces. When
the thicknesses of the dot are 50 nm, 100 nm and 200 nm,
the attraction forces are 2.3 × 10-10 N, 6.1 × 10-10 N and
1.9 × 10-9 N, respectively. It shows that when the thick-
ness of the dot doubles the force increases about three-
fold.
We then calculated the dot size dependence, which is
shown in Figure 7. In this calculation, we used ξ as a
parameter that is shown in the figure. Other parameters
were λ = 150 nm, C = 625 nm, d = 50 nm and µ = 75.
We can draw three conclusions from the figure. First, the
figure shows that as the coherence length increases, the
attraction force decreases. Second, all curves in Figure 7
have a plateau region from about R = 50 nm to R = 230
Figure 6. The dependence of the maximum pinning force
upon the thickness of the dot under the condition of ξ = 2
nm, λ = 150 nm, C = 625 nm, R = 94 nm and µ = 75.
Figure 7. The dependence of the maximum pinning force
upon the size of the dot for three values of
 . Other pa-
rameters were λ = 150 nm, C = 625 nm, d = 50 nm and µ =
75.

W. J. YEH ET AL.369
nm. In this region, the strength of the attraction varies
little. When R is larger than 230 nm the attraction force
decreases. This decrease is due to the restriction from the
lattice constant C. In the calculation, we chose C = 625
nm. When R is approaching 300 nm, the two adjacent
dots are very close. In this case, when a vortex moves to
the edge of the first dot, it experiences a maximum at-
traction from this dot to pull it back. At the same time,
due to the large value of the penetration length, part of
the vortex is already in the region occupied by the sec-
ond dot. The second dot also exerts a force on that vortex.
This is opposite to the first one, so that the total force
reduces. If we use a larger lattice constant, the plateau
region will extend farther to the right. Third, as the dot
size decreases below 100 nm, the forces show different
behaviors for different coherent lengths. When the dot
size reduces two different factors are at work. Number
one is that when the dot size reduces the demagnetization
factor reduces, which increases the force. Number two is
the mass of the dot. As the size of dot reduces, the fer-
romagnetic materials reduces, which results in a smaller
force. It seems that for small coherence length (ξ = 2 nm)
the demagnetization effect dominates. On the other hand,
for relatively large coherence length (ξ = 10 nm) the
mass effect dominates. When the coherence length is 5
nm, the force is almost constant when the dot size re-
duces. We need to point out that the coherence length of
cuprate at 77 K is about 4 nm, which is very close to 5
nm. It means that if we want to use ferromagnetic dot as
the external pinning for cuprate at 77 K, the dot size is
not a factor. Almost any size of dot will give the similar
pinning force.
We also studied the force dependence upon the mag-
netic permeability µ. The µ dependence is in the
pre-factor in Equation (11), which is (µ − 1)/[1 + N(µ −
1)]. In general, as µ decreases, the attraction force is also
reduced. The relationship between the force and µ is also
dependent upon the value of N. If N is zero in case of an
infinite long dot, then the force is proportional to (µ − 1).
The force is approximately proportional to µ, except
when µ is close to one. On the other hand, if N is 1 in
case of an infinite thin dot, the force is proportional to (µ −
1)/µ. The force is weakly dependent upon µ until µ is
close to one. Since in reality we do not have these ex-
treme conditions, we selected two cases to carry out the
calculation of the µ dependence. In case A, the thickness
of the dot was 50 nm and the value of N is 0.689. In case
B, the thickness of the dot was 500 nm and N equals to
0.125. In both cases, other parameters were ξ = 2 nm, λ =
150 nm, C = 625 nm, and R = 94 nm. The results are
depicted in Figure 8. For both cases, when the value of µ
decreases from 100, the attraction force for both cases
decreases in a slow pace until µ reaches 25. After that
Figure 8. The dependence of the maximum pinning force
upon the magnetic permeability µ for d = 50 nm and d =
500 nm, respectively. Other parameters were ξ = 2 nm, λ =
150 nm, C = 625 nm and R = 94 nm.
point the attraction force decreases dramatically. The
average initial values of µ for iron, cobalt and nickel are
150, 70 and 110, respectively [31]. All of them are much
higher than 25. Our result indicates that when choosing
ferromagnetic materials working as external pinning, the
µ value is not an important factor.
We also investigated the temperature dependence of
the attraction force. In this study, we assumed the ferro-
magnetic properties of dots did not change. We also as-
sumed that the ferromagnetic dots were deposited on a
cuprate thin film. The lengths of ξ and λ of the vortex in
the thin film change when the temperature changes. We
used the Ginzburg-Landau theory to calculate the values
of ξ and λ at different temperatures. Since the theory is
only valid when the temperatures are close the transition
temperature (Tc), besides zero degree we only calculated
a few points near Tc of cuprate, which we assume to be
90 K. At zero degree we used ξ0 = 2 nm and λ0 = 150 nm.
The formulas we used to calculate ξ and λ at other tem-
peratures were ξ(t) = 0.74ξ0/(1 − t)1/2 and λ(t) = λ0/[2(1 −
t)]1/2, which are the relations in the clean limit [32]. In
the calculation, other parameters were C = 625 nm, d =
50 nm, R = 0.15 C, and µ = 75. The result is shown in
Figure 9. It shows that the attraction force almost line-
arly decreases as the temperature increases.
Finally, we studied the magnetic field strength de-
pendence of the attraction force. As the field strength
increases, the vortex density increases and the field
strength at any place also enhances. As shown in Equa-
tion (11), the attraction force should be proportional to
the external field strength. To confirm this, we carried a
numerical calculation. In the calculation, we used the
following parameters: λ = 284 nm,
 = 4 nm, R = 40 nm,
d = 50 nm and µ = 75. The values of λ and ξ used in this
calculation resemble the values for cuprate at 77 K. In
the calculation, as the field strength changed, the density
of dots was also changed so that the matching condition
was always maintained. Figure 10 shows the result. It

W. J. YEH ET AL. 370
Figure 9. The temperature dependence of the maximum
pinning force. The values of  and  at different tempera-
tures were obtained from the Ginzburg-Landau theory
under the clean limit of cuprate. Other parameters were C
= 625 nm, d = 50 nm, R = 0.15 C, and µ = 75.
Figure 10. The magnetic field dependence of the maximum
pinning force under the condition of λ = 284 nm,  = 4 nm,
R = 40 nm, d = 50 nm and µ = 75. At any magnetic field, the
value of C was determined under the matching co ndition.
shows that in low fields the attraction force linearly in-
creases as the field strength increases as expected. This is
consistent with the experimental observation [12]. Ref-
erence [12] showed that when the magnetic field was
increased the pinning effect from magnetic dots also en-
hanced. As the magnetic field passes 40 mT, the curve
then starts to deviate from the linear behavior. The in-
crease slows down. When the magnetic field equals 40
mT, the value of C equals 205 nm. Because of the large
value of λ we used (λ = 284 nm), when the vortex moves
to the edge of the dot where the attraction reaches the
maximum, part of the vortex already feel the opposite
attraction from the adjacent magnetic dot, which results
in a smaller total force. This is the reason why at high
fields, the increase slows down from a linear relation.
5. Conclusions
We have developed a theoretical model to describe the
interactions between the magnetic dots and vortices in
the superconductor by using the London equation. The
absolute values of the pinning force under various condi-
tions have been calculated. The external attraction force
from a soft ferromagnetic dot with a thickness of 50 nm
could reach 3.5 × 10-11 N for a cuprate sample at 77 K,
which is about one order of magnitude stronger than the
intrinsic pinning force in cuprate. We also studied the
dependences of the attraction force on various parame-
ters. We found that the most effective way to increase the
external pinning force is to increase the thickness of dot.
When the thickness doubles, the force increases about
threefold. On the other hand, in a large range of the dot
size, the force remains approximately constant. We
found that the pining force is weakly dependent upon the
value of µ. We also investigated the temperature and
magnetic field dependences of the force. When tempera-
ture increases, the attraction force linearly decreases.
And when the magnetic field increases, the force en-
hances linearly in the low field region.
6. Acknowledgments
This work was partly supported by NSF grant PHY-
0754360.
7. References
[1] F. M. Sauerzopf, H. P. Wiesinger, H. W. Weber, G. W.
Crabtree and J. Z. Liu, “Magnetization of Neutron Irradi-
ated YBa2Cu3O7-δ Single Crystals,” Physica C, Vol.
162-164, 1989, pp. 751-752.
[2] L. Civale, A. D. Marwick, T. K. Worthington, M. A. Kirk,
J. R. Thompson, L. Krusin-elbaum, Y. Sun, J. R. Clem
and F. Holtzberg, “Vortex Confinement by Columnar
Defects in YBa2Cu3O7 Crystals: Enhanced Pinning at
High Fields and Temperatures,” Physical Review Letters,
Vol. 67, No. 5, 1991, pp. 648-561.
[3] J. R. Thompson, L. Krusin-Elbaum and D. K. Christen,
“Current-density Enhancements of the Highest-Tc Super-
conductors with GeV Protons,” Applied Physics Letters,
Vol. 71, No. 4, 1997, pp. 536-538.
[4] T. Kato, T. Shibauchi, Y. Matsuda, J. R. Thompson and L.
Krusin-Elbaum, “Interlayer Coherence in Bi2Sr2CaCu2O8+y
with Splayed Columnar Defects,” Physica C, Vol. 463-
465, 2007, pp. 240-244.
[5] M. Baert, V. V. Metlushko, R. Jonckheere, V. V. Mosh-
chalkov and Y. Bruynseraede, “Composite Flux-line Lat-
tices Stabilized in Superconducting Films by a Regular
Array of Artificial Defects,” Physical Review Letters, Vol.
74, No. 16, 1995, pp. 3269-3272.
[6] E. Rosseel, T. Puig, M. Baert, M. J. Van Bael, V. V.
Moshchalkov and Y. Bruynseraede, “Upper Critical Field
of Pb Films with an Antidot Lattice,” Physica C, Vol.
282-287, 1997, pp. 1567-1568.

W. J. YEH ET AL. 371
[7] A. V. Silhanek, L. V. Look, R. Jonckheere, B. Y. Zhu, S.
Raedts and V. V. Moshchalkov, “Enhanced Vortex Pin-
ning by a Composite Antidot Lattice in a Superconduct-
ing Pb Film,” Physical Review B, Vol. 72, No. 1, 2005,
pp. 1-6.
[8] S. L. Prischepa, A. A. Armenio, L. Maritato, V. N. Kush-
nir and S. Barbanera, “The Influence of a Submicrometre
Antidot Array on the Vortex Topology and the Pinning
Mechanism in Layered Superconductors”, Superconduc-
tor Science and Technology, Vol. 18, No. 1, 2005, pp.
152-157.
[9] J. I. Martin, M. Velez, J. Nogues and I. K. Schuller, “Flux
Pinning in a Superconductor by an Array of Submicro-
meter Magnetic Dot,” Physical Review Letters, Vol. 79,
No. 10, 1997, pp. 1929-1932.
[10] D. J. Morgan and J. B. Ketterson, “Asymmetric Flux
Pinning in a Regular Array of Magnetic Dipoles,” Physi-
cal Review Letters, Vol. 80, No. 16, 1998, pp. 3614-3617.
[11] M. Lange, M. J. V. Bael, Y. Bruynseraede and V. V.
Moshchalkov, “Nanoengineered Magnetic-Field-Induced
Superconductivity,” Physical Review Letters, Vol. 90, No.
19, 2003, pp. 1-4.
[12] W. J. Yeh, B. Cheng and B. L. Justus, “I–V Characteris-
tics of YBCO Thin Films with a Periodic Array of Ni
Dots,” Physica C, Vol. 388-389, 2003, pp. 433-434.
[13] J. Eisenmenger, M. Oettinger, C. Pfahler, A. Plettl and P.
Ziemann, “Temperature-dependent Matching in a Flux-line
Lattice Interacting with a Triangular Array of Pinning
Centers without Long-range Order,” Physical Review B,
Vol. 75, No. 14, 2007, p. 144514.
[14] M. V. Milosevic and F. M. Peeters, “Vortex-Antivortex
Lattices in Superconducting Films with Magnetic Pinning
Arrays,” Physical Review Letters, Vol. 93, No. 26, 2004,
p. 267006.
[15] M. V. Milosevic and F. M. Peeters, “Vortex Pinning in a
Superconducting Film Due to In-plane Magnetized Fer-
romagnets of Different Shapes: The London Approxima-
tion,” Physical Review B, Vol. 69, No. 10, 2004, p.
104522.
[16] M. V. Milosevic and F. M. Peeters, “Field-enhanced
Critical Parameters in Magnetically Nanostructured Su-
perconductors,” Europhysics Letters, Vol. 70, No. 5,
2005, pp. 670-676.
[17] M. V. Milosevic and F. M. Peeters, “Interaction between
a Superconducting Vortex and an Out-of-plane Magnet-
ized Ferromagnetic Disk: Influence of the Magnet Ge-
ometry,” Physical Review B, Vol. 68, No. 9, 2003, pp.
094510.
[18] M. V. Milosevic and F. M. Peeters, “Vortex-Antivortex
Lattices in Superconducting Films with Magnetic Pinning
Arrays,” Journal of Low Temperature Physics, Vol. 139,
No. 1, 2005, pp. 257-272.
[19] C. Reichhardt, C. J. Olson and F. Nori, “Nonequilibrium
Dynamic Phases and Plastic Flow of Driven Vortex Lat-
tices in Superconductors with Periodic Arrays of Pinning
Sites,” Physical Review B, Vol. 58, No. 10, 1998, pp.
6534-6564.
[20] C. Reichhardt and N. Gronbech-Jensen, “Collective Mul-
tivortex States in Periodic Arrays of Traps,” Physical Re-
view Letters, Vol. 85, No. 11, 2000, pp. 2372-2375.
[21] C. Reichhardt, G. T. Zimanyi, R. T. Scalettar, A. Hoff-
mann and I. K. Schuller, “Individual and Multiple Vortex
Pinning in Systems with Periodic Pinning Arrays,” Phys-
ical Review B, Vol. 64, No. 5, 2001, p. 052503.
[22] C. Reichhardt and C. J. O. Reichhardt, “Ratchet Effects
for Vortices in Superconductors with Periodic Pinning
Arrays,” Physica C, Vol. 404, No. 1-4, 2004, pp.
302-305.
[23] I. F. Lyuksyutov and V. Pokrovsky, “Magnetization Con-
trolled Superconductivity in a Film with Magnetic Dots,”
Physical Review Letters, Vol. 81, No. 11, 1998, pp.
2344-2347.
[24] S. Erdin, F. Kayali, I. F. Lyuksyutov and V. Pokrovsky,
“Interaction of Mesoscopic Magnetic Textures with Su-
perconductors,” Physical Review B, Vol. 66, No. 1, 2002.
[25] W. V. Pogosov, A. L. Rakhmanov and V. V. Mosh-
chalkov, “Vortex Lattice in the Presence of a Tunable Pe-
riodic Pinning Potential,” Physical Review B, Vol. 67, No.
1, 2003, p. 014532.
[26] W. V. Pogosov and V. V. Moshchalkov, “Vortex Lattice
Structure in Presence of an Artificial Periodic Pinning
Array,” Physica C, Vol. 404, No. 1-4, 2004, pp. 285-288.
[27] L. N. Bulaevskii, E. M. Chudnovsky and M. P. Maley,
“Magnetic Pinning in Superconductor-ferromagnet Mul-
tilayers,” Applied Physics Letters, Vol. 76, No. 18, 2000,
pp. 2594-2596.
[28] C. P. Poole, H. A. Farach and R. J. Creswick, “Super-
conductivity,” Academic Press, California, 1995.
[29] J. D. Jackson, “Classical Electrodynamics,” 3rd Edition,
John Wiley & Sons Ltd., Chichester, 1999.
[30] B. D. Cullity, “Introduction to Magnetic Materials,” Ad-
dison-Wesley Publishing Company, Massachusetts, 1972.
[31] E. U. Condon and H. Odishaw, “Handbook of Physics,”
2nd Edition, McGraw-Hill Book Company, New York,
1967.
[32] M. Tinkham, “Introduction to Superconductivity,” Mc-
Graw-Hill Book Company, New York, 1975.