Optics and Photonics Journal, 2013, 3, 240-249
http://dx.doi.org/10.4236/opj.2013.33039 Published Online July 2013 (http://www.scirp.org/journal/opj)
Optical Image Compression Using a Real Fourier Plane
Abdulsalam G. Alkholidi
Faculty of Engineering, Electrical Engineering Department, Sanaa University, Sanaa, Yemen
Received April 7, 2013; revised May 7, 2013; accepted May 17, 2013
Copyright © 2013 Abdulsalam G. Alkholidi. This is an open access article distributed under the Creative Commons Attribution Li-
cense, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
Hastening transmission by efficiently providing compression is our goal in this work. Image compression consists in
reducing information size representing an image. Elimination of redundancies and non-pertinent information enables
memory space minimization and thus fast data transmission. Optics can offer an alternative choice to overcome the
limitation of numerical compression algorithms. In this paper, we propose real-time optical image compression using a
real Fourier plane to save time required for compression by using the principles of coherent optics. Digital and optical
simulation results are presented and analyzed. An optical compression decompression setup is demonstrated using two
different SLMs (SEIKO and DisplayTech). The purpose of this method is to simplify our earlier method, improve the
quality of reconstructed image, and avoid the disadvantages of numerical algorithms.
Keywords: FT; Optical Compression; a Real Fourier Plane; Hologram; SLM
1. Introduction
In recent years, there has been much interest in image
compression algorithms which are proposed in this paper.
Our algorithm is oriented towards large size images. The
goal of this work is to minimize the time required for
compression with high compression ratio (Cr). One of the
current technological challenges in image compression is
to achieve real-time imaging rates with a minimal sacri-
fice in signal-to-noise ratio (SNR) [1]. We propose a no-
vel technique of image compression using a real Fourier-
plane capable of real-time image compression. In the
frame of the present work our objective is to simplify our
earlier optical image compression algorithm using the
JPEG and optical JPEG standards [2]. We intend to
eliminate the most complex part in the synoptic diagrams
of the set up implementation compression and decom-
pression described in [2,3].
To digitally decompress large images, they should be
first transmitted to a calculator to enable applying one or
several digital compression methods. The real-life appli-
cation of this technique; consists first in optically com-
pressing these images. Starting from an image, with size
(N × N) pixels (Figure 1(a)), we obtain a compressed
version of only (c × c) pixels as pointed out by Figure
1(f). This results in a decrease of the volume of informa-
tion to be transmitted to the calculator. The latter may
provide additional compression, by applying digital me-
thods. In this paper, we provide a detailed technical de-
scription of the proposed architecture. This exposition is
interested to serve as a reader-friendly starting point for
those interested in learning about optical JPEG com-
pression. Although many details are included in our pre-
sentation, some details were necessarily omitted to focus
on the main subject that is compression. The reader
should, therefore, refer to standards of optical JPEG
compression [2,3] before attempting an implementation.
Indeed, much work has been done toward developing
compression methods, most techniques reported, such as
presented in [4-8].
The remainder of this paper is structured as follows:
Section 2 provides a brief overview of the optical JPEG
standards. This is followed, in Section 3, by a detailed
description of mathematical approach of the proposed
algorithm. In Section 4, optical architecture of compres-
sion/decompression is presented. Section 5, an optical
setup of image compression/decompression of proposed
method is presented and the results are presented in Sec-
tion 6. Finally, we conclude with some closing remarks
in Section 7.
2. Optical JPEG Compression
By using the principle of coherent optics, optical JPEG
(OJPEG) compression and decompression; process the
whole image at once and do not divide it into blocks. The
disadvantage of OJPEG is the fact that its optical imple-
mentation is complicated [2,3]. To relax this constraint,
C
opyright © 2013 SciRes. OPJ

A. G. ALKHOLIDI 241
Figure 1. Synoptic diagram of the setup implementation of the optical image compression using a real Fourier plane, (a)
original image I (N × N) pixels, (b) replicated image I (2N × 2N) pixels, (c) convergent lens to calculate FT, (d) real spectrum
of replicated image, (e) information selection, (f) (c × c) pixels is the size of compressed spectrum to be transmitted.
we propose a new optical image compression method
using a real Fourier plane.
3. Mathematical Approach of Optical Image
Compression Using a Real Fourier Plane
The main steps to compress an image in this work are as
follows:
1) Replicate the original image (N × N) pixels as
showing in Figure 2. This operation comes down to
making the image even. We then obtain a (2N × 2N) pix-
els image with hermitian symmetry. Since the image is
initially real, its hermetian version is merely even.
2) By applying Equation (1) to an image of (2N × 2N)
pixels, we obtain Equation (2).
Equation (1) gives the discrete version of the FT re-
ferred to as the 2 dimensional DFT of an (N × N) pixels
image.


2
11
00
,
1,e
mp nq
j
NN NN
mn
Fpq
fmn
NN
 

 
 








(1)
with


0to 1pN


0to 1qN
The term f(m, n) stands for the discrete version of the
two-dimensional signal f(x, y).
For N = 2k, k is an integer, fast algorithms FFT to com-
pute DFT exist. For the obtained hermetian image, the
DFT is expressed as follows:
Figure 2. Characteristic replication of the input image.
 
2121 222
00
1
,,e
4
mp nq
NN jNN
mn
Fpq fmn
NN
 
 
 
 





 (2)
with


0to 21pN




0to 21qN


3) The real spectrum obtained using Equation (2) after
replication of the image Figure 3(d), is then quantified.
We note that the input image with (N × N) pixels pre-
sented in Figure 3(a) is real whereas its Fourier trans-
form is complex. The main difference between the OJPEG
compression presented in [2,3] and the proposed com-
pression technique is that the spectrum obtained of repli-
cated image (2N × 2N) pixels showing in Figure 2 is
complex for the first one as presented in Figures 3(a) and
(c), because we presented a mathematical approach for
this objective demonstrated in [3]. If we replicate an im-
age to obtain (2N × 2N) pixels, then its Fourier transform
is real even. This presents the core of this work; that is,


,

,
F
uvFu v


 (3)

A. G. ALKHOLIDI
242
(a) (b)
(c) (d)
Figure 3. (a) Input image, symbol lambda I(N × N) pixels, (b)
replicated image with I ((2N × 2N) pixels, (c) complex her-
metian spectrum obtained from (a), (c) real even spectrum
obtained from (b).
where “*” indicates the standard conjugate operation on
complex number. From this, it follows that:



,,
F
uvFu v, (4)
Which says that the spectrum of the Fourier is sym-
metric [10,11]. The two spectra (c) and (d) are symmetric.
But spectra (c) is symmetric complex and spectra (d) is
symmetric real even.
4) After the real Fourier spectra step, we proceed to
the quantification and selection. It consists firstly in map-
ping the spectra values on a set of selected values, (quan-
tization), and secondly in eliminating redundant informa-
tion in this spectra plane. These operations are performed
together, thanks to a single threshold:
The quantification: this operation consists of dividing
the values of the spectra by another matrix containing
quantization values. The optical implementation of this
operation is performed in the spectral domain by multi-
plying the spectrum coefficient by another computer ge-
nerated hologram containing values of quantization. The
filtering: to increase the compression ratio after quantiza-
tion, a threshold operation is used to retain only the part
of information that we want to transmit. This operation
corresponds in general at a low-pass filter to preserve the
low frequency information which is relevant for the spec-
trum obtained. High frequencies are omitted. The filter
size is then reduced to (c), expressed as follows:
s
NN
cQ

 (5)
 c × c is the size of compressed spectrum to be trans-
mitted,
 Qs is the quantification steps (in change the intensity
of laser’s energy).
Two compression parameters can be defined:
100 100
%
i
s
cc
TNN Q





100 %
ro i
CT (7)
 Ti is the transmitted information, percentage,
 Cro is the optical compression rate.
The compression rate for digital image compression
technique is defined as follows:
Original Image Size
Compressed Image Size
r
C (8)
The main difference between two compression tech-
niques is digital-JPEG reduces the number of bytes while
optical image compression, using a real Fourier plane the
number of pixels, is reduced as seen in Equations (7) and
(8).
The optical compression ratio Cro mentioned above
Equation (7) consists in comparing the number of pixels
remaining after compression with that of the initial image.
As this ratio takes into account the remaining number of
pixels, thus it is completely normal that the quality of the
image is degraded when the compression ratio increases.
The increase in the ratio means that there are fewer of
pixels to be transmitted and thus less information on the
image.
4. Optical Image Compression and
Decompression Architectures Using a Real
Fourier-Plane
4.1. Architecture of Optical Compression
We propose an optical architecture in a real Fourier plane
by using a DFT. This optical compression technique can
be processed numerically or optically. The synoptic dia-
gram of the optical setup is demonstrated in Figure 1.
The synoptic diagram presented in Figure 1 represents
successive operations. The first one consists of replicat-
ing the input image Figure 1(a) in a specific way Figure
1(b). The objectives of this replication operation are:
1) To obtain a real spectrum easy to compress in the
frequency domain as illustrated in Equations (6) and (7).
2) To avoid the noise order of zero generated by the
beam of LASER as demonstrated in Figure 4 decom-
pressed image.
The second stage performs the FT of this duplicated
image by using a convergent lens “L1” as shown in Fig-
ure 1(c). The real spectrum Figure 1(d) is multiplied by
the low-pass filter of Figure 1(e) to increase the com-
pression ratio after quantization. In fact, this filter is used
for the purpose of preserving the low frequency, and to
select the transmitted data and to obtain the compressed
optical part of information the input image. Figure 1(f),
this spectra, of size (c × c) pixels (see Equation (5)), con-
tains the data to be transmitted.
4.2. Architecture of Optical Decompression
 (6)
On the receiver side, transmitted data should be decom-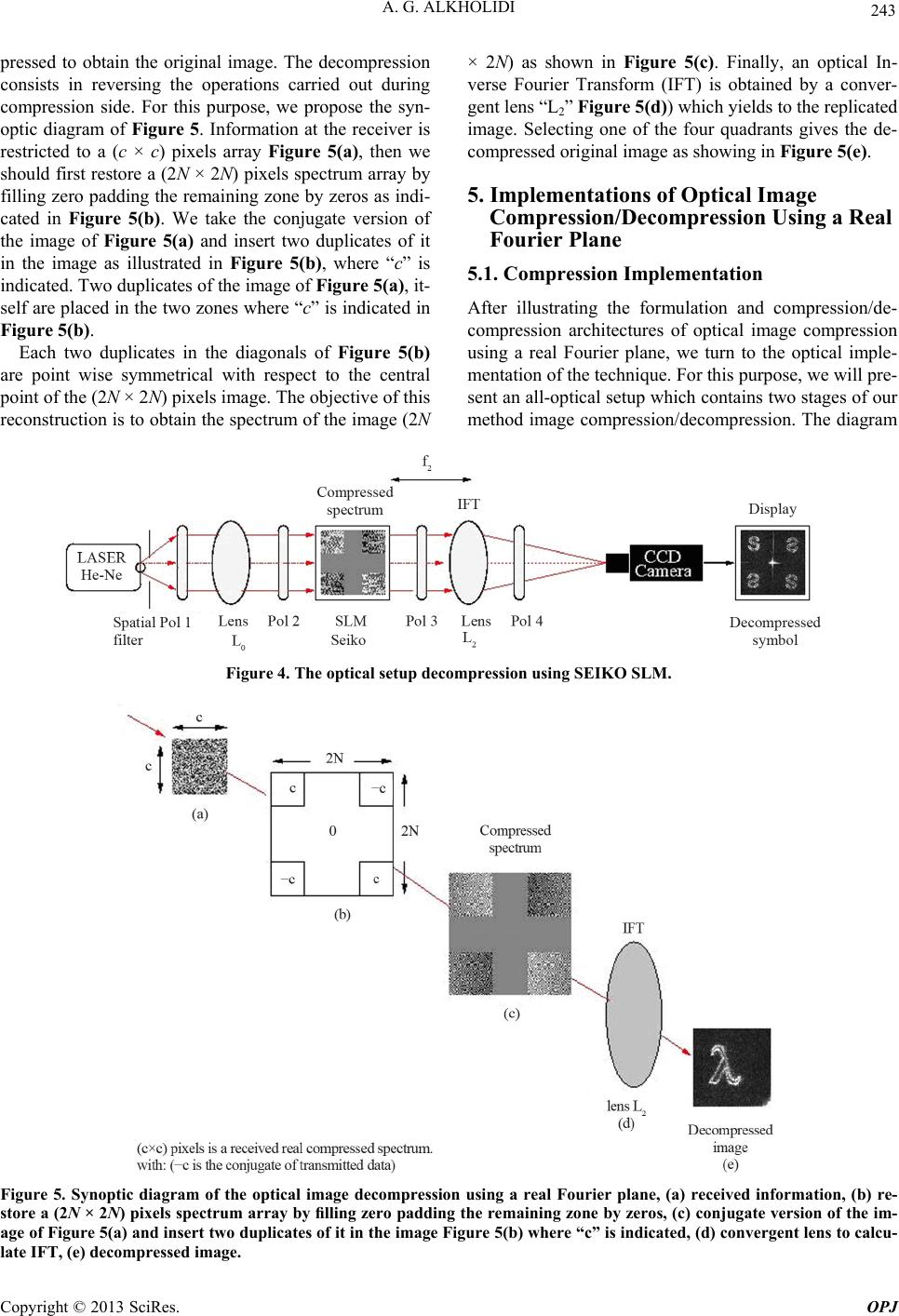

A. G. ALKHOLIDI
243
pressed to obtain the original image. The decompression
consists in reversing the operations carried out during
compression side. For this purpose, we propose the syn-
optic diagram of Figure 5. Information at the receiver is
restricted to a (c × c) pixels array Figure 5(a), then we
should first restore a (2N × 2N) pixels spectrum array by
filling zero padding the remaining zone by zeros as indi-
cated in Figure 5(b). We take the conjugate version of
the image of Figure 5(a) and insert two duplicates of it
in the image as illustrated in Figure 5(b), where “c” is
indicated. Two duplicates of the image of Figure 5(a), it-
self are placed in the two zones where “c” is indicated in
Figure 5(b).
Each two duplicates in the diagonals of Figure 5(b)
are point wise symmetrical with respect to the central
point of the (2N × 2N) pixels image. The objective of this
reconstruction is to obtain the spectrum of the image (2N
× 2N) as shown in Figure 5(c). Finally, an optical In-
verse Fourier Transform (IFT) is obtained by a conver-
gent lens “L2” Figure 5(d)) which yields to the replicated
image. Selecting one of the four quadrants gives the de-
compressed original image as showing in Figure 5(e).
5. Implementations of Optical Image
Compression/Decompression Using a Real
Fourier Plane
5.1. Compression Implementation
After illustrating the formulation and compression/de-
compression architectures of optical image compression
using a real Fourier plane, we turn to the optical imple-
mentation of the technique. For this purpose, we will pre-
sent an all-optical setup which contains two stages of our
method image compression/decompression. The diagram
Figure 4. The optical setup decompression using SEIKO SLM.
Figure 5. Synoptic diagram of the optical image decompression using a real Fourier plane, (a) received information, (b) re-
store a (2N × 2N) pixels spectrum array by filling zero padding the remaining zone by zeros, (c) conjugate version of the im-
age of Figure 5(a) and insert two duplicates of it in the image Figure 5(b) where “c” is indicated, (d) convergent lens to calcu-
late IFT, (e) decompressed image.

A. G. ALKHOLIDI
244
of the optical compression setup of the proposed method
is presented in Figure 6.
Technical characteristics of this montage of optical
image compression using a real Fourier plane. The mon-
tage presented in Figure 6 consists of the following dis-
positive:
A monochromatic light source LASER He-Ne source
(  = 633 nm, 25 µW), Spatial Filter, Three separators
cubes, two polarizers, two mirrors, two lens L0, L1, the
first one its focal is of 160 mm to be collimated the la-
ser’s beam and the second one to realize the Fourier
transform. Compression implementation setup consists
tow Spatial Light Modulators (SLM). A SLM generally
consists of an addressing material and a modulating ma-
terial. The optical property of the modulating material is
changed by write-in information, and phase or amplitude
of readout light is modulated in parallel, corresponding to
the write-in information [12].
The first one SLM-1 of 640 × 480 pixels from Seiko
with resolution of 42 µm is used to display the input
plane of size (2N × 2N) = (256 × 256) pixels as demon-
strated in Figure 6 (input plane). This VGA3 is a high
resolution SLM based on Thin Film Transistor (TFT)
twisted nematic (TN) display. It provides grey scale dis-
playing capability at standard video frame rates. The
second SLM-2 of 1280 × 780 pixels, from Display Tech
to display the hologram necessary to realize the low pass
filter (information selection).
The compression plane (output plane) consists of
camera CCD of size 753 × 582 pixels with a resolution of
6 µm [13].
The first step for proposed optical montage is to cal-
culate the focal distance (L1) of the Fourier lens. For that,
we are going to utilize the following equation:
1ef
fNdd


 (9)
where

is the operating beam wavelength, f1 is the
focal distance of L1, N is the number of pixels of the
various planes, di and do, respectively, represent the size
of the pixel (resolution) of the input and output planes.
1
66
6
256421013.210224.212 mm
633 10
ef
Nd d
f






 


After having described the different components util-
ized in this optical setup presented in Figure 6, we are
going to present the optical compression results. One of
the disadvantages of this implementation is difficult to
align the optical montage. The results of this multiplica-
tion, we obtain the spectra of compressed image (c × c)
pixels. That is registered using a CCD camera. The ob-
tained result considers a numerical version of optical
image compression using a real Fourier plane. The photo
of the setup is given in Figure 7.
Figure 8 shows the image of size (c × c) pixels that
considers the result of optical compression implementa-
tion using a real Fourier plane, contains the data to be
transmitted.
5.2. Decompression Implementation
After illustrating the optical compression implementation
stage, we turn to the optical decompression setup. For
this purpose, we will present an all-optical setup consist-
ing of different components for implementing the image
decompression using a real Fourier plane using two dif-
ferent SLMs. In this implementation, we are going to
implement two spectra:
Figure 6. The optical setup used to optical image compression using a real Fourier plane.

A. G. ALKHOLIDI 245
Figure 7. A photo of the setup used for the optical compression stage.
c
c
Figure 8. The result of optical compression implementation
using a real Fourier plane.
- Compressed spectrum in grey level as demonstrated
in Figure 4, where, we used SLM SEIKO.
- Binary compressed spectrum as demonstrated in Fig-
ure 9, where, we used DisplayTech SLM.
We used two SLM with different technical character-
istics to compare the decompressed images. In fact,
firstly we used the modulator SEIKO permits to display
an image with several levels of grey, but with a weak-
level of quality of reconstructed image. Secondly, we
used DesplayTech binary modulator that displays reve-
nue so important, but it does not permits to the display of
the specters with several levels of grey. For this purpose,
we propose the synoptic diagram of Figure 4. Informa-
tion at the receiver is restricted to (c × c) pixels. Two
polarizers are placed before and after the SLM in order to
operate in phase. A mask is used to isolate only the addi-
tive share of the SLM. The modulator is used to display
the hologram that includes (c × c) pixels representing the
compressed spectrum of the image obtained digitally
(Figures 10(a) and (b)).
6. Results of Optical Implementation
To validate the principle of proposed compression/de-
compression method of a real Fourier plane, we have
considered several images as shown in Figure 11.
In column (a), we see the different symbols and an
image used to validate our optical implementation of
compression/decompression stages. Four images are con-
sidered including three binary letters images, namely “
 ”,
“S”, and “Ψ” and, a gray level image, namely the famous
“Lena”. Each input image extends over 128 × 128 pixels.
In column (b), we have replicated each input image four
times. Indeed, each image is mirrored horizontally, ver-
tically and obliquely. In column (c), the calculated Opti-
cal Fourier Transform (OFT) of the different replicas is
shown. We have optically implemented the IFT of these
various spectra. These are used as references. The results
are given in column (d). In column (e), we see the dif-
ferent compressed spectra with our proposed method.
Finally, in column (f) the optically reconstructed versions
of decompressed images are shown. The results, shown
in column “f”, validate the principle of our implementa-
tion method of the optical image compression/decom-
pression using a real Fourier plane.
Figure 12 shows the optical implementation of the
compression/decompression of proposed method. The in-
put plane of this setup consists of a binary modulator
DisplayTech to display the binary compressed spectra as
demonstrated in Figure 12(e), (a) original image; (b)
replicated image; (c) replicated image spectra; (d) optical
output plane of the replicated image spectra; (e) com-
pressed spectra; (f) decompressed image. Finally, we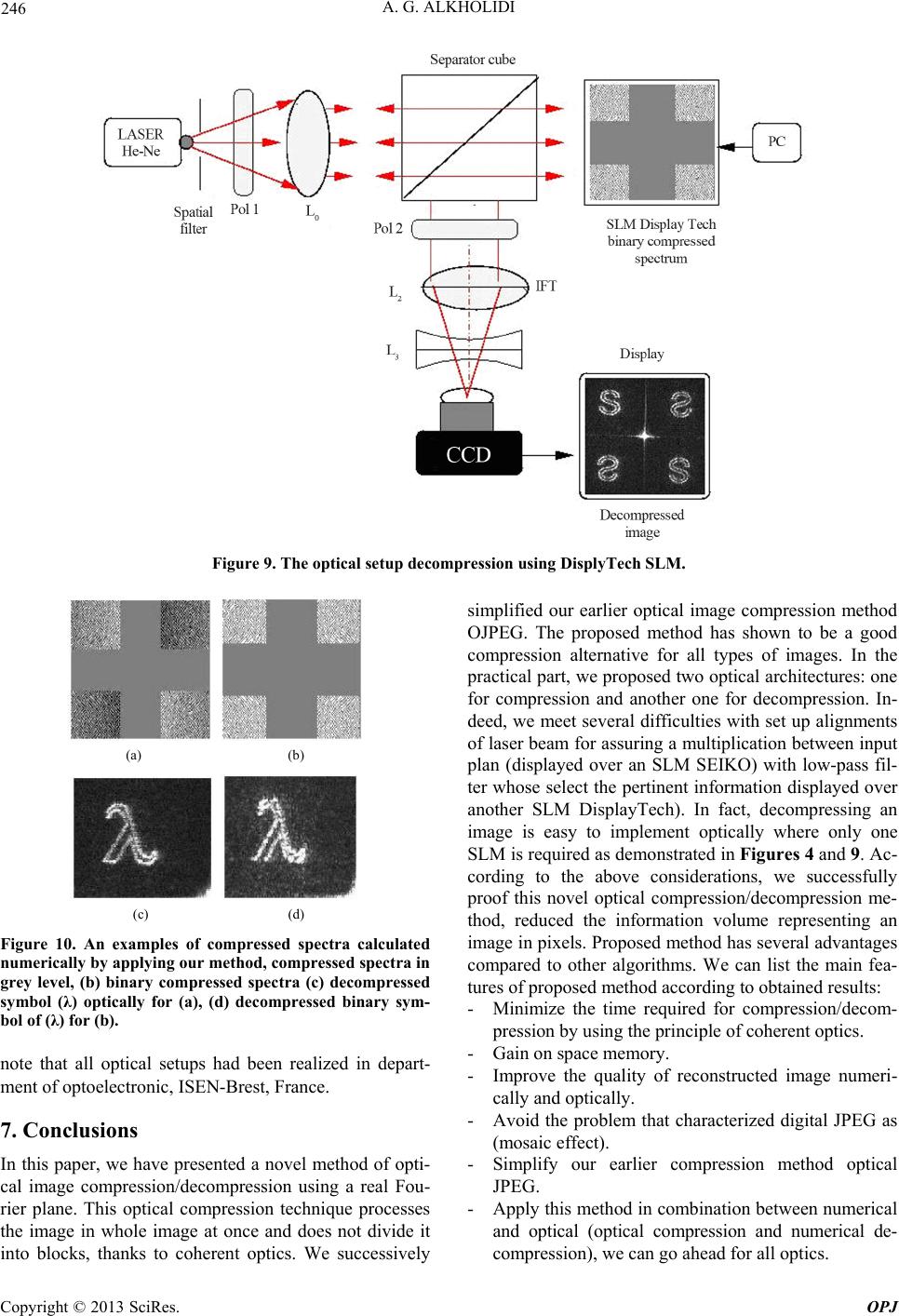

A. G. ALKHOLIDI
246
Figure 9. The optical setup decompression using DisplyTech SLM.
(a) (b)
(c) (d)
Figure 10. An examples of compressed spectra calculated
numerically by applying our method, compressed spectra in
grey level, (b) binary compressed spectra (c) decompressed
symbol (λ) optically for (a), (d) decompressed binary sym-
bol of (λ) for (b).
note that all optical setups had been realized in depart-
ment of optoelectronic, ISEN-Brest, France.
7. Conclusions
In this paper, we have presented a novel method of opti-
cal image compression/decompression using a real Fou-
rier plane. This optical compression technique processes
the image in whole image at once and does not divide it
into blocks, thanks to coherent optics. We successively
simplified our earlier optical image compression method
OJPEG. The proposed method has shown to be a good
compression alternative for all types of images. In the
practical part, we proposed two optical architectures: one
for compression and another one for decompression. In-
deed, we meet several difficulties with set up alignments
of laser beam for assuring a multiplication between input
plan (displayed over an SLM SEIKO) with low-pass fil-
ter whose select the pertinent information displayed over
another SLM DisplayTech). In fact, decompressing an
image is easy to implement optically where only one
SLM is required as demonstrated in Figures 4 and 9. Ac-
cording to the above considerations, we successfully
proof this novel optical compression/decompression me-
thod, reduced the information volume representing an
image in pixels. Proposed method has several advantages
compared to other algorithms. We can list the main fea-
tures of proposed method according to obtained results:
- Minimize the time required for compression/decom-
pression by using the principle of coherent optics.
- Gain on space memory.
- Improve the quality of reconstructed image numeri-
cally and optically.
- Avoid the problem that characterized digital JPEG as
(mosaic effect).
- Simplify our earlier compression method optical
JPEG.
- Apply this method in combination between numerical
and optical (optical compression and numerical de-
compression), we can go ahead for all optics.

A. G. ALKHOLIDI 247
(a)
(c)
(b)
(d)
(e)
(f)
Figure 11. Results of optical compression/decompressionsetup of the real Fourier plane using SEIKO modulator: (a) original
image I; (b) replicated image I; (c) replicated spectrum of the image; (d) optical output plane; (e) compressed spectra; (f)
decompressed image.

A. G. ALKHOLIDI
248
(a)
(c)
(b)
(d)
(e)
(f)
Figure 12. Validation results of optical compression/decompression implementation using a Display Tech modulator to dis-
play the binary compressed spectra, (a) input image I; (b) replicated image I; (c) replicated image spectra; (d) implementa-
tion of replicated image spectra; (e) compressed spectra; (f) decompressed image.
Finally the numerical and optical results obtained are
generally considered to be more robust as appear in Sec-
tion 6.
8. Acknowledgements
The author wants to thank Prof. Habib Hama (Moncton
University), and Prof. M. Sujr (Sanaa University) for
reading this paper and for their nice comments.
REFERENCES
[1] A. L. Oldenburg, J. J. Reynolds, D. L. Marks and S. A.
Boppart, “Fast-Fourier-Domain Delay Line for in Vivo

A. G. ALKHOLIDI 249
Optical Coherence Tomography with a Polygonal Scan-
ner,” Applied Optics, Vol. 42, No. 22, 2003, pp. 4606-
4611.
[2] A. Alkholidi, A. Alfalou and H. Hamam, “A New Ap-
proach for Optical Colored Image Compression Using the
JPEG Standards,” Signal Processing, Vol. 87, 2007, pp.
569-583.
[3] A. Alkholidi, “Analyse and Implementation of Compres-
sion/Decompression Processors Based on JPEG and JPEG
2000 Standards,” Ph.D. Thesis, Université de Bretagne
Ocedentale (UBO), Brest, 2007.
[4] A. Alkholidi, A. Cottour, A. Al falou, H. Hamam and G.
Keryer, “Real Time Optical 2-D Wavelet Transform
Based of the JPEG2000 Standards,” European Physical
Journal (EPJ), Applied Physics, Vol. 44, 2008, pp. 261-
272.
[5] A. Alfalou, et al., “Assessing the Performance of a Me-
thod of Simultaneous Compression and Encryption of
Multiple Images and Its Resistance against Various At-
tacks,” Optics Express, Vol. 21, No. 7, 2013, pp. 8025-
8043. doi:10.1364/OE.21.008025
[6] A. E. Shortt, T. J. Naughton and B. Javidi, “Compression
of Optically Encrypted Digital Holograms Using Artifi-
cial Neural Networks,” Journal of Display Technology,
Vol. 2, No. 4, 2006, pp. 401-410.
[7] C.-H. Chuang and Y.-L. Chen, “Steganographic Optical
Image Encryption System Based on Reversible Data Hi-
ding and Double Random Phase Encoding,” Optical En-
gineering, Vol. 52, No. 2, 2013, Article ID: 028201.
[8] X. Q. Zhou, et al., “Spatial-Frequency-Compression Scheme
for Diffuse Tomography with Dataset,” Applied Optics,
Vol. 52, No. 9, 2013, pp. 1779-1792.
[9] H. Wang, S. S. Han and M. Kolobov, “Quantum Limits in
Compressed Sensing of Optical Images,” Quantum Elec-
tronics and Laser Science Conference, San Jose, 6 May
2012.
[10] R. C. Gonzalez and R. E. Woods, “Digital Image Com-
pression,” Prentice Hall, 2009.
[11] W. Goodman, “Introduction to Fourier Optics,” MacGraw-
Hill, New York, 1968.
[12] Y. Suzuki, “Spatial Light Modulators for Phase-Only
Modulation,” IEEE, 1999, pp. 1312-1313.
[13] G. Ntogari, et al., “A Numerical Study of Optical Swit-
ches and Modulators Based on Ferroelectronic Liquid
Crystals,” Journal of Optics A: Pure and Applied Optics,
Vol. 7, 2004, pp. 82-87.