Journal of Modern Physics, 2010, 1, 349-356
doi:10.4236/jmp.2010.16049 Published Online December 2010 (http://www.SciRP.org/journal/jmp)
Characterization of Blood Flow in Capillaries by
Numerical Simulation
Tong Wang1, Zhongwen Xing2
1Department of Mathematics, Nanjing University of Aeronautics and Astronautics, Nanjing, China
2Department of Materials Science and Engineering National Laboratory of Solid State Microstructures,
Nanjing University, Nanjing, China
Received August 4, 2010; revised September 10, 2010; accepted September 15, 2010
Abstract
This paper presents a numerical investigation of the axisymmetric, pressure driven motion of single file
erythrocyte (i.e., red blood cell) suspensions flowing in capillaries of diameter 8-11 µm. Our study success-
fully recreates several important in vivo hemodynamic and hemorheological properties of microscopic blood
flow, such as parachute shape of the cells, blunt velocity profile, and the Fahraeus effect, and they have been
shown to have strong dependence on cell deformability, hematocrit and vessel size.
Keywords: Numerical Simulation, Blood Flow Dynamics, Red Blood Cell, Capillary, Rheology
1. Introduction
Investigation of blood flow dynamics and erythrocyte
(i.e., red blood cell) rheology in capillaries is of great
importance not only because they are the major site of
oxygen and nutrient exchange, but also because the
proper microcirculatory function is primarily determined
by the rheological behavior of red blood cells (RBCs) in
these vessels. In capillaries, blood can be viewed as a
suspension of RBCs in plasma due to the high volume
fraction (about 99%) of RBCs in the blood cells. It has
been shown that capillary flow dynamics is significantly
affected by arrangement, orientation and deformability of
RBCs in plasma suspension [1].
Measuring 5-11 µm in diameter, capillaries are the
smallest blood vessels in the human body. The average
size of normal red cells is approximately 7.7 µm in di-
ameter and varies in thickness from ~2.8 µm at the rim to
~1.4 µm at the center. They assume a biconcave-disc-
shape in the absence of flow. At the level of capillaries,
RBCs tend to travel in single file, separated by gaps of
plasma [2]. An important property of the RBC is that the
cell membrane is highly deformable. In capillaries, they
deform and assume an axisymmetric parachute-like
shape (coaxial with the flow axis) in order to reduce the
flow resistance, leaving a cell-free plasma layer between
the RBC and the vessel wall [3,4]. It is also observed that
under pathological conditions, such as malaria, infected
RBCs become more rigid than healthy ones. The de-
formability of RBC is a critical determinant of blood
flow in capillaries, and is the combined result of several
mechanical and physiological properties.
Another major determinant of blood property is the
hematocrit (Hct), which is defined as the volume fraction
of the RBCs to the total blood volume and varies from
29-41% for a one-year-old child to 38-46% for adults.
When the term hematocrit is applied to microvessels, it
can include two different estimates of red cell distribu-
tion, the tube hematocrit (HT), defined as the instantane-
ous volume fraction of RBCs in a specified volume of
capillary and the discharge hematocrit (HD), defined as
the proportion of RBCs flowing out the capillary. The
Fahraeus effect [5] is characterized as the reduction of
HT below HD which occurs in microvessels. The effect is
due to the fact that the mean velocity of the RBCs (Uc) is
higher than the mean bulk flow velocity (Um) [6]. The
ratio of these velocities decreases with increasing hema-
tocrit.
Indeed, the blood flow dynamics in capillaries has not
been extensively explored. Within this context, the ap-
plication of mathematical and numerical models has been
shown to provide useful information on dynamic charac-
teristics of blood flow under complex flow conditions
that is difficult to obtain through in vivo or in vitro ex-
periments. The nature of blood flow in capillaries re-
quires a different model, if not more complex, from those

T. WANG ET AL. 350
for blood flow in big and medium sized vessels in which
the fluid is well approximated by a continuum medium.
At the same time, in order to obtain a better understand-
ing of blood flow in capillaries, two other aspects must
be considered in the numerical simulation as well. One
aspect is that multiple cells must be considered to ac-
count for cell-cell hydrodynamic interaction because
under high Hct conditions, the interaction between RBCs
becomes significant. The other is that deformation of the
cell must also be considered in the model, as it is a major
determinant of many physiologically significant phe-
nomena, such as formation of the cell-free layer, and the
Fahraeus effect. Tsubota et al. [7] carried out a numerical
study on effects of Hct on blood flow properties in a
two-dimensional channel using particle method and sug-
gested that shape of the red cells and the flow in capil-
laries is significantly affected by the hematocrit level.
However, the study did not include the effect of the cell
deformability and vessel size. Pozrikidis [8] investigated
the axisymmetric motion of RBCs in cylindrical capil-
laries using a boundary-integral method. The effect of
capillary radius and cell spacing on the discharge hema-
tocrit and apparent viscosity was studied. Zhang et al. [9]
developed an immersed boundary lattice Boltzmann ap-
proach to investigate the blood flow in microvessels.
However, the deformability of the red cell was only con-
sidered to a limited extent in [8] and [9]. In addition,
there was a lack of quantitative analysis of the RBC and
the flow behaviors in the study of [9].
The objective of this study is to predict the blood flow
properties in capillaries using numerical methods. We
present two-dimensional computational simulations of
blood flow in vessels of diameter 8-11 µm at HT of
10-41%, taking into consideration the particulate nature
of blood and cell deformation. The simulation is based
on the numerical solution of the Navier-Stokes equations,
and the red blood cell membrane is modeled as mem-
brane particles connecting by springs. Also presented in
this paper are parametric simulation studies on the effect
of hematocrit, deformability, and size of the vessels on
the shape change of the cells, plug-flow velocity profile,
cell-free layer thickness, and the Fahraeus effect. A
qualitative/quantitative comparison between the simula-
tion results and experimental data is also presented in
this paper.
2. Numerical Simulations and Discussions
In capillary vessels, blood is considered as a multiphase
fluid because the size of the RBC is comparable to the
size of the vessel. It is anticipated that capillary flow
dynamics should be similar to that of a suspension of
deformable particles. Based on the fact that blood plasma,
the liquid component of blood in which the blood cells
are suspended, is composed of mostly water (90% by
volume), the plasma flow in capillaries is assumed to be
governed by the Navier-Stokes equations for the incom-
pressible, Newtonian fluid
p
t




 



uuu uf (1)
0

u (2)
where u and p are the fluid velocity and pressure any-
where in the flow; ρ is the fluid density; µ is the fluid
viscosity; f accounts for the external body force. Both ρ
and µ are assumed to be constant for the entire fluid.
The deformable shape of the RBCs is modeled by the
elastic spring model described in Appendix A. The
model has been validated and applied to a number of
blood flow studies [10,11]. It has been shown to have the
ability to capture the deformation of the RBCs under
various flow conditions [10,11], which is fundamental to
the successful simulation of the flow behavior. It takes
into consideration the structure of the RBC membrane
skeleton. The membrane of the cell has strong resistance
to changes in area/volume and shear deformation which
is consistent with other people’s findings [12]. It also
shows the ability of recovering to the initial biconcave
shape after the removal of the external flow field [11].
The motion of the deformable cells and fluid domain
are coupled together by the immersed boundary method
[13] described in Appendix B. This method is an innova-
tive approach to deal with the problem of modeling fluid
flows interacting with a flexible, elastic boundary. The
applications of immersed boundary method to the simu-
lation of deformable cells can be found in, e.g., [10,11,
14-16].
For the simulation, the RBCs are suspended in blood
plasma which is assumed to be incompressible, Newto-
nian and has a density ρ = 1.00 g/cm3 and a dynamic
viscosity µ = 0.012 g/(cm·s). The viscosity ratio which
describes the viscosity contrast of the fluid inside and
outside the RBC membrane is fixed at 1.0. The fluid
domain is a two dimensional channel of horizontal length
20-25 µm. The width of the channel is varied from 8 µm
to 11 µm. A single file of RBCs coaxial with the flow
axis is placed vertically with uniform center to center
distance, which can be adjusted to correspond varies of
hematocrit.
The parameters in the simulation of the shape change
of the RBCs are set as follows: the membrane mass m =
2.0 × 10-4 g and the membrane viscosity γ = 8.8 × 10-7
Ns/m. The penalty coefficient ks = kb × 104. The spring
constants are set as kl = kb. The bending constant is
closely related to the rigidity of the membrane. A higher

T. WANG ET AL.351
kb value results a less deformable cell. The biconcave
shape obtained for s* = 0.42 resembles the normal
physiological shape of the RBC very well and is used for
the simulations in the current study.
For all computations, the grid resolution for the com-
putational domain is 80 grid points per unit length with
the unit length equal to 10 µm. To obtain a Poiseuille
flow, a constant pressure gradient is prescribed as a body
force. Periodic boundary conditions are imposed at the
left and right boundary of the domain. The evolution of
the periodic file of cells from a specified initial configu-
ration with uniform cell spacing is computed. Simula-
tions from the unstressed biconcave shape (Figure 1(a))
are performed until steadily translating deformed shapes
(e.g., Figure 1(b)) are obtained in the flow.
2.1. RBC Deformation
The deformation of RBCs in plasma flow with varying
hematocrit, cell deformability and vessel diameter is
studied. Simulations are conducted in the channel de-
scribed above. As the flow starts, the RBCs change
quickly from its static biconcave shape to parachute
shape. At the mean time, RBCs move down stream with
an increasing velocity. The change of shape stops when
the hydrodynamic force is balanced by the elastic force
of the cell membrane and the cell velocity become con-
stant. The equilibrium shape strongly depends on the
hematocrit (Figure 2(a) and 2(b)) and the deformability
of the cell membrane (Figure 2(c)). It is also depends on
the width of the flow channel (Figure 2(d)). These re-
sults are in qualitative agreement with experimental [17]
and simulation results [7,8]. The vector fields of the flow
velocity are also shown in Figure 2.
We also wish to quantitatively study how the shape of
the red cells is affected by the factors such as hematocrit,
vessel diameter and the deformability of the cell. To this
purpose, equilibrium length L of the cell and the defor-
mation index DI, defined as DI = w/L, where L and w are
shown in Figure 1(b), are investigated in this paper.
Firstly, equilibrium length L is plotted versus hematocrit
for the channel width D = 8, 9, 10, and 11 µm in Figure
3(a). The length L increases almost linearly with the in-
crease of HT for all the vessels in the range of HT =
10-41%. Figure 3(b) shows deformation index DI de-
creases almost linearly with the increase of HT over the
same range for these vessels. In Figure 4, the cell-free
layer thickness H is shown to decrease with the increase
of HT for the 11 µm-capillary and the results are in good
agreement with the experimental results provided by
Albrecht et al. [18]. We also wish to investigate the ef-
fect of the deformability of the membrane on the size of
(a) (b)
Figure 1. RBC shape obtained using the spring model: (a)
Equilibrium shape of RBC under no-flow condition; (b)
Parachute shape of RBC in Poiseuille flow.
red cell in the blood flow. Figure 5(a) and Figure 5(b)
show the dependence of the cell length L and deforma-
tion index DI on membrane bending constant kb, respec-
tively. The length L (respectively deformation index DI)
increases (respectively decreases) with the increase of kb
and the rate of change is less severe for rigid cells.
2.2. Blunt Velocity Profile
Comparing to the parabolic profile of the Poiseuille flow
for the pure plasma, the velocity profile is flat topped in
the center region for the blood flow in capillaries con-
taining RBCs under the same pressure gradient. The ef-
fect of hematocrit, deformability of the cell, and vessel
size on the velocity profile has been investigated in this
paper.
The effect of increasing hematocrit on the velocity
profile is show in Figure 6(a) for a 10 µm-capillary. The
profile for HT = 10% appears to be parabolic, but with
significantly reduced centerline velocity. The flow shows
a more and more blunt profile with increasing tube he-
matocrit HT. The maximum velocity at the centerline
decreases rapidly when more RBCs are present. When
the tube hematocrit reaches 41%, the maximum velocity
at the centerline reduces to about 45% of that of the pure
plasma.
As shown in Figure 6(b), we adopted six different
bending constant kb values and compare the mean veloc-
ity in blood flow of RBC suspension of same tube he-
matocrit (HT = 21%). It is observed that the flow profile
is less blunt with the increase of the RBC deformability.
However, the distribution of axial velocity in the capil-
lary seems less sensitive to the change of deformabilty
than the hematocrit of the blood. Since a decrease in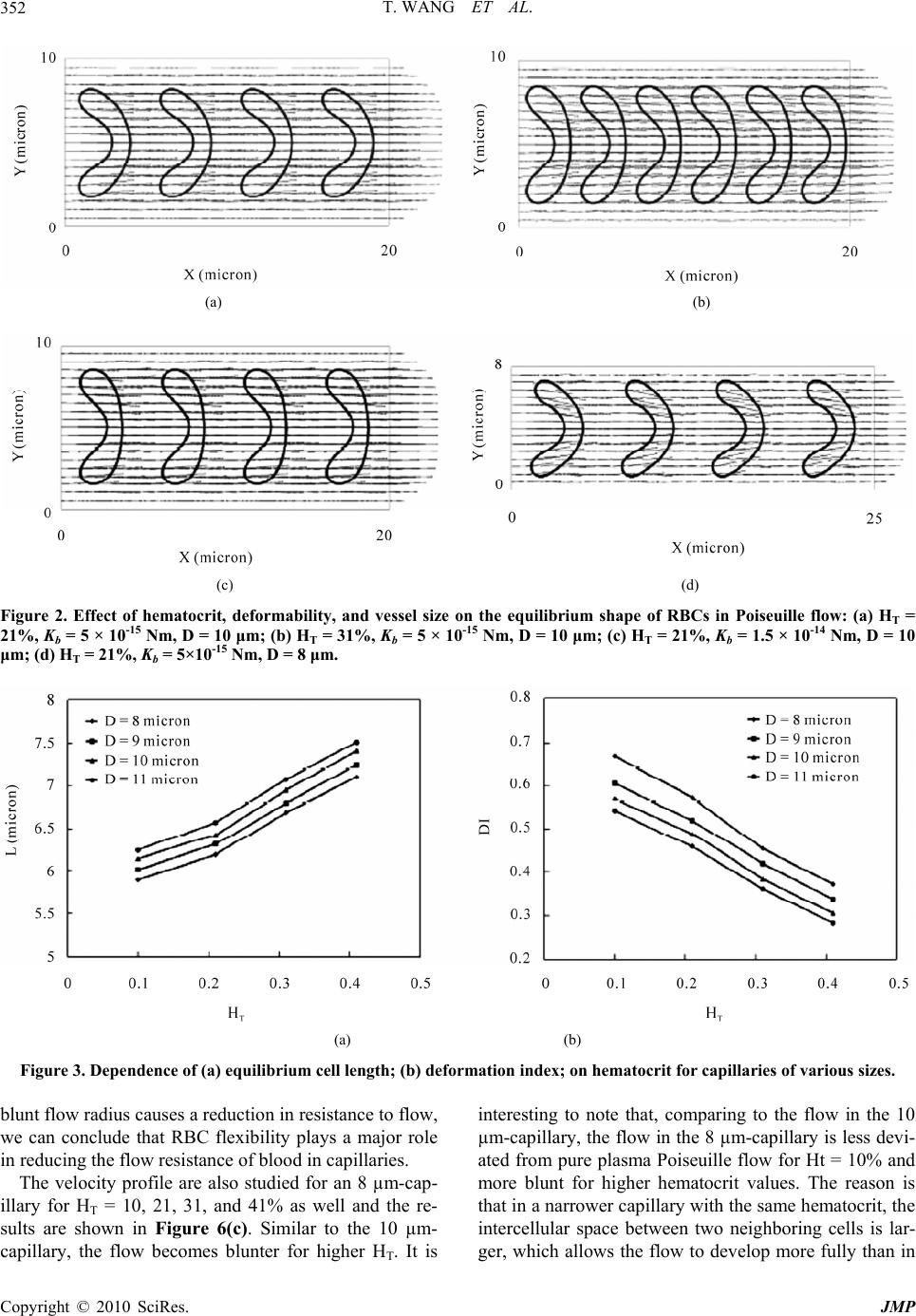

T. WANG ET AL. 352
(a) (b)
(c) (d)
Figure 2. Effect of hematocrit, deformability, and vessel size on the equilibrium shape of RBCs in Poiseuille flow: (a) HT =
21%, Kb = 5 × 10-15 Nm, D = 10 μm; (b) HT = 31%, Kb = 5 × 10-15 Nm, D = 10 μm; (c) HT = 21%, Kb = 1.5 × 10-14 Nm, D = 10
μm; (d) HT = 21%, Kb = 5×10-15 Nm, D = 8 μm.
(a) (b)
Figure 3. Dependence of (a) equilibrium cell length; (b) deformation index; on hematocrit for capillaries of various sizes.
blunt flow radius causes a reduction in resistance to flow,
we can conclude that RBC flexibility plays a major role
in reducing the flow resistance of blood in capillaries.
The velocity profile are also studied for an 8 µm-cap-
illary for HT = 10, 21, 31, and 41% as well and the re-
sults are shown in Figure 6(c). Similar to the 10 µm-
capillary, the flow becomes blunter for higher HT. It is
interesting to note that, comparing to the flow in the 10
µm-capillary, the flow in the 8 µm-capillary is less devi-
ated from pure plasma Poiseuille flow for Ht = 10% and
more blunt for higher hematocrit values. The reason is
that in a narrower capillary with the same hematocrit, the
intercellular space between two neighboring cells is lar-
ger, which allows the flow to develop more fully than in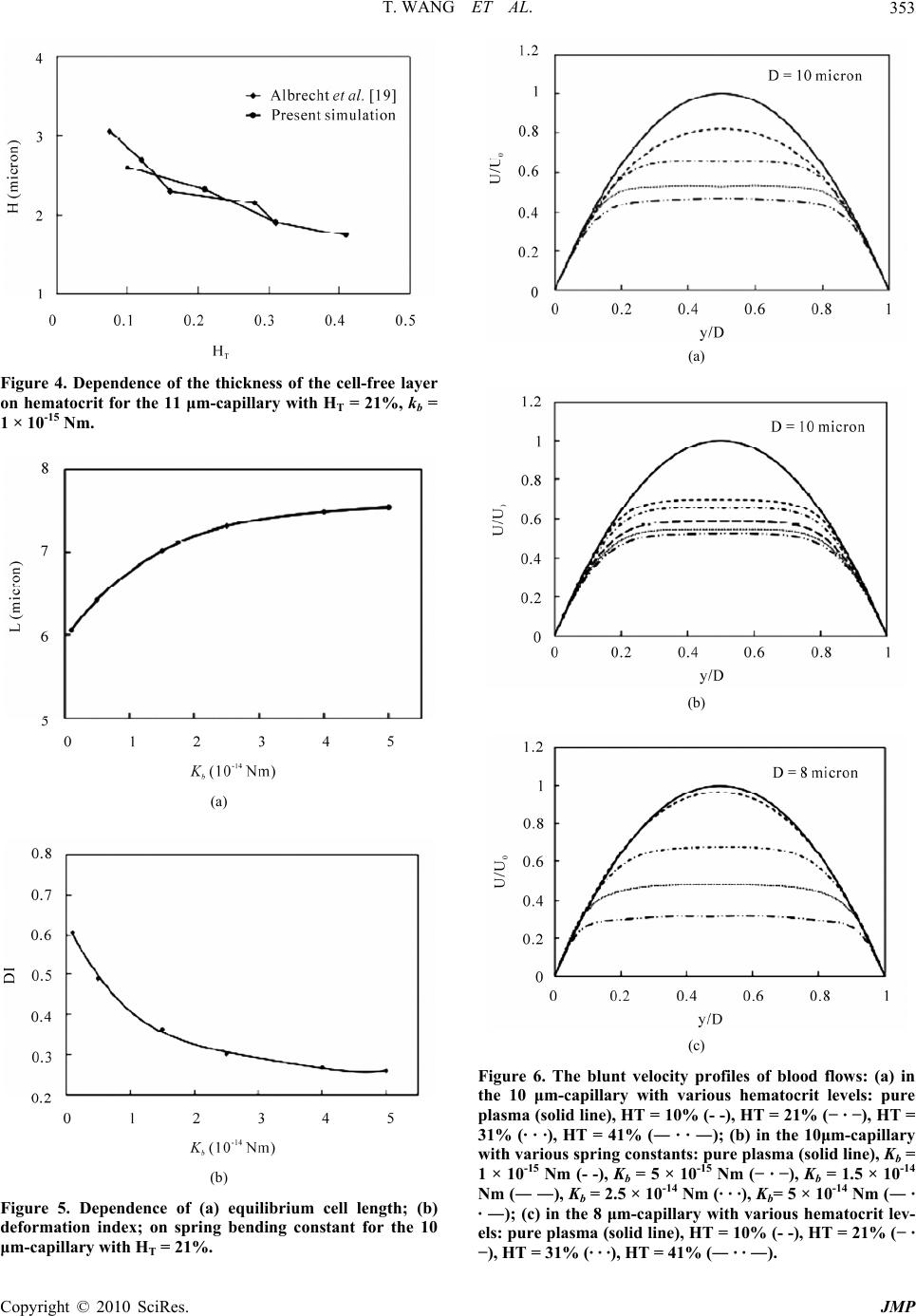

T. WANG ET AL.353
Figure 4. Dependence of the thickness of the cell-free layer
on hematocrit for the 11 μm-capillary with HT = 21%, kb =
1 × 10-15 Nm.
(a)
(b)
Figure 5. Dependence of (a) equilibrium cell length; (b)
deformation index; on spring bending constant for the 10
μm-capillary with HT = 21%.
(a)
(b)
(c)
Figure 6. The blunt velocity profiles of blood flows: (a) in
the 10 μm-capillary with various hematocrit levels: pure
plasma (solid line), HT = 10% (- -), HT = 21% (− · −), HT =
31% (· · ·), HT = 41% (― · · ―); (b) in the 10μm-capillary
with various spring constants: pure plasma (solid line), Kb =
1 × 10-15 Nm (- -), Kb = 5 × 10-15 Nm (− · −), Kb = 1.5 × 10-14
Nm (― ―), Kb = 2.5 × 10-14 Nm (· · ·), Kb= 5 × 10-14 Nm (― ·
· ―); (c) in the 8 μm-capillary with various hematocrit lev-
els: pure plasma (solid line), HT = 10% (- -), HT = 21% (− ·
−), HT = 31% (· · ·), HT = 41% (― · · ―).

T. WANG ET AL. 354
a wider capillary. However, this effect is only significant
when the hematocrit is low. As the hematocrit becomes
higher, the flow is severely blunted by the increasing
number of cells in the vessel.
2.3. The Fahraeus Effect
In capillary vessels, the red cells speed up relative to the
plasma as they squeeze through the capillary. Since they
must travel faster than the plasma, there must be fewer of
them present to maintain the same proportions of cells
and plasma as blood exits the capillary. This is the
so-called Fahraeus effect. The reduction of the tube he-
matocrit HT to the discharge hematocrit HD due to the
Fahraeus effect is related to the mean flow velocity Um
and the cell velocity Uc [6]
m T
D
c
U H
H
U
 (3)
In the laboratory study [18], the feed hematocrit HF
instead of tube hematocrit HT was used as a control pa-
rameter. It has been shown by Yen and Fung [19] that HT
< HF for the capillaries used in the study and therefore,
our numerical results shown in Figure 7 agree well with
the experimental results in [18] and simulation results of
[8] which illustrated that the hematocrit ratio increased
as the tube hematocrit increased.
The hematocrit ratio is also strongly related to the de-
formability of the red cells. Figure 8(a) shows the ratio
increases with the increase of kb rapidly when the cell is
more deformable and the increase become slower as the
cell become more rigid. On the other hand, the hema-
tocrit ratio is found to decrease linearly with the increase
of the deformation index (Figure 8(b)).
Figure 7. Dependence of hematocrit ratio on vessel size for
various hematocrit levels. The spring bending constant Kb =
5 × 10-15 Nm.
(a)
(b)
Figure 8. Dependence of hematocrit ratio on (a) spring
bending constant; (b) deformation index; for the 10 µm-
capillary with HT = 21%.
3. Conclusion
In summary, we have simulated the dynamics of the
blood flow and RBCs in capillary using a numerical ap-
proach. The results show that RBCs in narrow capillaries
change to parachute shape in the flow field. The profile
of the capillary flow was markedly blunt in comparison
to the parabolic one which characterizes the pure plasma
flow. The hematocrit ratio reduces from the value of
unity (the Fahraeus effect) in these capillaries. Our study
reveals that the RBC shape, bluntness of the flow profile,
and the reduction of the hematocrit ratio are strongly
depend on the tube hematocrit, deformation of the cell,
and the size of the vessel. These findings are consistent
qualitatively or quantitatively with other people’s ex-
perimental and numerical results. We also find that the
distribution of axial velocity in the capillary is more sen-

T. WANG ET AL. 355
sitive to the change of hematocrit than the deformability
of the cells. The results indicate that the pressure differ-
ence in the blood flow has to increase in the capillary
vessels in order to sustain the same flux rate of the red
blood cells when the hematocrit or the rigidity of the cell
increases. The study yields useful insights into under-
standing the dynamic characteristics of blood flow in
capillaries. The potential applications of this study in-
clude the analysis of some pathological conditions, such
as sickle cell disease (SCD), in which the RBCs become
hard, pointed and sticky and shaped like crescents or
sickles. This model could also be used to predict micro-
scopic hemodynamic and hemorheological behaviors in
more complex microcirculation situations, such as curved
and stenotic microvessels, branches and post-capillary
expansions.
4. Acknowledgements
This work was supported by the National Natural Sci-
ence Foundation of China (11074109), National Science
Foundation of Jiangsu Province in China (SBK2009
20627), and National Key Projects for Basic Research of
China (2010CB923404).
5. References
[1] C. Pozrikidis, “Modeling and Simulation of Capsules and
Biological Cells,” Chapman and Hall, London, 2003.
[2] T. W. Secomb, R. Skalak, N. Özkaya and J. F. Gross,
“Flow of Axisymmetric Red Blood Cells in Narrow Cap-
illaries,” Journal of Fluid Mechanics, Vol. 163, February
1986, pp. 405-423.
[3] N. Maeda, “Erythrocyte Rheology in Microcirculation,”
The Japanese Journal of Physiology, Vol. 46, 1996, pp.
1-14.
[4] H. Vink and B. R. Duling, “Identification of Distinct
Luminal Domains for Macromolecules, Erythrocytes, and
Leukocytes within Mammalian Capillaries,” Circulation
Research, Vol. 79, September 1996, pp. 581-598.
[5] R. Fahraeus, “The Suspension Stability of the Blood,”
Physiological Reviews, Vol. 9, April 1929, pp. 241-274.
[6] S. P. Sutera, V. Seshadri, P. A. Croce and R. M. Ho-
chmuth, “Capillary Blood Flow: II. Deformable Model
Cells in Tube Flow,” Microvascular Research, Vol. 2,
October 1970, pp. 420-433.
[7] K. Tsubota, S. Wada and T. Yamaguchi, “Simulation
Study on Effects of Hematocrit on Blood Flow Properties
Using Particle Method,” Journal of Biomechanical Sci-
ence and Engineering, Vol.1, 2006, pp.159-170.
[8] C. Pozrikidis, “Axisymmetric Motion of a File of Red
Blood Cells through Capillaries,” Physics of Fluids, Vol.
17, March 2005, pp. 1-14.
[9] J. Zhang, P. Johnson and A. Popel, “An Immersed
Boundary Lattice Boltzmann Approach to Simulate De-
formable Liquid Capsules and its Application to Micro-
scopic Blood Flows,” Physical Biology, Vol. 4, Decem-
ber 2007, pp. 285-295.
[10] T. Wang, T.-W. Pan, Z.W. Xing and R. Glowinski, “Nu-
merical Simulation of Rheology of Red Blood Cell
Rouleaux in Microchannels,” Physical Review E, Vol. 79,
April 200, pp. 1-11.
[11] T.-W. Pan and T. Wang, “Dynamical Simulation of Red
Blood Cell Rheology in Microvessels,” International
Journal of Numerical Analysis & Modeling, Vol. 6, 2009,
pp. 455-473.
[12] J. C. Hansen, R. Skalak, S. Chien and A. Hoger, “Influ-
ence of Network Topology on the Elasticity of the Red
Blood Cell Membrane Skeleton,” Biophysical Journal,
Vol. 72, May 1997, pp. 2369-2381.
[13] C. S. Peskin, “Numerical Analysis of Blood Flow in the
Heart,” Journal of Computational Physics, Vol. 25, No-
vember 1977, pp. 220-252.
[14] P. Bagchi, “Mesoscale Simulation of Blood Flow in
Small Vessels”, Biophysical Journal, vol. 92, March
2007, pp. 1858-1877.
[15] C. Eggleton and A. Popel, “Large Deformation of Red
Blood Cell Ghosts in a Simple Shear Flow,” Physics of
Fluids, Vol. 10, August 1998, pp. 1834-1845.
[16] Y. Liu and W. K. Liu, “Rheology of Red Blood Cell Ag-
gregation by Computer Simulation,” Journal of Compu-
tational Physics, Vol. 220, December 2006, pp. 139-154.
[17] Y. Suzuki, N. Tateishi, M. Soutani and N. Maeda,
“Deformation of Erythrocytes in Microvessels and Glass
Capillaries: Effects of Erythrocyte Deformability,” Mic-
rocirculation, Vol. 3, March 1996, pp. 49-57.
[18] K. H. Albrecht, P. Gaehtgens, A. Pries and M. Heuser,
“The Fahraeus Effect in Narrow Capillaries (i.d. 3.3 to
11.0 μm),” Microvascular Research, Vol. 18, September
1979, pp. 33-47.
[19] R. T. Yen and Y. C. Fung, “Inversion of Fahraeus Effect
and Effect of Mainstream Flow on Capillary Hematocrit,”
Journal of Applied Physiology, Vol. 42, April 1977, pp.
578-586.
[20] S. Wada and R. Kobayashi, “Numerical Simulation of
Various Shape Changes of a Swollen Red Blood Cell by
Decrease of Its Volume,” Transactions of the Japan So-
ciety Mechanical Engineering (Series A), Vol. 69, Janu-
ary 2003, pp. 14-21.

T. WANG ET AL. 356
Appendices
Appendix A. RBC Model
In two-dimensional simulations, the biconcave shape of
the RBC is approximated by the characteristic cross sec-
tion in the plane that is parallel to the flow direction if
the cell were in shear flow. This paper adopts the elastic
spring model that has been proposed by Wada and Ko-
bayashi [20] and used by Tsubota et al. [7] and Wang et al.
[10] to obtain the shape of RBC in the absence of exter-
nal force. Based on this model, the RBC membrane is
approximated by a group of membrane particles con-
necting with the neighboring membrane particles by
springs (Figure A1). The total elastic energy of the RBC
membrane is defined as E = El + Eb + Γs. In particular, El
is the energy for stretch/compression which is induced
by the change of the length l of the spring with respected
to its reference length l0
2
0
10
2
N
li
l
i
kll
El

 



(A1)
and Eb is the energy for bending due to the change in
angle θ between two neighboring springs

2
1
tan 2
2
N
b
b
i
k
E




i
(A2)
The shape change is stimulated by reducing the total
area of the circle s0 through a penalty function
2
2
se
s
e
kss
s


 


(A3)
In Equations (A1) and (A2), N is the total number of
the spring elements; kl and kb are spring constants for
changes in length and bending angle, respectively. In
Equation (A3), s and se are the time dependent area and
the equilibrium area of the RBC, respectively. Based on
the principle of virtual work, the elastic spring force act-
ing on the membrane particle i is
i
i
E
 Fr (A4)
with ri being the position of the i-th membrane particle.
Initially, the RBC is assumed to be a circle which is
discretized into a group of membrane particles so that
springs are formed by connecting the neighboring parti-
cles. When the area is reduced, each RBC membrane
particle moves according to the following equation of
motion
ii
m
Figure A1. The elastic spring model of the RBC membrane.
Here, (˙) denotes the time derivative; m and γ repre-
sent the mass and the viscosity of the membrane particle.
The position ri of the i-th membrane particle is solved by
a discrete analogue of Equation (A5) via a second-order
finite difference method. The total elastic energy stored
in the membrane decreases as the time elapse. The final
shape of the RBC for a given area ratio s* = se/s0 is ob-
tained as the total elastic energy is minimized.
Appendix B. Immersed Boundary Method
The boundary of the deformable structure is discretized
spatially into a set of boundary nodes. The force located
at the immersed boundary node X affects the nearby
fluid mesh nodes x through a 2-D discrete δ-function
Dh(X-x)






for -2
h
Dh 

FxFXX xXx (B1)
where h is the uniform finite element mesh size and



 
112 2hhh
DXxX   Xx x (B2)
with the 1-D discrete δ-functions being

1
1cos for ||2
42
0 for ||2
h
zzh
zhh
zh











(B3)
The movement of the immersed boundary node X is
also affected by the surrounding fluid and therefore is
enforced by summing the velocities at the nearby fluid
mesh nodes x weighted by the same discrete δ-function
 
for -2
h
hD h

2
UXuxX xXx (B4)
After each time step Δt, the position of the immersed
boundary node is updated by

tt tt
t
 XXUX (B5)
Equations (1) and (2) are numerically solved by a fi-
nite element technique combined with the immersed
boundary method described in this section.
i

rrF
  (A5)