 Engineering, 2013, 5, 587-600 http://dx.doi.org/10.4236/eng.2013.57071 Published Online July 2013 (http://www.scirp.org/journal/eng) Electronic Throttle Control System: Modeling, Identification and Model-Based Control Designs Robert N. K. Loh1, Witt Thanom1,2, Jan S. Pyko1,2, Anson Lee1,2 1Center for Robotics and Advanced Automation, Department of Electrical and Computer Engineering, Oakland University, Rochester, USA 2Electrical & Electronic Systems Engineering, Chrysler Group LLC, Auburn Hills, USA Email: tporntha@oakland.edu, loh@oakland.edu Received May 19, 2013; revised June 19, 2013; accepted June 26, 2013 Copyright © 2013 Robert N. K. Loh et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Electronic throttle control (ETC) system has worked its way to become a standard subsystem in most of the current automobiles as it has contributed much to the improvement of fuel economy, emissions, drivability and safety. Precision control of the subsystem, which consists of a dc motor driving a throttle plate, a pre-loaded return spring and a set of gear train to regulate airflow into the engine, seems rather straightforward and yet complex. The difficulties lie in the unknown system parameters, hard nonlinearity of the pre-loaded spring that pulls the throttle plate to its default position, and friction, among others. In this paper, we extend our previous results obtained for the modeling, unknown system parameters identification and control of a commercially available Bosch’s DV-E5 ETC system. Details of modeling and parameters identification based on laboratory experiments, data analysis, and knowledge of the system are provided. The parameters identification results were verified and validated by a real-time PID control implemented with an xPC Target. A nonlinear control design was then proposed utilizing the input-output feedback linearization approach and technique. In view of a recent massive auto recalls due to the controversial uncontrollable engine accelerations, the re- sults of this paper may inspire further research interest on the drive-by-wire technology. Keywords: ETC System; System Identification; Nonlinear Control; Input-Output Feedback Linearization; xPC Target-Based Control System 1. Introduction In the automotive industry, one of the fruitful technolo- gies that have emerged from the increasing regulations in terms of fuel economy, emission control, drivability and safety is the drive-by-wire technology that creates the electronic throttle control (ETC) system [1,2]. The sys- tem comprises of a throttle plate equipped with a pre- loaded spring and is driven by an electronic-controlled dc motor to regulate airflow in the intake manifold. In mod- ern vehicles, the engine control unit computes and maps the throttle plate’s angle to many entries such as accel- erator pedal position, engine speed, cruise control com- mand, and so forth in order to achieve optimal air-fuel mixtures in the combustion chambers, thereby maximiz- ing fuel economy and minimizing emissions. The ETC system, which responses to the prescribed reference from the engine control unit must operate with fast transient responses and precise control to regulate the throttle plate’s angular position [3,4]. In recent years, research in the ETC system and related areas has been very active in both academia and industry [5-20]. The research challenge lies mainly in the un- known system parameters, high nonlinearity characteris- tic of the throttle module caused by friction and a pre-loaded spring. In the area of modeling and identifica- tion, a series of laboratory experiments that yield the parameter values of an ETC model was presented in [5], and the complete model was verified through simulations and real-time implementation. In [6], an ETC model based on the LuGre friction model was developed. Fur- ther modifications including parameter verification based on several experiments were shown in [7]. In [8], the authors characterized the effects of transmission friction and nonlinearity of the return spring by means of com- puter simulations, experiments, and analytical calcula- tions. Another topic of research by the same authors in which an automatic parameter tuning method was adop- ted to enhance the control system robustness was pro- C opyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. 588 posed in [9]. Reference [10] proposed a discrete-time piecewise affine model of the ETC system, and applied the clustering-based procedure to identify the parameters. Yet another approach based on nonlinear optimization and genetic algorithms were applied to estimate the un- known ETC system parameters in [11]. Much research has been conducted in the area of con- trol strategies as well. Controller realizations based on proportional-integral-derivative (PID) algorithm supple- mented with friction feedback/feed-forward can be found in [8,12,13]. In addition, a comparative study of the per- formance and advantages among the three controllers: a PID, Linear Quadratic Regulator (LQR), and LQR-plus- Integral controllers was addressed in [13]. A linear- quadratic-Gaussian (LQG) based control was proposed in [14]. Researches that utilized the sliding mode control (SMC) technique applied to an ETC system can be found in [11,15,16], and neural networks-based SMC in [17]. In [18] the development of an adaptive control scheme that guarantees speed tracking was presented. In the system integration level, the authors of [19] considered the con- trol strategy for a vehicle with ETC and automatic trans- mission. They applied dynamic programming technique to optimize the transmission gear shift and throttle open- ing to maximize fuel economy and power demand from the driver’s accelerator pedal position. In [20], the au- thors proposed a throttle-control algorithm that compen- sates two sources of delays, in the throttle response and in the manifold filling, in order to improve the engine response. This paper enhances our previous research results in [5]. We provide in details the procedure of laboratory experiments for identifying each unknown system pa- rameter. Data and analytical computations are also pro- vided. A nonlinear control strategy based on the input- output feedback linearization approach is then investi- gated. The paper is organized as follows. Section 2 de- scribes the physical components and mathematical mod- eling of the ETC system. Section 3 elaborates in details the identification method of each system parameter. Step-by-step tests, experiments and detailed data analysis are provided to arrive at the set of system parameters. The parameters obtained were verified and validated in Section 4. The proposed design of a model-based non- linear controller for the ETC system is illustrated in Sec- tion 5, followed by the simulation results in Section 6. Finally, Section 7 contains the conclusion. 2. ETC System Modeling A pictorial view of a Bosch DV-E5 ETC system [21], particularly the throttle module, used in many vehicle models is shown in Figure 1. The module consists of: a throttle plate driven by an armature-controlled dc motor with two redundant angular position sensors; Throttle body DC motor Armature input voltage, v a (t) Throttle plateThrottle plate angle, (t) Figure 1. Pictorial view of the Bosch ETC system. throttle plate angle limiters acting as a mechanical stop at 90 when the throttle plate is in the fully open position, and approximately 7.5 in the fully closed position [12]. This small partial opening of the throt- tle plate provides enough air flow to allow the engine to run at its idle speed, allowing a driver to crawl a vehicle, sometimes referred to as limp home, to a safe place in the absence of throttle control full power; two sets of reduction gear trains with a total gear ratio of N = 20.68 obtained by physically counting the numbers of the gear teeth; a return spring which ensures a safe return of the throttle plate to its closed position when no driving torque is generated by the dc motor. A schematic representation of the ETC system of Fig- ure 1 is displayed in Figure 2. The mathematical model for the ETC system can be treated as a single-shaft mechanical system by transfer- ring all the model parameters to the throttle plate shaft (load) through the gear ratio. The parameters and nota- tions used in deriving the mathematical model of this particular ETC system are listed below: a R L: Resistance of the armature circuit, a: Inductance of the armature circuit, b : Back electromotive force (emf) coefficient re- ferred to the motor side, b : Back emf coefficient referred to the load side, m : Motor torque constant referred to the motor side, m : Motor torque constant referred to the load side, m : Motor moment of inertia, : Throttle plate moment of inertia, eq : Equivalent moment of inertial referred to the load side, m B: Motor viscous damping coefficient, B: Throttle plate viscous damping coefficient, eq : Equivalent viscous damping coefficient referred to the load side, B : Return spring stiffness, L T T: Spring pre-loaded torque, f: Frictional torque generated by the movement of the throttle plate, N: Gear ratio 0 Lmm L Nnn , b et: Voltage produced by emf, t L: Angular position of the throttle plate, Copyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. 589 Bm nm θm(t) nL va(t) KS M Jm + nL > nm Return eb t + JL La ia(t) Ra BL θL(t) m t TL(t) Figure 2. Schematic of the ETC system. Lt t : Angular velocity of the throttle plate, m t : Angular position of the motor, m Tt: Angular velocity of the motor, L: Load torque transmitted through the reduction gear trains, a vt it: Armature voltage, a With reference to Figure 2, the armature circuit of the ETC system is described by : Armature current. d d a aaabm it LRitKtv t a t . (1) Substituting mL N and bb KN into (1) yields d d a aaabL it LRitKtv t a t. (2) The torque balance equation is given by L mm mmma Tt tB tKit N . (3) The ETC system load torque in (3) is governed by L Tt sgn LLLLL LPLf TtJt Bt KtTT L (4) where sgn is the signum function defined by 1 if 0, sgn0 if 0, 1 if 0. L L L L (5) Combining (3) and (4) with mL N yields sgn , eqLeqLs L PLfLm a tBtK t TT Kit (6) where 2 eqm L NJ J, , and 2 eqm L BNBB mm 3. System Identification System parameter identification is, in general, one of the most critical and difficult tasks in system modeling, analysis and synthesis. The following approaches are commonly used: 1) application of mathematical system parameters identification algorithms and techniques [22, 23]; 2) estimation based on laboratory experiments; and 3) a combination of 1) and 2). In this section, we present a series of laboratory experiments to identify the pa- rameters of the Bosch ETC system model described in Section 2. The approach is practical and proved to be effective for the ETC system investigated. The details of each experiment are described as follows. 3.1. Stalled Motor Resistance Test In this experiment, the throttle plate was held fixed at its closed position. A slowly varying dc voltage was applied to the motor terminals which, in turn, caused the motor current to increase slowly. The data of the voltage and current were captured. Since the throttle plate was locked, that is, 0 Lt , and with the fact that the armature current changed very slowly, dd 0 a it, thus (2) is re- duced to a simple Ohm’s law aaa Ri tvt . (7) The plot of the armature voltage and armature current a vt a it in (7) is shown in Figure 3. The inverse of the slope of the approximated line yields the armature resistance which reads 1.15 a R . 3.2. Stalled Motor Inductance Test The throttle plate was still held fixed at the closed posi- tion. A step voltage a was applied to the stalled motor terminals. As a result, the back emf voltage V b et was zero because there was no angular velocity. Therefore, the armature circuit in (1) or (2) can be expressed as d d a ata it LRit t a V , (8) where t was the total armature circuit resistance con- sisting of the resistances of the armature circuit, current sensor and all the wiring in the measurement set up. The solution of the first-order differential Equation (8) with a step voltage and the initial condition R a V 00 a i is given by 1e t a at V it R , (9) NK. Equations (2) and (6), therefore, represent the ETC mathematical model referred to the load side. The immediate task now is to identify all the unknown parameters and constants: ,, aa LR ,, eq eq B,, bm K , , L T and T, which are needed to facilitate the designs of the model-based ETC feedback control systems in Sections 5 and 6. where at LR is the electrical time-constant of the dc motor. Figure 4 shows the oscilloscope-captured waveforms of the resulting motor voltage and current. At steady state, after 3 ms, the total resistance was ap- proximately 1.591.051.5 taa RVi . The time t Copyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. 590 00.5 11.5 22.5 33.5 4 0 0.5 1 1.5 2 2.5 3 3.5 Volta ge ( V) Current (A) Measured Approximated Figure 3. Stalled motor voltage versus current. -0.001 0 0.001 0.002 0.003 0.0040.005 -0.2 0 0. 2 0. 4 0. 6 0. 8 1 1. 2 1. 4 1. 6 1. 8 Time (s) Voltage (V) & Current (A) Voltage Current 100% 63% Figure 4. Stalled motor inductance te st. read from Figure 4 when the current reached approxi- mately 63% of its steady-state value was 1 ms; this yields t . Therefore, the motor inductance was obtained as 1.5 mH at LR . 3.3. Back Electromotive Force Test In this test, the throttle plate was manually placed at the fully open position and released. The return spring caused rapid return of the throttle plate to its closed posi- tion. The rapid closing of the throttle plate, in turn, me- chanically drove the dc motor through the reduction gears. As a result, the back emf voltage described by b et bbL tKe t, (10) was induced at the motor terminals. Figure 5 shows the back emf voltage and the throttle plate position captured by the oscilloscope during such self-closing of the throt- tle plate. Using the angular position data from Figure 5, the throttle plate velocity was calculated by d LL tt dt. The resulting angular velocity was plotted together with the angular position and back emf as shown in Figure 6. The back emf signal was filtered (not shown). Using (10), the back emf constant referred to the load side b = 0.4 V·s/rad was computed at time t = 0.2 s where the plate angular velocity was the most steady. Since we used the SI unit, it follows that the motor torque constant referred to the load side was 0.4 NmA mb KK [24]. The back emf constant of the dc motor b can be obtained from 0.0193 Vsrad bb KKN , where N = 20.68 is the gear ratio. It is important to mention that a different experiment, called a sensorless velocity meas- urement method, in which the dc motor was detached from the ETC module was performed in Section 3.5.1, and yielded a value 0.0185 Vsrad b K , which agreed with the value obtained above. The sensorless measure- 00.05 0.10.15 0.2 0.25 0.3 0.35 0 1 2 Time (s) Angular position (r a d) Back emf An gular posit ion 00.05 0.10.15 0.2 0.25 0.3 0.35 -10 0 10 Back emf (V) Figure 5. Plot of back emf versus angular position. 00.05 0.10.15 0.2 0.250.30.35 -12 -10 -8 -6 -4 -2 0 2 4 6 Time (s) Angular position ( r ad) , v elocity ( r ad/s ) , em f ( V) Bac k emf An gular position Angular velocity Figure 6. Plot of back emf, angular position and angular velocity. Copyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. 591 ment method is a more reliable method, because, among other things, the fact that the plate angular velocity was judged to be the “most steady” at in Figure 6 was somewhat arbitrary. The new method will be devel- oped in Section 3.5.1. 0.2 st 3.4. Static Loads Test The purpose of static loads test was to identify the fric- tion torque T, the spring pre-loaded torque L pro- duced by the return spring, and the return spring constant T . When the throttle plate was moving very slowly, that is, , the torque balance equation is given by, from (6) t 0 LL t sgn LsLPLfLma TtKt TTKit . (11) In order to measure the parameters in (11), the dc mo- tor was energized by a slowly increasing armature cur- rent. This caused a slow rotation of the throttle plate. The armature current and throttle plate angular position were captured by the oscilloscope as shown in Figure 7. It can clearly be seen from Figure 7 that a larger cur- rent was needed (approximately 1.7 A) to move the throttle plate towards opening than towards closing (ap- proximately 0.6 A). This was because the torque devel- oped by the motor had to overcome the torques produced by the return spring, sL t , L, and the friction torque, T T. Using the armature current data together with the motor constant 0.4 m obtained from the previous experiment in (11), the load torque equation becomes K sLPL f TtKt TT , (12) where during the plate opening, and during the plate closing. sgn 1 L 1 Lsgn Equation (12) can be visualized by the plot of the load torque against the angular position shown in Figure 8. Three approximate straight lines have been inserted. The 0 2 4 6810 12 1416 0 1 2 3 Time (s) Current (A ) Current Angle 0 2 4 6810 12 1416 0 0. 5 1 1. 5 2 Angular position (rad) 1.7 A 0.6 A 00.1 0.20.3 0.40.5 0.6 0.7 0.8 0.91 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 Load tor q ue (Nm) Angular position ( r ad) (0.112,0.096) (0.396,0.096)(0.680,0.096) (0.240,1.571)(0.524,1.571) (0.808,1.571) Figure 8. Throttle plate position versus load torque. iddle straight line representing the spring load torque, m LPL tT , lies exactly in the middle between the es. The right straight line represents the torque during the movement towards opening which is the spring load torque plus friction torque, other two lin LPLf tT T . The left straight line re plate closing which is the spring load torque minus friction torque, presents the torque during the LPLf tT T . The following parameters tly can be read direcfrom Fi ng pre-loaded torque is the minimum torque gure 8: The spri value on the middle line which reads 0.396 Nm PL T ; of the middle line yields the The inverse of the slope spring constant, 0.5240.3961.571 0.096 0.087Nmrad; sL KT Finally, the friction torque is easily obtained as: 0.6800.3960.284Nm f T (during the move- 0.5240.2400.284NT ment towards opening), or m f ment towards closing). (during the move- 3.5. Viscous Frictional Coefficient Test of the The equivalent viscous frictional coefficient eq B ETC unit referred to the load side is given by 2 eqmL BNBB (see (6)), where N = 20.68 is the gear ratio. Since B fication comes mostly from the lubricated and sealed throttle shaft joint, it is small and negligible, therefore 2 eq m BNB. Thus we only have to deal with the identim B. Note that the throttle plate movement is limited t90, but the viscous frictional coefficient is associated h the angular velocity and thus requires the dc motor to run freely. The need to run the motor freely can be accomplished by removing the dc motor from the ETC unit. Consider the torque balance of o wit Figure 7. Static loads test. Copyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. Copyright © 2013 SciRes. ENG 592 3.5.1. Sensorless Velocity Measurement Method equation of the detached dc motor The optical sensor was disconnected and the motor was mechanically driven by another dc motor with an arbi- trary velocity , the resulting induced back emf voltage b et shown in Figure 10(a) was recorded. mmmmfm m tB t T Tt , (13) where m T y represents static frictional torque of the mo- tor. At anconstant speed, 0 mt , therefore the fric- tional torque caused by visccient m B is given by ous coeffiTwo data processing runs were performed on the re- corded emf data. The first was filtered to get an average value (see Table 1); the second was Fast Fourier transformed (FFT) using MATLAB to obtain the associ- ated frequency f (see Table 1). The FFT result is dis- played in Figure 10(b). Since there were 8 ripples per revolution on the signals, the back emf constant can be calculated from ˆb e mmm TtBtT . fm (14) It is seen from (14) that if the instantaneous values of t and mt can be captured, the viscous coeffi- m B anic frictional torque m T cient d stat m T can be de- termin Since it ed. was desired to obtain the velocity measure- m ripples per re ˆˆ 4 28 b be Kff b e . (15) ent but the detached dc motor was not equipped with any velocity sensor, a 16 pulse-per-revolution optical sensor was attached to the motor shaft, and the detached dc motor was energized to run smoothly. The optical sensor signal, motor voltage and current were recorded by the oscilloscope as shown in Figure 9. Here, observe that the motor produced 8 The procedures above were repeated with different ar- bitrary constant velocities and the corresponding and b ˆb e were calculated. Figure 11 shows the result of the FFT, and the calculated data of each test is shown in Ta- ble 1. volution on the voltage and current waveforms caused by the non-uniformity of the magnetic field in the dc motor. This information is useful and can be used to cal- culate the motor angular velocity from a frequency measurement method proposed below, rather than using the optical sensor method conducted above. This is be- cause the dc motor was small and attaching the optical sensor to the motor shaft was not practically convenient to perform the measurements. The proposed frequency measurement approach may be called a sensorless veloc- ity measurement method and is detailed below. The overall average b calculated from Table 1 was 0.0185 V·s/rad which is very close to the result of b = 0.0193 V·s/rad obtained in Section 3.3 when the dc mo- tor was not removed from the ETC unit. The method of sensorless velocity measurement developed here was judged to be more reliable than the method of Section 3.3, and can be applied to the next parameters identification described in the sequel. 3.5.2. Identification of Viscous Friction Coefficient A series of step input voltages: 2, 4, 6, 8, 10 and 12 V, 0.10.11 0.120.13 0.14 0.150.16 0.170.18 -2 0 2 4 6 Optical sensor 0.10.11 0.120.13 0.14 0.150.16 0.170.18 2.95 2.955 2.96 2.965 Voltage (V) 0.10.11 0.120.13 0.14 0.150.16 0.170.18 0.3 0.4 0.5 0.6 0.7 Time (s) Current (A) 16 puls es/ revol ut i on of opti c al s ensor 8 pulses/revoluti on of motor c urrent ri pple Figure 9. Optical sensor, motor voltage and current signals.  R. N. K. LOH ET AL. 593 00.02 0.04 0.06 0.080.1 0 1 2 3 4 5 6 Time (s) Back emf (V) 0100 200300400 0 0.05 0.1 0.15 0.2 0.25 0.3 Frequ ency ( H z) Amplitude (a) (b) Figure 10. (a) Back emf voltage, and (b) its associated frequency. 0100 200 300 400 500 0 0.05 0.1 0.15 0.2 0.25 Frequency (Hz) Test #1 0100 200 300 400 500 0 0.05 0.1 0.15 0.2 0.25 Frequency (Hz) Test #2 0100 200 300 400 500 0 0.1 0.2 0.3 0.4 0.5 0.6 Frequency (Hz) Test #3 0100 200 300 400 500 0 0.1 0.2 0.3 0.4 0.5 0.6 Frequency (Hz) Test #4 Figure 11. Fast Fourier transform of different motor veloc Table 1. Result of sensorless verification test. Test # Frequency f i- ties. Average back emf ˆb e (V) (Hz) ˆ 4 bb ef (V·s/rad) 1 0.8753 61.0426 0.01827 2 1.9009 129.41 0.018703 3 3.7113 255.77 0.018475 4 4.6501 321.69 0.018405 Avge 1 era2.7844 91.97820.0185 ere applied to the armature circuit of the detached dc w motor. The voltages and currents were recorded. Figure 12 illustrates the oscilloscope-captured waveforms of the voltage and the current with the 2 V step input voltage. The responses of the other input voltages were similar but different in amplitudes and therefore were not shown here. For each of the step input voltages, the steady-state 00.5 11.5 -2 0 2 4 Time (s) Arm atur e volt ag)e (V 1. 5 00.5 11.5 -0.5 0 0. 5 1 Time (s) Armature current (A) Figure 12. Armature voltage and current responses. portere rocessed by FFT to obtain their associated frequencies f ions of the current data between 0.3 to 0.9 s w p and the angular velocities were calculated by 28 mf . The same portion of the current data, after averaging, were also used to calculate mma Ki the motor torque from T , where 0.0185 mb KK. Ta- ble 2 reports all data obtained from the experiments and calculations ab The angular velocity and the motor torque data from Table 2 were plott ove. ed and the MATLAB polyfit com- mand was used to perform the best fit of the data. The result is shown in Figure 13 which is also mathemati- cally represented by (14). At 0 m , the approximate static frictional torque of the dc motor read from Figure 13 was 3 6.9 10Tfm 5 2.05 10 Nm. Tpe of the fitted line was the approximate viscous coefficient of the dc motor: m B he slo Nm-s/rad. The viscous friction torque generated by the throttle shaft was small and therefore ig- tioned earlier in this section. The total viscous friction coefficient referred to the load side was therefore nored as men Copyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. 594 Table 2. Result of viscous friction coefficient test. Step Angular input ltage FFT Frequency velocity vo f (V) (Hz) m (rad/s) Average Mo measured to torque cu r rrent a i (A) m T (N·m) 2 95.2 74.80 0.405 0.0075 4 211.2 165.90 0.576 6 334.6 262.76 0.688 0.0127 8 457.9 359.61 0.813 0.0150 10 580.0 455.51 0.903 0.0167 12 704.5 553.33 0.934 0.0172 0.0106 00.02 0.040.06 0.080.10.12 0.140.16 0.18 0.2 -6 -4 -2 0 emf (V ) 00.02 0.040.06 0.080.10.12 0.140.16 0.18 0.2 -10 -5 0 Velocity (rad/s) 00.02 0.040.06 0.080.10.12 0.140.16 0.18 0.2 -100 0 100 Acceleration (rad/s 2 ) 00.02 0.040.06 0.080.10.12 0.140.16 0.18 0.2 -0.4 -0.2 0 Torque (Nm) Ti me ( s) Figure 13. Plot of torques versus angular velocities based on data from Table 2. 225 20.682.05 10 0.0088 Nmsrad. eq m BNB 3.6. Moment of Inertia Test back into the ETC unit ally released from the The back emf data In this test, the dc motor was put and the throttle plate was manu fully open position similar to the test in Section 3.3. Since the armature current was zero, the torque balance equation can be described by toteq LeqLsLPLf Tt JtBtKtTT .(16) b et during t vel and the angular po were captured he rapid self closing o throttle plate. The angular sition f the Lt tion ocity and angular accelera- were calculated from bb tetK , and () dd LL tt , respectively. The total torque tot Tt can be calculated from the right higure e measured and calculated values function of time. and side of (16) 14 shows thes as a . F Finally, the moment of inertia can be calculated from (16), eq totL Ttt . The calculated average mo- m 2 ent of inertia at the time interval of 0.04 to 0.08 s was eq J3 2.110 kgm . T identified all the unkn is to use the mathe- 6) to verify the pa- his value was the total moment of inertia of the whole ETC unit. At this point, we have own ETC system parameters and constants. The results are summarized in Table 3. 4. Parameters Verification The main objective of this section matical model described by (2) and ( rameters identified in Table 3. Two methods were em- ployed: SIMULINK simulation, and actual real-time control implementation of the ETC system using an xPC TargetBox. The xPC TargetBox is a real-time rapid pro- totyping device, which is widely used in both industries 0100 200300 400 500600 0. 005 0. 01 0. 015 0.02 An gular velocit y (rad/ s ) Torque ( Nm) Measured A pproxim ated m T Figure 14. Filtered back emf, velocity, acceleration and tor- que versus time. P lues Table 3. Results of ETC parameter identification. arameters and constants Symbols Identified va Armature resistance R a1.15 Armature measurement circuit resistance t R 1.5 Armature inductance mH a L 1.5 Back em f constant (load side) Vsrad b K 0. M 383 otor torque constant (load side) NmA m K 0.383 Spring constant Nmrad s K 0.087 Spring prque Equivalent viscousping e-loaded tor Nm PL T 0.396 Friction torque Nm f T 0.284 dam Nmsrad eq B 0. Equivalent moment of inertia 0.0021 0088 2 kg m eq J Copyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. Copyright © 2013 SciRes. ENG 595 ananalysis and synhesis, see for exam ULINK diagrm is as n 1 h d academia for control t ple [25,26]. The SIM Figure 15, while the act a show ental se x x. (19) where 21 , txt represent the angular position and the angular velocity of the throttle plate, respectively, 3 t is the armature current of the dc motor; u(t) is the armature voltage applied to the dc motor. The function 2 S defined by in ual control experimtup is as shown in Figure 16. A PID controller with the gains 9 p K, 6 i K and 0.1 d K was designed to meet the following performance criteria: 1) step response of the throttle plate angular position with no overshoot and steady-state error, and 2) settling time 100ms s t. Figure 17 shows the SIMULINK response of the an- gular position Lt with a reference input 1rt rad, together with the result captured b 2 2 21 1ex Sx , (20) is a smooth approximation of the signum function 2 sgn with a small positive number [30]. Figure 18 illustrates the approximated 2 sgn given by (20) with different . It is remarked that other signum ap- proximations are also possible, for example, the sig- moid-like function 222 xxxS , where is a small positive scalar [31]. However, the approximation function (20) will be used in this study. y the xPC Target ope in real time. It can be seen that the SIMULINK and the real-time control results were practically identical and the performance criteria were satisfied with no over- shoot and 100ms s t. Hence the parameters obtained in Table 3 were validated. These parameters together with the mathematical model described by (2) and (6) can now be used for other control analysis and synthesis for this particular ETC system. 5. Design of Model-Based Nonlinear Control Systems sc k lin- ear con- Applying the input-output feedback linearization me- thodology, we obtain 2, LhLhux fg xx 2 112 233425 , f yLhLLhu kxkxkxkS xk gf xx In this section, we applied the input-output feedbac earization technique [27-29] to design a nonlin troller for the ETC system. For ease of analysis and ref- erence, we define the following constants in the ETC system described by (2) and (6): 32 2 1211236 23 27 3 2 25 242438 d d ff yLhLLh u kk xkkkkxkkkx Sx kkkkS xkkku t g xx (21) 2341, , , , eq f m eq eq sBT KK kkkk JJ 567 8 1 , , , , eq eq ba eq a PL aa JJ KR T kkkk JLLL (17) The resulting model can be expressed in a con- trol-affine single-input single-output (SISO) nonlinear state-space form where 11 1 , ii ii Lh Lh LhLL h ff fgf xx xfxx xx gx are the Lie derivatives for , 1, 2, 3i o Lh h fxx, and 2 dSxt as 2 1122 1 2 0xx d is given by 3 32 6 4 27 5 383 0 kx kx 2 2e x 2 2 2 2 d d1ex Sx kxkS xku xkxkx xgx fx k , (18) t . (22) Equation (21) shows that the output relative degree is Km_bar Kb_bar (t ) (t ) (t ) Ks* (t )+Tpl Ste p i npu t Springs Sign Scope Kp 9 Ki 6 Kd 0.1 1 s 1 s 1 s 1 s Hard Limi t s Tf Beq 1/Jeq 0.4 Rt 0.4 1/La du/dt Battery 12 Ia emf Figure 15. ETC SIMULINK model with PID controller.  R. N. K. LOH ET AL. 596 Throttle Unit xPC TargetBox Figure 16. Pictorial view of computer controlled ETC sys- m with xPC Target. te 00.2 0.40.6 0.811.2 1.41.6 1.8 2 -0.2 0 0.2 0.4 0.6 0.8 1 1.2 Time s Angular p os iti on (rad) Step i nput Simulation xPC Target Figure 17. Comparison between real-time control and simu- lation. -20 -15 -10 -505 10 15 20 -1 -0.5 0 0. 5 1 Angual r vel oci t y (rad/ s) Magni tude Signum = 0.5 = 1.0 = 3.0 Figure 18. Approximated signum function with different.δ three and is equal to the dimension of the system. There- fore, the ETC system in (18) and (19) is fully linearizable with the nonlinear transformation given by . (23) It can be shown that the Jacobian matrix associated 1 2 11223 3425 x x kxkxkxkS xk zTx with (23) has the form 2 2 124 3 2 e 1e 10 01 2x x kkk k 0 0 Tx x, (24) which is nonsingular for all and therefore T(x) is a global diffeomorphism f. Referring to (23), the original nonlinear system in the x-coordinates de- scribed by (18) and (19) is transformed to a linear system in the z-coordinates as (25) 3 x or (18) ,v zB ,y Cz where A, B and C are in controllable canonical forms, and v(t) is the transformed input defined by zA vybD u xx, (26) where b(x) is the nonlinear cancellation factor an is a nonsingular scalar function. From (21) and (2 follows that d D(x) 6), it 2 121126 227 333 k kxkkkkxkkkx kk kkS x (27) 5422 4 2 2 d, d b Sx x kt 38 Dkx.k In order to achieve output tracking, we introduce the tracking error as (28) r etyty t where r t ective is to force is the reference input. The main obj 0et such that r yt as t ty . It fol- lows that 1, rr ez e yyy yy 2 3 , . rr rr z eyy zy y y v r (29) A suitable tracking control law for the transformed r y input v(t) is given by rr vy KeKTxY , (30) where T eeee, Tx is given in (23), T rrrr yyy Y, and the constant feedback gain 13 R is determined such that is Hur- witz, that is, all eigenvalues of lie in the open left- half complex plane. Finally, the linearizing fe control law can be obtained from (26) and is given by cl AABK cl A edback 1 uDbv xx, (31) whe in re v(t) is given by (30), and b(x) and D(x) are given (27) and (28), respectively. Substituting (31) into (18) Copyright © 2013 SciRes. ENG 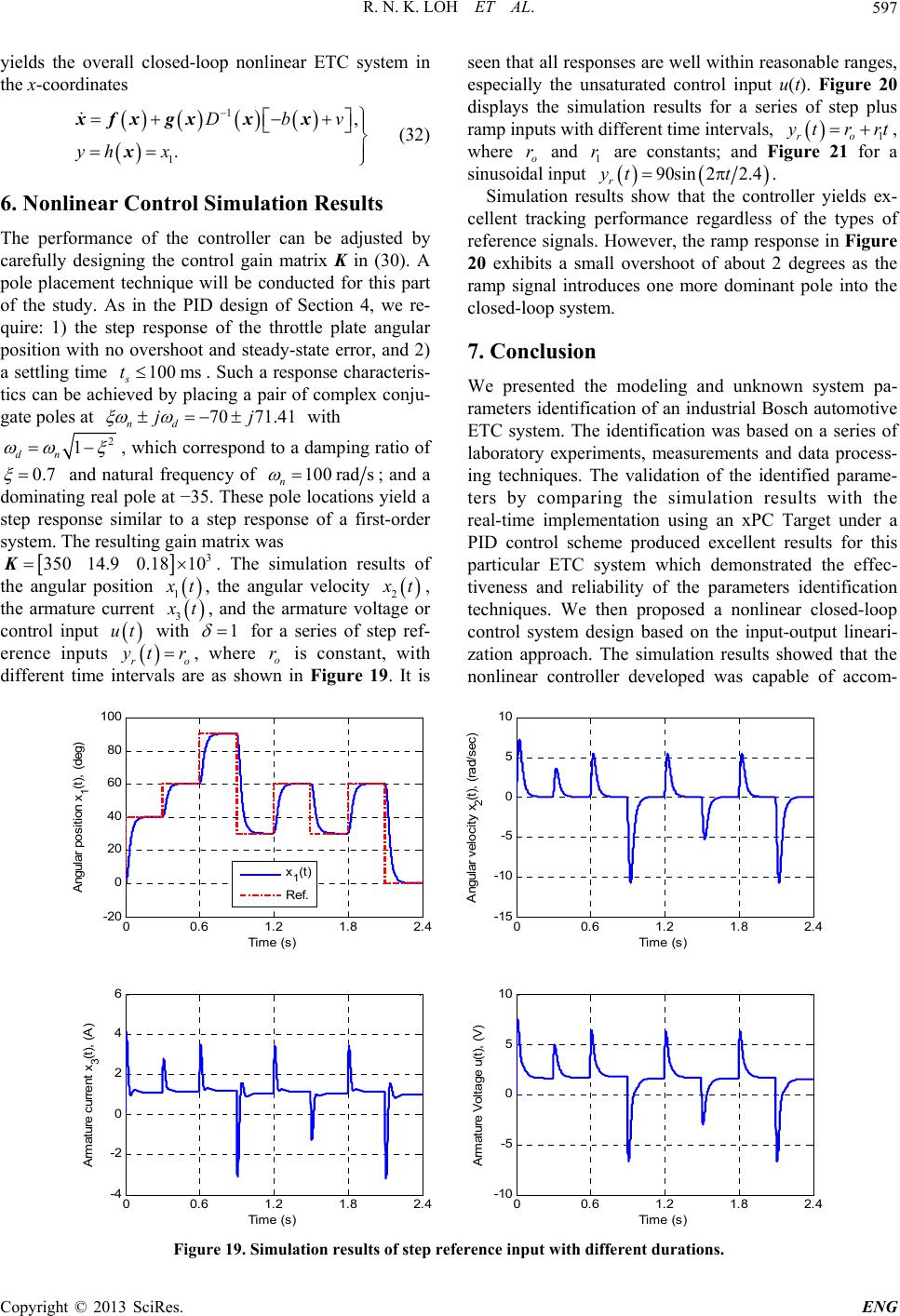 R. N. K. LOH ET AL. 597 yields the overall car ETC s in the x-coordinates losed-loop nonlineystem 1 1, . Dbv yh x x x x xfx gx (32) 6. Nonlinear Control Simulation R The performance of the controller can be adjusted by ca que will be conducted for this part of the study. As in the PID design of Sectio quire: 1) the step response of the throttle pl with no overshoot an and 2) g time S tics can be achju- gate poles at esults refully designing the control gain matrix K in (30). A pole placement techni n 4, we re- ate angular positiond steady-state error, a settlin0much a response characteris-10 s s t. ieved by placing a pair of complex con 707 nd jj1.41 with 2 1 dn , which correspoo a damping ratio of 0.7 nd t and natural frequency of 100 rads n ; and a dominating real pole at −35. These pole locations yield a step response similar to a step response of a first-order system. The resulting gain matrix was 3 350 14.90.1810K. The simulation results of the angular position 1 t, the angular velocity 2 t, the armature current 3 t, and the armature voltage or control input ut with 1 for a series of step ref- erence inputs ro tr, w different time intervals are as sh her seen that all responses are well within reasonable ranges, especially the unsaturated control input u(t). Figure 20 displays the simulation results for a series of step plus ramp inputs with different time intervals, 1ro trrt , where o and are constants; and Figure 21 for a sinusoidal input r1 r 90sin 22.4 r yt t . Simulation results show that the controller yields ex - cellent tracking performance regardless of the types of reference signals. However, the ramp response in Figure 20 exhibits a small overshoot of about 2 degrees as the ramp signal introduces one more dominant pole into the closed-loop system. 7. Conclusion We presented the modeling and unknown system pa- rameters identification of an industrial Bosch automotive ETC system. The identification was based on a series of laboratory experiments, measurements and data process- ing techniques. The validation of the identified parame- ters by comparing the simulation results with the real-time implementation using an xPC Target under a PID control scheme produced excellent results for this particular ETC system which demonstrated the effec- tiveness and reliability of the parameters identification techniques. We then proposed a nonlinear closed-loop control system design based on the input-output lineari- zation approach. The simulation results showed that the nonlinear controller developed was capable of accom- e is constan Figure 19 o r own in t, with . It is 00.6 1.2 1.8 2.4 -20 0 20 40 60 100 80 An gula r po sition x 1 (t) Time (s) , (deg) x 1 (t) Ref. 10 5 0 -5 -10 -1500.6 1.2 Angular velocity x 2 (t), (rad/ sec) Tim e (s)1.8 2.4 610 00.6 1.2 1.8 2.4 -4 -2 0 2 4 A rma tu Time (s) re current x 3 (t), (A) 5 0 -5 -1000.6 1.2 1.8 2.4 Ar m ature Volta ge u(t) , (V ) Tim e (s) ference input w i th diffe re nt dur ations. Figure 19. Simulation results of step re Copyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. 598 00.6 1.2 1.8 2.4 -20 0 20 40 60 80 100 Angular position x 1 (t), (deg) Time (s) x 1 (t) Ref. 00.6 1.2 1.8 2.4 -8 -6 -4 -2 0 2 4 6 Angular velocity x 2 (t), (rad/sec) Time (s) 00.6 1.2 1.8 2.4 -2 -1 0 1 2 3 4 Arm ature current x 3 (t), (A) Time (s)00.6 1.2 1.8 2.4 -6 -4 -2 0 2 4 6 8 Arm ature Voltage u(t), (V) Time (s) Figure 20. Simulation results of step plus ramp re ferenc e input with diffe re nt durations. 00.6 1.2 1.8 2. 4 -100 -50 0 50 100 An gu lar position x 1 (t ), (deg) Time (s) x 1 (t) Ref. 3 2 00.6 1.2 1.8 2.4 -3 -2 -1 0 1 Angular velocity x 2 (t), ec) Tim e (s) (rad/s 2.5 5 00.6 1.2 1.8 2. 4 0 0. 5 1 1. 5 24 Armature current x 3 (t ), (A ) Time (s) 3 2 1 0 -100.6 1.2 1.8 2.4 A rmature V ol tage u(t ), (V ) Tim e (s) Figure 21. Simulation results of sinusoidal refere nce input. plishing the tracking tasks for different types of reference inputs with excel this paper can be considered as an interesting and im- portant case study encompassing system modeling, sys- tem parameters identification, nonlinear controller de- signs, real-time control, and analytical solutions of the closed-loop trajectories of the nonlinear ETC system. d are applica- ble to similar and/or other types of ETC systems. In view of a recent massive auto recalls due to the controversial uncontrollable engine accelerations, the results of this paper may inspire further research interest on the drive- lent performance. The results presented The techniques and methodology develope in Copyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. 599 by-wire technology. REFERENCES [1] H. Streib and G. Bischof, “Electronic Throttle Control (ETC): A Cost Effective System for Improved Emissions, Fuel Economy, and Drivability,” SAE No. 960338, 1996. [2] W. Huber, B. Lieberoth-Leden, W. Maisch and A. Rep- pich, “Electronic Throttle Control,” Automotive Engi- neering, Vol. 99, No. 6, 1991, pp. 15-18. [3] T. Kowatari, T. Usui, and S. Tokumoto, “Optimization of an Electronic-Throttle-Control Actuator for Gasoline- Direct-Injection Engines,” SAE Paper No. 1999-01-0542, 1999. [4] C. Rossi, A. Tilli and A. Tonielli, “Robust Control of a Throttle Body for Drive by Wire Operation of Automo- tive Engines,” IEEE Transactions on Control Systems Technology, Vol. 8, No. 6, 2000, pp. 993-1002. doi:10.1109/87.880604 [5] R. N. K. Loh, T. Pornthanomwong, J. S. Pyko, A. Lee and M. N. Karsiti, “Modeling, Parameters Identification, and Control of an Electronic Throttle Control (ETC) Sys- tem,” Proceedings of 2007 International Conference on Intelligent and Advanced Syst pp. 1029-1035. doi:10.1109/I ems, Vol. 1, Malaysia, 2007, CIAS.2007.4658541 [6] C. C. de Wit, I. Kolmanovsky and J. Sun, “Adaptive Pulse Control of Electronic Throttle,” Proceedings of American Control Conference, Virginia, 2001, pp. 2872- 2877. [7] A. Contreras, I. Quiroz and C. C. de Wit, “Further Re- sults on Modeling and Identification of an Electronic Throttle Body,” Proceedings of 10th Mediterranean Conference on Control and Automation, Lisbon, 2002. [8] J. Deur, D. Pavkovic, N. Peric, M. Jansz and D. Hrovat, “An Electronic Throttle Control Strategy Including Com- pensation of Friction and Limp-Home Effects,” IEEE Transactions on Industry Applications, Vol. 40, No. 3, 2004, pp. 821-833. doi:10.1109/TIA.2004.827441 [9] J. Deur, D. Pavkovic, M. Jansz and N. Peric, “Automatic Tuning of Electronic Throttle Control Strategy,” ceedings of 11th Mediterranean Conference on Control and Automatio03. ode Control of g, “Model-Based Analysis and Tuning of Elec- e Control f the International Conference on Intelligent Systems (ICIS2005), Kala Lumpur, December 2005. [14] A. Kitahara, A. Sato, M. Hoshino, N. Kurihara and S. Shin, “LQG Based Electronic Throttle Control with a Two Degree of Freedom Structure,” Proceedings of 35th Conference on Decision and Control, Kobe, 11-13 De- cember 1995, pp. 1785- 1788. [15] M. Horn and M. Reichhartinger, “Second-Order Sliding Mode Control of Electronic Throttle Valves,” Interna- tional Workshop Variable Structure Systems 2008, Anta- lya, 2008, pp. 280-284. doi:10.1109/VSS.2008.4570721 [16] U. Ozguner, S. Hong and Y. Pan, “Discrete-Time Sliding Mode Control of Electronic Throttle Valve,” Proceedings of 40th IEEE Conference on Decision and Control, Or- lando, 4-7 December 2001, pp. 1819-1824. [17] M. Baric, I. Petrovic and N. Peric, “Neural Network- Based Sliding Mode Control of Electronic Throttle,” En- gineering Applications of Artificial Intelligence, Vol. 18, 2005, pp. 951-961. doi:10.1016/j.engappai.2005.03.008 [18] Z. Xu and P. Ioannou, “Adaptive Throttle Control for Speed Tracking,” California PATH Research Paper, UCB-ITS-PRR-94-09, April 1994. [19] D. Kim, H. Peng, S. Bai and J. M. Maguire, “Control of Electronic Throttle and Auto- EE Transactions on Control Sys- Pro- n (MED’03), Rhodes, 20 [10] M. Vasak, L. Mladenovic and N. Peric, “Clustering-Based Identification of a Piecewise Affine Electronic Throttle Model,” Proceedings of the 31st Annual Conference of IEEE Industrial Electronics Society, Vol. 1, Raleigh, 2005, pp. 177-182. [11] K. Nakano, U. Sawut, K. Higuchi and Y. Okajima, “Modeling and Observer-Based Sliding-M Electronic Throttle Systems,” ETCI Transactions on Electrical Engineering, Electronics, and Communications, Vol. 4, No. 1, 2006, pp. 22-28. [12] C. Yan tronic Throttle Controllers,” SAE Paper #2004-01-0524, 2004. [13] R. N. K. Loh, S. Elashhab, M. A. Zohdy and A. Lee, “Modeling and Design of an Automotive Throttl System,” Proceedings o Integrated Powertrain with matic Transmission,” IE tems Technology, Vol. 15, No. 3, 2007, pp. 474-482. doi:10.1109/TCST.2007.894641 [20] T. Aono and T. Kowatari, “Throttle-Control Algorithm for Improving Engine Response Based on Air-Intake Model and Throttle-Response Model,” IEEE Transac- tions on Industrial Electronics, Vol. 53, No. 3, 2006, pp. 915-921. doi:10.1109/TIE.2006.874263 [21] “Technical Customer Information Manual: DV-E5 Throt- tle Body for ETC Systems,” Robert Bosch GmbH, 2000. [22] L. Ljung, “System Identification: Theory for the User,” n, ns on Prentice Hall, Upper Saddle River, 1987. [23] T. Soderstrom and P. Stoica, “System Identification,” Prentice Hall, Upper Saddle River, 1989. [24] B. C. Kuo, “Automatic Control Systems,” 8th Editio Prentice Hall, Upper Saddle River, 2003. [25] P. S. Shiakolas and D. Piyabongkarn, “Development of a Real-Time Digital Control System with a Hardware- in-the-Loop Magnetic Levitation Device for Reinforce- ment of Controls Education,” IEEE Transactio Education, Vol. 46, No. 1, 2003, pp. 79-87. doi:10.1109/TE.2002.808268 [26] K. H. Low, H. Wang and M. Y. Wang, “On the Devel- opment of a Real Time Control System by Using xPC Target: Solution to Robotic System Control,” Proceed- ings of the 2005 IEEE International Conference on Automation Science and Engineering, Edmonton, 2005, pp. 345-350. [27] A. Isidori, “Nonlinear Control Systems,” Springer-Verlag, New York, 1995. doi:10.1007/978-1-84628-615-5 [28] H. K. Khalil, “Nonlinear Systems, ” 3rd Edition, Prentice Hall, Upper Saddle River, 2002. [29] H. Marquez, “Nonlinear Control Systems, Analysis and Copyright © 2013 SciRes. ENG  R. N. K. LOH ET AL. Copyright © 2013 SciRes. ENG 600 Link Manipulators Using neural Networks,” Mode Control Design,” Wiley Interscience, Hoboken, 2003. [30] H. A. Talebi, R. V. Patel and K. Khorasani, “Control of Flexible- Lecture Notes in Control and Information Sciences, Springer-Verlag, London, 2001. [31] C. Edwards and S. Spurgeon, “Sliding Theory and Applicationsm” Taylor & Francis, London, 1998.
|