 Journal of Modern Physics, 2013, 4, 983-990 http://dx.doi.org/10.4236/jmp.2013.47132 Published Online July 2013 (http://www.scirp.org/journal/jmp) Energy β-Conformal Change and Special Finsler Spaces Amr Soleiman1, Amira A. Ishan2 1Department of Mathematics, Faculty of Science, Benha University, Benha, Egypt 2Department of Mathematics, Taif University, Makkah, KSA Email: amrsoleiman@yahoo.com, amiraishan@hotmail.com Received February 18, 2013; revised March 21, 2013; accepted April 20, 2013 Copyright © 2013 Amr Soleiman, Amira A. Ishan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT The main aim of the present paper is to establish an intrinsic investigation of the energy β-conformal change of the most important special Finsler spaces, namely, Ch-recurrent, Cv-recurrent, C0-recurrent, Sv-recurrent, quasi-C-reducible, semi-C-reducible, C-reducible, P-reducible, C2-like, S3-like, P2-like and h-isotropic, ···, etc. Necessary and sufficient conditions for such special Finsler manifolds to be invariant under an energy β-conformal change are obtained. It should be pointed out that the present work is formulated in a prospective modern coordinate-free form. Keywords: Energy β-Conformal Change; Ch-Recurrent; Cv-Recurrent; C0-Recurrent; C2-Like; Quasi-C-Reducible; C-Reducible; Berwald Space; Sv-Recurrent; S3-Like; P2-Like; h-Isotropic 1. Introduction An important aim of Finsler geometry is the construction of a natural geometric framework of variational calculus and the creation of geometric models that are appropriate for dealing with different physical theories, such as gen- eral relativity, relativistic optics, particle physics and others. As opposed to Riemannian geometry, the extra degrees of freedom offered by Finsler geometry, due to the dependence of its geometric objects on the direc- tional arguments, make this geometry potentially more suitable for dealing with such physical theories at a deeper level. Studying Finsler geometry, however, one encounters substantial difficulties trying to seek analogues of classi- cal global, or sometimes even local, results of Rieman- nian geometry. These difficulties arise mainly from the fact that in Finsler geometry all geometric objects depend not only on positional coordinates, as in Riemannian geometry, but also on directional arguments. In Riemannian geometry, there is a canonical linear connection on the manifold M, whereas in Finsler ge- ometry there is a corresponding canonical linear connec- tion due to E. Cartan. However, this is not a connection on M but is a connection on T (TM), the tangent bundle of TM, or on π−1 (TM), the pullback of the tangent bun- dle TM by :TM M . The infinitesimal transforma- tions (changes) in Riemannian and Finsler geometry are important, not only in differential geometry, but also in application to other branches of science, especially in the process of geometrization of physical theories [1]. In [2], we investigated intrinsically energy β-confor- mal change of the fundamental linear connections on the pullback bundle of a Finsler manifold, namely, the Car- tan connection, the Berwald connection, the Chern con- nection and the Hashiguchi connection. Moreover, the change of their curvature tensors is obtained. The present paper is a continuation of [2] where we present an intrinsic investigation of energy β-conformal change of the most important special Finsler spaces, namely, Ch-recurrent, Cv-recurrent, C0-recurrent, Sv-re- current, quasi-C-reducible, semi-C-reducible. C-reducible, P-reducible, C2-like, S3-like, P2-like and h-isotropic, ··· , etc. Moreover, we obtain necessary and sufficient conditions for such special Finsler manifolds to be invariant under an energy β-conformal change. Finally, it should be pointed out that all results ob- tained are formulated in a prospective modern coordi- nate-free form. 2. Notation and Preliminaries In this section, we give a brief account of the basic con- cepts of the pullback approach to intrinsic Finsler ge- ometry necessary for this work. For more details, we refer to [3-6]. We assume, unless otherwise stated, that all geometric objects treated are of class C∞. The following notation will be used throughout this paper: M: a real paracompact differentiable manifold of finite C opyright © 2013 SciRes. JMP  A. SOLEIMAN, A. A. ISHAN 984 dimension n and of class C∞, : the R-algebra of differentiable functions on M, : the M : module of vector fields on M, :TM M :TM M : the tangent bundle of M, M : : the cotangent bundle of M, M : the subbundle of nonzero vectors tan- gent to M, VTM 1 :PT M M : the vertical subbundle of the bundle TTM, MT: the pullback of the tangent bun- dle TM by π, 1 :PTMT TM : the pullback of the cotangent bundle by π, :M 1 :M the : module of differentiable sections of , TM TM TM the : module of differentiable sections of , M 1 T iX: the interior product with respect to M , df: the exterior derivative of M, d: , L Lid, iL being the interior derivative with re- spect to a vector form L. Elements of will be called π-vector fields and will be denoted by barred letters. Tensor fields on will be called π-tensor fields. The fundamen- tal π-vector field is the π-vector field 1TM defined by ,uuu for all uM. We have the following short exact sequence of vector bundles, relating the tangent bundle T (TM) and the pull- back bundle : 1TM 1 00MT TMTM 1 , where the bundle morphisms ρ and γ are defined respec- tively by :,d TM and , where ju is the natural isomorphism ,:u uvj v : uu Mv Mv jT MTTM . The vector 1-form J on TM defined by :J is called the natural almost tangent structure of TM. The ver- tical vector field C on TM defined by :C is called the fundamental or the canonical (Liouville) ve- ctor field. Let D be a linear connection (or simply a connection) on the pullback bundle . We associate with D the map 1TM 1 :: X KTMTMXD called the connection (or the deflection) map of D. A tangent vector u TTM X TTM is said to be horizontal if . The vector space 0KX HTM : uu KX uTM 0 of the hori- zontal vectors at is called the horizontal space to M at u. The connection D is said to be regular if . uu u TTMVTMH TMuTM (1) If M is endowed with a regular connection, then the vector bundle maps 1 1 1 :, :, :. HTM VTM TMV TM TM TM KVTM TM are vector bundle isomorphisms. Let us denote 1 :HTM , this map will be called the horizontal map of the connection D. According to the direct sum decomposition (1), a regular connection D gives rise to a horizontal projector hD and a vertical projector vD, given by , DD hvI, (2) where I is the identity endomorphism on T (TM). The (classical) torsion tensor T of the connection D is defined by ,,, ,. YX YDYDXXY XY TM T The horizontal ((h)h-) and mixed ((h)hv-) torsion ten- sors, denoted by Q and T respectively, are defined by ,,,, , ,. QXYTXY TXYTXX XY M , The (classical) curvature tensor K of the connection D is defined by , ,, ,, . XY YXXY XYZDDZ DDZ DZ XYZ TM The horizontal (h-), mixed (hv-) and vertical (v-) cur- vature tensors, denoted by R, P and S respectively, are defined by ,, ,, ,, RXYZ KX YZ PXY S , , . KXYZ YZKX Y Z The contracted curvature tensors, denoted by , R ̂, P ̂ and respectively, are also known as the (v)h-, (v)hv- and (v)v-torsion tensors and are defined by ˆ S ˆ,, ˆ,, ,, ˆ RXYRXY PXY PXY XYSSXY , , . If M is endowed with a metric g on 1 πTM , we write :,,,, ,RXYZWgRXYZW (3) On a Finsler manifold , L, there are canonically Copyright © 2013 SciRes. JMP  A. SOLEIMAN, A. A. ISHAN 985 associated four linear connections on [7]: the Cartan connection , the Chern (Rund) connection Dc, the Hashiguchi connection 1 πTM D and the Berwald con- nection D◦. Each of these connections is regular with (h) hv-torsion T satisfying ,0TX . The following theorem guarantees the existence and uniqueness of the Cartan connection on the pullback bundle. Theorem 2.1. [8] Let , L be a Finsler manifold and g the Finsler metric defined by L. There exists a unique regular connection on π−1 (TM) such that (a) is metric : , 0g (b) The (h) h-torsion of vanishes: , 0Q (c) The (h) hv-torsion T of satisfies: ,,,, TXY ZgTX Z Y Definition 2.2. Let , L be a Finsler manifold and g the Finsler metric dened by L. We define: 1 :,XLgX, :g ħ : the angular metric tensor, ,,:, ,TXYZgTXY Z : the Cartan tensor, :CXTrY TXY ,: the contracted torsion, ,: CXC X: C ̅ is the π-vector field associated with the π-form C, ,: , v RicX YTrZSXZY : the vertical Ricci tensor, 0,: , vv Ric XYRic XY: the vertical Ricci map, 0 : v ScTr XRicX v : the vertical scalar curva- ture. Deicke theorem [9] can be formulated globally as fol- lows: Lemma 2.3. Let , L be a Finsler manifold. The following assertions are equivalent: (a) , L is Riemannian, (b) The (h)hv-torsion tensor T vanishes, (c) The π-form C vanishes. Concerning the Berwald connection on the pullback bundle, we have Theorem 2.4. [8] Let , L be a Finsler manifold. There exists a unique regular connection D◦ on such that 1TM D (a) = 0, hX (b) D◦ is torsion-free: T= 0, L (c) The (v)hv-torsion P◦ of D◦ vanishes : P ̂◦(X ̅,Y ̅) = 0. Such a connection is called the Berwald connection associated with the Finsler manifold , L. We terminate this section by some concepts and re- sults concerning the Klein-Grifone approach to ic Finsler geometry. For more details, we refer to [103]. ntrinsi -1 A semispray is a vector field X on TM, C∞ on M, C1 on TM, such that X . A semispray X which is homogeneous of degree 2 in the directional argument ,CX X , is called a spray. Proposition 2.5. [12] Let L be a Finsler mani- fold. The vector field G on TM defined by d G iE is a spray, where 2 2L:1E is the energy function and :d J dE . Such a spray is called the canonical spray. A nonlinear connection on M is a vector 1-form Γ on TM, C∞ on M, C0 on TM, such that ,. JJ J The horizontal and vertical projectors hΓ and vΓ asso- ciated with are defined by 12:2:,1hIvI . To each nonlinear connection Γ there is associated a semispray S defined by , where S' is an arbi- trary semispray. A nonlinear connection Γis homoge- neous if ShS ,C0 . The torsion of a nonlinear connec- tion Γ is the vector 2-form t on TM defined by :12t,J . The curvature of Γ is the vector 2-form on TM defined by R :12,hh R. A nonlinear connection Γ is said to be conservative if d0hE . Theorem 2.6. [11] On a Finsler manifold , L, there exists a unique conservative homogenous nonlinear connection with zero torsion. It is given by: ,, G where G is the canonical spray. Such a nonlinear connec- tion is called the canonical connection, the Barthel con- nection or the Cartan nonlinear connection associated with (M,L). It should be noted that the semispray associated with the Barthel connection is a spray, which is the canonical spray. 3. Energy β-Conformal Change and Special Finsler Spaces In [2], we investigated intrinsically a particular β-change, called an energy β-conformal change: 2222 ,e ,, x xy LxL, yB y (4) where , L is a Finsler manifold admitting a con- current π-vector field , :,Bg ; being the fundamental π-vector field and σ(x) is a function on M. Moreover, the relation between the two Barthel connec- tions Γ and , corresponding to this change, is obtained. The energy β-conformal change of the fundamental lin- ear connections on the pullback bundle of a Finsler manifold is studied. In this section, we introduce the effect of energy β-conformal change on some important special Finsler spaces. The intrinsic definitions of the special Finsler spaces treated here are quoted from [14]. Copyright © 2013 SciRes. JMP 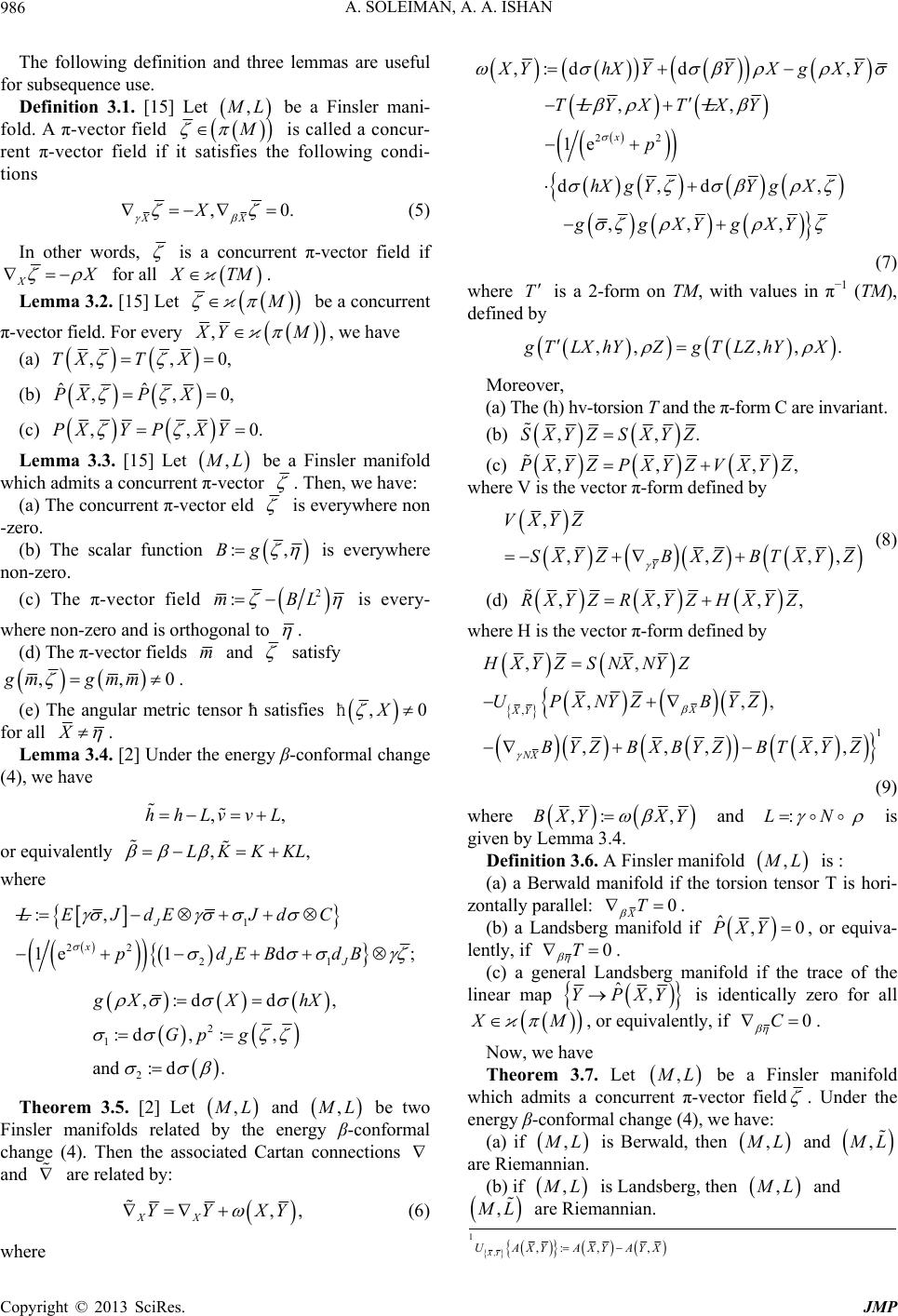 A. SOLEIMAN, A. A. ISHAN 986 The following definition and three lemmas are useful for subsequence use. Definition 3.1. [15] Let , L be a Finsler mani- fold. A π-vector field is called a concur- rent π-vector field if it satisfies the following condi- tions ,0 XX X . (5) In other words, is a concurrent π-vector field if X for all TM. Lemma 3.2. [15] Let M be a concurrent π-vector field. For every , YM , we have (a) 0,X,,TX T (b) ˆˆ ,,PXP X 0, (c) ,,PXY PXY 0. Lemma 3.3. [15] Let , L be a Finsler manifold which admits a concurrent π-vector . Then, we have: (a) The concurrent π-vector eld is everywhere non -zero. (b) The scalar function :,Bg is everywhere non-zero. (c) The π-vector field 2 :mBL is every- where non-zero and is orthogonal to . (d) The π-vector fields m and satisfy ,,gm gmm 0 . (e) The angular metric tensor ħ satisfies ,0X ħ for all X . Lemma 3.4. [2] Under the energy β-conformal change (4), we have ,,hhLvvL or equivalently ,,LK KKL where 1 22 21 :, 1e 1d; J x JJ LE JdEJdC pdEBdB 2 1 2 ,:d d :d, :, and: d. , XX Gp g hX Theorem 3.5. [2] Let , L and , L be two Finsler manifolds related by the energy β-conformal change (4). Then the associated Cartan connections and are related by: , XX YYXY , where (6) 22 :d d, ,, 1e d,d , ,, , x hX YYXgXY TYXTLXY p hXYY gX g L YgXY g gX ,XY (7) where T is a 2-form on TM, with values in π−1 (T by M), defined ,, ,, T.LXhYZgTLZhYX Moreover, v-torsion T and the π-form C are invariant. (a) The (h) h (b) ,,.SXYZ SXYZ (c) ,,,PXYZPXYZ VXYZ , wV is the vector π-form defined by here ,, ,, Y SX YZB XZBTXYZ (8) (d) ,VXYZ ,, ,RXYZRXYZ HXYZ , wH is the vector π-form defined by here ,,HXYZ SNXNYZ , 1 ,, ,, , ,, , X XY NX UP XNYZ BYZ BYZ BXBYBTZY X (9) where ,: ,BXY XY and :LN is given b Definiti on 3.6. A Fi y Lemma 3.4. nsler manifold , L n tenso is : hori- zo (a) a Berwald manifold if the torsior T is ntally parallel: 0 XT . (b) a Landsberga mnifold if ˆ,0PXY , or equiva- lently, if 0T . (c) a gerg manifold if t lin neral Landsbehe trace of the ear map ˆ,YPXY is identically zero for all M tly, if , or equivalen0C . Now, we have Theorem 3.7. Let , L ent π-v be a Finsler manifold which admits a concurrector field . Under the energy β-conformal change (4), we have: (a) if , L is Berwald, then , L and , L are Riem (b) if annian. , L is Landsberg, then , L and , L annian. are Riem 1 ,,: ,, XY UAXYAXYAYX Copyright © 2013 SciRes. JMP  A. SOLEIMAN, A. A. ISHAN 987 Proo f. (a) If , L is a Berwald manifold, then 0 XT . (Definition 3.6(a)). Hence ˆ0TP [16]- quently, the hv-curvature P va Hence, . Conse nishes [15]. 0,,, ,,PXYZ TXYZ by Proposi- tio of [15]. The result follows then n 3.4(d) from Deicke theorem (Lemma 2.3) and noting that under β-conformal change the (h)hv-torsion T is invariant (Theorem 3.5(a)). (b) The proof is similar to that of (a). Definition 3.8. A Finsler manifold , L is said to be ) Ch-recurrent if the (h)hv-torsion tensor T satisfies th : (a e condition o XTXT , where o is a π-form of order one. (b) Cv-recurrent if the (h)hv-torsion tensor T satisfies the condition ,,TYZ XTYZ . o X rent if the (h)hv-torsion tensor T satisfies th (c) C0-recur e condition ,,DT YZXTYZ . o X .9. Under the energy β-conform l change (4 Theorem 3a ), we have: (a) if , L is Ch-recurrent, then , L and , L arnnian. f , e Riema (b) i L is Cv-recurrent, then , L and , L arennian. f , Riema (c) i L is C0-recurrent, then , L and , L arnnian. f. e Riema Proo (a) We have [16] ,, ,, ˆˆ ,, ,,.,, ZW P gTYXWg TYXZ gT XWPZYgT XZPWY (10) Setting ,,,XYZW W in Equation (10), making use of ˆ0PX T ,,X (Lemma 3.2), ,Z [15] and ,,, ,PXYZT XY ,, , ZZ , TXYW gY (Proposi- tion 3.3 of [16]), we get TXW 0.T On the other hand, Definition 3.8(a) for X , yields . o TT The above two equations and Theorem 3.5(a) imply th ma 2.3, the result follows. 4], together wDefinition 3.10. A Finsler manifold (M,L) is said to r T has the from at 0.TT Hence, by Lem (b) and (c) follow from Theorem 4.7 of [1 ith Theorem 3.5(a). □ be: (a) quasi-C-reducible if dim 3M and the Cartan tenso ,, Z AY AZXCY (11) where A is a symmetric π-tensor field satisfying ,, ,,T XYZAXYCZCX ,0AX (b) semi-C-reducible if and the Cartan tensor T has the form dim 3M ,,TXYZ 2 1 ,, , , n YCZYZCXZXCY CCXCYCZ ħħħ (12) where 2:0CCC , g 1 μ and τ are scalar functions sat- isfyin . (c) Cm 3M and the Cartan tensor T has the f -reducible if orm di ,,TXYZ 11 ,, , n .YCZ YZCXZXCY ħħ+ħ (13) (d) C2-like if and the Cartan tensor T has the form dim 2M , .TXYCXCYCZ 2 , 1ZC Theorem 3.11. Under the energy β-conformal change (4), we have: (a) if , L is quasi-C-reducible provided that and , L ,0A , th , Len are Rieman- ni (b) if an. , L is Cible, the , L and -reducn , L are Riemannian. (c) if , L is semi-C-reducible,, then L and , L are C2-like. Proof. (M,L) is qua (a) Ifsi-C-reducible, then the Cartan ten- so fies Relation (11). Setting r T satis XY into Equation (11) and using the fact that 0as:, 0CTrXTX C and ,,, ,0TXYgTX Y , we get ,0. ACX From which together with the given assumption, ,0A , it follows that the π-orm C vanishes. Hence, by Lemma 2.3 and Theorem 3.5(a) imply that f Copyright © 2013 SciRes. JMP  A. SOLEIMAN, A. A. ISHAN 988 0C. Consequently, again by Lemma 2.3, C , L and , L bility by se are Riemannian manifolds. (b) Follows from the defining property of C-reduci- tting XY , taking into account Lemma 3.3(ea 2.3, Theorem 3.5(a) and ), Lemm 0C . (c) Let , L be semi-C-reducible. Setting XY and C in Equation (12), taking into account Lemma 3.2(a) and 0C , we get ,0.CC From which, since ħ ħand ,0 CC 0 , it follows that 0 . Consequently, again by E (12) quation , we get 2 ,, 1.TXYZC CXCYCZ (14) Now, unde r the energy β-conformal change (4 Theorem 3.5(a), Lemma 2.3 and the Relation [ ), from 2] 2 ,e,, ,, x XYg XYg XgY it follows that 2 ,, e,, x TXYZ TXYZ and . Hence, from Equation (14), we get 2 22 ex CC 2 1 .C CXCYCZ 15) Therefore, aefini- tion 3.10(d), the result follows. Definitio n 3 .12. The condition ,,TXYZ ( gain from Equations (14), (15) and D □ 2 ,,, 0,, XYZW YZWTX (1 will be called the T-condition. The more relaxed condition ,,,TXYZW :, , X LT YZW , 6) ,,, 0. XYZW CY (17) will be called the To-condition. Theorem 3.13. Under the energy β-conformal change (4), we have: ,: oX TXY L XCY (a) if , L satisfies the T-condition, then , L and , L are Riemannian. (b) if , Lsatisfies the To-condition, then , L and , L are Riemannian. Proof. (a) If , L satisfies the T-condition, then - by set ting W into Equation (16), taking into account that ,0TT X , we get ,X ,, 0.TXYZ r with 0BL This equation, togethe (Lem- ma 3.3(b)) and Theorem 3.5(a), impl thaty 0TT . Consequently, by Lemma 2.3, , L and , L are Riemannian manifolds. (b) Follows from Equation (17) by setting X , taking into account that CX (by 0, X CCY Y , XY TYZT X ,Z [16]), 0BL , together with 3.5(a) and Lemma 3.3. □ Definition 3.14. A Finsler m Theore m anifold , Lis said to be S3-like if 4M and the v-curvature tensor S has the form: dim 12 ,, , ,. n n ,,, v SXYZW Sc ZYWXWYZ ħ-ħħħ (18) Theorem 3.15. Under the energy β-conforma (4), if l change , L curvature te is S3-like with , then, the v- nsors S andvanis dim 4M h. S Proof. Setting Z in Equation (18), taking into accounct that t the fa ,0SXY position 3.4(a) of [13]) and (Pro ,,: YgX ħY, we immediately t ge 12 ,,0.Sc nnYX vXY ħħ Taking the trace of the above equation with respect to , noting that 1Tr n Y[14], we have –1, 0 v Sc nX ħ From which, s 0 (Lemma 3. ince ,Xħ3(e)), the vertical scalar curvature Scv vanishes. Now, again from Equation (18) togeth with Theorem 3.s. ld er 5(b), the result follow □ Definition 3.16. A Finsler manifo , L, where dim 3M, is said to be: (a) P2-like if the hv-curvature tensor P has the form: ,, ,,, ,,,PXYZW TXYW WTXYZ (19) where ω is a (1) π-form (positively homogeneous of de- gree 0). (b) P-reducible if the π-tensor field ˆˆ ,, :,,PXYZgPXYZ has the form ˆ,,PXYZ ,,,, YZYXXY ħħ (20) 2 ,, ,, ,,,:, XYZ XYZXYZ YZXA AAA,, XY Z Zħ Copyright © 2013 SciRes. JMP  A. SOLEIMAN, A. A. ISHAN 989 where δ is the π-form defined by 11. nC X gy β-conformal change (4), we have: (a) if Theorem 3.17. Under the ener , L is P-like, provided that 2 1 , then , L and , L are Riemannian. (b) if , L is P-reducible, provided that ,0XY (defined by Theorem 3.5(c)), , V then L , and L Landsberg. are (a) Setting Proof. Z in Equation (19), taking into mma 3.2, we im ac- count Pion 3.4- m roposit(a) of [15] and Le get ediately 1,0.TXY This, together with the given assumption and Theorem 3.5(a), follow that and T vanish. He by Lemma 2.3, T nce, , L and , L are Riemannian. (b) If , L is P-reducible, then, by Definition 3.16(b), the (v)hv-tosion ˆ P satisfy Relation (20). Set- ting r XY to Equ co ination (20) and taking into ac- unt that 0 , we get C ,0.CZ ħ From which, noting that , ħ0 (Lemma 3.3(e)), implies that 0C Theorem 3. . Hence, again, from Definition 3.16(b) and5(c) (under the given assumption), th H f e (v)hv-torsion tensors ence, by Defini- t ion 3.6, the resultollows. □ Definition 3.18. A Finsler manifold , ˆ0PP . L, where dim 3M, is said to be h-otropic if there exists a sca- lar ko such that the horizontal curvature tensor R has the fo is rm ,,,. o XYZk gXZYgYZX The R orem 3.19. Under the energy β-conformal change (4), we have: (a) if , L is h-isotropic, provided that ,0XYZ (defined by Theorem 3.5(d)), then the h-curvature tensors R and R of the Cartan connection va H ) if nish. (b , L is an h-isotropic Berwald manifold, provided that ,0HXYZ, then , L and , L are Riemannian. Proof. (a) From De we havfinition 3.18(a),e ,, , o kg XZYWgYZgg ,. R WX (2 Setting ,,,XYZW 1) Z 0,,,, o kgmYW ggWgYm . Taking the trace of this equation, we get ,0. o kn 1gm , since and m and noting that ,0RXY (Proposition 3.4(g) of [15]), we have From which ,,gm gmm (Lemma 0 3.3) and , the scalar ko vanishes. Now, ain, fromder the given as nd of the Cartan connection vanish (b) Follows from (a), taking Theorem 3.7 into account. n better plications of indices. of the present work, where dim 3Mag Equation (21) and Theorem 3.5(c) (un sumption), the h-curvature tensors R a R 4. Concluding Remark It should be pointed out that a global formulatio of dif- ferent aspects of Finsler geometry may give more insight into the infrastructure of physical theories and make a understanding on the essence of such theories without being trapped into the com This is one of the motivations all results obtained are formulated in a prospective mod- ern coordinate-free form. Moreover, it should be noted that the outcome of this work is twofold. Firstly, the local expressions of the obtained results, when calculated, co- incide with the existing local results. Secondly, new glo- bal proofs have been established. REFERENCES [1] T. Mestdag and V. Toth, Report Mathmatics Physics, Vol. 50, 2002, pp. 167-193. doi:10.1016/S0034-4877(02)80053-2 [2] A. Soleiman, International Journal of Geometric Meth- ods in Modern p. [3] H. Akbar-ZadFinsler Geometry,” siques des Es- ication Department Spaces with ed and A. Soleiman, Algebras, , 1965, pp. 90-191. 5802/aif.407 Physic, Vol. 9, 2012, 21 eh, “Initiation to Global Elsevier, San Diego, 2006. [4] P. Dazord, “Propriétés Globales des Géodé paces de Finsler,” Thése d’Etat, Publ Mathematics Lyon, 1969. [5] A. A. Tamim, “General Theory of Finsler Applications to Randers Spaces,” Ph.D. Thesis, Cairo University, Cairo, 1991. [6] N. L. Youssef, S. H. Abed and A. Soleiman, Balkan Journal of Geometry and Its Applications, Vol. 15, 2010, pp. 138-150. [7] N. L. Youssef, S. H. Abed and A. Soleiman, Tensor N. S., Vol. 71, 2009, pp. 187-208. [8] N. L. Youssef, S. H. Ab Groups and Geometries, Vol. 25, 2008, pp. 363-386. [9] F. Brickell, Proceedings of the American Mathematical Society, Vol. 16 [10] J. Grifone, Annales de L’Institut Fourier, Grenoble, Vol. 22, 1972, pp. 287-334. doi:10. [11] J. Grifone, Annales de L’Institut Fourier, Grenoble, Vol. 22, 1972, pp. 291-338. doi:10.5802/aif.431 Copyright © 2013 SciRes. JMP  A. SOLEIMAN, A. A. ISHAN Copyright © 2013 SciRes. JMP 990 0. [12] J. Klein and A. Voutier, Annales de L’Institut Fourier, Grenoble, Vol. 18, 1968, pp. 241-26 doi:10.5802/aif.282 [13] N. L. Youssef, Tensor, N. S., Vol. 36, 1982, pp. 275-280. 93. [16] [14] N. L. Youssef, S. H. Abed and A. Soleiman, Kyoto Jour- nal of Mathematics, Vol. 48, 2008, pp. 857-8 [15] N. L. Youssef, S. H. Abed and A. Soleiman, International Journal of Geometric Methods in Modern Physics, Vol. 6, 2009, pp. 1003-1031. N. L. Youssef, S. H. Abed and A. Soleiman, Journal of the Egyptian Mathematical Society, Vol. 18, 2010, pp. 67-90.
|