Paper Menu >>
Journal Menu >>
 Journal of Modern Physics, 2013, 4, 1-7 http://dx.doi.org/10.4236/jmp.2013.47A2001 Published Online July 2013 (http://www.scirp.org/journal/jmp) Thermal Modeling of Cylindrical LiFePO4 Batteries Mojtaba Shadman Rad1,2, Dmitri L. Danilov1, Morteza Baghalha2, Mohammad Kazemeini2, Peter H. L. Notten1,3* 1Department of Chemistry and Chemical Engineering, Eindhoven University of Technology, Eindhoven, The Netherlands 2Chemical & Petroleum Engineering Department, Sharif University of Technology, Tehran, Iran 3Department of Electrical Engineering, Eindhoven University of Technology, Eindhoven, The Netherlands Email: *P.H.L.Notten@TUE.nl Received May 4, 2013; revised June 6, 2013; accepted July 3, 2013 Copyright © 2013 Mojtaba Shadman Rad et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Thermal management of Li-ion batteries is important because of the high energy content and the risk of rapid tempera- ture development in the high current range. Reliable and safe operation of these batteries is seriously endangered by high temperatures. It is important to have a simple but accurate model to evaluate the thermal behavior of batteries un- der a variety of operating conditions and be able to predict the internal temperature as well. To achieve this goal, a ra- dial-axial model is developed to investigate the evolution of the temperature distribution in cylindrical Li-ion cells. Ex- perimental data on LiFePO4 cylindrical Li-ion batteries are used to determine the overpotentials and to estimate the State-of-Charge-dependent entropies from the previously developed adaptive thermal model [1]. The heat evolution is assumed to be uniform inside the battery. Heat exchange from the battery surfaces with the ambient is non-uniform, i.e. depends on the temperature of a particular point at the surface of the cell. Furthermore, the model was adapted for im- plementation in battery management systems. It is shown that the model can accurately predict the temperature distribu- tion inside the cell in a wide range of operating conditions. Good agreement with the measured temperature develop- ment has been achieved. Decreasing the heat conductivity coefficient during cell manufacturing and increasing the heat transfer coefficient during battery operation suppresses the temperature evolution. This modified model can be used for the scale-up of large size batteries and battery packs. Keywords: Lithium-Ion Batteries; Thermal Modeling; Entropy; Energy; Electrochemistry; Heat Transfer 1. Introduction A successful design of battery packs starts with the cor- rect accommodation of the thermal battery properties. Using high thermally resistant materials, such as binders in the electrodes and polymer separators is inevitable in constructing high performance batteries, but this limits the heat transfer inside the cells. Consequently, higher tem- peratures are expected at the core of the cells compared to its surface. However high temperatures are not permit- ted for safety and reliability reasons; they can accelerate battery degradation and even cause thermal runaway. In a battery management system (BMS), it is desirable to ac- curately predict the internal temperature evolution of the battery according to the state-of-charge (SOC), cell po- tential, current and surface temperature. Such a system re- quires an efficient thermal model with a limited number of measured parameters at each state. Therefore heat dis- sipation in a cell must be properly studied in order to avoid elevated temperatures where decomposition reac- tions of the electrodes and electrolyte are started [2]. A number of models have been developed to study the thermal behavior of Li-ion or Li-polymer batteries [1,3- 22]. Theoretical models, which are usually based on a combination of electrochemistry and physics, can give accurate predictions for various operating conditions [3- 10]. But these are complicated and need sophisticated measurements and estimation of transport properties, elec- trochemical reaction constants, etc. to be accurately solv- ed. Such models are well-suited for battery design pur- poses, though not optimal for the low computing-power environment of micro-controllers used in BMS [20]. On the other hand, experimental-based models employ bat- tery measurements on the cell level to determine equilib- rium potentials and, consequently, overpotentials and in some studies, entropy contributions in heat generation, but do not go into detail of the electrochemical processes occurring inside the cells [1,11-18,22]. The present paper represents combination of both ap- *Corresponding author. C opyright © 2013 SciRes. JMP  M. SHADMAN RAD ET AL. 2 proaches. An experimental-based methodology for accu- rate two-dimensional thermal modeling of cylindrical cells is proposed. Commercially available high power 2.3 Ah LiFePO4 batteries, which are an interesting option for hybrid electrical vehicles (HEVs) and full electrical ve- hicles (EVs), are used in this study. Previously developed lumped thermal model [1] is implemented for this cell chemistry to provide part of the input data of the two- dimensional model based on the experimental data and then for extension of the model. In the previous work, it was shown how one can explicitly determine the equi- librium potentials by polynomial extrapolation towards zero current, and obtain the overpotentials at various cur- rents and SoC. Then a back-estimation method was in- troduced to find the values of the entropy changes from the adapted thermal model. The main challenge and contribution of this work is to implement a proper two-dimensional model of heat dis- sipation by using overpotentials and temperature deriva- tives of the equilibrium potentials, which gives a proper rate of the heat generation. The developed model is ex- ported into Matlab, enabling a user-friendly implemen- tation into a BMS. COMSOL multiphysics is used for fi- nite element modeling, and then the model is exported to MATLAB for estimation of the various parameters. 2. Theoretical Considerations 2.1. Model Development Based on the differential energy balance in cylindrical coordinates, the following heat transport partial differ- rential equation (PDE) is obtained ,, in T kHtrz 2 2 pTk T C trrrz , (1) where is the density [g·m−3], p C the specific heat capacity [J·g−1·K−1], T the temperature [K], t time [s], k the thermal conductivity [W·m−1·K−1], r radial coordinate and z is the axial coordinate. Note that derivatives with respect to , the tangential coordinate, are absent since the considered problem possesses radial symmetry. The heat source term ,, in H trz [W·m−3] includes all bat- tery processes that contributes to the heat evolution, ac- cording to ,, s C ,, in H tHtrz V Ht rz , (2) where H t ,, [W] represents the overpotential heat, s H trz C t [W] the entropic heat and V [m3] is the volume of the battery. H ttIt , (3) where the overpotential t eq E E t [V] is defined as the difference between equilibrium cell potential and the operating cell potential teq tEtEt , (4) t t is always defined positive during charging and negative upon discharging. I(t) [A] specifies the current flowing through the individual electrodes which is by de- finition positive during charging and negative upon dis- charging. So ,, s H t is always positive. H trz is the entropic heat [W] which can be represented by ,, ,, s St H trzItTtrznF )( tS , (5) where n is the number of electrons that are transferred in the electrochemical reaction during the battery operation and F is the Faraday constant [96,486 C·mol−1]. [J·mol−1·K−1] expresses the entropy change of the indi- vidual electrochemical charge transfer reaction during battery operation and has been derived at our previous work [1], according to , eq E St nFT P , (6) where represents, in general terms, the reaction pro- gress, in our specific case the SoC of the cell. The initial condition for the partial differential equation (Equation (1)) for the whole cell is 0, ,a TrzT, (7) where a [K] is the ambient temperature. Denoting the radius of the cell as R and length of the cell as L energy conservation requires that on the surface of the cell there is a balance between heat conduction and sum of con- vection and radiation heat transfer, according to T 44 aa kThTTTT n, (8) where h is the average convective heat transfer coeffi- cient [W·m−2·K−1] between the cell and the environment, = 5.67 × 10-8 [J·s−1·m−2·K−4] is the Stefan-Boltzmann constant and is the emissivity factor of the surface material. T represents temperature gradient and is the outer normal vector of unit length. n 2.2. Experimental 2.3 Ah cylindrical A123 (ANR26650m1) LiFePO4 cells were investigated in this study. Temperature develop- ment as a function of applied current, potential and oper- ating regime was recorded. The experimental data were used to determine the overpotential and SoC-dependent entropy changes and to validate the thermal model. Cy- cling was performed with an 8-channel MACCOR 4000 battery tester. The temperature development was meas- ured on the middle of the surface of the cell by the poten- tial drop across PT100 type thermo-resistors connected to Copyright © 2013 SciRes. JMP  M. SHADMAN RAD ET AL. 3 battery tester via the auxiliary potential input. A water bath was used to control the ambient temperature in a cli- mate control box (Figure 1). To evaluate the thermal be- havior of the cells, three different temperatures were in- vestigated: 0˚C, 20˚C and 40˚C. Constant current-constant voltage (CCCV) charging was applied in this study. Charging was carried out at 1.6 A (= 0.7 C-rate) till the maximum cell potential of 3.6 V was attained. Charging was continued under constant vol- tage conditions at 3.6 V until the charging current drop- ped below 0.3 A (End-of-Charge). Subsequently, CCCV- charging was followed by a relaxation period of 180 min. Constant current (CC) was then applied to discharge the battery at various C-rates. Discharging was terminated at 2.0 V. The following rated currents were employed for discharging: 0.05, 0.10, 0.15, 0.20, 0.30, 0.50, 0.75, 1.00, 1.50 and 2.00 C-rates. 2.3. Model Parameters and Assumptions The battery specifications are summarized in Table 1. The battery consists of several components: organic elec- trolyte, dissolved lithium salts, polymer separator, cur- rent collectors, graphite and composite electrodes, sup- porting materials, metal casing, etc. So it is difficult to estimate the overall physical properties of the cell based on the physical properties of its constituents. Table 2 provides some proposed and estimated values of requir- ed physical properties of the main cell components. Surface emissivity factor of the batteries is as- sumed to be 0.65. The small observed variation in eq upon battery aging is neglected. Considering heat capaci- ties of the components, the average heat capacity of the cells is estimated to be 1.36 [J·g−1·K−1]. E Considering natural convection of air around a hori- zontally positioned cylinder, the following expression has been adopted for the heat transfer coefficient [23] 14 49 916 8 Pr Ra0.51 0.36 1 0.559 famb hd Nu k , (9) Figure 1. Experiment set-up. Table 1. Battery specifications. Parameter Value or description Diameter 25.85 mm Height 65.15 mm without terminals Mass Approx. 70 g Positive Electrode LiFePO4 Negative Electrode Porous Graphite Nominal Capacity 2.3 Ah at 0.2 C Table 2. Physical properties of the cell components. Cell (Avg.) Separator (PP) Cathode Anode CP [J·g−1·K−1]1.36 1.93-2.00 1.25 1.20 k [W·m−1·K−1]0.4 0.12-0.22 0.4 1.4 [g·m−3]2.047·1069.02 - 9.06·105 2.208·106 1.410·106 where f Nu Pr D Ra Gr is the average dimensionless Nusselt num- ber, h is the average natural (free) convection heat trans- fer coefficient [W·m−2·K−1], d the diameter of the bat- tery [m] and kamb is thermal conductivity of air [W·m−1·K−1]. Ra is the dimensionless Rayleigh number, defined as in which D Gr is the dimensionless Gra- shof number, 3 2 a D g TTD Gr and Pr p C k is the Prandtl number, g [m·s−2] is the gravity constant, [K−1] is the volumetric thermal expansion coefficient, which is defined as 1Ta for ideal gases. Parameters and represent the viscosity and kinematic viscosity of air, respectively. 3. Results and Discussion The thermal behavior of the batteries has been evaluated up to 2C-discharge rates at ambient temperature 20˚C. The results at this temperature are presented here as a common ambient temperature for the battery operations in electrical vehicles. However the battery measurements and simulation have also been performed at 0˚C and 40˚C to determine equilibrium potentials and derive en- tropy change values to further validation of the model. 3.1. EMF, Overpotential and Entropy Determination The measured cell potentials during cycling with various discharge C-rates at 20˚C are shown in Figure 2(a). The battery is charged to 3.6 V according to the standard charging regime in every cycle. During the subsequent 3 hours of relaxation under open-circuit conditions, the cell potential drops to about 3.4 V, after that discharging Copyright © 2013 SciRes. JMP  M. SHADMAN RAD ET AL. 4 (a) (b) Figure 2. (a) Cell potential development during charging (1), relaxation (2) and discharging (3) at various C-rates and (b) the corresponding temperature development. Ambient tem- perature is 20˚C. starts. The discharge cut-off potential is 2 V. Figure 2(b) represents the temperature development during cycling. It is clearly visible that the temperature evolution becomes more pronounced at higher C-rates. The temperature nor- mally increases during (dis)charging. However at some specific stages the temperature decreases. Since the over- potential heat is always positive, this can be explained only by a negative entropic heat contribution, which will be discussed later. The methodology developed in previous work [1] is used to determine the overpotentials and SoC-dependent entropy changes from the experimental data. Modeling starts with estimation of the equilibrium potential. Extra- polation of the measured cell potential towards 0 C-rate discharge current which has introduced in the previous works is used to determine the equilibrium potentials [1,24,25]. Figure 3 shows the measured potential curves, the determined dependence (black upper potential curve) and the overpotential curves (insert). eq E S S According to Equation (4) the overpotential can be ob- tained from the EMF and the cell potential discharge curves (see inset of Figure 3). The as-determined over- potentials serve as important input parameter to calculate the heat evolution Equation (3). Another heat contribu- tion (see Equation (4)) is related to the entropy. In order to reduce the complexity of the calculations 11 Qout-re- gions are considered. Values of in 11 subsequent nodes of the discrete grid, i.e. SoC from 0 to 1 with step 0.1 are treated as unknown optimizing parameters. These values are determined from an optimization proce- dure by a lumped thermal model based on battery meas- urements [1], considering the best agreement between experimentally measured and theoretical evolution of the surface cell temperature as criteria. Optimization has been performed across 10 cycle of (dis)charge as the cell mea- surements have been performed. values as a func- tion of SoC are displayed in Figure 4. The obtained val- ues for entropy changes are in consistence with the re- ported values for this battery by C. Forgez et al. [20]. S 3.2. 2D-Model It is assumed, that rate of heat generation is uniform across the cell and determined by overpotential and state- of-charge (SoC)-dependent entropic heat sources. In con- trast, the heat exchange at the battery surface with the ambient environment depends on temperature, and is therefore not uniform. Contributions from convective and radiation cooling are considered. The model is construc- ted in COMSOL 3.5a in radial-axial coordinates using the physical cell properties listed in Tables 1 and 2. The overpotential tS and values are used to calculate heat generation (Equations (2)-(5)). These values are us- ed as input parameter to radial-axial model for the heat generation. Natural heat convection of air around the cell and radiation are taken into consideration knowing that radiation is comparable to natural heat convection amounts. By using Equation (9) at an estimated average tempera- ture of 24˚C (which is estimated according to the experi- mental measurements of temperature) on the boarder of the cell, h is calculated to be 9 [W·m−2·K−1]. The physi- cal properties of the cell and air are assumed to be tem- perature-independent over a narrow temperature range upon each test which is less than 10˚C and an average ex- tent for each property is chosen. The grid used in the cal- culations is shown in Figure 5. Equation (1) with initial condition Equation (7) and boundary conditions Equation (8) can then be solved by a time-dependent solver. 3.3. Temperature Profiles The result of a COMSOL simulation is illustrated in Fig- re 6. As expected, the core temperature of the cell is u Copyright © 2013 SciRes. JMP 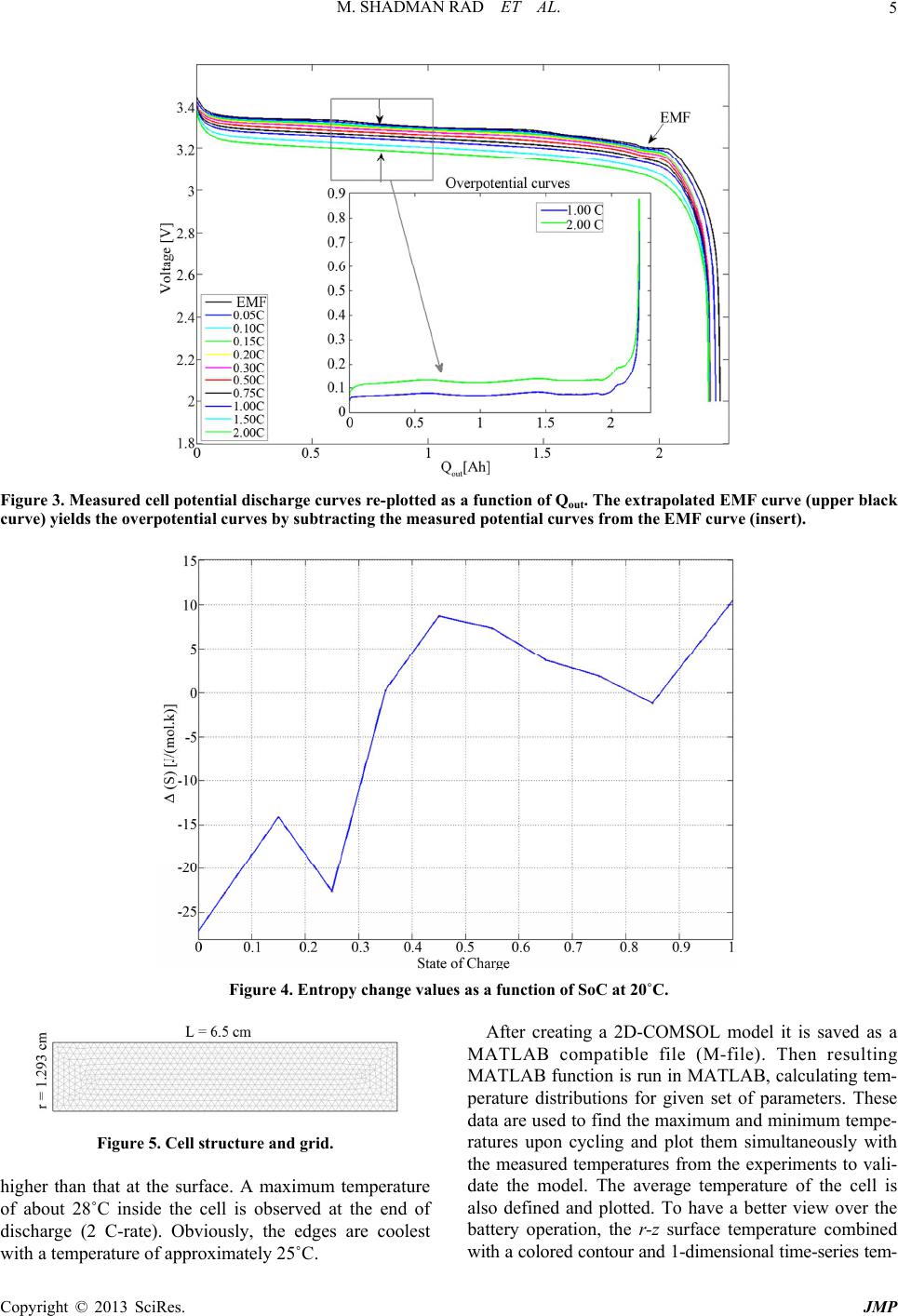 M. SHADMAN RAD ET AL. Copyright © 2013 SciRes. JMP 5 Figure 3. Measured cell potential discharge curves re-plotted as a function of Qout. The extrapolated EMF curve (upper black curve) yields the overpotential curves by subtracting the measured potential curves from the EMF curve (insert). Figure 4. Entropy change values as a function of SoC at 20˚C. After creating a 2D-COMSOL model it is saved as a MATLAB compatible file (M-file). Then resulting MATLAB function is run in MATLAB, calculating tem- perature distributions for given set of parameters. These data are used to find the maximum and minimum tempe- ratures upon cycling and plot them simultaneously with the measured temperatures from the experiments to vali- date the model. The average temperature of the cell is also defined and plotted. To have a better view over the battery operation, the r-z surface temperature combined with a colored contour and 1-dimensional time-series tem- Figure 5. Cell structure and grid. higher than that at the surface. A maximum temperature of about 28˚C inside the cell is observed at the end of discharge (2 C-rate). Obviously, the edges are coolest with a temperature of approximately 25˚C.  M. SHADMAN RAD ET AL. 6 perature plots were calculated, then time-series movie was created. The simulated temperature profiles of the cell at 2C-discharge and upon 3 hours of relaxation in the following period are shown in Figure 7. The temperature is measured on the surface of the cell during the experi- ments, while the heat generation occurs inside the cell. So, it is expected that measurements remain between the Figure 6. Temperature distribution inside the cell at the end of 2C-rate discharging at an ambient temperature of 20˚C. Figure 7. Minimum, maximum and average temperature profiles versus measured temperatures on the surface of the cell at 2C-rate discharge from MATLAB model. minimum and average temperature of the cell. A maxi- mum temperature difference around 3˚C is observed in the cell at the end of discharge. It is seen that even with moderately high discharge rate, which is not extreme case, the core temperature increases by 9˚C. The benefit of running the model in MATLAB is the ability to use it for optimization purposes. Moreover the physical properties of the cell or adjustable parameters for BMS can easily be changed and the results be evalu- ated individually in-line with other part of the model. To cease or moderate the temperature rise in the cell upon high discharge rates, it is possible to increase the heat transfer coefficient h. For instance it is possible to use a fan to apply force convection of air around the cell. On the other hand, heat conduction of the cell seems another limiting factor for effective temperature control over the cell. Therefore it is better to increase the k value during manufacturing the cell. A combination of different k and h values and the consequences on the minimum and ma- ximum temperatures and maximum temperature differ- ence across the cell are presented in Table 3. It is con- cluded that by increasing the thermal conductivity from 0.4 to 2 W·m−1·K−1, the gap between the minimum and maximum temperature in the cell decreases from 3˚C to less than 1˚C by running the MATLAB model with the new k value. However, it seems that increasing h can control the temperature rise. By increasing h by a factor of 4, the maximum internal temperature of the cell de- creases to 25.2˚C. However, the maximum temperature difference in the cell increases to 3.9˚C. More effective cooling can be done if the heat transfer coefficient in- creases, but the heat conduction of the cell decreases. A 3-dimensional view from the r-z surface temperature profile and contours and comparison with the maximum temperature at each moment has been plotted in Figure 8. The animated movie from the r-z surface temperature, con- tours and maximum temperature plot during the whole cycle is available as electronic file. 4. Conclusion A simple radial-axial model has been developed to eva- luate the thermal behavior of LiFePO4 batteries. The over- potential and SoC-dependent entropy change heating are two important sources of heat generation in the cell. The parameter values for these sources are obtained by im- plementing the previously developed lumped thermal model. The as-determined values for entropy changes are consistent with recent literature [20]. The model provides a good agreement with the experimentally measured tem- peratures upon cycling. The model is constructed and run in COMSOL 3.5a. It is combined with MATLAB to use optimization capabilities for validating the model with measured data. It is shown that the core temperature of the cell is much higher than that at the surface of the Copyright © 2013 SciRes. JMP 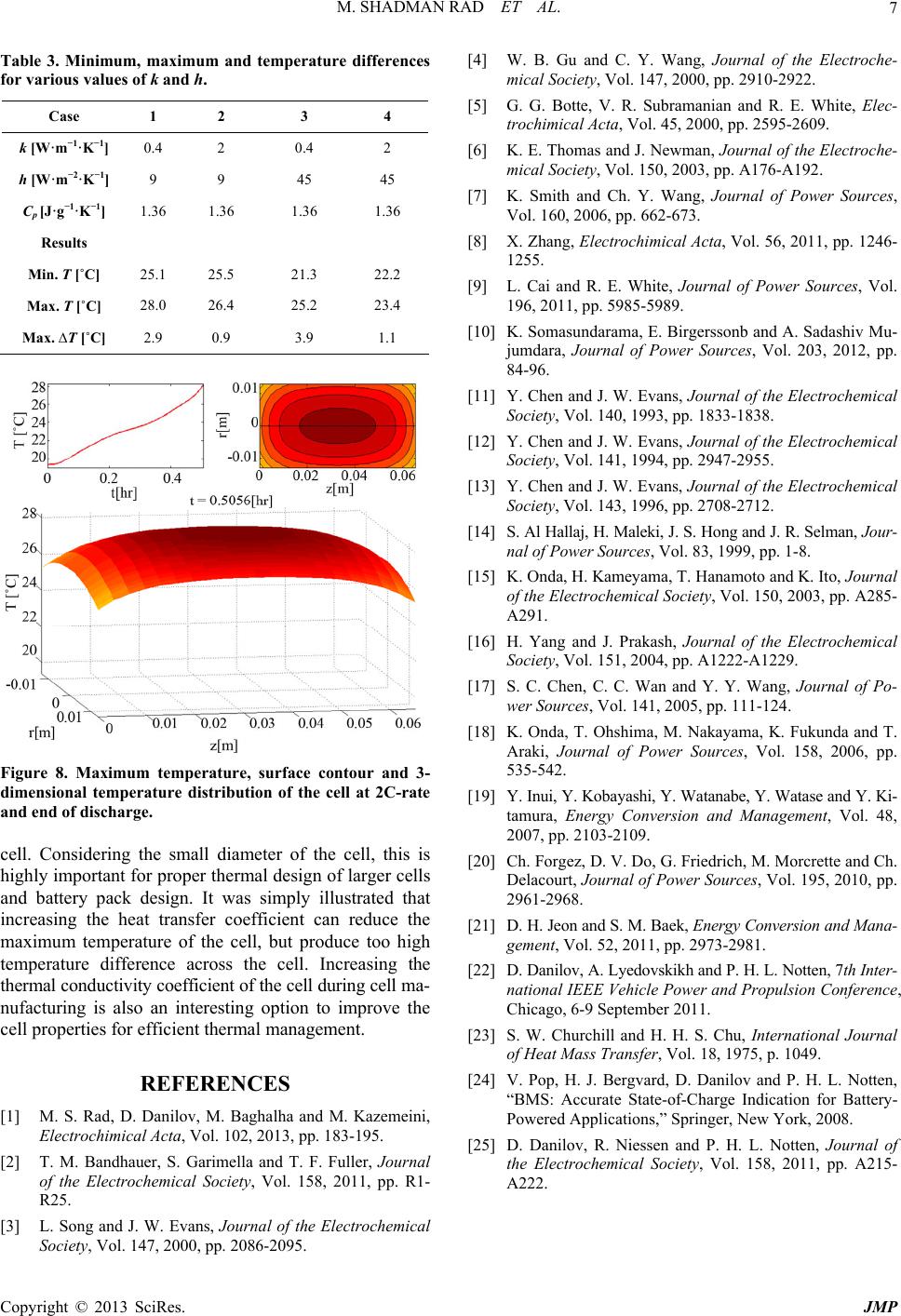 M. SHADMAN RAD ET AL. Copyright © 2013 SciRes. JMP 7 [4] W . B. Gu and C. Y. Wang, Journal of the Electroche- mical Society, Vol. 147, 2000, pp. 2910-2922. Table 3. Minimum, maximum and temperature differences for various values of k and h. Case 1 2 3 4 k [W·m−1·K−1] 0.4 2 0.4 2 h [W·m−2·K−1] 9 9 45 45 Cp [J·g−1·K−1] 1.36 1.36 1.36 1.36 Results Min. T [˚C] 25.1 25.5 21.3 22.2 Max. T [˚C] 28.0 26.4 25.2 23.4 Max. ∆T [˚C] 2.9 0.9 3.9 1.1 [5] G. G. Botte, V. R. Subramanian and R. E. White, Elec- trochimical Acta, Vol. 45, 2000, pp. 2595-2609. [6] K. E. Thomas and J. Newman, Journal of the Electroche- mical Society, Vol. 150, 2003, pp. A176-A192. [7] K. Smith and Ch. Y. Wang, Journal of Power Sources, Vol. 160, 2006, pp. 662-673. [8] X. Zhang, Electrochimical Acta, Vol. 56, 2011, pp. 1246- 1255. [9] L. Cai and R. E. White, Journal of Power Sources, Vol. 196, 2011, pp. 5985-5989. [10] K. Somasundarama, E. Birgerssonb and A. Sadashiv Mu- jumdara, Journal of Power Sources, Vol. 203, 2012, pp. 84-96. [11] Y. Chen and J. W. Evans, Journal of the Electrochemical Society, Vol. 140, 1993, pp. 1833-1838. [12] Y. Chen and J. W. Evans, Journal of the Electrochemical Society, Vol. 141, 1994, pp. 2947-2955. [13] Y. Chen and J. W. Evans, Journal of the Electrochemical Society, Vol. 143, 1996, pp. 2708-2712. [14] S. Al Hallaj, H. Maleki, J. S. Hong and J. R. Selman, Jour- nal of Power Sources, Vol. 83, 1999, pp. 1-8. [15] K. Onda, H. Kameyama, T. Hanamoto and K. Ito, Journal of the Electrochemical Society, Vol. 150, 2003, pp. A285- A291. [16] H. Yang and J. Prakash, Journal of the Electrochemical Society, Vol. 151, 2004, pp. A1222-A1229. [17] S. C. Chen, C. C. Wan and Y. Y. Wang, Journal of Po- wer Sources, Vol. 141, 2005, pp. 111-124. [18] K. Onda, T. Ohshima, M. Nakayama, K. Fukunda and T. Araki, Journal of Power Sources, Vol. 158, 2006, pp. 535-542. Figure 8. Maximum temperature, surface contour and 3- dimensional temperature distribution of the cell at 2C-rate and end of discharge. [19] Y. Inui, Y. Kobayashi, Y. Watanabe, Y. Watase and Y. Ki- tamura, Energy Conversion and Management, Vol. 48, 2007, pp. 2103-2109. cell. Considering the small diameter of the cell, this is highly important for proper thermal design of larger cells and battery pack design. It was simply illustrated that increasing the heat transfer coefficient can reduce the maximum temperature of the cell, but produce too high temperature difference across the cell. Increasing the thermal conductivity coefficient of the cell during cell ma- nufacturing is also an interesting option to improve the cell properties for efficient thermal management. [20] Ch. Forgez, D. V. Do, G. Friedrich, M. Morcrette and Ch. Delacourt, Journal of Power Sources, Vol. 195, 2010, pp. 2961-2968. [21] D. H. Jeon and S. M. Baek, Energy Conversi on an d Mana- gement, Vol. 52, 2011, pp. 2973-2981. [22] D. Danilov, A. Lyedovskikh and P. H. L. Notten, 7th Inter- national IEEE Vehicle Power and Propulsion Conference, Chicago, 6-9 September 2011. [23] S. W. Churchill and H. H. S. Chu, International Journal of Heat Mass Transfer, Vol. 18, 1975, p. 1049. REFERENCES [24] V. Pop, H. J. Bergvard, D. Danilov and P. H. L. Notten, “BMS: Accurate State-of-Charge Indication for Battery- Powered Applications,” Springer, New York, 2008. [1] M. S. Rad, D. Danilov, M. Baghalha and M. Kazemeini, Electrochimical Acta, Vol. 102, 2013, pp. 183-195. [25] D. Danilov, R. Niessen and P. H. L. Notten, Journal of the Electrochemical Society, Vol. 158, 2011, pp. A215- A222. [2] T. M. Bandhauer, S. Garimella and T. F. Fuller, Journal of the Electrochemical Society, Vol. 158, 2011, pp. R1- R25. [3] L. Song and J. W. Evans, Journal of the Electrochemical Society, Vol. 147, 2000, pp. 2086-2095. |

