Open Journal of Applied Sciences, 2013, 3, 94-98
doi:10.4236/ojapps.2013.31B1019 Published Online April 2013 (http://www.scirp.org/journal/ojapps)
Rogue Waves of the Kundu-Nonlinear Schrödinger
Equation
Chengchuang Zhang, Chuanzhong Li, Jingsong He
Department of Mathematics, Ningbo University, Ningbo 315211, China
Received 2013
ABSTRACT
This paper is based on the Darboux transformation of the Kundu-Nonlinear Schrödinger equation. The rogue wave so-
lutions are obtained from periodic seed solutions. After that, the higher order rogue wave solutions of the
Kundu-Nonlinear Schrödinger equation are given. Finally, we show that free parameters in eigenfunctions can adjust
the patterns of the higher order rogue waves.
Keywords: Darboux Transformation; Rogue Waves; Kundu-Nonlinear Schrödinger Equation
1. Introduction
It is remarked that the Darboux transformation is an effi-
cient method to generate the soliton solutions for inte-
grable equations [1]. The determinant representation of
n-fold Darboux transformation of AKNS system was
given in [2]. Recently, the rogue waves observed firstly
in the ocean [3], have been also studied extensively in
several fields, such as optical system [4], water tanks[5],
Bose-Einstein condensate [6-7],space plasma [8], and
even in a financial system [9]. It can be well-described
by the analytical expressions for the spectra of breather
solutions at the zero point. Furthermore there are several
interesting patterns of the higher order rogue waves [10].
In this paper, we shall study the rogue waves of the
Kundu-Nonlinear Schrödinger(Kundu-NLS) equation,


2* 2
2iQQQ QiQiQ
txxtx xxxx
  2
0,
(1)
where

is a arbitrary gauge function, denotes the
complex conjugate of Q.
*
Q
In Section 2, the Lax representation and two-fold
Darboux transformation of the Kundu-NLS equation will
be given. In Section 3, From a periodic seed solution,
breather solutions, the first-order rogue wave and higher
order rogue wave solutions of the Kundu-NLS equation
are given. The higher order rogue waves can be separated
into some different types by adjusting free parameters in
eigenfunctions. The final Section is a short summary.
2. Lax Representation and 2-fold Darboux
Transformation of the Kundu-NLS
Equation
Now, we concentrate on the Kundu-NLS equation.
The linear eigenvalue problem of Kundu-NLS equation
can be expressed in the form of Lax pair M and N as
30
(),

 
xMi V
  (2)
2
301
(22) ,

 
tNi VV
 (3)
with
30
*
10 0
,,
01 0




 



i
i
Qe
VQe



2
1*2
||( ).
() ||






i
x
i
x
iQ iQe
V
iQei Q




Here

, an arbitrary complex number, is called the
eigenvalue(or spectral parameter), denotes the com-
plex conjugate of ,
*
Q
Q

is a arbitrary gauge function,

is a real parameter and is called the eigenfunc-
tion associated with


of the Kundu-NLS equation.
Firstly, let us consider a matrix T of gauge transforma-
tion for the spectral problem (2) and (3) with the follow-
ing form [1] .

T
[1]

[1]
New function is supposed to
satisfy
[1]
,

[1][1][1] [1]
,


x
[1]
NT

x
TT
N
t
then matrix T should
satisfy following identities
, we obtain
M
[1
M
],TM
N
t
TT
[1][1][1] [1]1
[,]( [,]).


tx tx
M
NMNTMNMNT
This implies that, under the transformation [1]

T
[1]
,
it is crucial to construct a matrix T so that
M
and
have the same forms as that M and N. At the same
time, the old potentials(or seed solutions) in spectral ma-
trixes
[1]
N
M
and are mapped into new potentials(or
new solutions) in terms of transformed spectral matrixes
N

C. C. ZHANG ET AL. 95
[1]
M
and . With the help of symbolic computation,
MAPLE, after some analysis and some calculations, the
two-fold Darboux transformation of Kundu-NLS equa-
tion can be represented as follows:
[1]
N
2[2] [2]
2 1
(; ,

2341 0
211 212
221 222 2
, ,)
()
()
1
() ()

 
 



TItt
 
(4)
where
1,1
2,1
3,1
4,1
1

1,2 11,1 11,2
2,222,1 22,2
2
3,233,1 33,2
4,244,1 44,2
2
2
1,11,211,111,21 1,1
2
21 2,12,2 22,122,2 22,1
2
3,13,2 33,133,2 33,1
4,14,2 44,144,2 4
,
10 0
()
 
 
 
 
 
 
 
 










2
4,1
2
1,11,2 11,1 11,2 11,1
2
2,12,2 22,122,2 22,1 21
2
3,13,2 33,133,2 33,1
2
4,14,2 44,144,2 44,1
2
1,11,211,111,21 1,1
2
2,12,2 22,122,2 22,2 22
3,1 3,
,
() ,
100 0
01 0
)
0

 
 

 
 
 
 










2
1
(
2
233,13 3,233,2
2
4,14,2 44,144,2 44,2
2
1,11,211,111,21 1,1
2
222 2,12,2 22,122,222,2
2
3,13,23 3,13 3,233,2
2
4,14,2 44,144,2 44,2
2
,
.
10
()
0
 
 
 
  
 
 







Note that the above determinant representation is
given by solving following algebraic equations,
,1
22 1234
,2
(; ,,,)0
j
j
j
TT

 








,
where . Furthermore the new solution after
the two-fold Darboux transformation of Kundu-NLS
equations will be
1, 2, 3, 4j


2
112
2, i i
QQ t
e


2
[2]
(5)
and must hold for. Then we start
with one of the above as a seeding solution and use it
with Darboux transformations to obtain more compli-
cated ones.


2
112
t


*
2
121
 t1 t
3. Rouge Waves of Kundu-NLS Equation
It is well known that solitons and positon solutions have
been generated through Darboux transformation by as-
suming constant trivial solutions, while the plane-wave
solution results in the hierarchy of solutions related to
modulation instability. Rational solutions have never
been constructed in this way. In order to get rouge waves,
we must obtain Akhmediev breathers or Ma solitons.
Now, we can take a periodic seed solutions as i
Qce

,

ax bt

, are arbitrary real constants. Then
we can choose
,,abc

x

. Substitute the periodic seed solu-
tions into equation.(1.1), we can obtain a constraint rela-
tionship, 22
2120

c aba  . Define
22
:14244 4 2 ,
K
aaa   c



then the following wave function
is obtained in the form
1,1 2,1
12
1,2 2,2
,
 

 
 



111
()(( )())
2222
1,1 1,
 
 ixKxt ke


(6)
111
()(( )())
12222
1,2
(2 ),
2
 

 ixKxt
ii aiKk
e
c





(7)
111
()(( )())
2222
2,1 1,

 ixKxt ke


(8)
111
()(()())
12222
2,2
(2)
2
 

 ixKx t
ii aiKk
e
c





(9)
Here,
21
2
1
1 
 k
k n denotes the number of the
steps of the multi-fold Darboux transformation, 1
() ,

k
nw


k
wC
are some free parameters and

is a infinitesimal parame-
ter. We would like to construct more complicated wave
functions to derive more meaningful solutions in the fol-
lowing part, so we mix these four series of wave func-
tions together to derive new functions and
1,1
1,2

as follows,
** **
1,1 1,11,22,12,2
:()()()()    ,
)
(10)
** **
1, 21,11, 22 ,12 , 2
:()() ()( .

  (11)
It can be proved that 1,1

and 1,2  are also the so-
lution of Lax equations with spectral parameter

. Us-
ing these two wave functions 1,1 and 1,2 , the one-
fold Darboux transformation will lead to the construction
of breather solutions. Next, substituting
 
11

i


(1

)/2
into K, and letting K = 0, thus we can obtain 1,

a

1c

 . If we do the Taylor expansion to breather solu-
tions of the Kundu-NLS equation around 1c


,

C. C. ZHANG ET AL.
96
1(1)/2 a,

the first order rogue wave solutions of
the Kundu-NLS equation will be obtained,
222 2
222222
222
(21) 16(
)34]/[16(2 1)
1) 41].

  

caactix
c xcaact
a tcx

 

1[ 16
16 (

i
rw
Qce
axc t
cx

2
When we take 1.25,1, 0.75 ac

, the graph for
this first order rogue wave solutions of the Kundu-NLS
equation and corresponding density graph are shown in
Figure 1.
However, it is highly non-trivial to construct higher
rogue waves from the higher order breathers because of
the multi-degeneration of the eigenvalues. Similar to the
case of the NLS equation, the determinant representation
of the Darboux transformation provides a useful tool to
calculate this tedious expansion. Value(1)/2 a

ic

is a zero point of the eigenfunction 1,1 , 1,2 

,
and all 
j

 with

denoting a small parameter
when we consider the degeneration of the eigenfunction.
Therefore, let the first and second rows in expand
into the second power to
[2]
Q

and the third and forth rows
expand into the third power to

. By the two-fold Dar-
boux transformation, we can obtain the second order
rogue wave solutions of the Kundu-NLS equation. Here,
we can only draw the graph the second order rogue wave
solutions of the Kundu-NLS equation in Figure 2. Simi-
larly, we can obtain the third order rogue wave solutions
of the Kundu-NLS equation.Choose 1.25, 0.4,a

c
1

, the graph of the third order rogue wave solutions
of Kundu-NLS equation is drawn in Figure 3.
Until now, from the first order rogue wave to the third
order rogue wave, basic modes have been given when
1. But 1k has different values in dif-
ferent 1,1 and 1,2 . Next we discuss the impact about
1 to the higher order rogue waves. To the second
order rogue wave solutions,
0( 1)
 k
wk

k
w
w

()

have two free para- me-
ters for the Kundu-NLS equation. We choose 00,

w
1 the second order rogue wave is well separated
into three single rogue waves. These single rogue waves
exhibit a triangular shape. The graph is shown in Figure
4. Similar behavior is obtained using the third order
rogue wave solution,
200,w
(
)

have three free parameters.
Chooing ac1. 25, 0.43, 1,

01 2 ,
the third order rogue wave is well separated into six sin-
gle rogue waves, which perform in a triangular shape.
Then we choose 01
0, 1ww
, 1,
 w
0, 0 w
0, 0,
w1, 0ac.5

2, the third order rogue wave is composed of
six single rogue waves, which form a pentagon with one
peak in the center and the rest are located on the vertices
of the pentagon. Figure 5 and Figure 6 illustrate the
corresponding combination of different types of the third
order rogue wave.
1000w
Figure 1. The first order rogue wave solution Q.
Figure 2. The second order rogue wave solution Q when a =
–1.25, α = 1, c = 0.43.
Figure 3. The third order rogue wave solutionswhen a =
–1.25, c = 0.4, α = 1, when a = –1.25, α = 1, c = 0.75.
Q

C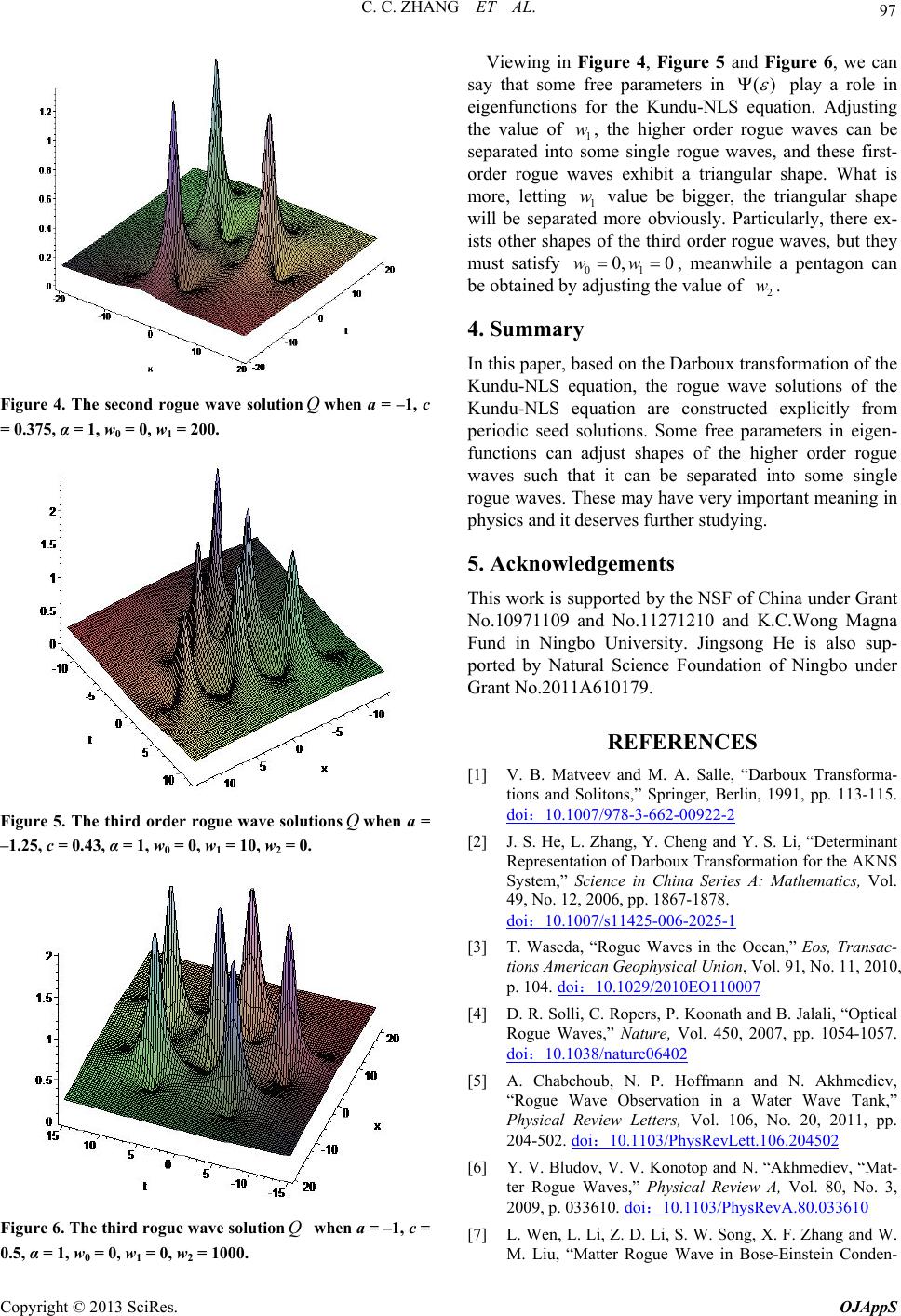. C. ZHANG ET AL. 97
Figure 4. The second rogue wave solutionwhen a = –1, c
= 0.375, α = 1, w0 = 0, w1 = 200.
Q
Figure 5. The third order rogue wave solutionswhen a =
–1.25, c = 0.43, α = 1, w0 = 0, w1 = 10, w2 = 0.
Q
Figure 6. The third rogue wave solution when a = –1, c =
0.5, α = 1, w0 = 0, w1 = 0, w2 = 1000.
Q
Viewing in Figure 4, Figure 5 and Figure 6, we can
say that some free parameters in ()

play a role in
eigenfunctions for the Kundu-NLS equation. Adjusting
the value of 1, the higher order rogue waves can be
separated into some single rogue waves, and these first-
order rogue waves exhibit a triangular shape. What is
more, letting 1 value be bigger, the triangular shape
will be separated more obviously. Particularly, there ex-
ists other shapes of the third order rogue waves, but they
must satisfy 01
w
w
0, 0

ww , meanwhile a pentagon can
be obtained by adjusting the value of .
2
w
4. Summary
In this paper, based on the Darboux transformation of the
Kundu-NLS equation, the rogue wave solutions of the
Kundu-NLS equation are constructed explicitly from
periodic seed solutions. Some free parameters in eigen-
functions can adjust shapes of the higher order rogue
waves such that it can be separated into some single
rogue waves. These may have very important meaning in
physics and it deserves further studying.
5. Acknowledgements
This work is supported by the NSF of China under Grant
No.10971109 and No.11271210 and K.C.Wong Magna
Fund in Ningbo University. Jingsong He is also sup-
ported by Natural Science Foundation of Ningbo under
Grant No.2011A610179.
REFERENCES
[1] V. B. Matveev and M. A. Salle, “Darboux Transforma-
tions and Solitons,” Springer, Berlin, 1991, pp. 113-115.
doi：10.1007/978-3-662-00922-2
[2] J. S. He, L. Zhang, Y. Cheng and Y. S. Li, “Determinant
Representation of Darboux Transformation for the AKNS
System,” Science in China Series A: Mathematics, Vol.
49, No. 12, 2006, pp. 1867-1878.
doi：10.1007/s11425-006-2025-1
[3] T. Waseda, “Rogue Waves in the Ocean,” Eos, Transac-
tions American Geophysical Union, Vol. 91, No. 11, 2010,
p. 104. doi：10.1029/2010EO110007
[4] D. R. Solli, C. Ropers, P. Koonath and B. Jalali, “Optical
Rogue Waves,” Nature, Vol. 450, 2007, pp. 1054-1057.
doi：10.1038/nature06402
[5] A. Chabchoub, N. P. Hoffmann and N. Akhmediev,
“Rogue Wave Observation in a Water Wave Tank,”
Physical Review Letters, Vol. 106, No. 20, 2011, pp.
204-502. doi：10.1103/PhysRevLett.106.204502
[6] Y. V. Bludov, V. V. Konotop and N. “Akhmediev, “Mat-
ter Rogue Waves,” Physical Review A, Vol. 80, No. 3,
2009, p. 033610. doi：10.1103/PhysRevA.80.033610
[7] L. Wen, L. Li, Z. D. Li, S. W. Song, X. F. Zhang and W.
M. Liu, “Matter Rogue Wave in Bose-Einstein Conden-

C. C. ZHANG ET AL.
98
sates with Attractive Atomic Interaction,” The European
Physical Journal D, Vol. 64, No. 2-3, 2011, pp. 473-478.
doi：10.1140/epjd/e2011-20485-4
[8] M. S. Ruderman, “Freak Waves in Laboratory and Space
Plasmas,” The European Physical Journal, Vol. 185, No.
1,2010, pp. 57-66. doi：10.1140/epjst/e2010-01238-7
[9] Z. Yan, “Financial Rogue Waves,” Communications in
Theoretical Physics, Vol. 54, No. 4, 2010, pp. 947-949.
doi：10.1088/0253-6102/54/5/31
[10] J. S. He, H. R. Zhang, L. H. Wang, K. Porsezian and A. S.
Fokas. “A Generating Mechanism for Higher Order
Rogue Waves,”.