J. Electromagnetic Analysis & Applications, 2010, 2, 672-676
doi:10.4236/jemaa.2010.212088 Published Online December 2010 (http://www.SciRP.org/journal/jemaa)
Theory of Carbon Nanotubes as Optical Nano
Waveguides
Afshin Moradi1,2
1Department of Nano Science, Kermanshah University of Technology, Kermanshah, Iran; 2Department of Nano Science, Institute for
Studies in Theoretical Physics and Mathematics (IPM), Tehran, Iran
Received November 5th, 2010; revised November 25th, 2010; accepted December 1st, 2010.
ABSTRACT
The propagation of surface plasmon waves in metallic single-walled carbon nanotubes is analyzed within the frame-
work of the classical electrodynamics. The conduction electrons of the system are modelled by an infinitesimally thin
layer of free-electron gas which is described by means of the semiclassical kinetic theory of the electron dynamics. The
effects of the energy band structure is taken into accoun t and a more accura te dispersion relation fo r surface plasmon
oscillations in the zig-zag and armchair nanotubes of metallic cha ra c ter is obtained.
Keywords: Carbon Nanotubes, Dispersion Relation , Plasmon Oscillations
1. Introduction
With the discovery by Iijima [1] of carbon nanotubes
(CNTs) structures, a new class of materials with a re-
duced dimensionality has been introduced. Metallic
CNTs are considered suitable candidates in the field of
plasmonics as new plasmonics waveguides [2-12]. These
new plasmonic waveguides can be built by some simple
and well-known methods such as CVD [12].
By using the classical electrodynamics and a semi-
classical kinetic theory, Slepyan et al [2], derived the
dispersion relation of surface waves in single-walled
carbon nanotubes (SWCNTs) and for the first time,
found that CNTs can be used as a nano waveguide for
controlling electro magnetic wave propagation in speci-
fied frequency ranges (for instance, infrared and optical).
In particular, by solving Maxwell and hydrodynamic
equations, the propagation of electromagnetic waves in
SWCNTs is studied in Reference [4,5] and it has been
shown that dispersion behaviors of the plasma waves
with TM and TE modes are quite similar. However, the
hydrodynamic theory, without any effects of the energy
band structure to be taken into account, can not be valid
enough for the investigations of plasmon waves propaga-
tion in CNTs.
SWCNTs are quasi one-dimensional material, which
could be regarded as a rolled-up graphene layer (i.e., a
mono-atomic layer of graphite) in the cylindrical form. It
has a radius of a few nanometers and lengths up to cen-
timeters. A graphene layer is a semi-metallic material.
Nevertheless, when a graphene layer is rolled up it may
become either metallic or semiconducting, depending
on its geometry. Figure 1 shows a graphene layer. The
geometric structure of a SWCNT is uniquely deter-
mined by the chiral vector


12
R,manam n ,
where m and n are integers, and a1 and a2 are the ele-
mentary vectors of the dimensional graphene lattice
(see Figure 1). The tube radius of the CNTs is given by
22 0,
2
c
a
rmmn

 n
where 0 is the lattice constant of the graphite
sheet and 0
0
1.42b
=3abA

 is the distance between the near-
est-neighboring carbon atoms. A SWCNTs is metallic if
3mn q

, where 0,1,2,q


q
Thus, armchair nano-
tubes are always metallic, whereas zig-zag nanotubes are
metallic only if 3m

with 1, 2,q
In this Letter, we study the energy band effects on the
dispersion relation of the surface plasmon waves in
SWCNTs of metallic character, by using the semiclassi-
cal kinetic theory of the electron dynamics. In compari-
son with previous investigatio ns [4,5] that focus on plas-
mon wave oscillations in a cylindrical electron gas as a
simple model of metallic tubes, present work stresses on
more exact analysis of geometrical effects, including the
radius and the chiral angle of the nanotube.

Theory of Carbon Nanotubes as Optical Nano Waveguides 673
Figure 1. Graphene sheet used in forming CNTs (The dots
illustrate the carbon atoms positions). The lattice basis vec-
tors are a1 and a2. The chiral vector
, where m and n are integers. The nanotubes
with are called zig-zag, those withare called
armchair and those with are called chiral.
12
Rma na
mn


,mn
n0mn
2. Formulation of the Problem
Let us consider both zig-zag and armchair
nanotubes as infinitesimally thin and infinitely
long cylindrical shells of radius c with its axis along
the -direction and regard the CNT to consist of
(,0)m
r
(,)mm
z

-electrons superimposed with equilibrium densities
(per unit area) 0. We assume that in equilibrium the n

-electron fluid has no velocity and is the perturbed
density (per unit area) of fluid, produced by the
n

-electrons themselves under the action of the electric
field generated by the fixed positive ions of the lattice.
Hydrodynamic theory describes electronic motion in
terms of two dynamical variables, namely the electron-
density fluctuation, and
(,)nxt

uxt

,=

,
z
uu

The
basic equations in this linearized hydrody- namic model
are the equations of motion, the equations of continuity,
 
0
,= nxt nuxt
t

,
, (1)
   
0
00
,=, ,
eff
uxt n
nn xteExtnu xt
tm

 

,,
ˆ
(2)
where

ˆ ,=zz ExtEe Ee




eff
m
is the tangential com-
ponent of the electromagnetic field, e is the element
charge, is the effective mass of the

-electrons and
1
=(/)(/ )
z
ezae




 differentiates only tangen-
tially to the nanotubes surface. In the right-hand side of
Equation (2), the first term arise from the internal
interaction force in the fluid with that is the
square of the speed of propagation of density
disturbances in a uniform 2D homogeneous electron
fluid. The second term is the force on
2
=/2
F


-electron fluid
due to the tangential component of the electric field,
evaluated at the nanotube surface and the last
term represents the effects of the scattering of the
electrons with the positive-charge background, where
=c rr

being the friction coefficient. We note that this term has
been neglected in the previous works [4,5].
Let us deal with the surface plasmon waves with TM
modes only in this paper, the similar result for TE mode
can be obtained. The electric field vector can be
expanded in the following Fourier forms (,Ex

im qz  
)t
 
=
(,)=,.
m
m
ExtdqE rqexpt 
 




 (3)
For the TM modes, the field components can be
expressed in terms of
z
m
E, and it is readily shown that
this satisfy
2
2=0
zm
m
E
r



2
1,
zm
dd
rE
rdr dr





2
/c
(4)
where and c is the light speed. The
parameter
222
=q  

is a real quantity in the region
<.c
q

(5)
This means that we deal with the slow transverse
magnetic waves. By eliminating the velocity field


,uxt, one can obtain the following equation from
Equations (1 ) and (2)
 
,. t 
22
2,= ,nx
tnxtE x
t

 




 
0
eff
n
e
tm
qz 
(6)
Upon solving Equation. (6) by means of the space-time
Fourier transforms for the induced density on
the cylindrical surface, we find ),( txn
 
=
,= ,
m
m
n xtdqNqexpit 
 






m (7)
where
0
=,
z
r




m
meff
n
ie
N E
m


c
m
qE (8)
and




2
m
22
=/
mc
iq  r. Now, we use the
appropriate boundary condition, we have
 
><
0
||=
e,
rm crrrm c rrm
cc
Er Er N

 (9)

Theory of Carbon Nanotubes as Optical Nano Waveguides 674
where 0

is the permittivity of free space and the radial
component rm and the azimuthal component Em
E

of
the electric field, are given by
 
2
=
zm
rm
dE r
q
Er idr

, (10)
and
 
2
=
mz
mq
Er Er
r


.
m

,

>,
(11)
On the other hand, the relevant solution of Equation (4)
is
   
0
=
zmz mcmc
Er EKrIrrr   (12)
and
   
0
=
zmz mcmc
Er EIrKrrr  (13)
where

m
I
x and

m
K
x are the modified Bessel
functions. Substituting Equations (12-13) into boundary
condition Equation (9), by using Equation (8), for
/cq

, one can obtain the dispersion equation as
below:
 
22
2222
22
=,
pcmc mc
cc
mm
irIrK
rr






r
(14)
where eff
is the eigen-frequency of
the

1/2
200
=/
pc
en rm 

-electron gas layer in metallic SWCNTs. The
solutions of Equation (14) yield complex frequencies
=ri i

 . It may be observed that the imaginary part
i

will be given simply by /2


. In fact, by writing
=/2
ri



, the solutions for finite damping will be
of the form

1/2
22 2
2222
22
=
42
pcmc mc
cc
mm
rIrKr
rr .i


 



 
 

 

(15)
The friction coefficient is the inverse of the electron
relaxation time

. For CNTs it is taken as =

12
310
s


=0
[13], so we have Hz. Formally
speaking, the dispersion characteristics of the surface
waves in the system is dependent on the nanotube
geometry (including the radius and the chiral angle of the
nanotube), the wave number, the angular momentum,
and the friction coefficient. However, it is easy to find
that by increasing friction coefficient, the dispersion
curves shift to lower frequencies, so in the following we
set
12
=1/3 10  

.
At this stage, from Equation (15), one can see for
investigation the dispersion characteristics of the zig-zag
and armchair SWCNTs, we have to give the values of
0. The parameter 0 takes into account the
influence of the atomic crystal field. By using the
semiclassical model of the
/eff nm /eff nm

-electron dynamics, Miano
and Villone [14], obtained the following estimation:
02
21,
F
eff c
n
mr


 (16)
where
F

is the velocity of the electrons at the Fermi
level
00
3
=.
2
F
b 


0

is a characteristic energy of the
graphene lattice and is the Planck constant; it results
that . The Equation (16) holds
for zig-zag nanotubes with , for armchair
nanotubes with and for chiral nanotubes with

02.7 3eV
 
=3 <60mq

6
10
<50
(0.9 1)/
Fms
 
m
=3q2nm

. In the range of validity of Equation (16),
the parameter decreases as the nanotube radius increases.
To see clearly the energy band effects on the
dispersion relation of the surface waves in SWCNTs, in
the following we consider long and short wavelength
limits of the Equation (15). For c, by using the
well-known asymptotic expressions [15],
r  
 
==(
2
2
xx
mm
e),
I
xandKxewith thefinite m
x
x



the dispersion relation can be written approximately as
2
22 2
0
=
F
c
e
r

 
. (17)
One can see unlike the case of Equation (3) in Ref. 5,
where the dispersion relation is independent of the
geometrical effects of the tube, the right-hand side of
Equation (17) in the present work, depends strongly on
the radius of the nanotube. It is easy to find that as the
values of the nanotube radius increases the values of
c
r

decrease.
In the opposite limit 0
c
r

, where the phase
velocity of the surface plasmon is comparable to the
velocity of light, surface plasmon oscillations couple
with the electromagnetic wave and retardation effects are
present. Retardation effects on low-dimensional plasmons
are investigated in details in Reference [16]. If we
neglect the retardation effects, by using the well-known
expressions of Bessel functions,
 
1
=(
12
m
m),
x
Ix m



0
2ln1.12
()=()for0and=for=0
2
m
m
m
Kxm Kxm
xx
3
then we may obtain for =0m

1/2
2
2
0
41.123
=0, 0ln,
F
c
e
mr



 



 



 (18)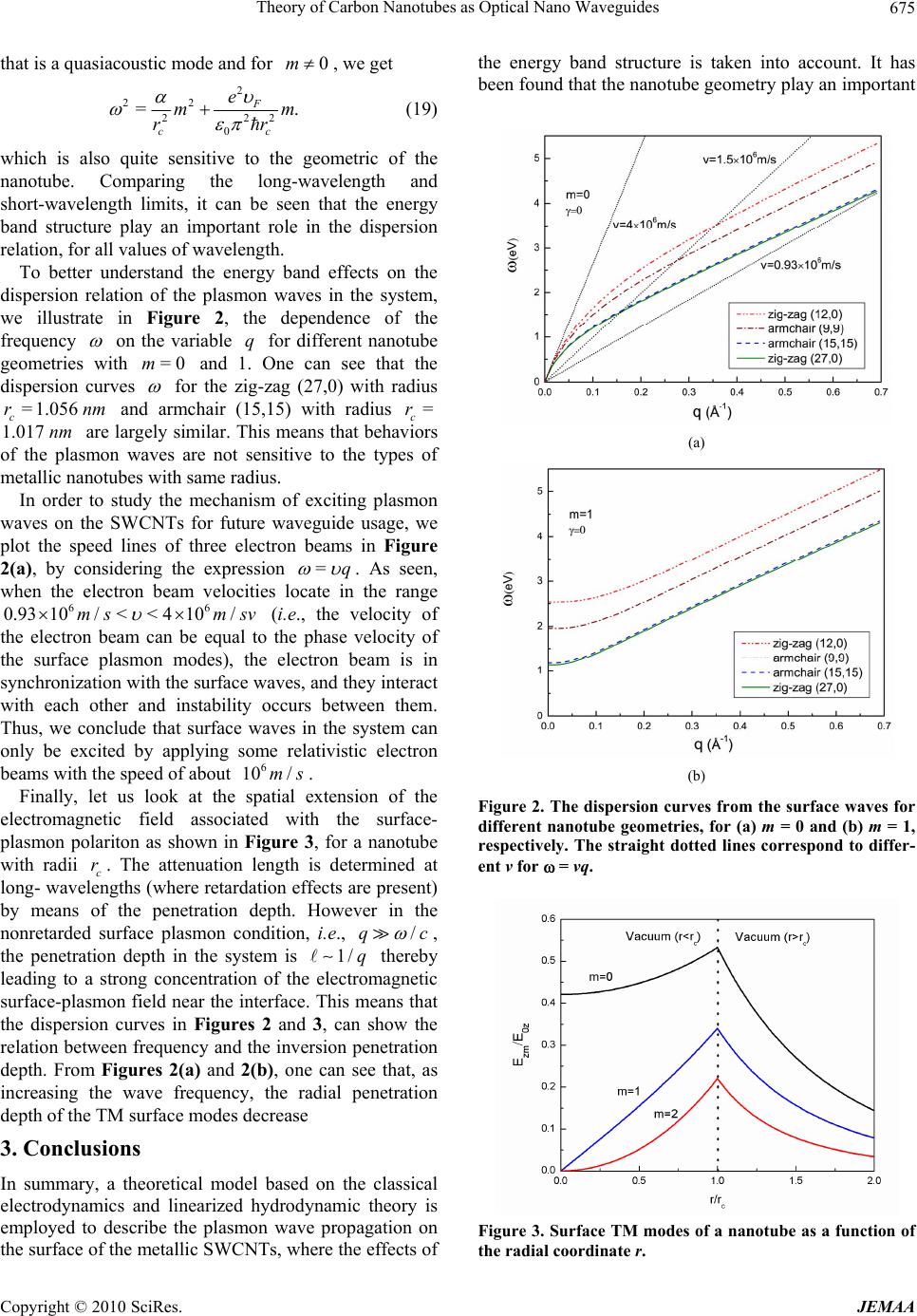

Theory of Carbon Nanotubes as Optical Nano Waveguides 675
that is a quasiacoustic mode and for , we get 0m
2
22
22
0
=
F
cc
e
m
rr
 

2 .m
(19)
which is also quite sensitive to the geometric of the
nanotube. Comparing the long-wavelength and
short-wavelength limits, it can be seen that the energy
band structure play an important role in the dispersion
relation, for all values of wavelength.
To better understand the energy band effects on the
dispersion relation of the plasmon waves in the system,
we illustrate in Figure 2, the dependence of the
frequency

on the variable for different nanotube
geometries with and 1. One can see that the
dispersion curves
q
=0m

for the zig-zag (27,0) with radius
and armchair (15,15) with radius
are largely similar. This means that behaviors
of the plasmon waves are not sensitive to the types of
metallic nanotubes with same radius.
=1.056
c
r
1.017 nm nm =
c
r
In order to study the mechanism of exciting plasmon
waves on the SWCNTs for future waveguide usage, we
plot the speed lines of three electron beams in Figure
2(a), by considering the expression =q


/s
. As seen,
when the electron beam velocities locate in the range
(i.e., the velocity of
the electron beam can be equal to the phase velocity of
the surface plasmon modes), the electron beam is in
synchronization with the surface waves, and they interact
with each other and instability occurs between them.
Thus, we conclude that surface waves in the system can
only be excited by applying some relativistic electron
beams with the speed of about .
6
0.9310/<< 410/ms msv  
6
10
6
m
Finally, let us look at the spatial extension of the
electromagnetic field associated with the surface-
plasmon polariton as shown in Figure 3, for a nanotube
with radii c. The attenuation length is determined at
long- wavelength s (where retardation effects are present)
by means of the penetration depth. However in the
nonretarded surface plasmon condition, i.e.,
r
/qc


q,
the penetration depth in the system is thereby
leading to a strong concentration of the electromagnetic
surface-plasmon field near the interface. This means that
the dispersion curves in Figures 2 and 3, can show the
relation between frequency and the inversion penetration
depth. From Figures 2(a) and 2(b), one can see that, as
increasing the wave frequency, the radial penetration
depth of the TM surface modes decrease
1/
3. Conclusions
In summary, a theoretical model based on the classical
electrodynamics and linearized hydrodynamic theory is
employed to describe the plasmon wave propagation on
the surface of the metallic SWCNTs, where the effects of
the energy band structure is taken into account. It has
been found that the nanotube geometry play an important
(a)
(b)
Figure 2. The dispersion curves from the surface waves for
different nanotube geometries, for (a) m = 0 and (b) m = 1,
respectively. The straight dotted lines correspond to differ-
ent v for  = vq.
Figure 3. Surfac e TM modes of a nanotube as a function of
the radial coordinate r.

Theory of Carbon Nanotubes as Optical Nano Waveguides 676
role in the dispersion relation of the surface waves, for
all value of wavelength. Also, numerical results show
that behaviors of the plasmon waves are not sensitive to
the types of metallic nanotubes with same radius. In
addition, the results obtained make us believe that the
hydrodynamic theory in conjunction with semiclassical
model is available and appropriates for studies of the
plasmon wave oscillations in CNTs, especially for dif-
ferent nanotube geometries.
REFERENCES
[1] S. Iijima, “Helical Microtubules of Graphitic Carbon,”
Nature, Vol. 354, No. 6348, 1991, pp. 56-58.
[2] G. Ya. Slepyan, S. A. Maksimenko, A. Lakhtakia, O. M.
Yevtushenko and A. V. Gusakov, “Electronic and
Electromagnetic Properties of Nanotubes,” Physical
Review B, Vol. 57, 1998, pp. 9485-9497.
[3] M. V. Shuba, S. A. Maksimenko and A. Lakhtakia,
“Electromagnetic Wave Propagation in an Almost
Circular Bundle of Closely Packed Metallic Carbon
Nanotubes,” Physics Review B, Vol. 76, No. 15, 2007, pp.
1-9.
[4] L. Wei and Y. N. Wang, “Electromagnetic Wave
Propagation in Single-Wall Carbon Nanotubes,” Physics
Letters A, Vol. 333, 2004, pp. 303-309.
[5] H. Khosravi and A. Moradi, “Comment on:
Electromagnetic Wave Propagation in Single-Wall
Carbon Nanotubes,” Physical Letters A, Vol. 364, 2007,
pp. 515-516.
[6] A. Moradi, “Guided Dispersion Characteristics of
Metallic Single-Walled Carbon Nanotubes in the
Presence of Dielectric Media,” Optics Communications,
Vol. 283, No. 1, 2010, pp. 160-163.
[7] D. J. Mowbray, Z. L. Miskovic, F. O. Goodman and Y.-N.
Wang, “Interactions of Fast Ions with Carbon Nanotubes:
Two-Fluid Model,” Physical Review B, Vol. 70, No. 19,
2004, pp. 1-7.
[8] D. J. Mowbray, S. Segui, J. Gervasoni, Z. L. Miskovi,
and N. R. Arista, “Plasmon Excitations on a Single-Wall
Carbon Nanotube by External Charges: Two-
Dimensional Two-Fluid Hydrodynamic Model,” Physical
Review B, Vol. 82, No. 3, 2010, pp. 1-14.
[9] C. Javaherian and B. Shokri, “Guided Dispersion
Characteristics of Metallic Single-Wall Carbon
Nanotubes,” Journal of Physics D, Vol. 42, No. 5, 2009,
pp. 1-6.
[10] L. Liu, Z. Han and S. He, “Novel Surface Plasmon
Waveguide for High Integration,” Optics Express, Vol.
13, No. 17, 2005, pp. 6645-6650.
[11] E. Ozbay, “Plasmonics: Merging Photonics and
Electronics at Nanoscale Dimensions,” Science, Vol. 311,
No. 5758, 2006, pp. 189-193.
[12] M. Su, B. Zheng and J. Liu, “A Scalable CVD Method
for the Synthesis of Single-Walled Carbon Nanotubes
with High Catalyst Productivity,” Chemical Physics
Letters, Vol. 322, No. 5, 2000, pp. 321-326.
[13] Y. Miyamoto, S. G. Louie and M. L. Cohen, “Chiral
Conductivities of Nanotubes,” Physical Review Letteras,
Vol. 76, No. 12, 1996, pp. 2121-2124.
[14] G. Miano and F. Villone, “An Integral Formulation for
the Electrodynamics of Metallic Carbon Nanotubes
Based on a Fluid Model,” IEEE Transaction on Antennas
and Propagation, Vol. 54, No. 10, 2006, pp. 2713-2724.
[15] M. Abramowitz and I. A. Stegum, Handbook of
Mathematical Funcyions, Dover, New York, 1965.
[16] L. Wendler and T. Kraft, “Retardation Effects on Intra-
and Intersubband Plasmons in Quantum Wells and Their
Manifestations in Grating-Coupler-Assisted Optical
Transmission,” Physical Review B, Vol. 60, No. 24, 1999,
pp. 16603-16610.