Journal of Modern Physics, 2013, 4, 55-63
http://dx.doi.org/10.4236/jmp.2013.47A1007 Published Online July 2013 (http://www.scirp.org/journal/jmp)
Modeling the Black Hole Recoil from the Nucleus of M83
Guilherme G. Ferrari1, Horacio Dottori1, Rubén J. Díaz2
1Instituto de Física, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil
2ICATE-CONICET, San Juan, Argentina
Received April 8, 2013; revised May 18, 2013; accepted June 23, 2013
Copyright © 2013 Guilherme G. Ferrari et al. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
GEMINI + GMOS and Chandra emission-line spectroscopy reveal that the Fanaroff-Riley II radio-source J133658.3-
295105 is a local object behind the barred-spiral galaxy M83 that is projected onto the galaxy’s disk at about 60" from
the galaxy’s optical nucleus. J133658.3-295105 and its radiolobes are aligned with the optical nucleus of M83 and two
other radio-sources neither of which are supernova remnants or HII regions. The optical nucleus of M83 is off-centered
by 2.7" (≈60 pc) with regard to the kinematic center. Its mass is within the range (1 - 4) × 106 Mʘ and the velocity dis-
persion at its center points to a non-resolved mass concentration of ≤106 Mʘ. In this paper we study the circumstances in
which the radio source would have been ejected from the central region of M83. We analyze different types of colli-
sions of binary and triple systems of super-massive black holes (SMBHs) by numerical simulations using a Post-New-
tonian approximation of order 7/2 (~1/c7). We developed an N-body code specially built to numerically integrate the
Post-Newtonian equations of motion with a symplectic method. Numerical experiments show that the code is robust
enough to handle virtually any mass ratio between particles and to follow the interaction up to a SMBH separation of
three Schwarzschild radii. We show that within the current Post-Newtonian approximation, a scenario in which one of
the three SMBHs suffers a slingshot-like kick is best suited to explain the ejection of J133658.3-295105, which si-
multaneously produces the recoil of the remaining BH pair, which drags together a subset of stars from the original
cluster forming a structure that mimics the off-center optical nucleus of M83. The simulation parameters are tuned to
reproduce the velocities and positions of J133658.3-295105 as well as the optical nucleus and the putative SMBH at its
center.
Keywords: Galaxies; Nuclei; Dynamics; Black Holes Interaction; Kick-Off
1. Introduction
The presence of the 6.3 keV Fe-Kα emission constrained
the distance of the Fanaroff-Riley II radio source
J133658.3-295105 to the vicinity of M83 [1]. The source
also shows Hα in emission receding with a radial velocity
on the order of 100 - 150 km/sec with respect to M83 [2].
The morphology of the radio emission distribution that
protrudes along a line joining the optical nucleus of M83
and J133658.3-295105 [1,3] suggests that the compact
object has been ejected from the optical nucleus (ON),
which is itself off-set with respect to the galaxy’s kine-
matic center. The ON has a mass of (1 - 4) ×106 Mʘ [4,5]
and it presents a velocity dispersion [5,6] that is com-
patible with the presence of a super-massive black hole
with MSMBH ≤ 106 M
ʘ or a spatially unresolved mass
concentration located at its centre.
There is growing evidence that most galaxies host
super-massive black holes (SMBHs) at their centers. The
correlation between SMBH mass and bulge velocity
dispersion in spiral galaxies [7,8] points to a concurrent
evolution of these systems in a hierarchical scenario of
disk-galaxy formation [9]. A paradigmatic outcome of a
merger of BHs is the recoil of the resulting BH [10,11] in
response to the anisotropic emission of gravitational
waves [11]. These results raise the questions on how a
SMBH can grow at the center of a galaxy through BH-
pair fusion alone, and whether this kind of merger always
leads to an amount of gravitational wave radiation that
ejects the pair off the nucleus.
A triple-BH encounter extends the possible scenarios,
because the ejection of one of the participant BHs may
occur far in advance of the merger of the remaining two
objects [12]. A triple-BH encounter seems to best explain
the jet of M87 [13] and may also open up the possibility
of explaining the double nucleus galaxy CID-42 [14].
We consider the by-product of the BHs interaction to
be important for the case of M83. Consequently, as con-
C
opyright © 2013 SciRes. JMP

G. G. FERRARI ET AL. 56
straints in the present scenario, we look at the ejection of
J133658.3-295105, its velocity with respect to ON, its
mass derived [1] from models based on black hole kine-
matics and emissivity [15], the offset position of ON, the
presence of a putative BH at its center and the approxi-
mate mass of this BH [5]. We do not attempt at this
modeling stage of our simulation, to reproduce either the
double radio-sources’ ejection which characterizes the
object J133658.3-295105 as one of the kind Fanaroff-
Riley II object, or the alignment of its three components
with the projected direction of ejection from the optical
nucleus. We analyze different types of collisions of binary
and triple SMBHs through numerical simulations using a
Post-Newtonian approximation of order 7/2 (~1/c7). For
this purpose, one of us (GGF) developed an N-body code
specially suited for numerically integrating the Post-New-
tonian equations of motion. In Section 2 we present the nu-
merical method and the equations of motion. In Section 3
we present numerical experiments with isolated binary and
triple SMBHs. In Section 4 we present the N-body simula-
tions of the SMBHs embedded in a cluster. Finally, in Sec-
tion 5 we compare our results to the central region of M83.
2. Numerical Methods
In our approach, Post-Newtonian equations are employed
in all interactions in which at least one SMBH is present,
while interactions between individual stars are computed
in Newtonian form with a softening length ~1/N, where
N is the total number of particles. We use a symplectic
integration method based on the time-transformed leap-
frog scheme [16], modified to account for the correct
time symmetry of the Post-Newtonian equations during
the numerical solution. The time symmetry was accom-
plished by a semi-implicit trapezoidal rule, which results
in only one (Newtonian and Post-Newtonian) force cal-
culation per timestep, while keeping energy conservation
within a difference of ≤10−12 relative to the initial value.
The simulations ended when the particles reached separa-
tions of the order of 3 Schwarzschild radii or when the
end-time was reached. We emphasize that the symplectic
integrators respect the system’s Hamiltonian structure,
conserving the symplectic form itself.
2.1. Post-Newtonian Equations of Motion
The Post-Newtonian (PN) equations are obtained from
Itoh’s works [17,18], who derived expressions for two
body interactions only. Here, we propose a generalization
of Itoh’s formalism for N-body equations of motion:

2
d1
d
nij
i
i
ji ij
Gm m
v
r

ij
ij
ij
mA
B
tr


 






rv


, (1)
where
A
and contain the different PN orders and are
functions of .
B
,,,,,
jiji j
rrvv
i
mm
ij ji

rr and ij ji

vv
ij
, are the relative distance and
velocity of particles and .
122.5
24 5
33.5
67 8
111
11 1
PN PNPN
PN PN
AA AA
ccc
AAO
cc c


 


(2)
122.5
24 5
33.5
678
111
11 1
PN PNPN
PN PN
BB BB
ccc
BBO
cc c


 


(3)
Because General Relativity (GR) is a non-linear theory,
such approximation is not strictly valid. Nevertheless, the
lack of a practical relativistic formulation for N-body
simulations [19] led us to use the present set of equations.
The PN corrections are taken into account for all the
timesteps, but they are only significant in close encounters
involving at least one BH. According to [17,18], A and B
refers respectively to the static and kinetic parts of the
equations of motion. Integer order corrections such as
1PN, 2PN and 3PN cause pericenter advance in binary
systems; nevertheless, they are conservative in the sense
that they secularly preserve the orbit’s semi-major axis.
Half-integer order corrections 2.5PN and 3.5PN are re-
sponsible for the orbital energy dissipation resulting from
the emission of gravitational waves. In the present simula-
tions, the particles are point masses without spin. Spin
effects should appear as spin-orbit coupling in order
1.5PN, spin-spin coupling in order 2PN and in the terms
of the reaction to gravitational radiation 2.5PN and 3.5PN
[20]. Although successive PN corrections are a cones-
quence of GR effects, the resulting equations of motion
have to be interpreted in terms of Newtonian dynamics
[20] that is, once a convenient coordinate system is cho-
sen, the results can be expressed in terms of positions,
velocities and accelerations and visualized as trajectories
in an absolute Euclidean space. Nevertheless, as the
equations of motion are intrinsically relativistic they
must be Lorentz invariant, must hold the correct perturb-
bative limit given by the Schwarzschild’s metric geodetic
when one of the masses tends to zero and they must be
conservative. In other words, the equations of motion
must allow a Lagrangian or Hamiltonian formulation
when radiation-reactions terms are switched off. We also
remark that compared with Aarseth’s 2.5PN formulation
[21], which implements equations reduced to the center of
mass, our Post-Newtonian equations allow free election of
the coordinate system’s origin.
3. Numerical Experiments
We first treated the Keplerian problem, which gives re-
sults similar to those obtained by [16], effectively obtain-

G. G. FERRARI ET AL. 57
of binary gravitational recoil without spin, with eccentrici-
ties of e = 0 and e = 0.9. In both cases a total mass for the
binary mass Mbinary = 107 M
ʘ was adopted. The initial
distance between the binary components was given in
each case by d0 = 2 × 10−5 pc for e = 0 and d0 = 2 × 10−4 pc
for e = 0.9, which give clight = 6.46 and 20.44, respectively.
This choice led to a similar time of coalescence in both
cases. The upper panels in Figure 4 show the time evo-
lution of the orbital separation for e = 0 and e = 0.9 while
the lower panels show the center of mass recoil in a posi-
tion vs. velocity diagram. The oscillation of the center of
mass velocity is due to the continuous radiation of gravi-
tational waves, which occurs in the direction opposite that
of the orbital velocity. The amplitude of this oscillation is
amplified according to the orbital eccentricity. The final
plunges of both systems are practically similar.
ing energy conservation within the machine precision. In
what follows we consider the onset of PN corrections in
the Keplerian problem.
3.1. Keplerian Problem with Post-Newtonian
Corrections
We adopted units where the gravitational constant G = 1.
We take m1 = m2 = 1, the orbit eccentricity e = 0.9 and
semi-major axis a = 1.0526 which corresponds to an
initial relative distance d0 = 2. We arbitrarily adopted a
speed of light clight = 16. As a matter of comparison, a
binary system with joint mass Mbinary = 106 Mʘ and d0 = 1
pc results in light velocity clight ≈ 4571 in the adopted units
system. Figure 1 shows a PN-integration during 1000
orbital periods where only conservative terms were taken
into account. The left panel shows that energy is con-
served to a precision better than one part in 1010. This
warrants that without radiation terms, the orbital semi-axis
does not suffer secular variation, and that, as expected, the
binary does not decay. The right panel shows the orbital
precession for the first ten revolutions.
3.1.2. Gravitational Recoil of SMBH Triplets
The chaotic nature of the three-body problem makes it
practically impossible to sweep the whole set of parame-
ters in triple-SMBH systems. We instead choose two sys-
tems with well known Newtonian evolution. Furthermore,
these two systems differ greatly from the point of view of
orbital stability. The first system is composed of three
equal mass bodies, which move in an 8-like orbit. This
system is extremely robust against small perturbations
[24,25] in Newtonian systems. The second system is the
so-called Pythagorean system, in which masses with a
ratio of 3:4:5 are located at the vertices of a traingle
whose sides have sizes proportional to the mass located
at the opposite vertex. We ran two simulations for each
of these systems, and their parameters are shown in
Table 1.
We then integrated the same system with the complete
set of PN equations until reaching a BH separation of
three Schwarzschild radii (RSch). In Figure 2, we show the
final phase of the orbital in-spiraling due to the gravita-
tional radiation emission. This simulation compares quail-
tatively well with Boyle’s numerical integration of gen-
eral relativistic equations [22, his Figure 3]. In Figure 3
we show the evolution of the orbital separation against the
period. The zoom in the right panel shows the spatial
distance at which the PN approximation loses validity.
The cross shows a separation of three Schwarzschild radii,
which ocurred when the simulation was interrupted. Model M111a corresponds to an 8-like orbit in which
the intermediate body is initially at the center of mass.
This model was integrated for a period of ≈1.05 × 1010
years. After that period the PN system differs slightly
from the Newtonian system (Figure 5, left panel). Al-
though 8-like systems are difficult to form [26] in mergers
3.1.1. Gravitational Recoil of a SMBH Pair
It has been determined [23] that the maximum velocity of
recoil in a binary system occurs when the mass ratio is q ≈
0.382. We adopted this mass ratio and simulated two cases
Figure 1. Left: energy conservation for a Keplerian binary (e = 0.9) integrated with conservative PN terms; Right: the orbital
precession during the first ten orbits.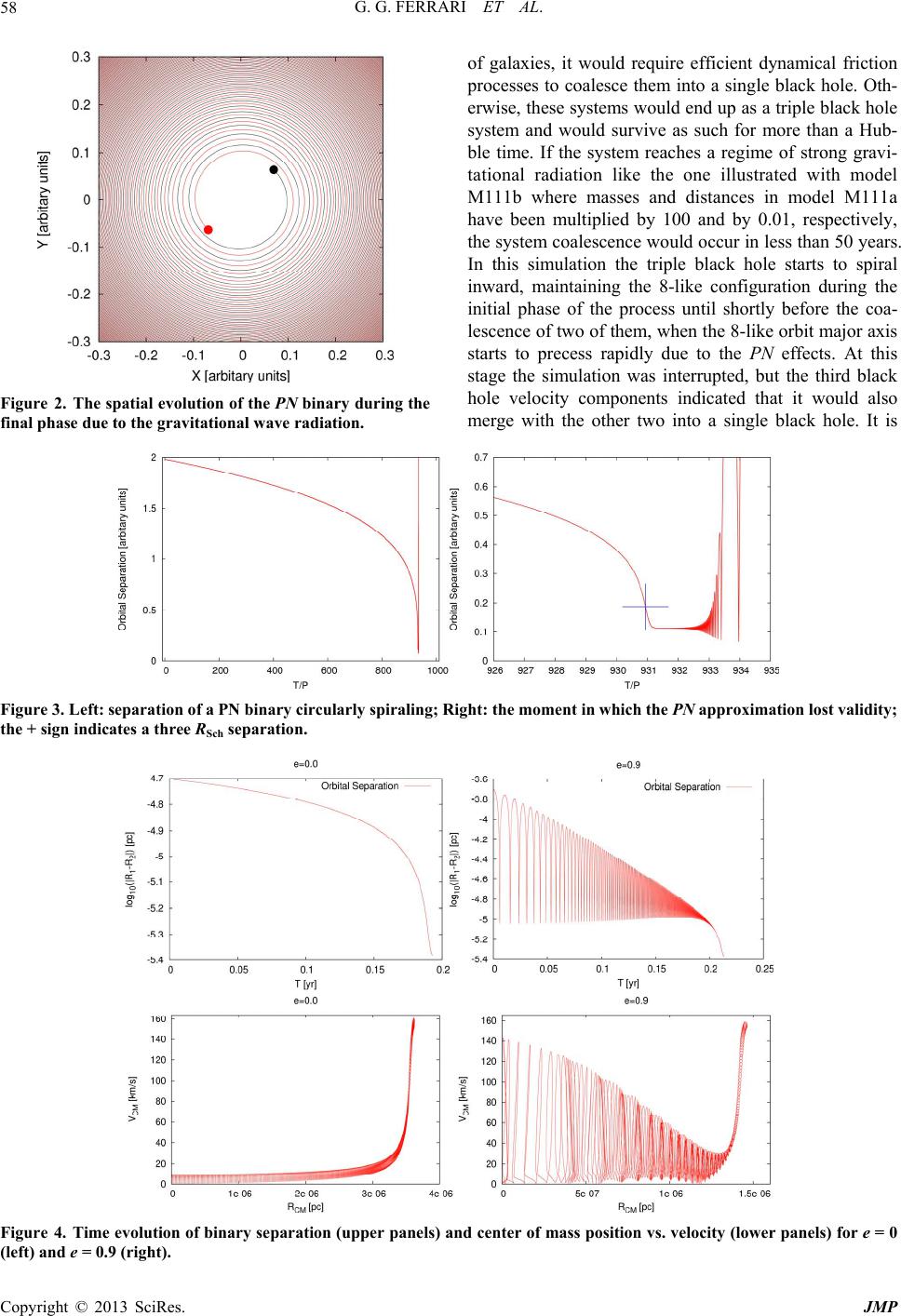

G. G. FERRARI ET AL. 58
Figure 2. The spatial evolution of the PN binary during the
final phase due to the gravitational wave radiation.
of galaxies, it would require efficient dynamical friction
processes to coalesce them into a single black hole. Oth-
erwise, these systems would end up as a triple black hole
system and would survive as such for more than a Hub-
ble time. If the system reaches a regime of strong gravi-
tational radiation like the one illustrated with model
M111b where masses and distances in model M111a
have been multiplied by 100 and by 0.01, respectively,
the system coalescence would occur in less than 50 years.
In this simulation the triple black hole starts to spiral
inward, maintaining the 8-like configuration during the
initial phase of the process until shortly before the coa-
lescence of two of them, when the 8-like orbit major axis
starts to precess rapidly due to the PN effects. At this
stage the simulation was interrupted, but the third black
hole velocity components indicated that it would also
merge with the other two into a single black hole. It is
Figure 3. Left: separation of a PN binary circularly spiraling; Right: the moment in which the PN approximation lost validity;
the + sign indicates a three RSch separation.
Figure 4. Time evolution of binary separation (upper panels) and center of mass position vs. velocity (lower panels) for e = 0
(left) and e = 0.9 (right).

G. G. FERRARI ET AL. 59
Figure 5. Left: orbital evolution during 1.05 × 1010 yr for model M111a. Right: orbital evolution of model M111b in which the
SMBH’s fusion occurs at ≈44.4 yr.
Table 1. Columns: 1) system type; 2) model (numbers refer
to mass ratio); 3) mass unit; 4) length unit; 5) speed of light
in system velocity units, which is defined by choosing [M]
and [L]).
System Model[M] (M◎) [L] (pc)clight
M111a 106 1 ≈4571
8-like configuration M111b108 0.001≈14.45
M345a 106 1 ≈4571
Pythagorean configuration M345b106 0.1 ≈1445
worth noting that in spite of the three masses being equal,
the gravitational recoil of the system is not inhibited,
because the presence of a third mass produces an asym-
metry in the emission of gravitational radiation.
Simulations of Pythagorean systems (models M345)
are presented in Figure 6. These kinds of systems are
more adequate for producing the ejection of the smaller
black hole in time intervals much shorter than the Hubble
time. Model M345a (Figure 6, upper left) initially evolves
like the Newtonian case. Nevertheless, the orbits are
deeply modified due to collisions with impact parameters
on the order of tens to hundreds RSch until the smallest of
the masses is kicked off from the system while the other
two follow as a binary black hole in the opposite direc-
tion. Due to the strong eccentricity of the pair orbit, they
reach the regime of strong gravitational radiation at
pericenter encounters (Figure 6, upper right) and they
finally merge in ≈ 7.38 × 104 years. The simulation was
interrupted when the distance reached 3 RSch. The total
simulation time was 5.27 × 105 years. The comparison of
the binary black hole coalescence time with Peter’s
formulae [27] suggests an orbital eccentricity as high as e
≈ 0.999 - 0.9999. The velocity of the smallest black hole
at the moment of ejection was ≈253 km/s while the black
hole pair recoils in the opposite direction at ≈84 km/s.
Model M345b represents a system in which distances
were diminished by a factor of ten (Figure 6, lower
panels). In this model an almost frontal collision between
the two more massive SMBHs leads to their coalescence
in ≈7.1 years.
4. N-Body Simulations Including SMBHs
4.1. Observational Constraints
The mass of ON has been estimated between 106 Mʘ and
(4 ± 2) × 106 Mʘ [5]. ON hosts a putative SMBH with a
mass of ≤106 Mʘ [5,6]. J133658.3-295105 is located at a
projected distance of approximately 1 kpc from ON,
receding with a radial velocity VR ≈ 130 km/s [2]. Using
Fujita’s model [15], the X-ray luminosity of J133658.3-
295105 was reproduced [1] with a SMBH mass on the
order of ≈106 M
ʘ moving at VR ≈ 250 km/s and an
inclination of 30˚ with respect to the galactic disk, which
fits well the observed radial velocity of J133658.3-
295105.
In the next Section we model the whole system with
the black holes embedded in a star cluster.
4.2. N-Body Simulation of a SMBH Triplet
Embedded in a Star Cluster
We performed N-body simulations of a star cluster con-
taining SMBHs to study the behavior of the system. Of
particularly importance was finding out if we could re-
produce the ejection of an object like J133658.3-295105
and its kinematics as well as find out if the position of
the off-centered nucleus might be a consequence of the
process of the SMBHs ejection. We constructed a sphere-
cal distribution of equal masses according to a Hernquist
profile [28] and an isotropic velocity distribution such
that the system is in initial virial equilibrium. We fol-
lowed prescriptions similar to those used by [29] for a
Plummer profile. The experiments were performed by
inserting different configurations of black holes and con-
straining their centers of mass to coincide with the clus-
ter’s potential center. In parallel, a rescaling was applied
to the positions and velocities in order to re-establish the
virial equilibrium of the whole (stars + SMBHs) system.
In Table 2, we present the models for the SMBHs con-
figurations M111 and M345. The parameter clight practi-
cally determines the SMBH system compactness, which

G. G. FERRARI ET AL. 60
Figure 6. Upper panels: orbital evolution of model M345a. The simulation lasts ≈5.27 × 105 yr. Upper right: we detached the
final coalescence phase of the more massive SMBHs pair, which took 7.38 × 104 yr. Lower panels: orbital evolution for 2646 yr
for model M345b. Lower right: final coalescence phase that took only 7.1 yr.
Table 2. Columns: 1) Model denomination (suffix a or b
only refers to the random numbers sequence used in their
construction); 2) Total number of particles (stars + 3 SMBHs);
3) Ratio between the SMBHs’ masses and the cluster total
mass (stars + 3 SMBHs); 4) Mass unit; 5) Length unit; 6)
speed of light in system velocity units, which is defined by
the choice of [M] and [L].
Model N MBH/Mclus [M] (M◎) [L] (pc)clight
M111-4k-20a 4096 0.2 107 10 ~4571
M111-4k-20b 4096 0.2 107 10 ~4571
M111-4k-25a 4096 0.25 8 × 106 10 ~5111
M111-4k-25b 4096 0.25 8 × 106 10 ~5111
M111-8k-25 8192 0.25 8 × 106 10 ~5111
M345-4k-20a 4096 0.2 107 10 ~4571
M345-4k-20b 4096 0.2 107 10 ~4571
M345-4k-25a 4096 0.25 8 × 106 10 ~5111
M345-4k-25b 4096 0.25 8 × 106 10 ~5111
M345-8k-25 8192 0.25 8 × 106 10 ~5111
allows a comparison with the isolated SMBH systems
quoted in Table 1 and discussed in the previous sections.
For the present simulations, we adopted a precision pa-
rameter η such that the energy error results are smaller
than 10−6 throughout the process. The adopted softening
parameter for the stars was ε = 4/N.
Figure 7 shows the evolution of the central SMBHs in
model M111-4k-25a. At approximately 1.4 Myr, two of
the SMBHs are ejected, reaching distances on the order
of 1 kpc in a time >10 Myr. The third SMBH remained in
the cluster center. As a consequence of the ejection, the
cluster swells up slightly. Figure 8 shows the evolution
of model M345-8k-25. At approximately 0.8 Myr, one of
the SMBHs is ejected, reaching distances on the order of
1 kpc in approximately 20 Myr. The remaining pair be-
came more bounded, showing that part of the ejection
energy was gained to the expense of their potential en-
ergy. The binary SMBH migrates and drags out a part of
the central cluster. The remainder of the cluster swells up
significantly. The binary SMBH becomes increasingly
bounded without reaching the strong gravitational radia-

G. G. FERRARI ET AL. 61
Figure 7. Snapshots of the evolution of the 8-like model M111-4k-25a. We show that two of the three equal mass SMBHs are
ejected in opposite directions, leaving the third at the center of the distribution of stars that swell up slightly but otherwise
remain centered at the original position.
Figure 8. We show the evolution of the Pythagorean system M345-8k-25. The M2 = 4 flies out, while the remaining pair M1 + M3
= 8 recoil more slowly, dragging a part of the embedding cluster.
tion regime in this period. It is worth noting that in this
case the ejected SMBH was the M2 = 4, and the SMBH-
pair that remained bound was the M1 + M3 = 8. For all
models the ejection of the isolated SMBH occured in ap-
proximately 0.1 to 2 Myr, reaching distances of 0.4 to 4
kpc until the end of the simulation.
Figure 9 shows the radial evolution of systems M111-
4k-25a and M345-8k-25. The SMBH velocities at the
ejection instant for the different models are presented in
Table 3. We note that the drag out of a part of the central
cluster only occurs if the velocity of the recoil of the
SMBH pair is up to about 1.5 times the initial velocity
dispersion of the star cluster.
5. Results and Discussion
In this paper we extended Itoh’s 3.5PN equations of mo-
tion to treat N-body problems. We study the behavior of
2-body and 3-body SMBH systems. For 3-body systems
we studied two idealized configurations, namely, the 8-
like system, with three equal mass bodies and the Py-
thagorean system with masses in the ratio 3:4:5.
Within the current PN approximation, the scenario with

G. G. FERRARI ET AL. 62
Figure 9. Time evolution of the radial position of each of the SMBHs for models M111-4k-25a (left) and M345-8k-25 (right).
Table 3. SMBH velocities at the moment of ejection for different models. Velocities are given in km/sec and relative to the
cluster’s initial velocity dispersion

0. Presented velocities correspond to the remaining SMBH center of mass, and values in
parenthesis correspond to the slingshotted SMBHs.
M111-4k-20a M111-4k-20b M111-4k-25a M111-4k-25b M111-8k-25
V (km/s) 89 (191) 58 (116) 12 (97,104) 97 (193) 48 (96)
V/ 
0 1.35 (2.91) 0.88 (1.77) 0.21 (1.64,1.76) 1.65 (3.29) 0.81 (1.63)
M345-4k-20a M345-4k-20b M345-4k-25a M345-4k-25b M345-8k-25
V (km/s) 51 (153) 69 (219) 43 (129) 39 (113) 62 (125)
V/ 
0 0.78 (2.33) 1.05 (3.34) 0.73 (2.20) 0.66 (1.92) 1.05 (2.13)
three SMBHs is best suited to explain the ejection of a
single SMBH. This kick-off reproduces well the projected
present position and the motion of the object J133658.3-
295105 away from the ON. The displacement of part of
the embedding cluster that accompanies the pair of re-
maining SMBH ranges over radial distances of 30 - 200 pc
on a timescale of 2 × 107 yr, which is in agreement with
the on-the-sky projected distance of the ON from the
kinematic center of M83 (60 pc). The accompanying
cluster can be dragged out if the recoil velocity of the
SMBH is less than ~1.5 times the initial velocity disper-
sion of the stars in the original cluster.
This simulation also furnishes a counterpart for the
mass concentration located at the kinematical center of
M83 [6], which is more extended than the ON [5]. This
feature is produced in the model by the remains of the
original star cluster, which swells up and stays centered
at the former kinematical center position.
Our results show that in 3-body SMBH systems the
recoil of an object like J133658.3-295105 may happen far
in advance of the strong gravitational wave radiation
regime.
Although the three SMBH models treated here are
idealistic, it is easy to see that one can construct more
realistic models that vary the mass ratios as well as their
configurations. Though a wider range of configurations
can be analyzed, we do not expect to achieve radically
different results than those presented here.
6. Acknowledgements
GGF and HAD thank CNPq, Brazil, for financial support
in the form of a fellowship and a research grant, respec-
tively. RD acknowledges support from the SECYT at the
National University of Cordoba and CONICET through
PIP-0523. The computation was carried out at CESUP-
UFRGS, Brazil.
REFERENCES
[1] H. Dottori, R. Diaz, J. Albacete-Colombo and D. Mast,
The Astrophysical Journal, Vol. 717, 2010, pp. L42-L46.
doi:10.1088/2041-8205/717/1/L42
[2] H. Dottori, R. Diaz and D. Mast, The Astronomical Jour-
nal, Vol. 136, 2008, pp. 2468-2472.
doi:10.1088/0004-6256/136/6/2468
[3] L. Maddox et al., The Astronomical Journal, Vol. 132,
2006, pp. 310-320. doi:10.1086/505024
[4] D. Elmegreen, F. Chromey and A. Warren, The Astro-
nomical Journal, Vol. 116, 1998, pp. 2834-2840.
doi:10.1086/300657
[5] I. Rodrigues, H. Dottori, R. Díaz, M. Agüero and D. Mast,
The Astronomical Journal, Vol. 137, 2009, pp. 4083-
4090. doi:10.1088/0004-6256/137/5/4083
[6] N. Thatte, M. Tecza and R. Genzel, Astronomy & Astro-

G. G. FERRARI ET AL. 63
physics, Vol. 364, 2000, pp. L47-L53.
[7] L. Ferrarese and D. Merrit, The Astrophysical Journal
Letters, Vol. 539, 2000, pp. L9-L12. doi:10.1086/312838
[8] K. Gebhardt, et al., The Astrophysical Journal Letters,
Vol. 539, 2000, pp. L13-L16. doi:10.1086/312840
[9] T. Okamoto, R. Nemmen and R. Bower, Monthly Notices
of the Royal Astronomical Society, Vol. 385, 2008, pp.
161-181. doi:10.1111/j.1365-2966.2008.12883.x
[10] E. Bonning, G. Shields and S. Salviander, The Astrophy-
sical Journal Letters, Vol. 666, 2007, pp. L13-L16.
doi:10.1086/521674
[11] L. Blecha and A. Loeb, Monthly Notices of the Royal
Astronomical Society, Vol. 390, 2006, pp. 1311-1325.
[12] M. Iwasawa, Y. Funato and J. Makino, The Astrophysical
Journal, Vol. 651, 2006, pp. 1059-1067.
doi:10.1086/507473
[13] D. Batcheldor, A. Robinson, D. Axon, E. Perlman and D.
Merritt, The Astrophysical Journal Letters, Vol. 717,
2010, pp. L6-L10. doi:10.1088/2041-8205/717/1/L6
[14] F. Civano, et al., The Astrophysical Journal, Vol. 717,
2010, pp. 209-222. doi:10.1088/0004-637X/717/1/209
[15] Y. Fujita, The Astrophysical Journal, Vol. 691, 2009, pp.
1050-1057. doi:10.1088/0004-637X/691/2/1050
[16] S. Mikkola and S. Aarseth, Celestial Mechanics and
Dynamical Astronomy, Vol. 84, 2002, pp. 343-354.
[17] Y. Itoh, Physical Review D, Vol. 69, 2004, Article ID:
064018.
[18] Y. Itoh, Physical Review D, Vol. 80, 2009, Article ID:
124003.
[19] Y. Chu, Physical Review D, Vol. 79, 2009, Article ID:
044031.
[20] L. Blanchet, Living Reviews in Relativity, Vol. 9, 2006.
doi:10.12942/lrr-2006-4
[21] S. Aarseth, Monthly Notices of the Royal Astronomical
Society, Vol. 378, 2007, pp. 285-292.
doi:10.1111/j.1365-2966.2007.11774.x
[22] M. Boyle, et al., Physical Review D, Vol. 76, 2007,
Article ID: 124038.
[23] M. Fitchett, Monthly Notices of the Royal Astronomical
Society, Vol. 203, 1983, pp. 1049-1062.
[24] C. Moore, Physical Review Letters, Vol. 70, 1993, pp.
3675-3679. doi:10.1103/PhysRevLett.70.3675
[25] A. Chenciner and R. Montgomery, Annals of Mathe-
matics, Vol. 152, No. 3, 2000, pp. 881-901.
doi:10.2307/2661357
[26] D. Heggie, Monthly Notices of the Royal Astronomical
Society, Vol. 318, 2000, pp. L61-L63.
doi:10.1046/j.1365-8711.2000.04027.x
[27] P. Peters, Physical Review, Vol. 136, 1964, pp. B1224-
B1232. doi:10.1103/PhysRev.136.B1224
[28] L. Hernquist, The Astrophysical Journal, Vol. 356, 1990,
pp. 359-364. doi:10.1086/168845
[29] S. Aarseth, M. Henon and R. Wielen, Astronomy & As-
trophysics, Vol. 37, 1974, pp. 183-187.