World Journal of Mechanics, 2013, 3, 230-235
doi:10.4236/wjm.2013.34023 Published Online July 2013 (http://www.scirp.org/journal/wjm)
The Numerical Simulation of Gas Turbine Inlet-Volute
Flow Field
Tao Jiang1, Kezhen Huang2
1Military Representative Office at the 426 Shipyad, Dalian, China
2China Ship Development and Design Center, Wuhan, China
Received April 18, 2013; revised May 20, 2013; accepted May 27, 2013
Copyright © 2013 Tao Jiang, Kezhen Huang. This is an open access article distributed under the Creative Commons Attribution Li-
cense, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
The structural and aerodynamic performance of the air inlet volute has an important influence on the performance of the
gas turbine. On one hand, it requires the airflow flowing through inlet volute as even as possible, in order to reduce the
pressure loss, to avoid a decrease in the effective output power and an increase of the fuel consumption rate of the in-
ternal combustion engin e which indicate the inefficiency of the en tire power unit; On the other hand, it requires the size
of the inlet volute to be as small as possible in order to save mounting space and production costs. The thesis builds the
structure model and develops flow fields numerical simulation of several different sizes of the inlet volutes. Further, the
unreasonable aerodynamic structure is improved according to the flow field characteristics and thereby, a better aero-
dynamic performance of the inlet volute is obtained.
Keywords: Axial Flow Compressor; Inlet Volute; Numerical Simulation; Pressure Loss; Uneven Degree
1. Introduction
The inlet volute structure and aerodynamic performance
is an important part of the gas turbine research [1]. Most
researches has focused on the impeller for the thought
that impeller has a greater impact on the compressor per-
formance so that the studies on the airflow of inlet volute
are fewer. Actually, inlet volute also has an important
impact on compressor performance. On one hand, it re-
quires that the airflow thr ough the inlet volute as even as
possible, the pressure loss as small as possible in order to
avoid the reduced efficiency of the entire power plant;
On the other hand, the size of the inlet volute should be
as small as possible to make it easier to arrange under the
premise of ensuring the performance requirements [2].
The evenness of air intake which influences the surge
line of compressor directly is one of the main factors to
ensure the normal operation of combustion engine. Gen-
erally, the flow field uneven degree value of the com-
pressor inlet volute outlet surface should be less than
15%. The pressure loss should be as small as possible
and the common design demands the total pressure loss
of entire air intake system (including the inlet volute and
other resistance units) not exceeds the maximum value
75 mm H2O. The thesis predicts the performance of a
certain type inlet volute, analyzes the internal flow
field characteristics to get the even degrees of inlet volute
at the outlet by means of numerical simulations which
provide a reliable basis for the manufacture of high-per-
formance inlet volute [3].
Volute is an important part of powered mechanical
plant which has applications in many fluid machineries,
such as centrifugal pumps, turbine, compressor, centri-
petal turbine etc. Though the volute is a stationary unit
for turbomachinery, its internal flow is a kind of three-
dimensional and vortex flow phenomenon [4]. The vo-
lute internal flow study focused on theoretical and ex-
perimental research early and theoretical study and de-
sign mostly based on the axisymmetric assumption of
free viscous flow and the runner outlet flow [5,6]. But it
is difficult to obtain a precise description of volute flow
through traditional methods for the sticky characteristic
in the actual flow and the volute inlet unevenness be-
cause of the limited number of leaves. With the devel-
opment of computer technology and computational fluid
dynamics, numerical methods have become an important
tool in the study of volute flows [7]. The studies of vo-
lute flow play a significant role for improving the effi-
ciency and performance of turbomachinery. Therefore, to
improve the efficiency of the volute and the volute de-
sign theory, experts and scholars at home and abroad

T. JIANG, K. Z. HUANG 231
have done a lot of work. They mainly concentrate on
three aspects:
1) Experimental test of the volute flow field;
2) Numerical simulation of the volute flow field;
3) Study on volute geometric characteristics .
2. Mathematical Calculation Model
Based on the inlet volute flow field aerodynamic charac-
teristics, it can be viewed as compressible viscous flow.
The conservative mass, momentum, and energy equa-
tions of full gas ignoring mass force and with constant
heat transfer coefficient
p
C and
F
C are:

p*
t

 
u0
(1)
   
pI
t

 
uuu

(2)

 
EE pI
t

 

uuq
(3)
For compressible gas, state equation connecting den-
sity and pressure (static pressure) should also be regarded
as a part of control equation.
In the above equation,

ij
I

 is unit tensor;

ij

 is viscous stress tensor. For the Newton fulid:
2
3
j
ii
in
ij
u
uu
uu
i
x
xx












 (4)

i
qq is heat flux vector. Assuming the fluid com-
ply with Fourier heat transfer law:
K
T q (5)
1
e2 E uu is the total energy of unit fluid and
e is the internal energy of unit mass of fluid. This is
Navier-Stokes equation of compressible viscous gas ig-
noring mass force.
For compressible gas, state equation should also be re-
garded as a part of control equation. Therefore,
pRT

 (6)
in the equation:

—density;
u—velocity vector;
p—pressure;
e—internal energy of unit mass of fluid;
K—thermal conductivity;
T—temperature;

—dynamic viscosity coefficient.
The dynamic viscosity coefficient varies with the tem-
perature change. Its value can be obtained through the
Sutherland equation generally used in engineering:

32
0
00
S
S
uT TT
T
uTTT
 
 
 (7)
In the equation, T0 = 273.15 K; Ts is the Sutherland
constant. Ts = 110.4 K in the air; μ0 is the dynamic vis-
cosity coefficient at an atmospheric pressure and tem-
perature of 273.15 K.
The thesis employs the Favre average because the flow
simulating is compressible. In fact, the Favre average is
time average for instantaneous pressure and density but
mass weighted average for other variables.
Firstly, the definition of Renault average is
 
2*
2
,,
t
t
ld
x
tx
t


  
ttt (8)
In the equation, t

is the time period which is large
enough compared with pulsation period of speed but
small enough as compared with the flowing size of the
macroscopic time. In the processing of the experiment
data, the exact selection of is very important, but
there is no need to care about its va lue du e to the ab sence
of
t
t

in the turbulence model.
The definition of mass weighted average is:
 
 
2*
2
2**
2
,,
,,
t
t
t
t
l
xtxt tt
t
l
d
d
x
tx
t







 


 


ttt
(9)
In the equation, *

  is the average velocity ac-
cording to the definition of Renault average.
Time average the control equations based on the Favre
average method, then we get the following form:

p*
t

0


v (10)
  

ij
pIpu u
t




 
uuu (11)
 
 j
EE
i
t
pIpu uq





 


，，
u (12)
pRT

 (13)
As indicated of the mass weighted averaged control
equations, they become not closed, because of a new
unknown quantity wh ich is a kind of stress caused by the
turbulent fluctuation called Renault stress. To make the
equations closed, a certain assumption must be made,
namely the establishment of the expression of the stress
(or the introduction of new turbulence model). The value

T. JIANG, K. Z. HUANG 232
of turbulent fluctuation and the average time can be
linked through these expressions or turbulence model
equations. There is no specific laws of physics can be
used to create turbulence model, therefore, the current
turbulence model can only be based on experimental ob-
servations.
According to Boussinesq and theoretical assumptions
of molecular motion:
2
3
j
ii
ijiij iij
jji
u
uu
uu uu
xxx
2
3






 




 (14)
In the equation, i different to u is the eddy vis-
cosity coefficient which is a function of the spatial coor-
dinates, depending on the flow state rather than a physi-
u
cal parameter.

222
1
2ijk
kuuu

 is the fuctuating
kinetic energy of unit mass fluid turbulence.
Now, define

222
1
33
tijk
puuu 2 k



and sub-
stitute (2.14) into the control equations:

p*
t

 
u0
(15)
   
eff
p
t

 
uuu

(16)
 

eff
EE
t
pI uq



  

u (17)
pRT

 (18)
In the equations, is a combined effective pres-
sure of and . eff
p
pt
p
2
3
eff t
ppp k

  (19)
Further , f or the

ij


 
2
3
j
ki
iji iji
kj
u
uu
uu uu
i
x
xx

 








(20)
Thereby, if the effective viscosity coefficient
, substitute it into the above equation, we get:
eff t
uuu
2
3
j
ki
ijeffij eff
kj
u
uu
uu
i
x
xx

 








(21)
So, the control equations of (15)-(18) are identical to
the formulas of (1)-(3), (6).
3. Numerical Modeling and Simulation
Two volute models are designed according to the turbine
shape and the inlet volute whose intake port is designed
in a circular shape is named Type A. The geometric
model in Figure 1.
Due to the irregularity of the model structure, it is dif-
ficult to generate the overall structure of the mesh. So it
is necessary to do the segmentation processing, then the
regular structures generate the structural mesh and the
irregular structures generate non-structural mesh. Note
that we must act from input to output, output to input or
from the middle to both sides to generate the mesh. The
mesh number is between 20 to 30 million. The results are
shown in Figure 2.
According to the model characteristics and perform-
ance requirements of an ideal gas as working fluid, the
given boundary conditions are as follows:
Input: mass flow inlet, the total temperature of 300 K;
Output: pressure on exports, the total temperature of
300 K, to adjust the inlet mass flow rate so that the exit
velocity can reach 100 m/s;
Solid wall: adiabatic, no-slip.
Make the numerical simulation of volute flow field
according to the control equations of the Favre averaged
Figure 1. Type A turbin volute.
Figure 2. Type A model mesh.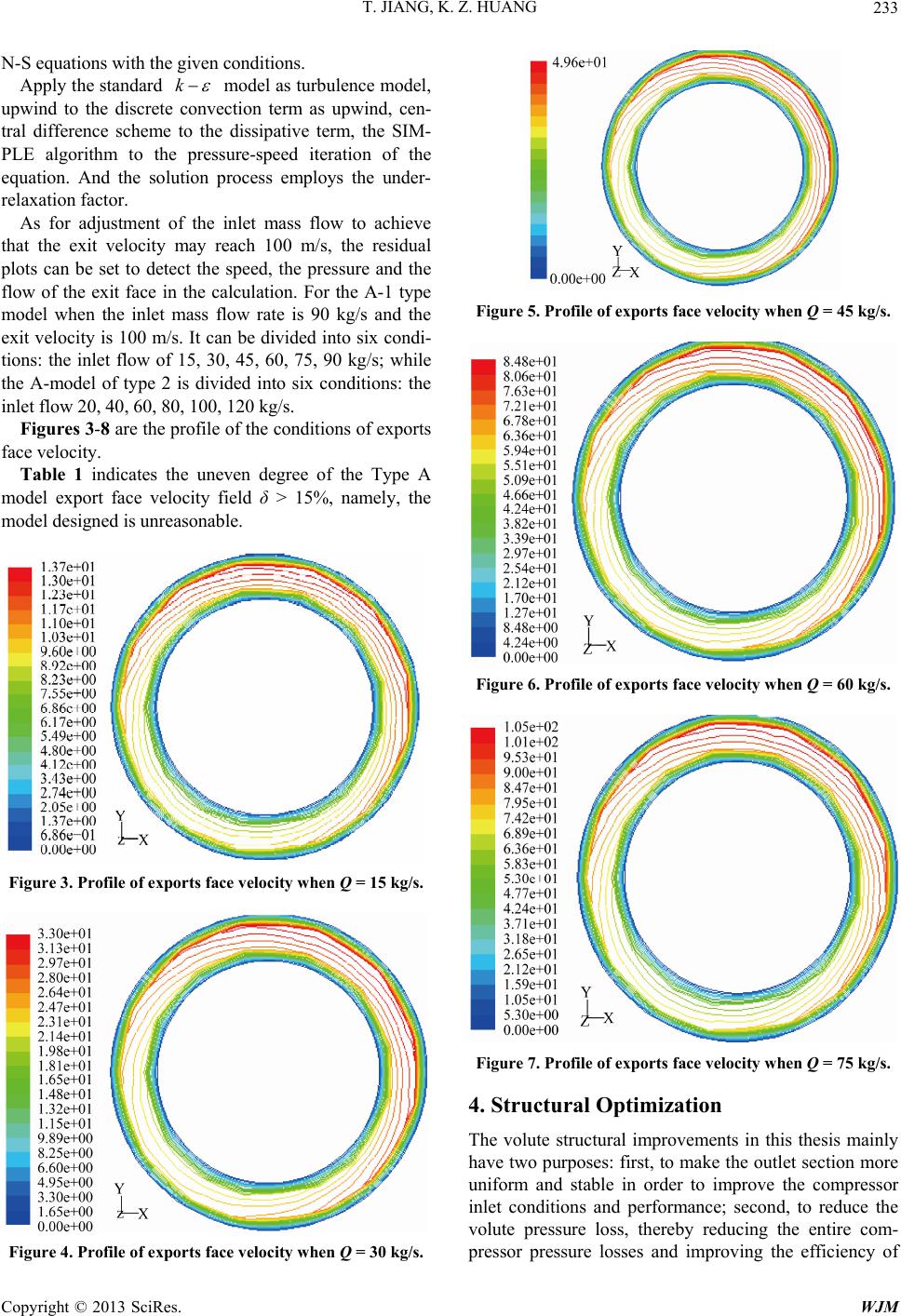

T. JIANG, K. Z. HUANG 233
N-S equations with the given conditions.
Apply the standard k

 model as turbulence model,
upwind to the discrete convection term as upwind, cen-
tral difference scheme to the dissipative term, the SIM-
PLE algorithm to the pressure-speed iteration of the
equation. And the solution process employs the under-
relaxation factor.
As for adjustment of the inlet mass flow to achieve
that the exit velocity may reach 100 m/s, the residual
plots can be set to detect the speed, the pressure and the
flow of the exit face in the calculation. For the A-1 type
model when the inlet mass flow rate is 90 kg/s and the
exit velocity is 100 m/s. It can be divided into six condi-
tions: the inlet flow of 15, 30, 45, 60, 75, 90 kg/s; while
the A-model of type 2 is divided into six conditions: the
inlet flow 20, 40, 60, 80, 100, 120 kg/s.
Figures 3-8 are the profile of the conditions of exports
face velocity.
Table 1 indicates the uneven degree of the Type A
model export face velocity field δ > 15%, namely, the
model designed is unreasonable.
Figure 3. Profile of exports face velocity when Q = 15 kg/s.
Figure 4. Profile of exports face velocity when Q = 30 kg/s.
Figure 5. Profile of exports face velocity when Q = 45 kg/s.
Figure 6. Profile of exports face velocity when Q = 60 kg/s.
Figure 7. Profile of exports face velocity when Q = 75 kg/s.
4. Structural Optimization
The volute structural improvements in this thesis mainly
have two purposes: first, to make the outlet section more
uniform and stable in order to improve the compressor
inlet conditions and performance; second, to reduce the
volute pressure loss, thereby reducing the entire com-
pressor pressure losses and improving the efficiency of

T. JIANG, K. Z. HUANG 234
Figure 8. Profile of exports face velocity when Q = 90 kg/s.
Table 1. Profile of exports face velocity when Q = 90 kg/s.
average max min
condition Entrance
flow m/s
The average
quality
1 15 15.54 16.36 13.52 18.28
2 30 31.48 33.98 27.82 19.06
3 45 47.85 49.75 41.76 19.16
4 60 65.48 67.96 56.46 19.29
5 75 83.10 86.21 71.42 19.09
6 90 101.27 104.17 84.93 19.11
compressor machine.
The pressure loss is mainly from the fluid turbulence
and the solid wall friction, therefore, the pressure energy
is scattered in the form of heat. In order to reduce the
pressure loss, strong turbulence of volute flow field
should be avoided, such as adding an air guide structure
in the airflow steering to slow the changes of the flow
field or improving structure components prone to cause
strong vortex.
Modifying the import and export is shown in Figure 9.
Make the numerical simulation of volute flow field
according to the control equations of the Favre averaged
N-S equations with the given conditions.
Apply the standard k

 model as turbulence model,
upwind to the discrete convection term as upwind, cen-
tral difference scheme to the dissipative term, the SIM-
PLE algorithm to the pressure-speed iteration of the
equation. And the solution process employs the under-
relaxation factor. As for adjustment of the inlet mass
flow to achieve that the exit velocity may reach 100 m/s,
it can be set to detect the speed, the pressure and the flow
of the exit face and in the calculation.
From the pressure loss comparison in Figure 10, the
pressure loss of Type B is the minimum. Based on the
average unevenness and pressure loss of each model, the
inlet volute should be designed in tapering structure
Figure 9. Type B mode.
Figure 10. Resistance characteristic curve of Type B model.
which can reduce the average unevenness of the model.
The former have required the unevenness of the volute to
be less than 15%. From the pressure loss analysis, the
inlet volute designed in tapering structure which in-
creases the pressure loss, however has relative little pres-
sure loss, so the Type B model is the prior model for the
improvement. The results could been seen in the Tables
2 and 3.
5. Conclusions
This thesis studies the inlet volute flow field characteris-
tics of compressor using numerical simulation method
and improves the volute structure. The conclusions are
summarized as follows:
1) Make numerical simulation on the compressor inlet
volute initial model and analysis of the characteristics of
about the volute structure improvement.
2) Make a variety of improvement attempts on the vo-
lute structure and improve numerical simulations under
the same conditions for each. The numerical simulation
results indicate that the tapered-structure volute reduces
the average unevenness of the outlet face while increases
the value in the outlet channel if adding a baffle.
3) The numerical simulation results on the improved
model structure after refinement show that the uneven-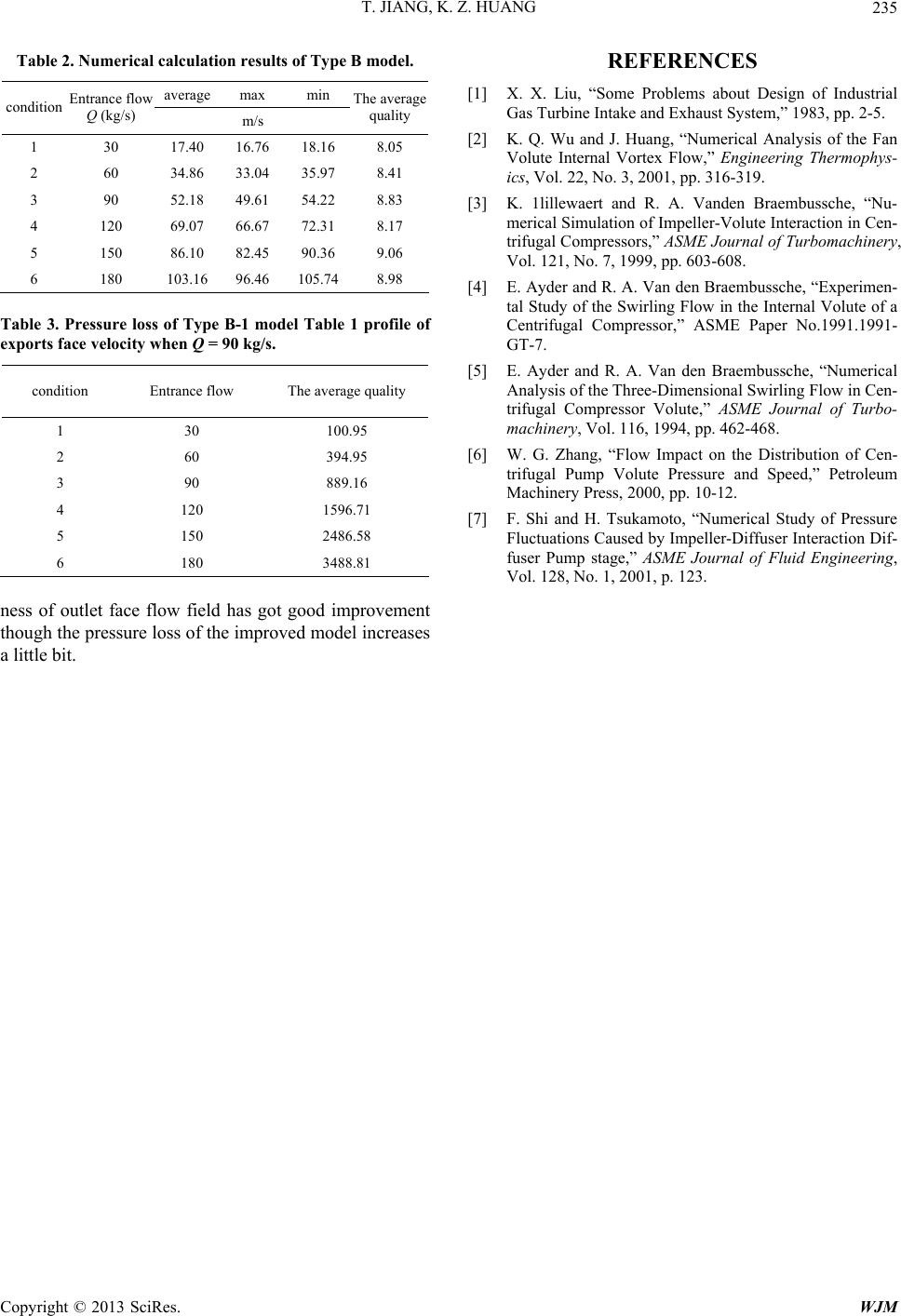

T. JIANG, K. Z. HUANG 235
Table 2. Numerical calculation results of Type B model.
average max min
condition Entrance flow
Q (kg/s) m/s
The average
quality
1 30 17.40 16.76 18.16 8.05
2 60 34.86 33.04 35.97 8.41
3 90 52.18 49.61 54.22 8.83
4 120 69.07 66.67 72.31 8.17
5 150 86.10 82.45 90.36 9.06
6 180 103.16 96.46 105.74 8.98
Table 3. Pressure loss of Type B-1 model Table 1 profile of
exports face velocity when Q = 90 kg/s.
condition Entrance flow The average quality
1 30 100.95
2 60 394.95
3 90 889.16
4 120 1596.71
5 150 2486.58
6 180 3488.81
ness of outlet face flow field has got good improvement
though the pr essure loss of the improved model increases
a little bit.
REFERENCES
[1] X. X. Liu, “Some Problems about Design of Industrial
Gas Turbine Intake and Exhaust System,” 1983, pp. 2-5.
[2] K. Q. Wu and J. Huang, “Numerical Analysis of the Fan
Volute Internal Vortex Flow,” Engineering Thermophys-
ics, Vol. 22, No. 3, 2001, pp. 316-319.
[3] K. 1lillewaert and R. A. Vanden Braembussche, “Nu-
merical Simulation of Impeller-Volute Interaction in Cen-
trifugal Compressors,” ASME Journal of Turbomachinery,
Vol. 121, No. 7, 1999, pp. 603-608.
[4] E. Ayder and R. A. Van den Braembussche, “Experimen-
tal Study of the Swirling Flow in the Internal Volute of a
Centrifugal Compressor,” ASME Paper No.1991.1991-
GT-7.
[5] E. Ayder and R. A. Van den Braembussche, “Numerical
Analysis of the Three-Dimensional Swirling Flow in Cen-
trifugal Compressor Volute,” ASME Journal of Turbo-
machinery, Vol. 116, 1994, pp. 462-468.
[6] W. G. Zhang, “Flow Impact on the Distribution of Cen-
trifugal Pump Volute Pressure and Speed,” Petroleum
Machinery Press, 2000, pp. 10-12.
[7] F. Shi and H. Tsukamoto, “Numerical Study of Pressure
Fluctuations Caused by Impeller-Diffuser Interaction Dif-
fuser Pump stage,” ASME Journal of Fluid Engineering,
Vol. 128, No. 1, 2001, p. 123.