Open Journal of Applied Sciences, 2013, 3, 270-277
doi:10.4236/ojapps.2013.33034 Published Online July 2013 (http://www.scirp.org/journal/ojapps)
Mean-Field Solution of the Mixed Spin-2 and Spin-5/2
Ising Ferrimagnetic System with Different
Single-Ion Anisotropies
Fathi Abubrig
Department of Physics, Faculty of Science, Elmergeb University, Zliten, Libya
Received December 26, 2012; revised February 13, 2013; accepted February 20, 2013
Copyright © 2013 Fathi Abubrig. This is an open access article distributed under the Creative Commons Attribution License, which
permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
The mixed spin-2 and spin-5/2 Ising ferrimagnetic system with different anisotropies
(
A
DzJ
)
for the spin-2 and
()
for the spin-5/2 is studied by the use of the mean-field theory based on the Bogoliubov inequality for the free
energy. First, the ground state phase diagram of the system at zero temperature is obtained on the
B
DzJ
()
,
AB
DzJDzJ
, different kinds of phase diagrams are achieved by changing the temperature and the values of the
single ion anisotropies
plane. Topologically
A
DzJ and B Dz des secr transition lines, first order phase transition lines
terminating at tricritical points, are found. The existence and dependence of a compensation temperature on single-ion
anisotropies is also investigated.
J. Besiond-orde
Keywords: Mixed Spin; Ising Model; Ferrimagnetic; Sublattice Magnetization; Tricritical Points
1. Introduction
In the last two decades, much attention has been paid to
the study of the magnetic properties of two-sublattice
mixed-spin ferrimagnetic Ising systems, because they are
well adapted to consider some types of ferrimagnetism,
namely the molecular-based magnetic materials [1-3]
which have less translational symmetry than their single-
spin counterparts since they consist of two interpenetrat-
ing sublattices and have increasing interest. In a ferri-
magnetic material, the different temperature dependences
of the sublattice magnetizations raise the possibility of
the existence of a compensation temperature: a tempera-
ture below the critical point where the total magnetiza-
tion is zero [4]. This interesting behaviour has important
applications in the field of thermomagnetic recording [5,
6]. For this reason, in recent years, there have been many
theoretical studies on the magnetic properties of systems
formed by two sublattices with different spins and with
different crystal field interactions.
One of the earliest and simplest of these models to be
studied was the mixed-spin Ising system consisting of
spin-1/2 and spin-S (S > 1/2) in a uniaxial crystal field.
The model for different values of S (S > 1/2) has been
investigated by acting on honey-comb lattice [7-9], as
well as on Bethe lattice [10,11]), mean field approxima-
tion [12], effective field theory with correlations [13-17],
cluster variational theory [11], renormalization-group tech-
nique [18] and Monte-Carlo simulation [19-21].
It should be mentioned that the effects of different
sublattice crystal-field interactions on the magnetic prop-
erties of the mixed spin-1 and spin-3/2 Ising ferromag-
netic system with different single-ion anisotropies have
been investigated with the use of an effective field theory
[22,23], mean field theory [24], a cluster variational me-
thod [25] and Monte Carlo simulation [26]. Recently,
The attention was devoted to the high order mixed spin
ferrimagnetic systems (mixed spin-3/2 and spin-2 ferri-
magnetic system mixed spin-2 and spin-5/2 ferrimagnetic
system and mixed spin-3/2 and spin-5/2 system) in order
to construct their phase diagrams in the temperature-
anisotropy plane and to consider their magnetic proper-
ties. Bobak and Dely investigated the effect of single-ion
anisotropy on the phase diagram of the mixed spin-3/2
and spin-2 Ising system by the use of a mean-field theory
based on the Bogoliubov inequality for the free energy

F. ABUBRIG 271
[27]. Albayrak also studied the mixed spin-3/2 and spin-2
Ising system with two different crystal-field interactions
on Bethe lattice by using the exact recursion equations
[28]. Bayram Deviren et al. have used the effective field
theory to study the magnetic properties of the ferrimag-
netic mixed spin-3/2 and spin-2 Ising model with crystal
field in a longitudinal magnetic field on a honeycomb
and a square lattice [29]. We should mention that an
early attempt to study the mixed-spin-2 and spin-5/2 sys-
tem on a honeycomb lattice was made by Kaneyoshi and
co-workers [30] within the frame work of the EFT. Na-
kamura [31,32] applied Monte Carlo (MC) simulations to
study the magnetic properties of a mixed spin-2 and
spin-5/2 system on a honeycomb lattice. Li et al. [33, 34]
studied the magnetic properties of the mixed spin-2 and
spin-5/2 system on a layered honeycomb lattice by a
multisublattice green-function technique to investigate
the magnetic properties of a mixed
() ()
24 21
AFeFeCOAN-CH,3, 5
nn
nn
ΙΙ ΙΙΙ
+

==
 3 and to
consider the compensation behaviour of the system. Wei
and co-worker [35] examined the internal energy, spe-
cific heat and initial susceptibility of the mixed spin-2
and spin-5/2 ferrimagnetic system with an interlayer
coupling by the use of the EFT with correlations. Albay-
rak [36] studied the critical behaviour of the mixed spin-
2 and spin-5/2 Ising ferrimagnetic system on Bethe lat-
tice. And he also examined the critical and the compen-
sation temperatures of the mixed spin-2 and spin-5/2
Ising ferrimagnetic system on Bethe lattice by using the
exact recursion equations. Keskin and Ertas [37] investi-
gated the Existence of a dynamic compensation tem-
perature of a mixed spin-2 and spin-5/2 Ising ferrimag-
netic system in an oscillating field.
In this paper, we studied the effects of two different
single-ion anisotropies in the phase diagram and in the
compensation temperature of the mixed spin-2 and spin-
5/2 Ising ferrimagnetic system within the theoretical frame-
work of the mean-field theory and we found some out-
standing features in the temperature dependences of total
and sublattice magnetizations.
The outline of this work is as follows. In Section 2, we
define the model and present the mean-field theory based
on the Bogoliubov inequality for the Gibbs free energy
and then, we describe a Landau expansion of the free
energy in the order parameter. In Section 3, we present
the results and the discussion about the phase diagrams
and compensation temperature for various values of the
single-ion anisotropies, as well as the temperature de-
pendences of the magnetizations in some particular cases.
Finally, in Section 4, we present our conclusions.
2. The Model and Calculation
We consider a mixed Ising spin-2 and spin-5/2 system
consisting of two sublattices A and B, which are arranged
alternately. The sublattice A are occupied by spins i,
which take the spin values of , while the sublat-
tice B are occupied by spins
S
2,1, 0±±
j
S, which take the spin
values of 52, 32,12.±± In each site of the lattice,
there is a single-ion anisotropy (A in the sublattices A
and
D
B
D in the sublattice B) acting in the spin-2 and
spin-5/2. The Hamiltunian of the system according to the
mean-field theory is given by
()
() ()
22
,
AB AB
ij AiBj
ij
HJSSDS DS=− −−

, (1)
where the first summation is carried out only over near-
est-neighbor pairs of spins on different sublattices and J
is the nearest-neighbour exchange interaction.
The most direct way of deriving the mean-field theory
is to use the variation principle for the Gibbs free energy,
() ()
00 0
0
GHG HHH≤Φ≡+ −, (2)
where is the true free energy described by Ham-
iltonian given in the relation (1), is the free
energy described by the trial Hamiltonian 0
()
GH
()
0
GH
H
which
depends on variational parameters and 0 denotes a
thermal average over the ensemble defined by

0
H
.
Depending on the choice of the trial Hamiltonian, one
can construct approximate methods of different accuracy.
However, owing to the complexity of the problem, we
consider in this work the simple choice of 0
H
, namely:
()
()
2
0
2,
AA
AiA i
iA
BB
BjBj
jB
HSDS
SDS
γ
γ
∈
∈


=− +






−+





 (3)
where A
γ
and
B
γ
are the two variational parameters
related to the molecular fields acting on the two different
sublattices, respectively. Through this approach, we found
the free energy and the equations of state (sublattice
magnetization per site
A
m
()() ()()
1ln12exp4cosh2 2exp cosh
2
1255 93 11
ln2expcosh 2expcosh 2expcosh
24 24242
111
,
222
AA AA
BB BB B
ABAA BB
gDD
N
DDD
zJmmmm
ββγββγ
β
ββγ ββγ ββ
β
γγ
Φ−
== ++ 

 
  
−++
    
  
 
−++
B
γ


(4)

F. ABUBRIG 272
where 1 ,
B
,
g
N
NkT
β
Φ
== is the total number of sites of the lattice and z is the coordination number.
The sublattice magnetization per site and
A
m
B
m are defined by 0
A
Ai
mS= and 0
B
Bj
mS=, thus
()()()
() ()()()
2sinh 2xp3sinh
cosh 2exp3cosh0.5exp4
AAA
AAAA A
D
mDD
βγβ βγ
βγβ βγβ
+−
=+−+ −
e (5)
and
() ()
() ()
53
5sinh3exp 4sinhexp 6sinh
122
53
2coshexp 4coshexp 6cosh
222
BBBB
B
BBBB
D
m
DD
βγββγβγ βγ
βγ ββγ ββγ

 
+− +−
 

 
 =  

+− +−
  

  

1
2
1
B
B

. (6)
Now, by minimizing the free energy (4) with respect
to A
γ
and
B
γ
, we obtain
,
ABB
zJm zJmA
γγ
==. (7)
The mean-field properties of the present model are
then given by Equations (4)-(7). Since the Equations (5)-
(7) have in general several solutions for the pair ,
the stable phase will be the one which minimizes the free
energy. When the system undergoes the second-order
transition from an ordered state , to the
paramagnetic state AB
, this part of the
phase diagram can be determined analytically.
()
,
AB
mm
()
0≠0,
AB
mm≠
)
0=
(
0,mm=
Because the magnetizations A and m
B
m are very
small in the neighborhood of second-order transition
point, we can expand Equations (4)-(6) to obtain a Lan-
dau-like expansion.
(
2468
0AAA A
)
g
gambmcmOm=++ + +, (8)
where the expansion coefficients are given by
()(
0
1ln 1
2AABB B
gXYXY
β
=−+++ +
)
Z



, (9)
22 4
2
12 1
1
24 8 32
tt t
aaaa
β
1
b


=−−



, (10)
43 2
2
11212 3
1
2768 19296
tt t
baccaa
β
c


=++



, (11)
() ()
74 8
52 32
5 22
45213214126
216 33
21152018423 768018432 245760
c atctt
ccctcaaaaaaa
t
β
 
 
=++ −−+−−
   
 
 
c (12)
with
12
1
21
925
,
1
RR
aRR
++
=++ 2
4,
1
AA
AA
X
Y
aXY
+
=++
12
3
12
81625 ,
1
RR
aRR
++
=++ 4
16 ,
1
AA
AA
X
Y
aXY
+
=++
12
5
12
72915625 ,
1
RR
aRR
++
=++ 6
64 ,
1
AA
AA
X
Y
aXY
+
=++
1
25 9,
B
BB
BB B
X
YZ
bXYZ
++
=++ 2
625 81,
B
BB
BB B
X
YZ
bXYZ
++
=++
3
15625 729,
B
BB
BB B
X
YZ
bXYZ
++
=++
()
3
2
213
3,
2
t
caa=−
(
2
22
3131
3412
4
t
cbaab=+−−
)
2
,
()
2
41212
1530 ,
4
t
cbbbb=−−−
()
3
3
5513
30 15,
4
t
caaaa=+−
()
()
43
66 2
61241612
1530 ,
12
t
caaaaaaa=−−
where
()
2exp 4,
AA
XD β =
()
2 exp254,
BB
XD β =
()
2exp ,
AA
YD β =
()
2exp 94 ,
BB
YD β =
()
2exp4,
BB
ZD β = ,
()
12exp 4A
RD β =−
()
22exp 6A
RD β =− .
In this way, critical and tricritical points are deter-
mined according to the following routine;
1) Second-order transition lines when a = 0 and b > 0;
2) Tricritical points when a = b = 0, and c > 0;
3) The first-order transition lines are determined by
comparing the corresponding Gibbs free energies of the
various solutions of Equations (5) and (6) for the pair
Even so, we have also checked that c > 0 in
all T, DA, DB space. The critical behaviour is the same for
both ferromagnetic (J > 0) and ferrimagnetic (J < 0)
systems, because the coefficients a, b and c are even
(
,
AB
mm
)
.
1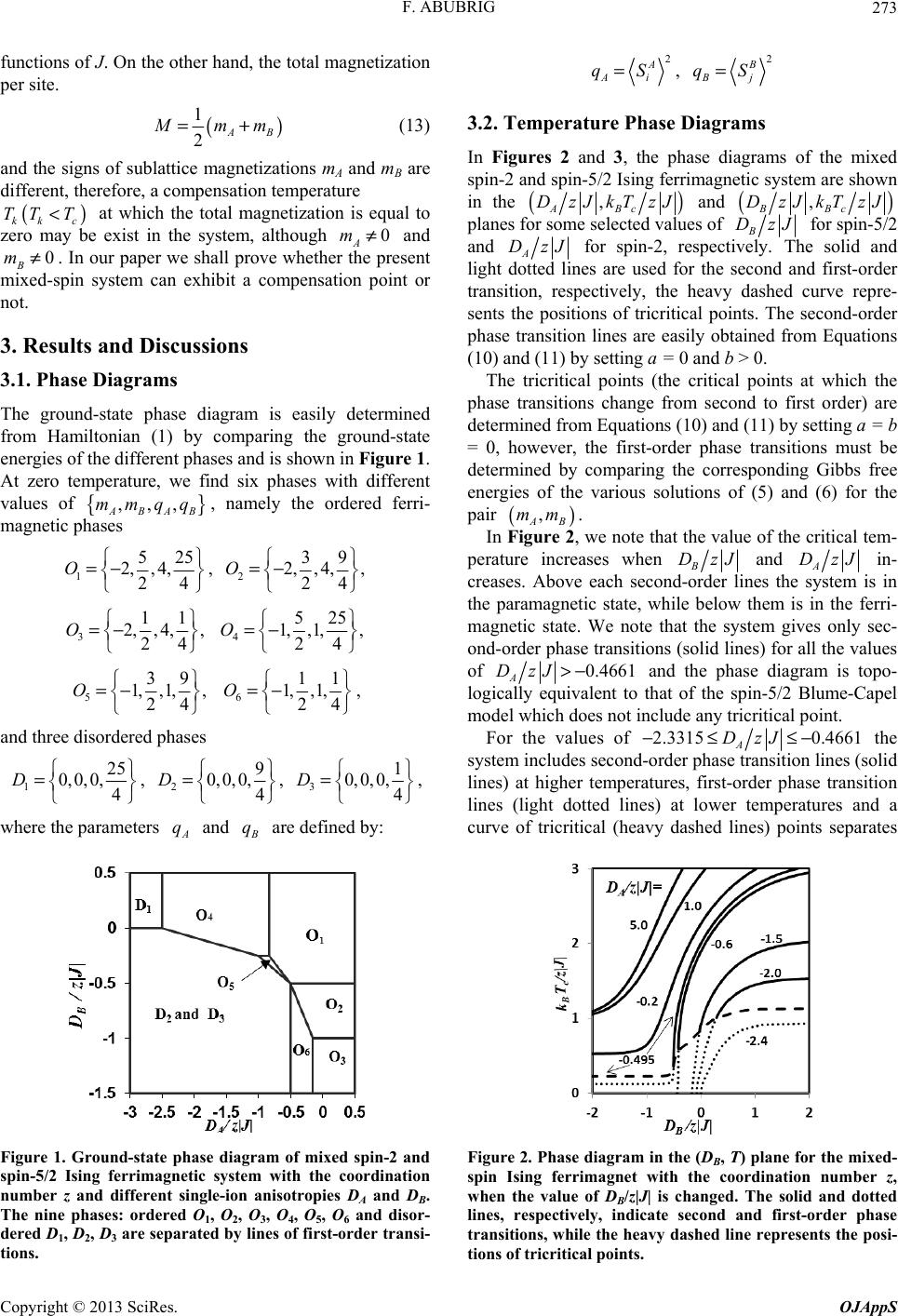

F. ABUBRIG 273
functions of J. On the other hand, the total magnetization
per site.
(
1
2AB
)
M
mm=+
(13)
and the signs of sublattice magnetizations mA and mB are
different, therefore, a compensation temperature
at which the total magnetization is equal to
zero may be exist in the system, although and
. In our paper we shall prove whether the present
mixed-spin system can exhibit a compensation point or
not.
(
kk c
TT T<
0
B
m≠
)
0
A
m≠
3. Results and Discussions
3.1. Phase Diagrams
The ground-state phase diagram is easily determined
from Hamiltonian (1) by comparing the ground-state
energies of the different phases and is shown in Figure 1.
At zero temperature, we find six phases with different
values of
{
}
,,,
ABAB
mmqq , namely the ordered ferri-
magnetic phases
1
525
2,,4,
24
O =−


, 2
39
2,,4,,
24
O =−


3
11
2,,4,,
24
O
=−


4
525
1, ,1,,
24
O
=−


5
39
1, ,1,,
24
O
=−


6
11
1, ,1,
24
O
=−


,
and three disordered phases
1
25
0, 0,0,4 D
=

, 2
9
0, 0,0,4 D
=

, 3
1
0, 0,0,4 D
=




,
where the parameters and
A
q
B
q are defined by:
Figure 1. Ground-state phase diagram of mixed spin-2 and
spin-5/2 Ising ferrimagnetic system with the coordination
number z and different single-ion anisotropies DA and DB.
The nine phases: ordered O1, O2, O3, O4, O5, O6 and disor-
dered D1, D2, D3 are separated by lines of first-order transi-
tions.
2
A
Ai
qS=, 2
B
Bj
qS=
3.2. Temperature Phase Diagrams
In Figures 2 and 3, the phase diagrams of the mixed
spin-2 and spin-5/2 Ising ferrimagnetic system are shown
in the
()
,
ABc
DzJkTzJ and
()
,
BBc
DzJkTzJ
planes for some selected values of B DzJ for spin-5/2
and A DzJ for spin-2, respectively. The solid and
light dotted lines are used for the second and first-order
transition, respectively, the heavy dashed curve repre-
sents the positions of tricritical points. The second-order
phase transition lines are easily obtained from Equations
(10) and (11) by setting a = 0 and b > 0.
The tricritical points (the critical points at which the
phase transitions change from second to first order) are
determined from Equations (10) and (11) by setting a = b
= 0, however, the first-order phase transitions must be
determined by comparing the corresponding Gibbs free
energies of the various solutions of (5) and (6) for the
pair .
()
,
AB
mm
In Figure 2, we note that the value of the critical tem-
perature increases when B DzJ and A DzJ in-
creases. Above each second-order lines the system is in
the paramagnetic state, while below them is in the ferri-
magnetic state. We note that the system gives only sec-
ond-order phase transitions (solid lines) for all the values
of 0.4661
A
DzJ>− and the phase diagram is topo-
logically equivalent to that of the spin-5/2 Blume-Capel
model which does not include any tricritical point.
For the values of 2.3315 0.4661
A
DzJ−≤ ≤− the
system includes second-order phase transition lines (solid
lines) at higher temperatures, first-order phase transition
lines (light dotted lines) at lower temperatures and a
curve of tricritical (heavy dashed lines) points separates
Figure 2. Phase diagram in the (DB, T) plane for the mixed-
spin Ising ferrimagnet with the coordination number z,
when the value of DB/z|J| is changed. The solid and dotted
lines, respectively, indicate second and first-order phase
transitions, while the heavy dashed line represents the posi-
tions of tricritical points.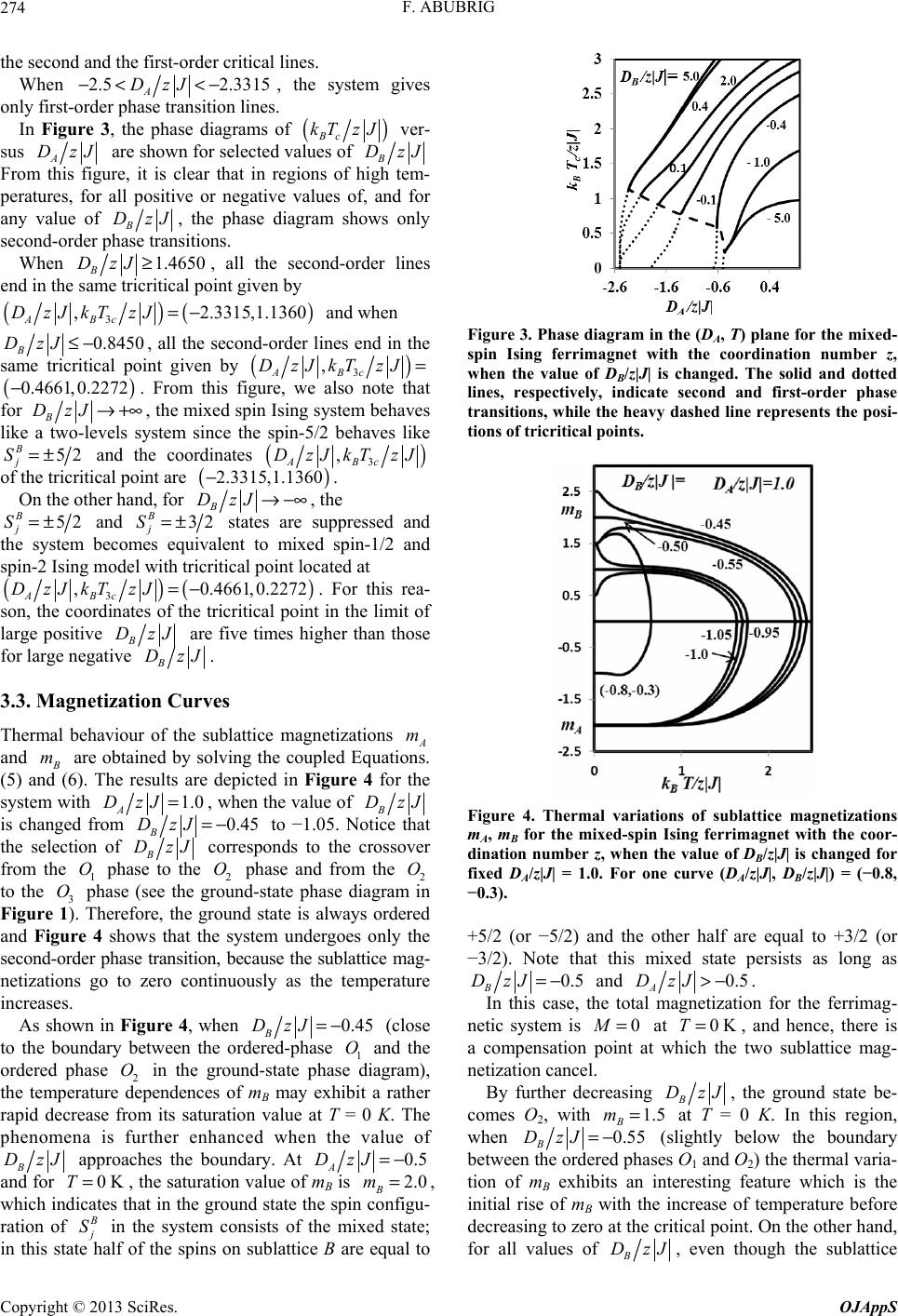

F. ABUBRIG 274
the second and the first-order critical lines.
When 2.5 2.3315
A
DzJ−<<−, the system gives
only first-order phase transition lines.
In Figure 3, the phase diagrams of
()
Bc
kTzJ ver-
sus A
DzJ are shown for selected values of B DzJ
From this figure, it is clear that in regions of high tem-
peratures, for all positive or negative values of, and for
any value of B
DzJ, the phase diagram shows only
second-order phase transitions.
When 1.4650
B
DzJ≥, all the second-order lines
end in the same tricritical point given by
() ()
3
, 2.3315,1.1360
ABc
DzJkTzJ=− and when
0.8450
B
DzJ≤− , all the second-order lines end in the
same tricritical point given by
(
3
,
ABc
DzJkTzJ=
)
)
. From this figure, we also note that
for
(
0.4661,0.2272−
B
DzJ→+∞, the mixed spin Ising system behaves
like a two-levels system since the spin-5/2 behaves like
52
B
j
S=± and the coordinates
()
3
,
ABc
DzJkTzJ
of the tricritical point are .
()
2.3315,1.1 360−
On the other hand, for B DzJ→−∞, the
52
B
j
S=± and 32
B
j
S=± states are suppressed and
the system becomes equivalent to mixed spin-1/2 and
spin-2 Ising model with tricritical point located at
() (
3
, 0.4661,0.2272
ABc
DzJkTzJ=−
)
. For this rea-
son, the coordinates of the tricritical point in the limit of
large positive B DzJ are five times higher than those
for large negative B DzJ.
3.3. Magnetization Curves
Thermal behaviour of the sublattice magnetizations A
and
m
B
m are obtained by solving the coupled Equations.
(5) and (6). The results are depicted in Figure 4 for the
system with 1.0
A
DzJ=, when the value of B DzJ
is changed from 0.45
B
DzJ=− to −1.05. Notice that
the selection of B
DzJ corresponds to the crossover
from the 1 phase to the 2 phase and from the 2
to the 3 phase (see the ground-state phase diagram in
Figure 1). Therefore, the ground state is always ordered
and Figure 4 shows that the system undergoes only the
second-order phase transition, because the sublattice mag-
netizations go to zero continuously as the temperature
increases.
O OO
O
As shown in Figure 4, when 0.45
B
DzJ=− (close
to the boundary between the ordered-phase 1 and the
ordered phase 2 in the ground-state phase diagram),
the temperature dependences of mB may exhibit a rather
rapid decrease from its saturation value at T = 0 K. The
phenomena is further enhanced when the value of
O
O
B
DzJ approaches the boundary. At 0.5
A
DzJ=−
and for , the saturation value of mB is ,
which indicates that in the ground state the spin configu-
ration of
0KT=2.0
B
m=
B
j
S in the system consists of the mixed state;
in this state half of the spins on sublattice B are equal to
Figure 3. Phase diagram in the (DA, T) plane for the mixed-
spin Ising ferrimagnet with the coordination number z,
when the value of DB/z|J| is changed. The solid and dotted
lines, respectively, indicate second and first-order phase
transitions, while the heavy dashed line represents the posi-
tions of tricritical points.
Figure 4. Thermal variations of sublattice magnetizations
mA, mB for the mixed-spin Ising ferrimagnet with the coor-
dination number z, when the value of DB/z|J| is changed for
fixed DA/z|J| = 1.0. For one curve (DA/z|J|, DB/z|J|) = (−0.8,
−0.3).
+5/2 (or −5/2) and the other half are equal to +3/2 (or
−3/2). Note that this mixed state persists as long as
0.5
B
DzJ=− and 0.5
A
DzJ>− .
In this case, the total magnetization for the ferrimag-
netic system is at , and hence, there is
a compensation point at which the two sublattice mag-
netization cancel.
0M=0KT=
By further decreasing B
DzJ, the ground state be-
comes O2, with at T = 0 K. In this region,
when
1.5
B
m=
0.55=−
B (slightly below the boundary
between the ordered phases O1 and O2) the thermal varia-
tion of mB exhibits an interesting feature which is the
initial rise of mB with the increase of temperature before
decreasing to zero at the critical point. On the other hand,
for all values of
DzJ
B
DzJ, even though the sublattice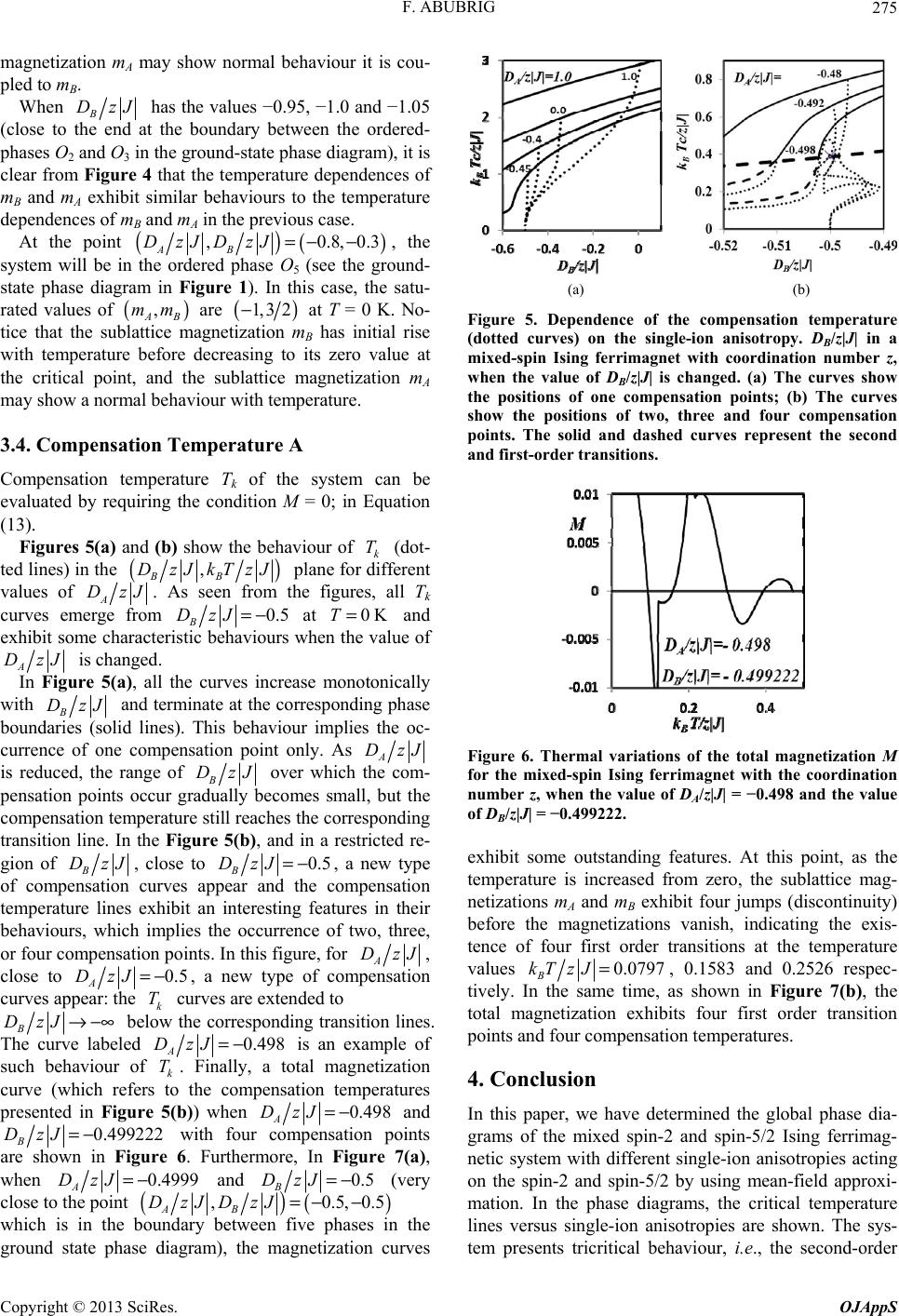

F. ABUBRIG 275
magnetization mA may show normal behaviour it is cou-
pled to mB.
When B DzJ has the values −0.95, −1.0 and −1.05
(close to the end at the boundary between the ordered-
phases O2 and O3 in the ground-state phase diagram), it is
clear from Figure 4 that the temperature dependences of
mB and mA exhibit similar behaviours to the temperature
dependences of mB and mA in the previous case.
At the point
()
()
,0.8,
AB
DzJDzJ=− −0.3, the
system will be in the ordered phase O5 (see the ground-
state phase diagram in Figure 1). In this case, the satu-
rated values of are
()
,
AB
mm
(
1, 32−
)
at T = 0 K. No-
tice that the sublattice magnetization mB has initial rise
with temperature before decreasing to its zero value at
the critical point, and the sublattice magnetization mA
may show a normal behaviour with temperature.
3.4. Compensation Temperature A
Compensation temperature Tk of the system can be
evaluated by requiring the condition M = 0; in Equation
(13).
Figures 5(a) and (b) show the behaviour of k (dot-
ted lines) in the
T
(
,
BB
DzJkTzJ
)
plane for different
values of A DzJ
. As seen from the figures, all Tk
curves emerge from 0.5
B
DzJ=− at and
exhibit some characteristic behaviours when the value of
0KT=
A
DzJ
is changed.
In Figure 5(a), all the curves increase monotonically
with B DzJ and terminate at the corresponding phase
boundaries (solid lines). This behaviour implies the oc-
currence of one compensation point only. As A DzJ
is reduced, the range of B
DzJ over which the com-
pensation points occur gradually becomes small, but the
compensation temperature still reaches the corresponding
transition line. In the Figure 5(b), and in a restricted re-
gion of B DzJ, close to 0.5
B
DzJ=− , a new type
of compensation curves appear and the compensation
temperature lines exhibit an interesting features in their
behaviours, which implies the occurrence of two, three,
or four compensation points. In this figure, for A DzJ,
close to 0.5
A
DzJ=− , a new type of compensation
curves appear: the curves are extended to
k
T
B
DzJ→−∞ below the corresponding transition lines.
The curve labeled 0.498
A
DzJ=− is an example of
such behaviour of k
T. Finally, a total magnetization
curve (which refers to the compensation temperatures
presented in Figure 5(b)) when 0.498
A
DzJ=− and
0.499222
B with four compensation points
are shown in Figure 6. Furthermore, In Figure 7(a),
when
DzJ=−
0.4999DzJ=−
A and 0.5 B
DzJ=− (very
close to the point
()
()
,0.5,0.5DzJDzJ=− −
AB
which is in the boundary between five phases in the
ground state phase diagram), the magnetization curves
(a) (b)
Figure 5. Dependence of the compensation temperature
(dotted curves) on the single-ion anisotropy. D
B/z|J| in a
mixed-spin Ising ferrimagnet with coordination number z,
when the value of DB/z|J| is changed. (a) The curves show
the positions of one compensation points; (b) The curves
show the positions of two, three and four compensation
points. The solid and dashed curves represent the second
and first-order transitions.
Figure 6. Thermal variations of the total magnetization M
for the mixed-spin Ising ferrimagnet with the coordination
number z, when the value of DA/z|J| = −0.498 and the value
of DB/z|J| = −0.499222.
exhibit some outstanding features. At this point, as the
temperature is increased from zero, the sublattice mag-
netizations mA and mB exhibit four jumps (discontinuity)
before the magnetizations vanish, indicating the exis-
tence of four first order transitions at the temperature
values 0.0797
B
kT zJ=, 0.1583 and 0.2526 respec-
tively. In the same time, as shown in Figure 7(b), the
total magnetization exhibits four first order transition
points and four compensation temperatures.
4. Conclusion
In this paper, we have determined the global phase dia-
grams of the mixed spin-2 and spin-5/2 Ising ferrimag-
netic system with different single-ion anisotropies acting
on the spin-2 and spin-5/2 by using mean-field approxi-
mation. In the phase diagrams, the critical temperature
lines versus single-ion anisotropies are shown. The sys-
tem presents tricritical behaviour, i.e., the second-order

F. ABUBRIG 276
(a)
(b)
Figure 7. Thermal variations of (a) The total magnetization
M; (b) The sublattice magnetizations mA, mB for the mixed-
spin Ising ferrimagnet with the coordination number z,
when the value of DA/z|J| = −0.4999 and the value of DB/z|J|
= −0.5.
phase transition line is separated from the first-order
transition line by a tricritical point. We also observed that
this mixed-spin ferrimagnetic system may exhibit one,
two, three or four compensation points. The theoretical
prediction of the possibility of compensation points and
the design and preparation of materials with such unusual
behaviour will certainly open a new area of research on
such materials.
REFERENCES
[1] O. Khan, “Molecular Magnetism,” VCH publishers, New
York, 1993.
[2] T. Kaneyoshi and Y. Nakamura, “A Theoretical Investi-
gation for Low-Dimensional Molecular-Based Magnetic
Materials,” Journal of Physics: Condensed Matter, Vol.
10, No. 13, 1998, p. 3003.
doi:10.1088/0953-8984/10/13/017
[3] T. Kaneyoshi, Y. Nakamura and S. Shin, “A Diluted
Mixed Spin-2 and Spin-5/2 Ferrimagnetic Ising System; a
Study of a Molecular-Based Magnet,” Journal of Physics:
Condensed Matter, Vol. 10, No. 31, 1998, p. 7025.
doi:10.1088/0953-8984/10/31/018
[4] L. Néel, “Propriétées Magnétiques des Ferrites; Férrimag-
nétisme et Antiferromagnétisme,” Annales de Physique
(Paris), Vol. 3, 1948, pp. 137-198.
[5] M. Mansuripur, “Magnetization Reversal, Coercivity, and
the Process of Thermomagnetic Recording in Thin Films
of Amorphous Rare Earth Transition Metal Alloys,” Jour-
nal of Applied Physics, Vol. 61, No. 4, 1987, pp. 1580-
1587. doi:10.1063/1.338094
[6] F. Tanaka, S. Tanaka and N. Imamura, “Magneto-Optical
Recording Characteristics of TbFeCo Media by Magnetic
Field Modulation Method,” Japan Journal of Applied
Physics, Vol. 26, 1987, pp. 231-235.
doi:10.1143/JJAP.26.231
[7] L. L. Goncaloves, “Uniaxial Anisotropy Effects in the Ising
Model: An Exactly Soluble Model,” Physica Scripta, Vol.
32, No. 3, 1985, p. 248. doi:10.1088/0031-8949/32/3/012
[8] L. L. Goncaloves, “Uniaxial Anisotropy Effects in the Ising
Model: An Exactly Soluble Model,” Physica Scripta, Vol.
33, No. 2, 1986, p. 192. doi:10.1088/0031-8949/33/2/018
[9] A. Dakhama and N. Benayad, “On the Existence of Com-
pensation Temperature in 2d Mixed-Spin Ising Ferri-
magnets: An Exactly Solvable Model,” Journal of Mag-
netism and Magnetic Materials, Vol. 213, No. 1-2, 2000,
pp. 117-125. doi:10.1016/S0304-8853(99)00606-X
[10] N. R. da Silva and S. R. Salinas, “Mixed-Spin Ising
Model on Beth Lattice,” Physical Review, Vol. 44, No. 2,
1991, pp. 852-855. doi:10.1103/PhysRevB.44.852
[11] J. W. Tucker, “The Ferrimagnetic Mixed Spin-1/2 and
Spin-1 Sing System,” Journal of Magnetism and Mag-
netic Materials, Vol. 195, No. 3, 1999, pp. 733-740.
doi:10.1016/S0304-8853(99)00302-9
[12] T. Kaneyoshi and J. C. Chen, “Mean-Field Analysis of a
Ferrimagnetic Mixed Spin System,” Journal of Magnet-
ism and Magnetic Materials, Vol. 98, No. 1-2, 1991, pp.
201-204. doi:10.1016/0304-8853(91)90444-F
[13] T. Kaneyoshi, “Curie Temperatures and Tricritical Points
in Mixed Ising Ferromagnetic Systems,” The Physical So-
ciety of Japan, Vol. 56, 1987, pp. 2675-2680.
doi:10.1143/JPSJ.56.2675
[14] T. Kaneyoshi, “Phase Transition of the Mixed Spin Sys-
tem with a Random Crystal Field,” Physica A, Vol. 153,
No. 3, 1988, pp. 556-566.
doi:10.1016/0378-4371(88)90240-3
[15] T. Kaneyoshi, M. Jascur and P. Tomczak, “The Ferri-
magnetic Mixed Spin-1/2 and Spin-3/2 Ising System,”
Journal of Physics: Condensed Matter, Vol. 4, No. 49,
1992, pp. L653-L658. doi:10.1088/0953-8984/4/49/002
[16] T. Kaneyoshi, “Tricritical Behavior of a Mixed Spin-1/2
and Spin-2 Ising System,” Physica A, Vol. 205, No. 4,
1994, pp. 677-686. doi:10.1016/0378-4371(94)90229-1
[17] A. Bobak and M. Jurcisin, “Discussion of Critical Behav-
iour in a Mixed-Spin Ising Model,” Physica A, Vol. 240,
No. 3-4, 1997, pp. 647-656.
doi:10.1016/S0378-4371(97)00044-7
[18] S. G. A. Quadros and S. R. Salinas, “Renormalization-
Group Calculations for a Mixed-Spin Ising Model,” Phy-
sica A: Statistical Mechanics and Its Applications, Vol.
206, No. 3-4, 1994, pp. 479-496.
[19] G.-M. Zhang and C.-Z. Yang, “Monte Carlo Study of the

F. ABUBRIG 277
Two-Dimensional Quadratic Ising Ferromagnet with Spins
S = 1/2 and S = 1 and with Crystal-Field Interactions,”
Physical Review B, Vol. 48, No. 13, 1993, pp. 9452-9455.
doi:10.1103/PhysRevB.48.9452
[20] G. M. Buendia and M. A. Novotny, “Numerical Study of
a Mixed Ising Ferrimagnetic System,” Journal of Physics:
Condensed Matter, Vol. 9, No. 27, 1997, pp. 5951-5964.
doi:10.1088/0953-8984/9/27/021
[21] G. M. Buendia and J. A. Liendo, “Monte Carlo Simula-
tion of a Mixed Spin-1/2 and Spin-3/2 Ising Ferrimag-
netic System,” Journal of Physic s: Condensed Matter, Vol.
9, No. 25, 1997, pp. 5439-5448.
doi:10.1088/0953-8984/9/25/011
[22] A. Bobak, “The Effect of Anisotropies on the Magnetic
Properties of a Mixed Spin-1 and Spin-3/2 Ising Ferri-
magnetic System,” Physica A, Vol. 258, No. 1-2, 1998,
pp. 140-156. doi:10.1016/S0378-4371(98)00233-7
[23] O. F. Bobak and D. H. Abubrig, “An Effective-Field
Study of the Mixed Spin-1 and Spin-3/2 Ising Ferrimag-
netic System,” Journal of Magnetism and Magnetic Ma-
terials, Vol. 246, No. 1-2, 2002, pp. 177-183.
doi:10.1016/S0304-8853(02)00048-3
[24] O. F. Abubrig, D. Horvath, A. Bobak and M. Jascur,
“Mean-Field Solution of the Mixed Spin-1 and Spin-3/2
Ising System with Different Single-Ion Anisotropies,” Phy-
sica A, Vol. 296, No. 3-4, 2001, pp. 437-450.
doi:10.1016/S0378-4371(01)00176-5
[25] J. W. Tucker, “Mixed Spin-1 and Spin-3/2 Blume-Capel
Ising Ferromagnet,” Journal of Magnetism and Mgnetic
Materials, Vol. 237, No. 2, 2001, pp. 215-224.
doi:10.1016/S0304-8853(01)00691-6
[26] Y. Nakamura and J. W. Tucker, “Monte Carlo Study of a
Mixed Spin-1 and Spin-3/2 Ising Ferromagnet,” IEEE
Transactions on Magnetics, Vol. 38, No. 5, 2002, pp.
2406-2408. doi:10.1109/TMAG.2002.803598
[27] A. Bobak and J. Dely, “Phase Transitions and Multicriti-
cal Points in the Mixed Spin-3/2 and Spin-2 Ising System
with a Single-Ion Anisotropy,” Journal of Magnetism and
Magnetic Materials, Vol. 310, No. 2, 2007, pp. 1419-
1421. doi:10.1016/j.jmmm.2006.10.427
[28] E. Albayrak, “The Critical and Compensation Tempera-
tures of the Mixed Spin-3/2 and Spin-2 Ising Model,”
Physica B: Condensed Matter, Vol. 391, No. 1, 2007, pp.
47-53. doi:10.1016/j.physb.2006.08.045
[29] B. Deviren, E. Kantar and M. Keskin, “Magnetic Proper-
ties of a Mixed Spin-3/2 and Spin-2 Ising Ferrimagnetic
System within the Effective-Field Theory,” Journal of the
Korean Physical Society, Vol. 56, No. 6, 2010, pp. 1738-
1747. doi:10.3938/jkps.56.1738
[30] Y. Nakamura, S. Shin and T. Kaneyoshi, “The Effects of
Transverse Field on the Magnetic Properties in a Diluted
Mixed Spin-2 and Spin-5/2 Ising System,” Physica B,
Vol. 284-288, 2000, pp. 1479-1480.
doi:10.1016/S0921-4526(99)02668-X
[31] Y. Nakamura, “Monte Carlo Study of a Mixed Spin-2 and
Spin-5/2 Ising System on a Honeycomb Lattice,” Journal
of Physics: Condensed Matter, Vol. 12, No. 17, 2000, pp.
4067-4074. doi:10.1088/0953-8984/12/17/312
[32] Y. Nakamura, “Existence of a Compensation Tempera-
ture of a Mixed Spin-2 and Spin-5/2 Ising Ferrimagnetic
System on a Layered Honeycomb Lattice,” Physical Re-
view B, Vol. 62, No. 17, 2000, pp. 11742-11746.
doi:10.1103/PhysRevB.62.11742
[33] J. Li, A. Du and G. Z. Wei, “Green Function Study of a
Mixed-Spin-2 and Spin-5/2 Heisenberg Ferrimagnetic Sys-
tem on a Honeycomb Lattice,” Physica Status Solidi (b),
Vol. 238, No. 1, 2003, pp. 191-197.
[34] J. Li, A. Du and G. Z. Wei, “The Compensation Behavior
of a Mixed-Spin-2 and Spin-5/2 Heisenberg Ferrimag-
netic System on a Honeycomb Lattice,” Physica B, Vol.
348, No. 1-4, 2004, pp. 79-88.
doi:10.1016/j.physb.2003.11.074
[35] G. Wei, Q. Zhang, Z. Xin and Y. Liang, “Internal Energy
and Initial Susceptibility of Mixed Spin-2 and Spin-5/2
Ferrimagnetic Ising System with Interlayer Coupling,” Jour-
nal of Magnetism and Magnetic Materials, Vol. 277, No
1-2, 2004, pp. 1-15. doi:10.1016/j.jmmm.2003.06.001
[36] E. Albayrak, “Mixed-Spin-2 and Spin-5/2 Blume-Emery-
Griffiths Model,” Physica A: Statistical Mechanics and
Its Applications, Vol. 375, No. 1, 2007, pp. 174-184.
[37] M. Keskin and M. Ertas, “Existence of a Dynamic Com-
pensation Temperature of a Mixed Spin-2 and Spin-5/2
Ising Ferrimagnetic System in an Oscillating Field,” Phy-
sical Review E, Vol. 80, No. 6, 2009, Article ID: 061140.
doi:10.1103/PhysRevE.80.061140